An Extended Kalman Filter-Based Attitude Tracking Algorithm for Star Sensors
Abstract
:1. Introduction
2. Algorithm Description
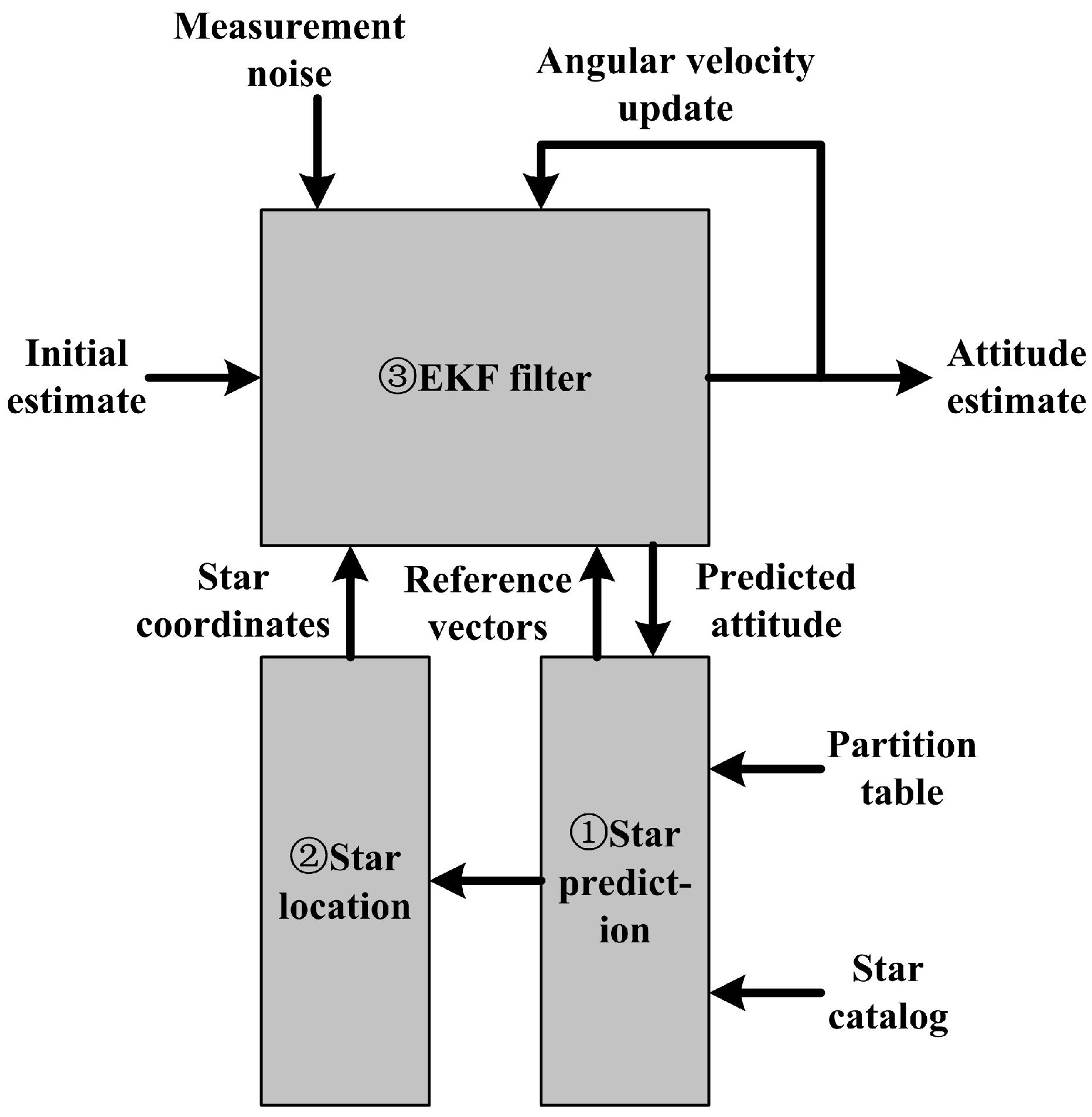
2.1. Tracking Models
- ①
- From EKF the attitude quaternion and its error covariance is extrapolated to the next frame in EKF. The expected attitude is used to access onboard partition table and star catalog by spherical polygon approach [1] to determine the centers of the star track windows. Meanwhile, the error covariance is used to determine the radius of the track windows.
- ②
- Get the stars to be measured [10] and evaluated in the track windows of star image. If there is only one star in a reference star’s neighborhood, the star in star image is matched with the star in reference star image. Further, the match can be checked by the inter-star angles between the reference stars and the observed stars.
- ③
- The coordinates of the matched stars in the observation star image are used as the measurements for EKF to estimate the optimal attitude quaternion of current frame and the angular velocity.
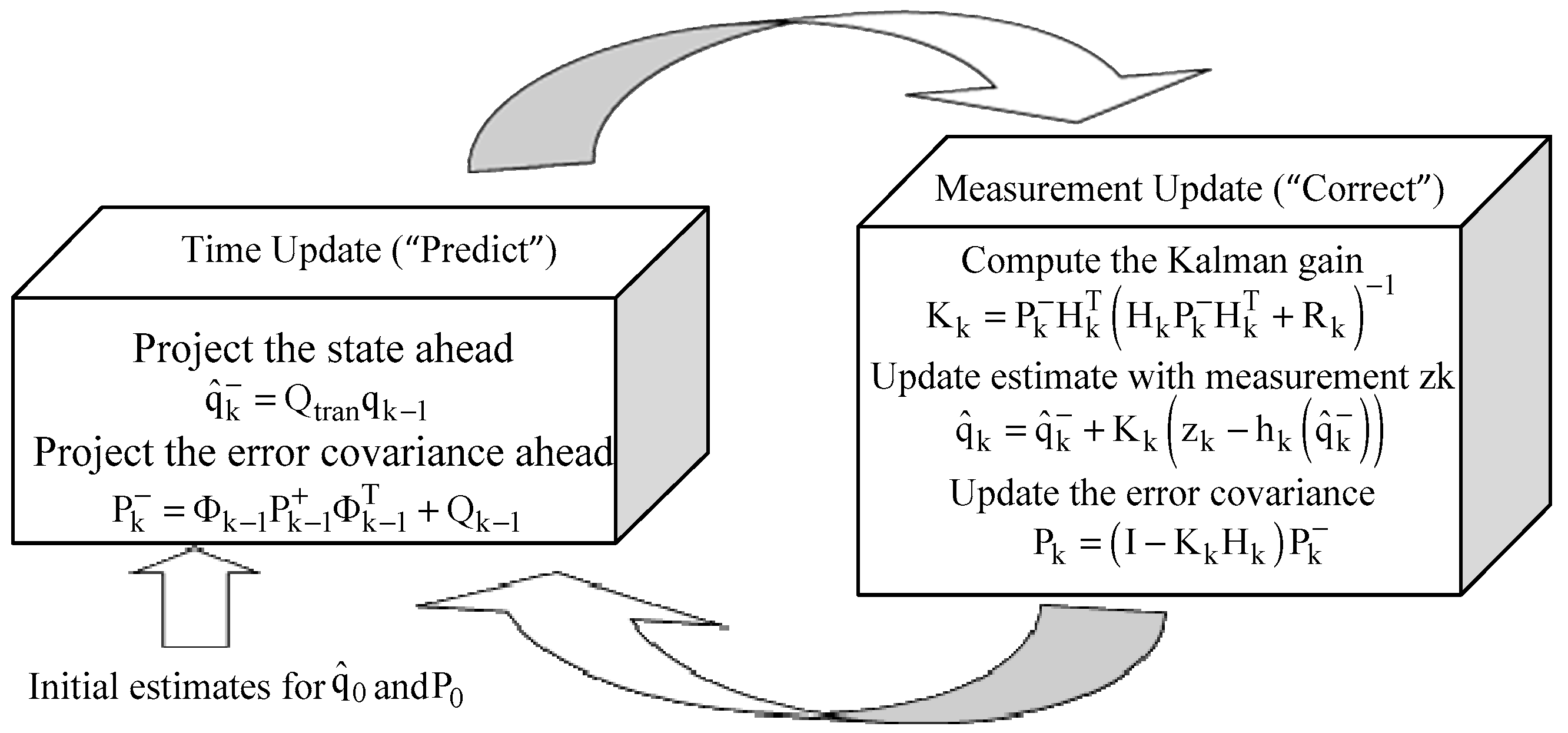
2.2. EKF Based Attitude Estimation
2.3. Star Catalog Partition
- ①
- The celestial sphere can be divided into twenty equivalent zones by an inscribed icosahedron which is shown in Figure 4a. A pyramid is formed by connecting the center of the celestial sphere with the three vertices on one face of the icosahedron. The pyramids divide the celestial sphere totally into twenty equivalent zones.
- ②
- Each of twenty regions is divided into several congruent equilateral triangles. As shown in the Figure 4b, each edge is divided into N + 1 segments, and each region is divided into triangles.
- ③
- When projected on the sphere, the vertices of these smaller triangles become the centers of sub-catalogs that completely cover the sphere, called sub-catalog centers. Each star in the catalog is then assigned to the sub-catalog of closest vertex. The sub-catalog centers number is computed as follows:
2.4. Initial Angular Velocity Estimation
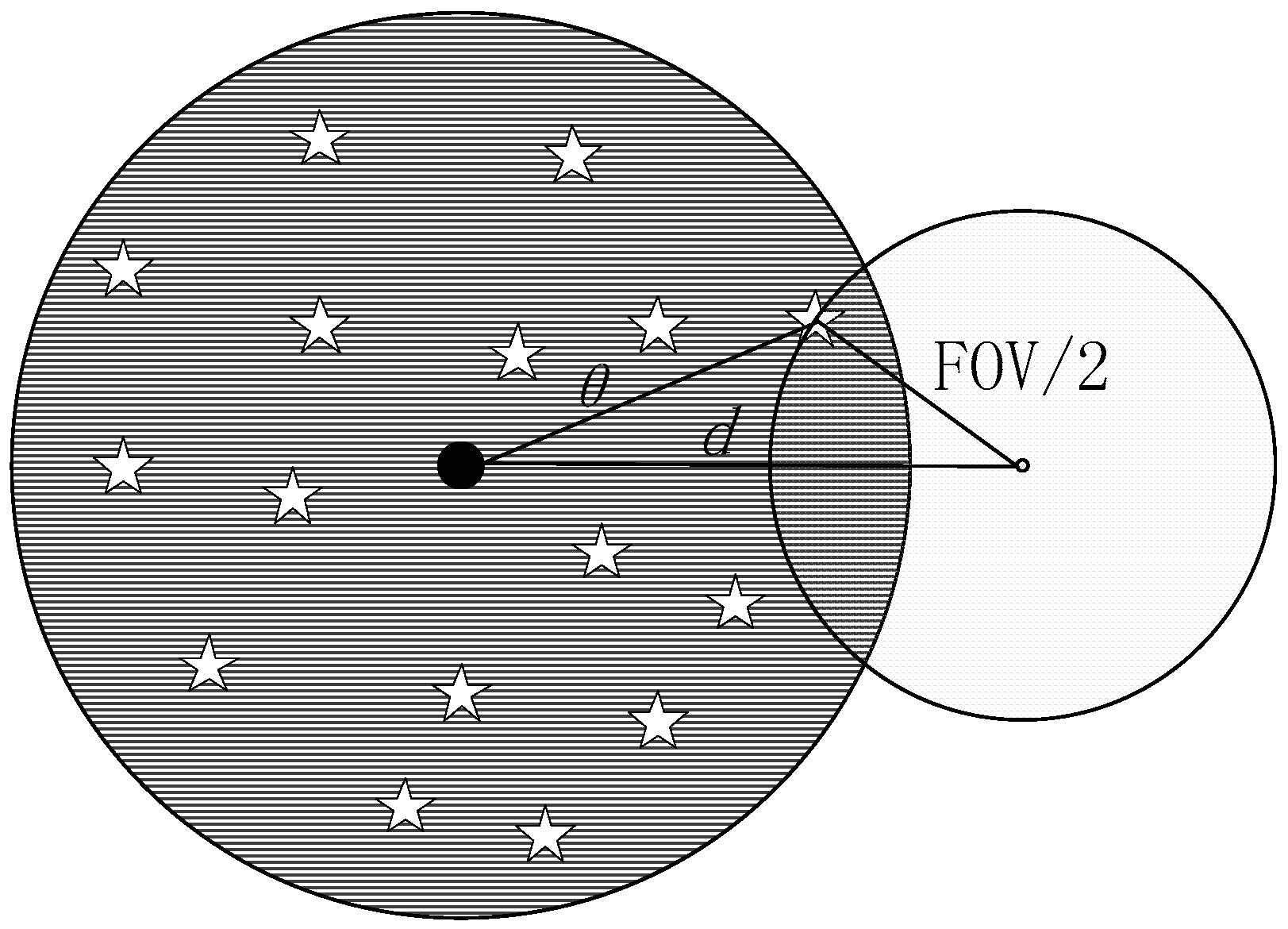
2.5. Track Window Radius Determination
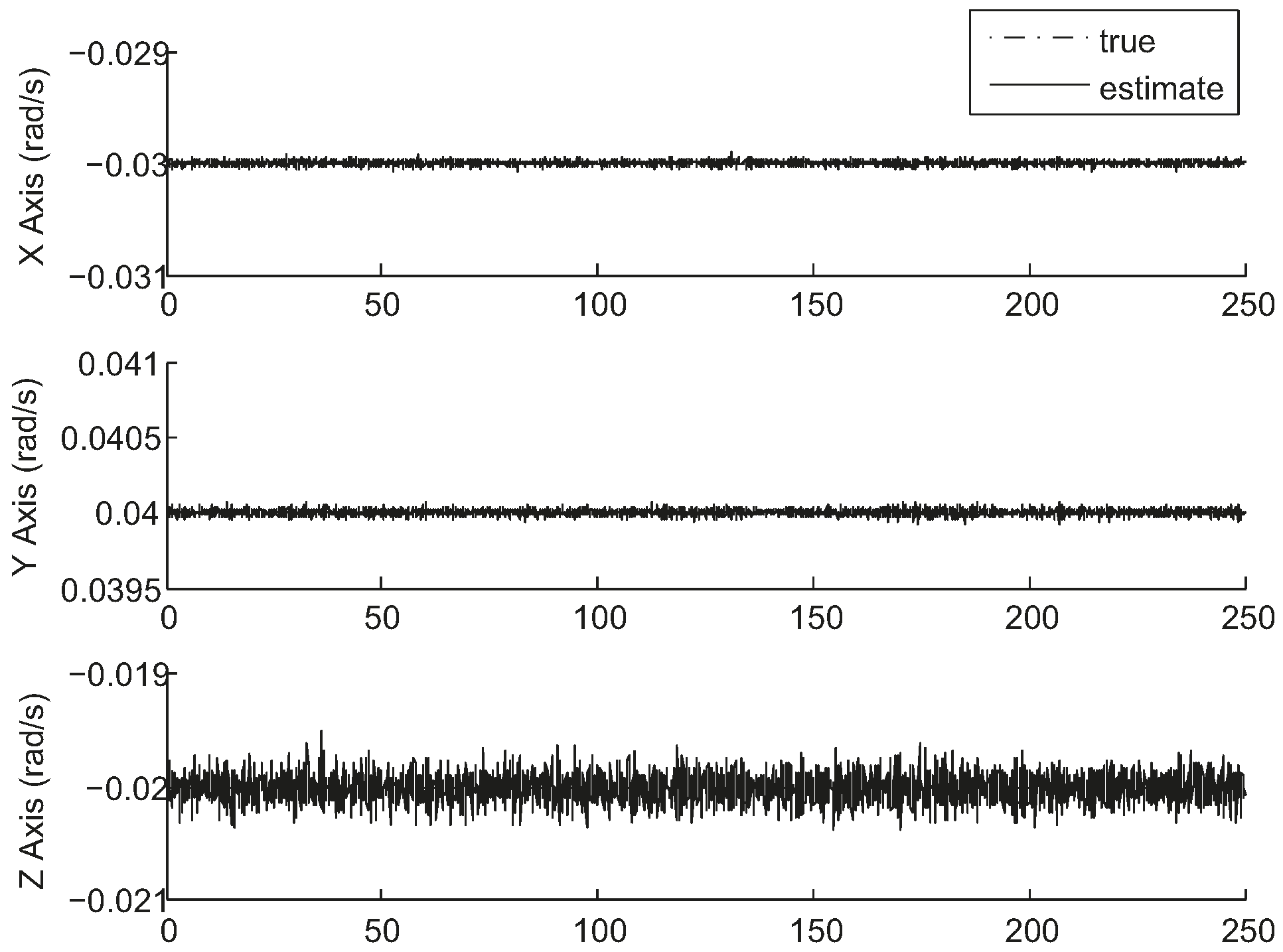
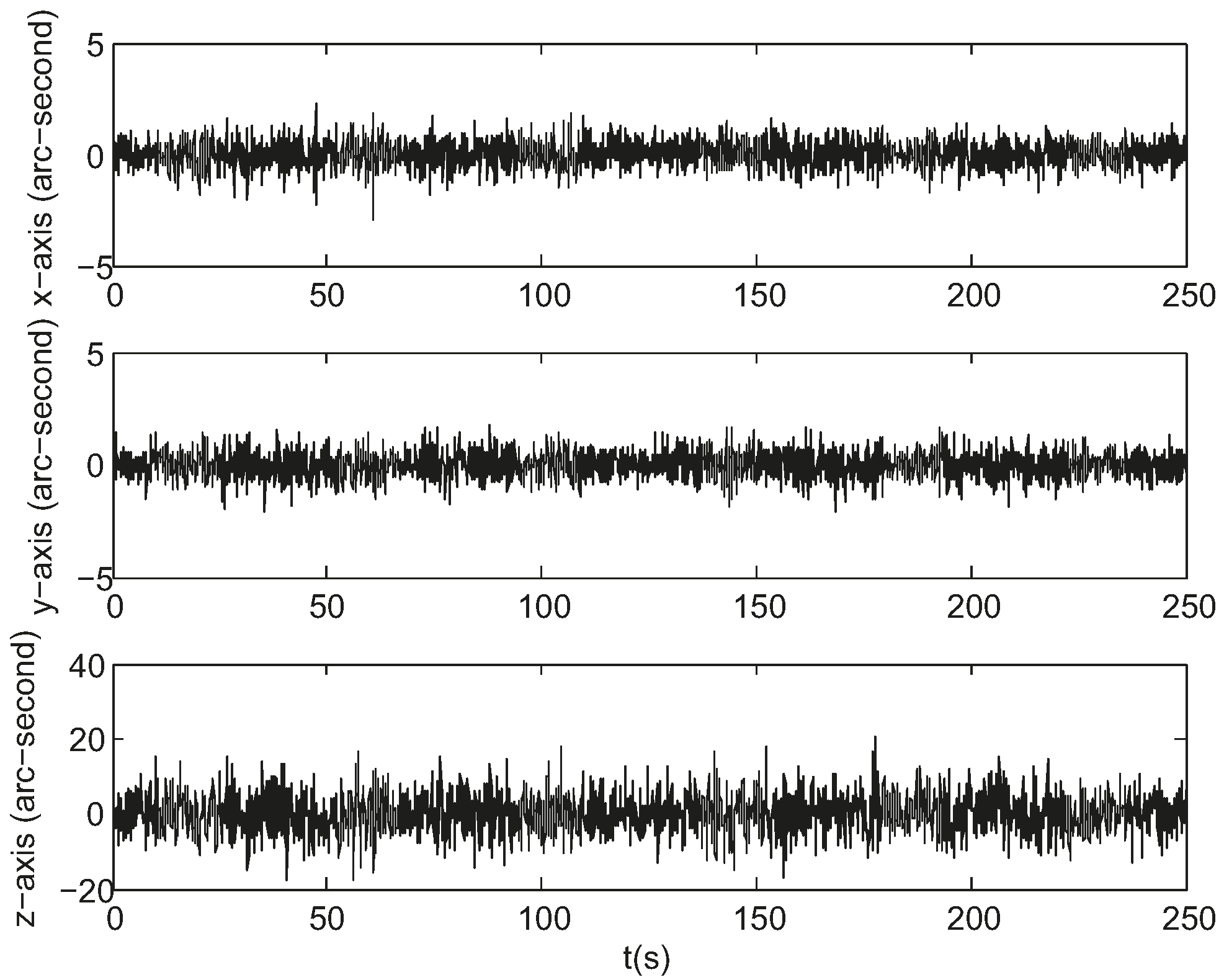
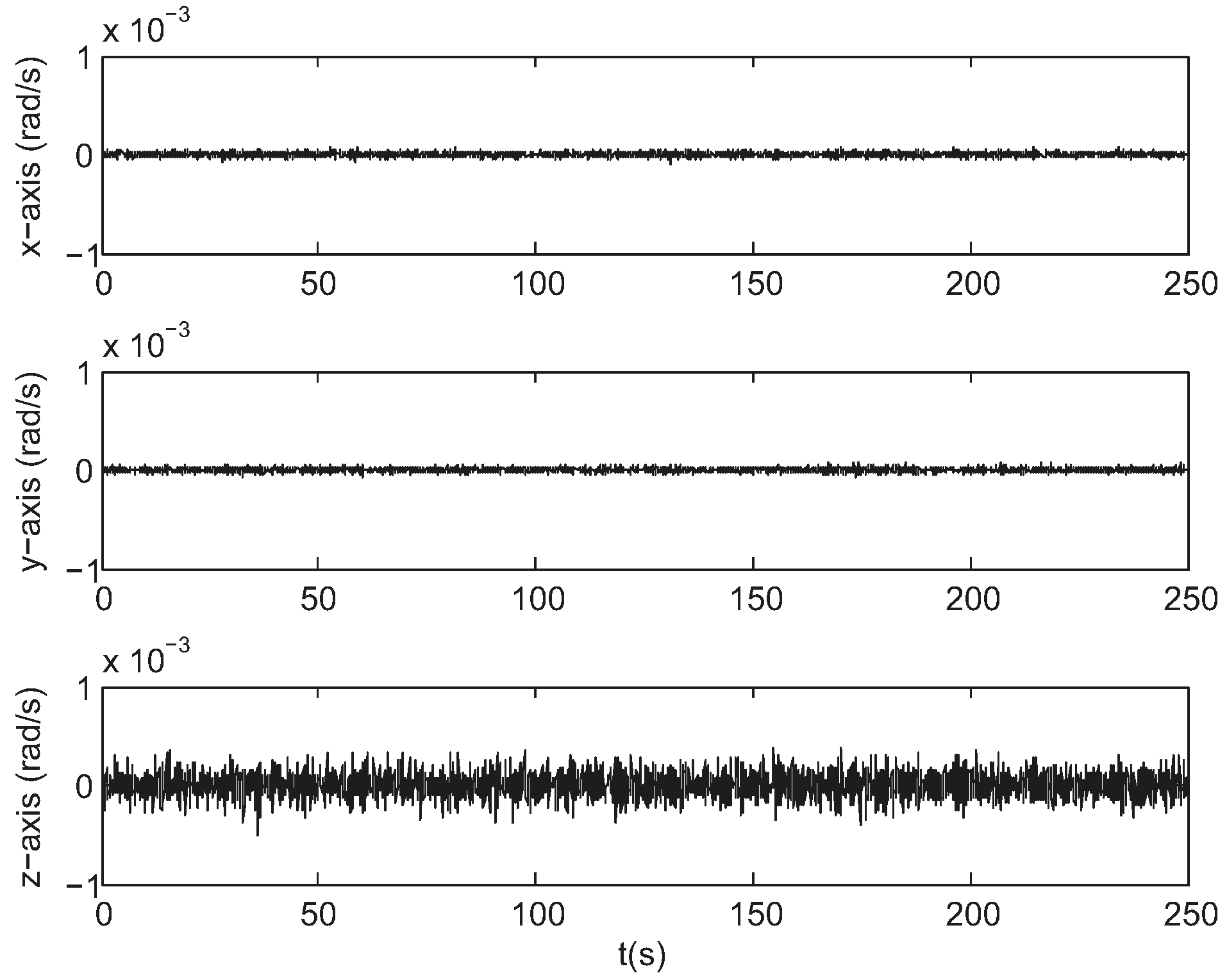
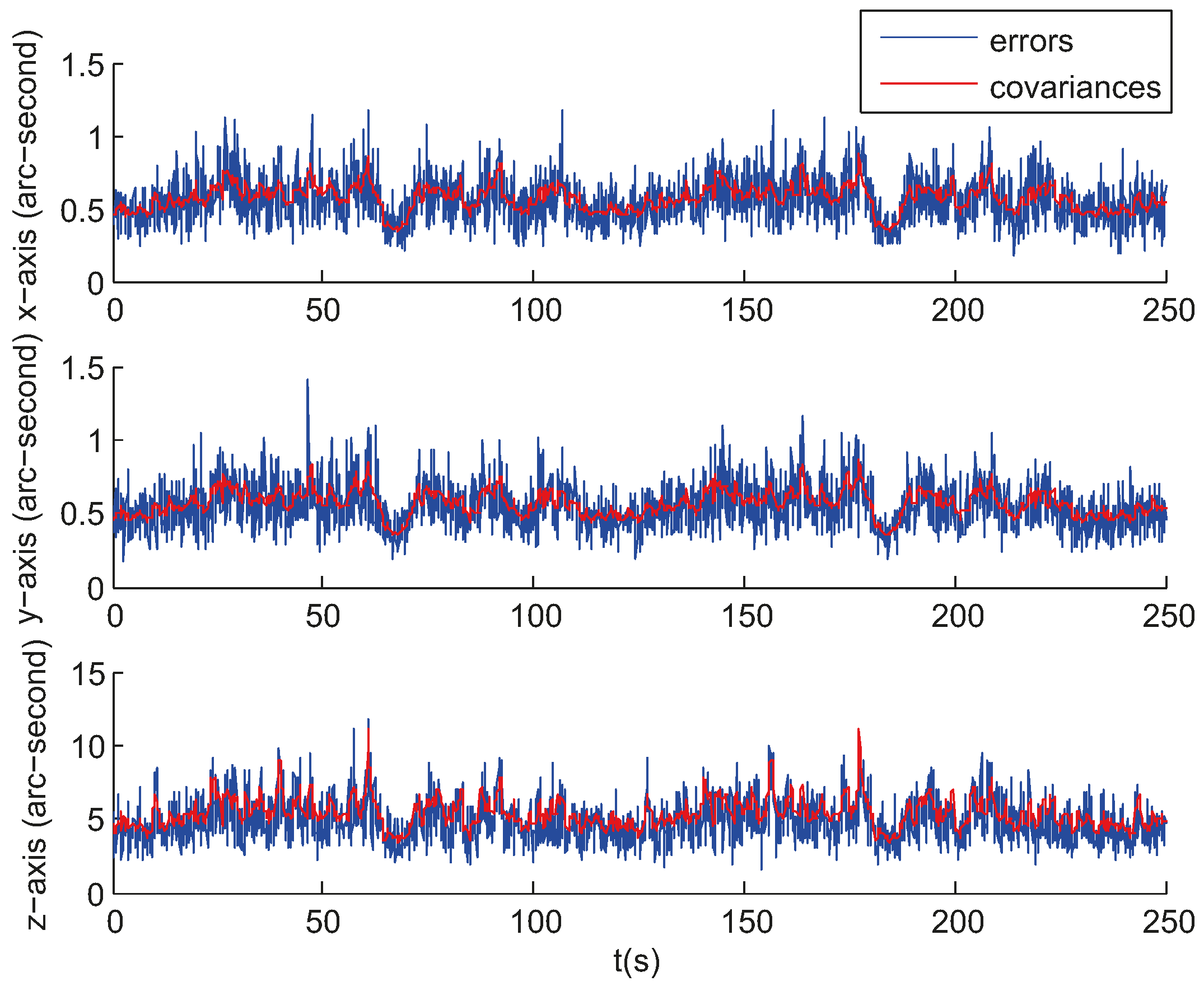
3. Simulation and Experiment
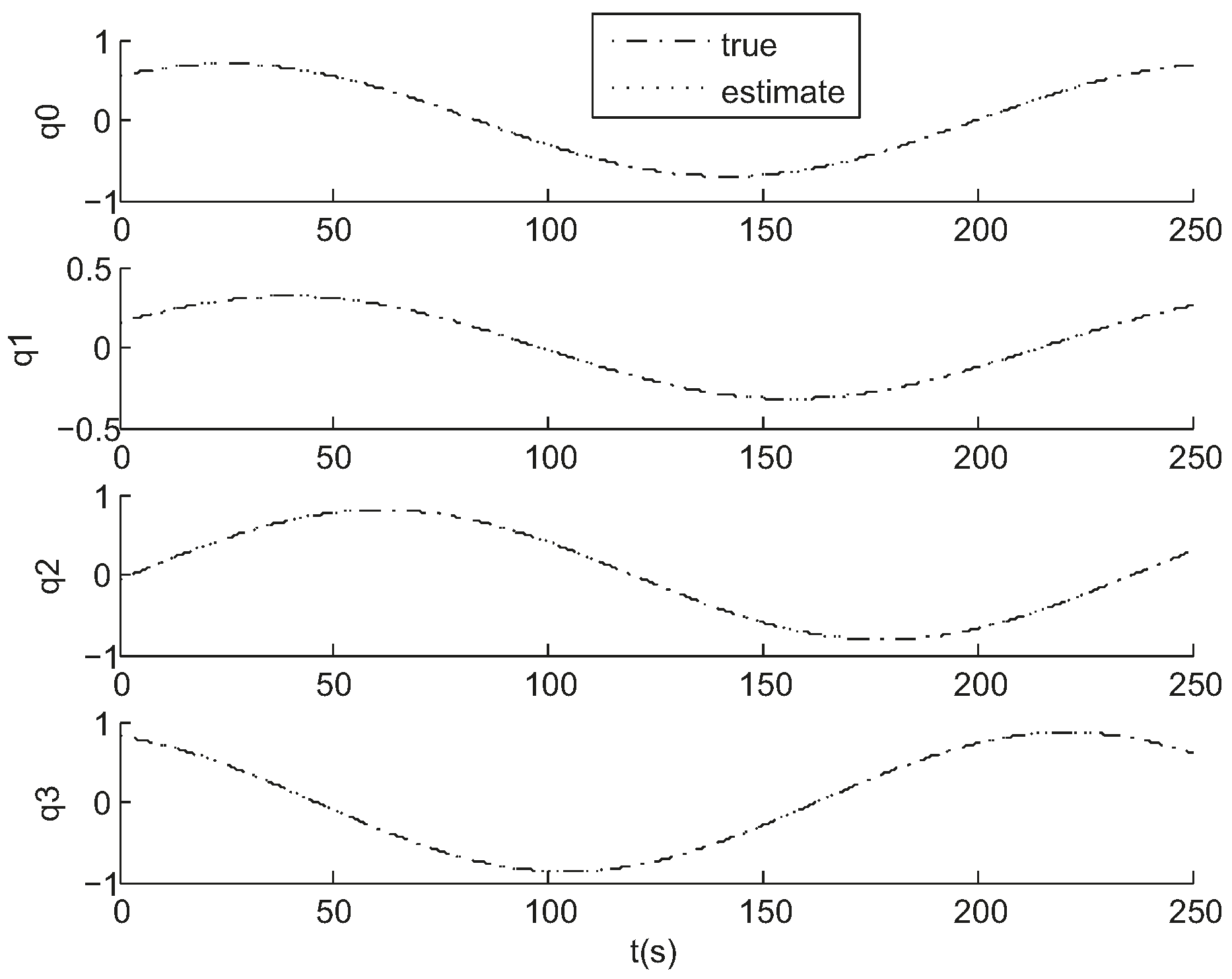
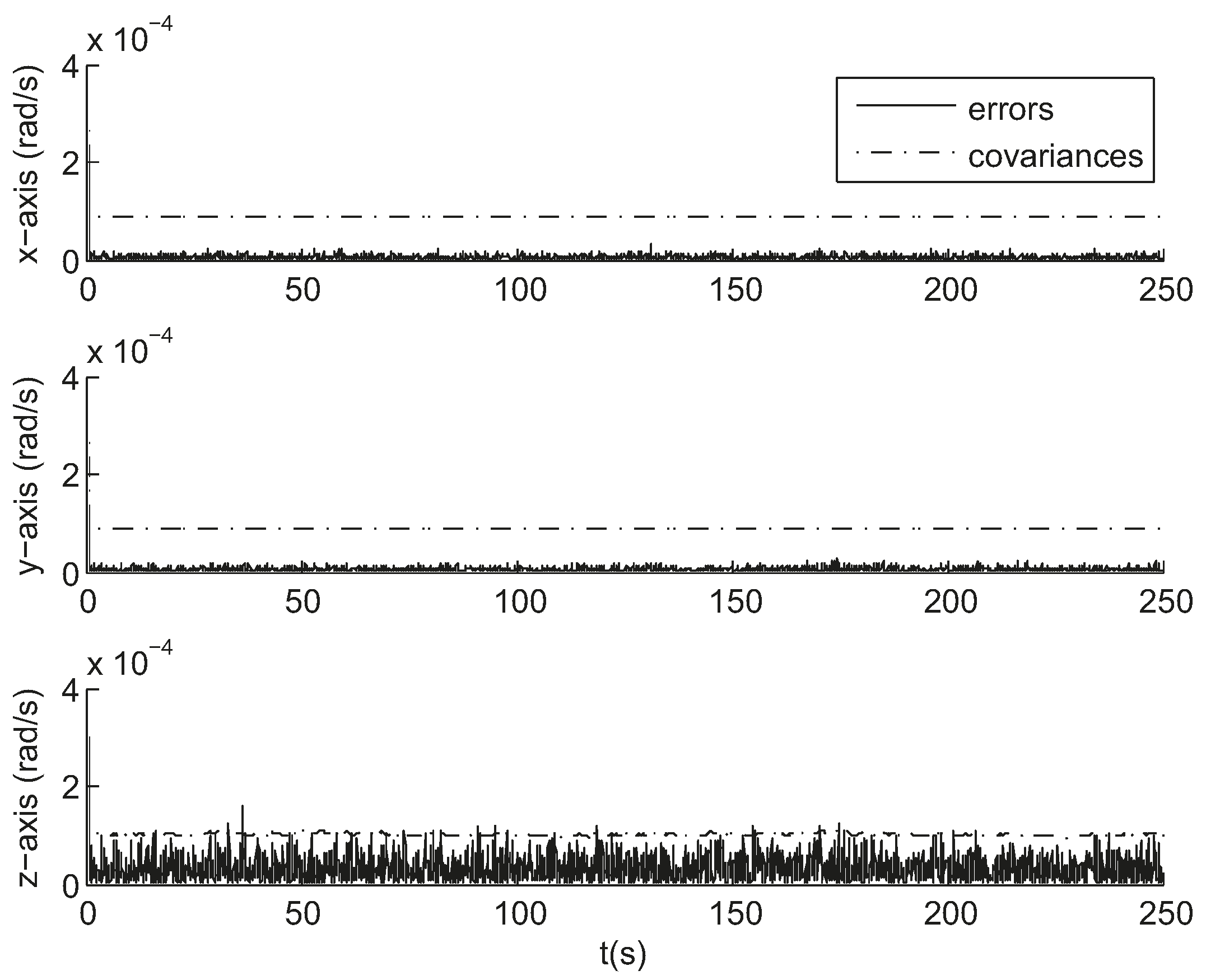
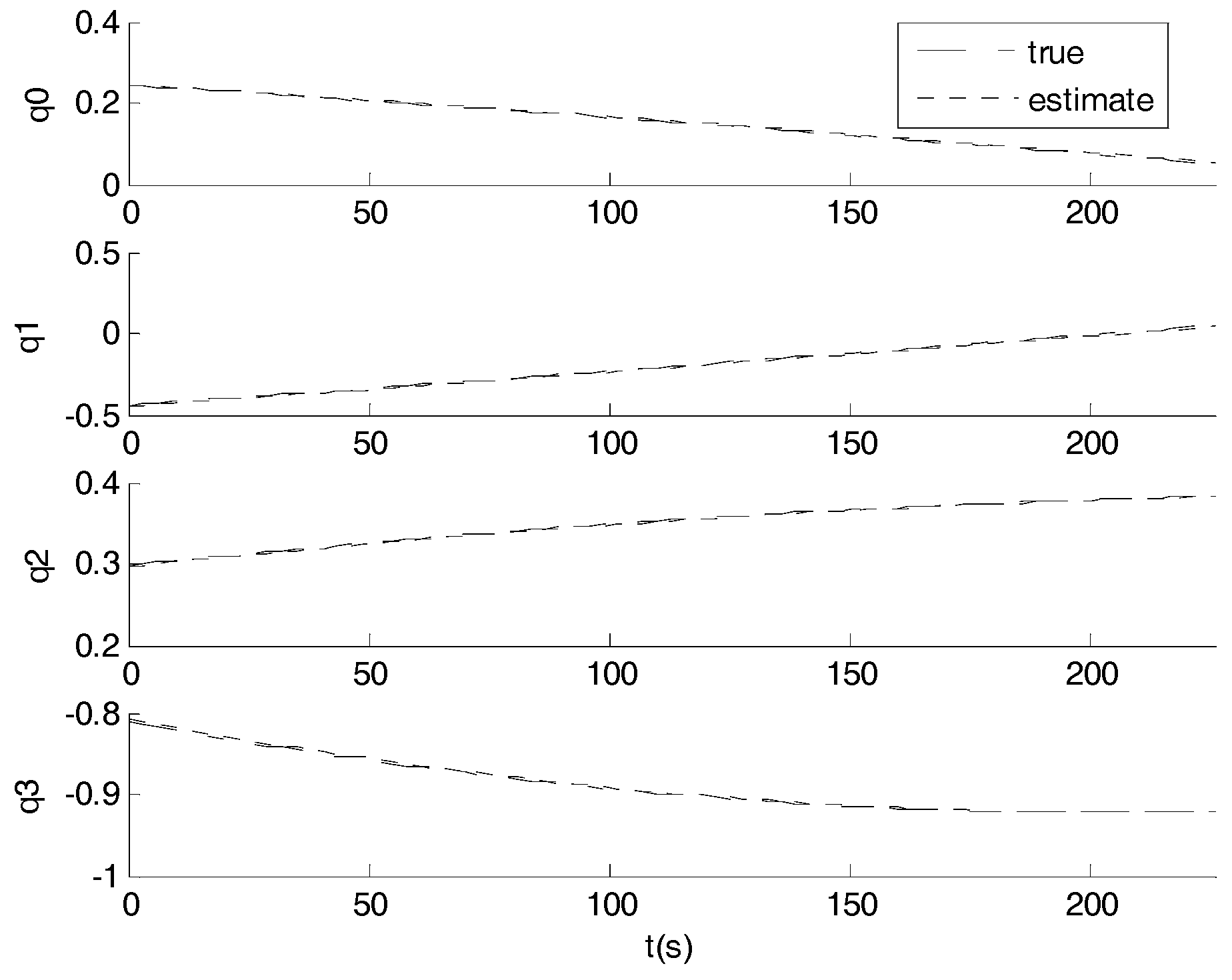
3.1. Simulation
3.2. Night Sky Experiments
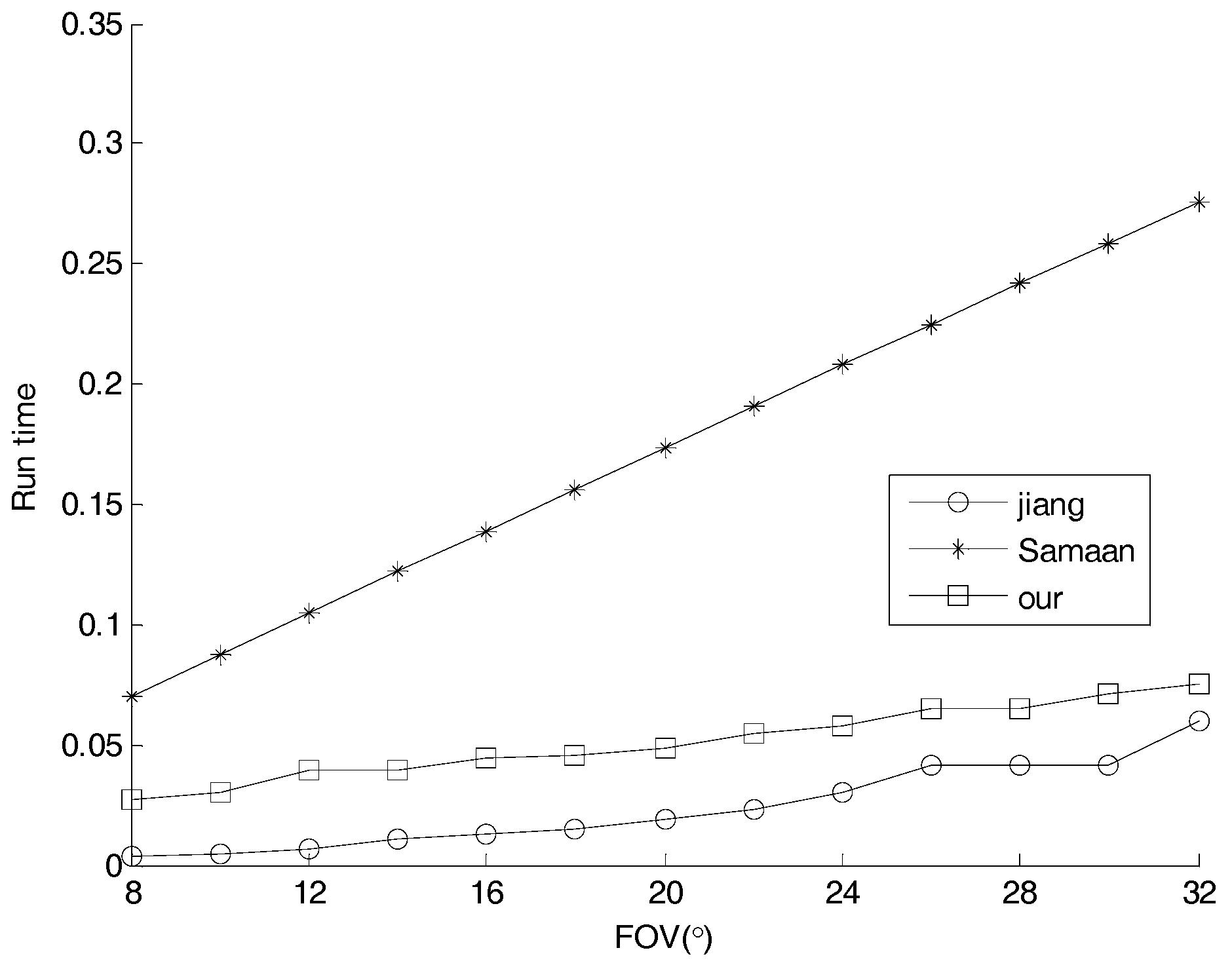
3.3. Comparison and Analysis
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Malak, A.; Samaan, D.M.; Junkins, J.L. Recursive Mode Star Identification Algorithms. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1–7. [Google Scholar]
- Benjamin, B.; Spratling, I.V.; Mortari, D. A Survey on Star Identification Algorithms. Algorithms 2009, 2, 93–107. [Google Scholar]
- Li, B.; Zhang, Y.; Li, H.; Wang, C. A star tracking algorithm suitable for star sensor. Proc. SPIE 2007. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, G.J.; Wei, X.; Li, X. Rapid star tracking algorithm for star sensor. IEEE Aerosp. Electron. Syst. Mag. 2009, 24, 23–33. [Google Scholar] [CrossRef]
- Shuster, M.D.; Oh, S.D. Three-axis attitude determination from vector observations. J. Guid. Control Dyn. 2012, 4, 70–77. [Google Scholar] [CrossRef]
- Mortari, D. Second Estimator of the Optimal Quaternion. J. Guid. Control Dyn. 2000, 23, 885–888. [Google Scholar] [CrossRef]
- Yu, W.; Jiang, J.; Zhang, G. Star tracking method based on multiexposure imaging for intensified star trackers. Appl. Opt. 2017, 56, 5961–5971. [Google Scholar] [CrossRef]
- Sun, T.; Xing, F.; Wang, X.; Li, J.; Wei, M.; You, Z. Effective star tracking method based on optical flow analysis for star trackers. Appl. Opt. 2016, 55, 10335–10340. [Google Scholar] [CrossRef] [PubMed]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; University of North Carolina at Chapel Hill: Chapel Hill, NC, USA, July 1995. [Google Scholar]
- Liebe, C.C. Accuracy performance of star trackers-a tutorial. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 587–599. [Google Scholar] [CrossRef]
- Markley, F.L. Parameterization of the Attitude, Spacecraft Attitude Determination and Control; D. Reidel Publishing Co.: Dordrecht, The Netherlands, 1978; pp. 410–420. [Google Scholar]
- Chou, J.C.K. Quaternion kinematic and dynamic differential equations. IEEE Trans. Robot. Autom. 1992, 8, 53–64. [Google Scholar] [CrossRef]
- Kreyszig, E. Advanced Engineering Mathematics; John Wiley and Sons: New York, NY, USA, 1983. [Google Scholar]
- Brogan, W.L. Modern Control Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1982. [Google Scholar]
- Active Pixel Sensor ASTRO APS. Available online: http://www.jena-optronik.de/en/aocs/astro-aps.html?file=tl_files/pdf/Data%20Sheet%20ASTRO%20APS.pdf (accessed on 17 August 2017).
- AA-STR APS Based Autonomous Star Tracker. Available online: http://www.leonardocompany.com/documents/63265270/65635102/Copia+di+A_STR_Autonomous_Star_Trackers_LQ_mm07786_.pdf?download_file (accessed on 17 August 2017).
- Michaels, D.; Speed, J. New Ball Aerospace star tracker achieves high tracking accuracy for a moving star field. Proc. SPIE 2004, 5430, 43–52. [Google Scholar]
- Blarre, L.; Perrimon, N.; Airey, S. New multiple head star sensor (HYDRA) description and development status: A highly autonomous, accurate and very robust system to pave the way for gyro-less very accurate AOCS systems. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005; pp. 1–9. [Google Scholar]
- Li, J.; Wei, X.; Zhang, G. Iterative algorithm for autonomous star identification. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 536–547. [Google Scholar] [CrossRef]
- Abreu, R. Stellar attitude determination accuracy with multiple-star-tracking advanced star tracker. Space Guid. Control Track. 1993, 1949, 216–227. [Google Scholar]
- Bar-Shalom, Y. Tracking and Data Association; Academic Press Professional, Inc.: Cambridge, MA, USA, 1987. [Google Scholar]








| Parameter | Description |
|---|---|
| The state transition function | |
| The linear term of the Taylor series expansion of the state transition function | |
| The process noise covariance matrix | |
| The state error covariance matrix | |
| The extended Kalman filter gain | |
| The measurement function | |
| The linear term of the Taylor series expansion of the measurement function | |
| The measurement noise covariance matrix |
| Element Index | Subcatalog Center Direction | Subcatalog Start Address in Guide Catalog | Subcatalog Length | Maximum Angle between the Guide Stars in the Subcatalog and the Center (Degree) |
|---|---|---|---|---|
| 1 | (−0.99244712, 0.06449312, 0.10435207) | 1 | 17 | 8.00 |
| 2 | (−0.99244712, −0.06449312, −0.10435207) | 18 | 9 | 6.37 |
| … | … | … | … | … |
| n | (0.99244712, −0.06449312, −0.10435207) | 4324 | 15 | 7.46 |
| Quaternion | Angular Velocity | |
|---|---|---|
| True Initial State | (0.54680, 0.15199, −0.06565, 0.82073) | (−0.03, 0.04, −0.02) rad/s |
| Initial State Estimate | (0.54679, 0.15199, −0.06566, 0.82074) | (−0.03115, 0.04046, −0.02086) rad/s |
| Error Covariance | (6 × 10−7, 1 × 10−8, 3 × 10−8, 3 × 10−7) | (8 × 10−4, 8 × 10−4, 8 × 10−4) (rad/s)2 |
| Process Noise | (1 × 10−9, 1 × 10−9, 1 × 10−9, 1 × 10−9) | (1 × 10−6, 1 × 10−6, 1 × 10−6) (rad/s)2 |
| Parameter | Value |
|---|---|
| Initial attitude | (0.24383, −0.44028, 0.29841, −0.81095) |
| Angular velocity | (0, 0.03491, 0) rad/s |
| Focal length | 44.27 mm |
| FOV | 14.5 degrees |
| Pixel array | 2048 × 2048 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wei, X.; Zhang, G. An Extended Kalman Filter-Based Attitude Tracking Algorithm for Star Sensors. Sensors 2017, 17, 1921. https://doi.org/10.3390/s17081921
Li J, Wei X, Zhang G. An Extended Kalman Filter-Based Attitude Tracking Algorithm for Star Sensors. Sensors. 2017; 17(8):1921. https://doi.org/10.3390/s17081921
Chicago/Turabian StyleLi, Jian, Xinguo Wei, and Guangjun Zhang. 2017. "An Extended Kalman Filter-Based Attitude Tracking Algorithm for Star Sensors" Sensors 17, no. 8: 1921. https://doi.org/10.3390/s17081921
APA StyleLi, J., Wei, X., & Zhang, G. (2017). An Extended Kalman Filter-Based Attitude Tracking Algorithm for Star Sensors. Sensors, 17(8), 1921. https://doi.org/10.3390/s17081921




