Accuracy of Flight Altitude Measured with Low-Cost GNSS, Radar and Barometer Sensors: Implications for Airborne Radiometric Surveys
Abstract
:1. Introduction
2. Instruments and Methods
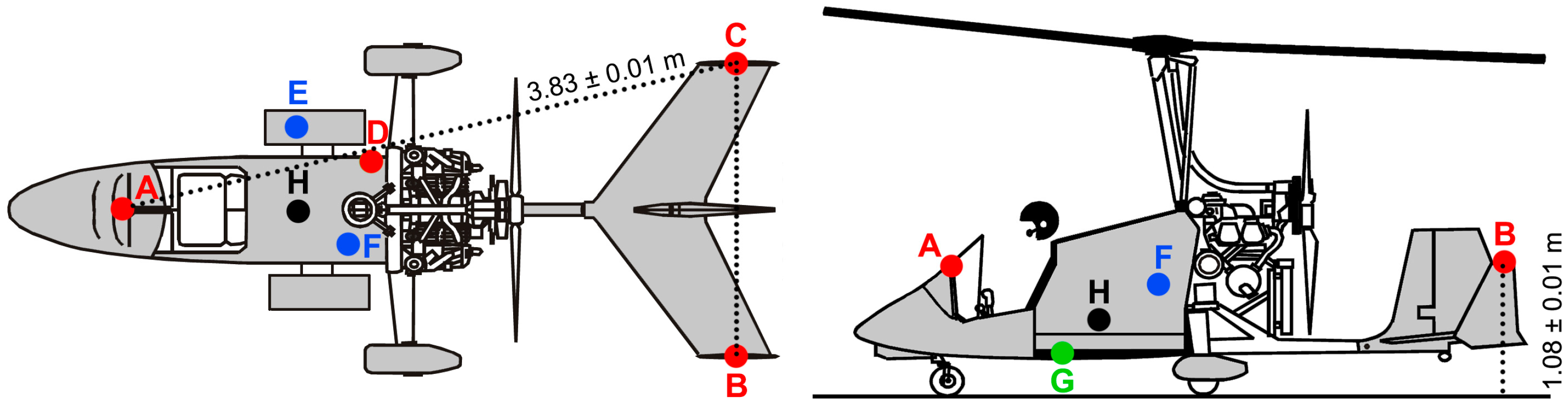
2.1. The Inertial Measurement Unit
2.2. The Radar Altimeter
2.3. The Three GNSS Receivers
- -
- code-only stand-alone solution (1 Hz), using a Kalman filter with constant-velocity dynamics;
- -
- code and phase double differences solution (0.2 Hz) with respect to the permanent station Madonna Dell’Acqua (Pisa) (43.7475° N, 10.3660° E, 2 a.s.l), using a Kalman filter with constant-velocity dynamics.
2.4. The two Pressure and Temperature Sensors
3. Results and Discussion
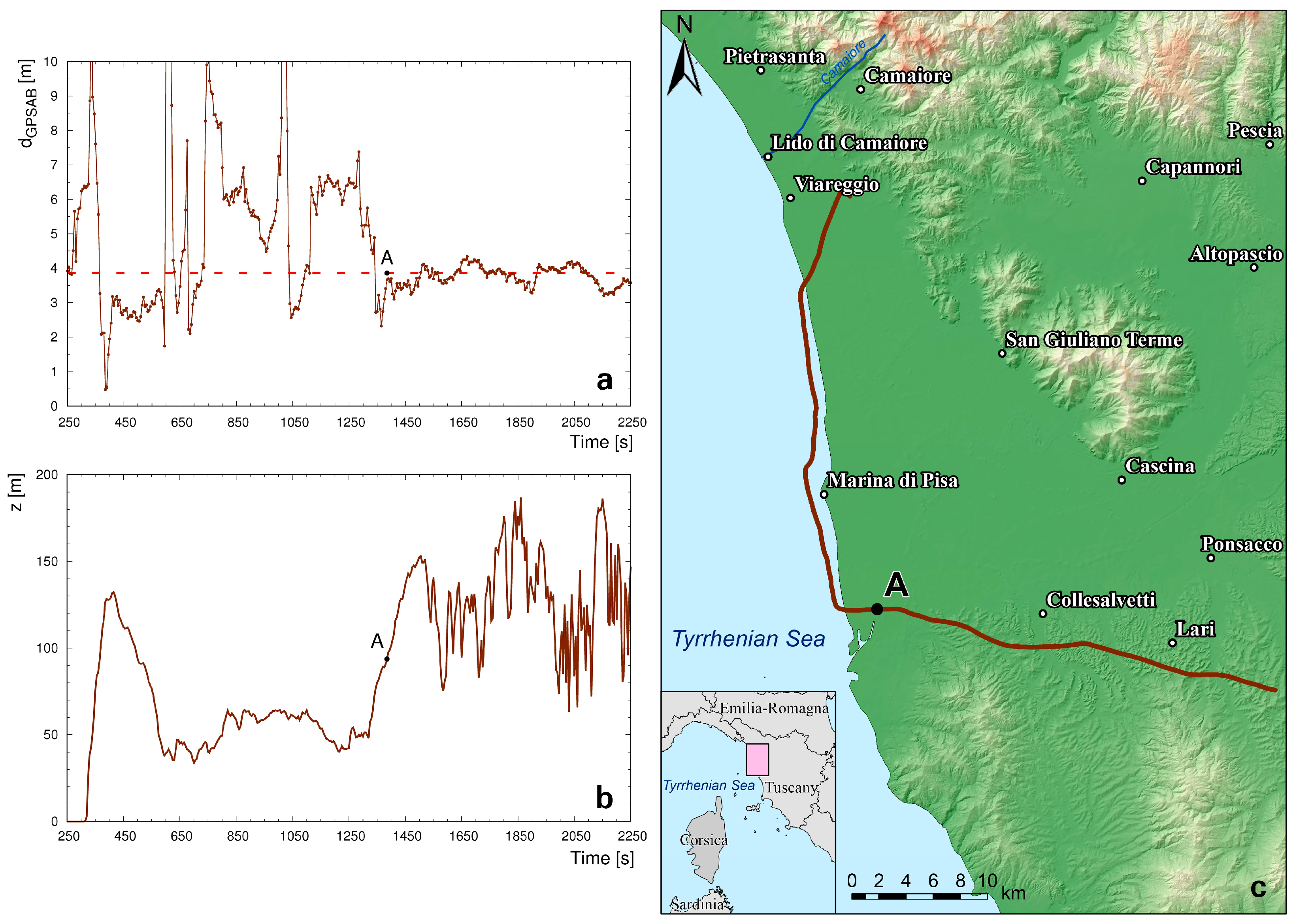
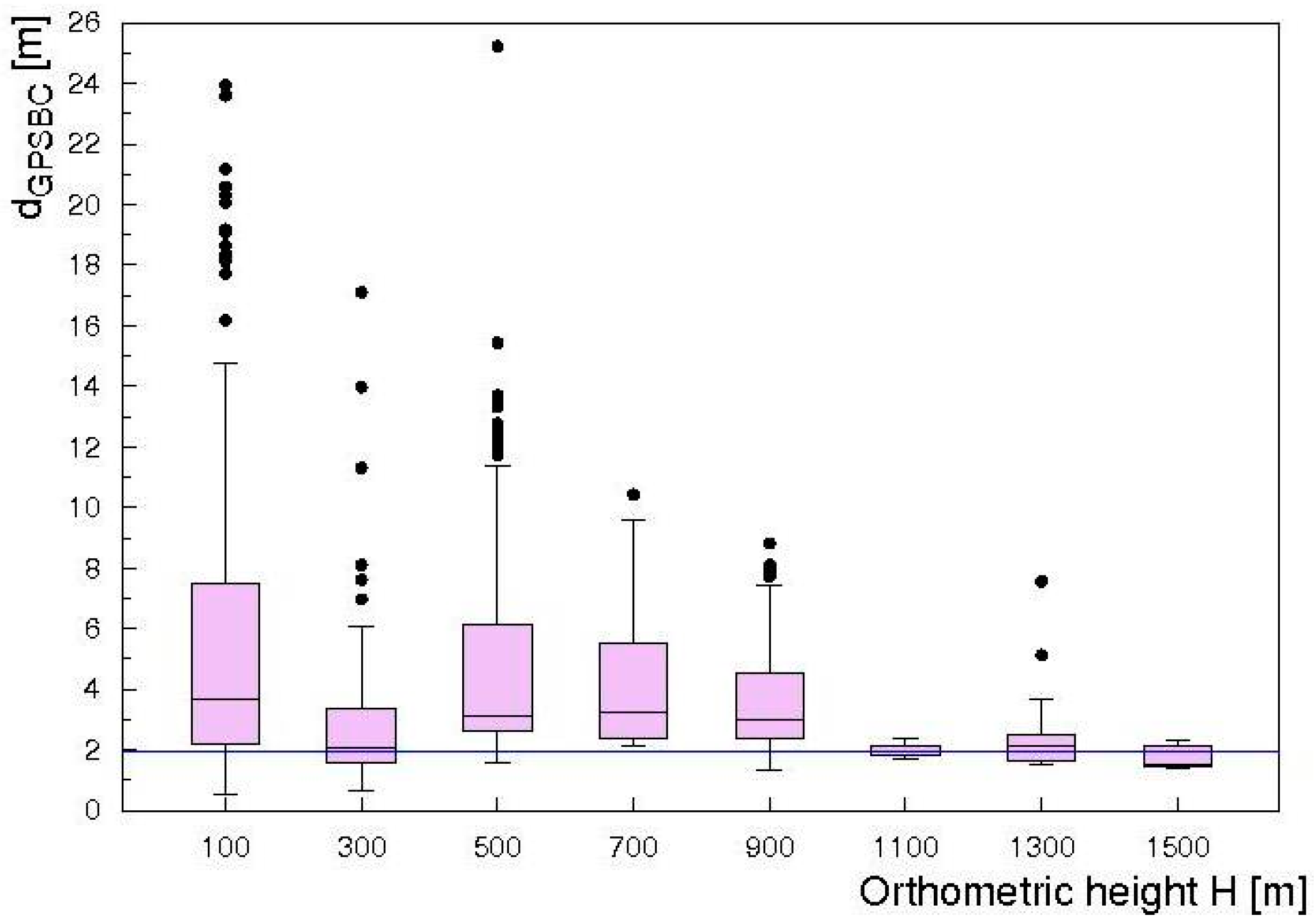
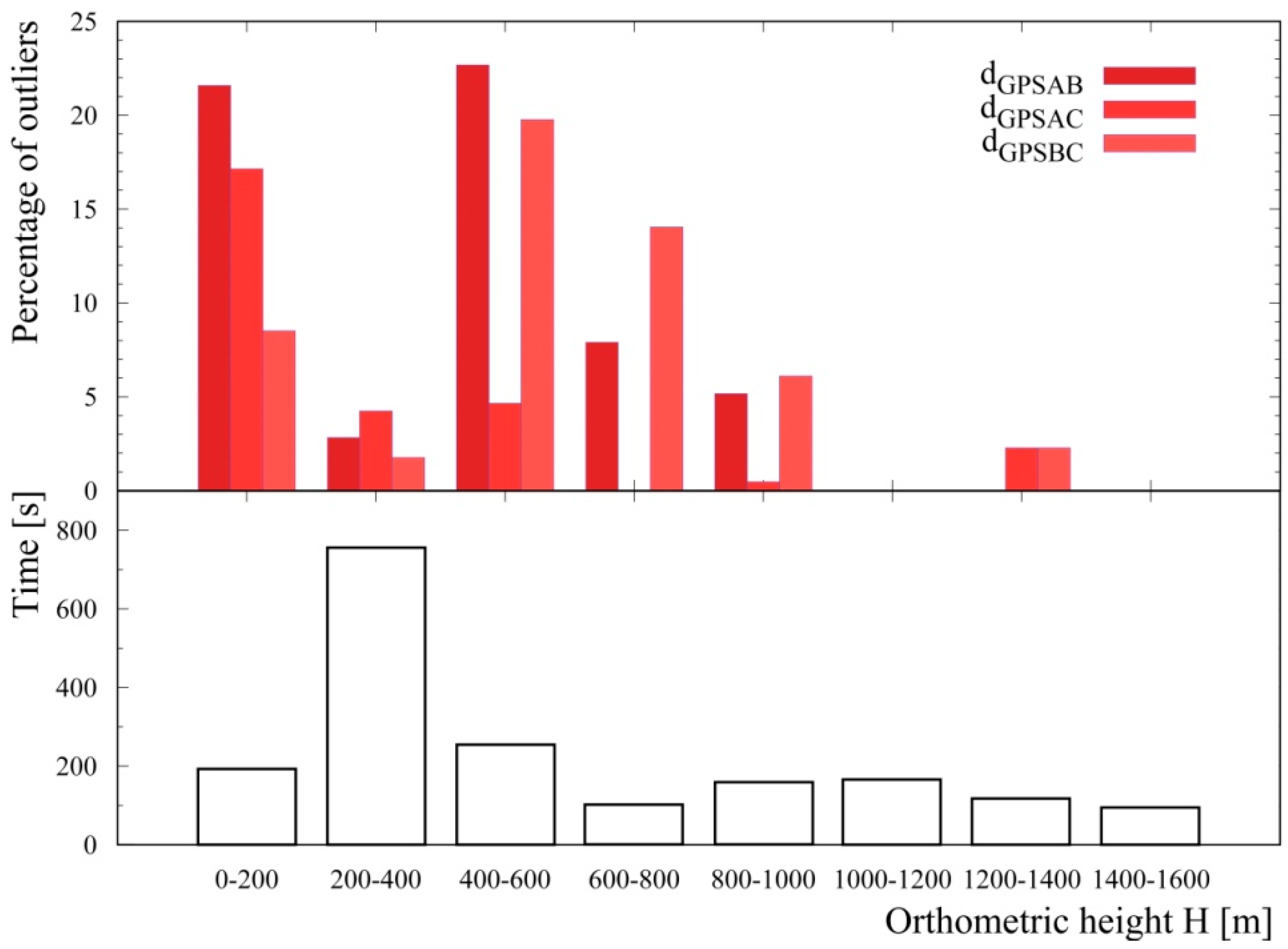
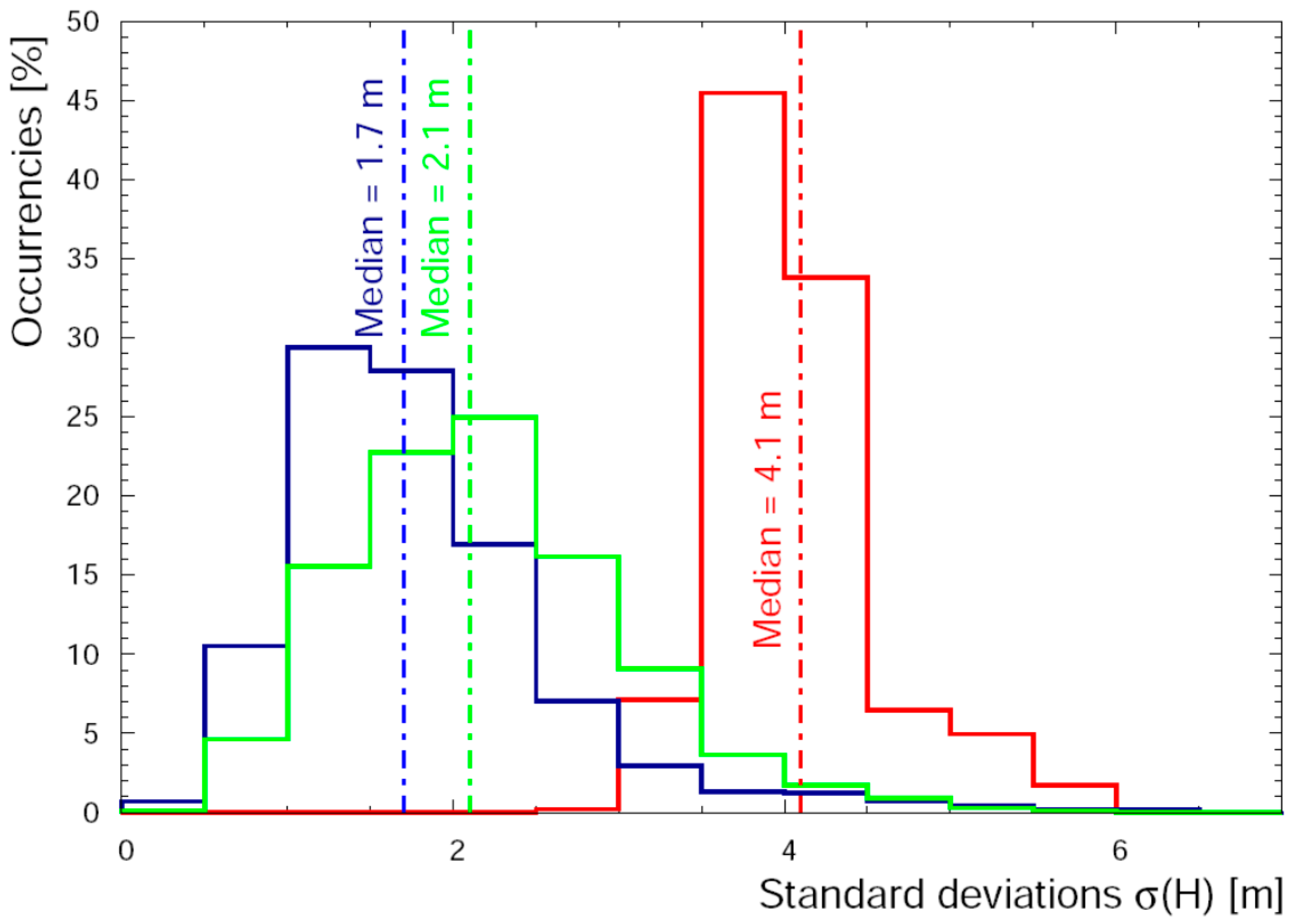
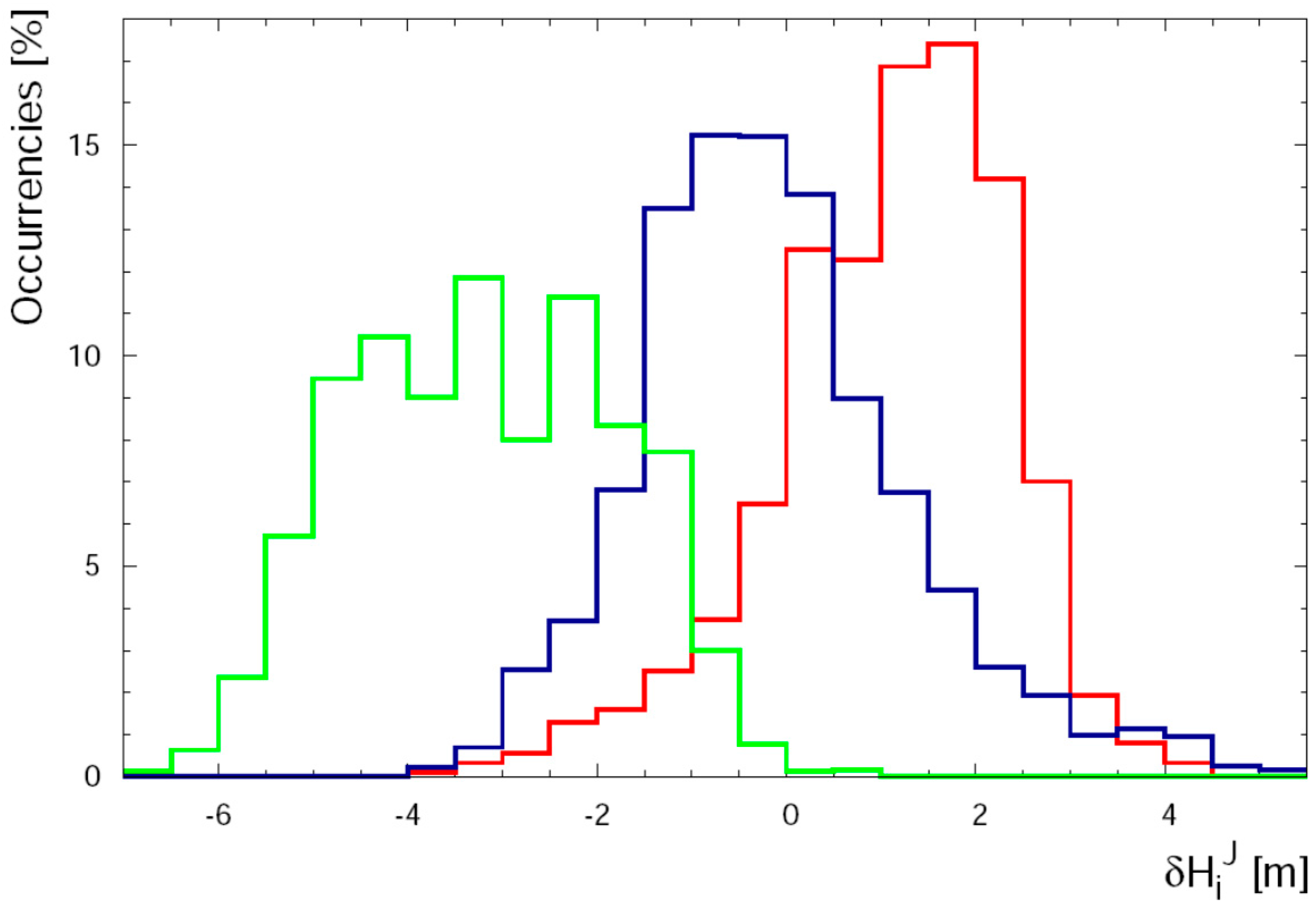
3.1. Analysis of DATASET 1
3.2. Analysis of DATASET 2
3.3. Effect of the Accuracy of the Flight Altitude on AGRS Measurements
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| F11 | |||||||
|---|---|---|---|---|---|---|---|
| GPSB | GPSA | GPSIMU | ALT | PT | PTIMU | ||
| GPSC | m | 0.994 ± 0.002 | 0.992 ± 0.003 | 0.981 ± 0.003 | 0.987 ± 0.002 | 0.996 ± 0.003 | 1.001 ± 0.003 |
| q | 0.21 ± 0.38 | −1.56 ± 0.49 | 2.62 ± 0.58 | 1.72 ± 0.39 | 0.48 ± 0.51 | 0.05 ± 0.55 | |
| r2 | 0.998 | 0.997 | 0.996 | 0.998 | 0.997 | 0.996 | |
| GPSB | m | 0.998 ± 0.003 | 0.987 ± 0.003 | 0.993 ± 0.002 | 1.001 ± 0.003 | 1.007 ± 0.003 | |
| q | 1.46 ± 0.44 | 2.49 ± 0.51 | 1.63 ± 0.33 | −0.43 ± 0.52 | 0.00 ± 0.56 | ||
| r2 | 0.998 | 0.997 | 0.999 | 0.997 | 0.996 | ||
| GPSA | m | 0.988 ± 0.003 | 0.993 ± 0.002 | 1.001 ± 0.003 | 1.008 ± 0.003 | ||
| q | 1.28 ± 0.545 | 0.40 ± 0.36 | −0.85 ± 0.49 | −1.31 ± 0.51 | |||
| r2 | 0.996 | 0.998 | 0.997 | 0.997 | |||
| GPSIMU | m | 1.003 ± 0.003 | 1.012 ± 0.002 | 1.019 ± 0.002 | |||
| q | −0.48 ± 0.46 | −1.95 ± 0.37 | −2.42 ± 0.38 | ||||
| r2 | 0.997 | 0.998 | 0.998 | ||||
| ALT | m | 1.008 ± 0.002 | 1.014 ± 0.003 | ||||
| q | −1.20 ± 0.40 | −1.63 ± 0.46 | |||||
| r2 | 0.998 | 0.997 | |||||
| PT | m | 1.007 ± 0.001 | |||||
| q | 0.44 ± 0.19 | ||||||
| r2 | 1.000 | ||||||
| F12 | |||||||
|---|---|---|---|---|---|---|---|
| GPSB | GPSA | GPSIMU | ALT | PT | PTIMU | ||
| GPSC | m | 1.016 ± 0.005 | 0.996 ± 0.006 | 1.015 ± 0.006 | 1.056 ± 0.007 | 1.015 ± 0.007 | 0.998 ± 0.007 |
| q | −2.67 ± 0.81 | 1.15 ± 1.01 | −3.65 ± 1.01 | −9.25 ± 1.27 | −1.70 ± 1.25 | 0.28 ± 1.21 | |
| r2 | 0.997 | 0.995 | 0.995 | 0.993 | 0.993 | 0.993 | |
| GPSB | m | 0.980 ± 0.004 | 0.998 ± 0.005 | 1.037 ± 0.008 | 0.997 ± 0.007 | 0.981 ± 0.007 | |
| q | 3.80 ± 0.70 | −0.77 ± 0.90 | −6.08 ± 1.36 | 1.25 ± 1.25 | 3.18 ± 1.19 | ||
| r2 | 0.998 | 0.996 | 0.992 | 0.993 | 0.993 | ||
| GPSA | m | 1.017 ± 0.005 | 1.057 ± 0.007 | 1.016 ± 0.008 | 1.000 ± 0.007 | ||
| q | −4.43 ± 0.95 | −9.93 ± 1.33 | −2.27 ± 1.38 | −0.35 ± 1.28 | |||
| r2 | 0.996 | 0.993 | 0.991 | 0.992 | |||
| GPSIMU | m | 1.036 ± 0.008 | 1.000 ± 0.004 | 0.983 ± 0.003 | |||
| q | −4.90 ± 1.42 | 1.93 ± 0.75 | 3.85 ± 0.63 | ||||
| r2 | 0.991 | 0.997 | 0.998 | ||||
| ALT | m | 0.957 ± 0.008 | 0.941 ± 0.008 | ||||
| q | 7.96 ± 1.38 | 9.92 ± 1.41 | |||||
| r2 | 0.99 | 0.99 | |||||
| PT | m | 0.983 ± 0.002 | |||||
| q | 2.07 ± 0.44 | ||||||
| r2 | 0.999 | ||||||
| F15 | |||||||
|---|---|---|---|---|---|---|---|
| GPSB | GPSA | GPSIMU | ALT | PT | PTIMU | ||
| GPSC | m | 0.896 ± 0.017 | 0.956 ± 0.008 | 1.015 ± 0.014 | 0.982 ± 0.007 | 0.991 ± 0.027 | 1.022 ± 0.026 |
| q | 5.68 ± 0.89 | 0.65 ± 0.43 | −7.34 ± 0.82 | 3.65 ± 0.35 | 3.92 ± 1.32 | 3.14 ± 1.25 | |
| r2 | 0.958 | 0.992 | 0.978 | 0.994 | 0.928 | 0.962 | |
| GPSB | m | 1.027 ± 0.019 | 1.108 ± 0.016 | 1.057 ± 0.019 | 1.079 ± 0.031 | 1.113 ± 0.030 | |
| q | −3.47 ± 1.05 | −13.05 ± 0.95 | −0.34 ± 0.92 | −0.63 ± 1.50 | −1.51 ± 1.41 | ||
| r2 | 0.958 | 0.975 | 0.964 | 0.968 | 0.921 | ||
| GPSA | m | 1.054 ± 0.017 | 1.022 ± 0.008 | 1.032 ± 0.028 | 1.061 ± 0.028 | ||
| q | −7.89 ± 0.97 | 3.37 ± 0.40 | 3.36 ± 1.38 | 2.97 ± 1.35 | |||
| r2 | 0.971 | 0.993 | 0.916 | 0.922 | |||
| GPSIMU | m | 0.952 ± 0.11 | 0.970 ± 0.025 | 1.001 ± 0.023 | |||
| q | 11.57 ± 0.54 | 11.38 ± 1.21 | 10.57 ± 1.11 | ||||
| r2 | 0.984 | 0.927 | 0.939 | ||||
| ALT | m | 1.009 ± 0.027 | 1.040 ± 0.026 | ||||
| q | 0.33 ± 1.31 | −0.45 ± 1.24 | |||||
| r2 | 0.921 | 0.931 | |||||
| PT | m | 1.020 ± 0.009 | |||||
| q | −0.28 ± 0.45 | ||||||
| r2 | 0.99 | ||||||
Appendix B
| F11 | ||||||
|---|---|---|---|---|---|---|
| GPSB | GPSA | GPSIMU | PT | PTIMU | ||
| GPSC | m | 0.9996 ± 0.0001 | 1.0007 ± 0.0001 | 1.0009 ± 0.0002 | 0.9994 ± 0.0002 | 0.9987 ± 0.0002 |
| q | 0.75 ± 0.11 | 0.11 ± 0.14 | 0.15 ± 0.21 | 1.57 ± 0.24 | 3.50 ± 0.26 | |
| r2 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| GPSB | m | 1.0011 ± 0.0002 | 1.0013 ± 0.0001 | 0.9998 ± 0.0002 | 0.9992 ± 0.0002 | |
| q | −0.64 ± 0.18 | −0.60 ± 0.16 | 0.82 ± 0.21 | 2.75 ± 0.23 | ||
| r2 | 1.000 | 1.000 | 1.000 | 1.000 | ||
| GPSA | m | 1.0002 ± 0.0002 | 0.9987 ± 0.0003 | 0.9980 ± 0.0003 | ||
| q | 0.05 ± 0.28 | 1.48 ± 0.30 | 3.40 ± 0.33 | |||
| r2 | 1.000 | 1.000 | 1.000 | |||
| GPSIMU | m | 0.9985 ± 0.0001 | 0.9979 ± 0.0001 | |||
| q | 1.41 ± 0.12 | 3.34 ± 0.11 | ||||
| r2 | 1.000 | 1.000 | ||||
| PT | m | 0.9994 ± 0.0001 | ||||
| q | 1.93 ± 0.11 | |||||
| r2 | 1.000 | |||||
| F14 | ||||||
|---|---|---|---|---|---|---|
| GPSB | GPSA | GPSIMU | PT | PTIMU | ||
| GPSC | m | 0.99997 ± 0.00005 | 0.9996 ± 0.0001 | 0.9977 ± 0.0001 | 0.9975 ± 0.0002 | 0.9982 ± 0.0002 |
| q | 0.18 ± 0.08 | 0.62 ± 0.10 | 5.64 ± 0.20 | 4.25 ± 0.26 | 3.37 ± 0.24 | |
| r2 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| GPSB | m | 99960 ± 0.00004 | 0.9977 ± 0.0001 | 0.9976 ± 0.0002 | 0.9982 ± 0.0002 | |
| q | 0.44 ± 0.06 | 5.47 ± 0.22 | 4.07 ± 0.28 | 3.19 ± 0.25 | ||
| r2 | 1 | 1.000 | 1.000 | 1.000 | ||
| GPSA | m | 0.9981 ± 0.0001 | 0.9980 ± 0.0002 | 0.9986 ± 0.0002 | ||
| q | 5.03 ± 0.21 | 3.63 ± 0.29 | 2.75 ± 0.25 | |||
| r2 | 1.000 | 1.000 | 1.000 | |||
| GPSIMU | m | 0.9998 ± 0.0001 | 1.0005 ± 0.0001 | |||
| q | −1.40 ± 0.21 | −2.28 ± 0.18 | ||||
| r2 | 1 | 1 | ||||
| PT | m | 1.0007 ± 0.0001 | ||||
| q | −0.87 ± 0.17 | |||||
| r2 | 1.000 | |||||
Appendix C

References
- Strati, V.; Baldoncini, M.; Bezzon, G.P.; Broggini, C.; Buso, G.P.; Caciolli, A.; Callegari, I.; Carmignani, L.; Colonna, T.; Fiorentini, G.; et al. Total natural radioactivity, Veneto (Italy). J. Maps 2015, 11, 545–551. [Google Scholar] [CrossRef]
- Xhixha, M.K.; Albèri, M.; Baldoncini, M.; Bezzon, G.P.; Buso, G.P.; Callegari, I.; Casini, L.; Cuccuru, S.; Fiorentini, G.; Guastaldi, E.; et al. Uranium distribution in the Variscan Basement of Northeastern Sardinia. J. Maps 2015, 1–8. [Google Scholar] [CrossRef]
- Wilford, J.; Minty, B. Chapter 16 The Use of Airborne Gamma-ray Imagery for Mapping Soils and Understanding Landscape Processes. Dev. Soil Sci. 2006, 31, 207–610. [Google Scholar]
- Mohamud, A.H.; Cózar, J.S.; Rodrigo-Naharro, J.; Pérez del Villar, L. Distribution of U and Th in an Iberian U-fertile granitic complex (NW, Spain): Airborne-radiometry, chemical and statistical approaches. J. Geochem. Explor. 2015, 148, 40–55. [Google Scholar] [CrossRef]
- Kock, P.; Raaf, C.; Samuelsson, C. On background radiation gradients—The use of airborne surveys when searching for orphan sources using mobile gamma-ray spectrometry. J. Environ. Radioact. 2014, 128, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Kurihara, Y.; Koike, Y.; Tanihata, I.; Fujiwara, M.; Sakaguchi, H.; Shinohara, A.; Yamamoto, H. Altitude distribution of radioactive cesium at Fuji volcano caused by Fukushima Daiichi Nuclear Power Station accident. J. Radioanal. Nucl. Chem. 2015, 303, 1613–1615. [Google Scholar] [CrossRef]
- Caciolli, A.; Baldoncini, M.; Bezzon, G.P.; Broggini, C.; Buso, G.P.; Callegari, I.; Colonna, T.; Fiorentini, G.; Guastaldi, E.; Mantovani, F.; et al. A new FSA approach for in situ γ ray spectroscopy. Sci. Total Environ. 2012, 414, 639–645. [Google Scholar] [CrossRef] [PubMed]
- Kock, P.; Lanke, J.; Samuelsson, C. A real-time statistical alarm method for mobile gamma spectrometry—Combining counts of pulses with spectral distribution of pulses. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2012, 681, 55–60. [Google Scholar] [CrossRef]
- Martin, P.G.; Payton, O.D.; Fardoulis, J.S.; Richards, D.A.; Yamashiki, Y.; Scott, T.B. Low altitude unmanned aerial vehicle for characterising remediation effectiveness following the FDNPP accident. J. Environ. Radioact. 2016, 151 Pt 1, 58–63. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Tang, X.-B.; Wang, P.; Meng, J.; Huang, X.; Wen, L.-S.; Chen, D. Spectrum correction algorithm for detectors in airborne radioactivity monitoring equipment NH-UAV based on a ratio processing method. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2015, 797, 290–296. [Google Scholar] [CrossRef]
- Martin, P.G.; Payton, O.D.; Fardoulis, J.S.; Richards, D.A.; Scott, T.B. The use of unmanned aerial systems for the mapping of legacy uranium mines. J. Environ. Radioact. 2015, 143, 135–140. [Google Scholar] [CrossRef] [PubMed]
- Druker, E. Processing of Airborne Gamma-Ray Spectrometry using Inversions. In Proceedings of the ASEG-PESA-AIG: 25th Geophysical Conference and Exhibition, Adelaide, Australia, 20 August 2016. [Google Scholar]
- Beekhuizen, J.; Heuvelink, G.B.M.; Biesemans, J.; Reusen, I. Effect of DEM Uncertainty on the Positional Accuracy of Airborne Imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1567–1577. [Google Scholar] [CrossRef]
- Baldoncini, M.; Albéri, M.; Bottardi, C.; Raptis, K.G.; Minty, B.; Strati, V.; Mantovani, F. Exploring atmospheric radon with airborne gamma-ray spectroscopy. Atmos. Environ. 2017. submitted. [Google Scholar]
- Baldoncini, M.; Albéri, M.; Bottardi, C.; Raptis, K.G.; Minty, B.; Strati, V.; Mantovani, F. Airborne gamma-ray spectroscopy for modeling cosmic radiation and effective dose in the lower atmosphere. IEEE Trans. Geosci. Remote Sens. 2017. submitted. [Google Scholar]
- Guastaldi, E.; Baldoncini, M.; Bezzon, G.; Broggini, C.; Buso, G.; Caciolli, A.; Carmignani, L.; Callegari, I.; Colonna, T.; Dule, K.; et al. A multivariate spatial interpolation of airborne γ-ray data using the geological constraints. Remote Sens. Environ. 2013, 137, 1–11. [Google Scholar] [CrossRef]
- Vydhyanathan, A.; Bellusci, G.; Luinge, H.; Slycke, P. The Next Generation Xsens Motion Trackers for Industrial Applications; Xsens: Enschede, The Netherlands, 2015. [Google Scholar]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Realini, E.; Reguzzoni, M. goGPS: Open source software for enhancing the accuracy of low-cost receivers by single-frequency relative kinematic positioning. Meas. Sci. Technol. 2013, 24. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Hoaglin, D.C.; Iglewicz, B.; Tukey, J.W. Performance of Some Resistant Rules for Outlier Labeling. J. Am. Statist. Assoc. 1986, 81, 991–999. [Google Scholar] [CrossRef]
- Smyrnaios, M.; Schön, S. GNSS Antenna Impact on the Resulting Multipath Effects in Carrier-Phase and Signal Amplitude. In Proceedings of the IAG Scientific Assembly, Postdam, Germany, 1–6 September 2013; Volume 143, pp. 735–742. [Google Scholar]
- Löfgren, J.S.; Haas, R.; Johansson, J.M. Monitoring coastal sea level using reflected GNSS signals. Adv. Space Res. 2011, 47, 213–220. [Google Scholar] [CrossRef]
- Löfgren, J.S.; Haas, R.; Scherneck, H.-G. Sea level time series and ocean tide analysis from multipath signals at five GPS sites in different parts of the world. J. Geodyn. 2014, 80, 66–80. [Google Scholar] [CrossRef]
- Tranquilla, J.M.; Carr, J.P. GPS Multipath Field Observations at Land and Water Sites. Navig. J. Inst. Navig. 1990, 37. [Google Scholar] [CrossRef]
- Gilardoni, M.; Reguzzoni, M.; Sampietro, D. GECO: A global gravity model by locally combining GOCE data and EGM2008. Stud. Geophys. Geod. 2016, 60, 228–247. [Google Scholar] [CrossRef]
- Society, P.S.A. A Quick Derivation Relating Altitude to Air Pressure; Portland State Aerospace Society: Portland, OR, USA, 2004. [Google Scholar]
- Parviainen, J.; Kantola, J.; Collin, J. Differential Barometry in Personal Navigation. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; pp. 148–152. [Google Scholar]
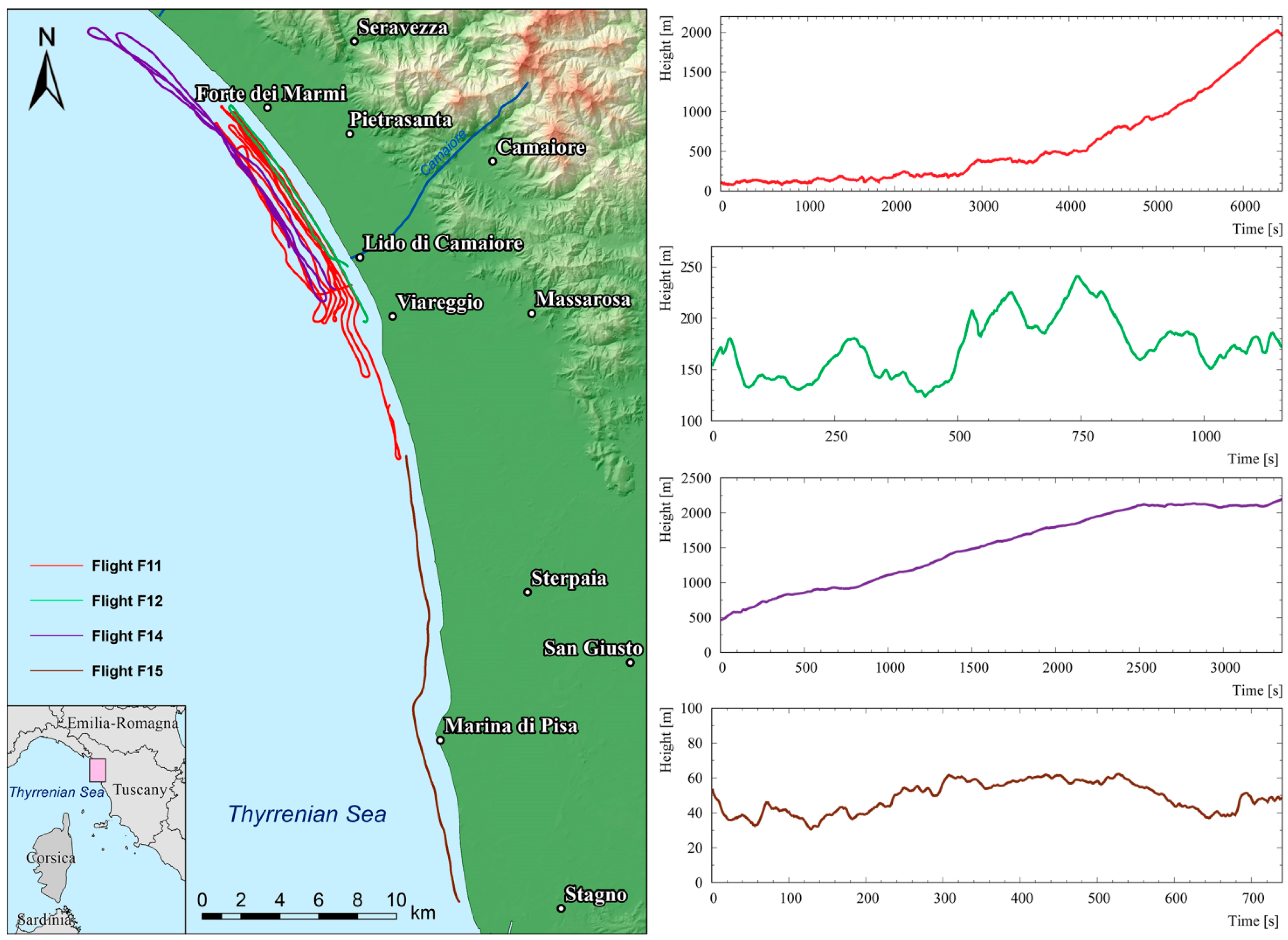




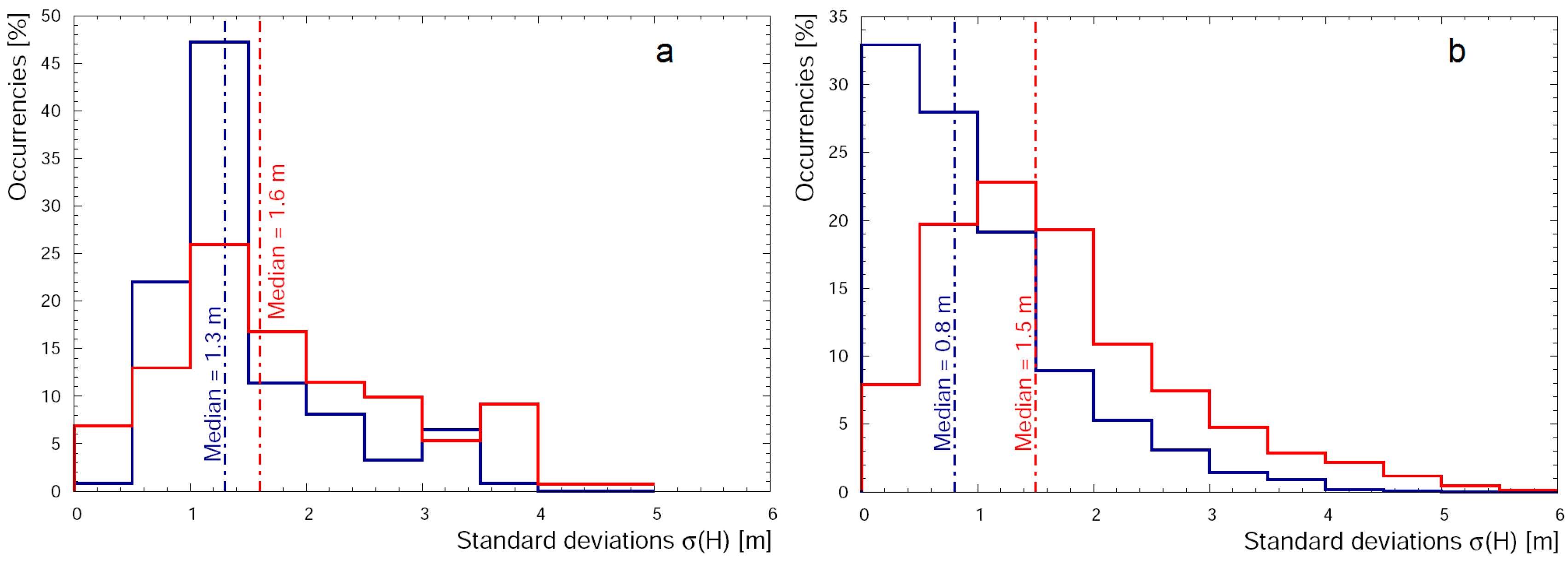
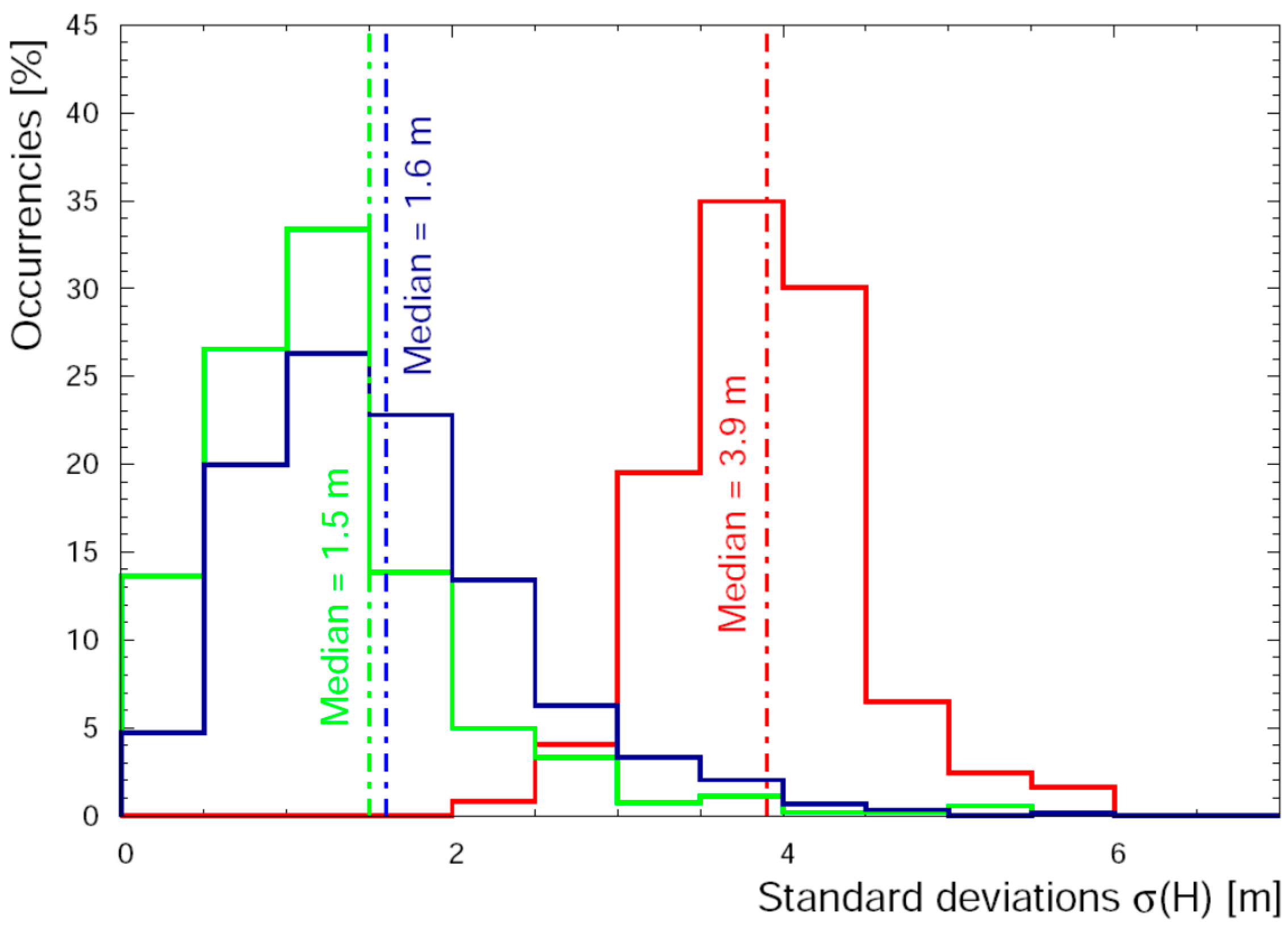
| Flight ID | Date | Time (CEST) | Hmin (m) | Hmax (m) | Acquisition Time (s) | Average Horizontal Speed (m/s) | Average Vertical Speed (m/s) |
|---|---|---|---|---|---|---|---|
| F11 | 30/03/16 | 17:42:11–19:29:38 | 79 | 2018 | 6447 | 18.9 | 0.8 |
| F12 | 31/03/16 | 18:13:55–18:33:12 | 129 | 237 | 1158 | 15.5 | 0.5 |
| F14 | 05/04/16 | 16:37:15–17:33:04 | 464 | 2194 | 3350 | 21.1 | 0.8 |
| F15 | 05/04/16 | 19:15:19–19:27:39 | 35 | 66 | 740 | 34.4 | 0.6 |
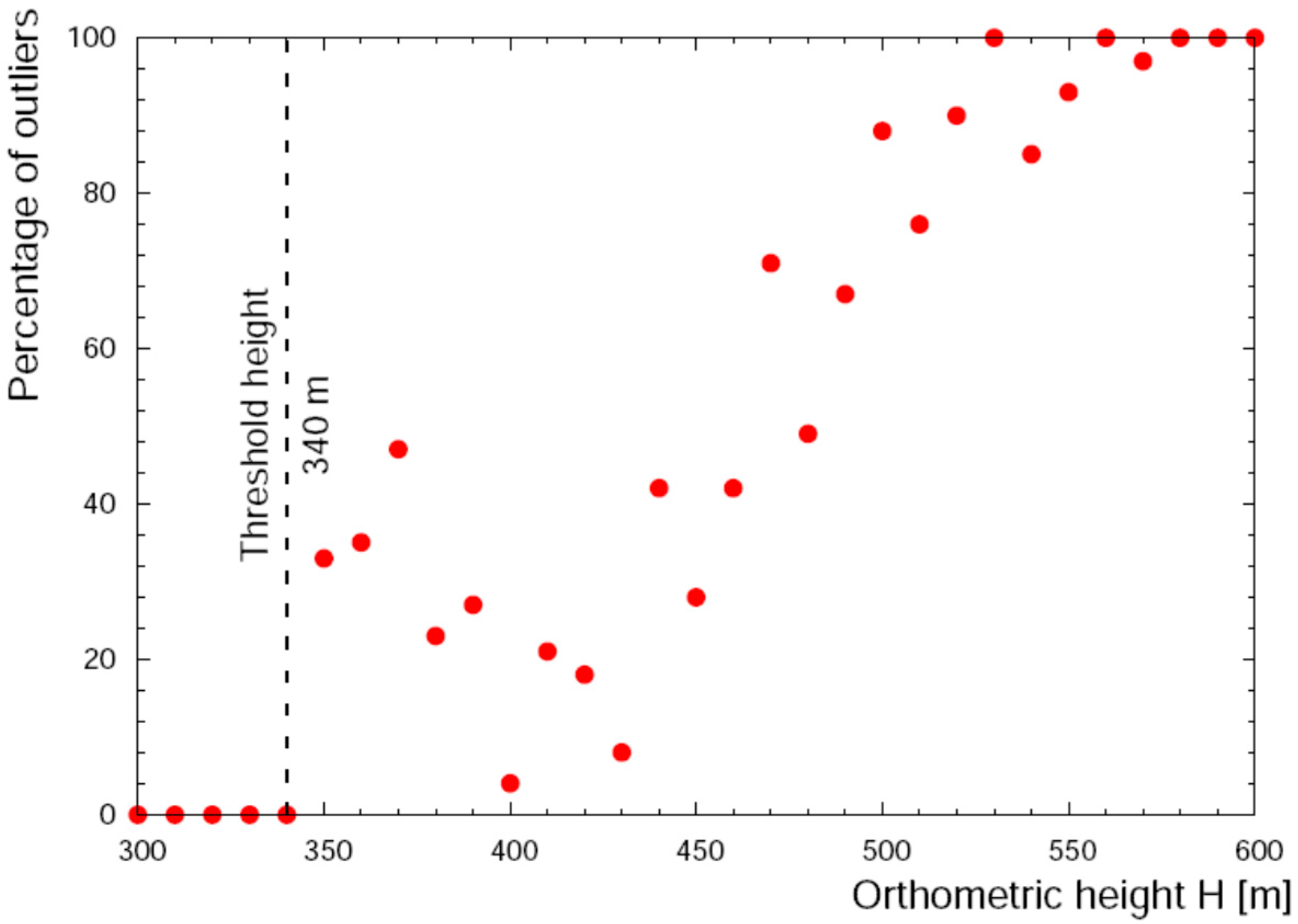
| Datasets | Frequency | α H < 340 m | β H > 340 m |
|---|---|---|---|
| DATASET 1 | 1.0 Hz (stand-alone) | 4803 | 6892 |
| DATASET 2 | 0.2 Hz (double-difference) | 960 | 1378 |
| DATASET 1α | ||||||||||||||
| GPSA [m] | GPSB [m] | GPSC [m] | GPSIMU [m] | ALT [m] | PTIMU [m] | PT [m] | ||||||||
| RMS | RMS | RMS | RMS | RMS | RMS | RMS | ||||||||
| F11 | −0.1 | 1.8 | 0.7 | 2.7 | 0.4 | 1.9 | 0.0 | 1.7 | 0.0 | 1.5 | −0.8 | 1.7 | −0.2 | 1.4 |
| F12 | −0.2 | 1.8 | −0.1 | 2.1 | 0.2 | 2.3 | 0.8 | 1.4 | −0.7 | 2.9 | 0.0 | 1.9 | 0.1 | 2.0 |
| F15 | 1.9 | 2.3 | 0.5 | 2.1 | 1.7 | 2.5 | 5.8 | 5.9 | −3.2 | 3.3 | −4.1 | 4.3 | −2.7 | 3.0 |
| DATASET 1β | ||||||||||||||
| GPSA [m] | GPSB [m] | GPSC [m] | GPSIMU[m] | ALT [m] | PTIMU [m] | PT [m] | ||||||||
| RMS | RMS | RMS | RMS | RMS | RMS | RMS | ||||||||
| F11 | 0.4 | 2.5 | 0.6 | 2.1 | 1.3 | 2.1 | −1.4 | 2.3 | / | / | −0.8 | 2.0 | −0.1 | 1.6 |
| F14 | 0.7 | 1.7 | 1.0 | 2.0 | 1.5 | 2.2 | −3.1 | 3.4 | / | / | −0.2 | 1.5 | −0.1 | 1.7 |
| DATASET 2α | ||||||||||||||
| GPSA [m] | GPSB [m] | GPSC [m] | GPSIMU[m] | ALT[m] | PTIMU [m] | PT [m] | ||||||||
| RMS | RMS | RMS | RMS | RMS | RMS | RMS | ||||||||
| F11 | −0.5 | 1.9 | 0.6 | 1.8 | −0.2 | 1.9 | 0.2 | 1.9 | 0.2 | 1.3 | −0.5 | 1.8 | 0.1 | 1.4 |
| F12 | −0.2 | 1.7 | 0.0 | 1.4 | 0.2 | 1.6 | 1.1 | 1.5 | −0.5 | 2.5 | 0.2 | 1.6 | −0.8 | 1.8 |
| F15 | 2.1 | 2.4 | 0.0 | 1.7 | 0.4 | 1.1 | 6.8 | 6.9 | −2.4 | 2.5 | −3.8 | 4.1 | −3.1 | 3.6 |
| DATASET 2β | ||||||||||||||
| GPSA [m] | GPSB [m] | GPSC [m] | GPSIMU[m] | ALT [m] | PTIMU [m] | PT [m] | ||||||||
| RMS | RMS | RMS | RMS | RMS | RMS | RMS | ||||||||
| F11 | 0.1 | 2.3 | 0.6 | 1.3 | 0.9 | 1.7 | −0.1 | 1.3 | / | / | −1.4 | 2.4 | −0.1 | 1.6 |
| F14 | 0.6 | 1.3 | 0.4 | 1.3 | 0.6 | 1.3 | −1.6 | 2.0 | / | / | −0.1 | 1.3 | 0.1 | 1.7 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albéri, M.; Baldoncini, M.; Bottardi, C.; Chiarelli, E.; Fiorentini, G.; Raptis, K.G.C.; Realini, E.; Reguzzoni, M.; Rossi, L.; Sampietro, D.; et al. Accuracy of Flight Altitude Measured with Low-Cost GNSS, Radar and Barometer Sensors: Implications for Airborne Radiometric Surveys. Sensors 2017, 17, 1889. https://doi.org/10.3390/s17081889
Albéri M, Baldoncini M, Bottardi C, Chiarelli E, Fiorentini G, Raptis KGC, Realini E, Reguzzoni M, Rossi L, Sampietro D, et al. Accuracy of Flight Altitude Measured with Low-Cost GNSS, Radar and Barometer Sensors: Implications for Airborne Radiometric Surveys. Sensors. 2017; 17(8):1889. https://doi.org/10.3390/s17081889
Chicago/Turabian StyleAlbéri, Matteo, Marica Baldoncini, Carlo Bottardi, Enrico Chiarelli, Giovanni Fiorentini, Kassandra Giulia Cristina Raptis, Eugenio Realini, Mirko Reguzzoni, Lorenzo Rossi, Daniele Sampietro, and et al. 2017. "Accuracy of Flight Altitude Measured with Low-Cost GNSS, Radar and Barometer Sensors: Implications for Airborne Radiometric Surveys" Sensors 17, no. 8: 1889. https://doi.org/10.3390/s17081889
APA StyleAlbéri, M., Baldoncini, M., Bottardi, C., Chiarelli, E., Fiorentini, G., Raptis, K. G. C., Realini, E., Reguzzoni, M., Rossi, L., Sampietro, D., Strati, V., & Mantovani, F. (2017). Accuracy of Flight Altitude Measured with Low-Cost GNSS, Radar and Barometer Sensors: Implications for Airborne Radiometric Surveys. Sensors, 17(8), 1889. https://doi.org/10.3390/s17081889











