On-Chip High-Finesse Fabry-Perot Microcavities for Optical Sensing and Quantum Information
Abstract
:1. Introduction
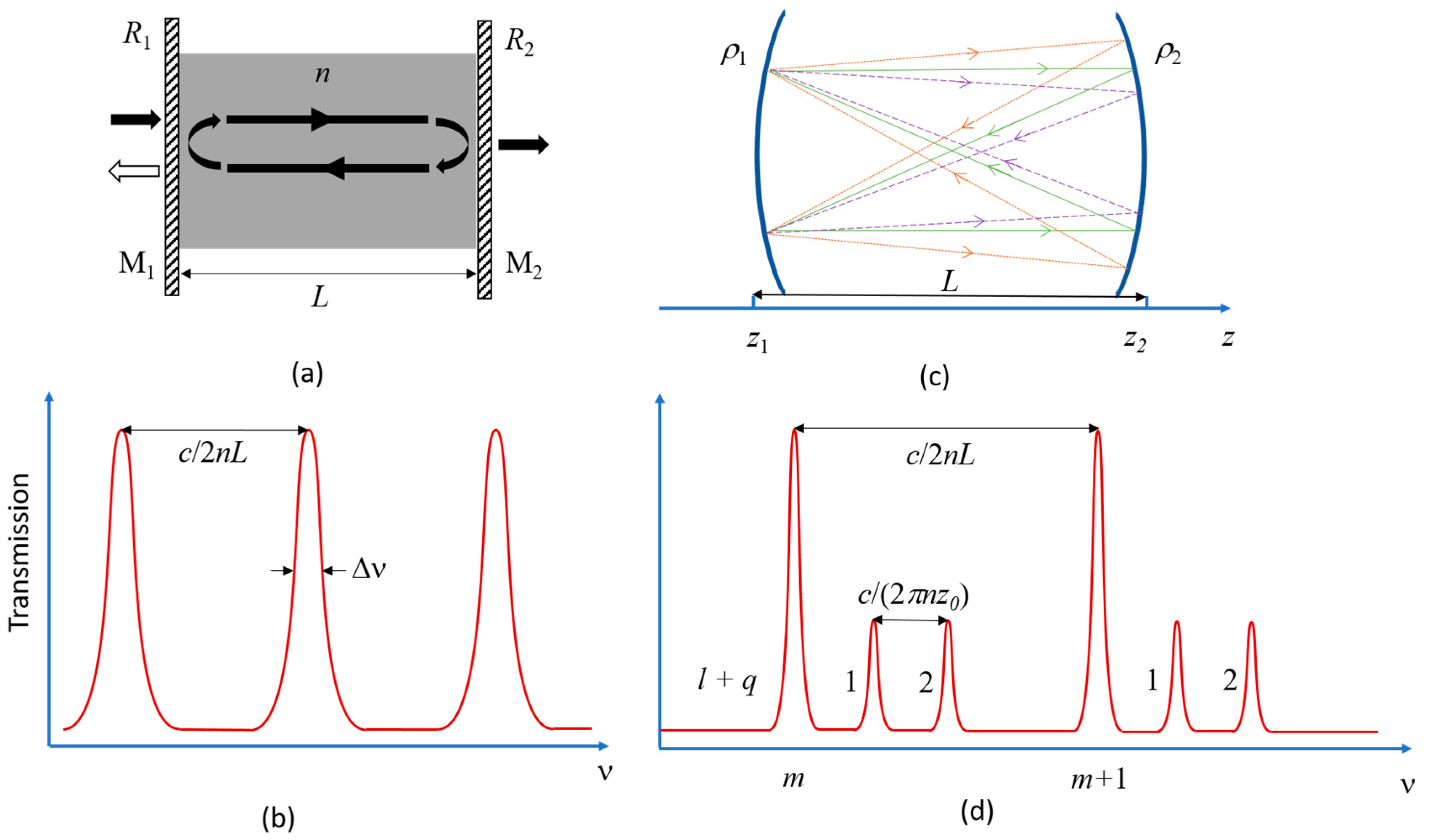
2. Background
3. FPCs for Sensing Applications
3.1. Refractometric Sensors—Background
3.2. Chip-Based FPCs for Refractometric Sensing
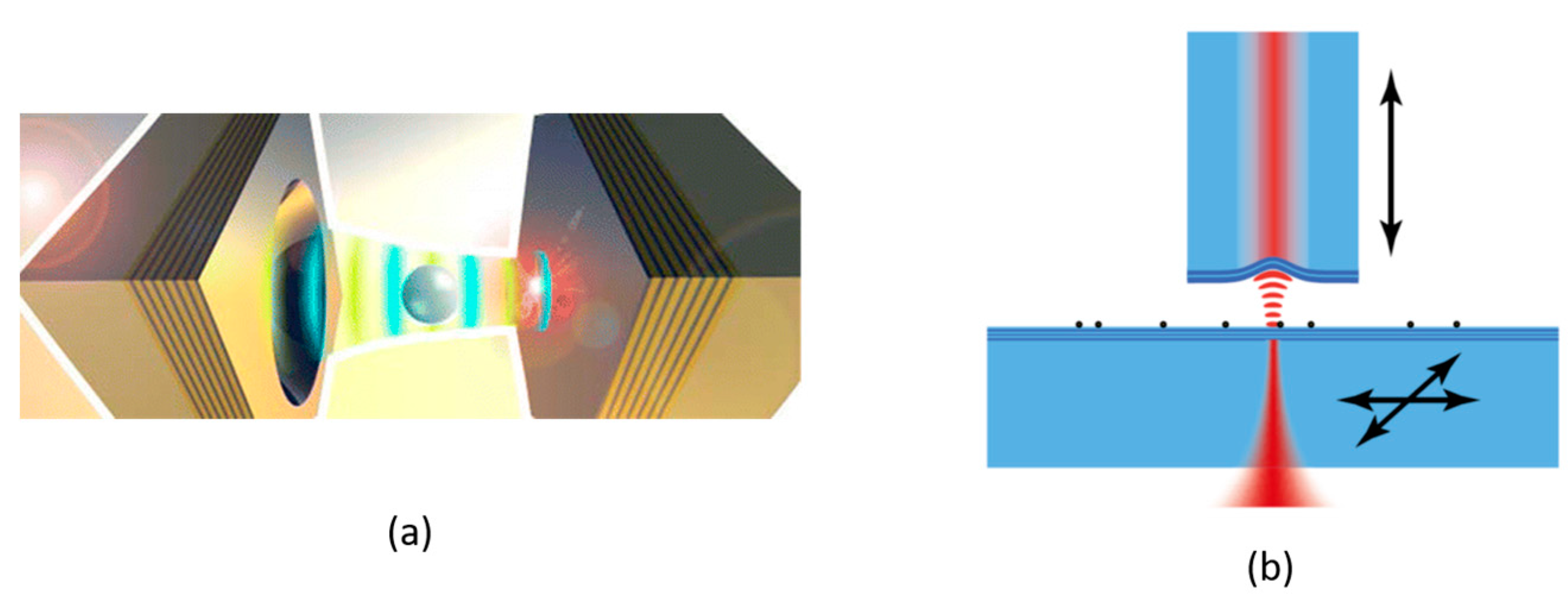
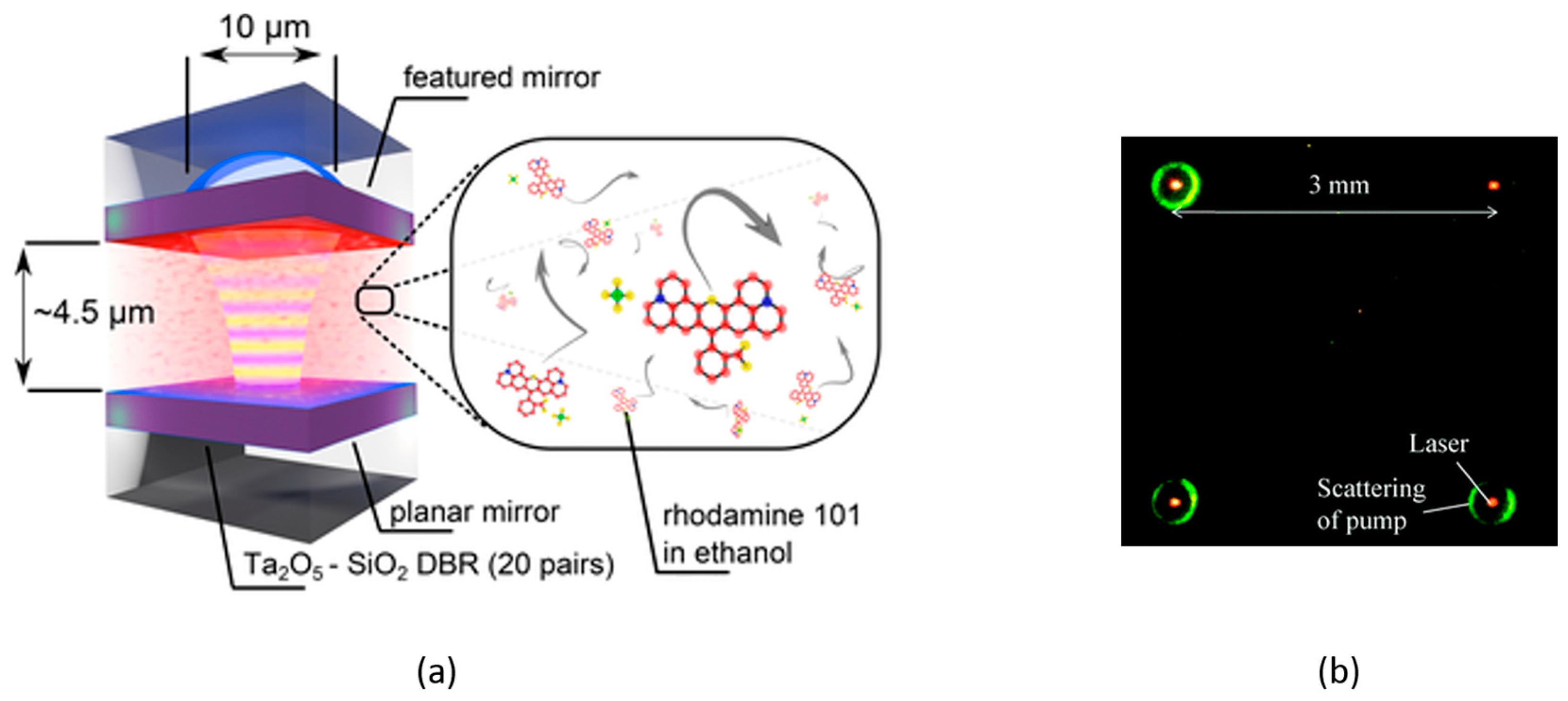
3.3. Open-Access FPC Lasers
4. FPCs for Cavity Quantum Electrodynamics Applications
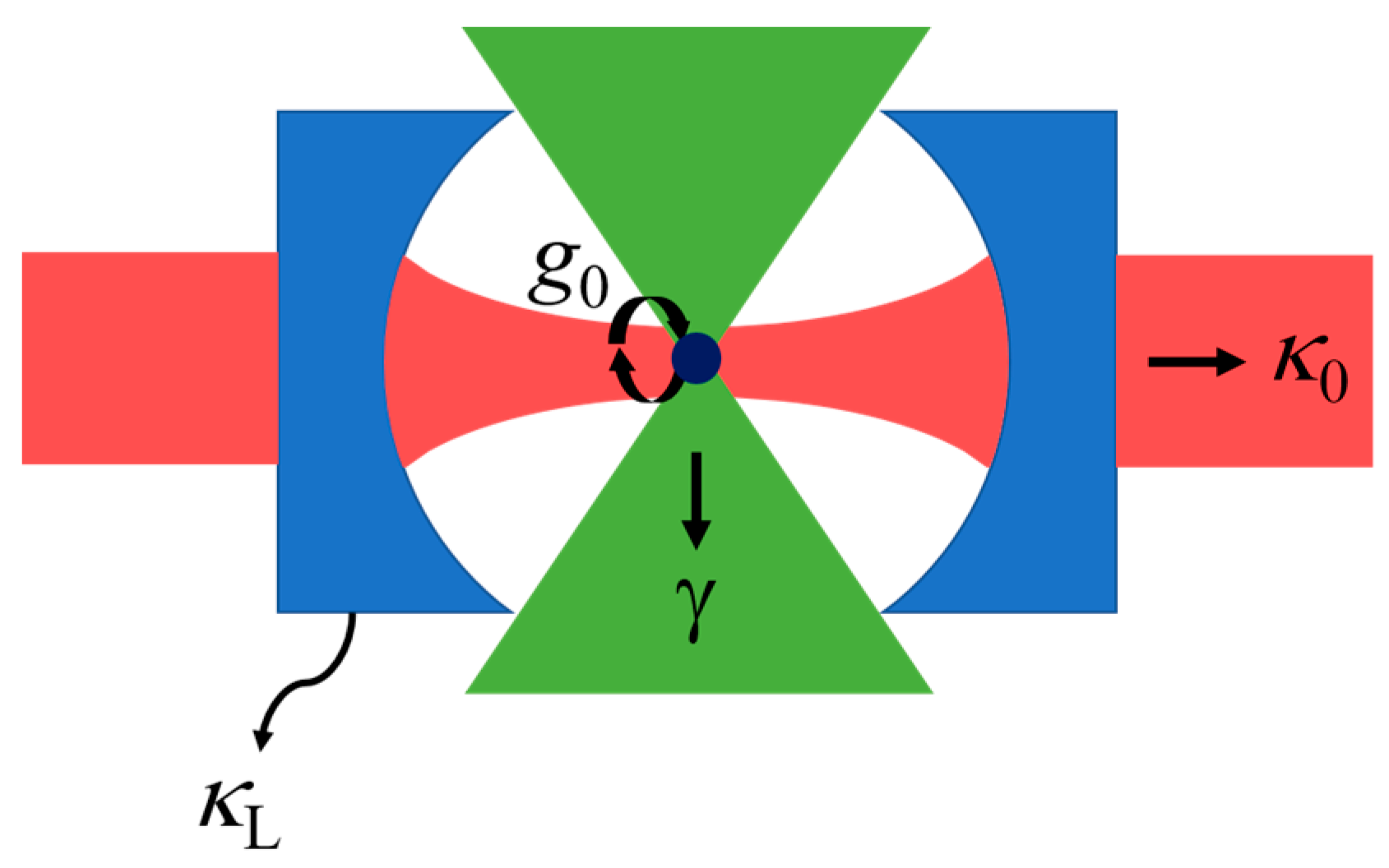
4.1. CQED—Overview
- (i)
- the ability to isolate quantum particles (e.g., atoms) from the external environment—i.e., to preserve quantum coherence on time-scales that are technologically useful, and;
- (ii)
- the ability to address, control, and store quantum states, and to build scalable systems with large numbers of quantum particles (‘qubits’).
4.2. Chip-Based FPCs for CQED
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Fowles, G.R. Introduction to Modern Optics; Dover Publications: Mineola, NY, USA, 1989. [Google Scholar]
- Atherton, P.D.; Reay, N.K.; Ring, J.; Hicks, T.R. Tunable Fabry-Perot Filters. Opt. Eng. 1981, 20, 206805. [Google Scholar] [CrossRef]
- Vahala, K.J. Optical microcavities. Nature 2003, 424, 839–846. [Google Scholar] [CrossRef] [PubMed]
- Schuler, L.P.; Milne, J.S.; Dell, J.M.; Faraone, L. MEMS-based microspectrometer technologies for NIR and MIR wavelengths. J. Phys. D. Appl. Phys. 2009, 42, 133001. [Google Scholar] [CrossRef]
- Yariv, A.; Yeh, P. Photonics: Optical Electronics in Modern Communications; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Hood, C.; Kimble, H.; Ye, J. Characterization of high-finesse mirrors: Loss, phase shifts, and mode structure in an optical cavity. Phys. Rev. A 2001, 64, 33804. [Google Scholar] [CrossRef]
- Tayebati, P.; Wang, P.; Azimi, M.; Maflah, L.; Vakhshoori, D. Microelectromechanical tunable filter with stable half symmetric cavity. Electron. Lett. 1998, 34, 1967. [Google Scholar] [CrossRef]
- Crocombe, R.A. MEMS technology moves process spectroscopy into a new dimension. Spectrosc. Eur. 2004, 16, 16–19. [Google Scholar]
- Ebermann, M.; Neumann, N.; Hiller, K.; Gittler, E.; Meinig, M.; Kurth, S. Recent advances in expanding the spectral range of MEMS Fabry-Perot filters. Proc. SPIE 2010, 75940V. [Google Scholar] [CrossRef]
- Dolan, P.R.; Hughes, G.M.; Grazioso, F.; Patton, B.R.; Smith, J.M. Femtoliter tunable optical cavity arrays. Opt. Lett. 2010, 35, 3556–3558. [Google Scholar] [CrossRef] [PubMed]
- Hunger, D.; Steinmetz, T.; Colombe, Y.; Deutsch, C.; Hänsch, T.W.; Reichel, J. A fiber Fabry–Perot cavity with high finesse. New J. Phys. 2010, 12, 65038. [Google Scholar] [CrossRef]
- Muller, A.; Flagg, E.B.; Lawall, J.R.; Solomon, G.S. Ultrahigh-finesse, low-mode-volume Fabry-Perot microcavity. Opt. Lett. 2010, 35, 2293–2295. [Google Scholar] [CrossRef] [PubMed]
- Greuter, L.; Starosielec, S.; Najer, D.; Ludwig, A.; Duempelmann, L.; Rohner, D.; Warburton, R.J. A small mode volume tunable microcavity: Development and characterization. Appl. Phys. Lett. 2014, 105, 121105. [Google Scholar] [CrossRef]
- Bitarafan, M.H.; Ramp, H.; Allen, T.W.; Potts, C.; Rojas, X.; MacDonald, A.J.R.; Davis, J.P.; DeCorby, R.G. Thermomechanical characterization of on-chip buckled dome Fabry–Perot microcavities. J. Opt. Soc. Am. B 2015, 32, 1214. [Google Scholar] [CrossRef]
- Potts, C.A.; Melnyk, A.; Ramp, H.; Bitarafan, M.H.; Vick, D.; LeBlanc, L.J.; Davis, J.P.; DeCorby, R.G. Tunable open-access microcavities for on-chip cavity quantum electrodynamics. Appl. Phys. Lett. 2016, 108, 41103. [Google Scholar] [CrossRef]
- Babic, D.I.; Corzine, S.W. Analytic expressions for the reflection delay, penetration depth, and absorptance of quarter-wave dielectric mirrors. IEEE J. Quantum Electron. 1992, 28, 514–524. [Google Scholar] [CrossRef]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics; Wiley-Interscience: New York, NY, USA, 2007. [Google Scholar]
- Syms, R.R.A. Principles of free-space optical microelectromechanical systems. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2008, 222, 1–18. [Google Scholar] [CrossRef]
- Siegman, A.E. Lasers; University Science Books: California, CA, USA, 1986. [Google Scholar]
- Allen, T.W.; Silverstone, J.; Ponnampalam, N.; Olsen, T.; Meldrum, A.; DeCorby, R.G. High-finesse cavities fabricated by buckling self-assembly of a-Si/SiO2 multilayers. Opt. Express 2011, 19, 18903–18909. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Zhou, C.; Zhang, T.; Chen, J.; Liu, S.; Fan, X. Optofluidic laser array based on stable high-Q Fabry–Pérot microcavities. Lab Chip 2015, 15, 3862–3869. [Google Scholar] [CrossRef] [PubMed]
- Fox, M. Quantum Optics: An Introduction; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Zijlstra, P.; Paulo, P.M.R.; Orrit, M. Optical detection of single non-absorbing molecules using the surface plasmon resonance of a gold nanorod. Nat. Nanotechnol. 2012, 7, 379–382. [Google Scholar] [CrossRef] [PubMed]
- Anker, J.N.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; Van Duyne, R.P. Biosensing with plasmonic nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Fan, X. Optical ring resonators for biochemical and chemical sensing. Anal. Bioanal. Chem. 2011, 399, 205–211. [Google Scholar] [CrossRef] [PubMed]
- White, I.M.; Zhu, H.; Suter, J.D.; Hanumegowda, N.M.; Oveys, H.; Zourob, M.; Fan, X. Refractometric sensors for lab-on-a-chip based on optical ring resonators. IEEE Sens. J. 2007, 7, 28–34. [Google Scholar] [CrossRef]
- Domachuk, P.; Littler, I.C.M.; Cronin-Golomb, M.; Eggleton, B.J. Compact resonant integrated microfluidic refractometer. Appl. Phys. Lett. 2006, 88, 1–4. [Google Scholar] [CrossRef]
- Dorfner, D.; Zabel, T.; Hürlimann, T.; Hauke, N.; Frandsen, L.; Rant, U.; Abstreiter, G.; Finley, J. Photonic crystal nanostructures for optical biosensing applications. Biosens. Bioelectron. 2009, 24, 3688–3692. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Salemink, H.W.M. Photonic crystal-based all-optical on-chip sensor. Opt. Express 2012, 20, 19912. [Google Scholar] [CrossRef] [PubMed]
- White, I.M.; Fan, X. On the performance quantification of resonant refractive index sensors. Opt. Express 2008, 16, 1020. [Google Scholar] [CrossRef] [PubMed]
- Song, W.Z.; Zhang, X.M.; Liu, A.Q.; Lim, C.S.; Yap, P.H.; Hosseini, H.M.M. Refractive index measurement of single living cells using on-chip Fabry-Pérot cavity. Appl. Phys. Lett. 2006, 89, 203901. [Google Scholar] [CrossRef]
- Campopiano, S.; Bernini, R.; Zeni, L.; Sarro, P.M. Microfluidic sensor based on integrated optical hollow waveguides. Opt. Lett. 2004, 29, 1894–1896. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.; Ali, M.; Lai, M.-H.; Lim, K.-S.; Ahmad, H. Chronology of Fabry-Perot Interferometer Fiber-Optic Sensors and Their Applications: A Review. Sensors 2014, 14, 7451–7488. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Li, H.; Reddy, K.; Shelar, H.S.; Nittoor, V.R.; Fan, X. Optofluidic Fabry–Pérot cavity biosensor with integrated flow-through micro-/nanochannels. Appl. Phys. Lett. 2011, 98, 41104. [Google Scholar] [CrossRef]
- Ran, Z.L.; Rao, Y.J.; Deng, H.Y.; Liao, X. Miniature in-line photonic crystal fiber etalon fabricated by 157 nm laser micromachining. Opt. Lett. 2007, 32, 3071. [Google Scholar] [CrossRef] [PubMed]
- Wei, T.; Han, Y.; Li, Y.; Tsai, H.-L.; Xiao, H. Temperature-insensitive miniaturized fiber inline Fabry-Perot interferometer for highly sensitive refractive index measurement. Opt. Express 2008, 16, 5764. [Google Scholar] [CrossRef] [PubMed]
- Trichet, A.A.P.; Foster, J.; Omori, N.E.; James, D.; Dolan, P.R.; Hughes, G.M.; Vallance, C.; Smith, J.M. Open-access optical microcavities for lab-on-a-chip refractive index sensing. Lab Chip 2014, 14, 4244–4249. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Sun, X.; Agarwal, A.; Kimerling, L.C. Design guidelines for optical resonator biochemical sensors. JOSA B 2009, 26, 1032–1041. [Google Scholar] [CrossRef]
- Cheema, M.I.; Shi, C.; Armani, A.M.; Kirk, A.G. Optimizing the Signal to Noise Ratio of Microcavity Sensors. IEEE Photonics Technol. Lett. 2014, 26, 2023–2026. [Google Scholar] [CrossRef]
- Yoshie, T.; Tang, L.; Su, S.-Y. Optical Microcavity: Sensing down to Single Molecules and Atoms. Sensors 2011, 11, 1972–1991. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Zhang, L.; Pang, W. Performance and noise analysis of optical microresonator-based biochemical sensors using intensity detection. Opt. Express 2016, 24, 18197. [Google Scholar] [CrossRef] [PubMed]
- Chin, L.K.; Liu, A.Q.; Lim, C.S.; Zhang, X.M.; Ng, J.H.; Hao, J.Z.; Takahashi, S. Differential single living cell refractometry using grating resonant cavity with optical trap. Cit. Appl. Phys. Lett. 2007, 91, 243901. [Google Scholar] [CrossRef]
- Chin, L.K.; Liu, A.Q.; Lim, C.S.; Lin, C.L.; Ayi, T.C.; Yap, P.H. An optofluidic volume refractometer using Fabry-Perot resonator with tunable liquid microlenses. Biomicrofluidics 2010, 4, 24107. [Google Scholar] [CrossRef] [PubMed]
- St-Gelais, R.; Masson, J.; Peter, Y.A. All-silicon integrated Fabry–Pérot cavity for volume refractive index measurement in microfluidic systems. Appl. Phys. Lett. 2009, 94, 243905. [Google Scholar] [CrossRef]
- Shao, H.; Kumar, D.; Lear, K.L. Single-cell detection using optofluidic intracavity spectroscopy. IEEE Sens. J. 2006, 6, 1543–1550. [Google Scholar] [CrossRef]
- Liu, P.; Huang, H.; Cao, T.; Tang, Z.; Liu, X.; Qi, Z.; Ren, M.; Wu, H. An optofluidics biosensor consisted of high-finesse Fabry-Perot resonator and micro-fluidic channel. Appl. Phys. Lett. 2012, 100, 1–5. [Google Scholar] [CrossRef]
- Liu, P.; Huang, H.; Cao, T.; Liu, X.; Qi, Z.; Tang, Z.; Zhang, J. An ultra-low detection-limit optofluidic biosensor with integrated dual-channel Fabry-P erot cavity. Appl. Phys. Lett. 2013, 163701, 2011–2015. [Google Scholar]
- Wu, H.; Huang, H.; Bai, M.; Liu, P.; Chao, M.; Hu, J.; Hao, J.; Cao, T. An ultra-low detection-limit optofluidic biosensor based on all glass Fabry-Perot cavity. Opt. Express 2014, 22, 31977. [Google Scholar] [CrossRef] [PubMed]
- Vallance, C.; Trichet, A.A.P.; James, D.; Dolan, P.R.; Smith, J.M. Open-access microcavities for chemical sensing. Nanotechnology 2016, 27, 274003. [Google Scholar] [CrossRef] [PubMed]
- Trichet, A.A.P.; Dolan, P.R.; James, D.; Hughes, G.M.; Vallance, C.; Smith, J.M. Nanoparticle Trapping and Characterization Using Open Microcavities. Nano Lett. 2016, 16, 6172–6177. [Google Scholar] [CrossRef] [PubMed]
- Mader, M.; Reichel, J.; Hänsch, T.W.; Hunger, D. A scanning cavity microscope. Nat. Commun. 2015, 6, 7249. [Google Scholar] [CrossRef] [PubMed]
- Kelkar, H.; Wang, D.; Martín-Cano, D.; Hoffmann, B.; Christiansen, S.; Götzinger, S.; Sandoghdar, V. Sensing nanoparticles with a cantilever-based scannable optical cavity of low finesse and sub- λ3 volume. Phys. Rev. Appl. 2015, 4, 1–11. [Google Scholar] [CrossRef]
- Liang, X.J.; Liu, A.Q.; Lim, C.S.; Ayi, T.C.; Yap, P.H. Determining refractive index of single living cell using an integrated microchip. Sensors Actuators A Phys. 2007, 133, 349–354. [Google Scholar] [CrossRef]
- Helbo, B.; Kristensen, A.; Menon, A. A micro-cavity fluidic dye laser. J. Micromechanics Microengineering 2003, 13, 307–311. [Google Scholar] [CrossRef]
- Hill, M.T.; Gather, M.C. Advances in small lasers. Nat. Photonics 2014, 8, 908–918. [Google Scholar] [CrossRef]
- Kuehne, A.J.C.; Gather, M.C. Organic Lasers: Recent Developments on Materials, Device Geometries, and Fabrication Techniques. Chem. Rev. 2016, 116, 12823–12864. [Google Scholar] [CrossRef] [PubMed]
- Patel, R.K.; Trichet, A.A.P.; Coles, D.M.; Dolan, P.R.; Fairclough, S.M.; Leontiadou, M.A.; Tsang, S.C.E.; Binks, D.J.; Jang, E.; Jang, H.; et al. Gain Spectroscopy of Solution-Based Semiconductor Nanocrystals in Tunable Optical Microcavities. Adv. Opt. Mater. 2016, 4, 285–290. [Google Scholar] [CrossRef]
- Coles, D.M.; Trichet, A.A.P.; Dolan, P.R.; Taylor, R.A.; Vallance, C.; Smith, J.M. Diffusion-driven continuous-wave-pumped organic dye lasers. Laser Photon. Rev. 2015, 9, 538–544. [Google Scholar] [CrossRef]
- Zhang, T.; Zhou, C.; Wang, W.; Chen, J. Generation of low-threshold optofluidic lasers in a stable Fabry-Pérot microcavity. Opt. Laser Technol. 2017, 91, 108–111. [Google Scholar] [CrossRef]
- Ladd, T.D.; Jelezko, F.; Laflamme, R.; Nakamura, Y.; Monroe, C.; O’Brien, J.L. Quantum computers. Nature 2010, 464, 45–53. [Google Scholar] [CrossRef] [PubMed]
- Gisin, N.; Thew, R. Quantum communication. Nat. Photonics 2007, 1, 165–171. [Google Scholar] [CrossRef]
- Thomas-Peter, N.; Smith, B.J.; Datta, A.; Zhang, L.; Dorner, U.; Walmsley, I.A. Real-World Quantum Sensors: Evaluating Resources for Precision Measurement. Phys. Rev. Lett. 2011, 107, 113603. [Google Scholar] [CrossRef] [PubMed]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in Quantum Metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
- Aharonovich, I.; Greentree, A.D.; Prawer, S. Diamond photonics. Nat. Photonics 2011, 5, 397–405. [Google Scholar] [CrossRef]
- Reiserer, A.; Rempe, G. Cavity-based quantum networks with single atoms and optical photons. Rev. Mod. Phys. 2015, 87, 1379–1418. [Google Scholar] [CrossRef]
- Mabuchi, H.; Doherty, A.C. Cavity Quantum Electrodynamics: Coherence in Context. Science 2002, 298, 1372–1377. [Google Scholar] [CrossRef] [PubMed]
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef] [PubMed]
- Ritter, S.; Nölleke, C.; Hahn, C.; Reiserer, A.; Neuzner, A.; Uphoff, M.; Mücke, M.; Figueroa, E.; Bochmann, J.; Rempe, G. An elementary quantum network of single atoms in optical cavities. Nature 2012, 484, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Liang, F.; Quan, Q. Detecting Single Gold Nanoparticles (1.8 nm) with Ultrahigh-Q Air-Mode Photonic Crystal Nanobeam Cavities. ACS Photonics 2015, 2, 1692–1697. [Google Scholar] [CrossRef]
- Miura, R.; Imamura, S.; Ohta, R.; Ishii, A.; Liu, X.; Shimada, T.; Iwamoto, S.; Arakawa, Y.; Kato, Y.K. Ultralow mode-volume photonic crystal nanobeam cavities for high-efficiency coupling to individual carbon nanotube emitters. Nat. Commun. 2014, 5, 5580. [Google Scholar] [CrossRef] [PubMed]
- Goban, A.; Hung, C.-L.; Yu, S.-P.; Hood, J.D.; Muniz, J.A.; Lee, J.H.; Martin, M.J.; McClung, A.C.; Choi, K.S.; Chang, D.E.; et al. Atom-light interactions in photonic crystals. Nat. Commun. 2014, 5, 3808. [Google Scholar] [CrossRef] [PubMed]
- Kaupp, H.; Hümmer, T.; Mader, M.; Schlederer, B.; Benedikter, J.; Haeusser, P.; Chang, H.C.; Fedder, H.; Hänsch, T.W.; Hunger, D. Purcell-Enhanced Single-Photon Emission from Nitrogen-Vacancy Centers Coupled to a Tunable Microcavity. Phys. Rev. Appl. 2016, 6, 1–10. [Google Scholar] [CrossRef]
- Steinmetz, T.; Colombe, Y.; Hunger, D.; Hänsch, T.W.; Balocchi, A.; Warburton, R.J.; Reichel, J. Stable fiber-based Fabry-Pérot cavity. Appl. Phys. Lett. 2006, 89, 111110. [Google Scholar] [CrossRef]
- Prakash, G.V.; Besombes, L.; Kelf, T.; Baumberg, J.J.; Bartlett, P.N.; Abdelsalam, M.E. Tunable resonant optical microcavities by self-assembled templating. Opt. Lett. 2004, 29, 1500. [Google Scholar] [CrossRef]
- Cui, G.; Hannigan, J.M.; Loeckenhoff, R.; Matinaga, F.M.; Raymer, M.G.; Bhongale, S.; Holland, M.; Mosor, S.; Chatterjee, S.; Gibbs, H.M.; et al. A hemispherical, high-solid-angle optical micro-cavity for cavity-QED studies. Opt. Express 2006, 14, 2289–2299. [Google Scholar] [CrossRef] [PubMed]
- Colombe, Y.; Steinmetz, T.; Dubois, G.; Linke, F.; Hunger, D.; Reichel, J. Strong atom–field coupling for Bose–Einstein condensates in an optical cavity on a chip. Nature 2007, 450, 272–276. [Google Scholar] [CrossRef] [PubMed]
- Biedermann, G.W.; Benito, F.M.; Fortier, K.M.; Stick, D.L.; Loyd, T.K.; Schwindt, P.D.D.; Nakakura, C.Y.; Jarecki, R.L.; Blain, M.G. Ultrasmooth microfabricated mirrors for quantum information. Appl. Phys. Lett. 2010, 97, 181110. [Google Scholar] [CrossRef]
- Derntl, C.; Schneider, M.; Schalko, J.; Bittner, A.; Schmiedmayer, J.; Schmid, U.; Trupke, M. Arrays of open, independently tunable microcavities. Opt. Express 2013, 15, 1023–1030. [Google Scholar] [CrossRef] [PubMed]
- Bitarafan, M.H.; DeCorby, R.G. Small-mode-volume, channel-connected Fabry-Perot microcavities on a chip. 2017; submitted. [Google Scholar]
- Trupke, M.; Hinds, E.A.; Eriksson, S.; Curtis, E.A.; Moktadir, Z.; Kukharenka, E.; Kraft, M. Microfabricated high-finesse optical cavity with open access and small volume. Appl. Phys. Lett. 2005, 87, 211106. [Google Scholar] [CrossRef]
- Trupke, M.; Goldwin, J.; Darquié, B.; Dutier, G.; Eriksson, S.; Ashmore, J.; Hinds, E.A. Atom Detection and Photon Production in a Scalable, Open, Optical Microcavity. Phys. Rev. Lett. 2007, 99, 63601. [Google Scholar] [CrossRef] [PubMed]
- Johnson, S.; Dolan, P.R.; Smith, J.M. Diamond Photonics for Distributed Quantum Networks. Prog. Quantum Electron. 2017. [Google Scholar] [CrossRef]
- Benedikter, J.; Hümmer, T.; Mader, M.; Schlederer, B.; Reichel, J.; Hänsch, T.W.; Hunger, D. Transverse-mode coupling and diffraction loss in tunable Fabry–Pérot microcavities. New J. Phys. 2015, 17, 53051. [Google Scholar] [CrossRef]
- Uphoff, M.; Brekenfeld, M.; Rempe, G.; Ritter, S. Frequency splitting of polarization eigenmodes in microscopic Fabry-Perot cavities. New J. Phys. 2015, 17, 1–9. [Google Scholar] [CrossRef]
- Najer, D.; Renggli, M.; Riedel, D.; Starosielec, S.; Warburton, R.J. Fabrication of mirror templates in silica with micron-sized radii of curvature. Appl. Phys. Lett. 2017, 110, 11101. [Google Scholar] [CrossRef]
- Purdy, T.P.; Stamper-Kurn, D.M. Integrating cavity quantum electrodynamics and ultracold-atom chips with on-chip dielectric mirrors and temperature stabilization. Appl. Phys. B 2008, 90, 401–405. [Google Scholar] [CrossRef]
- Epp, E.; Ponnampalam, N.; Newman, W.; Drobot, B.; McMullin, J.N.; Meldrum, A.F.; DeCorby, R.G. Hollow Bragg waveguides fabricated by controlled buckling of Si/SiO2 multilayers. Opt. Express 2010, 18, 24917–24925. [Google Scholar] [CrossRef] [PubMed]

| Ref. | Mirror Type | Mirror Material | Wavelength (nm) | Q | F | S (nm/RIU) | DL (RIU) | VM (λ3) |
|---|---|---|---|---|---|---|---|---|
| [32] | Planar | Au | 1550 | 330 | 5.2 | - | 1.4 × 10−3 * | - |
| [28] | Planar | FBG | 1550 | - | - | 6.825 | 2.7 × 10−3 * | - |
| [43] | Planar | FBG | 1258 | - | - | 32 * | 0.001 | - |
| [44] | Planar | Au | 1275 | 600 * | 18.79 | 960 | 0.01 | - |
| [45] | Planar | Si/Air | 1550 | 400 | 9 * | 907 | 1.7 × 10−5 | - |
| [46] | Planar | Au | 890 | 900 * | 30 | - | - | - |
| [47] | Planar | Ta2O5/SiO2 | 1550 | 861 | - | 1100 | 1.1 × 10−5 | - |
| [48] | Planar | Ta2O5/SiO2 | 1550 | 600 * | 14 * | - | 5.5 × 10−8 | - |
| [49] | Planar | Ta2O5/SiO2 | 1550 | 875 | 3 | 650 * | 2.0 × 10−9 | - |
| [38] | Curved | TiO2/SiO2 | 640 | - | 1000 | - | 3.5 × 10−4 | - |
| [50] | Curved | TiO2/SiO2 | 640 | 105 | 4000 | - | 3.5 × 10−4 | 3.8 |
| [51] | Curved | TiO2/SiO2 | 640 | 18000 | 4500 * | - | - | 1.7 |
| [52] | Curved | Ta2O5/SiO2 | 780 | 1.57 × 106 | 57,000 | - | - | 100 * |
| [53] | Curved | TiO2/SiO2 | 745/785 | 300 | 70 | - | - | 0.8 |
| Ref. | Fabrication Method | Mirror Material | Wavelength (nm) | Q | F | VM (λ3) | C |
|---|---|---|---|---|---|---|---|
| [74] | Deposition on microlens | TiO2/SiO2 | 780 | - | 1000 | 1260 | 2.1 |
| [75] | Self-assembled templating | Au | 747 * | 300 | 15 | 2.1 | - |
| [76] | Bubble trapping | TiO2/SiO2 | 750 | - | 200 | 74 * | - |
| [77] | Laser ablation | Ta2O5/SiO2 | 780 | - | 37,000 | - | 145 |
| [78] | Dry etching | Ta2O5/SiO2 | 780 | - | 64,000 | - | 200 |
| [81] | Wet etching | Au | 780 | 106 | 6000 | - | 39 |
| [11] | FIB milling | ZrO2/SiO2 | 637 | 104 | 460 | 8.5 | 10 * |
| [13] | Laser ablation | Ta2O5/SiO2 | 920 | 3.3 × 106 | 1.5 × 105 | 51 | - |
| [86] | Laser ablation | Ta2O5/SiO2 | 637 | 105 | 2.5 × 104 | - | - |
| [87] | Dry etching | Ta2O5/SiO2 | 780 | 1.4 × 107 * | 2 × 105 | - | 50 |
| [16] | Buckling delamination | Ta2O5/SiO2 | 780 | - | 3500 | 35 | 32 |
| [80] | Buckling delamination | Si/SiO2 | 1550 | 1800 | 1800 | 1.3 | 50 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bitarafan, M.H.; DeCorby, R.G. On-Chip High-Finesse Fabry-Perot Microcavities for Optical Sensing and Quantum Information. Sensors 2017, 17, 1748. https://doi.org/10.3390/s17081748
Bitarafan MH, DeCorby RG. On-Chip High-Finesse Fabry-Perot Microcavities for Optical Sensing and Quantum Information. Sensors. 2017; 17(8):1748. https://doi.org/10.3390/s17081748
Chicago/Turabian StyleBitarafan, Mohammad H., and Ray G. DeCorby. 2017. "On-Chip High-Finesse Fabry-Perot Microcavities for Optical Sensing and Quantum Information" Sensors 17, no. 8: 1748. https://doi.org/10.3390/s17081748
APA StyleBitarafan, M. H., & DeCorby, R. G. (2017). On-Chip High-Finesse Fabry-Perot Microcavities for Optical Sensing and Quantum Information. Sensors, 17(8), 1748. https://doi.org/10.3390/s17081748




