Double-Layer Compressive Sensing Based Efficient DOA Estimation in WSAN with Block Data Loss
Abstract
1. Introduction
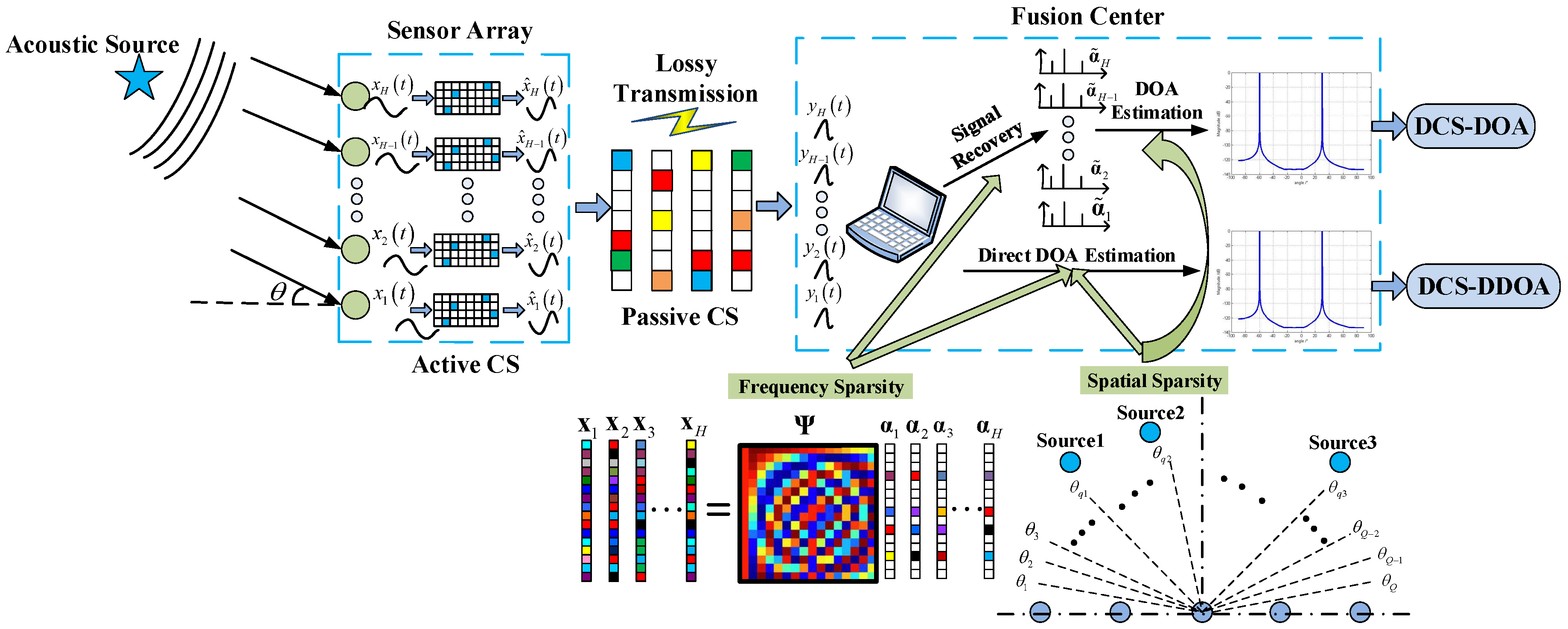
- A double-layer compressive sensing framework is proposed to eliminate the adverse effects of block data loss on DOA estimation in WSAN. Specifically, we model the random packet loss during transmission as a passive CS process and introduce an active CS process at each array sensor to address the block data loss problem.
- We present the mutual coherence of the equivalent measurement matrix and the absolute off-diagonal entries’ distribution of the corresponding Gram matrix under the double-layer CS framework, which account for the satisfactory DOA estimation performance.
- A direct DOA estimation technique (DCS-DDOA) is proposed under the double-layer CS framework to avoid the error propagation problem in DCS-DOA. A joint frequency and spatial domain sparse representation of the sensor array data is constructed and exploited to directly perform DOA estimation at the FC.
2. Background
2.1. Compressive Sensing
2.2. DOA Estimation
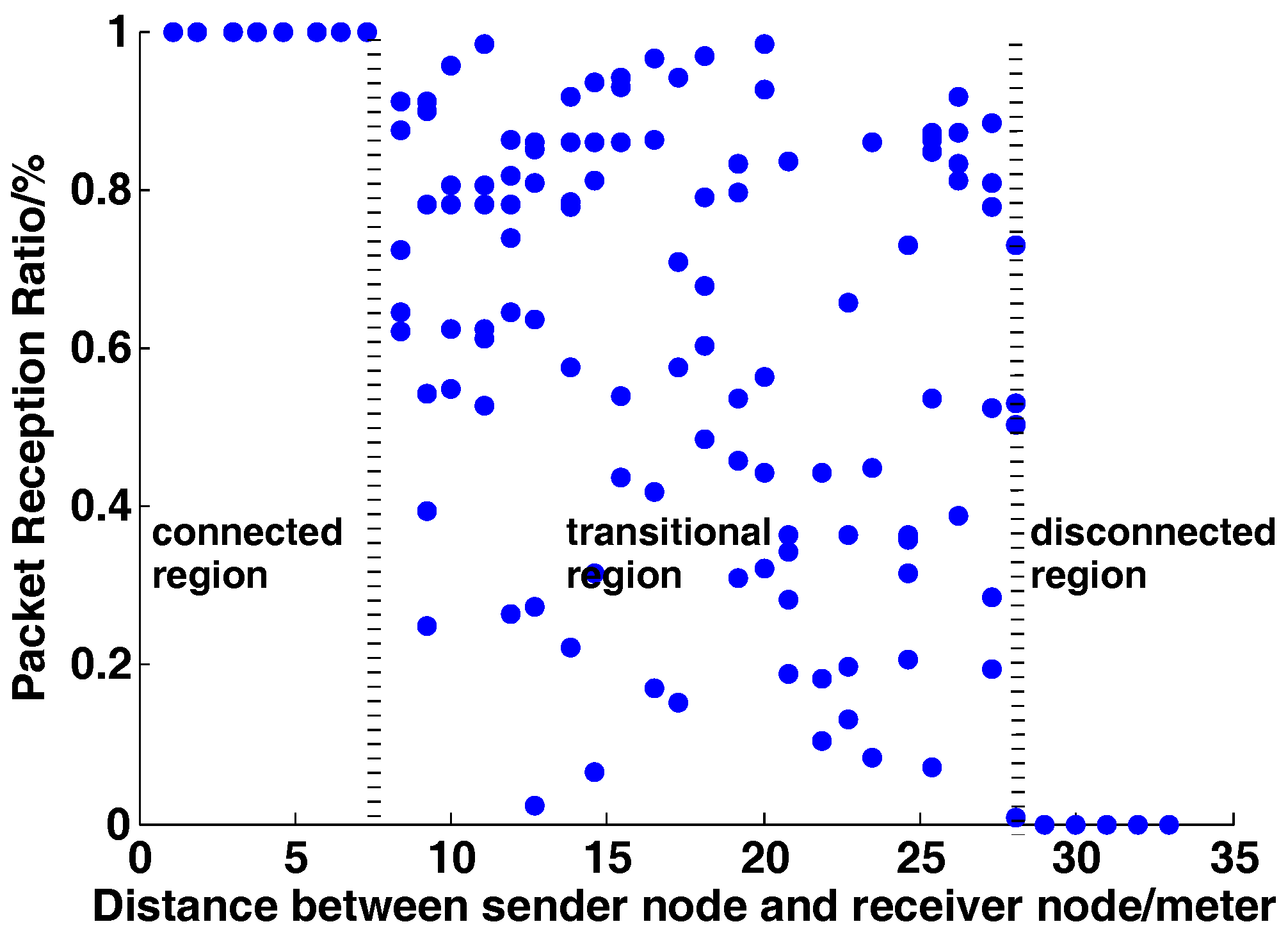
2.3. Lossy Wireless Links
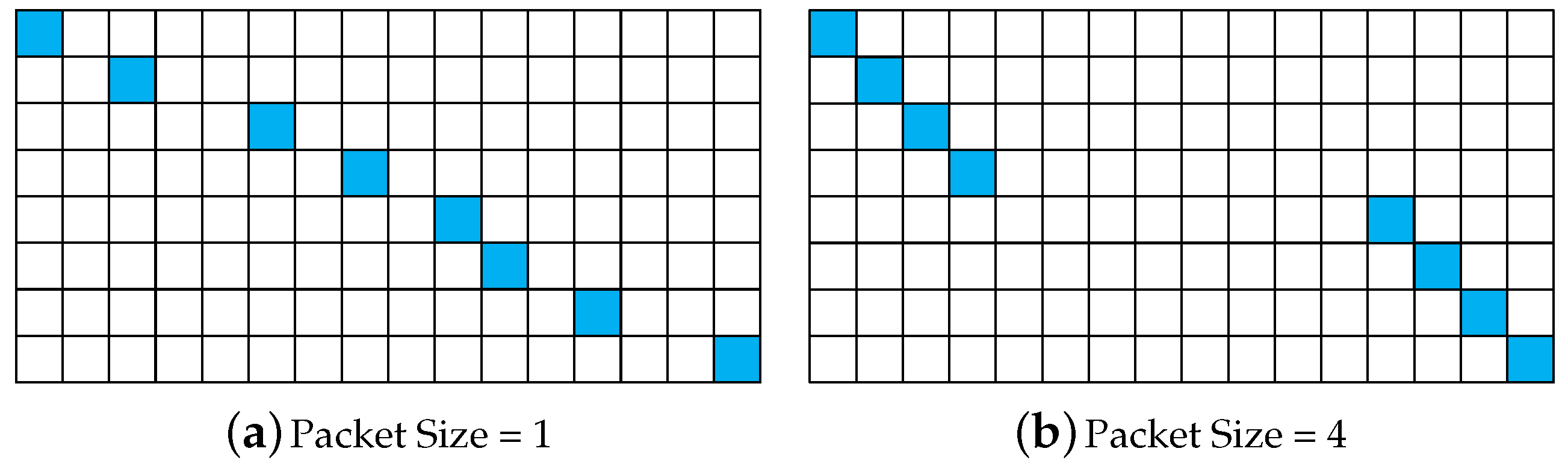
2.4. Block Data Loss
3. Double-Layer CS Framework-Based DOA Estimation
3.1. Double-Layer CS Framework
3.2. DOA Estimation by DCS-DOA
3.2.1. Signal Recovery
3.2.2. DOA Estimation
3.3. Improved DOA Estimation by DCS-DDOA
3.3.1. Joint Sparse Representation
3.3.2. Direct DOA Estimation
4. Experimental Results
4.1. Simulation Settings
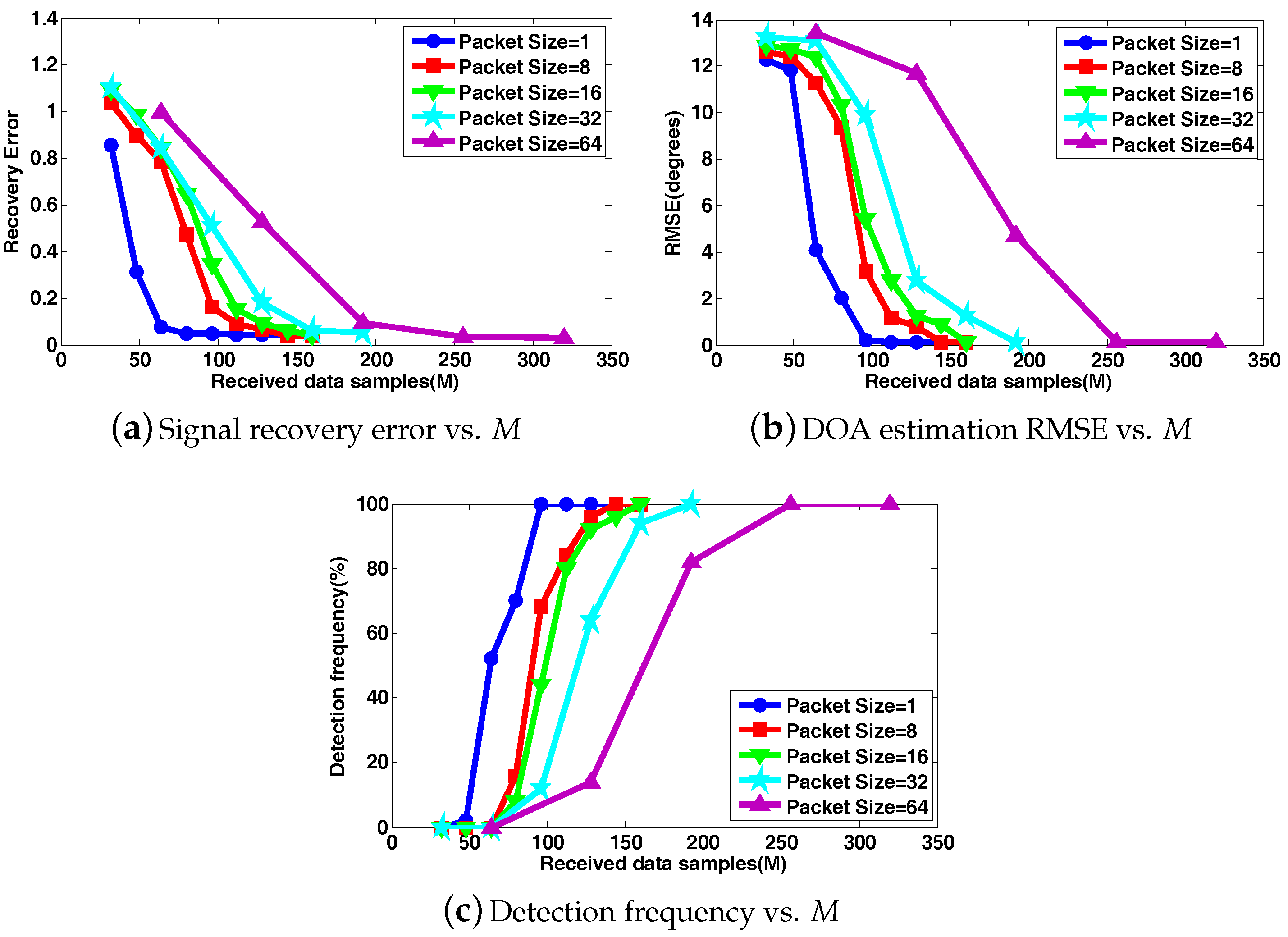
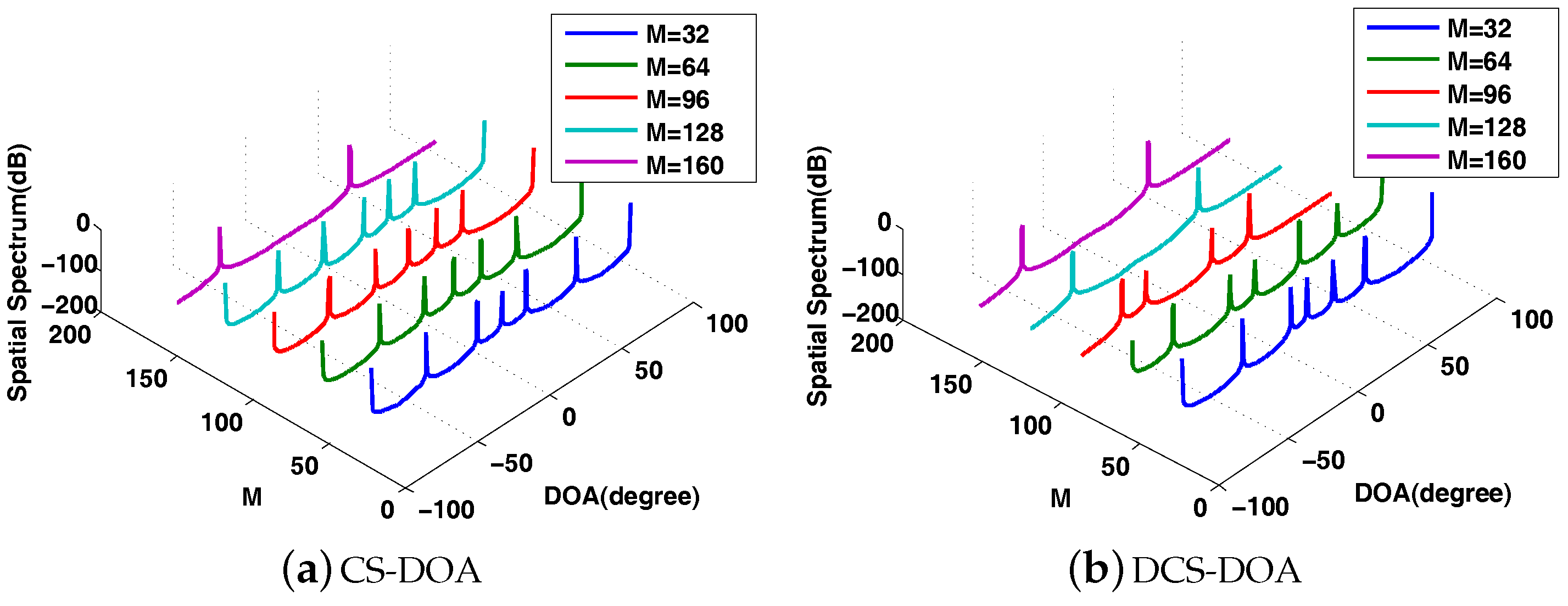
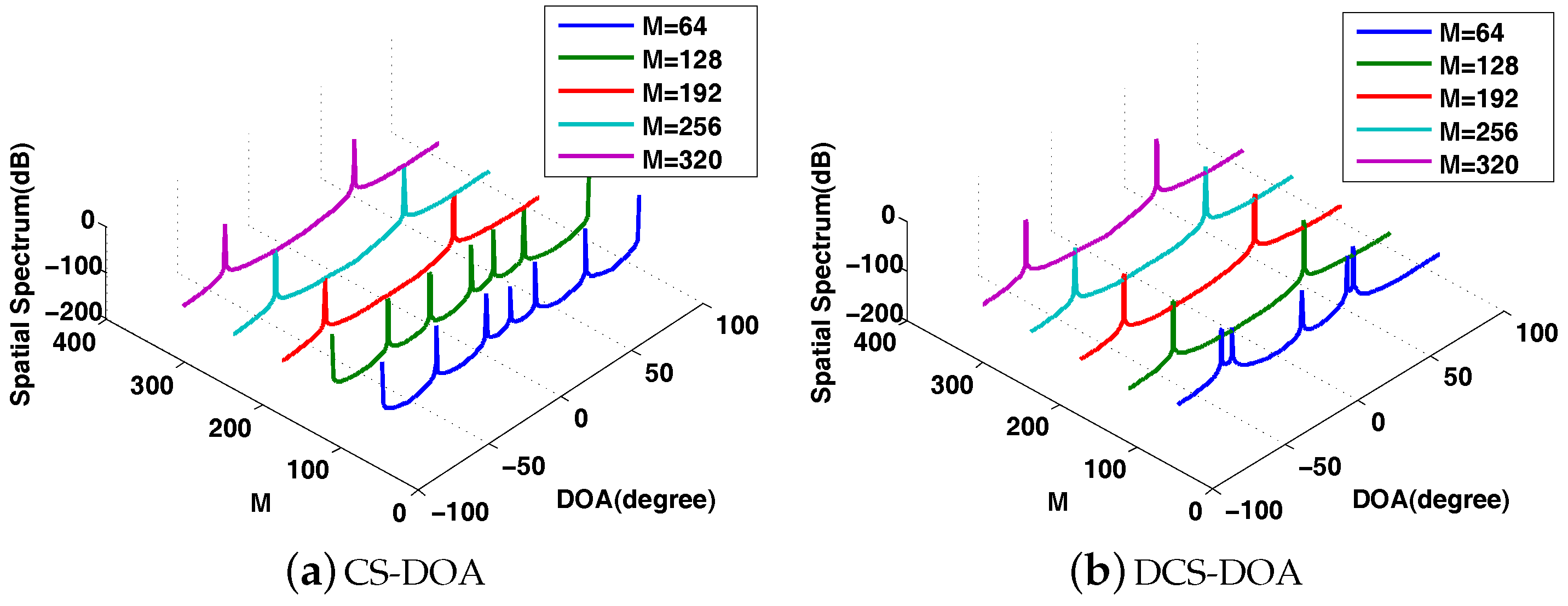
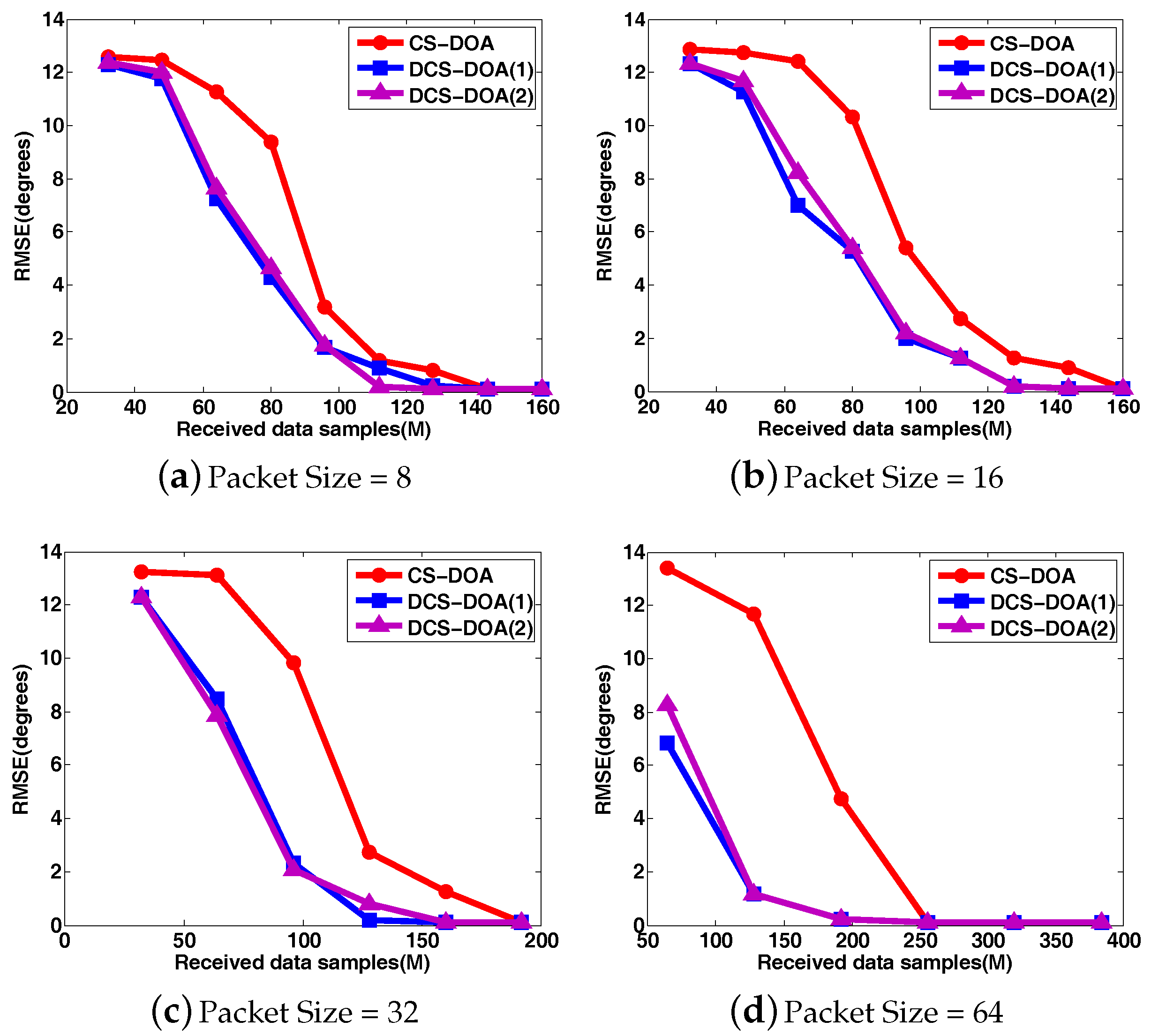
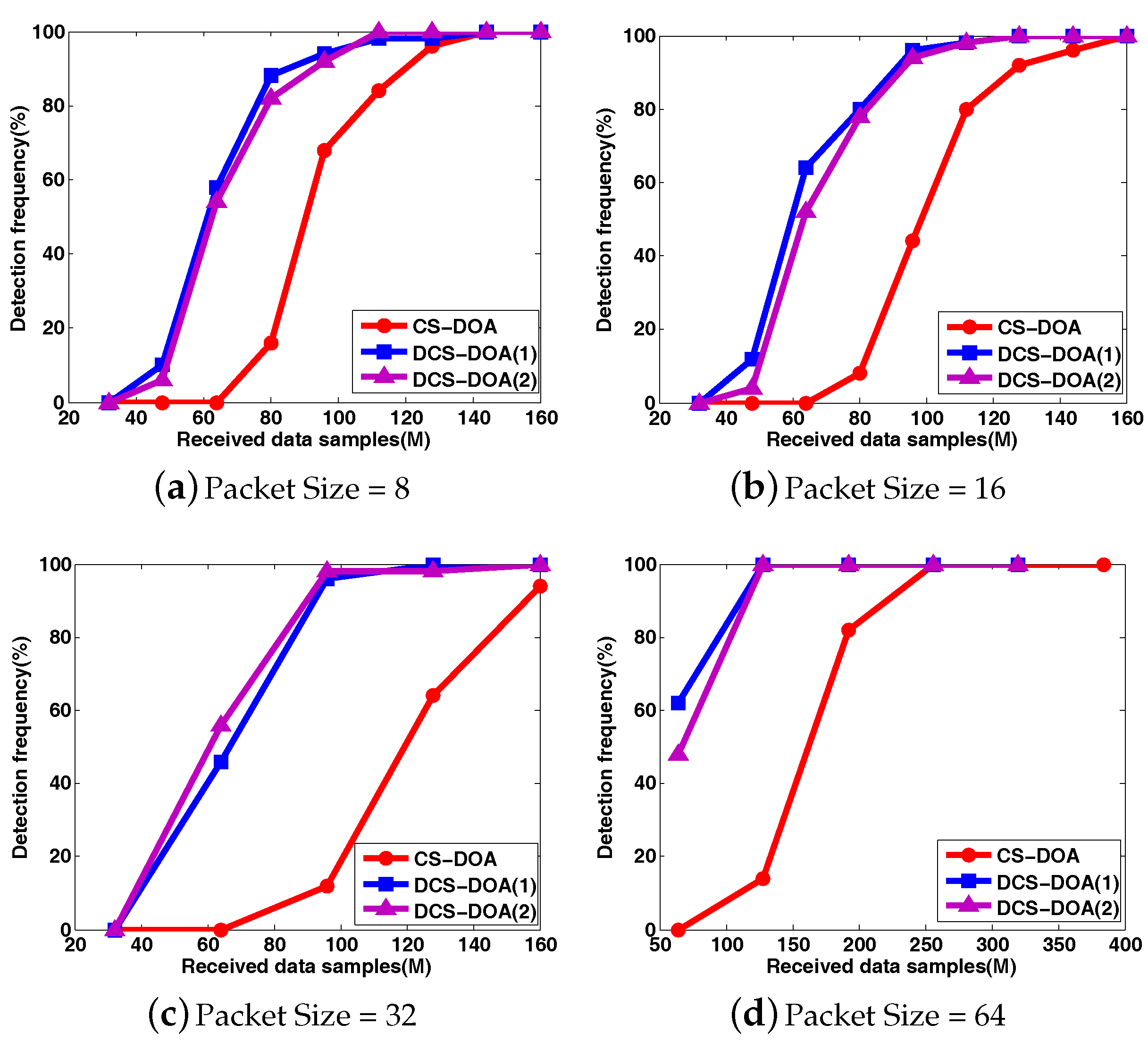
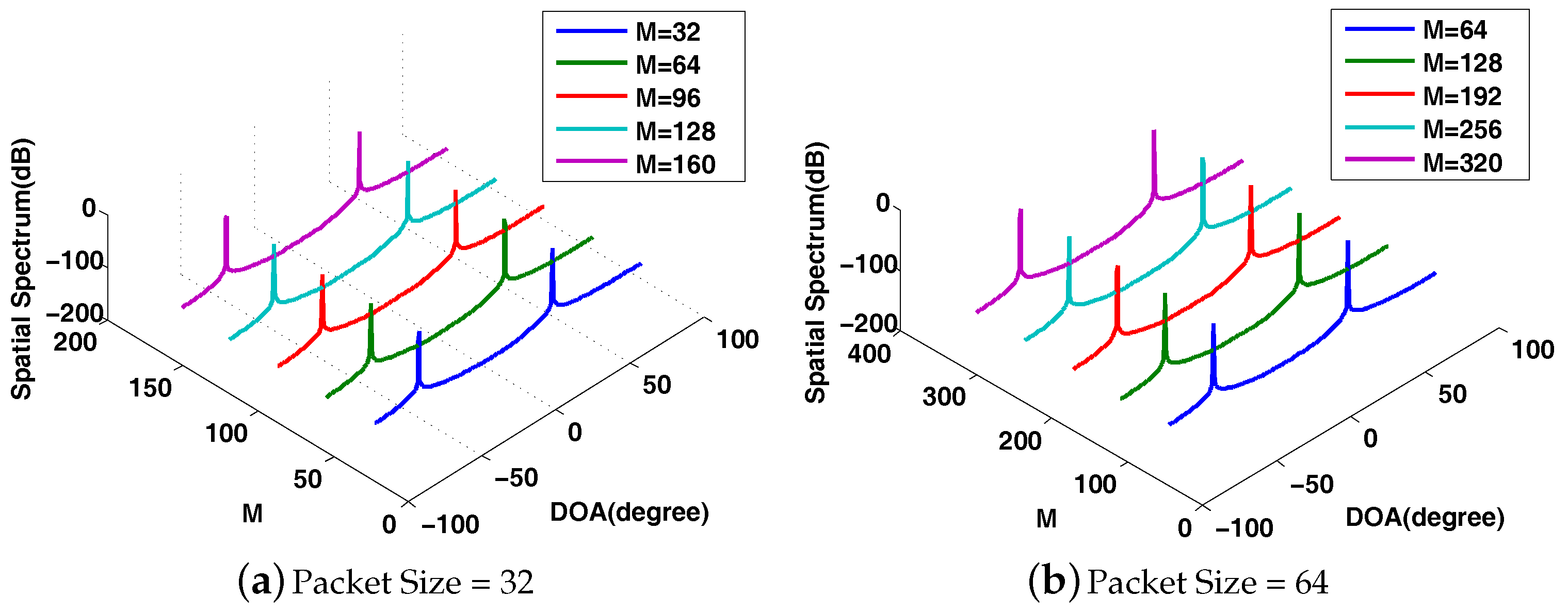
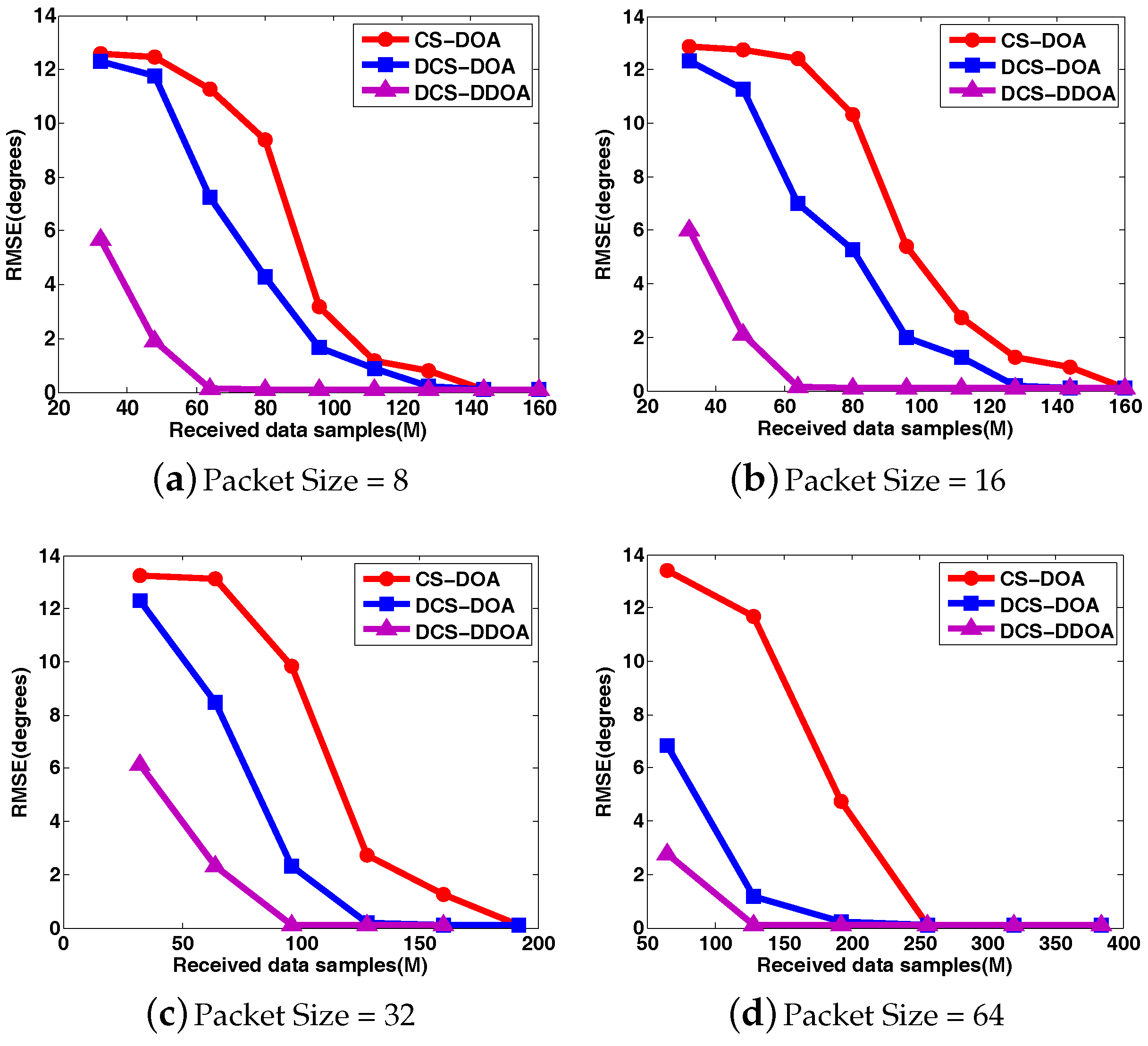
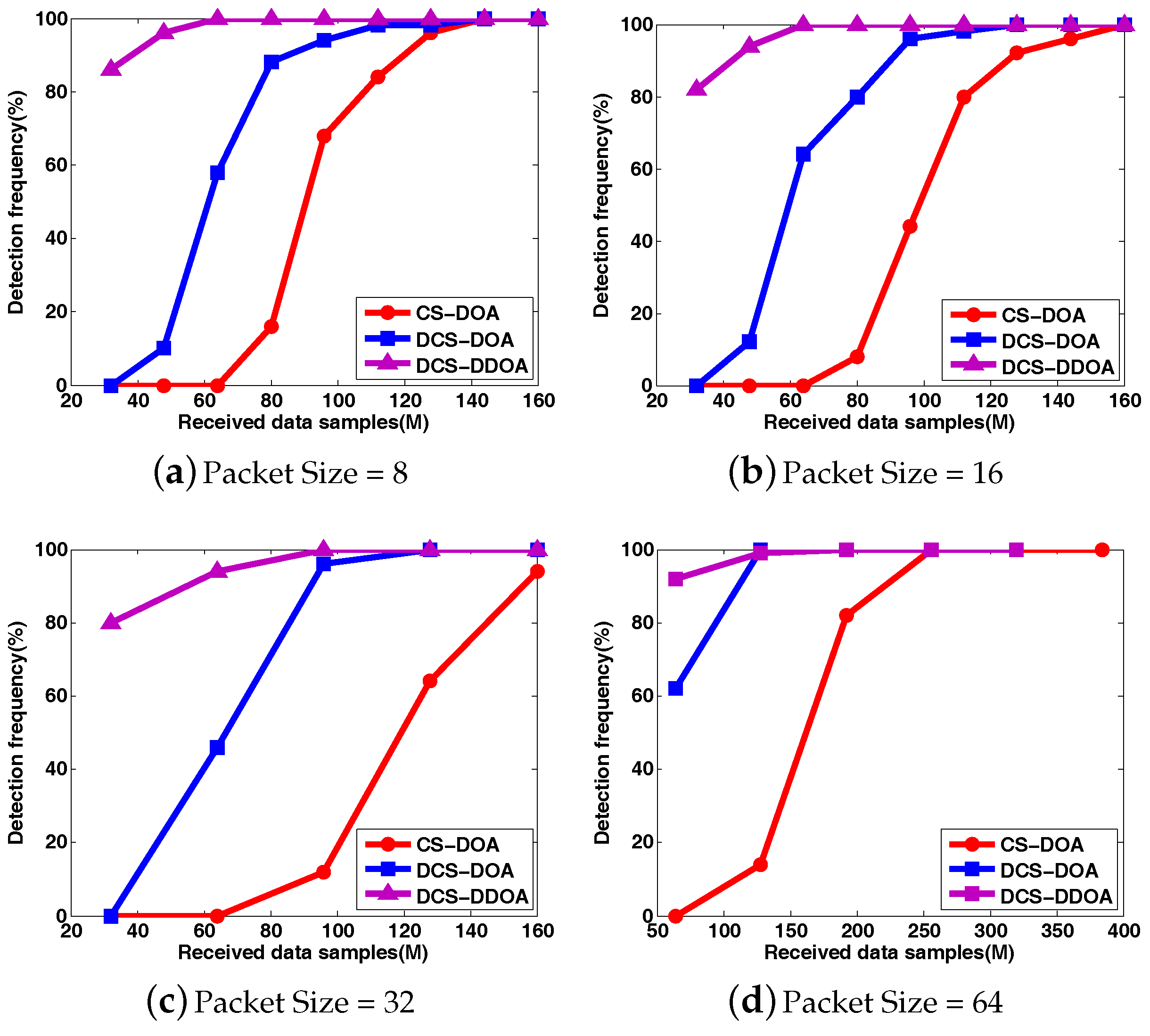
4.2. Performance Analysis for DCS-DOA
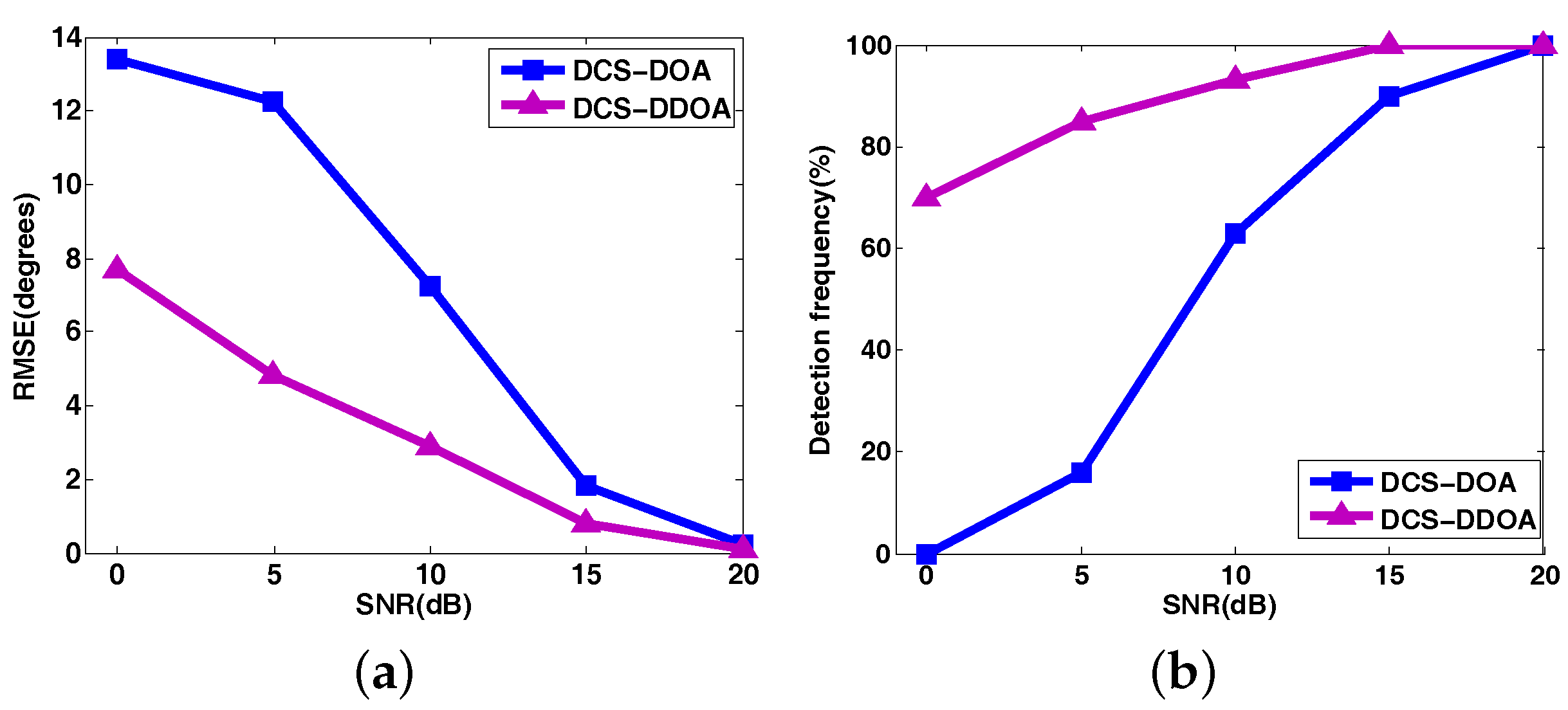
4.3. Performance Analysis for DCS-DDOA
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: the parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Nagata, Y.; Fujioka, T.; Abe, M. Two-Dimensional DOA Estimation of Sound Sources Based on Weighted Wiener Gain Exploiting Two-Directional Microphones. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 416–429. [Google Scholar] [CrossRef]
- Malioutov, D.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2003, 53, 3010–3022. [Google Scholar] [CrossRef]
- Shao, H.J.; Zhang, X.P.; Wang, Z. Novel closed-form auxiliary variables based algorithms for sensor node localization using AOA. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2014), Florence, Italy, 4–9 May 2014; pp. 1414–1418. [Google Scholar]
- Shao, H.J.; Zhang, X.P.; Wang, Z. Efficient Closed-Form Algorithms for AOA Based Self-Localization of Sensor Nodes Using Auxiliary Variables. IEEE Trans. Signal Process. 2014, 62, 2580–2594. [Google Scholar] [CrossRef]
- Winder, A.A. II. Sonar system technology. IEEE Trans. Sonics Ultrason. 1975, 22, 291–332. [Google Scholar] [CrossRef]
- Baldacci, A.; Haralabus, G. Signal processing for an active sonar system suitable for advanced sensor technology applications and environmental adaptation schemes. In Proceedings of the IEEE 2006 14th European Signal Processing Conference, Florence, Italy, 4–8 September 2006; pp. 1–5. [Google Scholar]
- Akyildiz, I.F.; Pompili, D.; Melodia, T. Underwater acoustic sensor networks: Research challenges. Ad Hoc Netw. 2005, 3, 257–279. [Google Scholar] [CrossRef]
- Ali, A.M.; Yao, K.; Collier, T.C.; Taylor, C.E.; Blumstein, D.T.; Girod, L. An empirical study of collaborative acoustic source localization. J. Signal Process. Syst. 2009, 57, 415–436. [Google Scholar] [CrossRef]
- Yu, K.; Zhang, Y.D.; Bao, M.; Hu, Y.H. DOA Estimation From One-Bit Compressed Array Data via Joint Sparse Representation. IEEE Signal Process. Lett. 2016, 23, 1279–1283. [Google Scholar] [CrossRef]
- Baccour, N.; Koubâa, A.; Mottola, L.; Iga, M.A.; Youssef, H.; Boano, C.A.; Alves, M. Radio link quality estimation in wireless sensor networks: A survey. Acm Trans. Sens. Netw. 2012, 8, 688. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2005, 59, 410–412. [Google Scholar] [CrossRef]
- Candes, E. Robust uncertainity principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Candes, E.J.; Wakin, M.B. An Introduction To Compressive Sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Kong, L.; Xia, M.; Liu, X.Y.; Wu, M.Y.; Liu, X. Data loss and reconstruction in sensor networks. In Proceedings of the IEEE INFOCOM, Turin, Italy, 14–19 April 2013; pp. 1654–1662. [Google Scholar]
- Bao, Y.; Li, H.; Sun, X.; Yu, Y.; Ou, J. Compressive sampling-based data loss recovery for wireless sensor networks used in civil structural health monitoring. Struct. Health Monit. 2012, 12, 78–95. [Google Scholar] [CrossRef]
- Charbiwala, Z.; Chakraborty, S.; Zahedi, S.; Kim, Y.; Srivastava, M.; He, T.; Bisdikian, C. Compressive Oversampling for Robust Data Transmission in Sensor Networks. In Proceedings of the IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; Volume 11, pp. 1–9. [Google Scholar]
- Wu, L.; Yu, K.; Cao, D.; Hu, Y.; Wang, Z. Efficient Sparse Signal Transmission over a Lossy Link Using Compressive Sensing. Sensors 2015, 15, 19880–19911. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L.; Elad, M. Optimally sparse representation in general (nonorthogonal) dictionaries via l1 minimization. Proc. Natl. Acad. Sci. USA 2003, 100, 2197–2202. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.M.; Huang, Z.T.; Zhou, Y.Y. Direction-of-Arrival Estimation of Wideband Signals via Covariance Matrix Sparse Representation. IEEE Trans. Signal Process. 2011, 59, 4256–4270. [Google Scholar] [CrossRef]
- Luo, J.A.; Zhang, X.P.; Wang, Z. A new sub-band information fusion method for wideband DOA estimation using sparse signal representation. In Proceedings of the International Conference on Acoustics, Speech, and Signal processing (ICASSP 2013), Vancouver, BC, Canada, 26–31 May 2013; pp. 4016–4020. [Google Scholar]
- Shen, Q.; Liu, W.; Cui, W.; Wu, S.; Zhang, Y.D.; Amin, M.G. Low-Complexity Direction-of-Arrival Estimation Based on Wideband Co-Prime Arrays. IEEE/ACM Trans. Audio Speech Lang. Process. 2015, 23, 1445–1456. [Google Scholar] [CrossRef]
- Zamalloa, M.Z.; Krishnamachari, B. An analysis of unreliability and asymmetry in low-power wireless links. Acm Trans. Sens. Netw. Tosn Homepage 2007, 3, 2198–2216. [Google Scholar] [CrossRef]
- Lettieri, P.; Srivastava, M.B. Adaptive frame length control for improving wireless link throughput, range, and energy efficiency. In Proceedings of the IEEE INFOCOM, San Francisco, CA, USA, 29 March–2 April 1998; Volume 2, pp. 564–571. [Google Scholar]
- Lv, X.; Bi, G.; Wan, C. The Group Lasso for Stable Recovery of Block-Sparse Signal Representations. IEEE Trans. Signal Process. 2011, 59, 1371–1382. [Google Scholar] [CrossRef]
- SeDuMi. Available online: http://sedumi.ie.lehigh.edu/ (accessed on 15 December 2016).
- Carlin, M.; Rocca, P.; Oliveri, G.; Viani, F.; Massa, A. Directions-of-arrival estimation through Bayesian compressive sensing strategies. IEEE Trans. Antennas Propag. 2013, 61, 3828–3838. [Google Scholar] [CrossRef]







| Notations | Explanations |
|---|---|
| raw data samples at the h-th array sensor | |
| Fourier sparsifying dictionary | |
| sparse representation of under the basis | |
| the active CS projection matrix adopted at each array sensor | |
| newly-generated data samples after a projection on | |
| the passive CS measurement matrix modeling the packet loss | |
| received data samples at the FC from the h-th array sensor | |
| recovered data samples for the h-th array sensor at the FC |
| Single-Layer CS | Double-Layer CS | |||
|---|---|---|---|---|
| Packet Size | ||||
| 1 | 0.2859 | 0.2297 | 0.2825 | 0.2306 |
| 8 | 0.5911 | 0.3328 | 0.2905 | 0.2269 |
| 16 | 0.7489 | 0.4077 | 0.2920 | 0.2311 |
| 32 | 0.8866 | 0.5118 | 0.2927 | 0.2296 |
| 64 | 0.9745 | 0.5616 | 0.2929 | 0.2308 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, P.; Wu, L.; Yu, K.; Shao, H.; Wang, Z. Double-Layer Compressive Sensing Based Efficient DOA Estimation in WSAN with Block Data Loss. Sensors 2017, 17, 1688. https://doi.org/10.3390/s17071688
Sun P, Wu L, Yu K, Shao H, Wang Z. Double-Layer Compressive Sensing Based Efficient DOA Estimation in WSAN with Block Data Loss. Sensors. 2017; 17(7):1688. https://doi.org/10.3390/s17071688
Chicago/Turabian StyleSun, Peng, Liantao Wu, Kai Yu, Huajie Shao, and Zhi Wang. 2017. "Double-Layer Compressive Sensing Based Efficient DOA Estimation in WSAN with Block Data Loss" Sensors 17, no. 7: 1688. https://doi.org/10.3390/s17071688
APA StyleSun, P., Wu, L., Yu, K., Shao, H., & Wang, Z. (2017). Double-Layer Compressive Sensing Based Efficient DOA Estimation in WSAN with Block Data Loss. Sensors, 17(7), 1688. https://doi.org/10.3390/s17071688





