1. Introduction
Electromagnetic (EM) waves interacts with matter in different ways. It depends on the radiation power, its frequency and the characteristic of the physical medium with which it interacts. In consequence, electromagnetic waves of different frequency interact differently with the medium through which they propagate. This interaction may be analyzed in the receiver measuring the parameters which characterize the signal (amplitude, propagation speed, phase, frequency, etc.). Matter is characterized by electromagnetic parameters (permittivity, conductivity, permeability) which can be used to detect it [
1]. Different frequency and different matter parameters induce different interaction mechanisms: the medium can be analyzed measuring in the receiver after the interaction. This paper proposes an experimental approach to design sensors using these interactions and the theoretical model presented in [
2].
This paper is organized as follows:
Section 2 reviews related works (electromagnetic waves and its interaction with the medium).
Section 3 proposes a new method which uses waves at different frequencies and measures using a differential method. In
Section 4, advantages and disadvantages over the conventional scenarios are treated. In
Section 5, experiments including software simulation of wave propagation dielectric medium are realized. In
Section 6 a new microstrip sensor and differential measures are proposed. Finally,
Section 7 provides conclusions and future works.
2. Related Work
Several disciplines exploit the interaction between electromagnetic waves and matter to detect and characterize the crossed medium. Biological systems or earth sciences that include the study of geology, the atmosphere, hydrosphere, biosphere, and the large-scale structure of the Earth’s interior use electromagnetic parameters like permittivity (), conductivity () and medium permeability (). Numerical values of these parameters characterize the analyzed medium. Frequency of electromagnetic wave is one of the main characteristics of the electromagnetic waves used in these applications.
Propagation speed, signal absorption and phase shift of electromagnetic waves in different transmissions depends on the radiation frequencies, and the electromagnetic parameters of the medium through which the waves propagate. These characteristics are used in different applications, measuring in receivers signals transmitted by wave emitters. In the study of geology, ground penetration radar [
3] uses radar pulses to image the subsurface, the materials composition in the first layers of soil are detected analyzing its dielectric constant or relative permittivity (
). Permittivity characterizes the analyzed medium and it depends on the frequency [
4]. Different frequencies transmitted follow a procedure in which the emission, reception and analysis is realized. Effective permittivity of the material (
) is calculated using the time of arrival (
) of the electromagnetic wave in its reflection with the various layers which make up the subsoil. The arrival time of the signal depends on the frequency range (
f) and the crossed medium, represented by its permittivity. The relations formed are arrival time (
) function of frequency (
f) and medium effective permittivity (
).
In other scenarios like weather radars [
5,
6], the composition environment and variation in time are two aspects to analyze. Meteorological radars analyze the rainfall. In this case, the energy reflected in the rain drops are measure and analyzed. Here, the characteristics of medium analyzed is known (water) the objective is to calculate its volumetric density and its size in the form of a drop [
7]. In this applications the relation between the energy received, working frequency and the rate of rainfall is analyzed [
8]. Ionosphere analysis in [
9] review the current state of knowledge of the European plasma environment with electromagnetic radiation and effects of the atmosphere on radio and radar signals is treated in [
10].
Other important applications where effects of electromagnetic waves are critical are the biological systems. Understanding potential health and safety risks in medical applications and therapies [
11] depend on the knowledge of the interaction with electromagnetic radiation. For a long time, the biological interaction medium-electromagnetic waves has produced numerous works [
12,
13], that use electromagnetic radiation with different frequencies, applications and biological scenarios. Electromagnetic waves are considered non-invasive methods that can characterize biological tissues [
14]. Theoretical bases, experimental methods and practical applications analyze dielectric properties [
15] using frequency spectra of electromagnetic radiation. Dielectric properties of the human skin is analyzed with new dielectric sensors configurations [
16]. One of the latest trends in research for the construction of wireless sensors are microstrip patch sensors [
17]. The basic idea of the microwave sensors is to measure the dielectric constant in a composite material (soil, water, biological, building structures) [
18]. Microstrip configuration and coplanar circuits [
19] are used in research works about human skin measurements during glucose excursions and wearable sensors.
The recent state of the art in physiological monitoring using wearable sensors, as review in [
20,
21], is the culmination of a decade of experimental developments from measurements in laboratory with instrumentation to design devices that permit continuous measurements. Accurate measures of the dielectric properties of the tissues does not depend only on these sensors, other requirements like sensor integration into the device, adapted user interface, data storage and analysis, pattern recognition and events with alerts are required [
22].
3. Differential Measurement Model
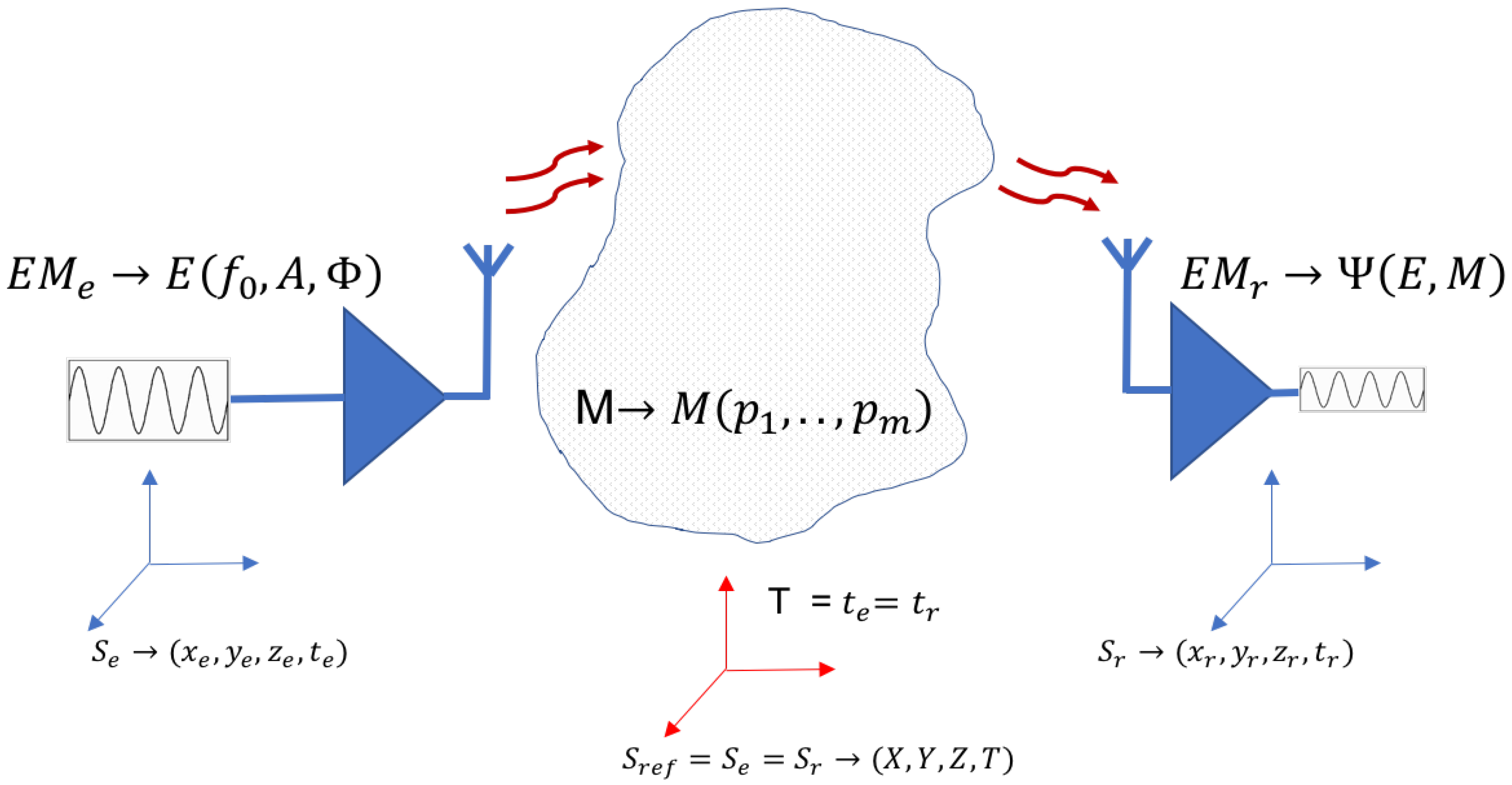
The interaction between EM radiation and medium analyzed uses positional and temporal reference systems
(
Figure 1). Transmission and reception are calibrated and synchronized as a preliminary step to use in an application that characterizes the medium analyzed.
In geolocation systems, the position of triangulation devices and the synchronization of the clocks embedded in all devices is a necessary condition for addressing the task of determining the position of the receiver. In remote sensing applications, where the transmitter and receiver are not situated on the same device, temporal references (clocks embedded) must be synchronized. Once the necessary relation has been established between the referenced systems, a working EM with at a frequency band is used to induce the desired interaction and to obtain the information in the receiver. Calibration or synchronization of the system should be managed and maintained at all times.
The maintenance of these references in all devices has a cost which must be assumed into its functioning or operations. Electromagnetic wave emitted (
E) is characterized by its Frequency (
), Amplitude (
A) and Polarization (
). Signal received is a function (
) that depends on signal emitted (
E) and the medium, expressed by its parameters (
). The function analyzed in the receiver is
(
Figure 1).
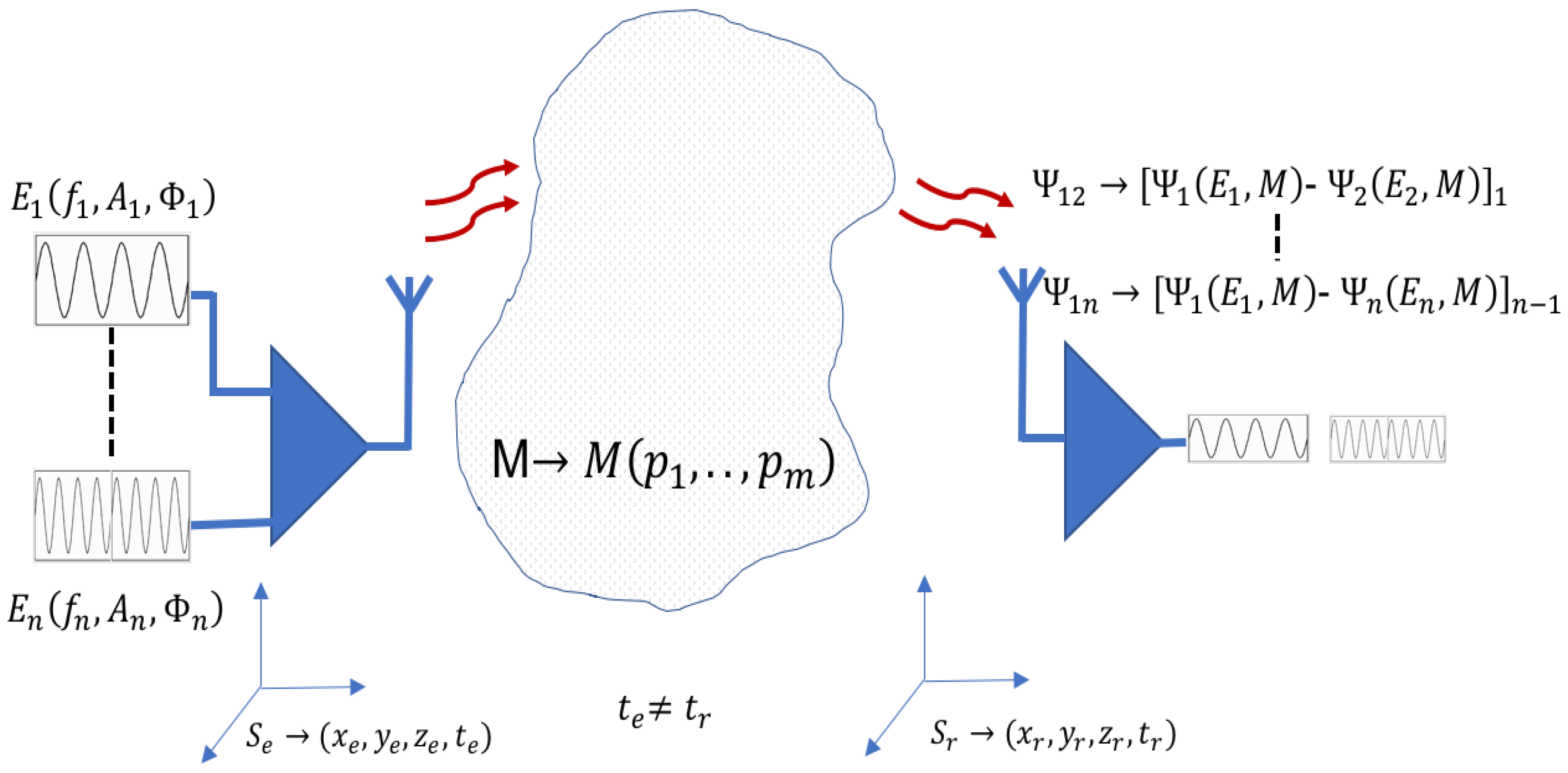
Conventional treatment uses absolute measures on the receivers in synchronized reference systems. In contrast to this conventional signal treatment a differential measure model is proposed (
Figure 2). In this new proposal, measured magnitude in the receiver (arrival time, signal amplitude, etc.) are relative. Differential measurements work with independent temporal references and enable the application of solutions with independent positional reference systems. Theoretical model is shown in
Table 1.
In the differential measurement model, if the wave-medium interaction depends on the frequency and the medium, different frequencies will produce different measures in the receiver for the same medium and symmetrically, different medium parameters produce different measures for the same frequency. Using these differences, measured in the receiver, the parameters of analyzed medium can be identified. Differential treatment of the signal without time synchronization introduces operating advantages over the conventional treatment: it achieves some independence from the positional and temporal reference systems. Treatment with different frequencies and differential measures take advantage from information obtained on the interaction with each frequency, useful in the systems where the medium is parametrized. In addition differential measures compensate undesirable interference such as common interference or noises. With the aim of showing the differential method advantages, an example for positioning systems is analyzed below.
If the distance d between the transmitter and the receiver is known, different speeds of propagation using different signal frequencies or different propagation conditions can identify the parameters of the medium analyzed. This treatment could be used in applications where an unknown medium should be determined.
This work proposes to measure differences in the reception of EM waves. Two treatments can be used:
If the wave-medium interaction is known, the link distance (emitter-receiver) can be estimated using differential measures in the receiver. This treatment is useful for location systems.
If the distance emitter-receiver or some environment conditions are known, medium parameters can be estimated using differential measures in the receiver. This treatment is useful for medium detection systems.
In this paper, the work analyzes the model proposed and simulates differential measures to develop sensors in applications that detect dielectric mediums.
Differences with Similar Methods
The differential method proposed uses similar techniques and technologies that already exist like stripline or microstrip [
23]. In these methods electromagnetic transmission use absolute measures to calculate characteristic impedances. Hence, stripline or microstrip configuration reduces wave propagation speed (
) according to relative permittivity (
) of the dielectric substrate:
Likewise, the characteristic impedance in stripline and microstrip (
) is dependent on geometrical dimensions (width, thickness and height) and the dielectric constant of the material used. If dielectric and dimensions are known, transmission processes are known, and vice-versa, if measures of transmission are known dielectric constant of materials can be characterized. In these and other similar cases, transmission and materials are analyzed using absolute measures of electromagnetic variables in a receiver device. The method proposed in this work uses striplines, microstrip or similar technologies extending its capabilities through a new model of utilization. In this way Equation (
1) becomes:
Basically, wave propagation speed () measured in conventional methods is replaced by differential speed measures (), using similar techniques and configurations. Wave propagation speed is one of the possible differential measures. Losses, wave phases and others electromagnetic measures can also be used in a differential mode. To obtain differential measures, reference materials are used in new configuration sensors proposed in this method (being another difference in relation to the current systems).
5. Simulation of wave Propagation in Dielectric Medium
The differential model uses different frequencies or different interactions induced by the medium through which the wave propagates. A dispersive medium (frequency dependent) is analyzed to determine the theoretical applicability. Dispersive medium are environments in which parameters like dielectric constant, permittivity or conductivity become dependent on the frequency. In this case, interactions in signal propagation like propagation speed or signal reduction (absorption) are frequency dependent. EM pulse propagation in different dielectric materials can be simulated using the numerical method Finite-Difference Time-Domain (FDTD) [
24]. FDTD are full-wave techniques used to solve problems in electromagnetic that employs finite differences as approximations. This numerical method proposes computational algorithms (in this simulation Yee algorithm) to resolve the Maxwell equations in time and space domain. The FDTD formulation is a direct solution of Maxwell equations:
In Equation (
3) the medium parameters are dielectric permittivity (
), conductivity (
) and permeability (
). This parameters represent the interaction of electric (
E) and magnetic (
H) fields. Finite Difference Algorithm is used to analyze electric and magnetic fields in space-time domain. A simulation using FDTD algorithm [
25] is implemented in a numerical computing environment (MATLAB). Different simulations using this platform are performed to analyze differences between electromagnetic waves when arrive to receiver.
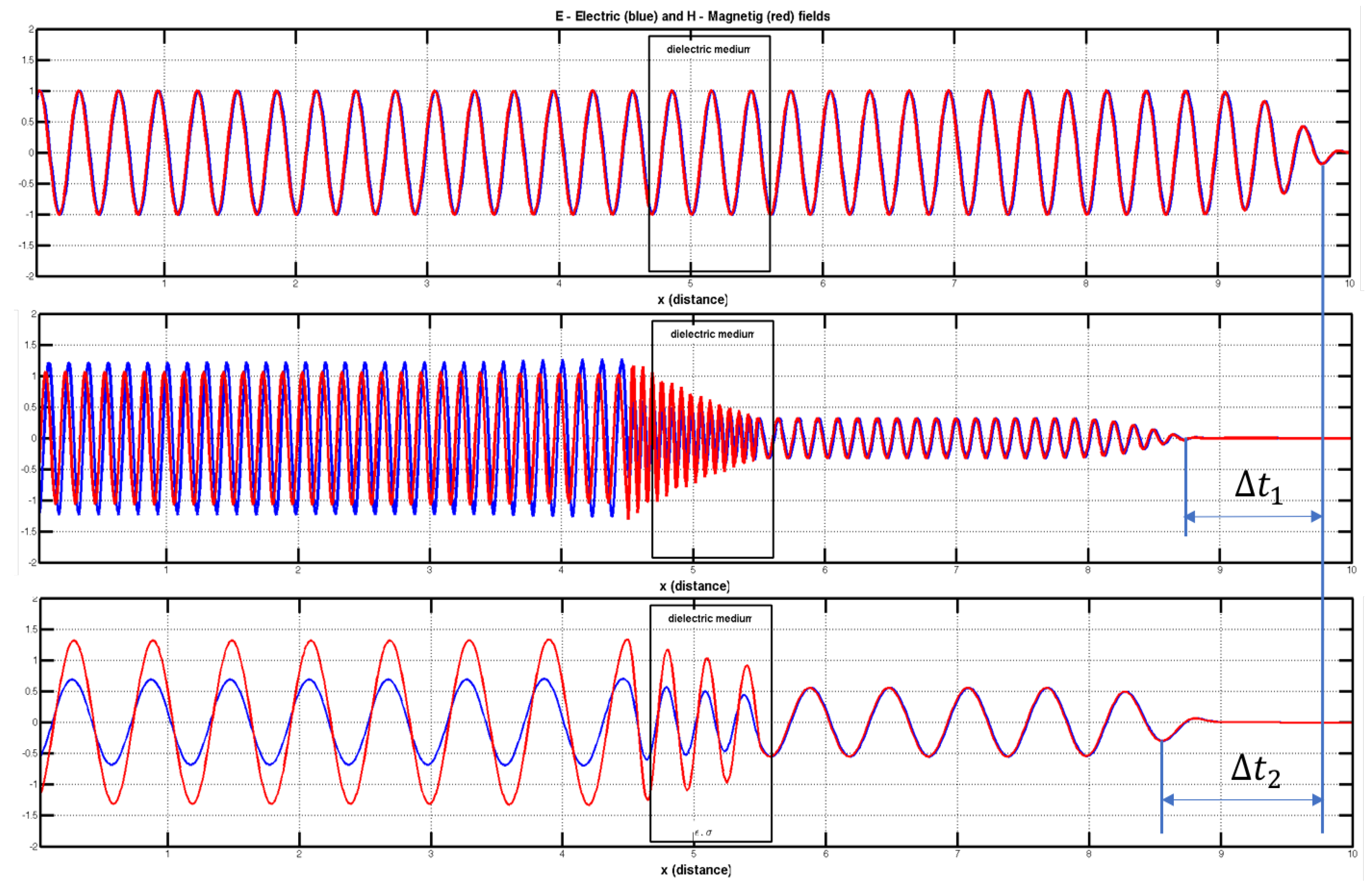
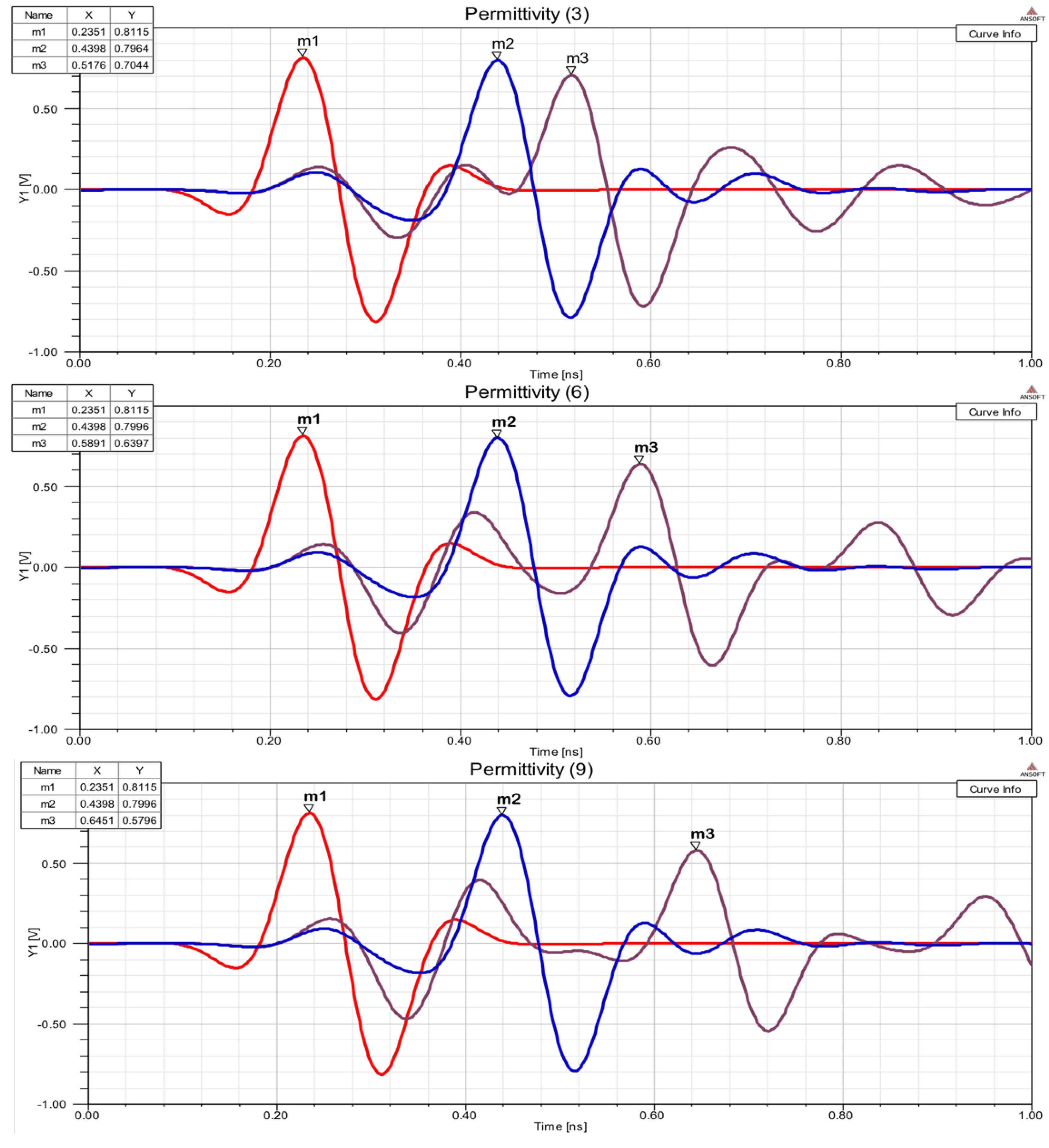
Figure 3 shows the result in a dielectric and dispersive medium. This simulation shows how this differences are induced and confirm the first method hypothesis.
Figure 3 shows the effect that the model wants to use: different frequency produce differences in receiver. The simulations demonstrate a relation between time differences measured in receiver port and dielectric medium crossed. This first simulations with FDTD algorithms shows trends and effects of interaction with a general resolution. It serves to confirm the working hypotheses.
To show if differential measures can be used to take advantage of this interactions a simulation in a specialized software for EM interactions. This platform is Ansoft HFSS 13.0 software. This tool is used to simulate complex geometries using Finite Element Method (FEM) to compute electrical behavior of high speed and high frequency components. The HFSS most accurately characterizes the electrical performance of the components and effectively evaluates various parameters.
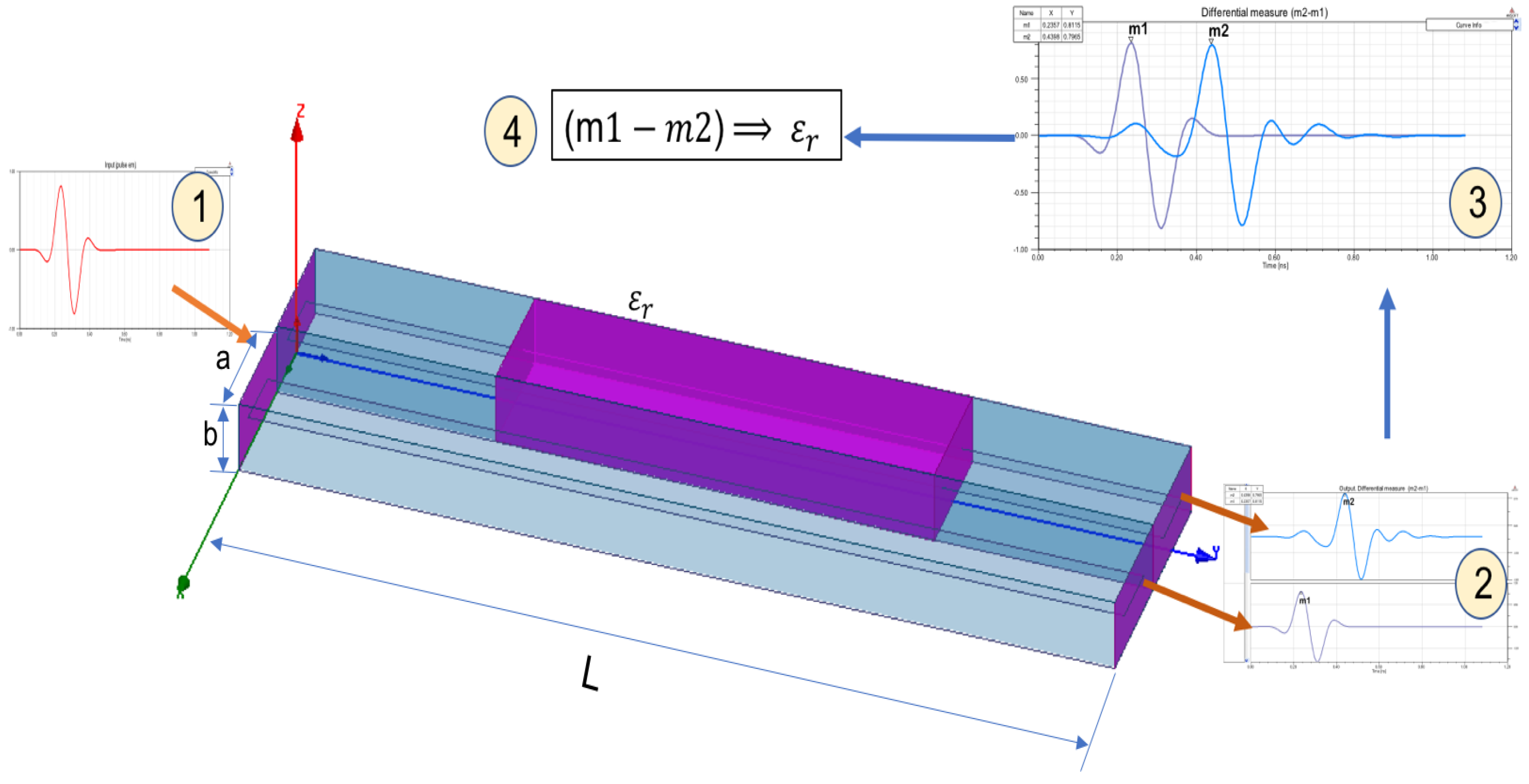
Figure 5 shows the simulation results. One wave is transmitted within two parallel waveguides with different dielectric constant (
) to produce different speed of propagation. One of the waveguides have
(air) and the other have an unknown dielectric material (
). Dielectric permittivity (
) of this material can be characterized using differential measures in the output ports.
It is assumed a medium with unknown dielectric permittivity (
) which is constant in a range of frequencies
. An equation system to calculate
is proposed. Dielectric Medium and wave speed, in dielectric medium, are related by Equation (
5).
Equations system proposed to different
are shown in Equations (
5)–(
7).
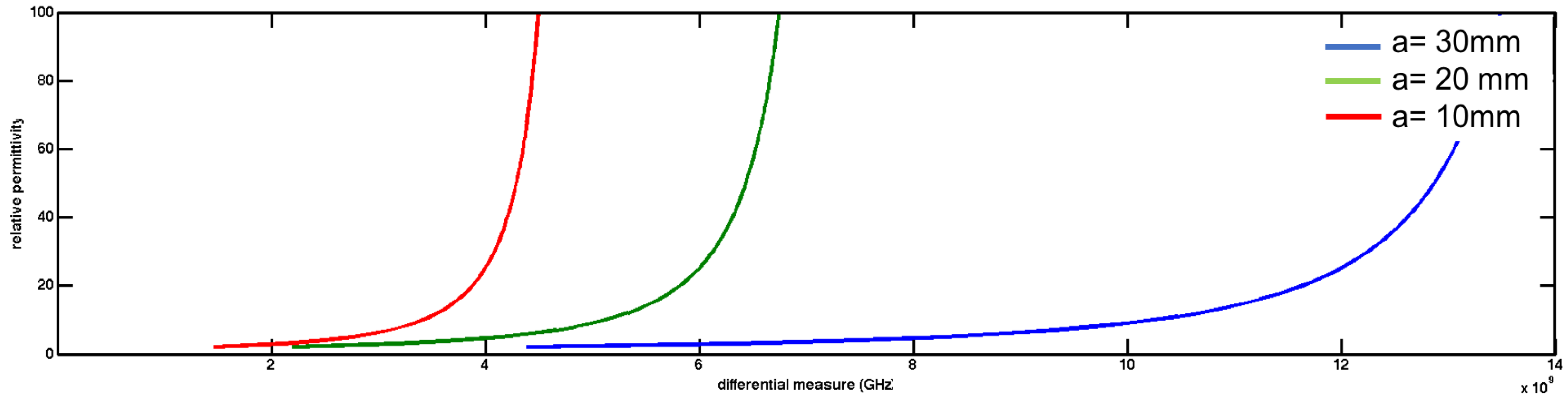
Waveguide long is
mm, width (
mm) and height (
mm). The length of the dielectric material is
mm. A broadband excitation pulse (1–10 GHz) is introduced on input waveguide port. Output ports receive signal at times
and
. There are a
obtained on output. This difference is used in Equation system (
5).
Using the dimensions an data simulation (
Figure 4), a relation between
measured and
can be calculated. This relation is shown in:
Time analysis realized using electromagnetic wave transmission in rectangular waveguide, applying Equation (
7) are shown in
Table 2 and
Figure 5.
Air is the dielectric medium in line 1 (
) and a dispersive medium unknown in line 2
, with the waveguide walls conducting. In a rectangular waveguide is possible to propagate various modes of electromagnetic waves. Three modes of transmission TE (Transverse electric mode), TM (Transverse Magnetic mode) and TEM (Transverse Electric and Magnetic) are possible. In the rectangular waveguide supports TE and TM are supported and not TEM. A rectangular waveguide cannot propagate below a certain frequency which is called the cutoff frequency. The dominant mode in the rectangular waveguide considered is TE10 which has the lowest cutoff frequency. The cutoff frequency in a rectangular waveguide is given in Equation (
8). The
Figure 6 shows calculated permittivity using Equation (
9).
Different
induces changes on
. Calculation and simulation results are shown in
Table 3. Like in time domain, if
is known in a transmission line,
can be calculated using measures differences
in:
6. Microstrip Sensor and Differential Measures
Polymers, biopolymers, biological tissues, food products, porous materials, agricultural soil, plants, and others can all be considered as complex and dispersive systems. Measurement of the properties of dielectric has significant application areas like the aerospace, automotive, food industry, pharmaceutical, medicine, agriculture, defense industry and microwave device fabrication. Developments in the determination of material properties and their contribution to various industries for a wide range of applications are known [
26].
Initially, sensors for detecting the properties of materials were waveguides and open-ended probes that were usually bulky and heavy [
27]. Soon planar microwave components brought the possibility of usage of planar, small sensing devices that are used for characterization of a material. Rectangular microstrip patch antenna as a sensor for permittivity measurement is presented in [
17]. A microwave sensor operating in the X-band (8.2 to 12.4 GHz) for detecting thickness or permittivity changes in one layer of multilayered dielectric structures is presented in [
28]. A novel soil-moisture sensor based in a microstrip sensor placed in the soil is tested at 1.2 GHz in [
29]. Tissue measurement using electromagnetic field and microstrip electrodes are analyzed in [
17]. The latest references show that the dielectric materials can be specifically investigated and modeled by electromagnetic sensors with microstrip transmission. The current state of the art in continuous monitoring using electromagnetic wearable sensors, presented in [
30], represents the design of broadband devices that permit continuous measurements in everyday life situations [
15]. These sensors measure evolution and changes in dielectric constant and correlate these changes with the variation in blood glucose. By incorporating a number of sensors with differing geometric characteristics (microstrip dimensions), it is possible to show that a different penetration depth of the electromagnetic field into the tissue could be achieved.
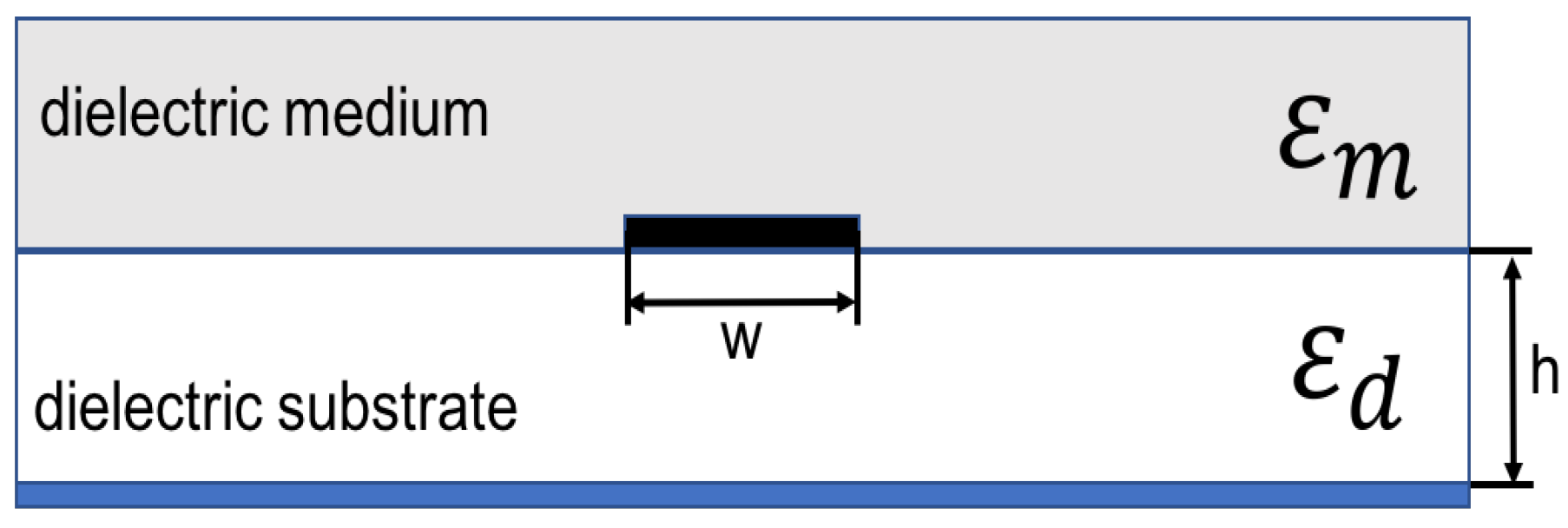
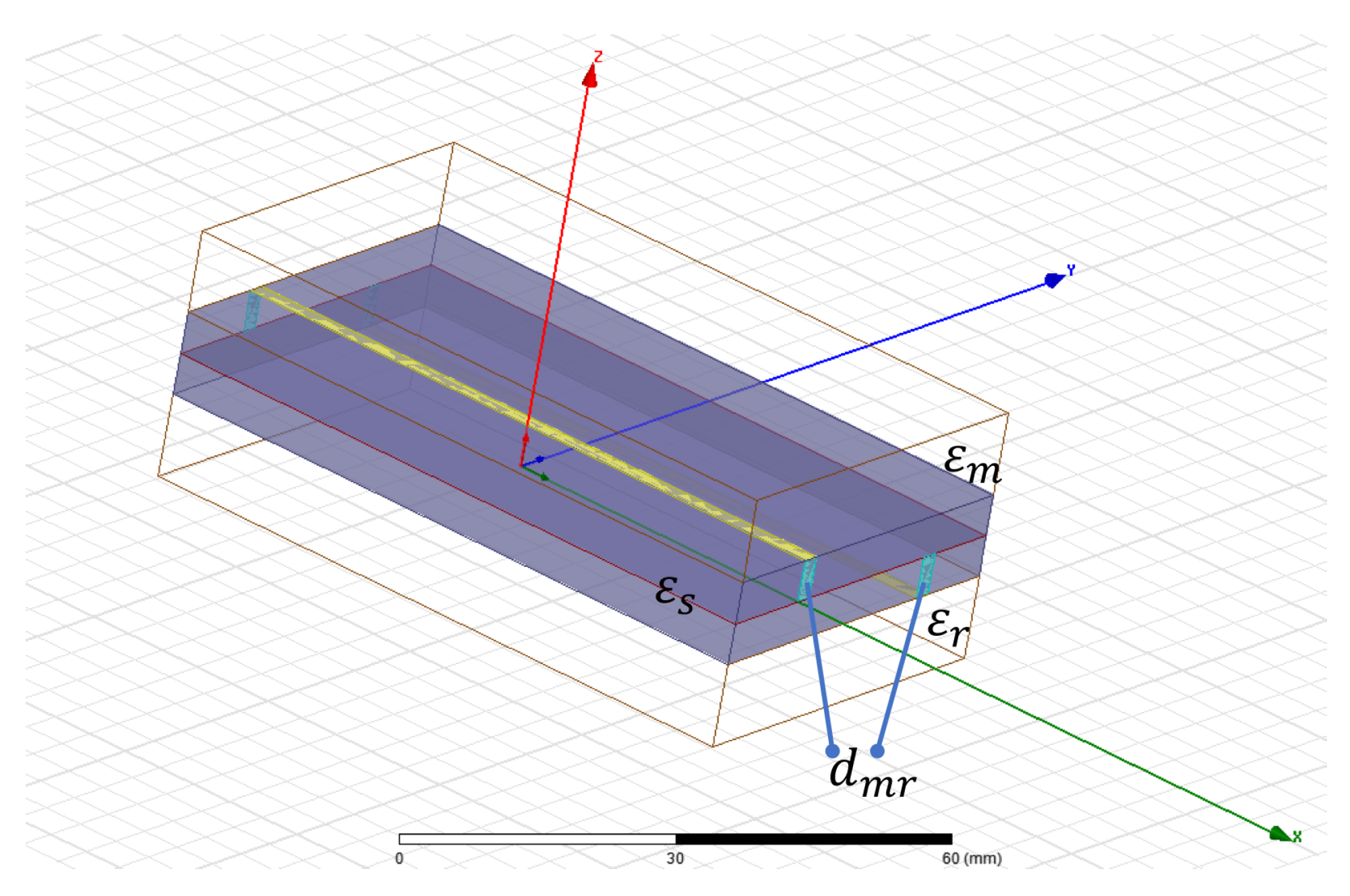
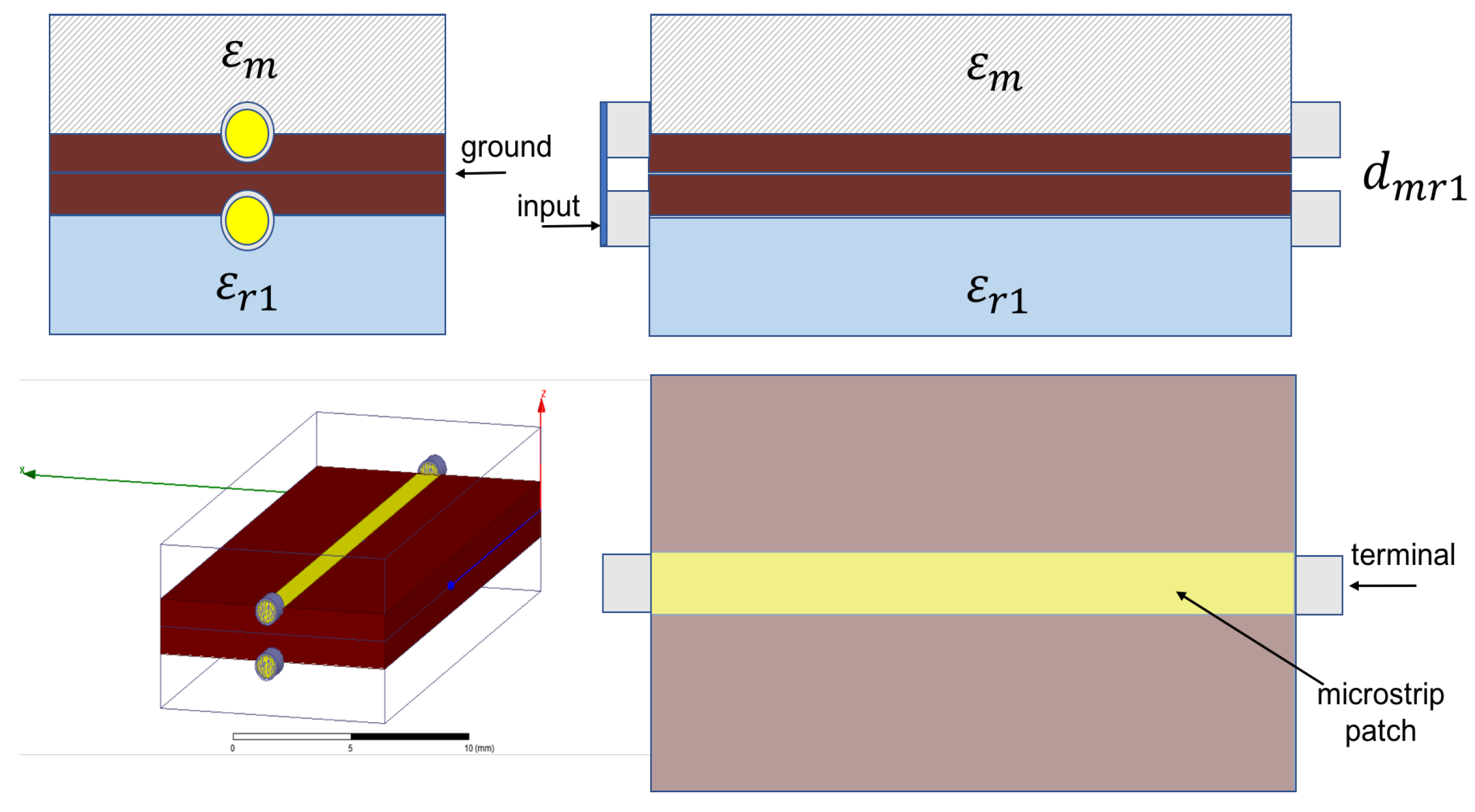
In
Figure 8a microstip sensor is shown. The influence of the material that must to be detected on signal propagation is reflected in effective permittivity of the microstrip, which depends on medium placed over miscrostrip (unknown material with
), and dielectric substrate (known
), from which microstrip sensor is made. Effective permittivity of the microstrip shown in
Figure 8 is defined in Equation (
10).
In
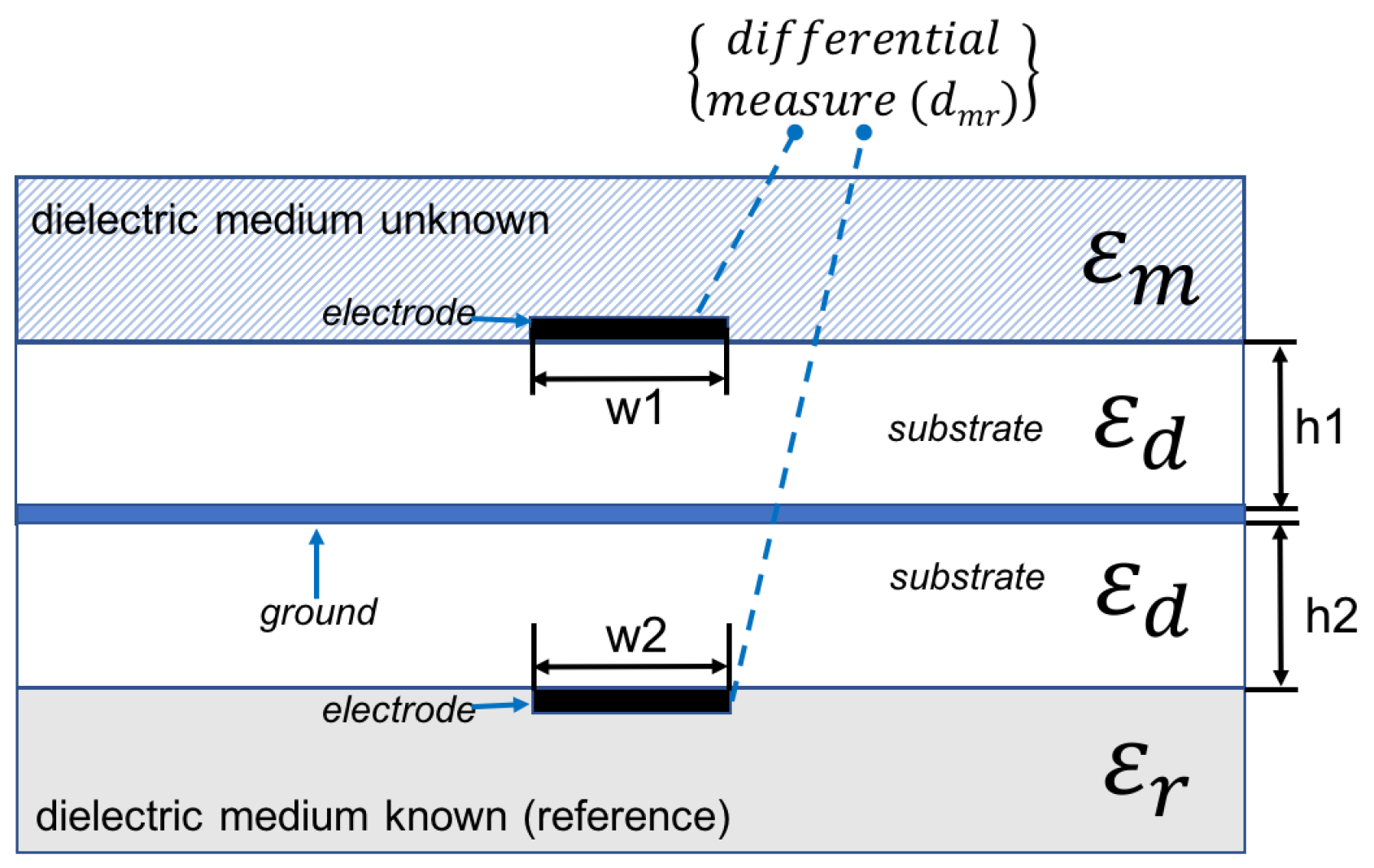
Figure 9, differential measure and microstip design is shown. In
Figure 10, a sensitive analysis is realized. The aim is to obtain information of unknown medium with differential measures. The sensor used in this study has a combination of two electrodes of similar geometries separated and surrounded by a ground electrode. The electrodes are made of copper. The substrate material comprises of a standard dielectric used in circuit board, FR4 (standard circuit board material composed of fiber glass and epoxy resin). To complete the electromagnetic field simulations, different assumptions were made. These assumptions include the reduction of the 3D to a 2D simulated space. Since the lengths of the electrodes (60 mm) is larger than their width (2 mm), in any profile across the longer size of electrodes (except the electrode ends) the field distribution is simplified with the 2D distribution. It was shown in [
31] that the simulation error caused by such reduction is smaller than
.
Theoretically, considering
Figure 11 structure:
If is then .
If is then , , knowing and microstrip dimensions.
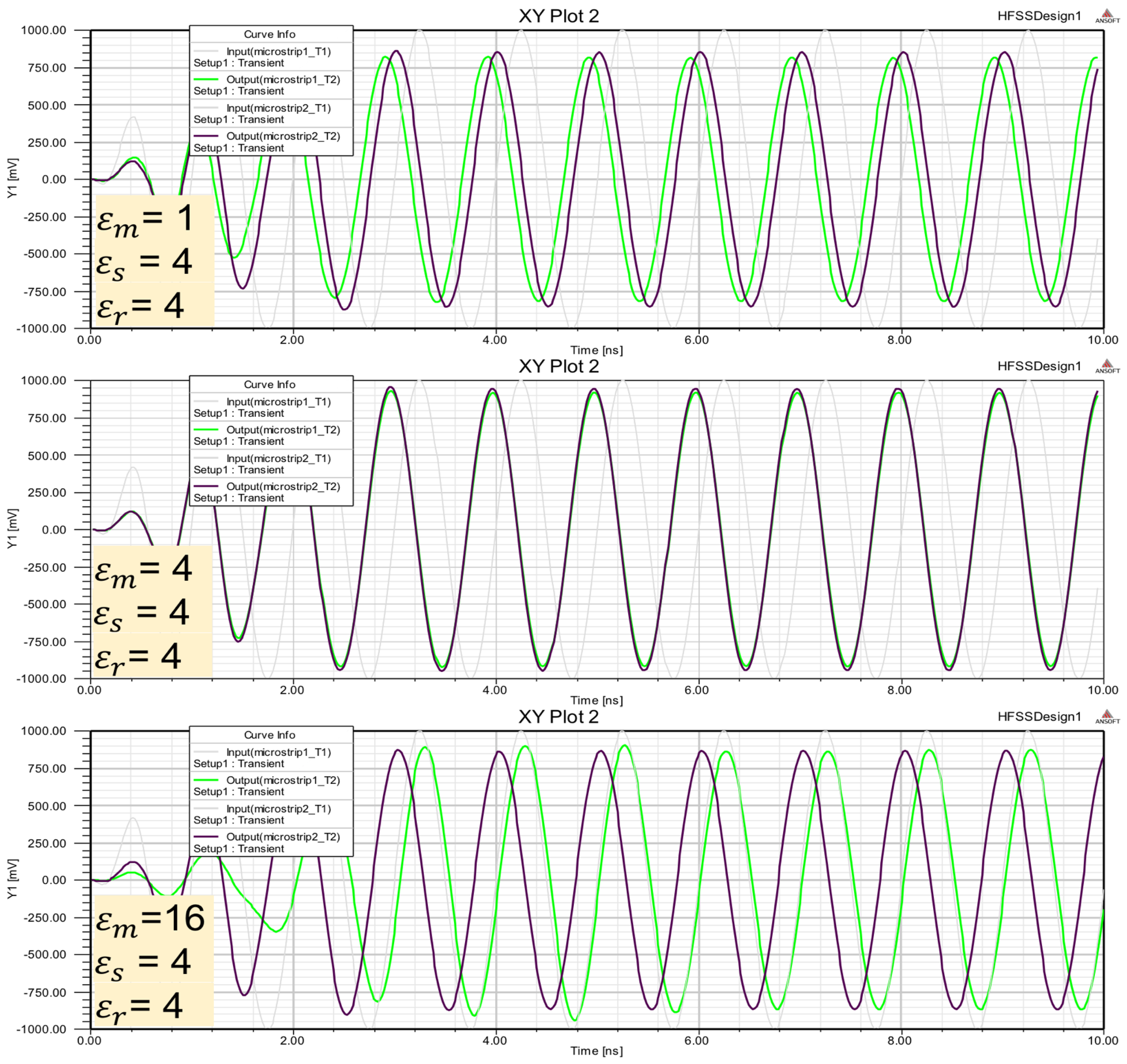
A numeric simulation was realized using HFSS software (
Figure 11) to test these assumptions.
Estimations of the wave phase incursion
in the different sub-domains of the system sensor-medium where:
f is frequency in
,
m/s,
is the dielectric permittivity of the sub-domain and
l is its linear size. The electromagnetic wave propagation processes can be neglected if
in selected frequency range, and thus the electromagnetic field can be assumed to have an electrostatic character. According to the electrostatic approach, the sensor coupled to skin and under-lying tissue can be considered as a lump capacitance element
C in parallel with the resistance
R. Thus, the description of the microstrip sensor can be reduced to an
resonant circuit. Parameters
C and
R are t unknown functions of these space distributions. The simplification of the sensor to a resonant circuit with lumped elements, allows to consider the sensor coupled to the medium unknown in terms of
C and
R parameters. Unknown medium are characterized by differential measure (
). The influence of dielectric medium on signal propagation is reflected in effective permittivity of the microstrip, which depends on medium placed over miscrostrip, in this case a dielectric material known and other unknown. There are several differential measures in
that can show unknown material information:
Differential phase shift
Differential electrical field
Other differential measures (impedances, signal loss, etc.)
Differential phase shift and electric field energy are analyzed in simulations on microstrip configuration shown in
Figure 9.
6.1. Differential Measure Based in Phase Shift
A sinusoidal signal (
) is considered. This signal propagates along the transmission line in order to determine the impact of the physical parameters of the microstrip measuring phase shift. At the beginning of line, at the moment
, the phase of the signal is
. At the end of the line, the moment is
, and its phase is
. The phase (
) at the end depends on electrical length (
), and the wavelength on dielectric medium (
):
like propagation velocity in the medium (
) and the wavelength (
) are :
then:
Using microstrip line configuration (
Figure 11) differential measure are:
is measured at the end of the line,
is a reference (known permittivity) and the
is the unknown permittivity, calculated using HFSS simulation. The thickness of the dielectric substrate is 0.8 mm. The width of the microstrip line is
mm, while the length is 25 mm. Substrate material is FR4_epoxy (with
and a surface of
mm).
Numerical data in
Table 4 shows the differential measures obtained at the end of microstrip line, considering frequencies between 1 and 8 GHz (rows) and a reference permittivity of
.
Simulations in HFSS software is shown in
Figure 12.
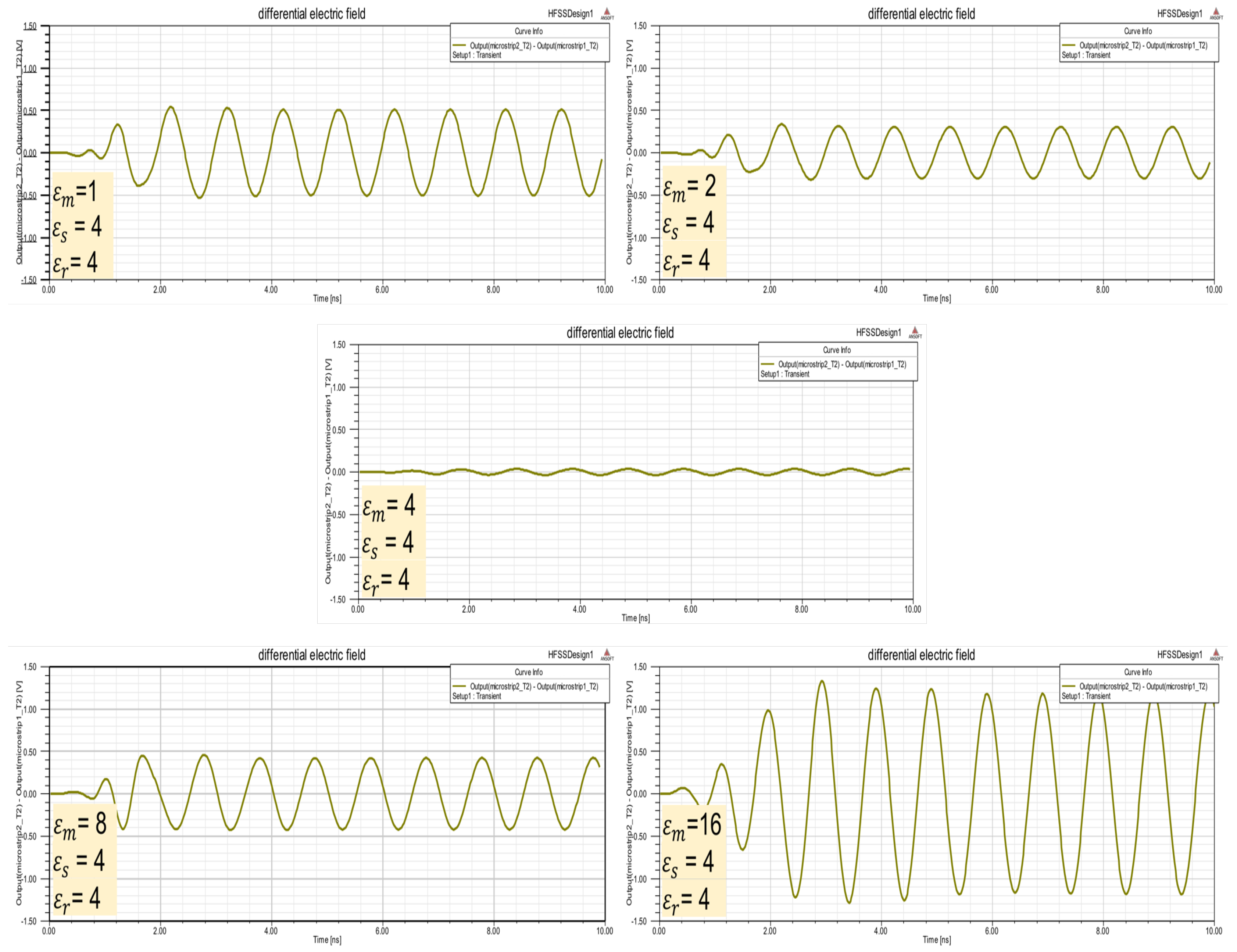
6.2. Differential Measure Based in Electrical Field
A sinusoidal signal (
) is considered. This signal propagates along the transmission line in order to determine electrical fields on the microstrip lines. Signal propagates along
x:
where
In dilectric medium
, substituting these in Equations (
18), (
19) and simplifying:
Considering dielectric medium, differential measures are:
Using HFSS software and construction shown in
Figure 11, differential electric field obtained in
is in
Figure 13. This table differential measurements confirm that when the unknown permittivity (
) is different to reference permittivity (
) electric field increases.
6.3. Microstrip Sensors
Differential electric field and phase shift simulations confirm potential use of sensors based on microstrip lines (
Figure 14). Permittivity of an unknown material can be characterized using microstrip lines configuration. Accuracy values depend on different factors that must be considered (temperature, connection terminals, materials, etc.) and it is not easy to obtain. Nevertheless, reference permittivities can be used to detect if unknown material has the same permittivity or approximate. In these cases detector sensors have easy applicability. An example of this functionality is simulated using a microstrip formed by three modules (
Figure 15). The goal is to detect if material permittivity is between minimum and maximum local values, and if it is near to the medium value. This example is useful when permittivity is variable over time (biological tissues) and it is necessary to detect limit values.
Electric fields and phase shift sign obtained in
Table 5 provide data to design an heuristic model based in rules like:
Analyzing numeric results in multi reference microstrip simulation, some rules have been defined.
6.4. Simulation Platform and Other Electromagnetic Effects (Dielectric Losses and Materials)
This work analyze a new way to take advantage of current technologies (microstrip, stripline transmission, etc.) proposing a method to design sensors using configurations that measure signal differences. Hardware devices that produce and measure those differences must be adapted or built. This work validates this new method using a software platform that reproduce real conditions: ANSYS HFSS. This software is an industry standard for simulating high-frequency electromagnetic fields. Its gold-standard accuracy, advanced solvers and high-performance computing technologies make it an essential tool for researchers and engineers tasked with executing accurate and rapid test and design in high-frequency and high-speed electronic devices and platforms. HFSS offers state-of the-art solver technologies based on finite element, integral equation, asymptotic and advanced hybrid methods to solve a wide range of microwave, RF and high-speed digital applications [
32]. Other effects like dielectric losses can be used to calculate material permittivity. If substrate used as a reference produce different losses than the unknown material substrate then the differences measured in receiver can be used in differential functions to determinate unknown material.
The simulation method is tested using relative dielectric constant of air and solids materials in range , without conductivity (). For other materials with more dielectric constant and conductivity, differences obtained will be more measurable. Reference material has values. These values represent solids with reference permittivity known. In real development, references are known and can be different.
First, potential differences are theoretically calculated, using this model, to analyze measurable signals in the receiver. Finally, sensors will be built to take advantage of these differences.