Spatiotemporal Recurrent Convolutional Networks for Traffic Prediction in Transportation Networks
Abstract
:1. Introduction
- We developed a hybrid model named the SRCN that combines DCNNs and LSTMs to forecast network-wide traffic speeds.
- We proposed a novel traffic network representation method, which can retain the structure of the transport network at a fine scale.
- The special-temporal features of network traffic are modeled as a video, where each traffic condition is treated as one frame of the video. In the proposed SRCN architecture, the DCNNs capture the near- and far-side spatial dependencies from the perspective of the network, whereas the LSTMs learn the long-term temporal dependency. By the integration of DCNNs and LSTMs, we analyze the spatiotemporal network-wide traffic data.
2. Literature Review
2.1. Parametric Approaches
2.2. Nonparametric Approaches
3. Methodology
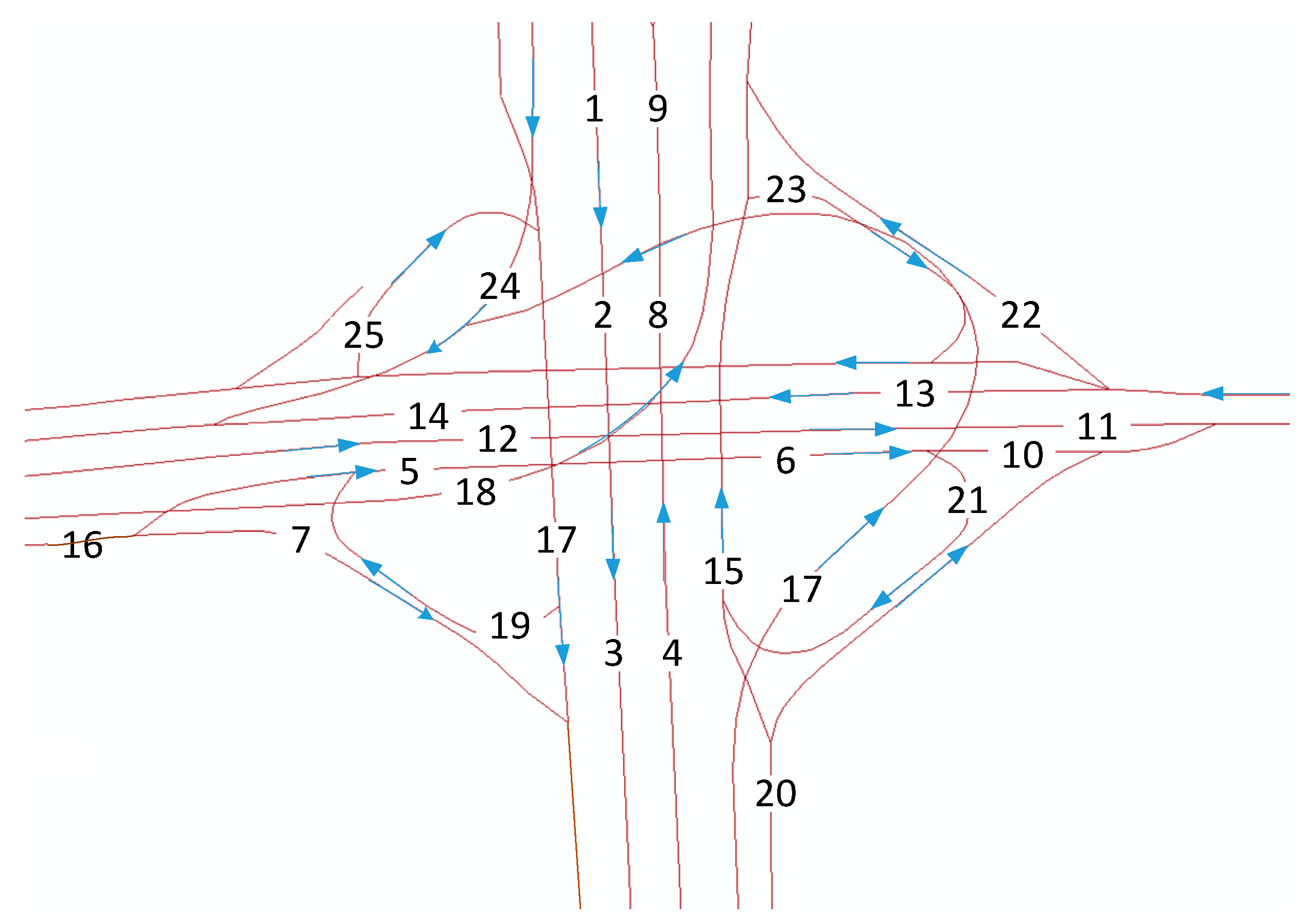
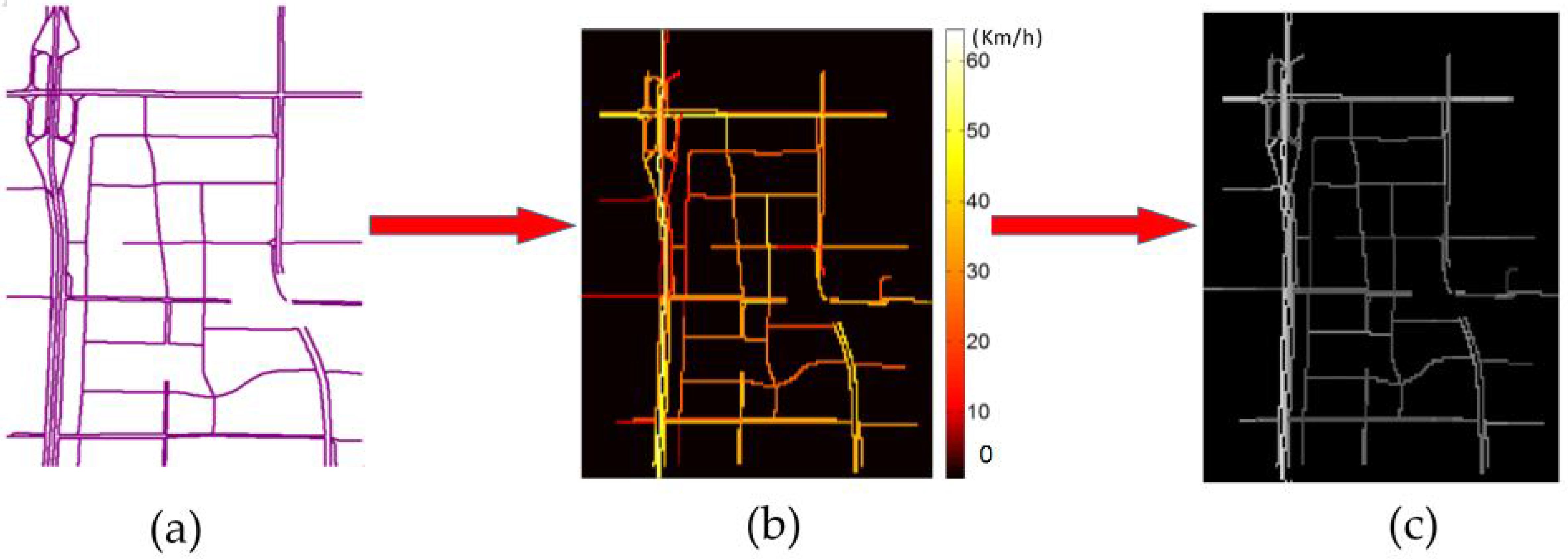
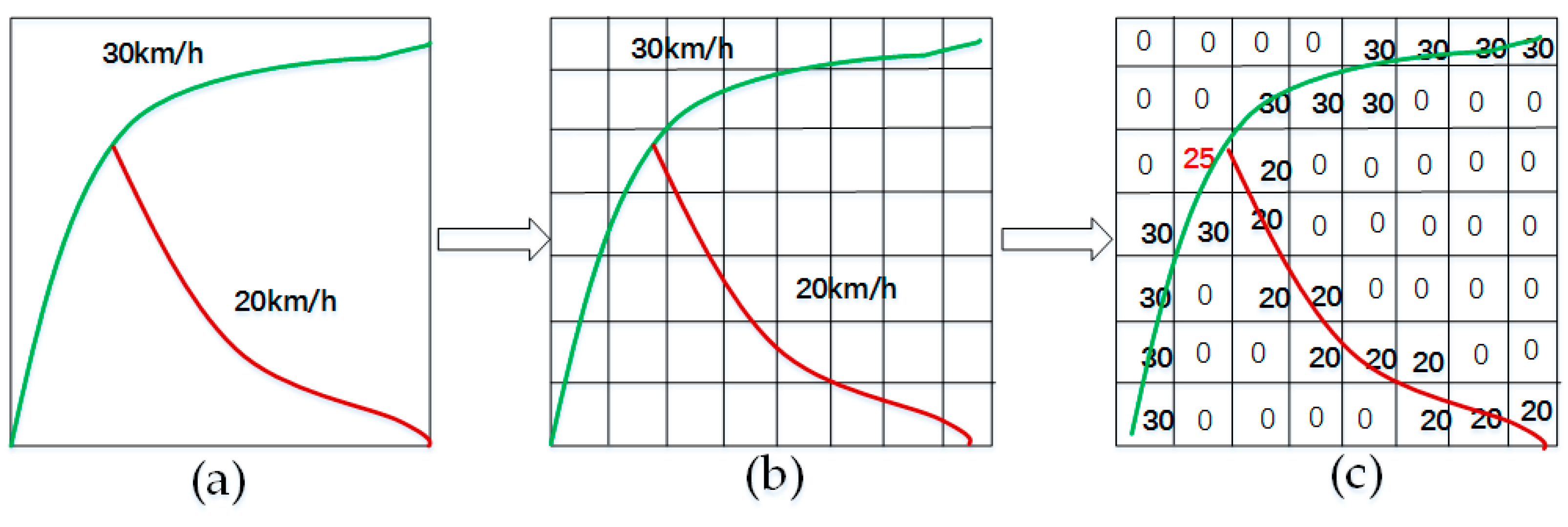
3.1. Network Representation
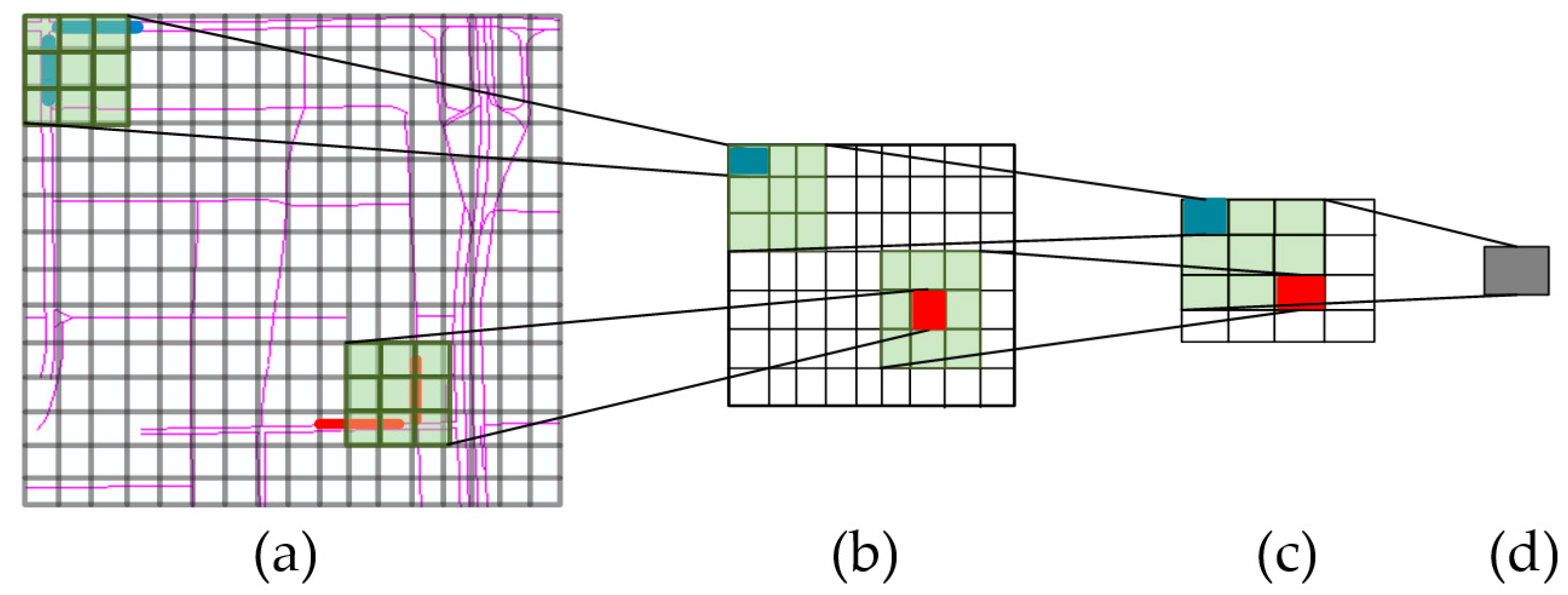
3.2. Spatial Features Captured by a CNN
3.3. Long Short-Term Temporal Features
3.4. Spatiotemporal Recurrent Convolutional Networks
4. Empirical Study
4.1. Data Source
4.2. Implementation
4.3. Comparison and Analysis of Results
4.4. Short-Term Prediction
4.5. Long-Term Prediction
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Asif, M.T.; Dauwels, J.; Goh, C.Y.; Oran, A. Spatiotemporal Patterns in Large-Scale Traffic Speed Prediction. IEEE Trans. Intell. Transp. Syst. 2014, 15, 794–804. [Google Scholar] [CrossRef]
- Ma, X.; Liu, C.; Wen, H.; Wang, Y.; Wu, Y.J. Understanding commuting patterns using transit smart card data. J. Transp. Geogr. 2017, 58, 135–145. [Google Scholar] [CrossRef]
- Yang, S. On feature selection for traffic congestion prediction. Transp. Res. Part C 2013, 26, 160–169. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Y.; Qi, D.; Li, R.; Yi, X. DNN-based prediction model for spatio-temporal data. In Proceedings of the ACM Sigspatial International Conference on Advances in Geographic Information Systems, San Francisco, CA, USA, 31 October–3 November 2016. [Google Scholar]
- He, Z.; Zheng, L.; Chen, P.; Guan, W. Mapping to Cells: A Simple Method to Extract Traffic Dynamics from Probe Vehicle Data. Comput. Aided Civ. Infrastruct. Eng. 2017, 32, 252–267. [Google Scholar] [CrossRef]
- Walker, J.; Gupta, A.; Hebert, M. Dense Optical Flow Prediction from a Static Image. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 2443–2451. [Google Scholar]
- Pavel, M.S.; Schulz, H.; Behnke, S. Object class segmentation of RGB-D video using recurrent convolutional neural networks. Neural Netw. 2017, 88, 105–113. [Google Scholar] [CrossRef] [PubMed]
- Qin, P.; Xu, W.; Guo, J. An empirical convolutional neural network approach for semantic relation classification. Neurocomputing 2016, 190, 1–9. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Y.; Qi, D. Deep Spatio-Temporal Residual Networks for Citywide Crowd Flows Prediction. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence (AAAI-17), San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Yu, H.; Wang, Y.; Wang, Y. Large-Scale Transportation Network Congestion Evolution Prediction Using Deep Learning Theory. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Chen, W.; Wu, X.; Chen, P.C.; Liu, J. LSTM network: A deep learning approach for short-term traffic forecast. IET Intell. Transp. Syst. 2017, 11, 68–75. [Google Scholar] [CrossRef]
- Van Lint, H.; van Hinsbergen, C. Short-Term Traffic and Travel Time Prediction Models. Transp. Res. E Circ. 2012, 22, 22–41. [Google Scholar]
- Hamed, M.M.; Al-Masaeid, H.R.; Said, Z.M.B. Short-Term Prediction of Traffic Volume in Urban Arterials. J. Transp. Eng. 1995, 121, 249–254. [Google Scholar] [CrossRef]
- Ding, Q.Y.; Wang, X.F.; Zhang, X.Y.; Sun, Z.Q. Forecasting Traffic Volume with Space-Time ARIMA Model. Adv. Mater. Res. 2010, 156–157, 979–983. [Google Scholar] [CrossRef]
- Chandra, S.R.; Al-Deek, H. Predictions of Freeway Traffic Speeds and Volumes Using Vector Autoregressive Models. J. Intell. Transp. Syst. 2009, 13, 53–72. [Google Scholar] [CrossRef]
- Guo, J.; Huang, W.; Williams, B.M. Adaptive Kalman filter approach for stochastic short-term traffic flow rate prediction and uncertainty quantification. Transp. Res. Part C Emerg. Technol. 2014, 43, 50–64. [Google Scholar] [CrossRef]
- Van Lint, J.W.C. Online Learning Solutions for Freeway Travel Time Prediction. IEEE Trans. Intell. Transp. Syst. 2008, 9, 38–47. [Google Scholar] [CrossRef]
- Chen, H.; Grant-Muller, S. Use of sequential learning for short-term traffic flow forecasting. Transp. Res. Part C Emerg. Technol. 2001, 9, 319–336. [Google Scholar] [CrossRef]
- Hosseini, S.H.; Moshiri, B.; Rahimi-Kian, A.; Araabi, B.N. Short-term traffic flow forecasting by mutual information and artificial neural networks. In Proceedings of the IEEE International Conference on Industrial Technology, Athens, Greece, 19–21 March 2012; pp. 1136–1141. [Google Scholar]
- Williams, B.; Durvasula, P.; Brown, D. Urban Freeway Traffic Flow Prediction: Application of Seasonal Autoregressive Integrated Moving Average and Exponential Smoothing Models. Transp. Res. Rec. 1998, 1644, 132–141. [Google Scholar] [CrossRef]
- Chan, K.Y.; Dillon, T.S.; Singh, J.; Chang, E. Neural-Network-Based Models for Short-Term Traffic Flow Forecasting Using a Hybrid Exponential Smoothing and Levenberg-Marquardt Algorithm. IEEE Trans. Intell. Transp. Syst. 2012, 13, 644–654. [Google Scholar] [CrossRef]
- Evgeniou, T.; Pontil, M.; Poggio, T. Regularization Networks and Support Vector Machines. Adv. Comput. Math. 2000, 13, 1–50. [Google Scholar] [CrossRef]
- Wang, J.; Shi, Q. Short-Term Traffic Speed Forecasting Hybrid Model Based on Chaos-Wndash Analysis-Support Vector Machine theory. Transp. Res. Part C Emerg. Technol. 2013, 27, 219–232. [Google Scholar] [CrossRef]
- Cong, Y.; Wang, J.; Li, X. Traffic Flow Forecasting by a Least Squares Support Vector Machine with a Fruit Fly Optimization Algorithm. Procedia Eng. 2016, 137, 59–68. [Google Scholar] [CrossRef]
- Gu, Y.; Wei, D.; Zhao, M. A New Intelligent Model for Short Time Traffic Flow Prediction via EMD and PSO-SVM. Lect. Notes Electr. Eng. 2012, 113, 59–66. [Google Scholar]
- Yang, Z.; Mei, D.; Yang, Q.; Zhou, H.; Li, X. Traffic Flow Prediction Model for Large-Scale Road Network Based on Cloud Computing. Math. Probl. Eng. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Karlaftis, M.G.; Vlahogianni, E.I. Statistical methods versus neural networks in transportation research: Differences, similarities and some insights. Transp. Res. Part C Emerg. Technol. 2011, 19, 387–399. [Google Scholar] [CrossRef]
- Huang, S.H.; Ran, B. An Application of Neural Network on Traffic Speed Prediction under Adverse Weather Condition. In Proceedings of the Transportation Research Board Annual Meeting, Washington, DC, USA, 12–16 January 2003. [Google Scholar]
- Khotanzad, A.; Sadek, N. Multi-scale high-speed network traffic prediction using combination of neural networks. In Proceedings of the International Joint Conference on Neural Networks, Portland, OR, USA 20–24 July 2003; Volume 2, pp. 1071–1075. [Google Scholar]
- Qiu, C.; Wang, C.; Zuo, X.; Fang, B. A Bayesian regularized neural network approach to short-term traffic speed prediction. In Proceedings of the 2011 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Anchorage, AK, USA, 9–12 October 2011; pp. 2215–2220. [Google Scholar]
- Huang, W.; Song, G.; Hong, H.; Xie, K. Deep Architecture for Traffic Flow Prediction: Deep Belief Networks With Multitask Learning. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2191–2201. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z. Traffic Flow Prediction with Big Data: A Deep Learning Approach. IEEE Trans. Intell. Transp. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
- Tan, H.; Xuan, X.; Wu, Y.; Zhong, Z.; Ran, B. A Comparison of Traffic Flow Prediction Methods Based on DBN. In Proceedings of the Cota International Conference of Transportation Professionals, Shanghai, China, 6–9 June 2016; pp. 273–283. [Google Scholar]
- Yang, H.F.; Dillon, T.S.; Chen, Y.P. Optimized Structure of the Traffic Flow Forecasting Model with a Deep Learning Approach. IEEE Trans. Neural Netw. Learn. Syst. 2016, 99, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Tian, Y.; Pan, L. Predicting Short-Term Traffic Flow by Long Short-Term Memory Recurrent Neural Network. In Proceedings of the IEEE International Conference on Smart City Socialcom Sustaincom, Chengdu, China, 19–21 December 2015; pp. 153–158. [Google Scholar]
- Chen, Y.; Lv, Y.; Li, Z.; Wang, F. Long short-term memory model for traffic congestion prediction with online open data. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 132–137. [Google Scholar]
- Fu, R.; Zhang, Z.; Li, L. Using LSTM and GRU neural network methods for traffic flow prediction. In Proceedings of the Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 11–13 November 2016; pp. 324–328. [Google Scholar]
- Wu, Y.; Tan, H. Short-Term Traffic Flow Forecasting with Spatial-Temporal Correlation in a Hybrid Deep Learning Framework. 2016. Available online: https://arxiv.org/abs/1612.01022 (accessed on 22 June 2017).
- He, Z.; Zheng, L. Visualizing Traffic Dynamics Based on Floating Car Data. J. Transp. Eng. Part A Syst. 2017, 143. [Google Scholar] [CrossRef]
- Vinyals, O.; Toshev, A.; Bengio, S.; Erhan, D. Show and Tell: A Neural Image Caption Generator. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3156–3164. [Google Scholar]
- Donahue, J.; Hendricks, L.A.; Rohrbach, M.; Venugopalan, S.; Guadarrama, S.; Saenko, K.; Darrell, T. Long-Term Recurrent Convolutional Networks for Visual Recognition and Description. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 677–691. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yu, L.C.; Lai, K.R.; Zhang, X. Dimensional Sentiment Analysis Using a Regional CNN-LSTM Model. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics, Berlin, Germany, 7–12 August 2016; pp. 225–230. [Google Scholar]
- Lecun, Y.; Bengio, Y. Convolutional Networks for Images, Speech, and Time-Series. In The Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 9, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.; Srivastava, N; Swersky, K. Lecture 6a Overview of Mini-Batch Gradient Descent. Lecture Notes Distributed in CSC321 of University of Toronto. 2014. Available online: http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf (accessed on 22 June 2017).
- Schaul, T.; Antonoglou, I.; Silver, D. Unit Tests for Stochastic Optimization. Nihon Naika Gakkai Zasshi J. Jpn. Soc. Int. Med. 2014, 102, 1474–1483. [Google Scholar]
- Sturm, B.L.; Santos, J.F.; Bental, O.; Korshunova, I. Music Transcription Modelling and Composition Using Deep Learning. 2016. Available online: https://arxiv.org/abs/1604.08723 (accessed on 22 June 2017).
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Ma, X.; Dai, Z.; He, Z.; Ma, J.; Wang, Y.; Wang, Y. Learning traffic as images: A deep convolutional neural network for large-scale transportation network speed prediction. Sensors 2017, 17, 818. [Google Scholar] [CrossRef] [PubMed]
- Chollet, F. Keras. Available online: https://github.com/fchollet/keras (accessed on 22 June 2017).
- Ryan, J.; Summerville, A.J.; Mateas, M.; Wardrip-Fruin, N. Translating Player Dialogue into Meaning Representations Using LSTMs. In Proceedings of the Intelligent Virtual Agents Conference, Los Angeles, CA, USA, 20–23 September 2016; pp. 383–386. [Google Scholar]
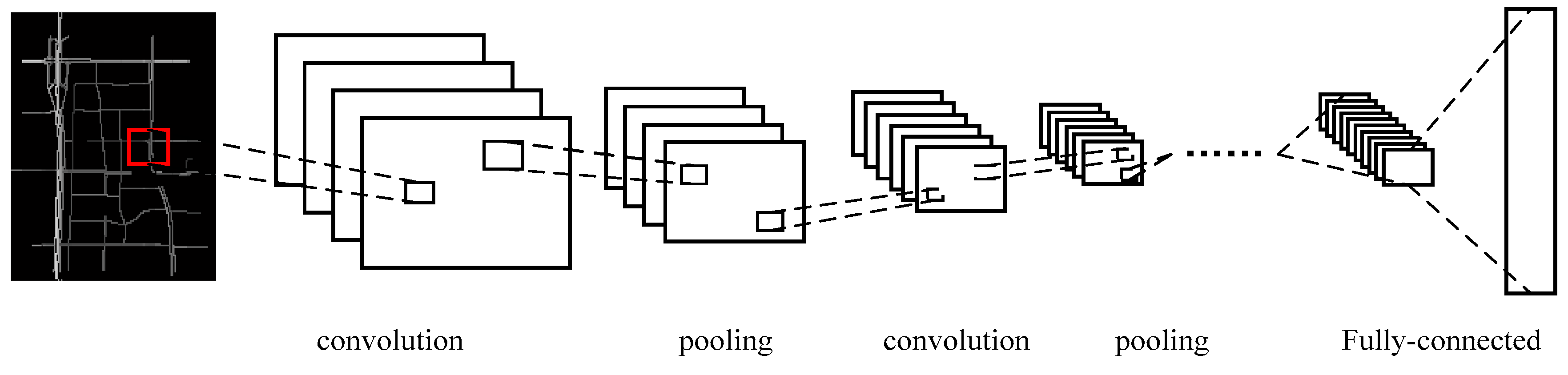
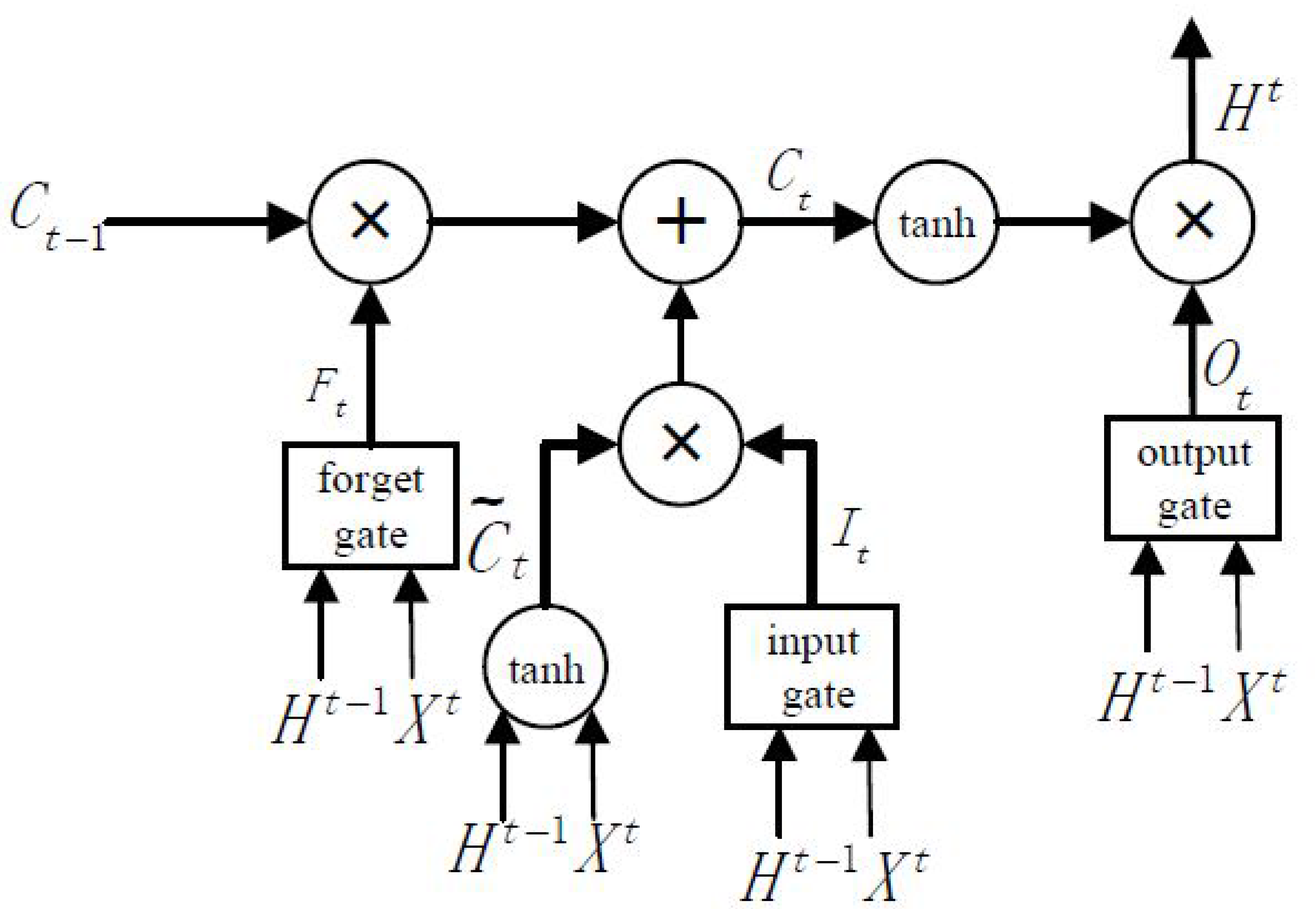
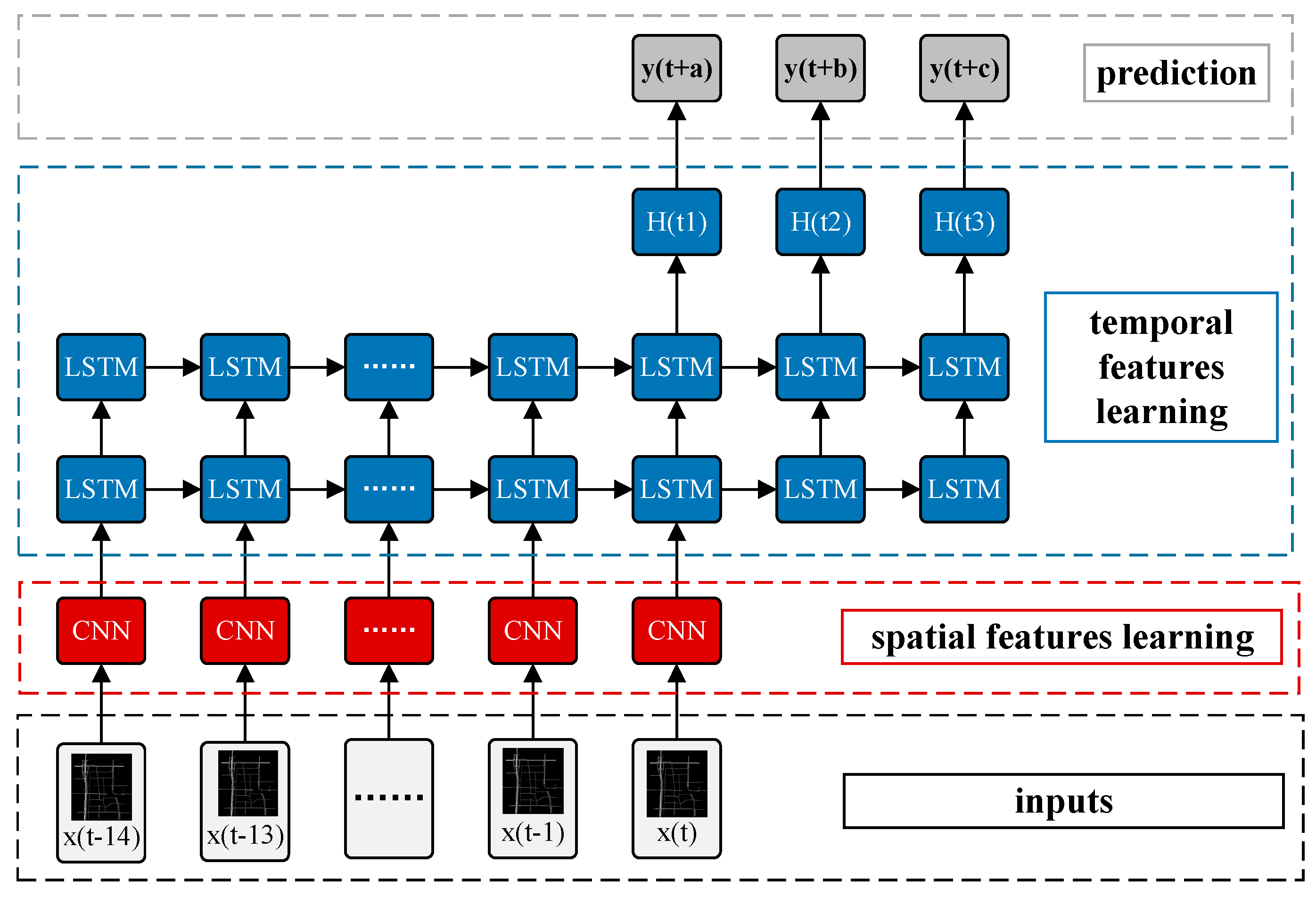
| Layer | Name | Channels | Size |
|---|---|---|---|
| 0 | Inputs | 1 | (163,148) |
| 1 | Convolution | 16 | (3,3) |
| Max-pooling | 16 | (2,2) | |
| Activation (relu) | —— | —— | |
| Batch-normalization | —— | —— | |
| 2 | Convolution | 32 | (3,3) |
| Max-pooling | 32 | (2,2) | |
| Activation (relu) | —— | —— | |
| Batch-normalization | —— | —— | |
| 3 | Convolution | 64 | (3,3) |
| Activation (relu) | —— | —— | |
| Batch-normalization | —— | —— | |
| 4 | Convolution | 64 | (3,3) |
| Activation (relu) | —— | —— | |
| Batch-normalization | —— | —— | |
| 5 | Convolution | 128 | (3,3) |
| Max-pooling | 128 | (2,2) | |
| Activation (relu) | —— | —— | |
| Batch-normalization | —— | —— | |
| 6 | Flatten | —— | —— |
| 7 | Fully connected | —— | 278 |
| 8 | Lstm1 | —— | 800 |
| Activation (tanh) | —— | ||
| 9 | Lstm2 | —— | 800 |
| Activation (tanh) | —— | —— | |
| 10 | Dropout (0.2) | —— | —— |
| 11 | Fully connected | —— | 278 |
| Time Steps | 2 min | 4 min | 6 min | Average Error | |||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | MAPE | RMSE | MAPE | RMSE | MAPE | RMSE | MAPE | RMSE | |
| SRCNs | 0.1269 | 4.9258 | 0.1271 | 5.0124 | 0.1272 | 5.0612 | 0.1270 | 4.9998 | |
| LSTMs | 0.1630 | 6.1521 | 0.1731 | 6.8721 | 0.1781 | 7.0016 | 0.1714 | 6.7527 | |
| SAEs | 0.1591 | 6.2319 | 0.1718 | 6.8737 | 0.1742 | 7.2602 | 0.1684 | 6.7886 | |
| DCNNs | 0.1622 | 6.6509 | 0.1724 | 6.8516 | 0.1775 | 7.2845 | 0.1707 | 6.9290 | |
| SVM | 0.1803 | 7.6036 | 0.2016 | 8.0132 | 0.2123 | 8.2346 | 0.1984 | 7.9505 | |
| Time Steps | 20 min | 40 min | 60 min | Average Error | |||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | MAPE | RMSE | MAPE | RMSE | MAPE | RMSE | MAPE | RMSE | |
| SRCNs | 0.1661 | 6.0569 | 0.1753 | 6.5631 | 0.1889 | 6.8516 | 0.1768 | 6.4905 | |
| LSTMs | 0.1700 | 7.1857 | 0.1872 | 7.7322 | 0.2003 | 7.9843 | 0.1858 | 7.6340 | |
| SAEs | 0.2045 | 7.2374 | 0.2139 | 7.9737 | 0.2228 | 8.2881 | 0.2137 | 7.8331 | |
| DCNNs | 0.2018 | 7.6608 | 0.2531 | 8.8613 | 0.3264 | 12.5846 | 0.2604 | 9.7022 | |
| SVM | 0.3469 | 12.9577 | 0.3480 | 13.181 | 0.3621 | 13.4676 | 0.3542 | 13.2021 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Wu, Z.; Wang, S.; Wang, Y.; Ma, X. Spatiotemporal Recurrent Convolutional Networks for Traffic Prediction in Transportation Networks. Sensors 2017, 17, 1501. https://doi.org/10.3390/s17071501
Yu H, Wu Z, Wang S, Wang Y, Ma X. Spatiotemporal Recurrent Convolutional Networks for Traffic Prediction in Transportation Networks. Sensors. 2017; 17(7):1501. https://doi.org/10.3390/s17071501
Chicago/Turabian StyleYu, Haiyang, Zhihai Wu, Shuqin Wang, Yunpeng Wang, and Xiaolei Ma. 2017. "Spatiotemporal Recurrent Convolutional Networks for Traffic Prediction in Transportation Networks" Sensors 17, no. 7: 1501. https://doi.org/10.3390/s17071501
APA StyleYu, H., Wu, Z., Wang, S., Wang, Y., & Ma, X. (2017). Spatiotemporal Recurrent Convolutional Networks for Traffic Prediction in Transportation Networks. Sensors, 17(7), 1501. https://doi.org/10.3390/s17071501





