Vicarious Calibration of sUAS Microbolometer Temperature Imagery for Estimation of Radiometric Land Surface Temperature
Abstract
:1. Introduction
1.1. Microbolometers UAS Temperature Cameras
1.2. Atmospheric Correction of Surface Temperature
2. Materials and Methods
2.1. Study Site
2.2. AggieAir sUAS
2.3. Methods
3. Results and Discussion
3.1. Before Flight
3.2. During Flight
3.3. After Flight
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Handcock, R.N.; Torgersen, C.E.; Cherkauer, K.A.; Gillespie, A.R.; Klement, T.; Faux, R.N.; Jing, T. Thermal Infrared Remote Sensing of Water Temperature in Riverine Landscapes. In Carbonneau/Fluvial Remote Sensing for Science and Management; Carbonneau, P.E., Piegay, H., Eds.; Wiley-Blackwell: Hoboken, UK; Hoboken, NJ, USA, 2012; pp. 85–113. [Google Scholar]
- Petropoulos, G.P. Remote Sensing of Energy Fluxes and Soil Moisture Content; CRC Press: Boca Raton, FL, USA, 2013; p. 546. [Google Scholar]
- Blonquist, J.M., Jr.; Norman, J.M.; Bugbee, B. Automated measurement of canopy stomatal conductance based on infrared temperature. Agric. For. Meteorol. 2009, 149, 2183–2197. [Google Scholar] [CrossRef]
- Apogee Instruments. Available online: http://www.apogeeinstruments.com/infraredradiometer/ (accessed on 24 February 2017).
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ. 2012, 122, 50–65. [Google Scholar] [CrossRef]
- Jackson, R.D.; Pinter, P.J. Detection of Water Stress in Wheat by Measurement of Reflected Solar and Emitted Thermal IR Radiation. In Proceedings of the Spectral Signatures of Objects in Remote Sensing, Avigion, France, 8–11 September 1981; pp. 399–406. [Google Scholar]
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Kogan, F.N. Operational space technology for global vegetation assessment. Bull. Am. Meteorol. Soc. 2001, 82, 1949–1964. [Google Scholar] [CrossRef]
- UMACCI Committee. Abrupt Impacts of Climate Change. Committee on Understanding and Monitoring Abrupt Climate Change and Its Impacts; National Academies Press: Washington, DC, USA, 2013; Volume 16, p. 201. [Google Scholar]
- Câmara, G. The Future of the CBERS Program: A View from Brazil. In Proceedings of the CBERS Chinese Users Conference, Beijing, China, 21 October 2003. [Google Scholar]
- Jensen, A.M.; McKee, M.; Chen, Y. Calibrating thermal imagery from an unmanned aerial system—AggieAir. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 21–26 July 2013; pp. 542–545. [Google Scholar]
- Cherkauer, K.A.; Burges, S.J.; Handcock, R.N.; Kay, J.E.; Kampf, S.K.; Gillespie, A.R. Assessing Satellite-Based and Aircraft-Based Thermal Infrared Remote Sensing for Monitoring Pacific Northwest River Temperature. J. Am. Water Resour. Assoc. 2005, 41, 1149–1159. [Google Scholar] [CrossRef]
- Hoffmann, H.; Nieto, H.; Jensen, R.; Guzinski, R.; Zarco-Tejada, P.; Friborg, T. Estimating evaporation with thermal UAV data and two-source energy balance models. Hydrol. Earth Syst. Sci. 2016, 20, 697–713. [Google Scholar] [CrossRef]
- Elarab, M.; Ticlavilca, A.M.; Torres-Rua, A.F.; Maslova, I.; McKee, M. Estimating chlorophyll with thermal and broadband multispectral high resolution imagery from an unmanned aerial system using relevance vector machines for precision agriculture. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 32–42. [Google Scholar] [CrossRef]
- Berni, J.A.J.; Zarco-Tejada, P.J.; Sepulcre-Cantó, G.; Fereres, E.; Villalobos, F. Mapping canopy conductance and CWSI in olive orchards using high resolution thermal remote sensing imagery. Remote Sens. Environ. 2009, 113, 2380–2388. [Google Scholar] [CrossRef]
- Hassan-Esfahani, L.; Torres-Rua, A.; Jensen, A.; McKee, M. Assessment of Surface Soil Moisture Using High-Resolution Multi-Spectral Imagery and Artificial Neural Networks. Remote Sens. 2015, 7, 2627–2646. [Google Scholar] [CrossRef]
- Torres-Rua, A.; Al Arab, M.; Hassan-Esfahani, L.; Jensen, A.; McKee, M. Development of unmanned aerial systems for use in precision agriculture: The AggieAir experience. In Proceedings of the 2015 IEEE Conference on Technologies for Sustainability (SusTech), Ogden, UT, USA, 30 July–1 August 2015; pp. 77–82. [Google Scholar]
- Hassan-Esfahani, L. High Resolution Multi-Spectral Imagery and Learning Machines in Precision Irrigation Water Management. Ph.D. Dissertation, Utah State University, Logan, UT, USA, 2015. [Google Scholar]
- Paul, G.; Gowda, P.H.; Prasad, P.V.V.; Howell, T.A.; Staggenborg, S.A.; Neale, C.M.U. Lysimetric evaluation of SEBAL using high resolution airborne imagery from BEAREX08. Adv. Water Resour. 2013, 59, 157–168. [Google Scholar] [CrossRef]
- Xia, T.; Kustas, W.P.; Anderson, M.C.; Alfieri, J.G.; Gao, F.; McKee, L.; Prueger, J.H.; Geli, H.M.E.; Neale, C.M.U.; Sanchez, L.; et al. Mapping evapotranspiration with high-resolution aircraft imagery over vineyards using one- and two-source modeling schemes. Hydrol. Earth Syst. Sci. 2016, 20, 1523–1545. [Google Scholar] [CrossRef]
- Neale, C.M.U.; Jayanthi, H.; Wright, J.L. Irrigation water management using high resolution airborne remote sensing. Irrig. Drain. Syst. 2005, 19, 321–336. [Google Scholar] [CrossRef]
- Glenn, E.P.; Neale, C.M.U.; Hunsaker, D.J.; Nagler, P.L. Vegetation index-based crop coefficients to estimate evapotranspiration by remote sensing in agricultural and natural ecosystems. Hydrol. Process. 2011, 25, 4050–4062. [Google Scholar] [CrossRef]
- Prueger, J.H.; Alfieri, J.G.; Hipps, L.E.; Kustas, W.P.; Chavez, J.L.; Evett, S.R.; Anderson, M.C.; French, A.N.; Neale, C.M.U.; McKee, L.G.; et al. Patch scale turbulence over dryland and irrigated surfaces in a semi-arid landscape under advective conditions during BEAREX08. Adv. Water Resour. 2012, 50, 106–119. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Barsi, J.A.; Barker, J.L.; Schott, J.R. An Atmospheric Correction Parameter Calculator for a single thermal band earth-sensing instrument. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS) (IEEE Cat. No.03CH37477), Toulouse, France, 21–25 July 2003; Volume 5, pp. 3014–3016. [Google Scholar]
- McCarville, D.; Buenemann, M.; Bleiweiss, M.; Barsi, J. Atmospheric correction of Landsat thermal infrared data: A calculator based on North American Regional Reanalysis (NARR) data. In Proceedings of the American Society for Photogrammetry and Remote Sensing Conference, Milwaukee, WI, USA, 1–5 May 2011; p. 12. [Google Scholar]
- Barsi, J.; Schott, J.; Hook, S.; Raqueno, N.; Markham, B.; Radocinski, R. Landsat-8 Thermal Infrared Sensor (TIRS) Vicarious Radiometric Calibration. Remote Sens. 2014, 6, 11607–11626. [Google Scholar] [CrossRef]
- Kotchenova, S.Y.; Vermote, E.F. Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data. Part II. Homogeneous Lambertian and anisotropic surfaces. Appl. Opt. 2007, 46, 4455–4464. [Google Scholar] [CrossRef] [PubMed]
- Kotchenova, S.Y.; Vermote, E.F.; Matarrese, R.; Klemm, F.J., Jr. Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data. Part I: Path radiance. Appl. Opt. 2006, 45, 6762–6774. [Google Scholar] [CrossRef] [PubMed]
- Kotchenova, S.Y.; Vermote, E.F.; Levy, R.; Lyapustin, A. Radiative transfer codes for atmospheric correction and aerosol retrieval: Intercomparison study. Appl. Opt. 2008, 47, 2215–2226. [Google Scholar] [CrossRef] [PubMed]
- Liddiard, K.C. The active microbolometer: A new concept in infrared detection. In Microelectronics, MEMS, and Nanotechnology; International Society for Optics and Photonics: Bellingham, DC, USA, 2004; pp. 227–238. [Google Scholar]
- Green, W.J.; Maurer, D.E. Merlin microbolometer camera calibration. In Proceedings of the Infrared Imaging Systems: Design, Analysis, Modeling, and Testing XII, Orlando, FL, USA, 16 April 2001. [Google Scholar]
- Behnken, B.N.; Karunasiri, G.; Chamberlin, D.R.; Robrish, P.R.; Faist, J. Real-time imaging using a 2.8 THz quantum cascade laser and uncooled infrared microbolometer camera. Opt. Lett. 2008, 33, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Irish, R.R. Landsat 7 Science Data Users Handbook; NASA Contract. Rep. NASA CR 2000; National Aeronautics and Space Administration: Houston, TX, USA, 2000.
- United States Geological Survey (USGS). Landsat 8 Data Users Handbook; USGS: Reston, VA, USA, 2016.
- Drinkwater, M.; Rebhan, H. Sentinel-3: Mission Requirements Document; EOP-SMO/1151/MD-md; European Space Agency (ESA): Paris, France, 2007; pp. 19–22. [Google Scholar]
- FLIR Systems, I. FLIR Systems|Thermal Imaging, Night Vision and Infrared Camera Systems. Available online: http://www.flir.com/home/ (accessed on 22 December 2016).
- Infrared & Thermal Camera Specialists. Available online: http://www.infraredcamerasinc.com/ (accessed on 22 December 2016).
- Srivastava, P.K.; Han, D.; Rico-Ramirez, M.A.; Bray, M.; Islam, T.; Gupta, M.; Dai, Q. Estimation of land surface temperature from atmospherically corrected LANDSAT TM image using 6S and NCEP global reanalysis product. Environ. Earth Sci. 2014, 72, 5183–5196. [Google Scholar] [CrossRef]
- Liang, S.; Fang, H.; Chen, M. Atmospheric correction of Landsat ETM+ land surface imagery—Part I: Methods. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2490–2498. [Google Scholar] [CrossRef]
- Liang, S.; Fang, H.; Chen, M.; Shuey, C.J.; Walthall, C.; Daughtry, C.; Morisette, J.; Schaaf, C.; Strahler, A. Validating MODIS land surface reflectance and albedo products: Methods and preliminary results. Remote Sens. Environ. 2002, 83, 149–162. [Google Scholar] [CrossRef]
- Gilmore, D.G.; Donabedian, M. Spacecraft Thermal Control Handbook: Cryogenics; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2003. [Google Scholar]
- Vollmer, M.; Möllmann, K.-P. Infrared Thermal Imaging: Fundamentals, Research and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Schott, J.R.; Brown, S.D.; Barsi, J.A. Calibration of thermal infrared sensors. In Thermal Remote Sensing in Land Surface Processing; Luvall, J.C., Ed.; CRC PRESS: Boca Raton, FL, USA, 2004. [Google Scholar]
- Berk, A.; Conforti, P.; Hawes, F. An accelerated line-by-line option for MODTRAN combining on-the-fly generation of line center absorption within 0.1 cm-1 bins and pre-computed line tails. In SPIE Defense + Security; International Society for Optics and Photonics: Baltimore, MD, USA, 20 April 2015; pp. 947217-1–947217-11. [Google Scholar]
- Berk, A.; Conforti, P.; Kennett, R.; Perkins, T.; Hawes, F.; van den Bosch, J. MODTRAN6: A major upgrade of the MODTRAN radiative transfer code. In SPIE Defense + Security; International Society for Optics and Photonics: Baltimore, MD, USA, 5 May 2014; pp. 90880H-1–90880H-7. [Google Scholar]
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Sabatini, R.; Richardson, M.A.; Jia, H.; Zammit-Mangion, D. Airborne laser systems for atmospheric sounding in the near infrared. In SPIE Photonics Europe; International Society for Optics and Photonics: Brussels, Belgium, 16 April 2012; pp. 843314-1–843314-40. [Google Scholar]
- Evans, H.; Lange, J.; Schmitz, J. The Phenomenology of Intelligence-Focused Remote Sensing: Volume 1: Electro-Optical Remote Sensing; Riverside Research: New York, NY, USA, 2013. [Google Scholar]
- E. & J. Gallo Winery. Available online: http://www.gallo.com/ (accessed on 21 June 2017).
- Harvey, M.C.; Luketina, K. Thermal Infrared Cameras and Drones: A Match Made in Heaven for Cost-Effective Geothermal Exploration, Monitoring and Development. In Proceedings of the 37th New Zealand Geothermal Workshop, Taupo, New Zealand, 18–20 November 2015; Volume 18, p. 20. [Google Scholar]
- Cassis, L.A.; Urbas, A.; Lodder, R.A. Hyperspectral integrated computational imaging. Anal. Bioanal. Chem. 2005, 382, 868–872. [Google Scholar] [CrossRef] [PubMed]
- Harvey, M.; Harvey, C.; Rowland, J.; Luketina, K. Drones in Geothermal Exploration: Thermal Infrared Imagery, Aerial Photos and Digital Elevation Models. In Proceedings of the 6th African Rift Geothermal Conference, Addis Ababa, Ethiopia, 2–4 November 2016; p. 12. [Google Scholar]
- Nugent, P.W. Wide-angle Infrared Cloud Imaging for Cloud Cover Statistics. Master’s Thesis, Montana State University, Bozeman, USA, 2008. [Google Scholar]
- PalmerWahl. Available online: http://www.palmerwahl.com/ (accessed on 21 June 2017).
- AgiSoft, L. Agisoft PhotoScan Professional Edition, version 1.0.3; Agisoft PhotoScan: St. Petersburg, Russia, 2014. [Google Scholar]
- Trimble. Available online: http://www.trimble.com/ (accessed on 21 June 2017).
- Torres-Rua, A.F.; Ticlavilca, A.M.; Walker, W.R.; McKee, M. Machine Learning Approaches for Error Correction of Hydraulic Simulation Models for Canal Flow Schemes. J. Irrig. Drain. Eng. 2012, 138, 999–1010. [Google Scholar] [CrossRef]
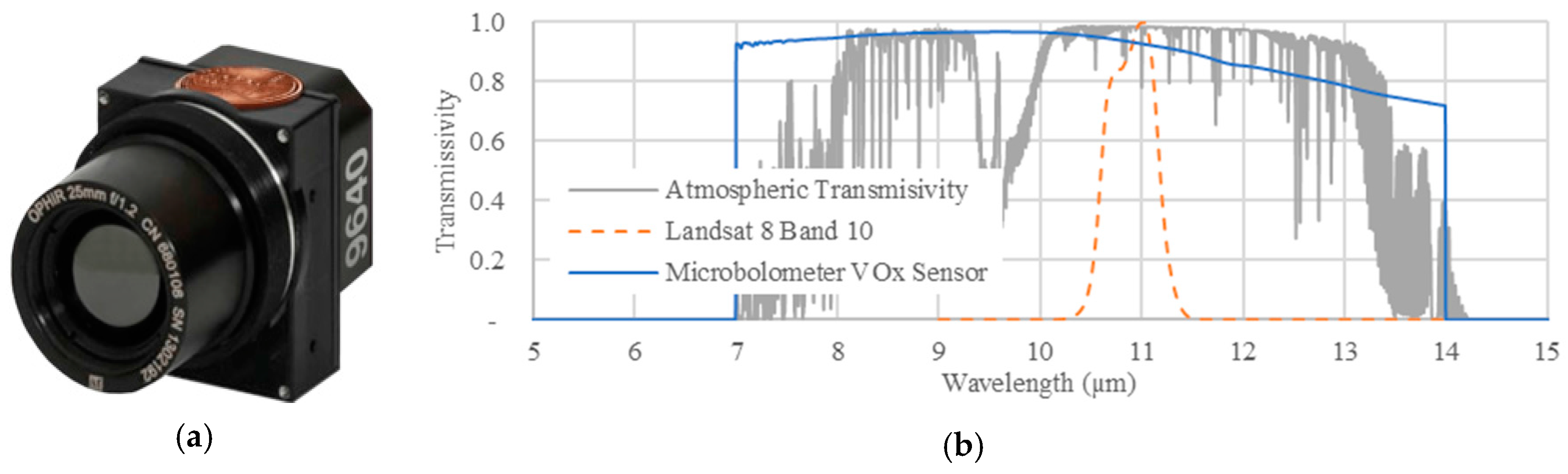
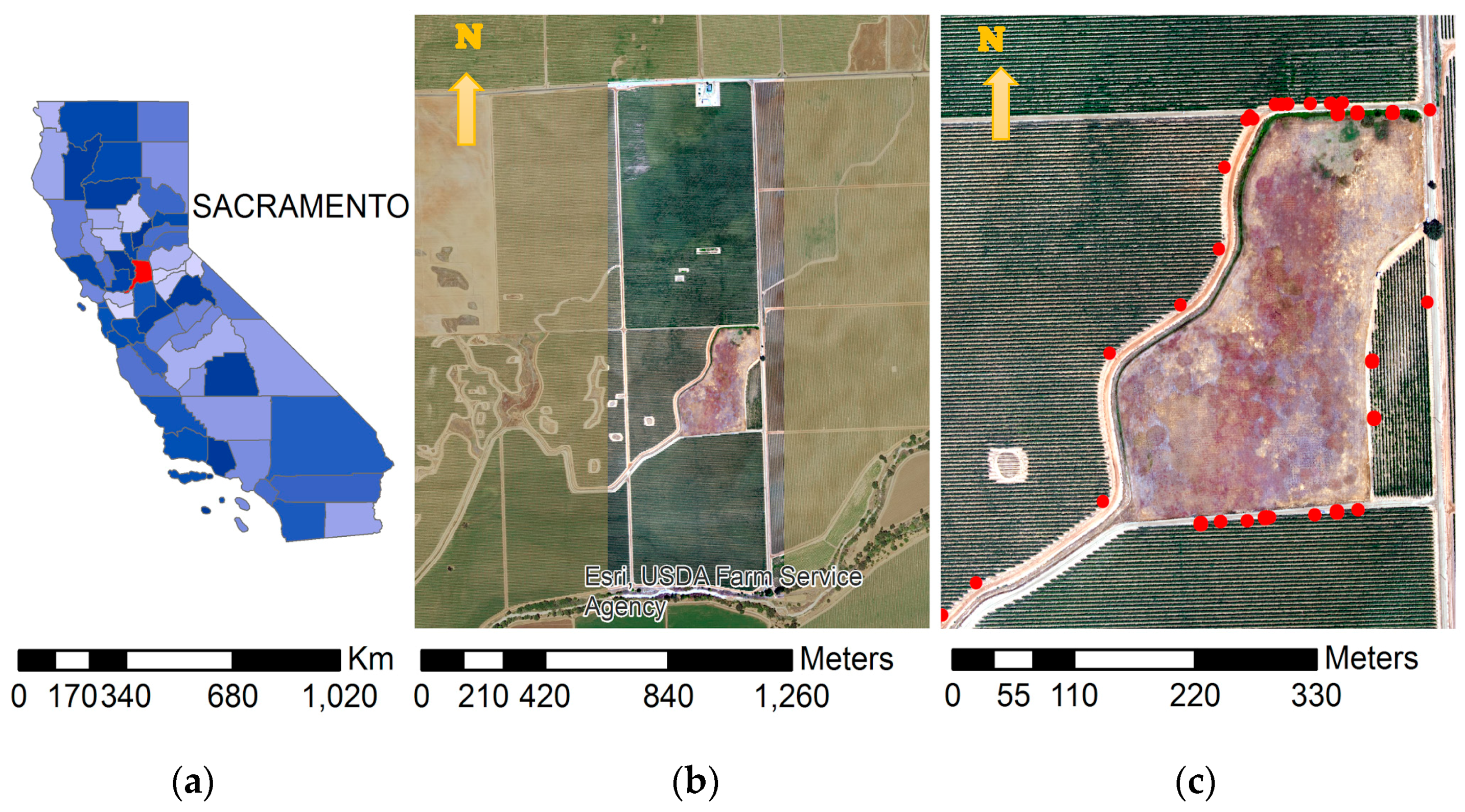


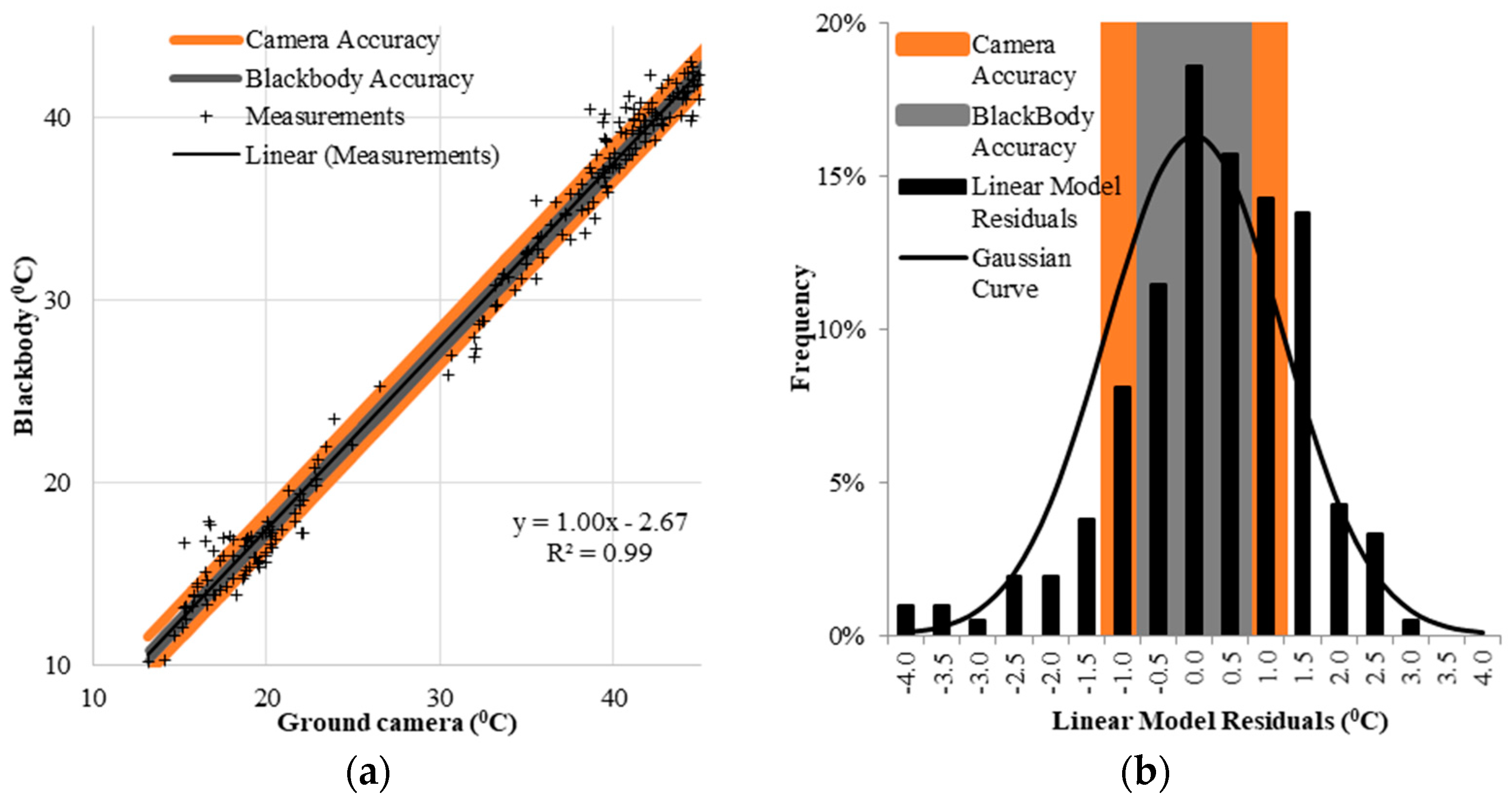

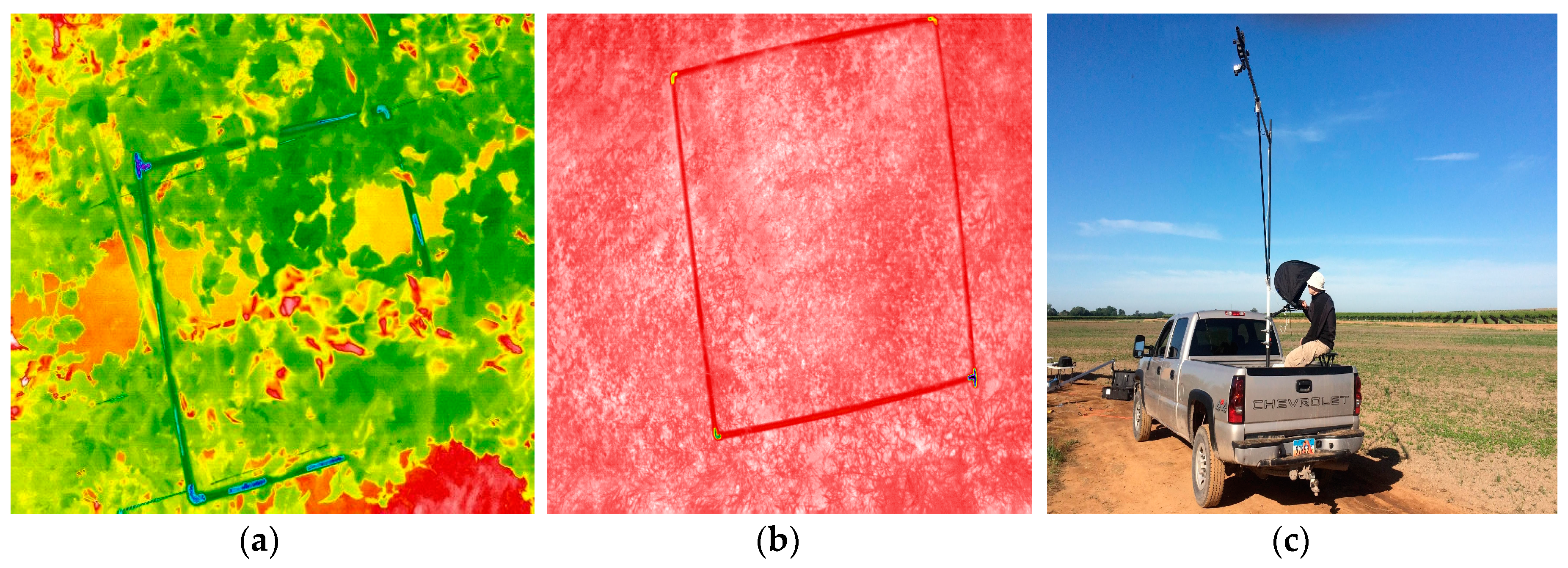

| Instrument | Blackbody | 2014 | 2015–2016 |
|---|---|---|---|
| Brand/Model | Wahl Palmer/WD1042 | ICI/7640-P | ICI/9640-P |
| Weight (gr) | 1000 | 148 | 141 |
| Image Size (pixel) | -- | 640 by 480 | 640 by 480 |
| Spectral Range (μm) | -- | 7 to 14 | 7 to 14 |
| Spectral Band Centre (μm) | -- | 10.35 | 10.35 |
| Operating Range | −40 to 70 °C | −20 to 100 °C | −40 to 140 °C |
| Reported Accuracy | ±0.2 °C | ±1.0 °C or ± 1.0% | ±1.0 °C |
| Reported Emissivity | 0.95 ± 0.02 | 1.0 | 1.0 |
| NIST Traceable? | YES | NOT REPORTED | NOT REPORTED |
| Date | Early Morning Flights | Landsat Overpass Flights | Mid-Afternoon Flights | |||
|---|---|---|---|---|---|---|
| Launch | Landing | Launch | Landing | Launch | Landing | |
| 09 August 2014 | 7:10 AM | 7:30 AM | 11:30 AM | 11:50 AM | No UAS flight | |
| 02 June 2015 | 6:51 AM | 7:32 AM | 11:21 AM | 12:06 PM | 2:54 PM | 3:20 PM |
| 11 July 2015 | 6:37AM | 7:11 AM | 11:26 AM | 12:00 PM | 2:58 PM | 3:31 PM |
| 02 May 2016 | 8:13 AM | 8:35 AM | 12:53 PM | 1:17 PM | 3:52 PM | 4:16 PM |
| 03 May 2016 | 8:40 AM | 9:06 AM | No UAS flight | 1:35 PM | 2:00 PM | |
| Steps | Activity Description |
|---|---|
| Before Flight | • Camera—blackbody temperature measurement • GPS survey of ground temperature sampling locations |
| During Flight | • Temperature ground sampling |
| After Flight | • Ground/sUAS temperature pixel extraction • Calibration of Radiative Transfer Model • sUAS temperature image correction |
| Model | Slope (95% Confidence Bounds) | Bias (95% Confidence Bounds) | R2 | RMSE (C°) | Reported Camera Accuracy (C°) | Reported Blackbody Accuracy (C°) |
|---|---|---|---|---|---|---|
| Linear | 1.00 (0.99 1.02) | −2.67 (−3.19–2.22) | 0.99 | 1.23 | ±1.00 | ±0.35 |
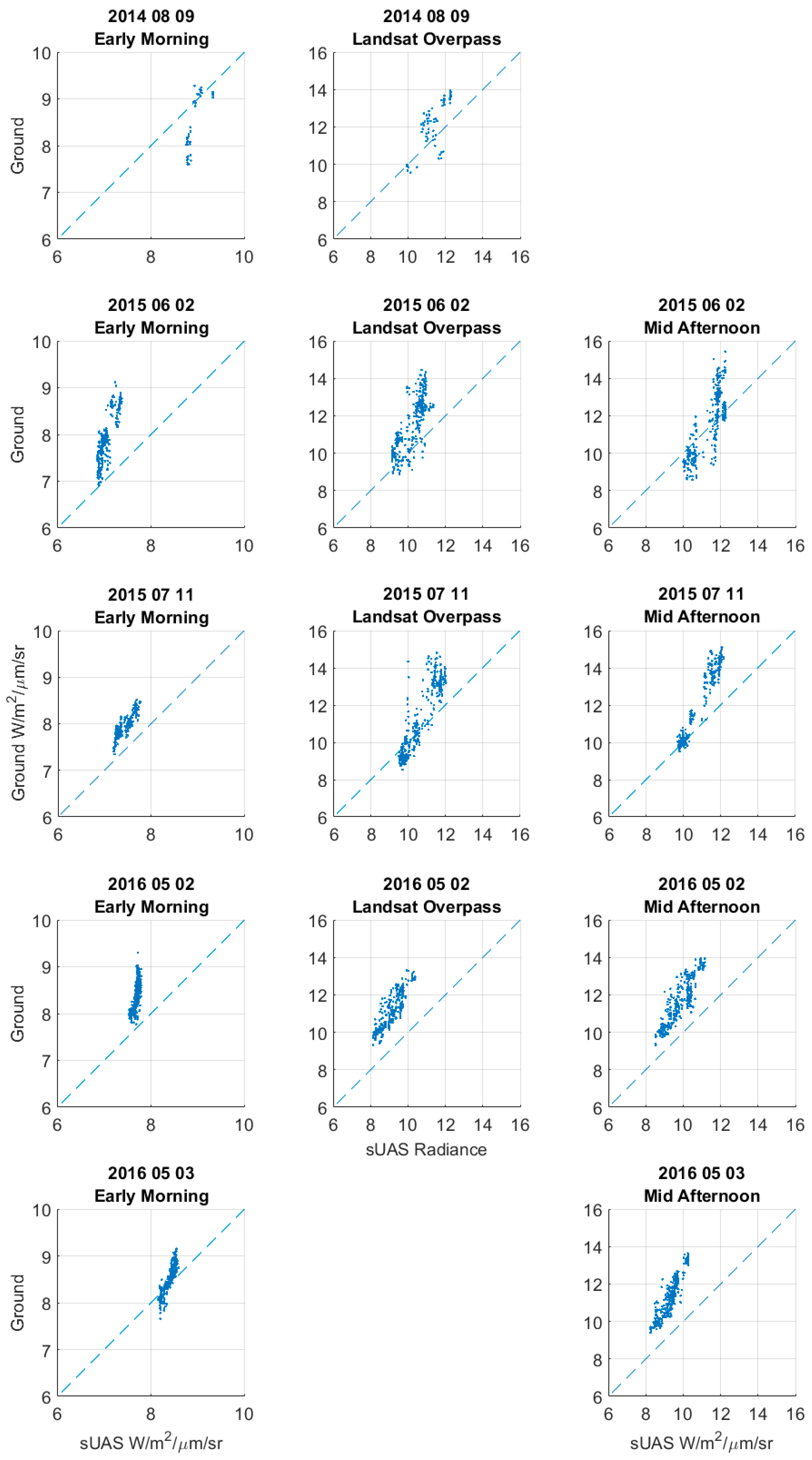
| Date | Flight Time | τ (95% Confidence Bounds) | Lu (95% Confidence Bounds) W/m2/μm/sr | r2 | RMSE W/m2/μm/sr | Used Pixels |
|---|---|---|---|---|---|---|
| 8/9/2014 | Early Morning | 0.40 (0.51 0.33) | −5.54 (−9.38–3.03) | 0.65 | 0.37 | 48 |
| Landsat Overpass | 0.69 (0.88 0.57) | −2.94 (−6.75–0.45) | 0.58 | 0.84 | 63 | |
| 6/2/2015 | Early Morning | 0.35 (0.38 0.33) | −4.28 (−5.10–3.56) | 0.71 | 0.26 | 336 |
| Landsat Overpass | 0.57 (0.62 0.53) | −3.61 (−4.88–2.53) | 0.62 | 0.88 | 330 | |
| Mid Afternoon | 0.53 (0.58 0.50) | −5.17 (−6.49–4.04) | 0.68 | 0.97 | 330 | |
| 7/11/2015 | Early Morning | 0.81 (0.88 0.76) | −0.94 (−1.58–0.39) | 0.73 | 0.12 | 283 |
| Landsat Overpass | 0.49 (0.52 0.47) | −5.08 (−5.86–4.38) | 0.83 | 0.77 | 352 | |
| Mid Afternoon | 0.47 (0.48 0.45) | −5.21 (−5.71–4.74) | 0.94 | 0.47 | 278 | |
| 5/2/2016 | Early Morning | 0.29 (0.33 0.27) | −5.23 (−6.66–4.05) | 0.53 | 0.21 | 343 |
| Landsat Overpass | 0.62 (0.63 0.60) | −2.21 (−2.49–1.94) | 0.95 | 0.46 | 299 | |
| Mid Afternoon | 0.65 (0.69 0.62) | −2.25 (−2.94–1.62) | 0.79 | 0.55 | 299 | |
| 5/3/2016 | Early Morning | 0.43 (0.45 0.41) | −4.74 (−5.49–4.07) | 0.8 | 0.13 | 326 |
| Mid Afternoon | 0.52 (0.55 0.50) | −3.38 (−4.01–2.82) | 0.83 | 0.43 | 349 |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres-Rua, A. Vicarious Calibration of sUAS Microbolometer Temperature Imagery for Estimation of Radiometric Land Surface Temperature. Sensors 2017, 17, 1499. https://doi.org/10.3390/s17071499
Torres-Rua A. Vicarious Calibration of sUAS Microbolometer Temperature Imagery for Estimation of Radiometric Land Surface Temperature. Sensors. 2017; 17(7):1499. https://doi.org/10.3390/s17071499
Chicago/Turabian StyleTorres-Rua, Alfonso. 2017. "Vicarious Calibration of sUAS Microbolometer Temperature Imagery for Estimation of Radiometric Land Surface Temperature" Sensors 17, no. 7: 1499. https://doi.org/10.3390/s17071499
APA StyleTorres-Rua, A. (2017). Vicarious Calibration of sUAS Microbolometer Temperature Imagery for Estimation of Radiometric Land Surface Temperature. Sensors, 17(7), 1499. https://doi.org/10.3390/s17071499





