1. Introduction
As critical components in rotating machinery, bearings that are not in a good condition can cause frequent machinery breakdowns [
1], and these faults may result in equipment instability, poor efficiency, and even major production-safety accidents [
2]. A stable machine-condition monitoring (MCM) system is required to guarantee the optimal states of the bearings during operation [
3]. Various physical properties can be utilized to monitor and diagnose the bearing faults. Most MCM systems in the industrial field are based on vibration signals, which are easy to acquire and can provide complete information [
4].
In modern industries, some problems exist in online wired MCM systems, such as installation difficulty and high cost, limited power supply and additional long cables. The wireless sensor network (WSN) offers a novel approach to improve the traditional wired MCM systems [
5], and it has some advantages such as rapid deployment, removability, and low energy consumption [
6]. However, the WSN manifests a number of limitations when applied in vibration-based MCM systems. According to the Nyquist–Shannon sampling theorem, an analog-to-digital converter (ADC) in WSN nodes needs to work at a high frequency because of the high speeds of rolling bearings [
7], so does the data processing rates. For effective condition monitoring and fault diagnosis, mass memory should be used to store large packets of vibration signals. In addition, transmitting huge amounts of data via radio-frequency modules increases the time and energy consumption [
8]. Thus, reducing the data size before transmission is the best way to solve the above-mentioned problems.
Many compression methods have been introduced for the machinery vibration signals in WSN. However, a serious problem is that almost all these methods require collecting original vibration signals according to sample theorem, and then applying complex algorithms to compress data in node processers. Essentially, this processing does not reduce the workload. As an emerged theory, Compressed Sensing (CS) [
9] shows great promise in compressing/reconstructing data with low energy consumption. CS framework utilizes a nonlinear projection to preserve the original information in a small quantity of measurement vectors, and then reconstruct the original signals through optimization algorithms [
10]. When CS is introduced in WSN systems, signal-acquisition and data-compression can be processed simultaneously in a sensor node, while the reconstruction process is operated at remote host computers [
11]. This huge advantage promotes the application of CS in vibration-based MCM systems using WSN.
For the first few years after the introduction of CS, not much attention to its application was paid in the machinery-condition monitoring field. For the past two years, a few researchers have been studying the use of CS in machinery fault diagnosis. Zhou [
12] mentioned an approach based on sparse representation for fault diagnosis in induction motors. The original feature vectors that described the different faults were extracted from the training samples and kept as the reference. Then, it compared the original feature vectors and real-time features, which are extracted from real time signals to identify the fault. The features extraction was based on orthogonal sparse basis representation, and the sparse solution problem was solved by l1-minimization. Zhang [
13] proposed a bearing-fault diagnosis method, which combined the CS theory with the K-SVD dictionary learning algorithm. Several over-complete dictionaries were trained using the historical data of particular operating states. Only with the over-complete dictionary that represents the same fault type with the original signal, the reconstruction signal with matching pursuit (MP) algorithm has the smallest error. The bearing fault can be identified in accordance with the differences. Wang [
14] developed a framework for remote machine-condition monitoring based on CS. The faults signals were transformed to the projection space by a measurement matrix that achieved the compressed acquisition and then the compressed data was transmitted to the host computer. Fast iterative shrinkage-thresholding algorithm and parallel proximal decomposition algorithm were combined for CS reconstruction. The reconstructed signals preserve the time-frequency representation signatures of the fault signals and the condition states were diagnosed with traditional methods. Zhu [
15] introduced the CS and sparse-decomposition theory for machine and process monitoring. Reference [
15] focused on several state-of-the-art applications, especially, the sparse-decomposition-based fault diagnosis. The referenced fault-diagnosis methods were all based on the fact that the fault signal could be constructed using weighted linear combinations of the fault samples in the learned dictionary. The fault types can be identified by comparing the representation coefficients and the reconstruction errors. Wang [
16] studied a multiple down-sampling method combined with CS for bearing-fault diagnosis. CS was used to further reduce the amount of data which had been processed by the down-sampling method. Then, the compressive data were partially reconstructed by setting a proper sparsity degree via MP algorithm. The fault features could be identified through the incomplete reconstruction signals which included the specific harmonic components. Du [
17] proposed a feature-identification scheme with CS, which did not need to recover the entire original data. The fault features could be extracted directly and quickly in the compressed domain. Reference [
17] introduced an alternating direction method of multipliers to solve the CS reconstruction problem.
Through the literature review, we noticed that bearings faults were diagnosed based on the features that were extracted from the entirely or partially reconstructed signals from compressed samples. Therefore, the accuracy level of recovered signal directly influenced the feature extraction and fault recognition. The aforementioned methods can identify faults that have demonstrated distinct and known fault features, especially they are effective when the bearings have a single point of failure. When the bearings have compound faults or unknown fault, however, the signals will present complicated waveforms. Under this circumstance, complete information recovery of the vibration signals is important. Therefore, a high-precision reconstruction algorithm plays a vital role. Almost all the above-mentioned methods use traditional CS reconstruction algorithms. Although these algorithms have good popularity, they are not quite suitable for bearing vibration signals, because these algorithms consider only the sparsity property of the vibration signals. In general, the bearing vibration signals not only have the sparsity property, but also have specific structural features. The structured sparsity model transcends the simple sparsity models. They reduce the size of measurements required to recover a signal steadily. On the other hand, during reconstruction, they enable the users to differentiate the useful signal from the interference in a better manner [
18]. Thus, by utilizing the structured sparsity model, it is possible to outperform the state-of-the-art conventional reconstruction algorithms.
Block sparse Bayesian learning (BSBL) [
19] has the potential to solve the reconstruction problem. BSBL derives from Sparse Bayesian learning (SBL) methodology [
20], which was first proposed for regression and classification in machine learning and was introduced for signals with block structures. BSBL not only recovers signals with block structures but also considers the intra-block correlation. BSBL outperforms the traditional CS algorithms and has the capacity to recover non-sparse signals with high precision. It has been successfully applied in the monitoring of fetal electrocardiogram (FECG) and electroencephalogram (EEG) via wireless body-area networks [
21]. However, until now, it has not attracted much attention in the field of machinery vibration signals.
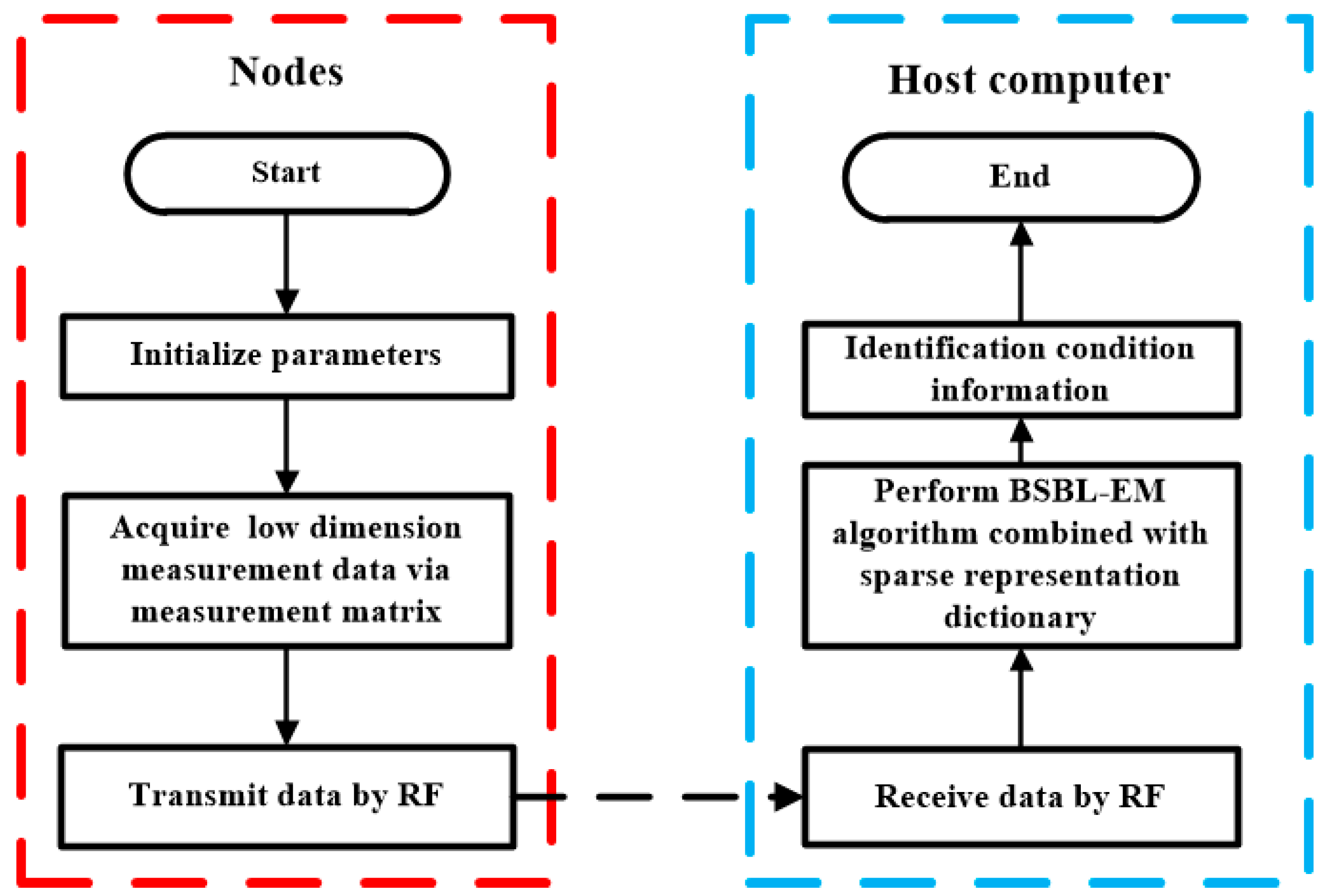
Based on the properties of the bearing vibration signals and related CS theory, this paper proposed a new reconstruction method combining BSBL and sparsity in transform domain to improve the recovery accuracy. The low-dimension measurement data were acquired in the sensor nodes of WSN, transmitted to workstations via radio frequency (RF) and then recovered using proposed method in the host computer. The bearing conditions can be identified on the basis of reconstructed signals. Experimental results show the reconstruction performance is better than the conventional reconstruction algorithms.
The remainder is organized as follows:
Section 2 introduces the principle of Compressed Sensing and BSBL.
Section 3 details the bearing vibration signal features and commonly used transform domains. The proposed method for bearing-condition monitoring via WSN is also presented in this section.
Section 4 presents the experiment results and analysis for the reconstruction methods of the bearing vibration signals. We analyze the reconstruction performances and compare the results of BSBL with other methods, and also discuss the influences of the block sizes and signal-noise ratio.
4. Experiments and Analysis
Experiments were carried out using the bearing vibration signals provided by Case Western Reserve University. A series of experiments were performed to verify the performance of the reconstruction methods and the BSBL-EM was compared with some typical recovery algorithms. This paper also analyzed how the performance of the BSBL-EM is affected by various parameters.
4.1. Comparison with Traditional Reconstruction Algorithms
Firstly, the BSBL-EM was verified the reconstructed performance in DCT and WPT domains. In the experiment, a bearing-vibration signal consisting of 2000 samples was chosen and in the condition of inner-ring fault. According to the features of bearing vibration signals, we chose sym6 as the wavelet packet base function. A Gaussian random matrix of size 800 × 2000 was used as the measurement matrix. The observation data can be obtained according to Equation (3). The block size of BSBL-EM in this experiment was set as 25.
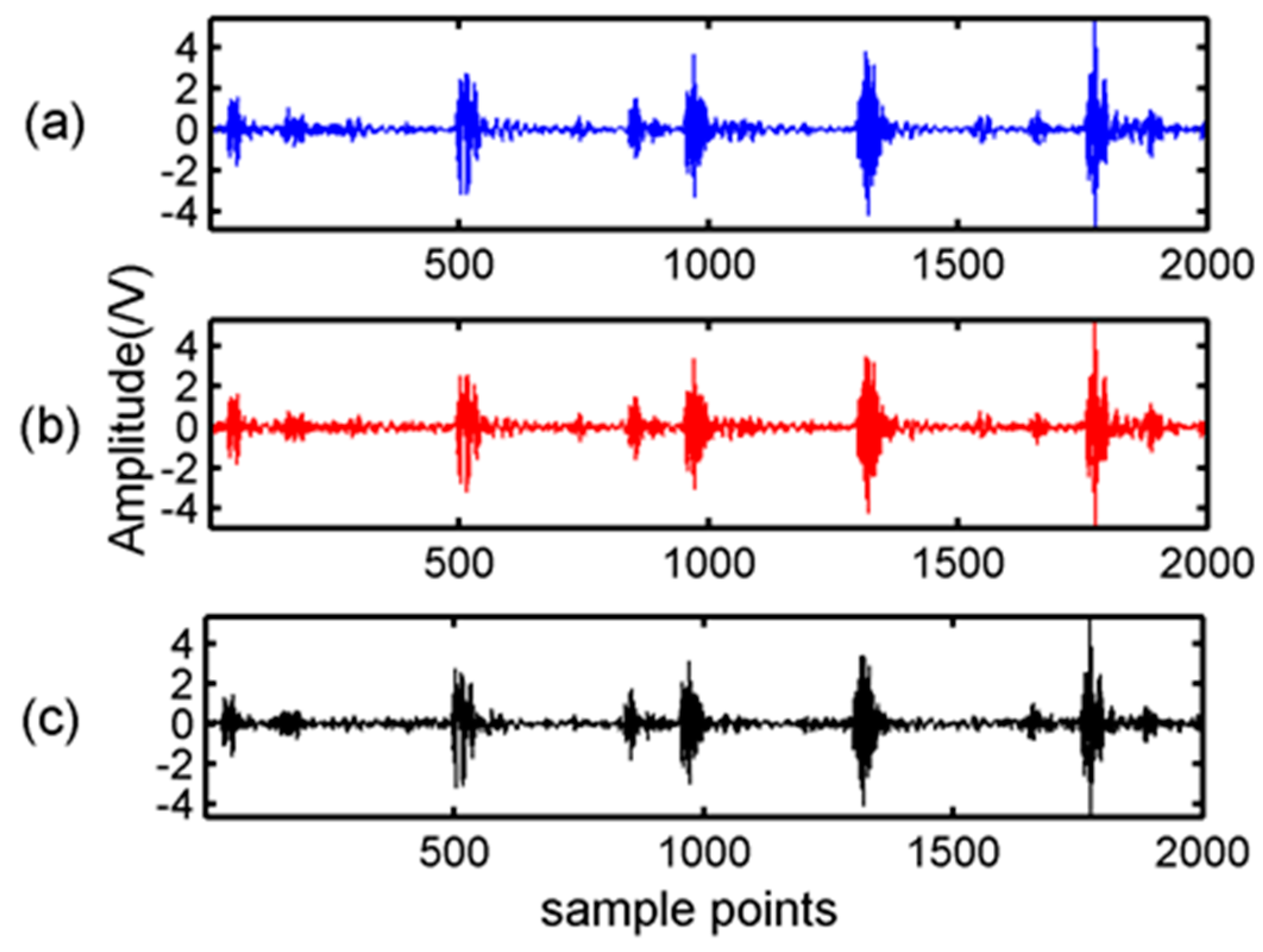
Figure 3 showed the original signal and the signal recovered by BSBL-EM with DCT and WPT.
Secondly, BSBL-EM was compared with four classical reconstruction algorithms: BP (Basis Pursuit) [
9], OMP (Orthogonal matching pursuit) [
26], IST (Iterative Soft Thresholding) [
36], and LASSO (Least Absolute Shrinkage and Selection Operator) [
37] in DCT and WPT domains. These algorithms do not exploit the block structures of the signals. Another common feature in these four algorithms is that they do not need to know the sparsity degree or other prior information.
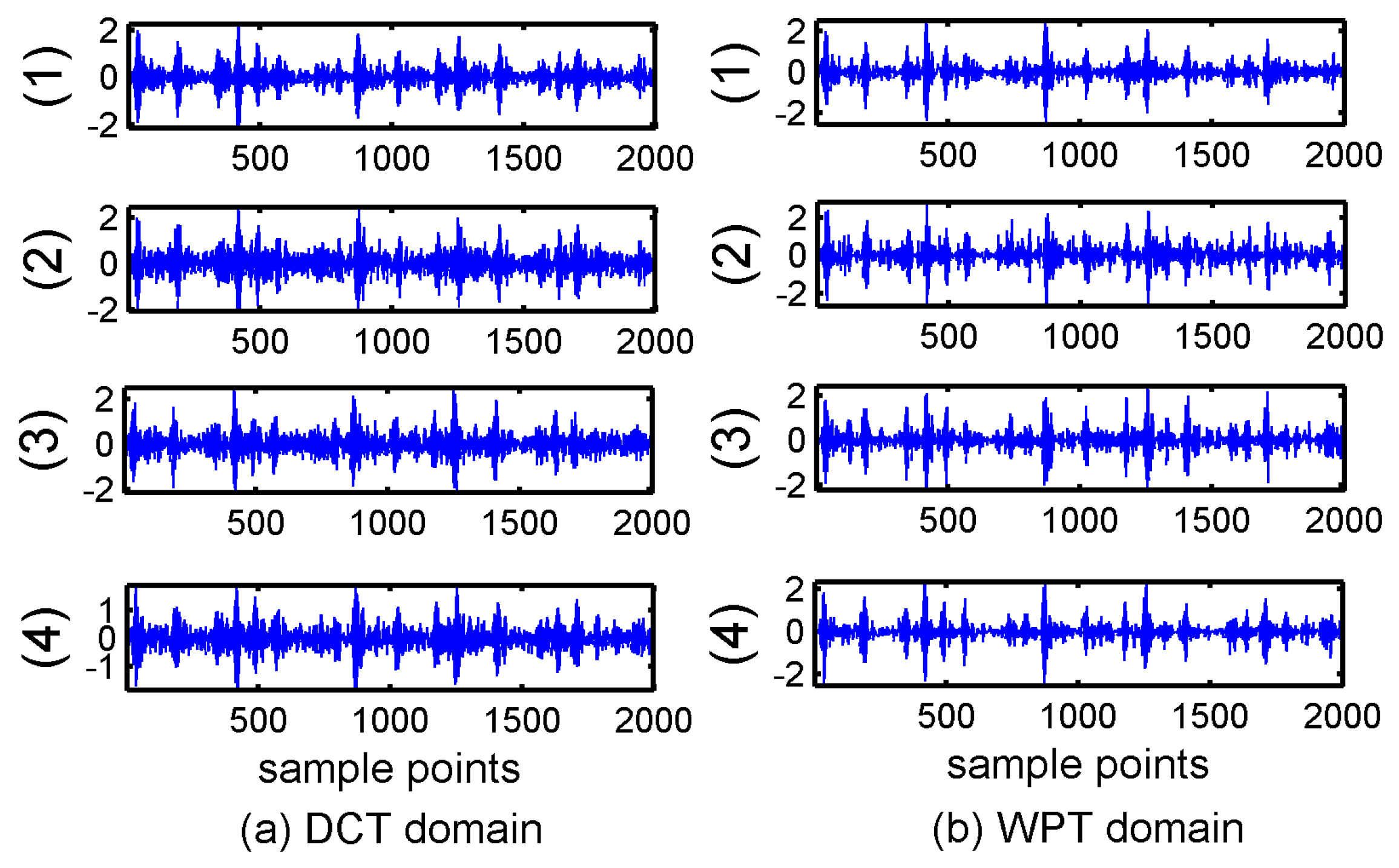
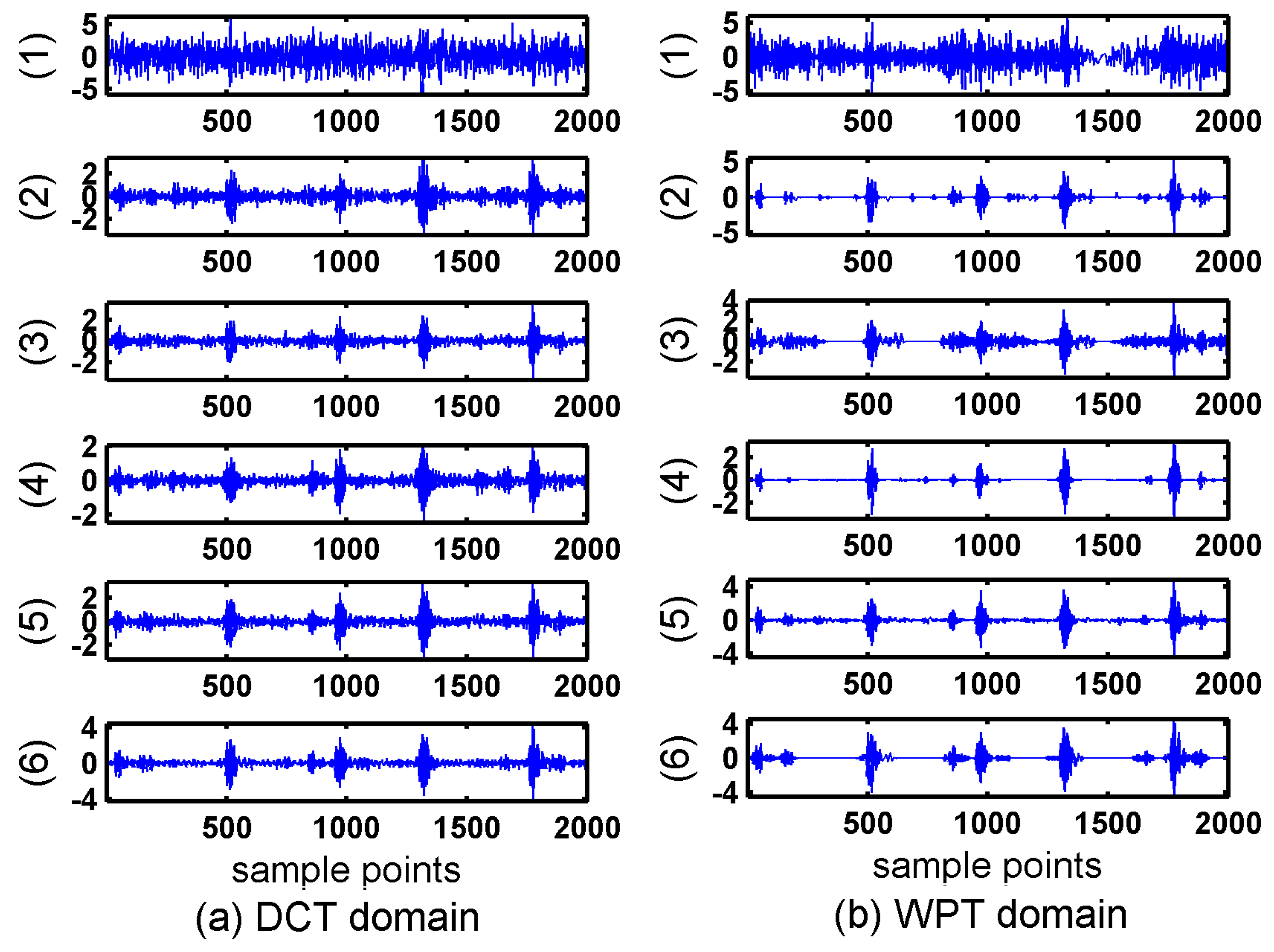
Figure 4 showed the reconstruction results of the four algorithms.
It can be seen in
Figure 3 and
Figure 4 that the reconstruction signals with traditional algorithms in DCT domain and WPT domain had larger differences. The signals recovered using the traditional algorithms in DCT domain contained large amounts of noise and the signals recovered using BSBL-EM have less noise. Moreover, the reconstruction signals with BSBL-EM in two domains had similar precision. Thus, the use of the block-sparsity property to recover the original signal is an obvious advantage of the BSBL framework.
In the conditioning monitoring system based on Compressed Sensing, the compression ratio is an important factor to the performance of reconstruction signals. In Equation (1), the measurement matrix
(
) fulfilled the compressive sampling in the projection space. The compression ratio (CR) can be defined as:
where
is the length of the original signal and
is the length of the compressed signal.
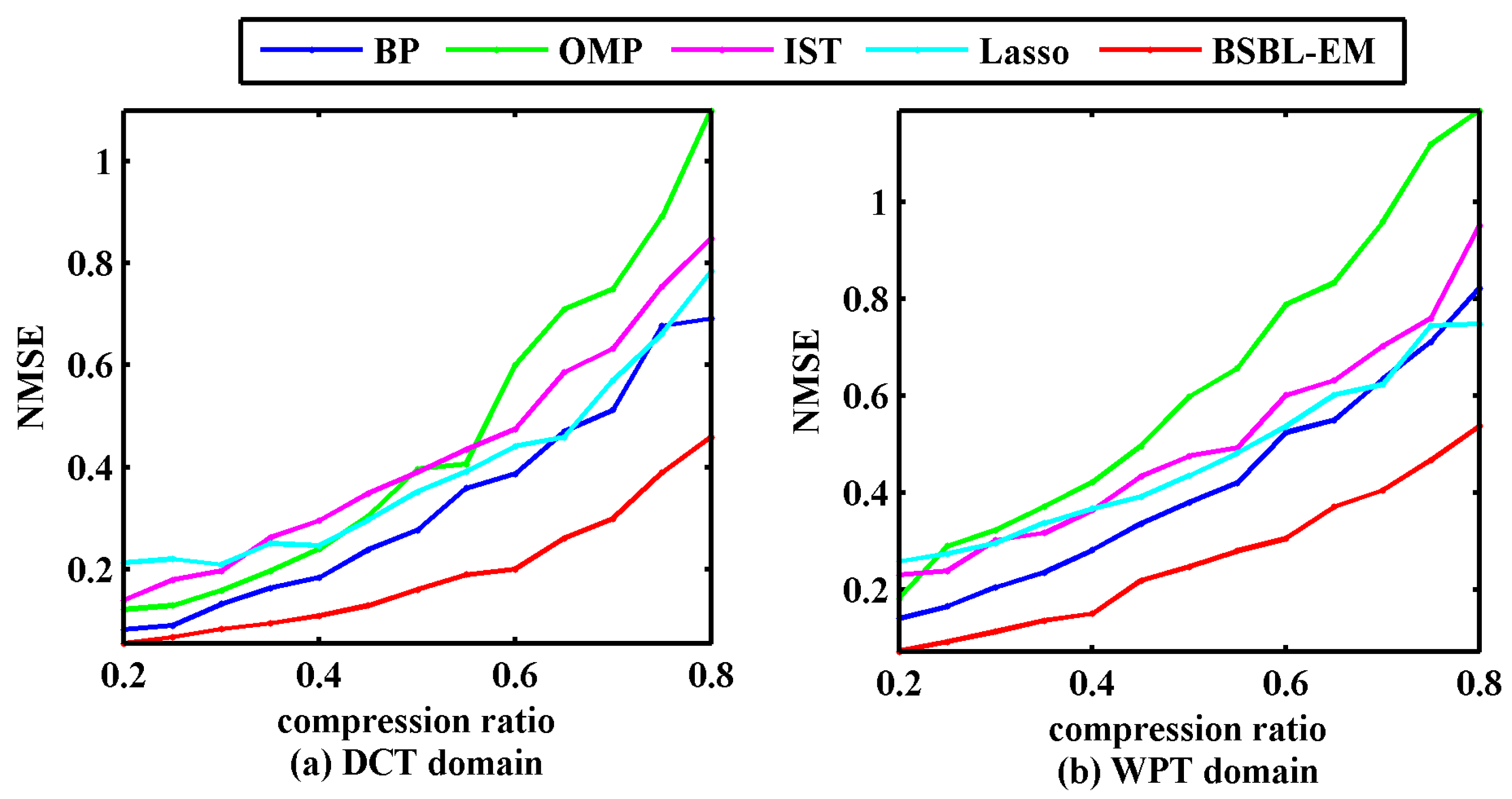
To further evaluate the performance of the BSBL, we experimented with the four traditional algorithms and the BSBL-EM at different compression ratios, i.e., 20–80%. The normalized mean square error (
) was used as the evaluation criterion for reconstruction performance. The expression of
is Equation (14).
where
is reconstruction signal and
is the original signal.
Figure 5 displays the NMSEs between the original signals and the signals reconstructed via different algorithms.
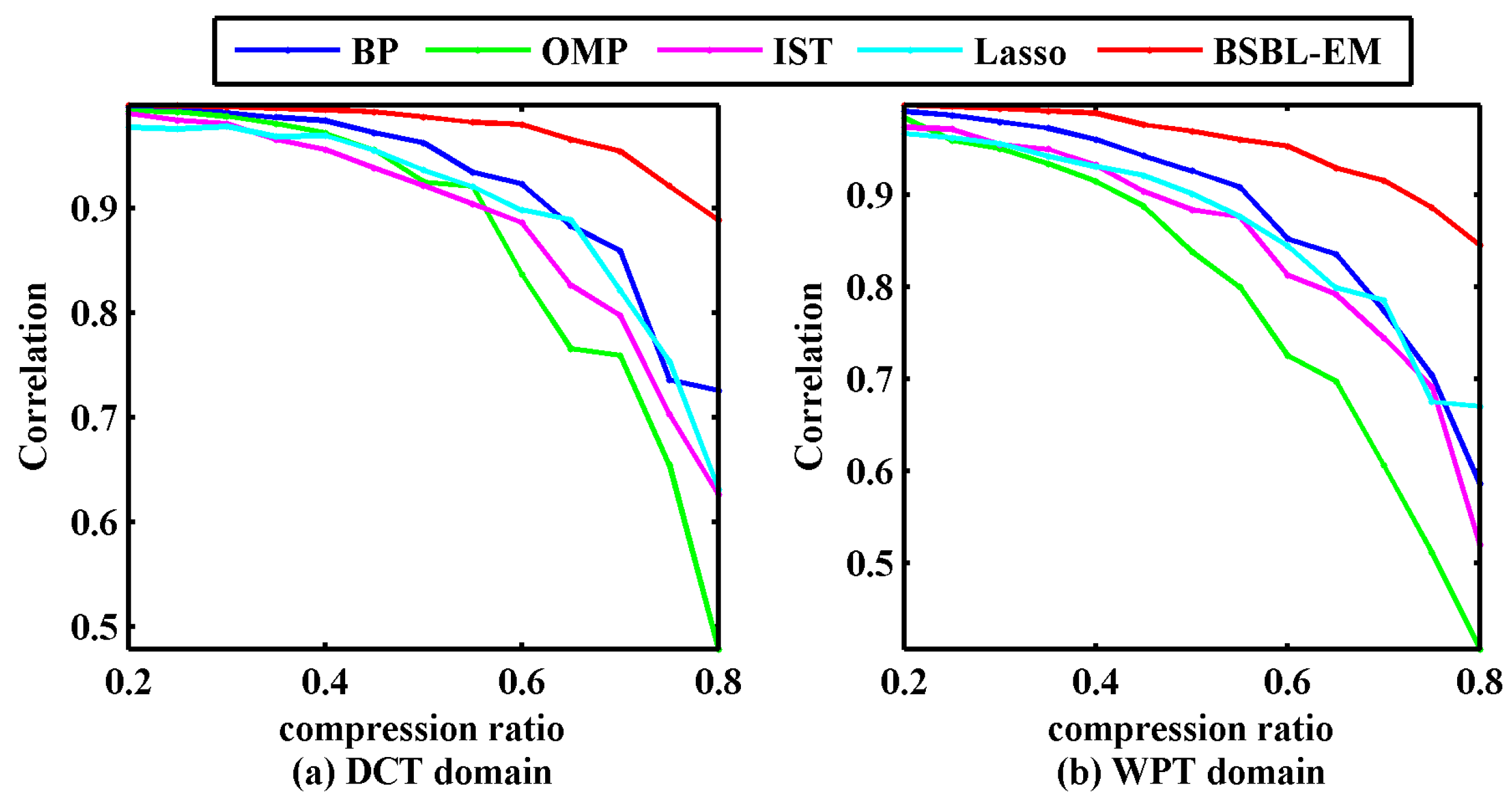
It can be seen that the reconstructed signals with BSBL-EM had smaller errors compared with the other algorithms in the given range of compression ratio. Although the NMSE can describe the reconstruction errors, NMSEs have no ability to display the similarities between original signal and the reconstructed signal. We used the Pearson correlation coefficient as Equation (14) to evaluate the similarity between the reconstructed signals and the raw signals.
where
is the Pearson correlation coefficient, and
and
are the reconstructed and raw signals, respectively.
Figure 6 displays the correlation coefficients between the original signals and the signals reconstructed via different algorithms under the given compression rates.
In
Figure 6, the experimental results indicated that the correlation coefficient between the reconstructed signal using BSBL-EM and the original signal was above 90% when the compressibility was under 70%, irrespective of whether the sparsity representation method was DCT or WPT. This implied that BSBL-EM can recover the bearing vibration signals with satisfactory quality, ensuring subsequent fault diagnosis with high fidelity.
4.2. Comparison with Other Reconstruction Algorithms Utilizing Block-Sparsity Property
In
Section 4.1, BSBL-EM was compared with four traditional CS algorithms which did not utilize the block-sparsity property of the bearing vibration signal. In this section, we compared the BSBL-EM with some algorithms that are based on the block structure of the original signal.
Sparsity representations dictionaries were DCT matrix and WPT matrix in this experiment as well. A segment of the bearing vibration signal, consisting of 2000 samples, was chosen for the experiment, and this signal was in the condition of the outer-ring fault. Other parameters were set to be the same as those used in
Section 4.1.
Figure 7 shows the original signal and the signal recovered using BSBL-EM.
The compared algorithms were Block-OMP [
30], BM-MAP-OMP [
32], JSMP [
31], Group Lasso [
38], Group BP [
39], and StructOMP [
40]. All these algorithms exploit the block structures of the signals. A common feature of all these compared algorithms is that they all need to know the prior information.
Figure 8 shows the reconstruction results of the compared algorithms with DCT and WPT.
It can be seen in
Figure 8 that the additional noise was serious when using the DCT. Although the noise is less when using WPT, most detail coefficients in WPT domain cannot be reconstructed successfully and the distortion in the reconstructed signals were obvious. The signals recovered via the Block OMP algorithm lost all the original information. In order to evaluate the quality of reconstruction via these block-sparsity algorithms, the outer-ring fault signal was also processed using the traditional algorithms mentioned in
Section 4.1.
Figure 9 shows the results of traditional algorithms in DCT and WPT domains.
Figure 8 and
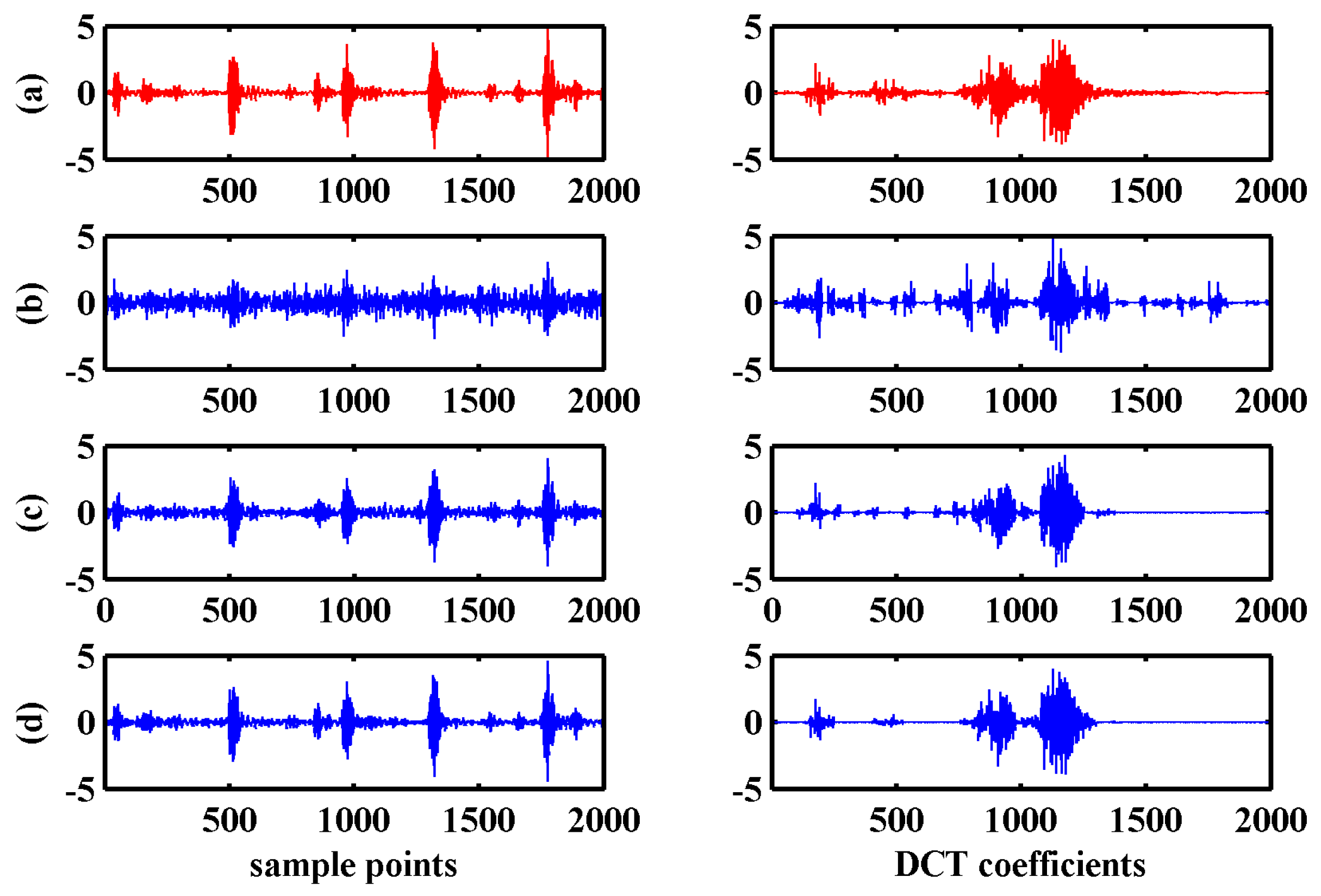
Figure 9 display an unexpected phenomenon. In general, the algorithms that utilize the structural properties should demonstrate better performances. However, except for the BSBL-EM, none of the algorithms using the block-sparsity property showed a precision higher than that of the traditional algorithms, in particular, the signals recovered in the wavelet packet domain. This problem can be analyzed from three angles. Firstly, it has been mentioned that the block-sparsity reconstruction methods need to know some prior information, such as the block position and size, which will directly affect the recovery results. However, the block sparse structures are actually obscure even though the energy clusters at some positions. There are also vast numbers of small coefficients at other positions, regardless of the DCT or WPT domain. Most algorithms that use the block sparse structure have been experimented under ideal conditions that have less noise, in the past researches. However, practical applications are different from numerical simulations. The structural properties of the original signal are often implicit and noise is inevitable. Secondly, these block-sparsity algorithms require corresponding structural features matched with the specific signals. However, the characteristics of the bearing vibration signals in DCT and WPT domain have great differences, as displayed in
Figure 1c,d. Finally, the bearing vibration signals are typical non-stationary signals; therefore, the sparsity appears divergent in different transform domains, for example in this paper the coefficients in WPT domain showed better sparsity and block partitions than DCT domain, therefore the reconstructed results under most circumstances had better performances. Most algorithms that utilize block structures cannot achieve good reconstructed performances for the complex real bearing signals if it lacks the prior information about the block structures. In other words, excessive dependence on prior information results in the algorithms using the block-sparsity property demonstrating worse adaptability than the traditional algorithms in practical applications
BSBL framework is different from most of the algorithms that utilize the block-sparsity property. As we can see in
Figure 7, the signals recovered by the BSBL-EM were almost the same whatever in DCT domain or WPT domain. BSBL-EM can well reconstruct the signal when the coefficients have inconspicuous blocks in transformation domain, even if the coefficients are non-stationary. Moreover, this algorithm only needs a minimum number of prior knowledge, namely the signals characterizing sparsity and block partitions, so the application of BSBL is as simple as that of the traditional CS algorithms.
4.3. Effect of Block Sizes in BSBL-EM
The improved performance of BSBL-EM over most of the typical algorithms had been displayed in the past two comparison experiments. Except the sparsity, block structure is the only prior condition needed when reconstructing the signal with BSBL-EM. In this section, we investigated the effects of different block sizes in BSBL-EM and showed the results.
In the previous experiments, the size of each block was 25. For the block-sparsity algorithm, the block size is a key factor, so how does it affect the performance of BSBL-EM? To examine this, we used various block sizes to complete reconstruction, and the reconstructed results were satisfactory for all conditions. The raw data in this experiment are the inner-ring fault state and the measurement matrix is a Gaussian random matrix of size
and the sparse representation dictionary is a DCT matrix. The criteria for evaluating the reconstruction performance were NMSE and correlation coefficient. The block sizes ranged from 5 to 100.
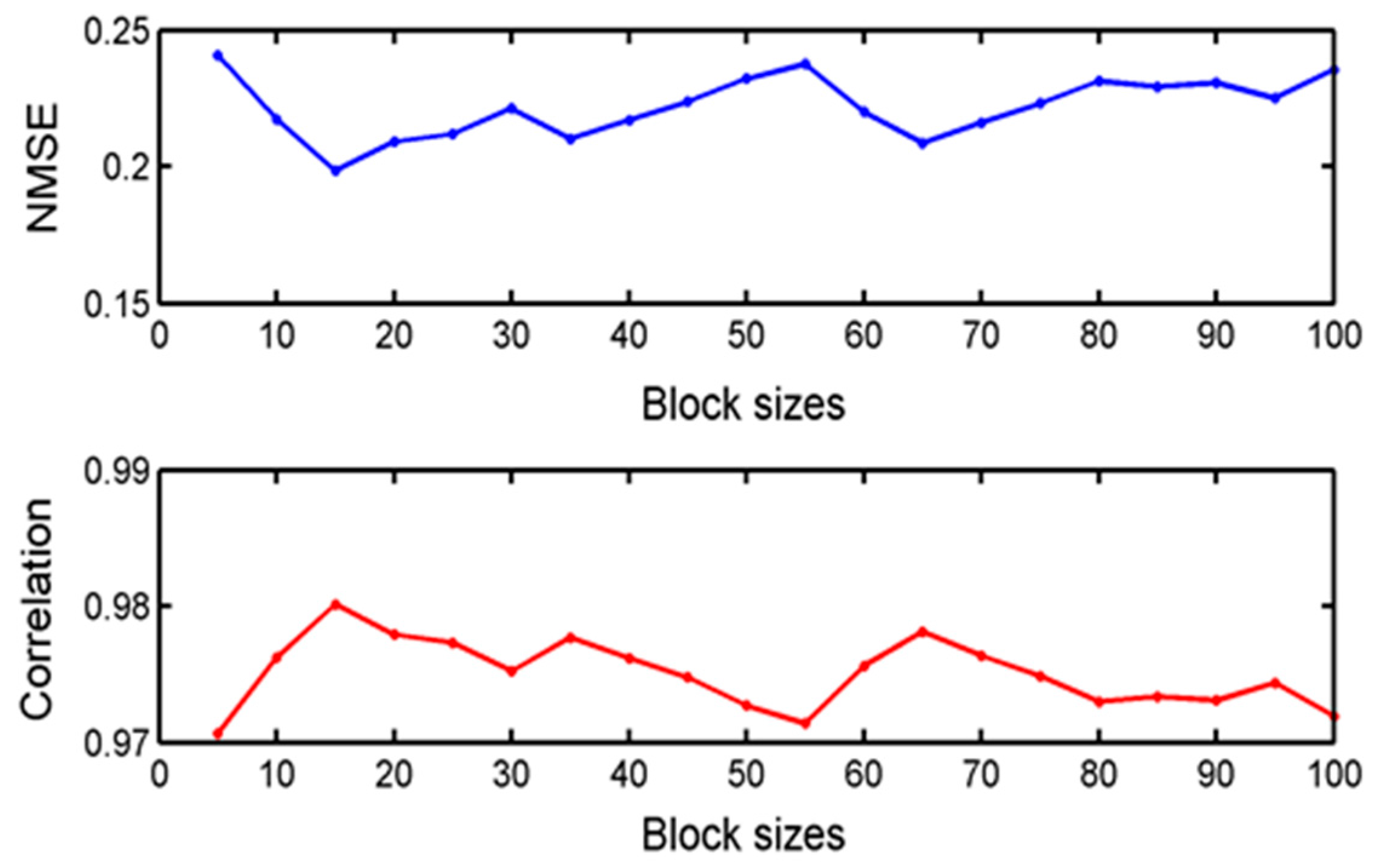
Figure 10 displays the reconstructed performances of BSBL-EM for various block partitions.
According to the two evaluation criteria, the differences between the various reconstructed signals were very small. Therefore, we can consider that the performance of BSBL-EM is not sensitive to the block partitions and the effects of block partitions can be ignored.
4.4. Effect of SNR
In most industrial fields, the bearing vibration signals contain different levels of noise. Most often, denoising processes for acquiring data are necessary for the subsequent fault diagnosis. Therefore, it is natural to question whether the BSBL-EM can reconstruct the original signal with less noise, while at the same time, preserve important information.
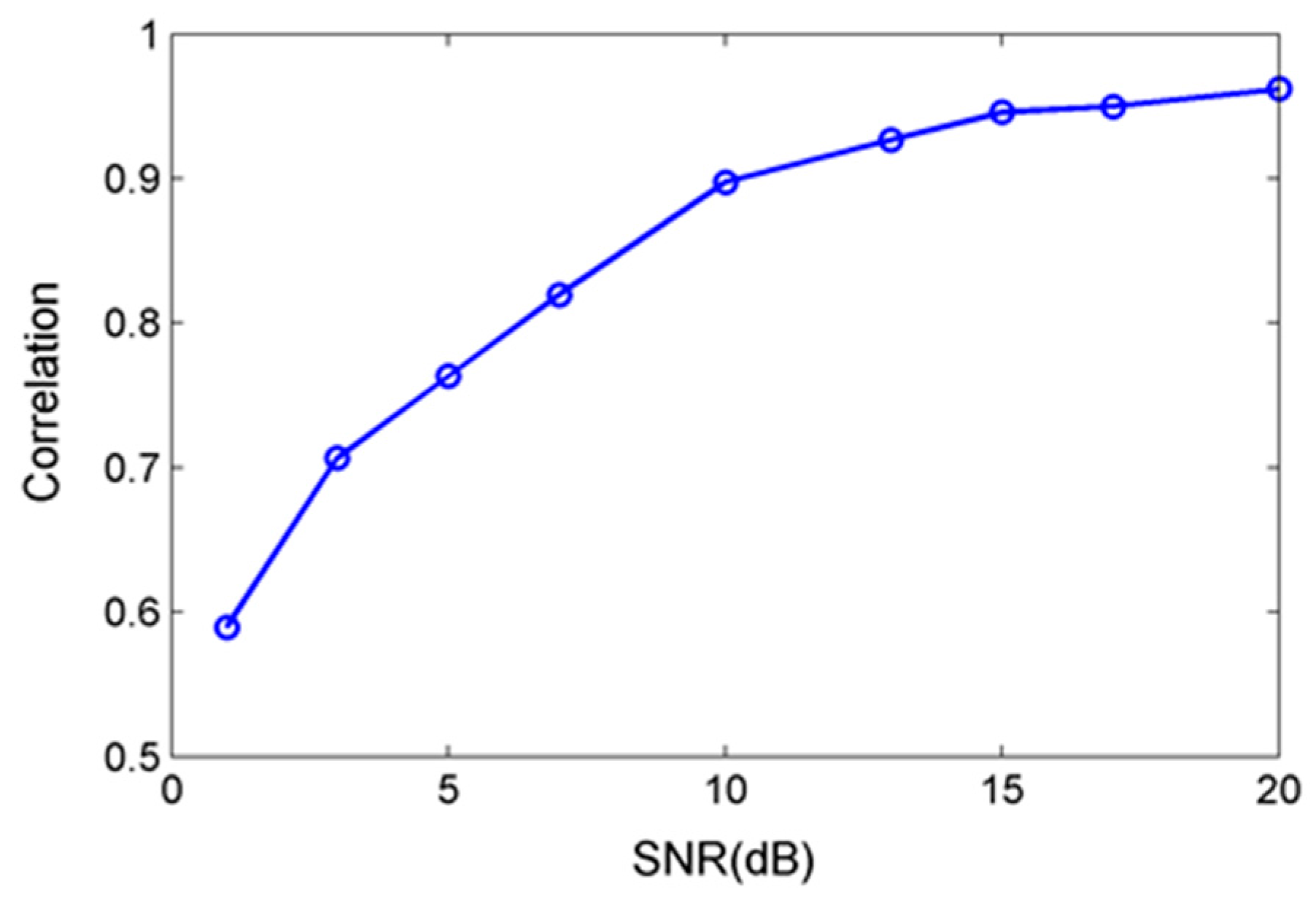
We studied the effects of signal-to-noise ratio (SNR) and BSBL-EM will estimate noise model parameter λ according to the learning rule in Equation (11). This section explores the reconstruction effects under various noise levels. The original data were bearing outer-ring fault signals added white Gaussian noise with different SNR, measurement matrix was the same Gaussian random matrix as the previous experiment and the sparse representation dictionary was DCT matrix.
Figure 11 compares the original signal and DCT coefficients with the reconstructed ones under different noise levels.
As shown in
Figure 11, the reconstruction effects were good using BSBL-EM with low SNR. The reconstructed DCT coefficients and signals were similar to the original signals when the SNR is higher than 10 dB.
Figure 12 shows the correlation coefficient between the original signals without noise and the reconstruction signals at different noise levels with SNR less than 20 dB.
There was a great difference between the reconstructed signal and original one under the low SNR. However, the reconstructed DCT coefficients still had similarity. The reconstruction performance was significantly improved with the increase of SNR. When the SNR exceeds 10 dB, the reconstructed signal had small difference with original ones and the correlation coefficient can reach more than 0.9.
4.5. Effect of Wavelet Packet Paremeters
In the past experiments, we used wavelet packet transformation matrix as the sparse representation matrix. Actually, the wavelet packet transformation matrixes have different forms, which depend on the wavelet kernels and decomposition levels. In the section, we discuss the CS reconstruction performance influenced by various wavelet packet parameters.
The experiment data were the same as in
Section 4.1. The measurement matrix was Gaussian random matrix and the reconstruction algorithm was BSBL-EM. Firstly, we set the basic wavelet types as variable. The contrastive wavelet kernels were db4, db5, db6, sym4, sym5 and sym6. The wavelet kernels were similar to the waveforms of bearing vibration signals. The correlation coefficient of reconstruction signals and original signal with different compression ratios is displayed in
Figure 13.
It can be seen in
Figure 13 that various wavelets kernels have little influence to reconstruction performance.
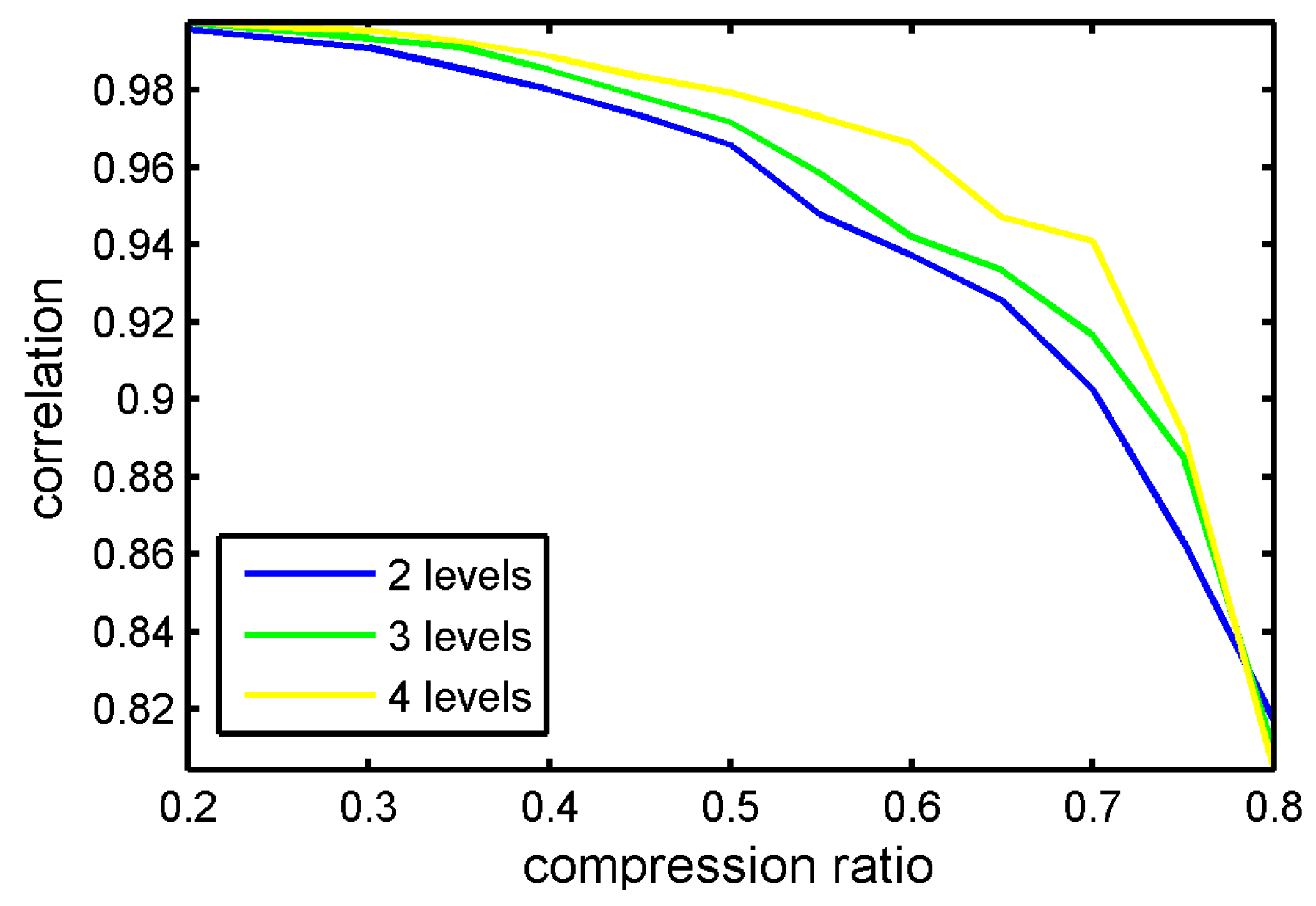
Figure 14 displays the CS reconstruction performance with different levels. In this experiment, the chosen wavelet kernel was sym6.
In
Figure 14, the correlation coefficients showed slight improvements with the increase of wavelet decomposition levels; however, this change was not obvious. Therefore, it is no necessary to increase the decomposition levels to improve the performance. Actually, the reconstruction algorithms have the greatest influence on CS reconstruction performance.
4.6. Faults Classification
In the above sections, we only evaluated the CS performance with NMSE and correlation coefficients, which only quantitatively presented the reconstruction accuracy. The ultimate purpose of machinery condition monitoring system is identifying the bearing faults types. Will this compressed sampling and reconstruction affect the identification accuracy? In this section, we perform the faults classification using the test signals, which were reconstructed by BSBL-EM.
The faults classification method was based on feature extraction and pattern recognition. We decomposed the bearing vibration signals with sym6 wavelet packet by five levels and extracted the wavelet packet energy spectrum in 32 decomposition nodes. This wavelet packet energy spectrum was used as the feature vector. The pattern recognition method was support vector machine (SVM).
The training data were bearing vibration signals which include seven states. The states were normal, and six faults. The fault types consisted of inner-ring fault, rolling-element fault, and outer-ring fault. Each fault type was divided into two fault diameters, 7 mils and 21 mils. The number of training data totally was 1400, which consists of 200 sets of data for each bearing state. The number of testing data was totally 280, which consists of 40 sets of data for each bearing states. In each set of data, the sample points were 2000. We tested the faults classification result at different compression ratios. The measurement matrix was a Gaussian random matrix and the reconstruction algorithm was BSBL-EM. The training samples and testing sample are shown in
Table 1 and
Table 2, respectively.
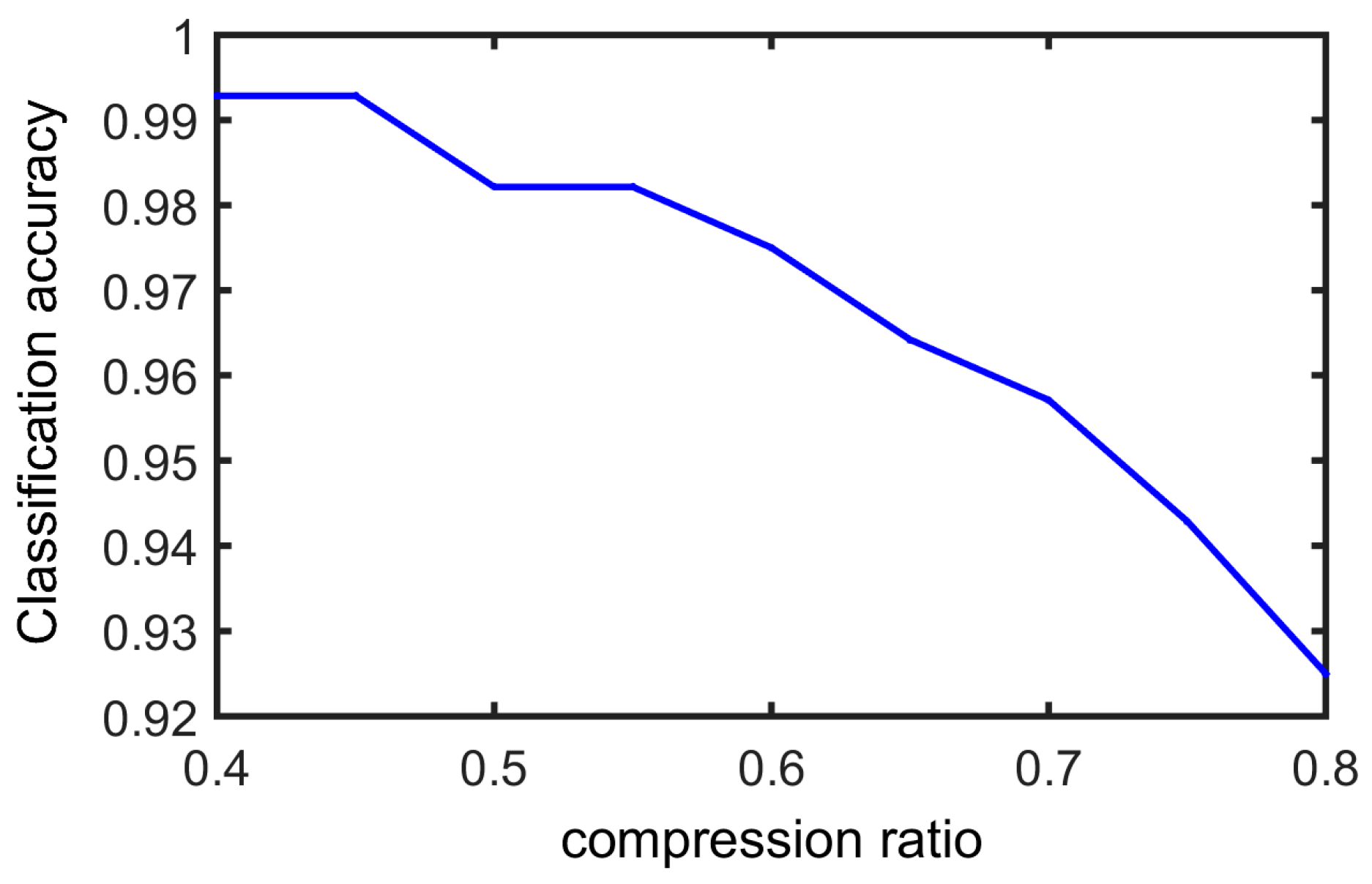
In this experiment, we test the faults classification accuracy with different CS compression ratios.
Figure 15 displays the fault classification result.
It can be seen that reconstruction signals were able to preserve most of the fault information. When the compression ratio was very high, for example 80%, some information was lost and there was the lowest accuracy value; however, when the CR was lower than 70%, all types of bearing faults can be identified accurately. The successful rate of faults classification can be close to 100% when the CR is 40%.