Current Research in Lidar Technology Used for the Remote Sensing of Atmospheric Aerosols
Abstract
:1. Introduction
- their high variability in space and time and, as a consequence, on their non-localized distribution, mostly due to medium- and long-range transport and short mean life time;
- the geographical extension of the sources: some are localized, others are distributed over large volumes;
- the large number of processes that lead to their production;
- the numerous and heterogeneous processes through which aerosols can interact during their lifetime: nucleation, condensation, coagulation and deposition.
2. General Concepts about Lidar Sensors and Aerosol Optical Properties Involved in Lidar Measurements
3. Typical Configurations of Aerosol Lidars
3.1. 1β Elastic (Including Ceilometers)
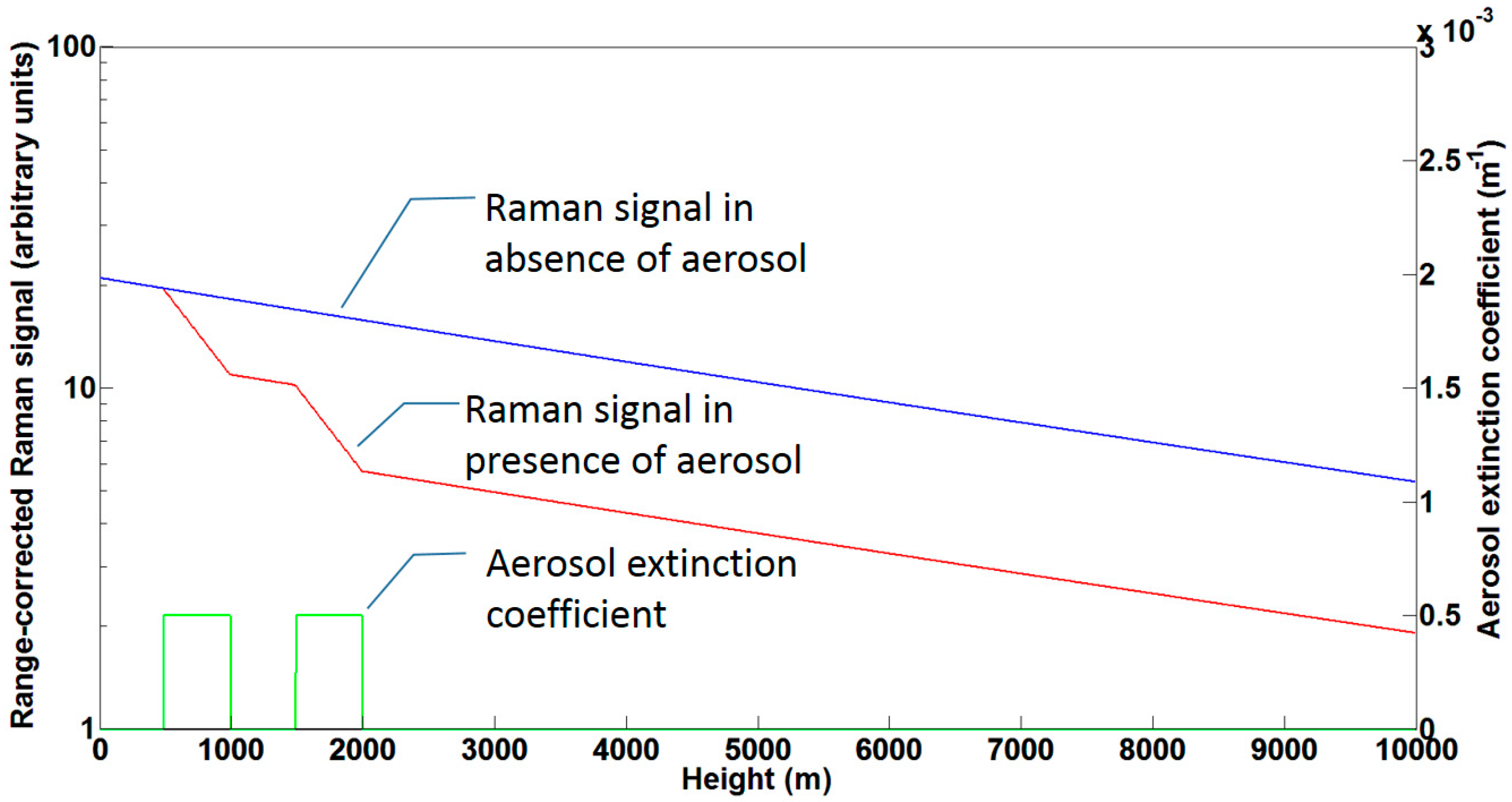
3.2. 1β + 1α Vibro-Rotational and Pure Rotational Raman
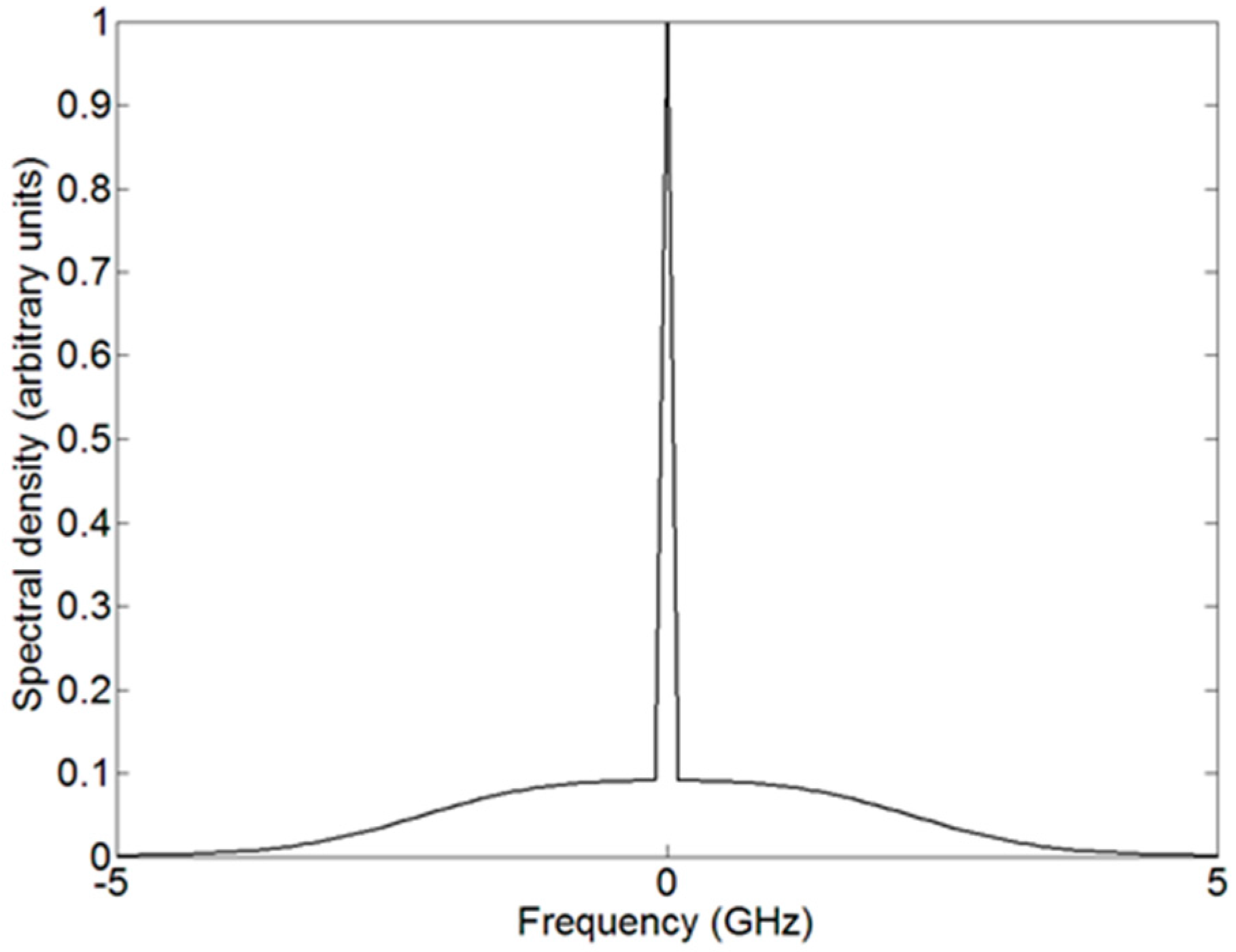
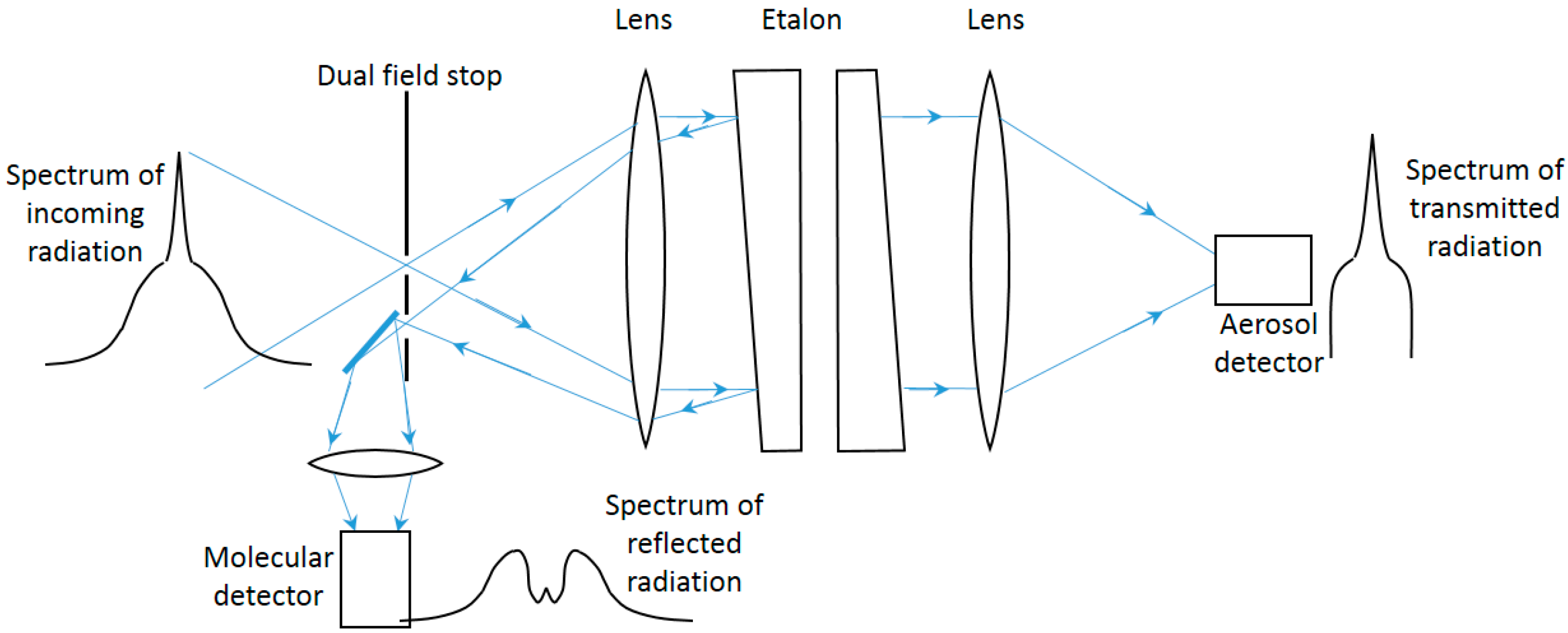
3.3. HSRL
3.4. Depolarization-Sensitive System
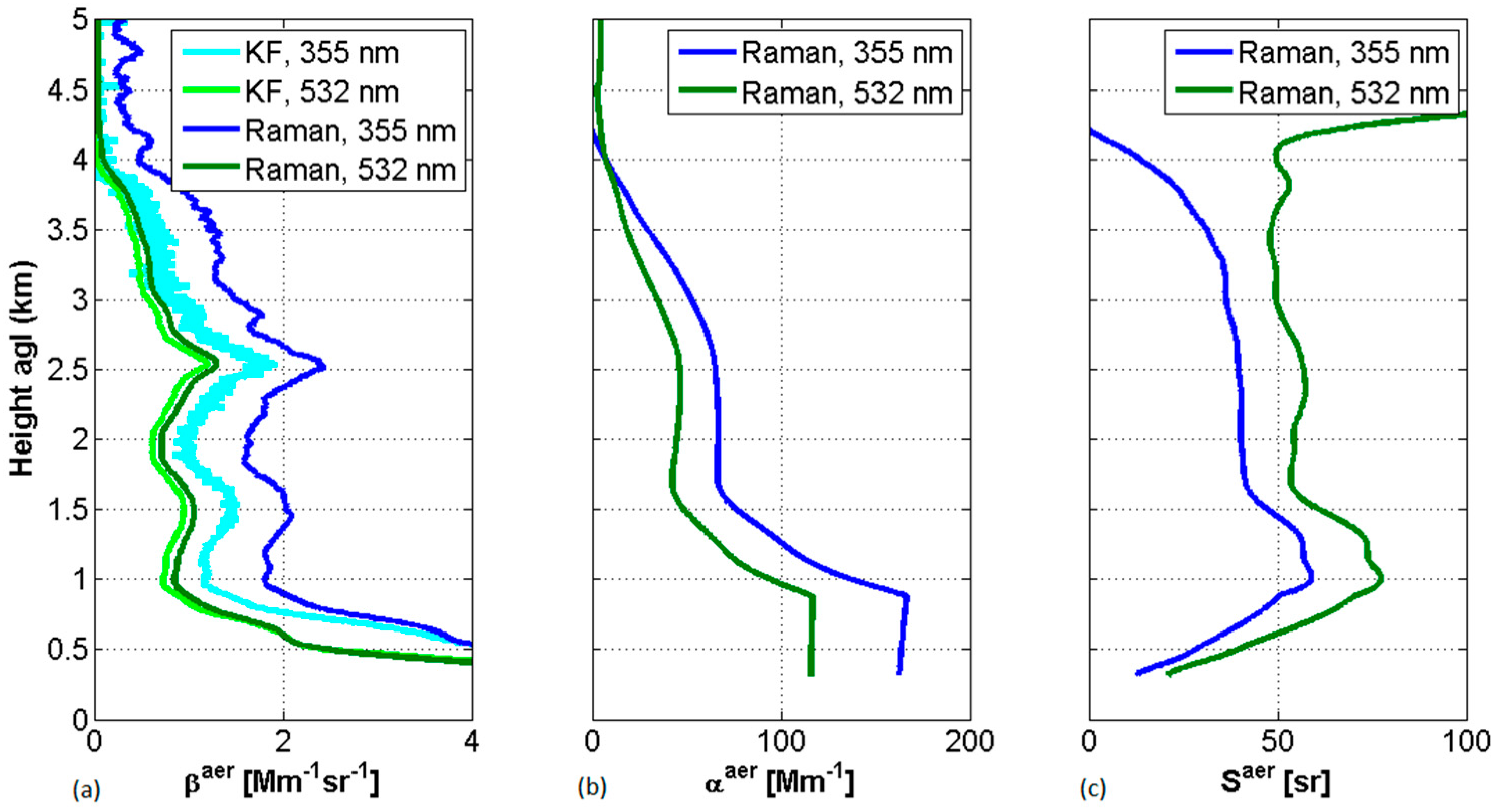
3.5. Multi-Wavelength Lidars
- Multi-wavelength elastic, vibro-rotational Raman and polarization-sensitive systems
- Multi-wavelength HSRL and polarization-sensitive systems
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Collis, R.T.H.; Russell, P.B. Lidar measurements of Particles and Gases by Elastic Backscattering and Differential Absorption. In Laser Monitoring of the Atmosphere; Hinkley, E., Ed.; Springer: New York, NY, USA, 1976; pp. 71–151. [Google Scholar]
- Huffaker, R.M.; Hardesty, R.M. Remote sensing of atmospheric wind velocities using solid-state and CO2 coherent laser systems. Proc. IEEE 1996, 84, 181–204. [Google Scholar] [CrossRef]
- Collis, R.T.H.; Fernald, F.G.; Ligda, M.G.H. Laser Radar Echoes from a Stratified Clear Atmosphere. Nature 1964, 203, 1274–1275. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Pal, S.R.; Steinbrecht, W.; Carswell, A.I. Automated method for lidar determination of cloud-base height and vertical extent. Appl. Opt. 1992, 31, 1488–1494. [Google Scholar] [CrossRef] [PubMed]
- Fernald, F.G.; Herman, B.M.; Reagan, J.A. Determination of aerosol height distribution by lidar. J. Appl. Meteorol. 1972, 11, 482–489. [Google Scholar] [CrossRef]
- Fernald, F.G. Analysis of atmospheric lidar observations: Some comments. Appl. Opt. 1984, 23, 652–653. [Google Scholar] [CrossRef] [PubMed]
- Klett, J.D. Lidar inversion with variable backscatter extinction ratios. Appl. Opt. 1985, 24, 1638–1643. [Google Scholar] [CrossRef] [PubMed]
- Potter, J.F. Two-frequency lidar inversion technique. Appl. Opt. 1987, 26, 1250–1256. [Google Scholar] [CrossRef] [PubMed]
- Sicard, M.; Chazette, P.; Pelon, J.; Won, J.G.; Yoon, S.-C. Variational Method for the Retrieval of the Optical Thickness and the Backscatter Coefficient from Multiangle Lidar Profiles. Appl. Opt. 2002, 41, 493–502. [Google Scholar] [CrossRef] [PubMed]
- Ansmann, A.; Riebesell, M.; Weitkamp, C. Measurement of atmospheric aerosol extinction profiles with a Raman lidar. Opt. Lett. 1990, 15, 746–748. [Google Scholar] [CrossRef] [PubMed]
- Ansmann, A.; Wandinger, U.; Riebesell, M.; Weitkamp, C.; Michaelis, W. Independent measurement of extinction and backscatter profiles in cirrus clouds by using a combined Raman elastic-backscatter lidar. Appl. Opt. 1992, 31, 7113–7131. [Google Scholar] [CrossRef] [PubMed]
- Gimmestad, G.G. Reexamination of depolarization in lidar measurements. Appl. Opt. 2008, 47, 3795–3802. [Google Scholar] [CrossRef] [PubMed]
- Müller, D.; Wandinger, U.; Ansmann, A. Microphysical particle parameters from extinction and backscatter lidar data by inversion with regularization: Theory. Appl. Opt. 1999, 38, 2346–2357. [Google Scholar] [CrossRef] [PubMed]
- Müller, D.; Wandinger, U.; Ansmann, A. Microphysical particle parameters from extinction and backscatter lidar data by inversion with regularization: Simulation. Appl. Opt. 1999, 38, 2358–2368. [Google Scholar] [CrossRef] [PubMed]
- Müller, D.; Wagner, F.; Wandinger, U.; Ansmann, A.; Wendisch, M.; Althausen, D.; von Hoyningen-Huene, W. Microphysical particle parameters from extinction and backscatter lidar data by inversion with regularization: Experiment. Appl. Opt. 2000, 39, 1879–1892. [Google Scholar] [CrossRef]
- Veselovskii, I.; Kolgotin, A.; Griaznov, V.; Müller, D.; Wandinger, U.; Whitemann, D.N. Inversion with regularization for the retrieval of tropospheric aerosol parameters from multiwavelength lidar sounding. Appl. Opt. 2002, 41, 3685–3699. [Google Scholar] [CrossRef] [PubMed]
- Veselovskii, I.; Whiteman, D.N.; Kolgotin, A.; Andrews, E.; Korenskii, M. Demonstration of aerosol property profiling by multiwavelength lidar under varying relative humidity conditions. J. Atmos. Ocean. Technol. 2009, 26, 1543–1557. [Google Scholar] [CrossRef]
- Bockmann, C.; Mironova, I.; Schneidenbach, L.; Nessler, R. Microphysical aerosol parameters from multiwavelength lidar. J. Opt. Soc. Am. A 2005, 22, 518–528. [Google Scholar] [CrossRef]
- Chaikovsky, A.; Dubovik, O.; Holben, B.; Bril, A.; Goloub, P.; Tanré, D.; Pappalardo, G.; Wandinger, U.; Chaikovskaya, L.; Denisov, S.; et al. Lidar-Radiometer Inversion Code (LIRIC) for the retrieval of vertical aerosol properties from combined lidar/radiometer data: Development and distribution in EARLINET. Atmos. Meas. Tech. 2016, 9, 1181–1205. [Google Scholar] [CrossRef]
- Lopatin, A.; Dubovik, O.; Chaikovsky, A.; Goloub, P.; Lapyonok, T.; Tanré, D.; Litvinov, P. Enhancement of aerosol characterization using synergy of lidar and sun-photometer coincident observations: The GARRLiC algorithm. Atmos. Meas. Tech. 2013, 6, 2065–2088. [Google Scholar] [CrossRef]
- Dubovik, O.; Lapyonok, T.; Litvinov, P.; Herman, M.; Fuertes, D.; Ducos, F.; Torres, B.; Derimian, Y.; Huang, X.; Lopatin, A.; et al. GRASP: A versatile algorithm for characterizing the atmosphere. SPIE Newsroom 2014, 2–5. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Koren, I.; Remer, L.A.; Tanré, D.; Ginoux, P.; Fan, S. Dust transport and deposition observed from the Terra-Moderate Resolution Imaging Spectroradiometer (MODIS) spacecraft over the Atlantic Ocean. J. Geophys. Res. D Atmos. 2005, 110, 1–16. [Google Scholar] [CrossRef]
- Shimizu, A.; Sugimoto, N.; Matsui, I.; Arao, K.; Uno, I.; Murayama, T.; Kagawa, N.; Aoki, K.; Uchiyama, A.; Yamazaki, A.A. Continuous observations of Asian dust and other aerosols by polarization lidars in China and Japan during ACE-Asia. J. Geophys. Res. D Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Tesche, M.; Ansmann, A.; Müller, D.; Althausen, D.; Mattis, I.; Heese, B.; Freudenthaler, V.; Wiegner, M.; Esselborn, M.; Pisani, G.; et al. Vertical profiling of Saharan dust with Raman lidars and airborne HSRL in southern Morocco during SAMUM. Tellus. Ser. B Chem. Phys. Meteorol. 2009, 61, 144–164. [Google Scholar] [CrossRef]
- Ansmann, A.; Seifert, P.; Tesche, M.; Wandinger, U. Profiling of fine and coarse particle mass: Case studies of Saharan dust and Eyjafjallajökull/Grimsvötn volcanic plumes. Atmos. Chem. Phys. 2012, 12, 9399–9415. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2001: The Scientific Basis; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001. [Google Scholar]
- Beer, A. Determination of the absorption of red light in colored liquids. Ann. Phys. Chem. 1852, 86, 78–88. [Google Scholar] [CrossRef]
- Bissonnette, L.R. Multiple-scattering lidar equation. Appl. Opt. 1996, 35, 6449–6465. [Google Scholar] [CrossRef] [PubMed]
- Halldórsson, T.; Langerholc, J. Geometrical form factors for the lidar function. Appl. Opt. 1978, 17, 240–244. [Google Scholar] [CrossRef] [PubMed]
- Stelmaszczyk, K.; Dell’Aglio, M.; Chudzyński, S.; Stacewicz, T.; Wöste, L. Analytical function for lidar geometrical compression form-factor calculations. Appl. Opt. 2005, 44, 1323–1331. [Google Scholar] [CrossRef] [PubMed]
- Comeron, A.; Sicard, M.; Kumar, D.; Rocadenbosch, F. Use of a field lens for improving the overlap function of a lidar system employing an optical fiber in the receiver assembly. Appl. Opt. 2011, 50, 5538–5544. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.; Rocadenbosch, F. Determination of the overlap factor and its enhancement for medium-size tropospheric lidar systems: A ray-tracing approach. J. Appl. Remote Sens. 2013, 7, 1–15. [Google Scholar] [CrossRef]
- Bösenberg, J.; Hoff, R. Plan for the Implementation of the GAW Aerosol Lidar Observation Network (GALION); GAW Report No. 178 (WMO Technical Document. No. 1443); GAW Aerosol Research: Hamburg, Germany, 2007. [Google Scholar]
- Hitschfeld, W.; Bordan, J. Errors inherent in the radar measurement of rainfall at attenuating wavelengths. J. Appl. Meteorol. 1954, 11, 58–67. [Google Scholar] [CrossRef]
- Kaul, B.V. Laser Sensing the Aerosol Pollution in the Atmosphere. Ph.D. Thesis, Institute of Atmospheric Optics, Tomsk State University, Tomsk, Russia, 1976. (In Russian). [Google Scholar]
- Klett, J.D. Stable analytical inversion solution for processing lidar returns. Appl. Opt. 1981, 20, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Ince, E.L. Ordinary Differential Equations; Dover Publications: New York, NY, USA, 1956. [Google Scholar]
- Rocadenbosch, F.; Frasier, S.; Kumar, D.; Vega, D.L.; Gregorio, E.; Sicard, M. Backscatter Error Bounds for the Elastic Lidar Two-Component Inversion Algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4791–4803. [Google Scholar] [CrossRef]
- Bodhaine, B.A.; Wood, N.B.; Dutton, E.G.; Slusser, J.R. On Rayleigh Optical Depth Calculations. J. Atmos. Ocean. Technol. 1999, 16, 1854–1861. [Google Scholar] [CrossRef]
- Pedros, R.; Estelles, V.; Sicard, M.; Gomez-Amo, J.L.; Utrillas, M.P.; Martinez-Lozano, J.A.; Rocadenbosch, F.; Perez, C.; Recio, J.M.B. Climatology of the Aerosol Extinction-to-Backscatter Ratio from Sun-Photometric Measurements. IEEE Trans. Geosci. Remote Sens. 2010, 48, 237–249. [Google Scholar] [CrossRef]
- Wandinger, U.; Müller, D.; Böckmann, C.; Althausen, D.; Matthias, V.; Bösenberg, J.; Weiß, V.; Fiebig, M.; Wendisch, M.; Stohl, A.; et al. Optical and microphysical characterization of biomass-burning and industrial-pollution aerosols from multiwavelength lidar and aircraft measurements. J. Geophys. Res. Atmos. 2002, 107, LAC 7-1–LAC 7-20. [Google Scholar] [CrossRef]
- Mattis, I.; Ansmann, A.; Müller, D.; Wandinger, U.; Althausen, D. Multilayer aerosol observations with dual-wavelength Raman lidar in the framework of EARLINET. J. Geophys. Res. D Atmos. 2004, 109, 1–15. [Google Scholar] [CrossRef]
- Ansmann, A. Ground-truth aerosol lidar observations: Can the Klett solutions obtained from ground and space be equal for the same aerosol case? Appl. Opt. 2006, 45, 3367–3371. [Google Scholar] [CrossRef] [PubMed]
- Comerón, A.; Rocadenbosch, F.; López, M.A.; Rodríguez, A.; Muñoz, C.; García-Vizcaíno, D.; Sicard, M. Effects of noise on lidar data inversion with the backward algorithm. Appl. Opt. 2004, 43, 2572–2577. [Google Scholar] [CrossRef] [PubMed]
- Sicard, M.; Comerón, A.; Rocadenbosch, F.; Rodríguez, A.; Muñoz, C. Quasi-analytical determination of noise-induced error limits in lidar retrieval of aerosol backscatter coefficient by the elastic, two-component algorithm. Appl. Opt. 2009, 48, 176–182. [Google Scholar] [CrossRef] [PubMed]
- Di Girolamo, P.; Ambrico, P.F.; Amodeo, A.; Boselli, A.; Pappalardo, G.; Spinelli, N. Aerosol observations by lidar in the nocturnal boundary layer. Appl. Opt. 1999, 38, 4585. [Google Scholar] [CrossRef] [PubMed]
- Kunz, G.J. Transmission as an input boundary value for an analytical solution of a single-scatter lidar equation. Appl. Opt. 1996, 35, 3255–3260. [Google Scholar] [CrossRef] [PubMed]
- Aerosol RObotic NETwork, AERONET. Available online: https://aeronet.gsfc.nasa.gov/ (accessed on 18 April 2017).
- Kovalev, V.A. Stable near-end solution of the lidar equation for clear atmospheres. Appl. Opt. 2003, 42, 585–591. [Google Scholar] [CrossRef] [PubMed]
- Kovalev, V.; Wold, C.; Petkov, A.; Hao, W.M. Modified technique for processing multiangle lidar data measured in clear and moderately polluted atmospheres. Appl. Opt. 2011, 50, 4957. [Google Scholar] [CrossRef]
- Wiegner, M.; Madonna, F.; Binietoglou, I.; Forkel, R.; Gasteiger, J.; Geiß, A.; Pappalardo, G.; Schäfer, K.; Thomas, W. What is the benefit of ceilometers for aerosol remote sensing? An answer from EARLINET. Atmos. Meas. Tech. 2014, 7, 1979–1997. [Google Scholar] [CrossRef]
- Madonna, F.; Amato, F.; Hey, J.V.; Pappalardo, G. Ceilometer aerosol profiling versus Raman lidar in the frame of the INTERACT campaign of ACTRIS. Atmos. Meas. Tech. 2015, 8, 2207–2223. [Google Scholar] [CrossRef]
- Coulter, R.L. A Comparison of Three Methods for Measuring Mixing-Layer Height. J. Appl. Meteorol. 1979, 18, 1495–1499. [Google Scholar] [CrossRef]
- Schafer, R.W. What Is a Savitzky-Golay Filter? [Lecture Notes]. IEEE Signal Process. Mag. 2011, 28, 111–117. [Google Scholar] [CrossRef]
- Iarlori, M.; Madonna, F.; Rizi, V.; Trickl, T.; Amodeo, A. Effective resolution concepts for lidar observations. Atmos. Meas. Tech. 2015, 8, 5157–5176. [Google Scholar] [CrossRef]
- Wandinger, U.; Ansmann, A. Experimental determination of the lidar overlap profile with Raman lidar. Appl. Opt. 2002, 41, 511–514. [Google Scholar] [CrossRef] [PubMed]
- Tesche, M.; Ansmann, A.; Müller, D.; Althausen, D.; Engelmann, R.; Freudenthaler, V.; Groß, S. Vertically resolved separation of dust and smoke over Cape Verde using multiwavelength Raman and polarization lidars during Saharan Mineral Dust Experiment 2008. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Veselovskii, I.; Whiteman, D.N.; Korenskiy, M.; Suvorina, A.; Perez-Ramirez, D. Use of rotational Raman measurements in multiwavelength aerosol lidar for evaluation of particle backscattering and extinction. Atmos. Meas. Tech. 2015, 8, 4111–4122. [Google Scholar] [CrossRef]
- Shipley, S.T.; Tracy, D.H.; Eloranta, E.W.; Trauger, J.T.; Sroga, J.T.; Roesler, F.L.; Weinman, J.A. High spectral resolution lidar to measure optical scattering properties of atmospheric aerosols. 1: Theory and instrumentation. Appl. Opt. 1983, 22, 3716–3724. [Google Scholar] [CrossRef] [PubMed]
- Sroga, J.T.; Eloranta, E.W.; Shipley, S.T.; Roesler, F.L.; Tryon, P.J. High spectral resolution lidar to measure optical scattering properties of atmospheric aerosols. 2: Calibration and data analysis. Appl. Opt. 1983, 22, 3725–3732. [Google Scholar] [CrossRef] [PubMed]
- Eloranta, E.E. Lidar: Range-Resolved Optical Remote Sensing of the Atmosphere; Weitkamp, C., Ed.; Springer: New York, NY, USA, 2005; pp. 143–164. [Google Scholar]
- Nishizawa, T.; Sugimoto, N.; Matsui, I.; Shimizu, A.; Tatarov, B.; Okamoto, H. Algorithm to Retrieve Aerosol Optical Properties From High-Spectral-Resolution Lidar and Polarization Mie-Scattering Lidar Measurements. IEEE Trans. Geosci. Remote Sens. 2008, 46, 4094–4103. [Google Scholar] [CrossRef]
- Dabas, A.; Denneulin, M.L.; Flamant, P.; Loth, C.; Garnier, A.; Dolfi-Bouteyre, A. Correcting winds measured with a Rayleigh Doppler lidar from pressure and temperature effects. Tellus Ser. A 2008, 60, 206–215. [Google Scholar] [CrossRef]
- Schotland, R.M.; Sassen, K.; Stone, R. Observations by Lidar of Linear Depolarization Ratios for Hydrometeors. J. Appl. Meteorol. 1971, 10, 1011–1017. [Google Scholar] [CrossRef]
- Sassen, K. The Polarization Lidar Technique for Cloud Research: A Review and Current Assessment. Bull. Am. Meteorol. Soc. 1991, 72, 1848–1866. [Google Scholar] [CrossRef]
- Sassen, K. Lidar: Range-Resolved Optical Remote Sensing of the Atmosphere; Weitkamp, C., Ed.; Springer: New York, NY, USA, 2005; pp. 19–42. [Google Scholar]
- Freudenthaler, V.; Homburg, F.; Jäger, H. Optical parameters of contrails from lidar measurements: Linear depolarization. Geophys. Res. Lett. 1996, 23, 3715–3718. [Google Scholar] [CrossRef]
- Sassen, K. Contrail-Cirrus and Their Potential for Regional Climate Change. Bull. Am. Meteorol. Soc. 1997, 78, 1885–1903. [Google Scholar] [CrossRef]
- Freudenthaler, V.; Esselborn, M.; Wiegner, M.; Heese, B.; Tesche, M.; Ansmann, A.; Müller, D.; Althausen, D.; Wirth, M.; Fix, A.; et al. Depolarization ratio profiling at several wavelengths in pure Saharan dust during SAMUM 2006. Tellus. Ser. B Chem. Phys. Meteorol. 2009, 61, 165–179. [Google Scholar] [CrossRef]
- Roy, G.; Bissonnette, L.R. Strong dependence of rain-induced lidar depolarization on the illumination angle: Experimental evidence and geometrical-optics interpretation. Appl. Opt. 2001, 40, 4770–4789. [Google Scholar] [CrossRef] [PubMed]
- Wandinger, U.; Ansmann, A.; Mattis, I.; Müller, D.; Pappalardo, G. CALIPSO and beyong: Long-term ground-based support of space-borne aerosols and cloud lidar missions. In Proceedings of the 24th International Laser Radar Conference, Colorado, CO, USA, 23–27 June 2008; pp. 715–718. [Google Scholar]
- Müller, D.; Ansmann, A.; Mattis, I.; Tesche, M.; Wandinger, U.; Althausen, D.; Pisani, G. Aerosol-type-dependent lidar ratios observed with Raman lidar. J. Geophys. Res. 2007, 112, D16202. [Google Scholar] [CrossRef]
- Behrendt, A.; Nakamura, T. Calculation of the calibration constant of polarization lidar and its dependency on atmospheric temperature. Opt. Express 2002, 10, 805. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Gómez, A.; Sicard, M.; Muñoz-Porcar, C.; Barragán, R.; Comerón, A.; Rocadenbosch, F.; Vidal, E. Depolarization channel for Barcelona lidar: Implementation and preliminary measurements. In Proceedings of the 28th International Laser Radar Conference, Bucharest, Romania, 25–30 June 2017. [Google Scholar]
- Engelmann, R.; Kanitz, T.; Baars, H.; Heese, B.; Althausen, D.; Skupin, A.; Wandinger, U.; Komppula, M.; Stachlewska, I.S.; Amiridis, V.; et al. The automated multiwavelength Raman polarization and water-vapor lidar PollyXT: The neXT generation. Atmos. Meas. Tech. 2016, 9, 1767–1784. [Google Scholar] [CrossRef]
- Haarig, M.; Engelmann, R.; Ansmann, A.; Veselovskii, I.; Whiteman, D.N.; Althausen, D. 1064nm rotational Raman lidar for particle extinction and lidar-ratio profiling: Cirrus case study. Atmos. Meas. Tech. 2016, 9, 4269–4278. [Google Scholar] [CrossRef]
- Bovchaliuk, V.; Goloub, P.; Podvin, T.; Veselovskii, I.; Tanre, D.; Chaikovsky, A.; Dubovik, O.; Mortier, A.; Lopatin, A.; Korenskiy, M.; et al. Comparison of aerosol properties retrieved using GARRLiC, LIRIC, and Raman algorithms applied to multi-wavelength lidar and sun/sky-photometer data. Atmos. Meas. Tech. 2016, 9, 3391–3405. [Google Scholar] [CrossRef]

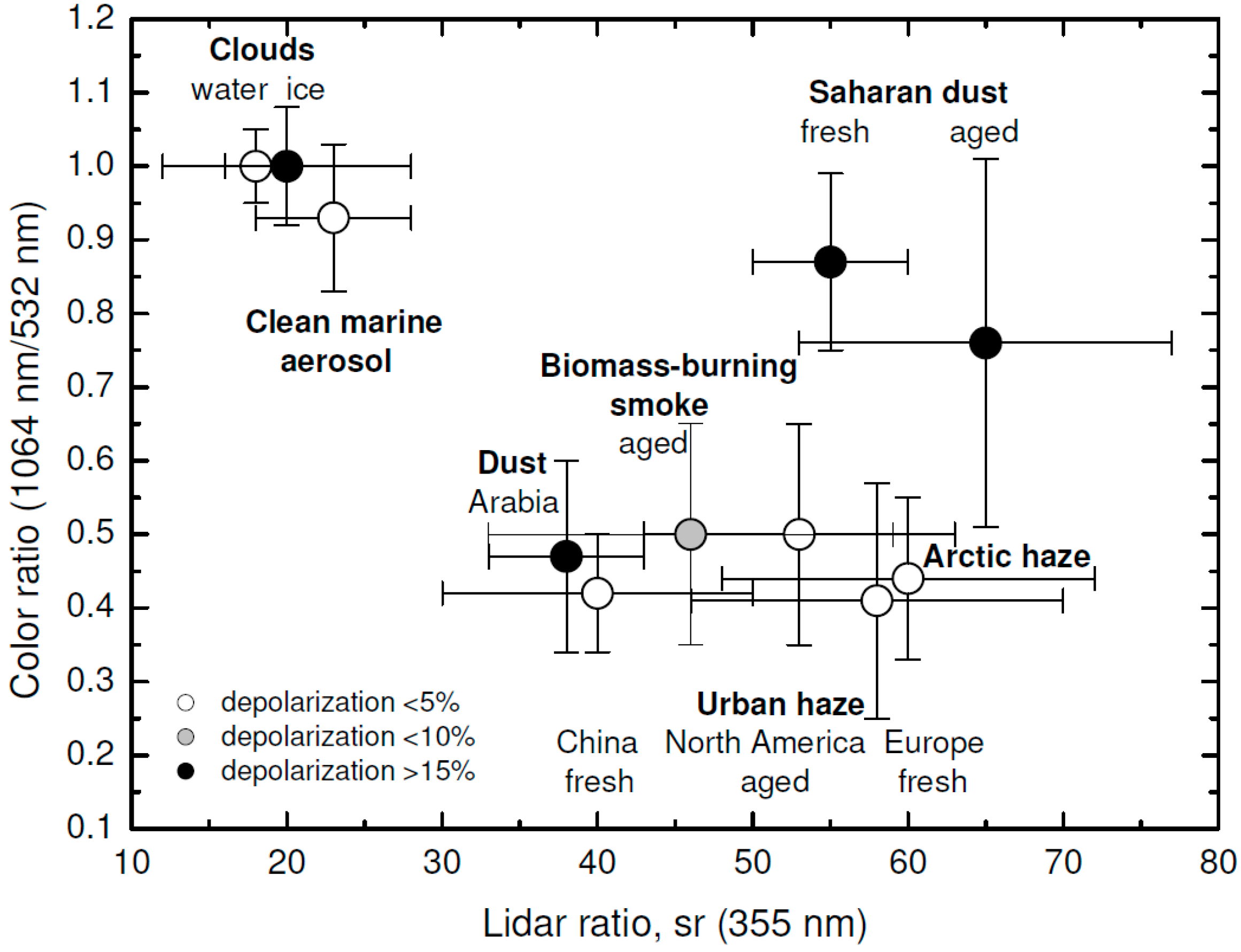
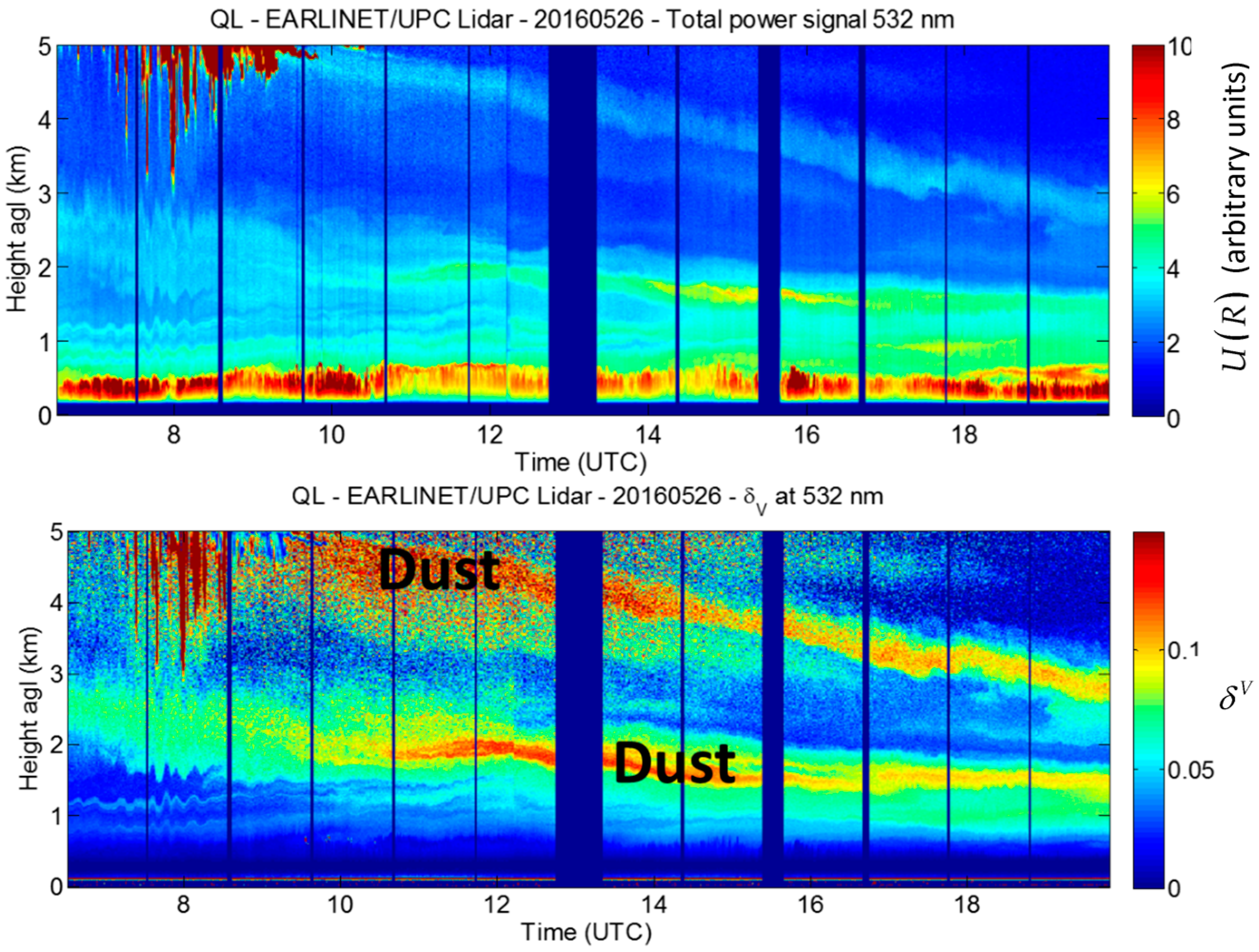
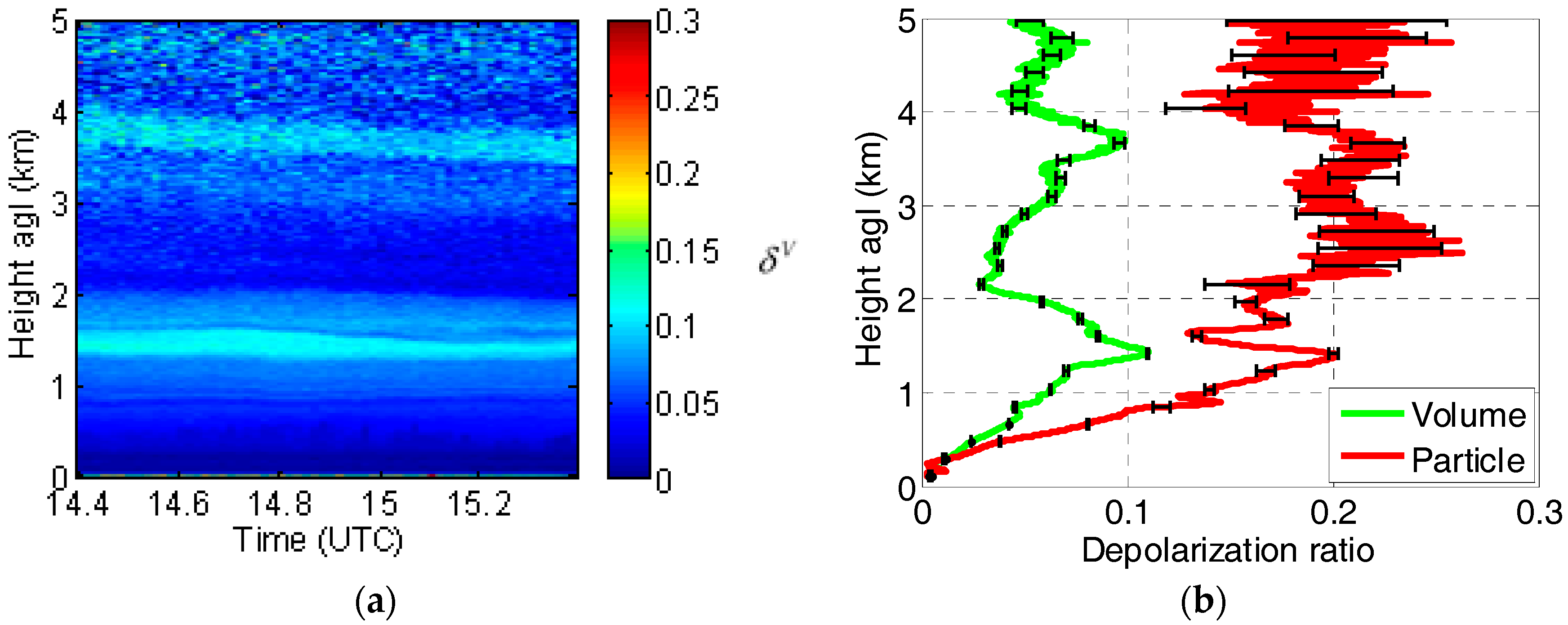
| Properties | Parameters | Configuration | References | |
|---|---|---|---|---|
| Structural | PBL height | 1β and > | [3,4] | |
| Lofted layer base, top and thickness | 1β and > | |||
| Cloud base, top and thickness | 1β and > | [5] | ||
| Optical | Backscatter coefficient | 1β and >; multi-angular | [6,7,8,9,10] | |
| Extinction coefficient | 1β + 1α and > | [11,12] | ||
| Microphysical | Shape | 1β + 1δ | [13] | |
| Size | reff, ω0, C, n domain | 3β + 2α | [14,15,16,17,18,19] | |
| βm,s, αm,s, Cm,s, Vm,s | 3β + 1δ + Sun-Photometer | [20,21,22] | ||
| reff | 2β + MODIS *-derived optical properties | [23] | ||
| βm, Cm | 1β + 1δ if 2 or 3 aerosol types of different depolarization ratios can be identified | [24,25,26] | ||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Comerón, A.; Muñoz-Porcar, C.; Rocadenbosch, F.; Rodríguez-Gómez, A.; Sicard, M. Current Research in Lidar Technology Used for the Remote Sensing of Atmospheric Aerosols. Sensors 2017, 17, 1450. https://doi.org/10.3390/s17061450
Comerón A, Muñoz-Porcar C, Rocadenbosch F, Rodríguez-Gómez A, Sicard M. Current Research in Lidar Technology Used for the Remote Sensing of Atmospheric Aerosols. Sensors. 2017; 17(6):1450. https://doi.org/10.3390/s17061450
Chicago/Turabian StyleComerón, Adolfo, Constantino Muñoz-Porcar, Francesc Rocadenbosch, Alejandro Rodríguez-Gómez, and Michaël Sicard. 2017. "Current Research in Lidar Technology Used for the Remote Sensing of Atmospheric Aerosols" Sensors 17, no. 6: 1450. https://doi.org/10.3390/s17061450
APA StyleComerón, A., Muñoz-Porcar, C., Rocadenbosch, F., Rodríguez-Gómez, A., & Sicard, M. (2017). Current Research in Lidar Technology Used for the Remote Sensing of Atmospheric Aerosols. Sensors, 17(6), 1450. https://doi.org/10.3390/s17061450







