Torsional Ultrasound Sensor Optimization for Soft Tissue Characterization
Abstract
:1. Introduction
2. Methods
- Phase 1: Modelization of the torsional wave propagation in tissue, including a sensitivity test on the parameters of the excitation wave.
- Phase 2: Joint modelization of tissue-transducer interaction. Optimization of the transducer under maximum POD (Probability Of Detection) criterion.
2.1. Robust Probability of Detection
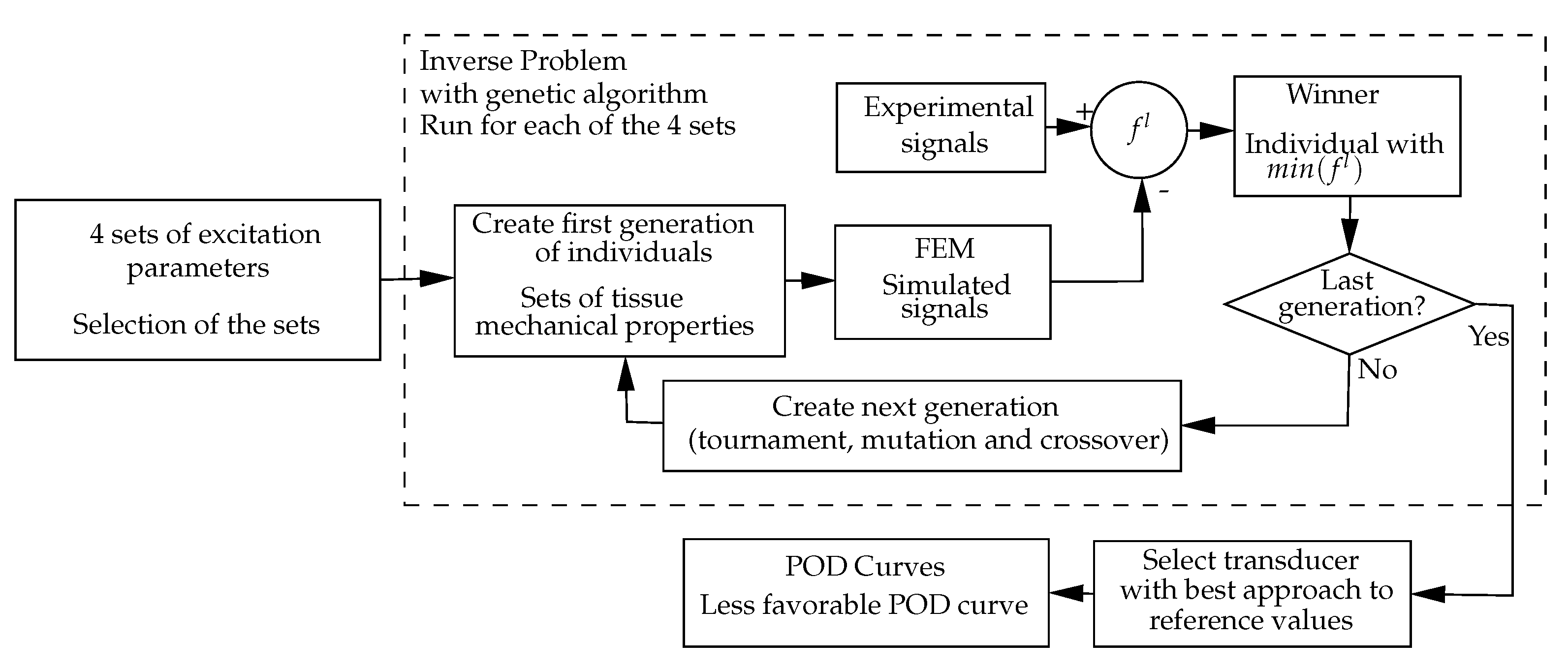
2.2. Inverse Problem
2.3. Phase 1: Modelization of Torsional Wave Propagation in Tissue
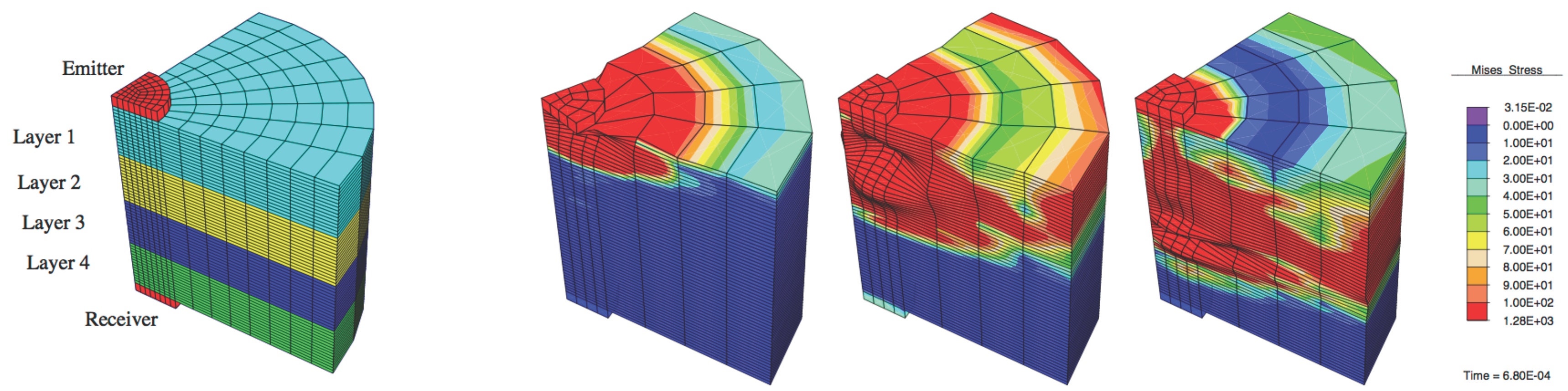
- A linear elastic, attenuating and multilayered physical model, solved by finite elements, was used to simulate the torsional wave propagation.
- An inverse problem is proposed to characterize the mechanical properties of the tissue and detect pathology.
- The inverse problem is applied to several sets of excitation parameters (geometry and emitted waveforms), to see the capability of the method to select that with best detection.
- The use of the semi-analytic POD estimator with the selected excitation, to measure its capability of detection.
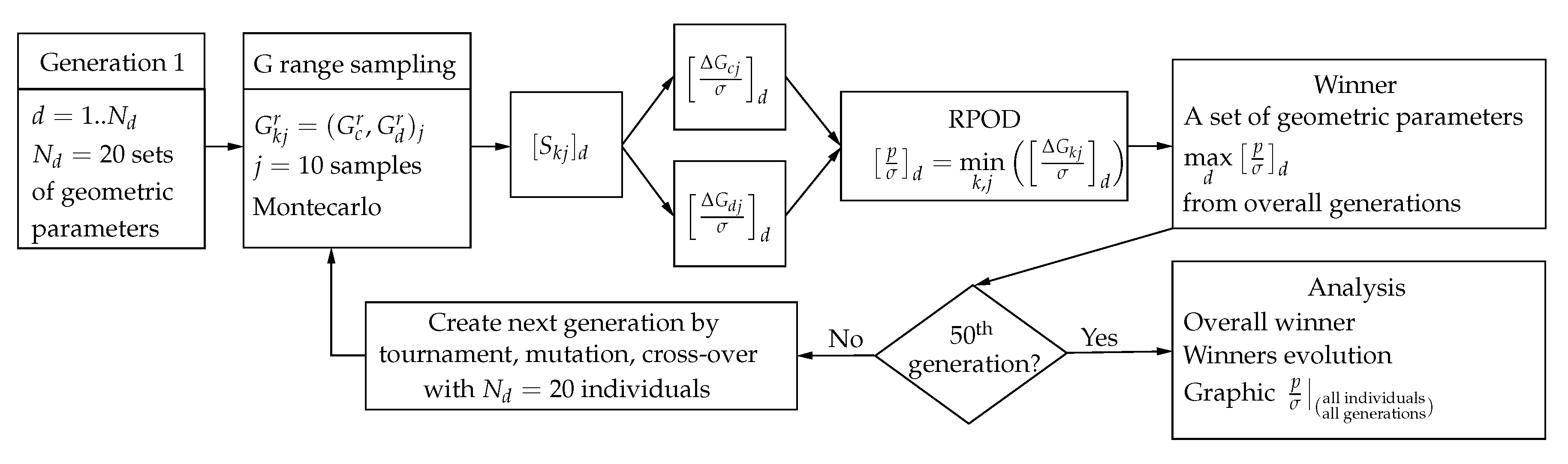
- The calculation process is outlined in Figure 3.
2.4. Phase 2: Tissue-Transducer Modelization, Optimization with RPOD
3. Results
4. Discussion and Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wells, P.N.; Liang, H.D. Medical ultrasound: Imaging of soft tissue strain and elasticity. J. R. Soc. Interface 2011, 8, 1521–1549. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Taylor, L.S.; Rubens, D.J.; Parker, K.J. Sonoelastographic imaging of interference patterns for estimation of the shear velocity of homogeneous biomaterials. Phys. Med. Biol. 2004, 49, 911. [Google Scholar] [CrossRef] [PubMed]
- Glazounov, A.; Zhang, Q.; Kim, C. Torsional actuator based on mechanically amplified shear piezoelectric response. Sens. Actuators A Phys. 2000, 79, 22–30. [Google Scholar] [CrossRef]
- Harkness, P.; Lucas, M.; Cardoni, A. Coupling and degenerating modes in longitudinal–torsional step horns. Ultrasonics 2012, 52, 980–988. [Google Scholar] [CrossRef] [PubMed]
- Szabo, T. Diagnostic Ultrasound Imaging: Inside Out; Academic Press: Oxford, UK, 2004. [Google Scholar]
- Thijssen, J.; Verhoef, W.; Cloostermans, M. Optimization of ultrasonic transducers. Ultrasonics 1985, 23, 41–46. [Google Scholar] [CrossRef]
- Heikkola, E.; Laitinen, M. Model-based optimization of ultrasonic transducers. Ultrason. Sonochemistry 2005, 12, 53–57. [Google Scholar] [CrossRef] [PubMed]
- Schröder, A.; Rautenberg, J.; Henning, B. Evaluation of cost functions for FEA based transducer optimization. Phys. Procedia 2010, 3, 1003–1009. [Google Scholar] [CrossRef]
- Heikkola, E.; Miettinen, K.; Nieminen, P. Multiobjective optimization of an ultrasonic transducer using NIMBUS. Ultrasonics 2006, 44, 368–380. [Google Scholar] [CrossRef] [PubMed]
- Fu, B.; Hemsel, T.; Wallaschek, J. Piezoelectric transducer design via multiobjective optimization. Ultrasonics 2006, 44, e747–e752. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Kwon, O. Vibration characteristics of piezoelectric torsional transducers. J. Sound Vib. 2003, 264, 453–473. [Google Scholar] [CrossRef]
- Kaneko, S.; Nomoto, S.; Yamamori, H.; Ohya, K. Load characteristics of a bolted Langevin torsional transducer. Ultrasonics 1996, 34, 239–241. [Google Scholar] [CrossRef]
- Lin, S. Study on the Langevin piezoelectric ceramic ultrasonic transducer of longitudinal–flexural composite vibrational mode. Ultrasonics 2006, 44, 109–114. [Google Scholar] [CrossRef] [PubMed]
- Aoyagi, M.; Suzuki, T.; Tomikawa, Y. Characteristics of a bolt-clamped torsional vibrator using shear-mode piezo-ceramics sandwiched in the axial direction. Ultrasonics 1996, 34, 219–222. [Google Scholar] [CrossRef]
- Harada, T.; Ishikawa, N.; Kanda, T.; Suzumori, K.; Yamada, Y.; Sotowa, K. Droplet generation using a torsional Langevin-type transducer and a micropore plate. Sens. Actuators A Phys. 2009, 155, 168–174. [Google Scholar] [CrossRef]
- Li, J.; Liu, P.; Ding, H.; Cao, W. Modeling characterization and optimization design for PZT transducer used in Near Field Acoustic Levitation. Sens. Actuators A Phys. 2011, 171, 260–265. [Google Scholar] [CrossRef]
- Lin, H.; Fang, W. A rib-reinforced micro torsional mirror driven by electrostatic torque generators. Sens. Actuators A Phys. 2003, 105, 1–9. [Google Scholar] [CrossRef]
- Kwun, H.; Jolly, W.; Light, G.; Wheeler, E. Effects of variations in design parameters of ultrasonic transducers on performance characteristics. Ultrasonics 1988, 26, 65–72. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, X.; Zhang, D.; Wu, Y. Development of novel ultrasonic transducers for microelectronics packaging. J. Mater. Process. Technol. 2009, 209, 1291–1301. [Google Scholar] [CrossRef]
- Murav’evaa, O.V.; Len’kovb, S.V.; Murashova, S.A. Torsional waves excited by electromagnetic acoustic transducers during guided-wave acoustic inspection of pipelines. Acoust. Phys. 2016, 62, 117–124. [Google Scholar] [CrossRef]
- Kwun, H.; Teller, C.M. Magnetostrictive generation and detection of longitudinal, torsional, and flexural waves in a steel rod. J. Acoust. Soc. Am. 1994, 96, 1202–1204. [Google Scholar] [CrossRef]
- Fan, Z.; Lowe, M.J.S.; Castaings, M.; Bacon, C. Torsional waves propagation along a waveguide of arbitrary cross section immersed in a perfect fluid. J. Acoust. Soc. Am. 2008, 124, 2002–2010. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.O.; Bau, H.H. Instrument for simultaneous measurement of density and viscosity. Rev. Sci. Instrum. 1989, 60, 1111–1115. [Google Scholar] [CrossRef]
- Spratt, W.K.; Vetelino, J.F.; Lynnworth, L.C. Torsional Ultrasonic Waveguide Sensor. IEEE Int. Ultrason. Symp. 2010, 702–706. [Google Scholar]
- Ophir, J.; Alam, S.; Garra, B.; Kallel, F.; Konofagou, E.; Krouskop, T.; Varghese, T. Elastography: Ultrasonic estimation and imaging of the elastic properties of tissues. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 1999, 213, 203–233. [Google Scholar] [CrossRef] [PubMed]
- Van Kervel, S.; Thijssen, J. A calculation scheme for the optimum design of ultrasonic transducers. Ultrasonics 1983, 21, 134–140. [Google Scholar] [CrossRef]
- Sunny, Y.; Bawiec, C.; Nguyen, A.; Samuels, J.; Weingarten, M.; Zubkov, L.; Lewin, P. Optimization of un-tethered, low voltage, 20–100 kHz flexural transducers for biomedical ultrasonics applications. Ultrasonics 2012, 52, 943–948. [Google Scholar] [CrossRef] [PubMed]
- Rus, G.; Bochud, N.; Melchor, J.; Alaminos, M.; Campos, A.; Linde, B.B.; Pączkowski, J.; Ponikwicki, N. Dispersive model selection and reconstruction for tissue culture ultrasonic monitoring. AIP Conf. Proc. 2012, 1433, 375–378. [Google Scholar] [CrossRef]
- Peralta, L.; Molina, F.; Melchor, J.; Gómez, L.; Massó, P.; Florido, J.; Rus, G. Transient elastography to assess the cervical ripening during pregnancy: A preliminary study. Ultraschall Med.-Eur. J. Ultrasound 2015. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, J.M.M. Mechanics of Nonlinear Ultrasound in Tissue. Ph.D. Thesis, Universidad de Granada, Granada, Spain, 2016. [Google Scholar]
- Melchor, J.; Rus, G. Torsional ultrasonic transducer computational design optimization. Ultrasonics 2014, 54, 1950–1962. [Google Scholar] [CrossRef] [PubMed]
- Hadj Henni, A.; Schmitt, C.; Trop, I.; Cloutier, G. Shear wave induced resonance elastography of spherical masses with polarized torsional waves. Appl. Phys. Lett. 2012, 100, 133702. [Google Scholar] [CrossRef] [PubMed]
- Ekeom, D.; Henni, A.H.; Cloutier, G. Design of a phased array for the generation of adaptive radiation force along a path surrounding a breast lesion for dynamic ultrasound elastography imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 552–561. [Google Scholar] [CrossRef] [PubMed]
- Ouared, A.; Montagnon, E.; Cloutier, G. Generation of remote adaptive torsional shear waves with an octagonal phased array to enhance displacements and reduce variability of shear wave speeds: Comparison with quasi-plane shear wavefronts. Phys. Med. Biol. 2015, 60, 8161. [Google Scholar] [CrossRef] [PubMed]
- Ouared, A.; Kazemirad, S.; Montagnon, E.; Cloutier, G. Ultrasound viscoelasticity assessment using an adaptive torsional shear wave propagation method. Med. Phys. 2016, 43, 1603–1614. [Google Scholar] [CrossRef] [PubMed]
- Mattei, G.; Ahluwalia, A. Sample, testing and analysis variables affecting liver mechanical properties: A review. Acta Biomater. 2016, 45, 60–71. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Stiadle, J.M.; Lau, H.K.; Zerdoum, A.B.; Jia, X.; Thibeault, S.L.; Kiick, K.L. Tissue engineering-based therapeutic strategies for vocal fold repair and regeneration. Biomaterials 2016, 108, 91–110. [Google Scholar] [CrossRef] [PubMed]
- Jiao, T.; Farran, A.; Jia, X.; Clifton, R.J. High frequency measurements of viscoelastic properties of hydrogels for vocal fold regeneration. Exp. Mech. 2009, 49, 235–246. [Google Scholar] [CrossRef] [PubMed]
- Moster, D.; Lie, R.T.; Markestad, T. Long-term medical and social consequences of preterm birth. N. Engl. J. Med. 2008, 17, 262–273. [Google Scholar] [CrossRef] [PubMed]
- Blondel, B.; Macfarlane, A.; Gissler, M.; Breart, G.; Zeitlin, J. Preterm birth and multiple pregnancy in European countries participating in the PERISTAT project. BJOG 2006, 113, 528–535. [Google Scholar] [CrossRef] [PubMed]
- Bercoff, J.; Tanter, M.; Fink, M. Supersonic shear imaging: A new technique for soft tissue elasticity mapping. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2004, 51, 396–409. [Google Scholar] [CrossRef] [PubMed]
- Rus, G.; Lee, S.Y.; Chang, S.Y.; Wooh, S.C. Optimized damage detection of steel plates from noisy impact test. Int. J. Numer. Methods Eng. 2006, 68, 707–727. [Google Scholar] [CrossRef]
- Rade, L.; Westergren, B. Mathematics Handbook for Science and Engineering; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Goldberg, D. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Gallego, R.; Rus, G. Identification of cracks and cavities using the topological sensitivity boundary integral equation. Comput. Mech. 2004, 33, 154–163. [Google Scholar] [CrossRef]
- Taylor, R.L.; Govindjee, S. FEAP Manual; University of Berkeley: Berkeley, CA, USA, 2003. [Google Scholar]
- Yonetsu, K.; Ohki, M.; Kumazawa, S.; Eida, S.; Sumi, M.; Nakamura, T. Parotid tumors: Differentiation of benign and malignant tumors with quantitative sonographic analyses. Ultrasound Med. Biol. 2004, 30, 567–574. [Google Scholar] [CrossRef] [PubMed]
| Step | Target | Outcome | Tools or Inputs |
|---|---|---|---|
| 1. Problem configuration | Problem geometry, boundary conditions, configuration, sets of excitation parameters | Problem definition. 4 sets of excitation parameters to test | |
| 2. Forward physical model selection | Simulate propagation with the excitation parameters | Physical model: differential equations | Outcome from step 1: geometry, materials, etc. |
| 3. Finite element model (FEM) | Computational implementation of the physical model | Computational code of the model | Outcomes from steps 1 and 2. |
| 4. Discretization study and FEM test | Convergence study
Balance computational burden-time Assure accuracy of simulations | Spatial element Time interval FEM checked | Forward model (FEM) Geometrical parameters and tissue mechanical properties L-S wave speed check |
| 5. Inverse problem with genetic algorithm (GA) | Design and implementation Evaluate GA’s convergence - Quality of identification - Convergence speed Apply IP to 4 excitation parameter sets | Observed right behaviour and identification on the mechanical properties of the tissue Winner: excitation parameter set with best identification | FEM Cost functional for GA optimization: misfit function Synthetic signals |
| 6. POD evaluation of the winner | POD estimator evaluation
Checking coherency on results | Graphics of POD on modifications of mechanical parameters of tissue No perceived anomalies | Forward model Winner parameter set POD estimator |
| Transducer | f (kHz) | b (kHz) | r (mm) |
|---|---|---|---|
| Design 1 | 6.32 | 6.32 | 10 |
| Design 2 | 20 | 20 | 10 |
| Design 3 | 2 | 1 | 10 |
| Design 4 | 6.32 | 3.16 | 20 |
| Material | Young Modulus E (MPa) | Poisson Ratio ν | Density ρ (kg/m3) | Thickness a (mm) | Attenuation |
|---|---|---|---|---|---|
| Layer 1 | 20 | 0.48 | 1070 | 10 | 1836.07 |
| Layer 2 | 920 | 10 | |||
| Layer 3 | 1070 | 10 | |||
| Layer 4 | 20 | 0.48 | 1070 | 10 | 1836.07 |
| Step | Target | Results | Tools or Inputs |
|---|---|---|---|
| 1. Selection of the forward model | Simulate generation, propagation, and reception of waves | Physical model: differential equations | Initial transducer design: geometry, materials, etc. |
| 2. Finite element model (FEM) | Computational implementation of the physical model | Computational code of the model | Physical model Boundary conditions(geometry and properties of conceptual design, etc.) |
| 3. Discretization analysis | Convergence enhancement Balance computational burden-time | Spatial element Time interval | FEM Initial geometry and mechanical properties |
| 4. Validation of FEM results | Check accuracy on simulations | Test discrepancies using simplified models | Approximated analytic model of torsional waves for comparison ([31]). |
| 5. Sensitivity test on mechanical properties of tissue and parameters of the transducer geometry ([31]) | To know the response to transducer geometry and tissue propagation Select materials Reduce P-wave generation and propagation Maximize amplitude of received torsional wave New check of the FEM | Material influence Select a transducer geometry among tested vanishing P-wave Ranges of mechanical properties in tissue with low P-wave propagation Ranges of P-wave existence | FEM Materials to test Variation ranges of the transducer parameters (geometry) |
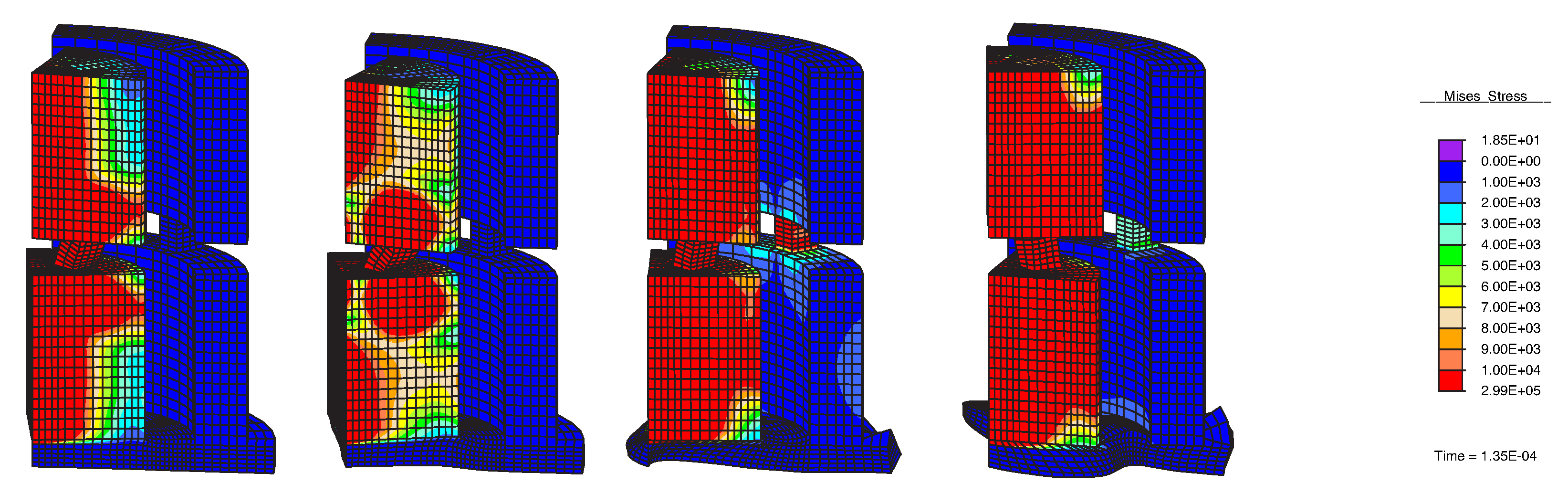
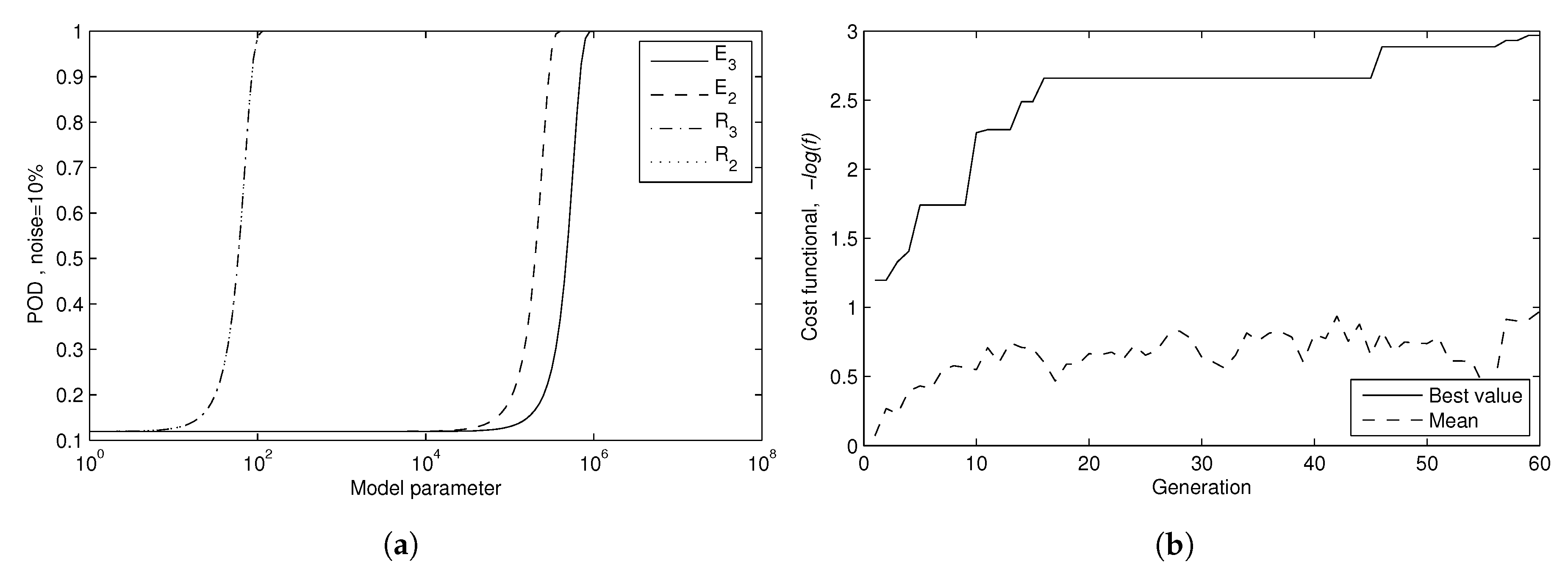
| 6. Inverse problem as a new test of the forward problem | New check of the FEM Quality of identification of tissue mechanical properties | Valid identification of mechanical properties of the tissue (Figure 5) | FEM Cost function for GA optimization: Misfit function |
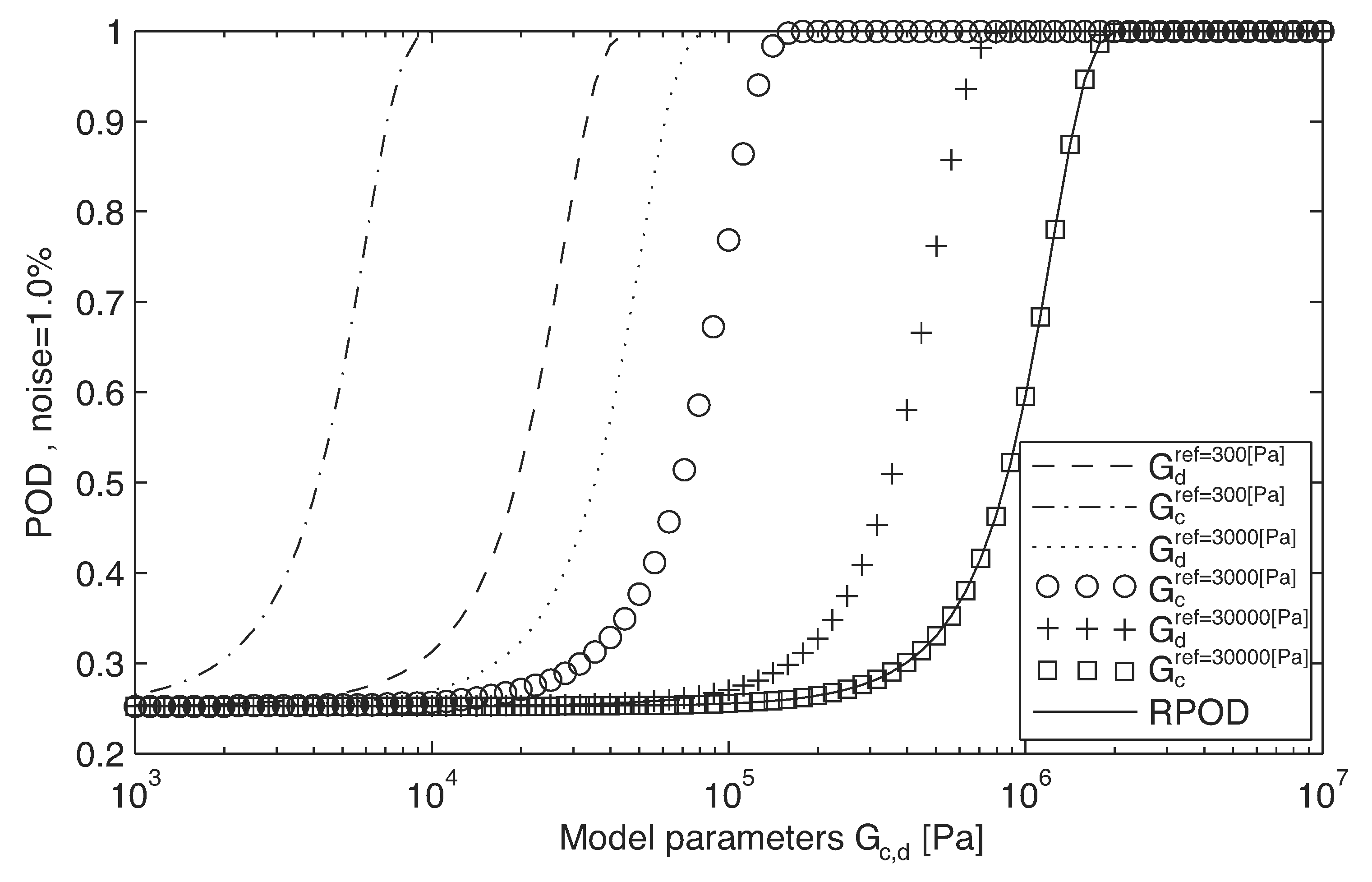
| 7. Evaluation of RPOD for best sensor in step 5 ([31]) | Test RPOD estimator Evaluate POD for three values of tissue shear modulus of reference (0.3, 3 and 30 kPa) Testing coherency on results | POD graphics (Figure 6) on a range of values of Select the initial parameters for optimization No apparent anomalies | FEM POD estimator |
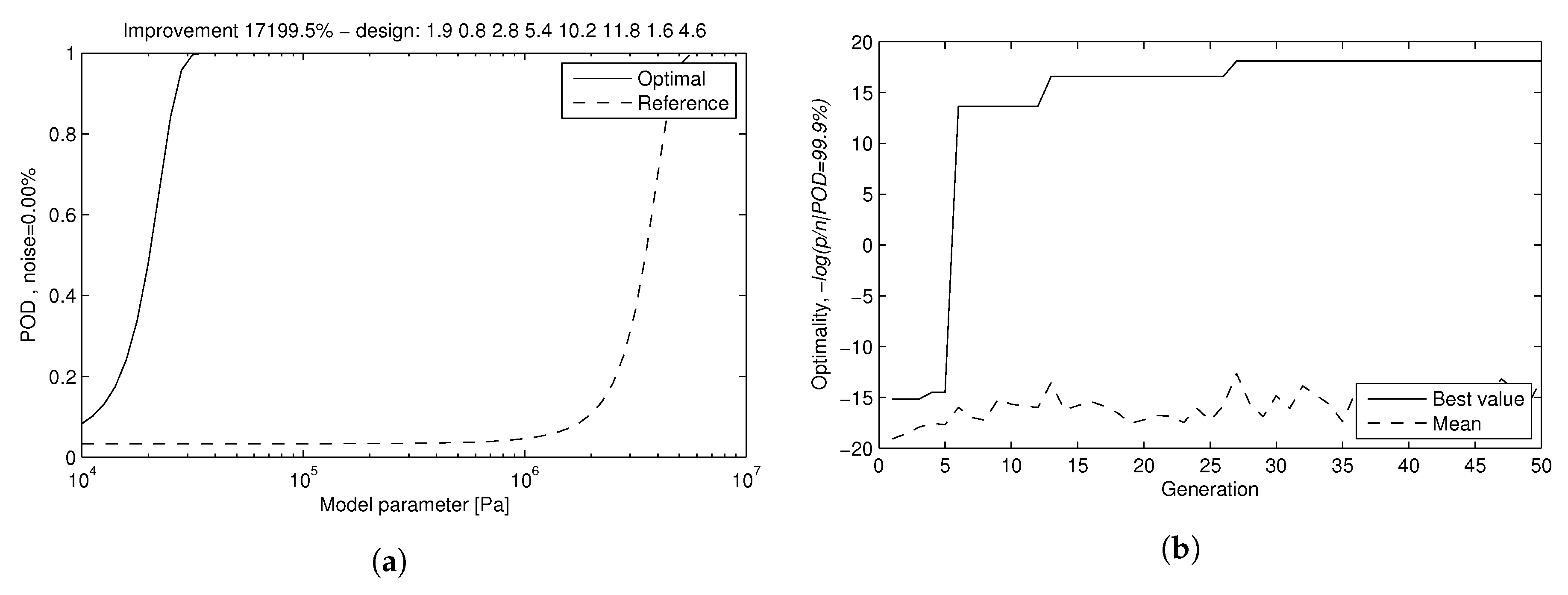
| 8. Transducer optimization with best RPOD criterion | Find transducer design (geometry) with maximum RPOD Evaluate improvement in RPOD | Select the optimal geometric design with the worst response to mechanical properties Quantification of improvement | FEM RPOD estimator GA design with RPOD as function to maximize |
| IP Results | (MPa) | (MPa) | f (kHz) | b (kHz) | rs (mm) | ||
|---|---|---|---|---|---|---|---|
| Reference Values | 27.3861 | 5.4772 | 2.2361 | 2.2361 | |||
| Design 1 | 30.4330 (11%) | 5.3381 (3%) | 1.6567 (26%) | 3.3893 (52%) | 6.32 | 6.32 | 10 |
| Design 2 | 25.2412 (8%) | 5.9172 (8%) | 1.7507 (22%) | 3.2839 (47%) | 20 | 20 | 10 |
| Design 3 | 29.1313 (6%) | 5.1269 (6%) | 2.4648 (10%) | 1.7845 (20%) | 2 | 1 | 10 |
| Design 4 | 30.6323 (12%) | 5.0484 (8%) | 2.5155 (12%) | 1.7478 (22%) | 6.32 | 3.16 | 20 |
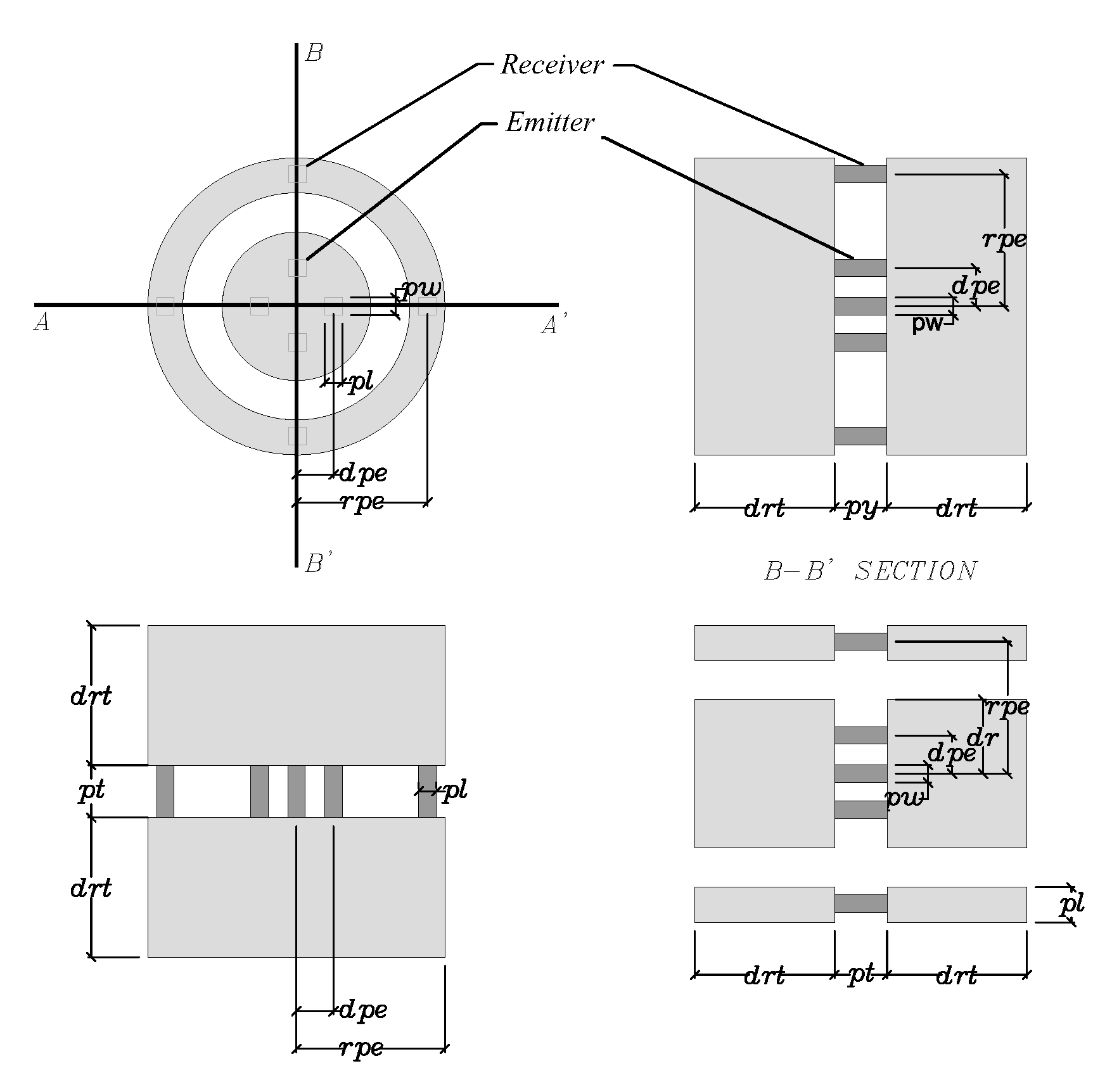
| Design Parameters (mm) | Range | Initial Value | Optimal Value | Label |
|---|---|---|---|---|
| Piezoelectric Length | (0.5, 2) | 1 | 0.8 | pl |
| Piezoelectric Width | (0.75, 2) | 1 | 1.9 | pw |
| Piezoelectric Thickness | (0.4, 4) | 2 | 2.8 | pt |
| Disc Radius | (1.75, 5.75) | 4.25 | 5.1 | dr |
| Disc Piezoelectric Eccentricity | (1.5, 3.5) | 2.5 | 2.7 | dpe |
| Ring Width | (1.5, 2.5) | 2 | 1.6 | rw |
| Ring Piezoelectric Eccentricity | (5.75, 8.5) | 7.5 | 5.9 | rpe |
| Disc-Ring Thickness | (3, 13) | 8 | 4.6 | drt |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melchor, J.; Muñoz, R.; Rus, G. Torsional Ultrasound Sensor Optimization for Soft Tissue Characterization. Sensors 2017, 17, 1402. https://doi.org/10.3390/s17061402
Melchor J, Muñoz R, Rus G. Torsional Ultrasound Sensor Optimization for Soft Tissue Characterization. Sensors. 2017; 17(6):1402. https://doi.org/10.3390/s17061402
Chicago/Turabian StyleMelchor, Juan, Rafael Muñoz, and Guillermo Rus. 2017. "Torsional Ultrasound Sensor Optimization for Soft Tissue Characterization" Sensors 17, no. 6: 1402. https://doi.org/10.3390/s17061402
APA StyleMelchor, J., Muñoz, R., & Rus, G. (2017). Torsional Ultrasound Sensor Optimization for Soft Tissue Characterization. Sensors, 17(6), 1402. https://doi.org/10.3390/s17061402






