Analysis and Validation of Contactless Time-Gated Interrogation Technique for Quartz Resonator Sensors
Abstract
:1. Introduction
2. Operating Principle
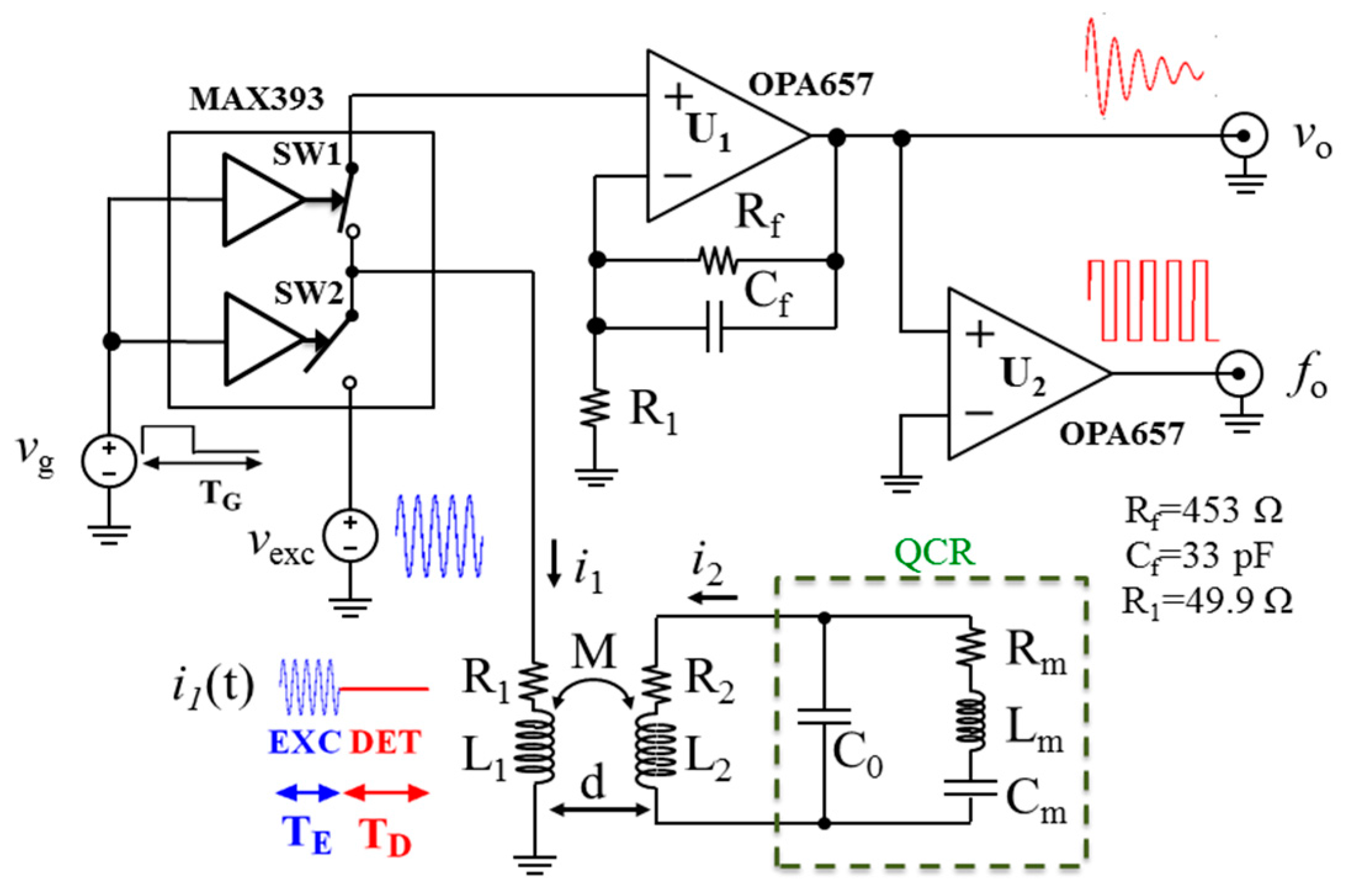
2.1. Theoretical Analysis and Equivalent Model
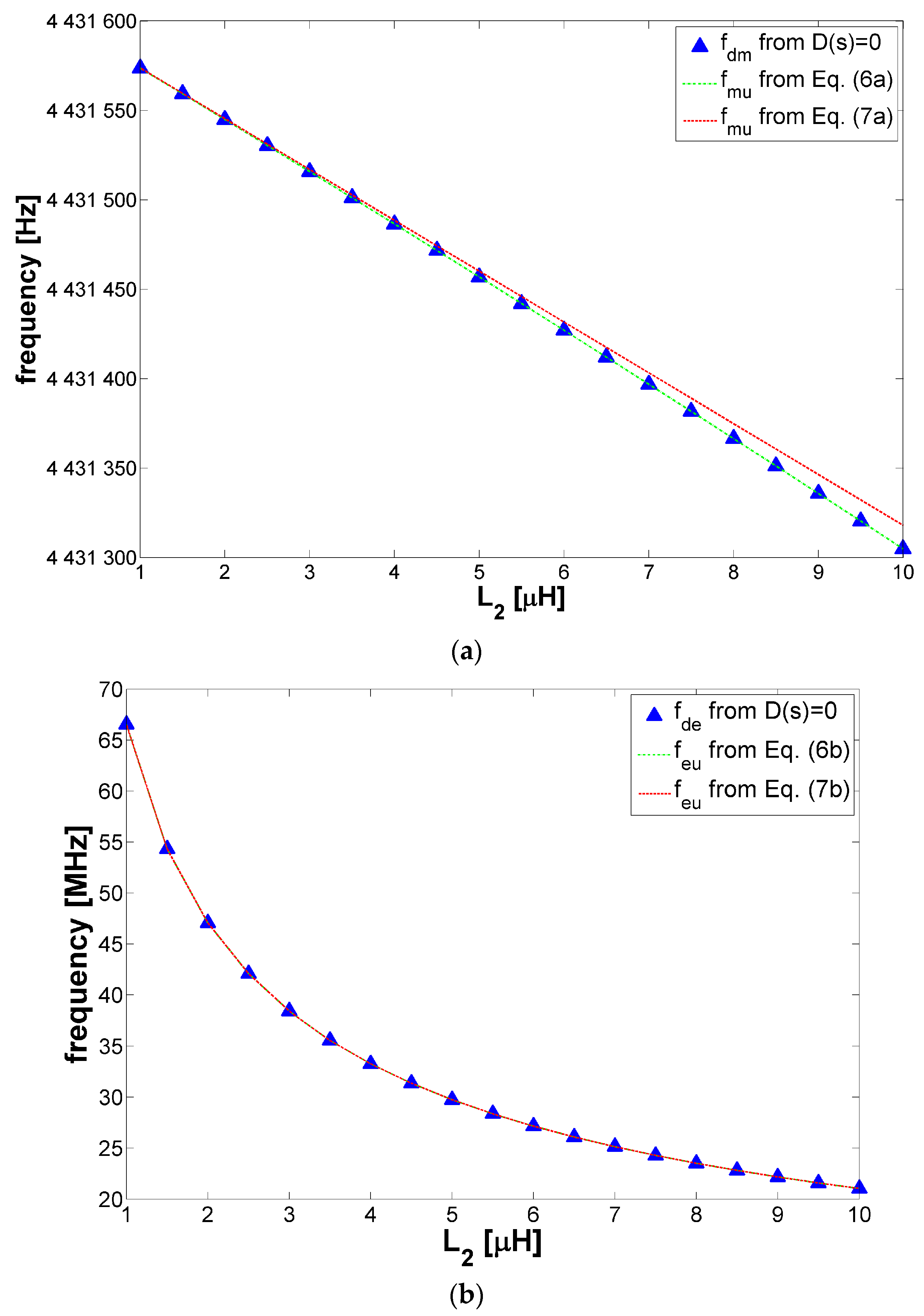
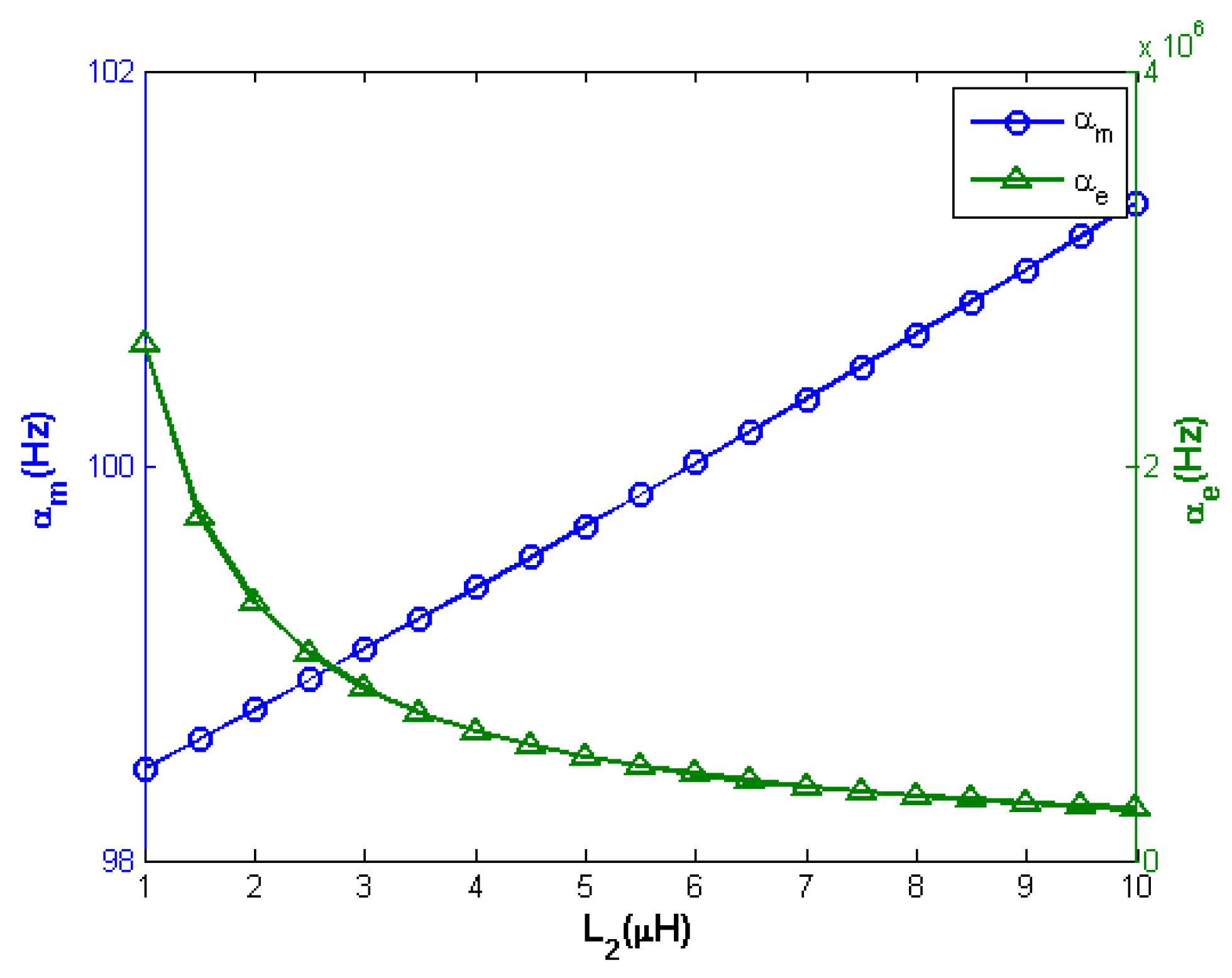
2.2. Numerical Analysis
2.3. Additional Remarks
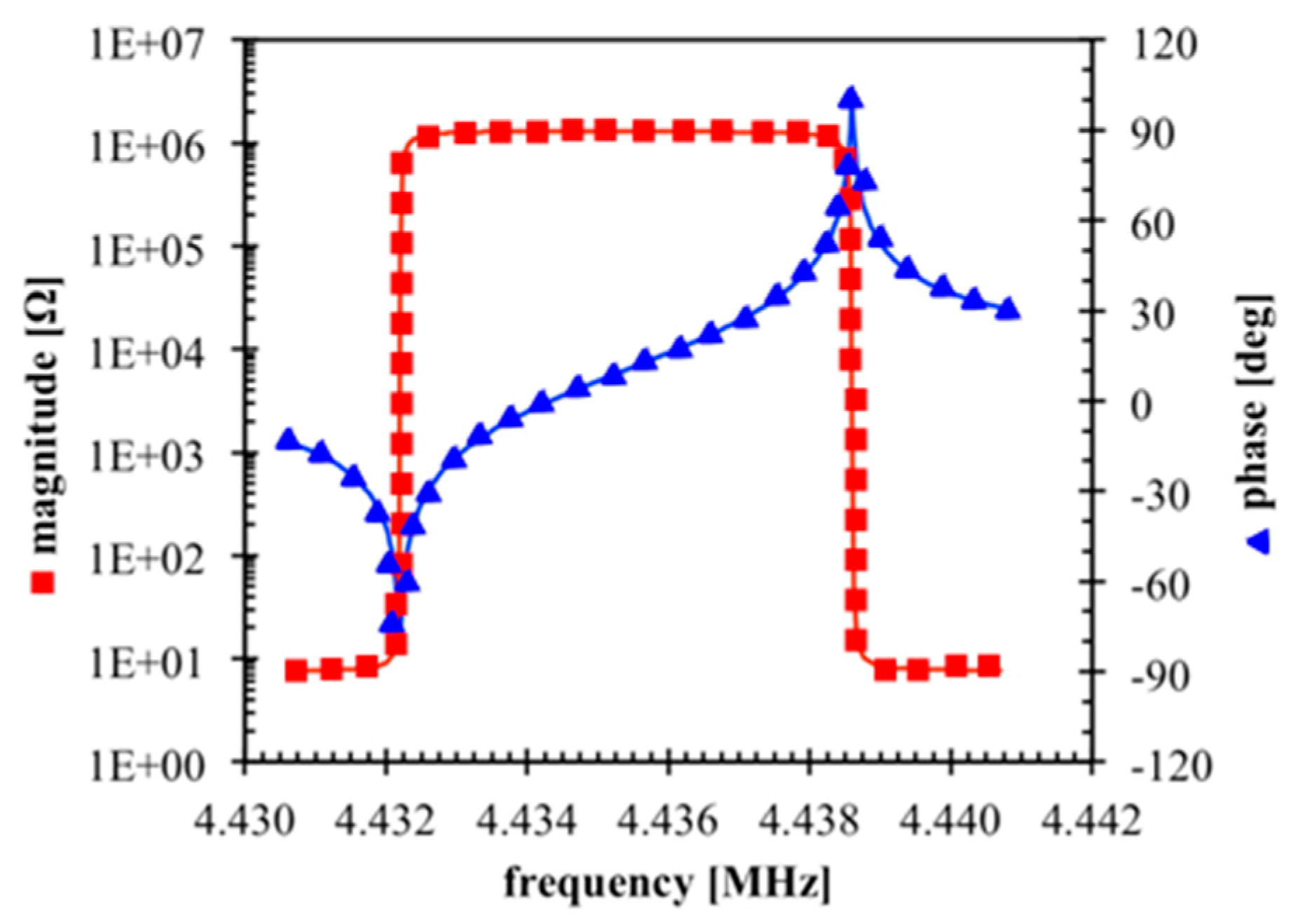
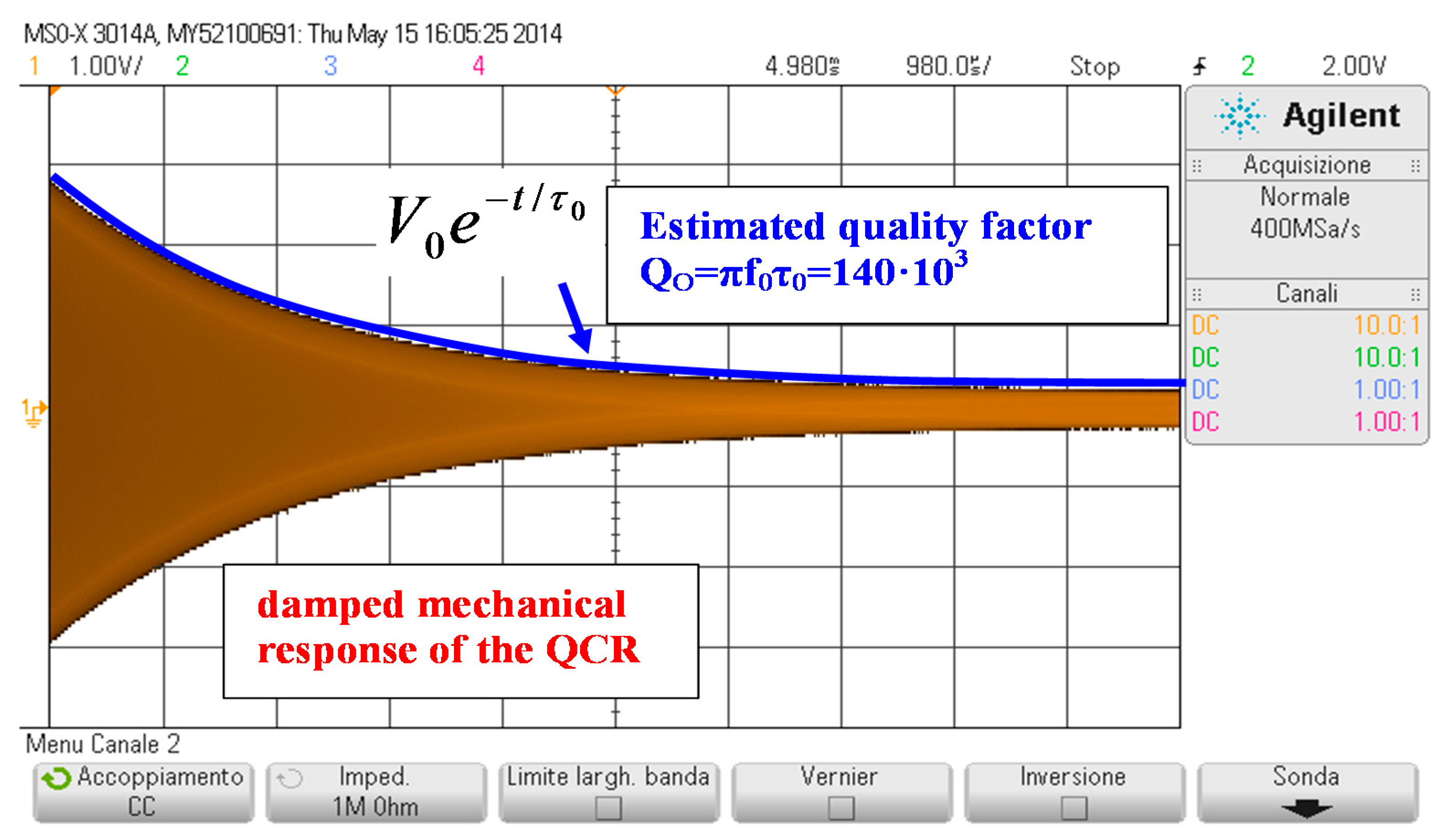
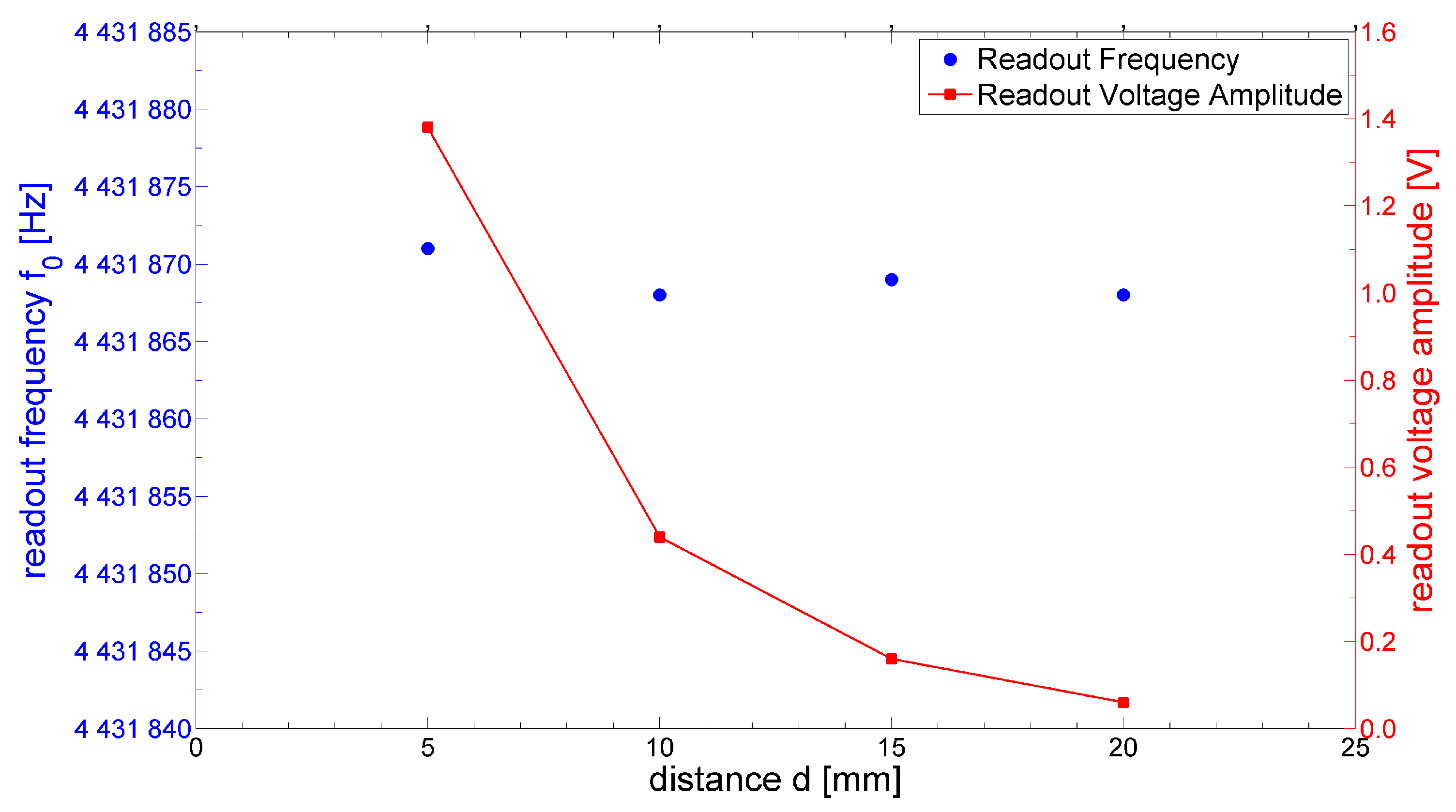
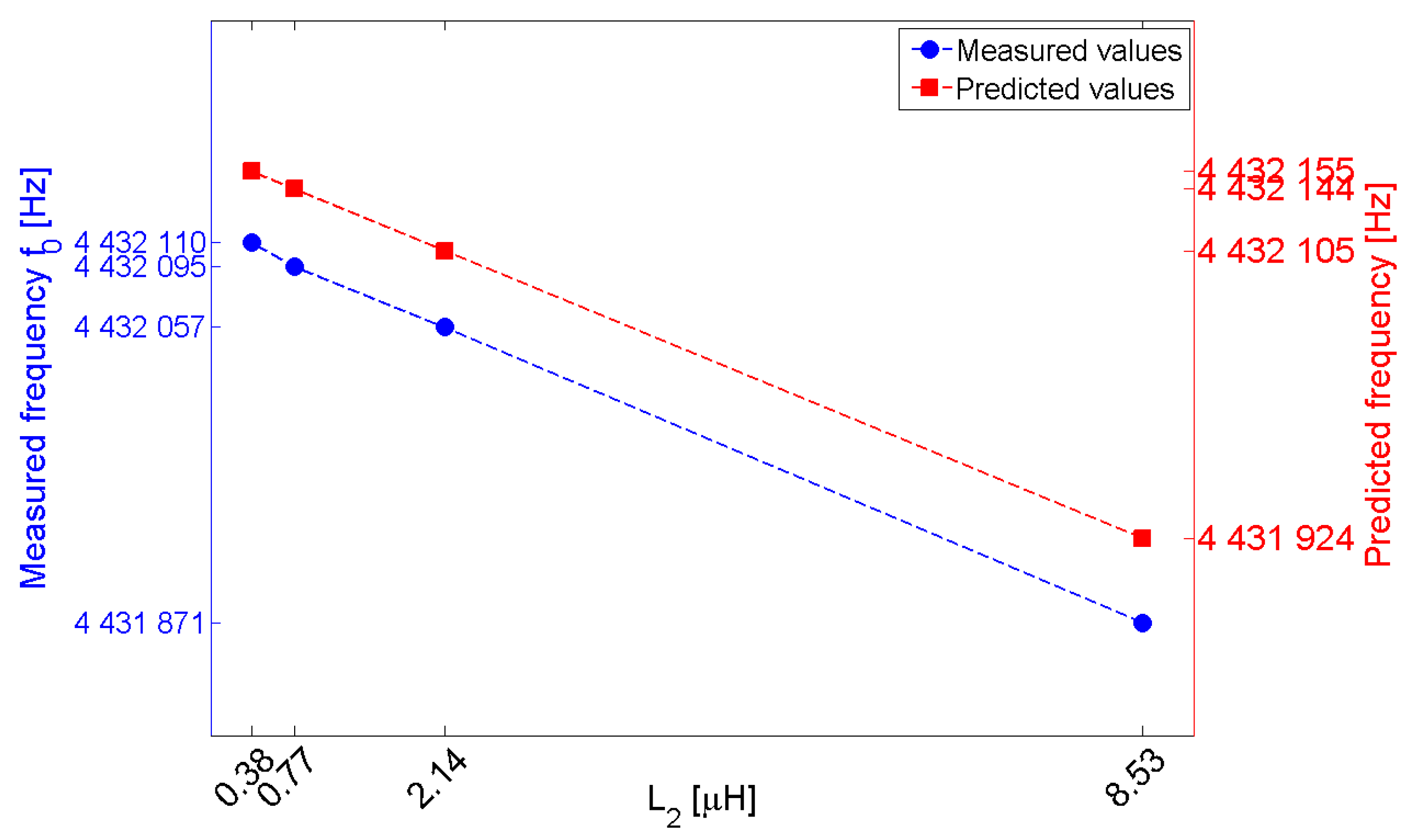
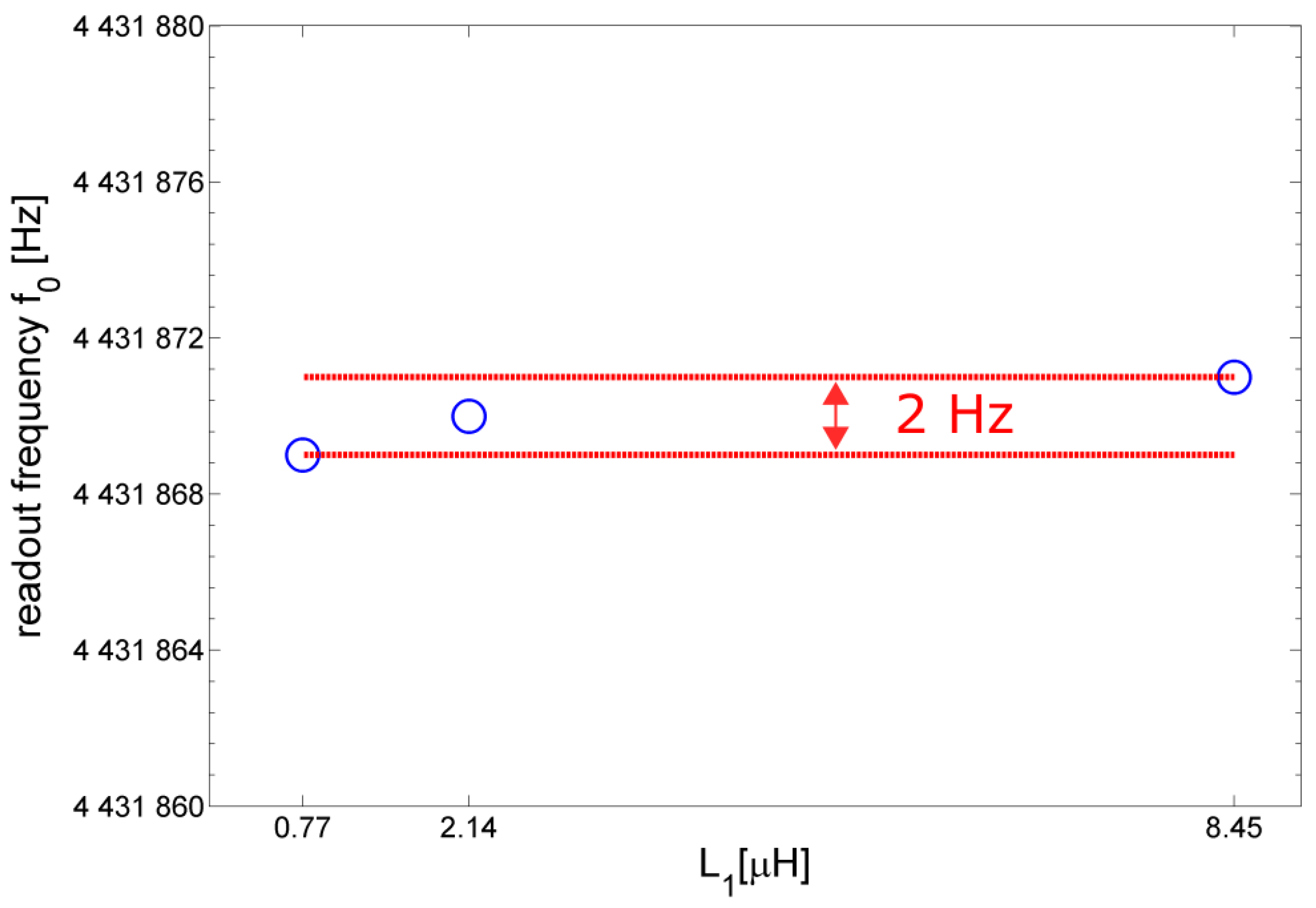
3. Experimental Validation
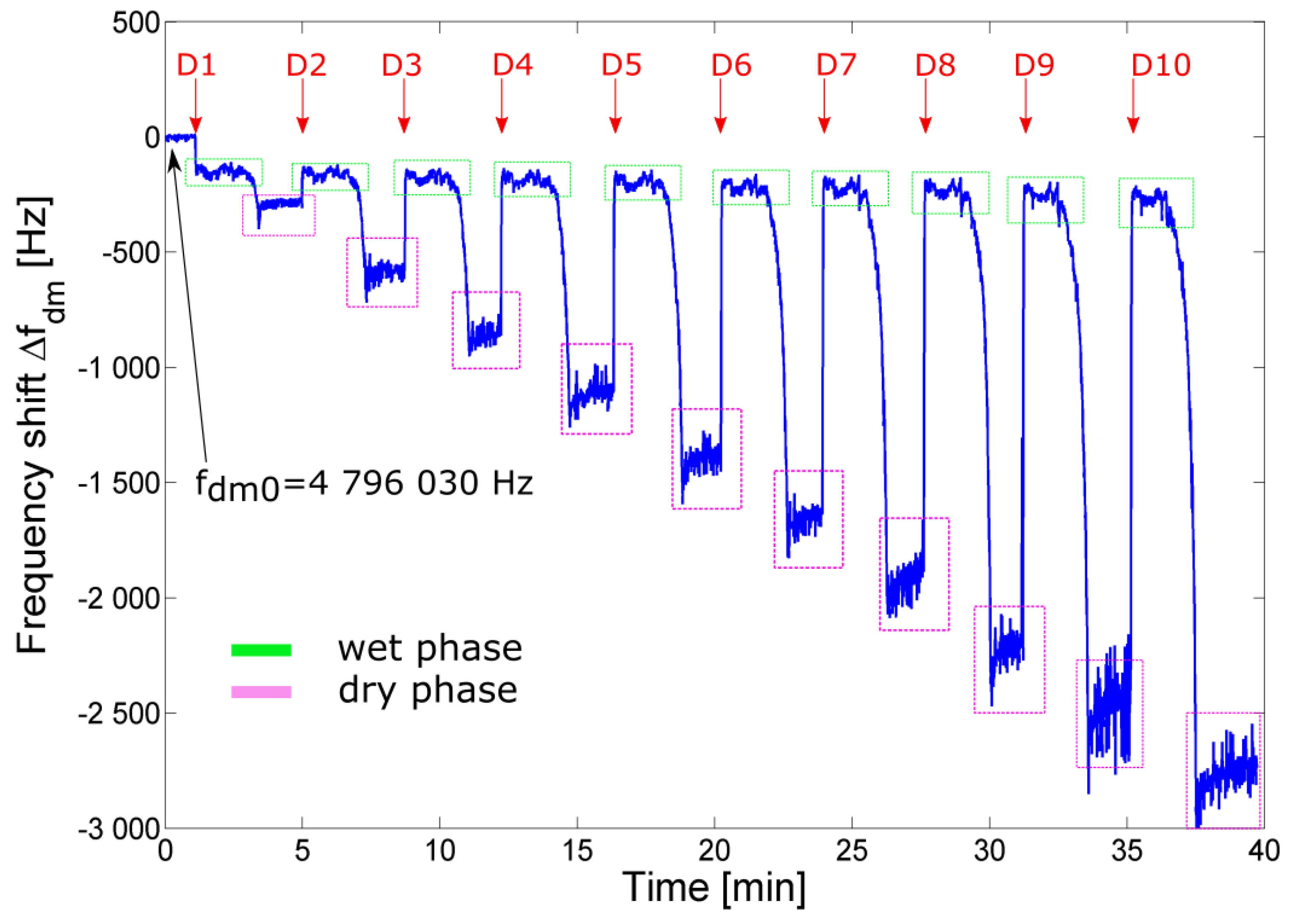
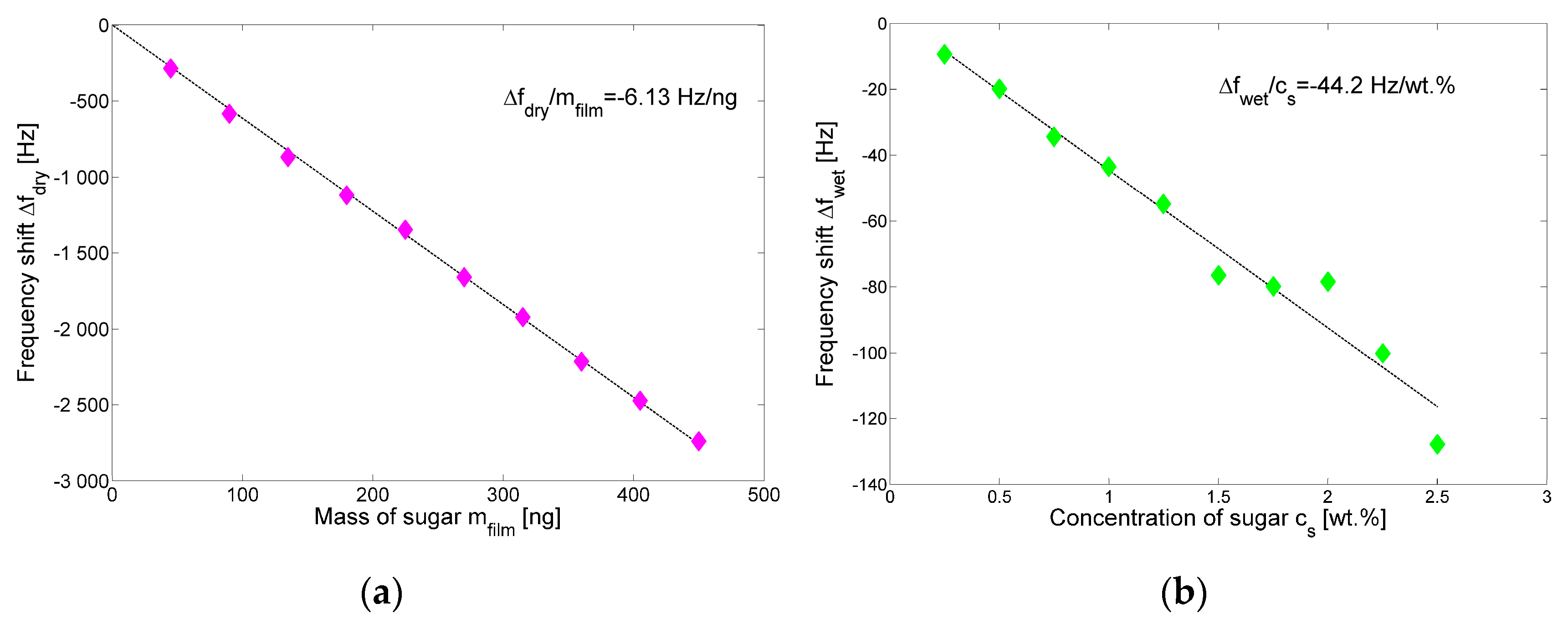
4. Liquid Solution Microdroplet Measurements
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vig, J.R. Introduction to Quartz Frequency Standards. Available online: https://ieee-uffc.org/frequency-control/learning-resources/introduction-to-quartz-frequency-standards-by-john-r-vig/ (accessed on 29 May 2017).
- Benes, E.; Gröschl, M.; Burger, W.; Schmid, M. Sensors based on piezoelectric resonators. Sens. Actuators A Phys. 1995, 48, 1–21. [Google Scholar] [CrossRef]
- Ballantine, D.S., Jr.; White, R.M.; Martin, S.J.; Ricco, A.J.; Zellers, E.T.; Frye, G.C.; Wohltjen, H.; Levy, M.; Stern, R. Acoustic wave sensors and responses. In Acoustic Wave Sensors: Theory, Design, and Physico-Chemical Applications; Academic Press: Cambridge, MA, USA, 1997; pp. 36–149. [Google Scholar]
- Ferrari, V.; Lucklum, R. Overview of acoustic-wave microsensors. In Piezoelectric Transducers and Applications, 2nd ed.; Arnau, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 39–62. [Google Scholar]
- Mecea, V.M.; Carlsson, J.O.; Bucur, R.V. Extensions of the quartz-crystal-microbalance technique. Sens. Actuators A Phys. 1996, 53, 371–378. [Google Scholar] [CrossRef]
- Ferreira, G.N.M.; da-Silva, A.C.; Tomé, B. Acoustic wave biosensors: Physical models and biological applications of quartz crystal microbalance. Trends Biotechnol. 2009, 27, 689–697. [Google Scholar] [CrossRef] [PubMed]
- Janshoff, A.; Galla, H.J.; Steinem, C. Piezoelectric mass-sensing devices as biosensors—An alternative to optical biosensors? Angew. Chem. Int. Ed. 2000, 39, 4004–4032. [Google Scholar] [CrossRef]
- Janshoff, A.; Steinem, C. Quartz Crystal Microbalance for Bioanalytical Applications. Sens. Update 2001, 9, 313–354. [Google Scholar] [CrossRef]
- Buttry, D.A.; Ward, M.D. Measurement of interfacial processes at electrode surfaces with the electrochemical quartz crystal microbalance. Chem. Rev. 1992, 92, 1355–1379. [Google Scholar] [CrossRef]
- Ferrari, M.; Ferrari, V. An oscillator circuit for dual-harmonic tracking of frequency and resistance in quartz resonator sensors. Meas. Sci. Technol. 2009, 20, 124005–124016. [Google Scholar] [CrossRef]
- Ferrari, M.; Ferrari, V.; Marioli, D. Interface Circuit for Multiple-Harmonic Analysis on Quartz Resonator Sensors to Investigate on Liquid Solution Microdroplets. Sens. Actuators B Chem. 2009, 146, 489–494. [Google Scholar] [CrossRef]
- Sell, J.K.A.; Niedermayer, O.; Jakoby, B. Reactance-locked loop for driving resonant sensors. In Proceedings of the 2012 IEEE International Instrumentation and Measurement Technology Conference, Graz, Austria, 13–16 May 2012; pp. 1113–1116. [Google Scholar]
- Lucklum, R.; Doerner, S.; Schneider, T.; Schlatt-Masuth, B.; Jacobs, T.; Hauptmann, P. Real Time Kinetic Analysis with Quartz Crystal Resonator Sensors. In Proceedings of the 2006 IEEE International Frequency Control Symposium and Exposition, Miami, FL, USA, 4–7 June 2006; pp. 528–534. [Google Scholar]
- Rodahl, M.; Hook, F.; Krozer, A.; Brzezinski, P.; Kasemo, B. Quartz crystal microbalance setup for frequency and Q-factor measurements in gaseous and liquid environments. Rev. Sci. Instrum. 1995, 66, 3924–3930. [Google Scholar] [CrossRef]
- Ferrari, M.; Ferrari, V.; Guizzetti, M.; Marioli, D. An autonomous battery-less sensor module powered by piezoelectric energy harvesting with RF transmission of multiple measurement signals. Smart Mater. Struct. 2009, 18, 085023. [Google Scholar] [CrossRef]
- Dalola, S.; Ferrari, M.; Ferrari, V.; Guizzetti, M.; Marioli, D.; Taroni, A. Characterization of thermoelectric modules for powering autonomous sensors. IEEE Trans. Instrum. Meas. 2009, 58, 99–107. [Google Scholar] [CrossRef]
- Abad, E.; Zampolli, S.; Marco, S.; Scorzoni, A.; Mazzolai, B.; Juarros, A.; Gómez, D.; Elmi, I.; Cardinali, G.C.; Gómez, J.M. Flexible tag microlab development: Gas sensors integration in RFID flexible tags for food logistic. Sens. Actuators B Chem. 2007, 127, 2–7. [Google Scholar] [CrossRef]
- Pohl, A. A review of wireless SAW sensors. IEEE Trans. Ultrason. Ferroelectr. 2000, 47, 317–332. [Google Scholar] [CrossRef] [PubMed]
- Pohl, A.; Ostermayer, G.; Seifert, F. Wireless sensing using oscillator circuits locked to remote high-Q SAW resonators. IEEE Trans. Ultrason. Ferroelectr. 1998, 45, 1161–1168. [Google Scholar] [CrossRef] [PubMed]
- Ogi, H.; Motoshisa, K.; Matsumoto, T.; Hatanaka, K.; Hirao, M. Isolated electrodeless high-frequency quartz crystal microbalance for immunosensors. Anal. Chem. 2006, 78, 6903–6909. [Google Scholar] [CrossRef] [PubMed]
- Volpe, L.S.; Ferrari, M.; Ferrari, V.; Arnau-Vives, A.; Perrot, H. Contactless confined readout of quartz crystal resonator sensors. In Proceedings of the 2005 IEEE Sensor, Irvine, CA, USA, 30 October–3 November 2005; pp. 457–460. [Google Scholar]
- Wu, W.; Greve, D.W.; Oppenheimer, I.J. Inductively coupled sensing using a quartz crystal microbalance. In Proceedings of the 2008 IEEE Ultrasonics Symposium, Beijing, China, 2–5 November 2008; pp. 1018–1021. [Google Scholar]
- Ferrari, M.; Baù, M.; Tonoli, E.; Ferrari, V. Piezoelectric resonant sensors with contactless interrogation for mass-sensitive and acoustic-load detection. Sens. Actuators A Phys. 2013, 202, 100–105. [Google Scholar] [CrossRef]
- Baù, M.; Tonoli, E.; Ferrari, V.; Marioli, D. Contactless electromagnetic switched interrogation of micromechanical cantilever resonators. Sens. Actuators A Phys. 2011, 172, 195–203. [Google Scholar] [CrossRef]
- Tonoli, E.; Baù, M.; Ferrari, V. Contactless Time-Gated Technique for Electromagnetic Interrogation of Micromechanical Resonator Sensors. Sens. Lett. 2013, 11, 294–298. [Google Scholar] [CrossRef]
- Jiang, H.; Chang, Z.; Pertijs, M.A.P. A 30 ppm < 80 nJ Ring-Down-Based Readout Circuit for Resonant Sensors. IEEE J. Solid State Circuits 2016, 51, 187–195. [Google Scholar]
- Ferrari, M.; Baù, M.; Pagnoni, M.; Ferrari, V. Compact DDS-Based System for Contactless Interrogation of Resonant Sensors Based on Time-Gated Technique. In Proceedings of the 2014 IEEE Sensors Conference, Valencia, Spain, 2–5 November 2014; pp. 907–910. [Google Scholar]
- Royer, D.; Dieulesaint, E. Piezoelectric transducers for bulk waves. In Elastic Waves in Solids; Springer: Berlin/Heidelberg, Germany, 2000; pp. 6–30. [Google Scholar]
- Ferrari, M.; Baù, M.; Masud, M.; Ferrari, V. A Time-Gated Contactless Interrogation System for Frequency and Quality Factor Tracking in QCR to Investigate on Liquid Solution Microdroplets. Procedia Eng. 2016, 168, 704–707. [Google Scholar] [CrossRef]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baù, M.; Ferrari, M.; Ferrari, V. Analysis and Validation of Contactless Time-Gated Interrogation Technique for Quartz Resonator Sensors. Sensors 2017, 17, 1264. https://doi.org/10.3390/s17061264
Baù M, Ferrari M, Ferrari V. Analysis and Validation of Contactless Time-Gated Interrogation Technique for Quartz Resonator Sensors. Sensors. 2017; 17(6):1264. https://doi.org/10.3390/s17061264
Chicago/Turabian StyleBaù, Marco, Marco Ferrari, and Vittorio Ferrari. 2017. "Analysis and Validation of Contactless Time-Gated Interrogation Technique for Quartz Resonator Sensors" Sensors 17, no. 6: 1264. https://doi.org/10.3390/s17061264
APA StyleBaù, M., Ferrari, M., & Ferrari, V. (2017). Analysis and Validation of Contactless Time-Gated Interrogation Technique for Quartz Resonator Sensors. Sensors, 17(6), 1264. https://doi.org/10.3390/s17061264







