Improved Accuracy of the Asymmetric Second-Order Vegetation Isoline Equation over the RED–NIR Reflectance Space
Abstract
:1. Introduction
2. Background
2.1. Two Approximations of the Vegetation Isoline Equations
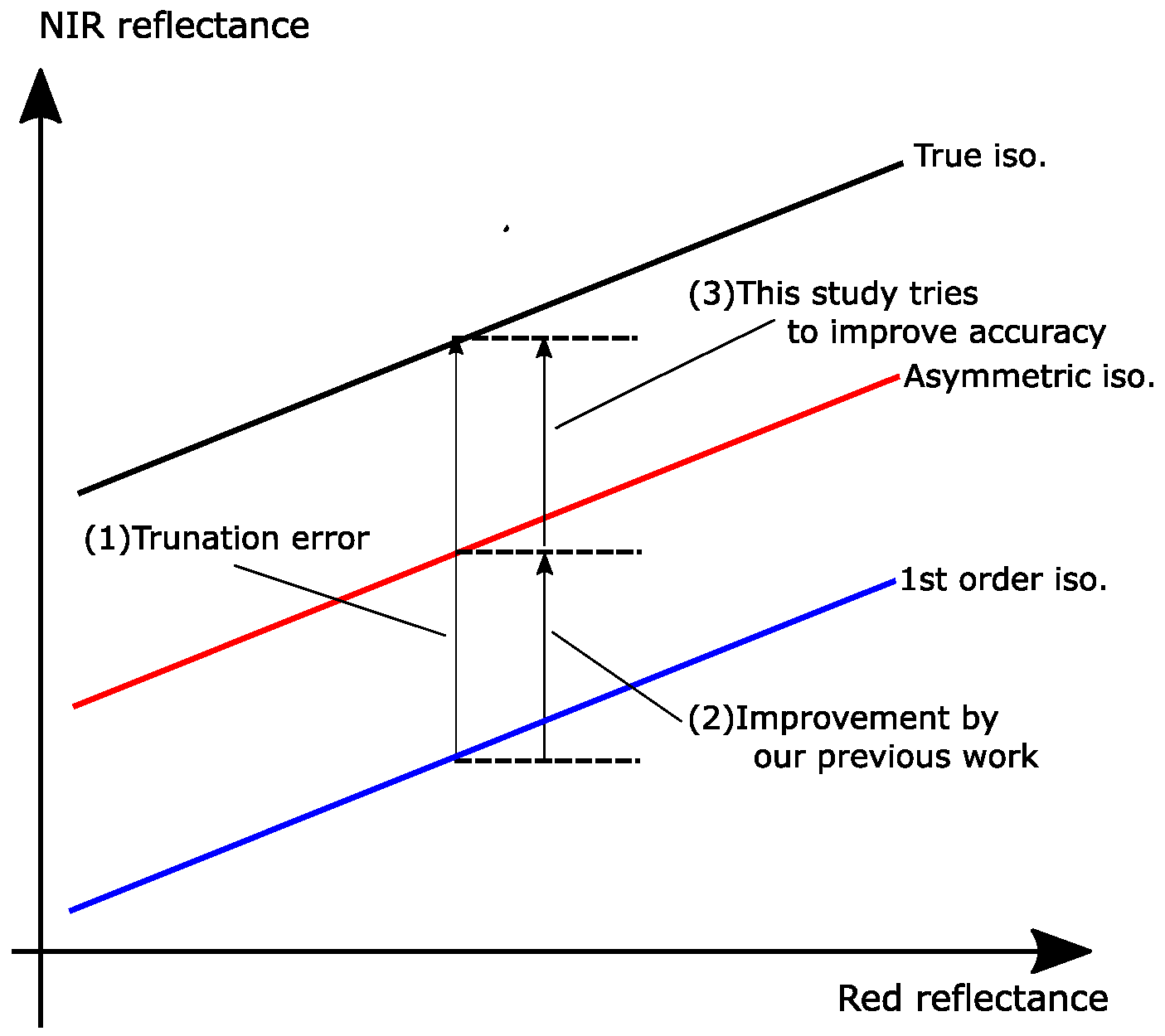
2.2. Errors in the Vegetation Isoline Equations
3. Approaches
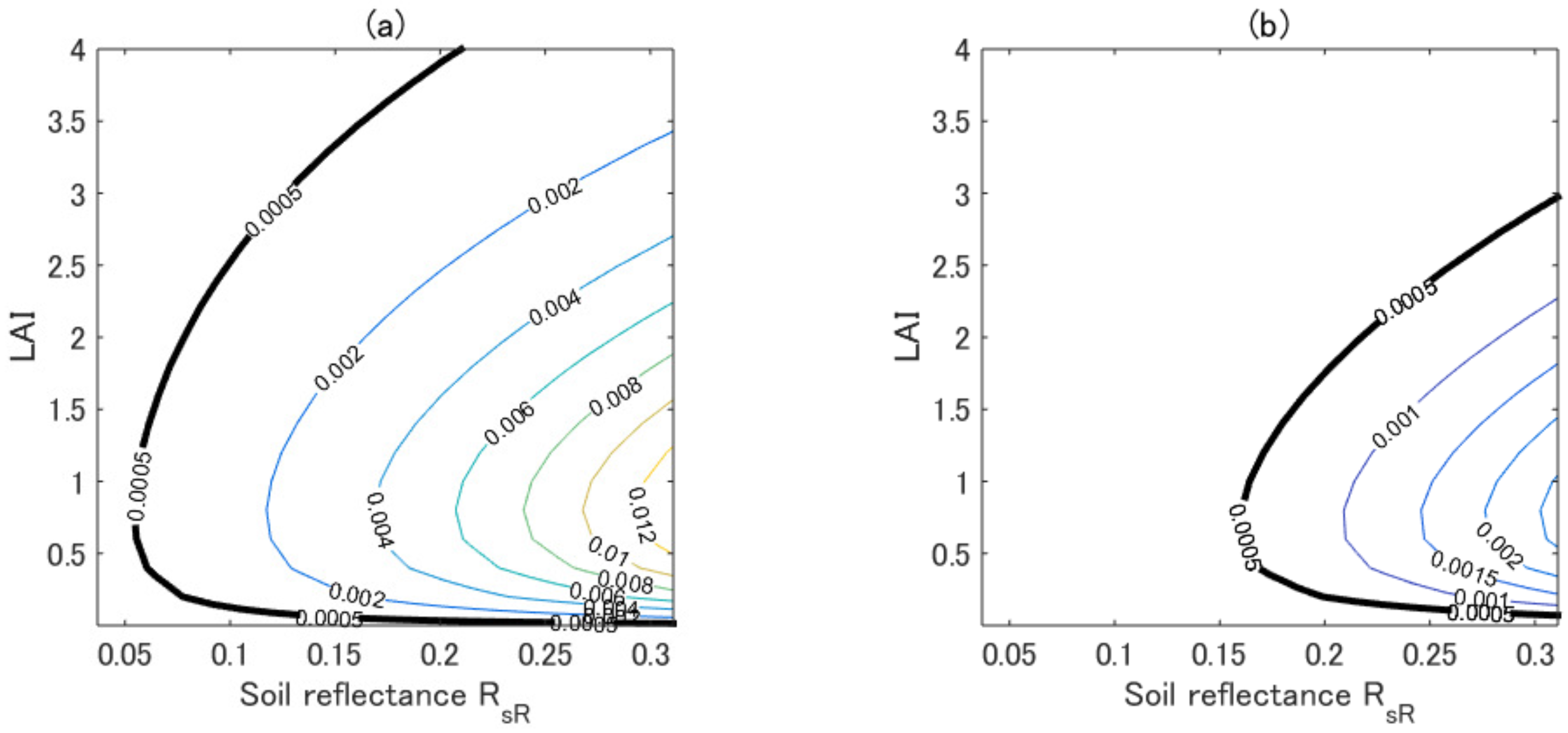
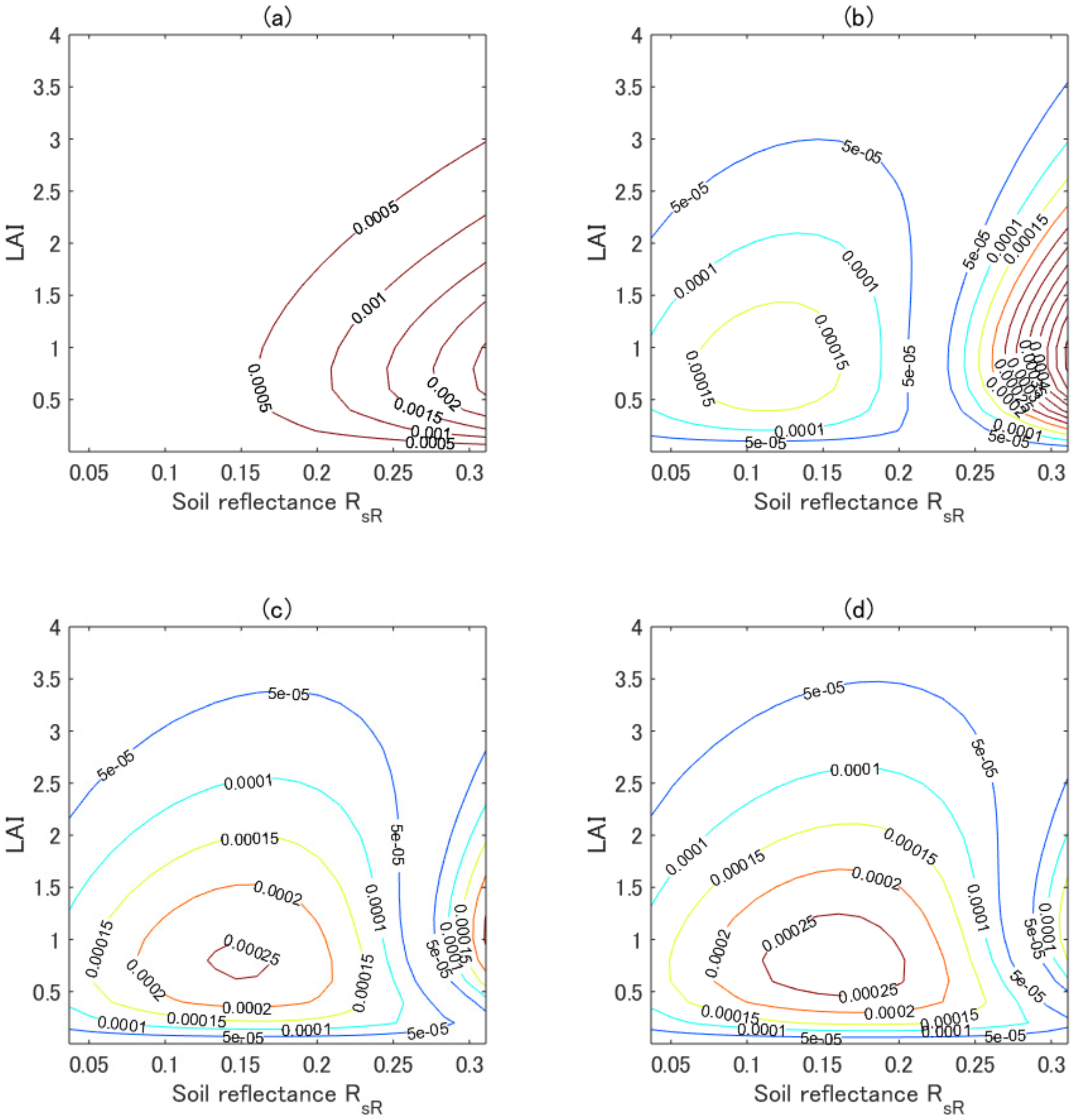
4. Results of the Numerical Simulations
4.1. Parameter Settings for the Numerical Experiments
4.2. Numerical Procedure Used for the Isoline Parameter Retrieval
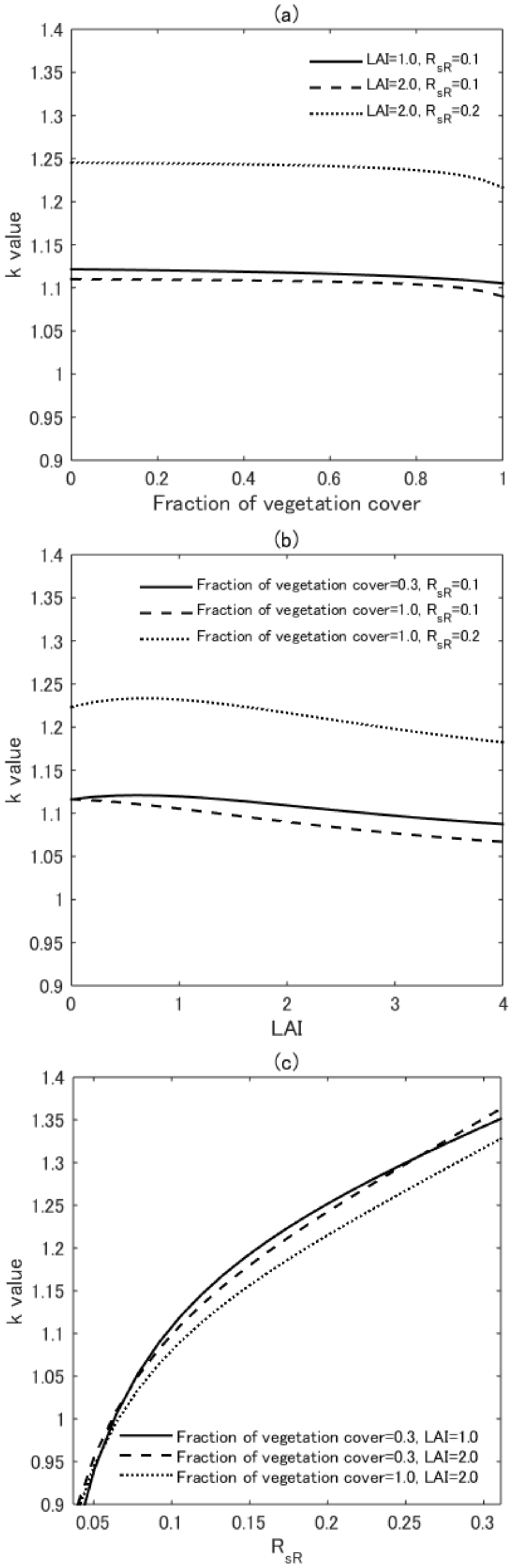
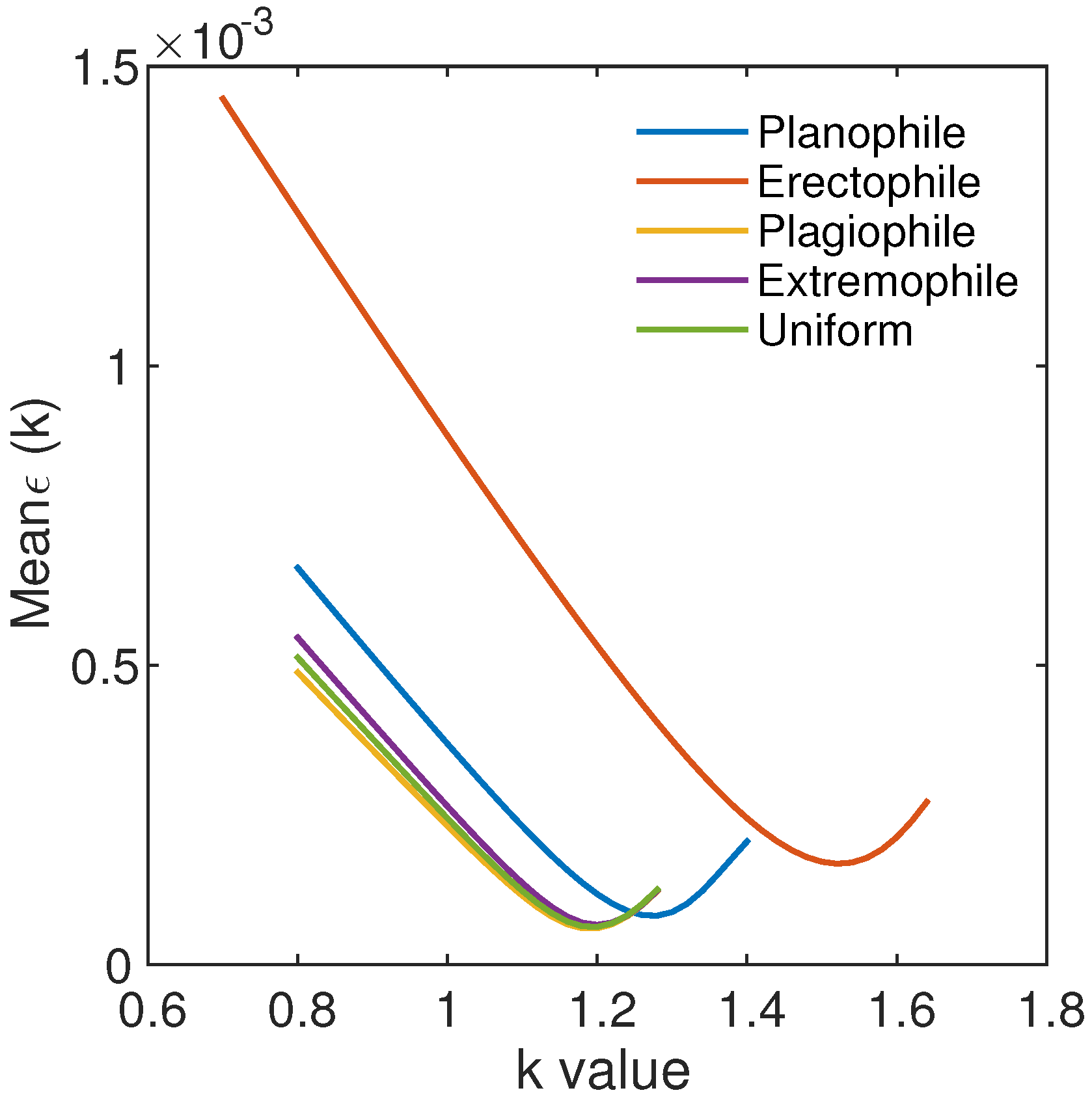
4.3. Variations in k
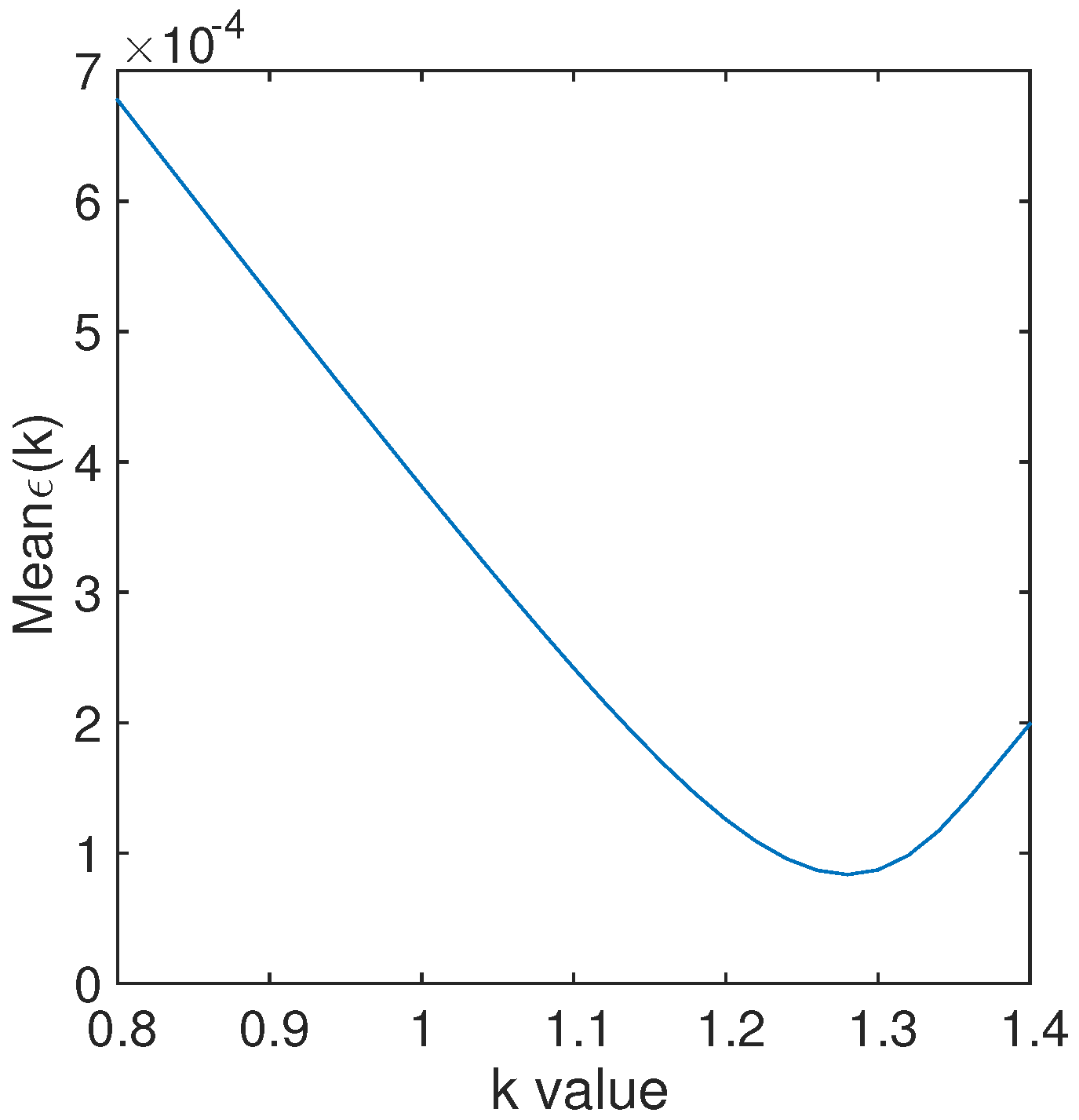
4.4. Optimum k-Values ()
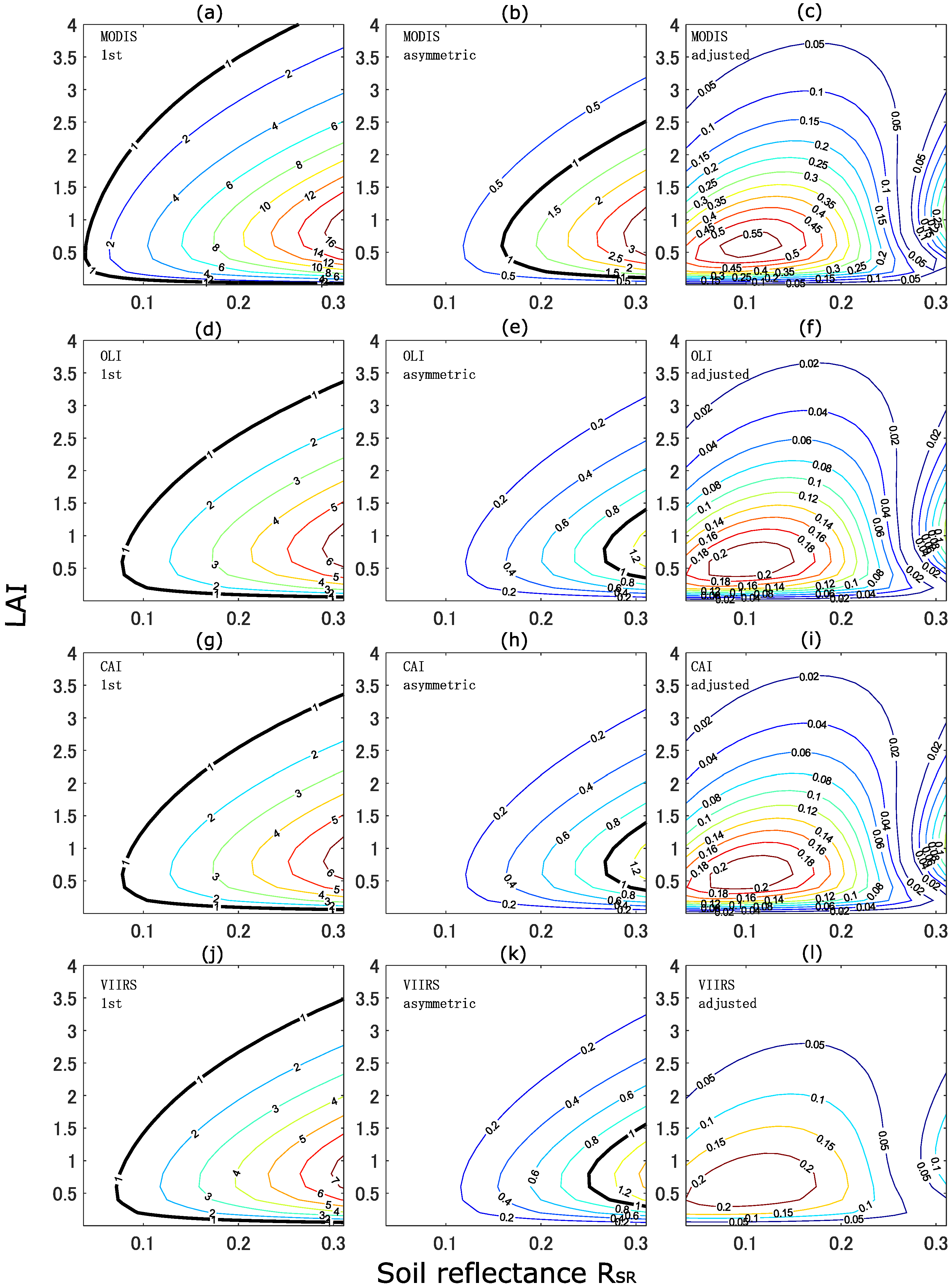
4.5. Evaluation of = 1.29
4.6. Evaluation of = 1.29 for Various LADs and Variations in the Optimum k-Value
4.7. Comparison with the Noise-Equivalent Errors in Satellite Sensors
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Miura, T.; Huete, A.R. Performance of three reflectance calibration methods for airborne hyperspectral spectrometer data. Sensors 2009, 9, 794–813. [Google Scholar] [CrossRef] [PubMed]
- Miura, T.; Yoshioka, H.; Fujiwara, K.; Yamamoto, H. Inter-comparison of ASTER and MODIS surface reflectance and vegetation index products for synergistic applications to natural resource monitoring. Sensors 2008, 8, 2480–2499. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Liu, Y. A Generalized Model for Intersensor NDVI Calibration and Its Comparison With Regression Approaches. IEEE Trans. Geosci. Remote Sens. 2016, PP, 1–11. [Google Scholar] [CrossRef]
- Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.R.; Myneni, R.B. Global Data Sets of Vegetation Leaf Area Index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g Derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the Period 1981 to 2011. Remote Sens. 2013, 5, 927. [Google Scholar]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.; Liang, S.; Li, X.; Wang, J. Development of the adjoint model of a canopy radiative transfer model for sensitivity study and inversion of leaf area index. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2028–2037. [Google Scholar] [CrossRef]
- Vina, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of different vegetation indices for the remote assessment of green leaf area index of crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Baret, F.; Guyot, G.; Major, D. TSAVI: A vegetation index which minimizes soil brightness effects on LAI and APAR estimation. In Proceedings of the 1989 International 12th Canadian Symposium on Remote Sensing Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 10–14 July 1989; Volume 3, pp. 1355–1358.
- Kaufman, Y.J.; Tanre, D. Atmospherically resistant vegetation index (ARVI) for EOS-MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]
- Huete, A.; Justice, C.; Liu, H. Development of vegetation and soil indices for MODIS-EOS. Remote Sens. Environ. 1994, 49, 224–234. [Google Scholar] [CrossRef]
- Gilabert, M.; González-Piqueras, J.; Garcıa-Haro, F.; Meliá, J. A generalized soil-adjusted vegetation index. Remote Sens. Environ. 2002, 82, 303–310. [Google Scholar] [CrossRef]
- Chen, D.; Huang, J.; Jackson, T.J. Vegetation water content estimation for corn and soybeans using spectral indices derived from MODIS near- and short-wave infrared bands. Remote Sens. Environ. 2005, 98, 225–236. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to Topographic Effects: A Case Study in High-density Cypress Forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Verstraete, M.M.; Pinty, B. Designing optimal spectral indexes for remote sensing applications. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1254–1265. [Google Scholar] [CrossRef]
- Yoshioka, H.; Miura, T.; Huete, A.; Ganapol, B. Analysis of vegetation isolines in red-NIR reflectance space. Remote Sens. Environ. 2000, 74, 313–326. [Google Scholar] [CrossRef]
- Yoshioka, H.; Miura, T.; Demattê, J.A.; Batchily, K.; Huete, A.R. Derivation of soil line influence on two-band vegetation indices and vegetation isolines. Remote Sens. 2009, 1, 842–857. [Google Scholar] [CrossRef]
- Yoshioka, H.; Yamamoto, H.; Miura, T. Use of an isoline-based inversion technique to retrieve a leaf area index for inter-sensor calibration of spectral vegetation index. In Proceedings of the International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; Volume 3, pp. 1639–1641.
- Kallel, A.; Le Hégarat-Mascle, S.; Ottlé, C.; Hubert-Moy, L. Determination of vegetation cover fraction by inversion of a four-parameter model based on isoline parametrization. Remote Sens. Environ. 2007, 111, 553–566. [Google Scholar] [CrossRef]
- Yoshioka, H.; Miura, T.; Obata, K. Derivation of relationships between spectral vegetation indices from multiple sensors based on vegetation isolines. Remote Sens. 2012, 4, 583–597. [Google Scholar] [CrossRef]
- Obata, K.; Miura, T.; Yoshioka, H.; Huete, A.R. Derivation of a MODIS-compatible enhanced vegetation index from visible infrared imaging radiometer suite spectral reflectances using vegetation isoline equations. J. Appl. Remote Sens. 2013, 7, 073467. [Google Scholar] [CrossRef]
- Miura, M.; Obata, K.; Yoshioka, H. Vegetation isoline equations with first-and second-order interaction terms for modeling a canopy-soil system of layers in the red and near-infrared reflectance space. J. Appl. Remote Sens. 2015, 9, 095987. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F.; Andrieu, B.; Danson, F.; Jaggard, K. Extraction of vegetation biophysical parameters by inversion of the PROSPECT+ SAIL models on sugar beet canopy reflectance data. Application to TM and AVIRIS sensors. Remote Sens. Environ. 1995, 52, 163–172. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+ SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Yoshioka, H.; Huete, A.R.; Miura, T. Derivation of vegetation isoline equations in red-NIR reflectance space. IEEE Trans. Geosci. Remote Sens. 2000, 38, 838–848. [Google Scholar] [CrossRef]
- Yoshioka, H.; Miura, T.; Huete, A.R. An isoline-based translation technique of spectral vegetation index using EO-1 Hyperion data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1363–1372. [Google Scholar] [CrossRef]
- Yoshioka, H. Vegetation isoline equations for an atmosphere-canopy-soil system. IEEE Trans. Geosci. Remote Sens. 2004, 42, 166–175. [Google Scholar] [CrossRef]
- Miura, M.; Obata, K.; Yoshioka, H. Vegetation isoline equations for analysis of hyper-spectral data with higher order interaction terms. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 1031–1034.
- Miura, M.; Obata, K.; Yoshioka, H. Vegetation isoline equations for atmosphere-canopy-soil system of layer with second order interaction term. In Proceedings of the SPIE Optical Engineering+ Applications. International Society for Optics and Photonics, San Diego, CA, USA, 1–5 August 2010; p. 780906.
- Obata, K.; Miura, T.; Yoshioka, H.; Huete, A.R.; Vargas, M. Spectral Cross-Calibration of VIIRS Enhanced Vegetation Index with MODIS: A Case Study Using Year-Long Global Data. Remote Sens. 2016, 8, 34. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Justice, C.O.; Vermote, E.; Townshend, J.R.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.; Loveland, T.; Woodcock, C.; Allen, R.; Anderson, M.; Helder, D.; Irons, J.; Johnson, D.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Yokota, T.; Yoshida, Y.; Eguchi, N.; Ota, Y.; Tanaka, T.; Watanabe, H.; Maksyutov, S. Global concentrations of CO2 and CH4 retrieved from GOSAT: First preliminary results. Sola 2009, 5, 160–163. [Google Scholar] [CrossRef]
- Cao, C.; Xiong, J.; Blonski, S.; Liu, Q.; Uprety, S.; Shao, X.; Bai, Y.; Weng, F. Suomi NPP VIIRS sensor data record verification, validation, and long-term performance monitoring. J. Geophys. Res. 2013, 118, 11664–11678. [Google Scholar] [CrossRef]
- Xiong, X.; Sun, J.; Xie, X.; Barnes, W.L.; Salomonson, V.V. On-Orbit Calibration and Performance of Aqua MODIS Reflective Solar Bands. IEEE Trans. Geosci. Remote Sens. 2010, 48, 535–546. [Google Scholar] [CrossRef]
- Morfitt, R.; Barsi, J.; Levy, R.; Markham, B.; Micijevic, E.; Ong, L.; Scaramuzza, P.; Vanderwerff, K. Landsat-8 Operational Land Imager (OLI) Radiometric Performance On-Orbit. Remote Sens. 2015, 7, 2208. [Google Scholar] [CrossRef]
- Fukuda, S.; Nakajima, T.; Takenaka, H.; Higurashi, A.; Kikuchi, N.; Nakajima, T.Y.; Ishida, H. New approaches to removing cloud shadows and evaluating the 380 nm surface reflectance for improved aerosol optical thickness retrievals from the GOSAT/TANSO-Cloud and Aerosol Imager. J. Geophys. Res. 2013, 118, 13,520–13,531. [Google Scholar] [CrossRef]
- Xiong, X.; Butler, J.; Chiang, K.; Efremova, B.; Fulbright, J.; Lei, N.; McIntire, J.; Oudrari, H.; Sun, J.; Wang, Z.; Wu, A. VIIRS on-orbit calibration methodology and performance. J. Geophys. Res. 2014, 119, 5065–5078. [Google Scholar] [CrossRef]

| Geometry | |
|---|---|
| Solar zenith angle | |
| Observation zenith angle | |
| Relative azimuth angle | |
| Pixel Heterogeneous Property | |
| Fraction of vegetation cover (FVC) | 0.0–1.0 |
| Canopy Properties | |
| Leaf area index (LAI) | 0.0–4.0 |
| Hotspot size parameter | 0.01 |
| Leaf Structural and Chemical Properties | |
| Leaf angle distribution (LAD) | Spherical, Planophile, Erectophile |
| Plagiophile, Extremophile, Uniform | |
| Leaf mesophyll structure | 1.5 |
| Chlorophyll-a and -b | 40 |
| Carotenoid content | 8 |
| Leaf mass per area | 0.009 |
| Equivalent water thickness | 0.01 cm |
| Brown pigment content | 0 |
| Soil Properties | |
| Wet soil reflectances at 655 and 865 nm | 0.037 and 0.071 |
| Dry soil reflectances at 655 and 865 nm | 0.311 and 0.412 |
| Soil factor (mixture ratio of wet and dry soils) | 0.0–1.0 [0.0: wet soil; 1.0: dry soil] |
| LAD: Spherical | ||||||
|---|---|---|---|---|---|---|
| 1.25 | 1.26 | 1.27 | 1.28 | 1.29 | 1.30 | |
| Mean | ||||||
| STD | ||||||
| MAX | ||||||
| LAD: Spherical | |||||
|---|---|---|---|---|---|
| First-Order | Asymmetric | Adjusted Asymmetric | adj./first | adj./asym. | |
| Mean | 4.0% | 22.1% | |||
| STD | 2.9% | 13.9% | |||
| MAX | 3.2% | 16.1% | |||
| LAD: Planophile | |||||
|---|---|---|---|---|---|
| first-order isoline | asymmetric isoline | adjusted isoline | adj./1st | adj./asym. | |
| Mean | 4.1% | 22.7% | |||
| STD | 2.8% | 13.8% | |||
| MAX | 2.8% | 14.6% | |||
| LAD: Erectophile | |||||
| first-order isoline | asymmetric isoline | adjusted isoline | adj./1st | adj./asym. | |
| Mean | 12.6% | 44.1% | |||
| STD | 15.6% | 49.4% | |||
| MAX | 15.8% | 50.9% | |||
| LAD: Plagiophile | |||||
| first-order isoline | asymmetric isoline | adjusted isoline | adj./1st | adj./asym. | |
| Mean | 7.9% | 58.4% | |||
| STD | 6.2% | 39.4% | |||
| MAX | 6.9% | 48.0% | |||
| LAD: Extremophile | |||||
| first-order isoline | asymmetric isoline | adjusted isoline | adj./1st | adj./asym. | |
| Mean | 7.2% | 51.9% | |||
| STD | 5.5% | 33.6% | |||
| MAX | 5.7% | 38.3% | |||
| LAD: Uniform | |||||
| first-order isoline | asymmetric isoline | adjusted isoline | adj./1st | adj./asym. | |
| Mean | 7.7% | 56.6% | |||
| STD | 5.9% | 37.3% | |||
| MAX | 6.5% | 44.4% | |||
| LAD | Optimum k | Mean | STD | MAX |
|---|---|---|---|---|
| Planophile | 1.28 | |||
| Erectophile | 1.53 | |||
| Plagiophile | 1.19 | |||
| Extremophile | 1.2 | |||
| Uniform | 1.20 |
| MODIS | Landsat8 OLI | GOSAT-CAI | VIIRS | |
|---|---|---|---|---|
| Red band | 201 | 227 | 200 | 209 |
| NIR band | 530 | 201 | 200 | 225 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miura, M.; Obata, K.; Taniguchi, K.; Yoshioka, H. Improved Accuracy of the Asymmetric Second-Order Vegetation Isoline Equation over the RED–NIR Reflectance Space. Sensors 2017, 17, 450. https://doi.org/10.3390/s17030450
Miura M, Obata K, Taniguchi K, Yoshioka H. Improved Accuracy of the Asymmetric Second-Order Vegetation Isoline Equation over the RED–NIR Reflectance Space. Sensors. 2017; 17(3):450. https://doi.org/10.3390/s17030450
Chicago/Turabian StyleMiura, Munenori, Kenta Obata, Kenta Taniguchi, and Hiroki Yoshioka. 2017. "Improved Accuracy of the Asymmetric Second-Order Vegetation Isoline Equation over the RED–NIR Reflectance Space" Sensors 17, no. 3: 450. https://doi.org/10.3390/s17030450
APA StyleMiura, M., Obata, K., Taniguchi, K., & Yoshioka, H. (2017). Improved Accuracy of the Asymmetric Second-Order Vegetation Isoline Equation over the RED–NIR Reflectance Space. Sensors, 17(3), 450. https://doi.org/10.3390/s17030450






