1. Introduction
With the rapid advance of wireless technology in recent years, the development of WBASN has been accelerated in an effort to monitor patients and support applications used for telemedicine [
1,
2,
3]. As the population is growing rapidly around the world, the demand for healthcare systems will consequently increase. Especially the population aged between 60 and 80 is expected to double in 2050, compared to the number in 2010. Thus, technological development in WBASNs is essential. Millions of people die every year from diseases such as cancer and cardiovascular disease, where early detection and treatment can dramatically reduce the mortality rate. Therefore, future healthcare systems should provide preventive services. Wearable devices that can be attached to the body, to monitor and analyze a bio-signal, are typically used as effective precautionary measures, for early disease detection. Many studies have been conducted to address various problems that may occur in the WBASN environment, where these wearable devices are used.
The WBASN can be configured by several wireless technologies that have advantages and disadvantages depending on each radio technology [
4]. In this paper, we focus on the IEEE 802.15.6 standard. A study group on the WBASN communication standard was approved as Task Group 6 (TG6) of the IEEE 802.15 working group, in January 2008. The first draft of the WBASN standard was ratified in February 2012 [
5]. The purpose of WBASN communication standardization is “to provide an international standard for a short-range (i.e., about human body range), low power, and highly reliable wireless communication for use in close proximity to, or inside, a human body” [
1].
The WBASN has distinctive features compared with the existing wireless networks [
6]. In the WBASN environment, there are many WBASN networks where communication ranges overlap with each other. Thus, interference may occur between each WBASN network, because of limited frequency resources [
7]. This inter-WBASN interference may cause problems that affect each user, such as a decrease in the throughput, or an increase in the packet loss rate. In general, inter-WBASN interference is maximized when there is no coordination between each network. Generally speaking, techniques for reducing interference can be classified as centralized and distributed methods. With centralized methods, a central coordinator is deployed like a base station, which regulates the media access control (MAC) and transmit power of each sensor node that is dependent on a WBASN, to reduce the effect of interference on each hub. However, since each user in the WBASN environment is highly mobile, and user-dependent WBASNs operate independently of each other, central coordinator based interference mitigation methods are not suitable for deployment with WBASNs. Therefore, distributed methods are used to mitigate interference in the WBASN environment.
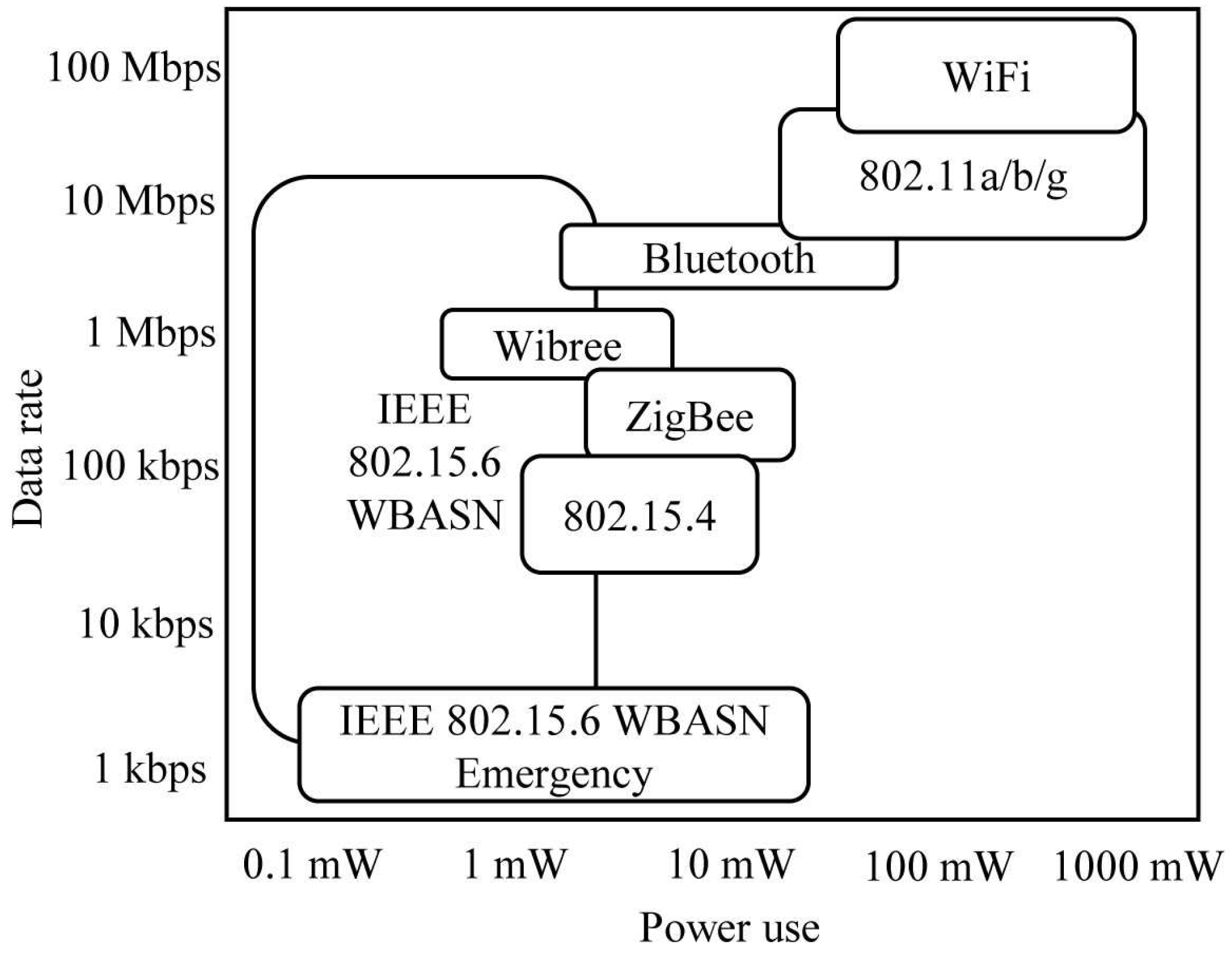
Figure 1 shows the transmission power requirements and data rates for different wireless technologies [
1]. From this image, it can be seen that the transmit power required in a WBASN environment is significantly lower than with other networks. Since the sensor nodes in the WBASN, for collecting biometric data, may exist on the inside, and on the surface of a human body, lower power consumptions are required for WBASN technology than with existing wireless technologies, in consideration of the specific absorption rate (SAR) of electromagnetic waves. In spite of the limited transmit power of WBASNs, the range of transmission rates required for each application is very broad. This is because the types of data measured by the sensor nodes vary depending on the application, and the required data rate varies depending on the type of data being transmitted. Since a maximum data rate of about 10 Mbps and low power consumption are required in the WBASN environment, the WBASN protocol requires higher energy efficiency than existing protocols. Depending on the type of application being used in a WBASN, the differences in the required data rate may be very large. As a result, some sensor nodes may use an unnecessarily large transmission power, reducing their energy efficiency, as well as the performance of other nodes. In addition, since the types of applications utilized in a WBASN are different, the data rate required for satisfying quality of service (QoS) may also be different for each WBASN. A required transmission rate based on the QoS is directly related to fair treatment of users in the network [
8]. If the difference in required data rate for a satisfactory QoS is not taken into consideration, users in the network could be provided with an unfair service. For example, allocating the same amount of resources to a voice service of relatively low quality, and a high-quality video service, does not provide each user with fair treatment. Therefore, in the WBASN environment it is necessary to consider different QoS requirements according to the applications employed in WBASNs.
The remainder of this paper is organized as follows. In
Section 2, we present the related works. In
Section 3, we describe the general system models and parameters of the WBASN. In
Section 4, we explain the Cucker–Smale model, which is the basis of the proposed algorithm. In
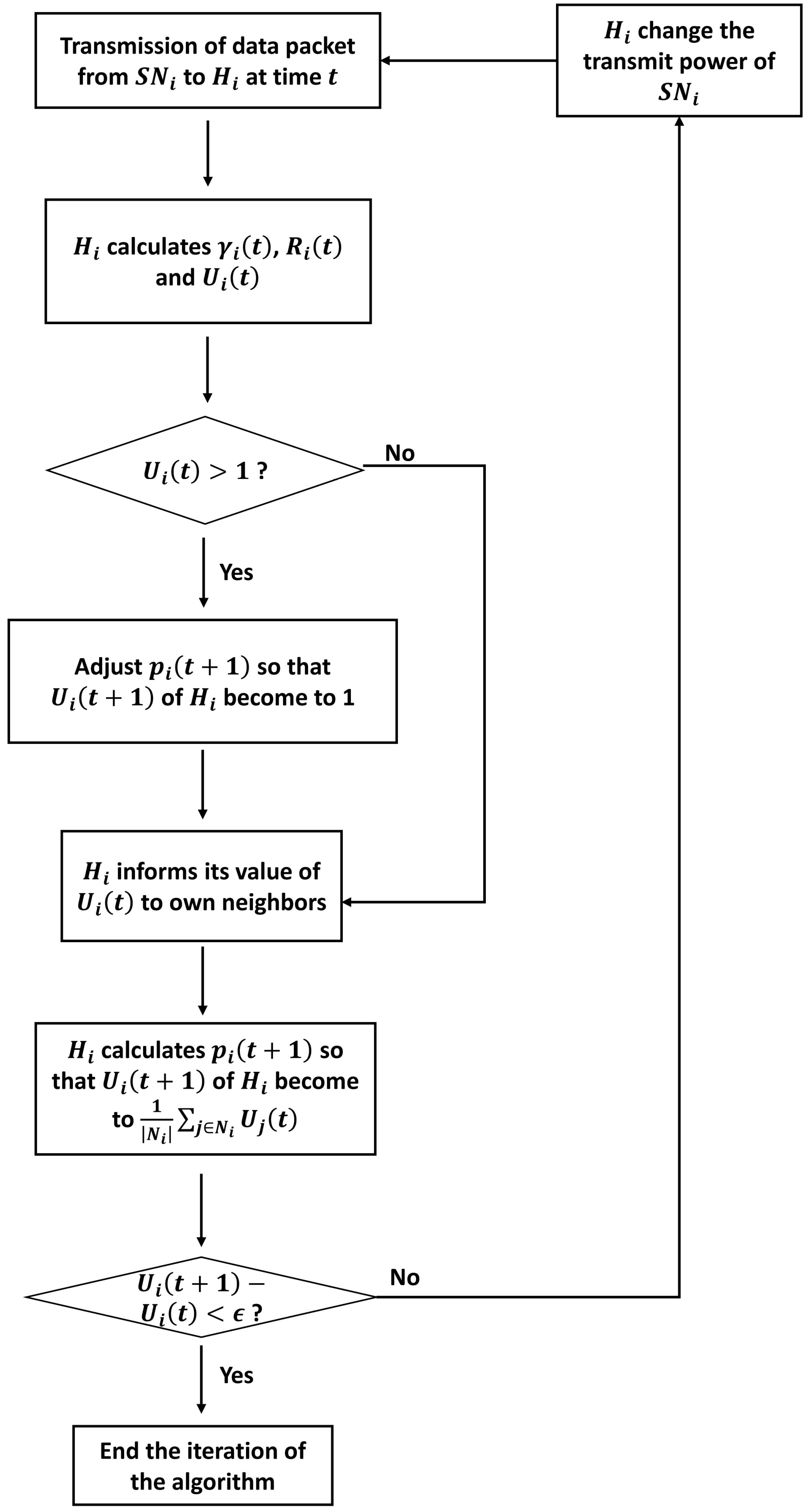
Section 5, we introduce the operation of the proposed transmission power control algorithm in WBASN. In
Section 6, we evaluate the performance of the proposed algorithm. Finally, we conclude this paper in
Section 7.
2. Related Works
The interference problem has been dealt with in the existing network [
9]. It is important to design the wireless network by considering the signal-to-interference-ratio (SINR), as indicated by the wide literature available on the topic, which we review in this section. The obtained SINR is proportional to a variety of performance metrics including throughput [
10]. However, the frequencies assigned to two connections may incur interference to one another, resulting in quality loss of the signal [
11]. For this reasons, several studies in the traditional wireless networks had conducted to mitigate interference. Resource allocation schemes in wireless network have been proposed to assign channel and to associate the users with access points (APs) by considering SINR. To address the co-channel interference problems, a biological behavior-based network resource management method is proposed [
12]. A solution to user association with the AP is proposed to guarantee the best quality of service considering SINR [
13]. In the cellular networks or the broadcasting systems, the efficiency of SINR is an important factor and the optimization of the SINR problem have been conducted. The planning methodologies in the cellular network that allow to minimize interference overhead while maintaining the established network coverage are introduced [
14]. A solution method for SINR constraints problem in the cellular network is proposed that combines combinatorial Benders decomposition, classical Benders decomposition, and valid cuts in a nested way [
15]. A two-stage heuristic methodology composed of power and frequency assignment stages is proposed so as to minimize the loss from mutual interference in the broadcasting system [
16]. An optimization problem of transmission powers so as to guarantee the required SINR in the broadcasting system can be formulated as a mixed integer linear program, and the analysis on the behavior of this model is proposed [
17]. To solve the interference problem caused by the coexistence of a plurality of WBASNs that are dependent on a specific individual, unlike earlier works for the existing wireless networks, many studies considering features of the WBASN have been conducted. The asynchronous inter-network interference avoidance (AIIA) scheme has been proposed, to reduce the magnitude of mutual interference that occurs in situations where two or more WBASNs share the same channel, so that the active interval in each WBASN frame is not allocated at the same time [
18]. AIIA is based on a hybrid technique of carrier sense multiple access with collision avoidance (CSMA/CA) and time division multiple access (TDMA). In this scheme, information relating to time occupied in a TDMA interval is periodically exchanged and recorded in the AIIA table. The coordinator in each WBASN can check if its TDMA interval conflicts with the time occupied by a neighbor, based on the information in the AIIA table. If a collision is predicted, the coordinator occupies another time slot. A technique for adjusting the modulation parameter, data rate, and duty cycle, linearly, according to the SINR of the receiver has been proposed, to solve co-channel interference [
19].
Transmission power control plays an important role in mitigating interference in a wireless network. The coverage extension of base stations (BSs) can be enhanced by mitigating interference in the cellular networks [
20]. In this scheme, the optimization of BS parameters leads to improving the system performance. The overall power consumption of AP is also decreased by interference management in the wireless local area network (WLAN) [
21]. This approach adapts the branch-and-benders-cut method to solve the non-linear power design problem on the interference management. Many studies have been conducted on methods to improve performance in the WBASN environment by adjusting transmission power. The received signal strength indicator (RSSI) is one of the commonly used parameters for power control algorithm. Due to inter-sensor node interference caused by body movement or variance of channel status, a method for detecting changes to the link quality using the received signal strength indicator (RSSI), and adjusting the transmission power, is proposed [
22]. An energy efficient transmission power control scheme in an on-demand way to adapt to varying channel environments is proposed [
23]. A power control schemes based on the reinforcement learning (RL) and mathematical optimization are proposed to consider interference. To determine the optimal combination of beamforming and power control in sensor arrays, the RL algorithm is proposed [
24]. In this case, the power configuration set of this kind of scheme could be explored by [
25]. A method for channel and power allocation based on a RL mechanism and convex optimization is proposed [
26]. Studies on game theory-based algorithm have been conducted in existing wireless networks to obtain the optimal transmission power that maximizes system performance. The non-cooperative differential game is used to control transmit power of wireless powered sensor network [
27]. This scheme extends working hours and improves throughput by optimal power control. The proactive power update (PAPU) algorithm applied this theory to WBASN environments with the purpose of maximizing the data rate of the entire WBASN networks [
7]. The scheme recognizes changes in SINR or transmission power of neighboring WBASNs, and determines whether to adjust the transmission power. If a coordinator decides to adjust transmission power, the optimal power that increases the transmission rate is found using the Nash equilibrium, based on the quality of the channel, interference from other WBASNs, noise, and other predetermined power parameters.
Besides, studies on various problem occurring in WBASN have been conducted. Researches on using relays have conducted to improve performance of far nodes. In the system of using relay node, routing is essential to improve network lifetime and system performance. A global routing scheme using Dijkstra’s algorithm is proposed with a novel cost function specialized for balancing energy consumption [
28]. A relay selection scheme is proposed to maximize the lifetime of WBASNs through formulating and solving an optimization problem where relay selection of each node acts as optimization variable [
29]. Traffic uncertainty causes degradation of network performance and interruption to operate protocols [
30]. Therefore, design of network protocol should take into account some uncertain factors in order to make it realistic [
31]. In the WBASN, the sensed data is generated by event-driven and this makes the algorithm to be outdated. For this reason, some optimization schemes are proposed to consider the event-driven data generation. A heuristic approach combining deterministic and probabilistic variable fixing strategies is proposed for WBASN optimal design, formulated as an integer programming problem [
32]. An original optimization algorithm is proposed that exploits suitable linear relaxations to guide a randomized fixing of the variables [
33]. It is supported by an exact large variable neighborhood search. Several robust algorithms considered the SINR. The robust optimization scheme using SINR is proposed to deal with the jamming problem in wireless networks [
34]. The stochastic programming-based convex optimization with the probabilistic SINR constraints is proposed to optimize the transmission power [
35]. A stochastic revenue optimization model based on bid pricing model for cellular networks is proposed [
36]. There also exist techniques that integrate various functions of wireless networks. An integrated optimization is proposed to handle the collide functions and to allocate the radio resources [
37]. An optimal cross layer design is developed in order to construct hierarchical system [
38].
In conventional studies, the objective of transmission power control schemes is to minimize the energy consumption [
21], or to maximize the data rate in considering interference occurred in inter-WBASN [
7]. Actually, determining the data rate according to QoS requirements in wireless environment is one of the important issues rather than merely considering high transmission rates or energy efficiency [
39]. However, as these schemes do not consider the QoS of each user in the WBASN environment, transmission power could operate regardless of the required data rate. Thus, there may be a limit in the ability to provide fair QoS to the users in WBASNs. In this paper, we propose an algorithm that can achieve fair QoS satisfaction across all users in WBASNs considering different QoS levels of the users. First of all, a utility function, which indicates how closely the current data rate matches the required data rate, is defined. Next, based on information from neighboring WBASNs, each network derives the transmission power needed for a QoS satisfaction value equal to the average QoS satisfaction value of the neighboring WBASNs. We use the Cucker–Smale model [
40] in calculating the appropriate transmission power for each user. The Cucker–Smale model is typically used to simulate phenomena in which organisms move in groups, based on individual behavior with simple rules, using limited information. The model is thus suitable for the WBASN environment, where the transmission power must be controlled in a distributed manner, because it uses only information available from the neighboring nodes. In addition, the Cucker–Smale model can be applied to solving the problem of fair distribution of a satisfactory QoS in all neighboring WBASNs, because it synchronizes the specific variables of each entity to the same value.
3. System Model
In this paper, we employ IEEE 802.15.6-based system as a target system [
5]. In IEEE 802.15.6, multiple nodes belong to one coordinator (or hub). The hub shall operate in one of the three access modes: ‘beacon mode with superframe’, ‘non-beacon mode with superframe’, and ’non-beacon mode without superframe’. The superframe is divided into contention-based period and managed access period (MAP) as shown in
Figure 2. In the contention-based period, there are three types of access phases: exclusive access phase (EAP), random access phase (RAP), and contention access period (CAP). In this period, sensor nodes use CSMA/CA or slotted ALOHA methods to access medium. Otherwise, in the MAP, it is possible to allocate resource by scheduling such as TDMA. If the beacon signal is available, the hub can determine whether to use each access phase or not, and broadcast some information such as the value of the utility function. For this reason, the beacon mode with superframe is used to facilitate a WBASN in our system.
A WBASN can consist of a hub and multiple sensor nodes. Each sensor node has a different QoS requirement, which leads to scheduling issue on resource allocation in the given MAC protocol. In this paper, we assumed that there is no intra-WBASN collision by assuming the TDMA-based WBASN protocol such as IEEE 802.15.6, in order to focus on the performance evaluation of our algorithm proposed in the context of control over inter-WBASN collision. The hub allocates time resources of the MAP to each sensor node by using the beacon signal.
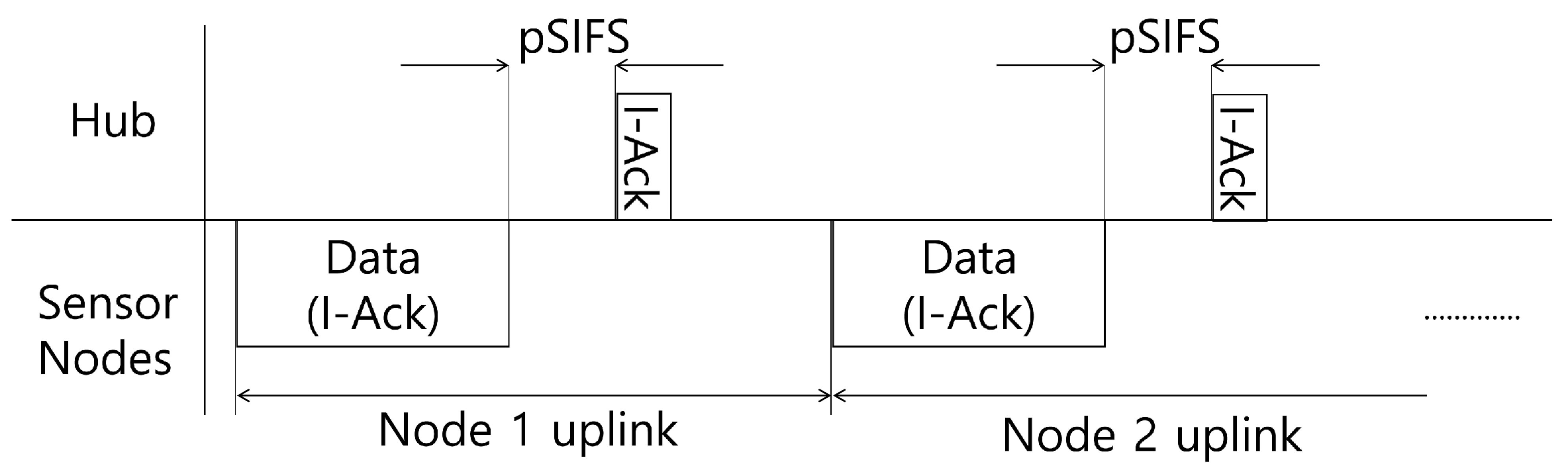
Figure 3 shows medium access in the MAP. Each sensor node periodically generates data and transmits it at the allocated time interval. At this time, the sensor node set the Ack field in the MAC header to immediate-Ack (I-Ack). After data transmission is completed, the hub sends back I-Ack including the information of calculated transmission power to the sensor node. The sensor node can adjust its power level by using the power information in the I-Ack.
It is assumed that a single sensor node
exists in
because contention-free MAC scheme is assumed to avoid intra-WBASN collision between sensor nodes associated with a WBASN, as shown in many studies on previous power control schemes in the WBASN environment [
41,
42,
43,
44]. As shown in
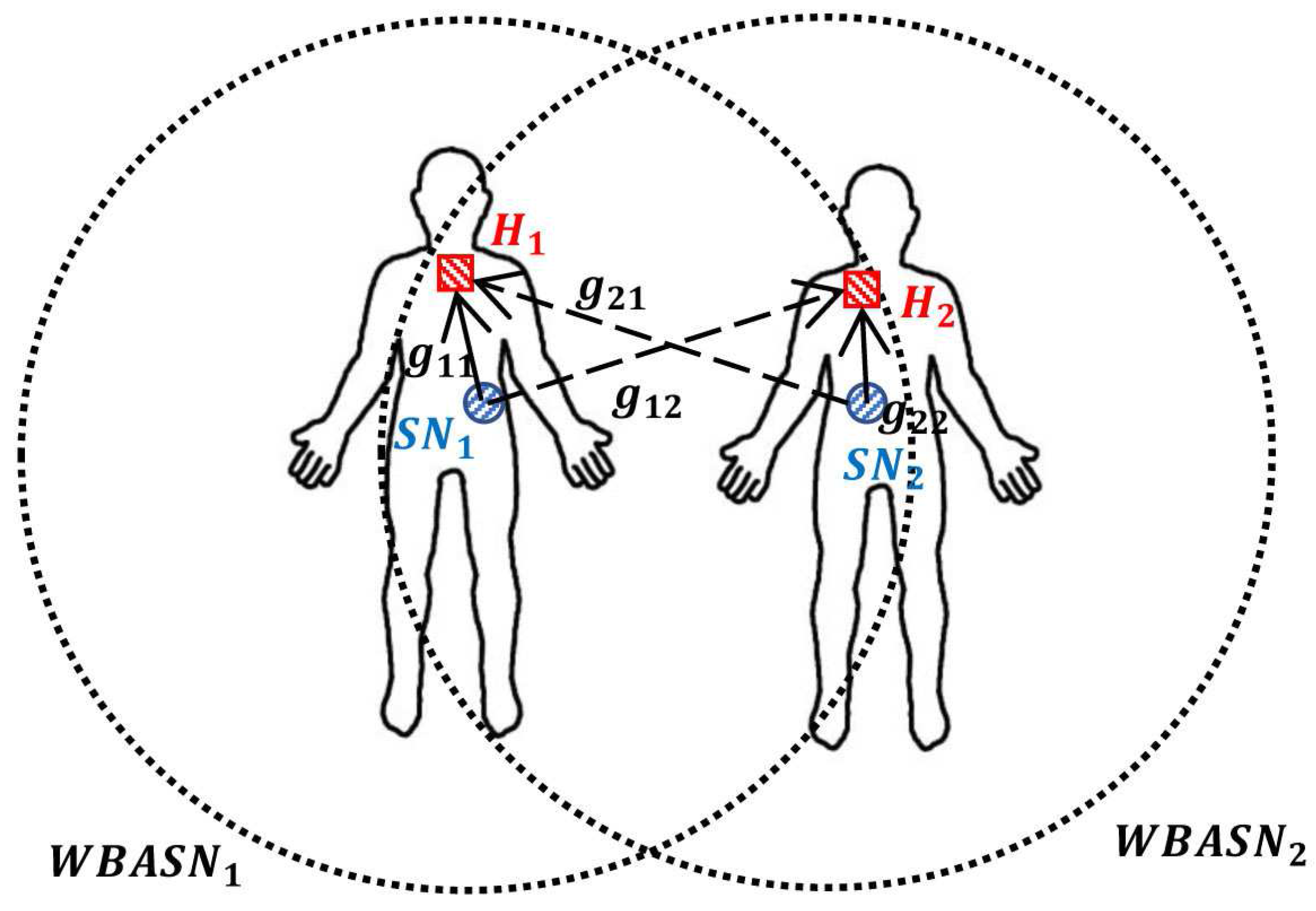
Figure 4, there may be other WBASNs within transmission range, which may cause interference. Suppose that each user
i constitutes a single WBASN
and one hub
in
collects information from each sensor node. The coefficient
represents the channel gain between the transmitter
i and the receiver
j, i.e., The coefficient
represents intra-WBASN channel gain in the WBASN when
, and inter-WBASN interference gain between different WBASNs when
. For example, in
Figure 4,
tries to transmit measured data to
in
, which it belongs to, and, at the same time,
tries to transmit data to
in
, which causes interference to each other’s network.
The SINR,
, of the
i-th WBASN at time
t is:
where
is the transmission power of
,
is the set of neighboring nodes within transmission range of
, and
is additive white Gaussian noise (AWGN). According to Shannon’s theory, the data rate,
, of the
i-th WBASN at time
t is described as follows:
where
B is the bandwidth of the channel. Finally, the energy efficiency,
, of the
i-th WBASN at time
t is defined as,
6. Simulation Results
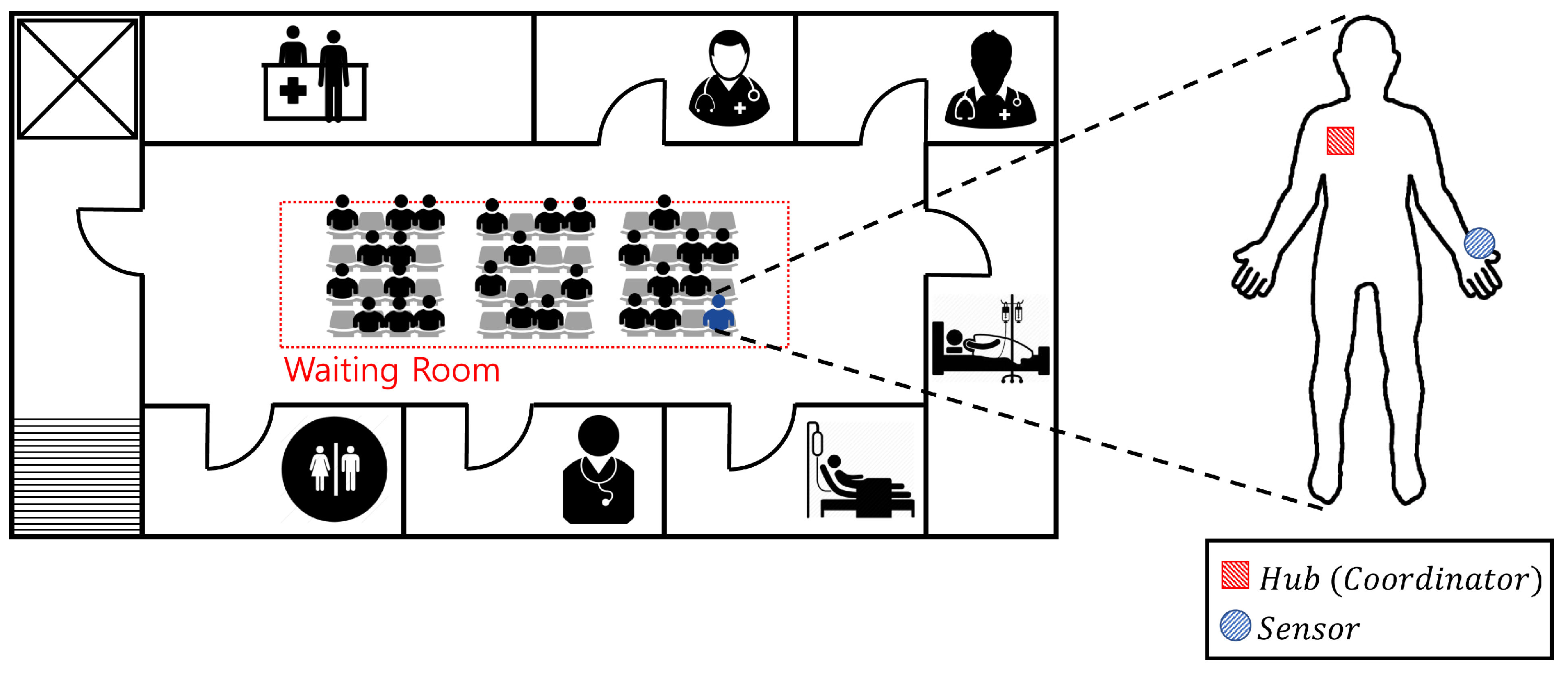
In this section, we evaluate the performance of the proposed algorithm using Monte-Carlo simulations. We assume the network topology proposed in
Section 2. Each WBASN operates in beacon mode according to the IEEE 802.15.6 standard, and exchanges utility information. A hospital waiting room was considered, as a dense environment where interference could occur.
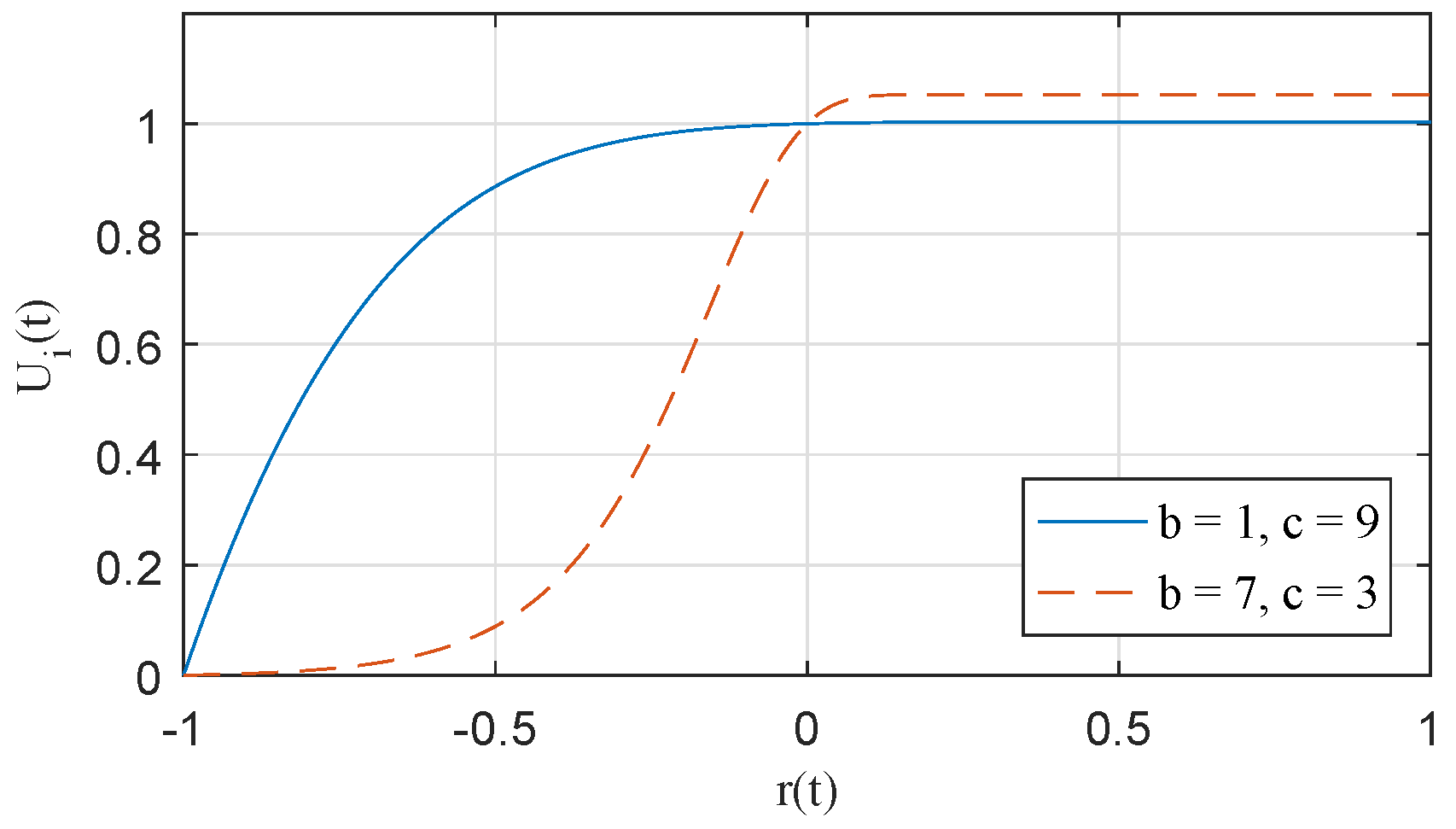
Figure 7 depicts the network environment, assuming a hospital waiting room. The area is set to 14 m × 4 m, where the maximum number of WBASNs is 48. In all subsequent simulations, we will use a logarithmically-shaped utility function, with control parameters
and
.
Table 2 summarizes the applications used in the simulations detailed in this paper, and considers the requirements for various services used in the WBASN [
1,
46,
47].
The simulation considers an uplink situation where measured data is transmitted from the sensor node to the coordinator. The channel gain in decibels is given by
, where
d is the distance [
48].
Table 3 summarizes the commonly-used parameters in this paper.
Furthermore, we compared the performance of the proposed algorithm with two algorithms: PAPU and transmission power control for body area network (TPC-BAN). PAPU controls transmission power based on game theory and aims to increase the transmission rate within a given power limit, and calculates the Nash equilibrium using the best response concept to determine the optimized transmission power value by distributed processing [
7]. This algorithm is adapted to update the transmit power according to the occurrence of the event. There are two kinds of events. The first one occurs when the transmission power is adjusted in the other network, and the second event occurs when the SINR variation according to the time is equal to or greater than a predetermined threshold value. When an event occurs, the hub changes the transmit power according to the best response and informs the neighboring network of the change of the transmit power of the hub by broadcasting. TPC-BAN controls transmission power using the detected RSSI [
23]. In TPC-BAN, the hub updates its own average RSSI by giving weighted parameter in order to mitigate the effects of instantaneous channel mutation. The hub determines whether to control transmission power or not by comparing the average RSSI value with the predetermined target reception power. If the average RSSI value is located in the offset range of the target RSSI, the hub does not change the power of sensor node. However, if the average RSSI value is out of the offset range of the target RSSI, the hub changes the transmission power of the sensor node. The algorithm periodically updates its average RSSI and adjusts the transmit power of the sensor nodes until it reaches the offset range of the target RSSI.
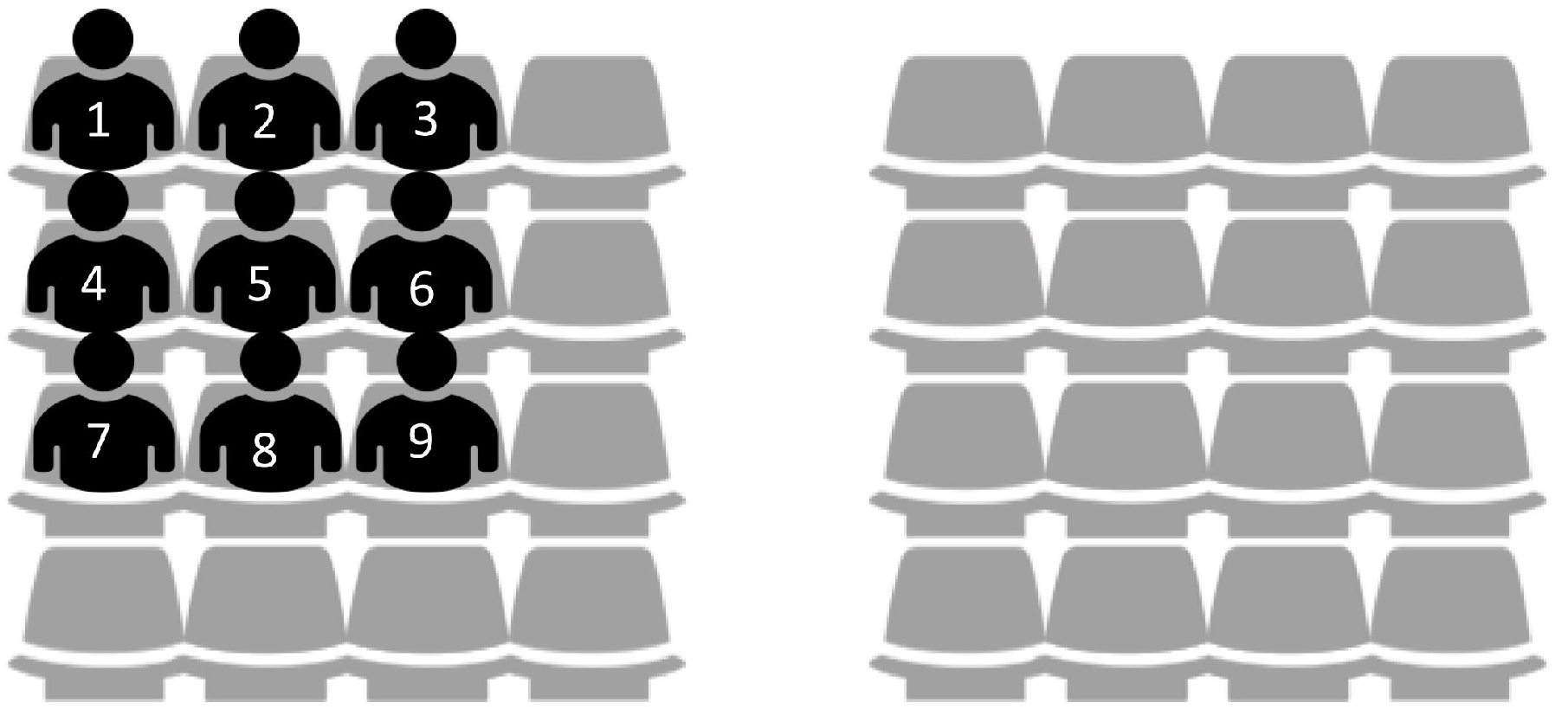
To verify the performance of the proposed algorithm, we create a network environment where nine WBASNs are placed close together, at specific locations, as shown in
Figure 8.
Table 4 shows information of applications used by each WBASN in this environment.
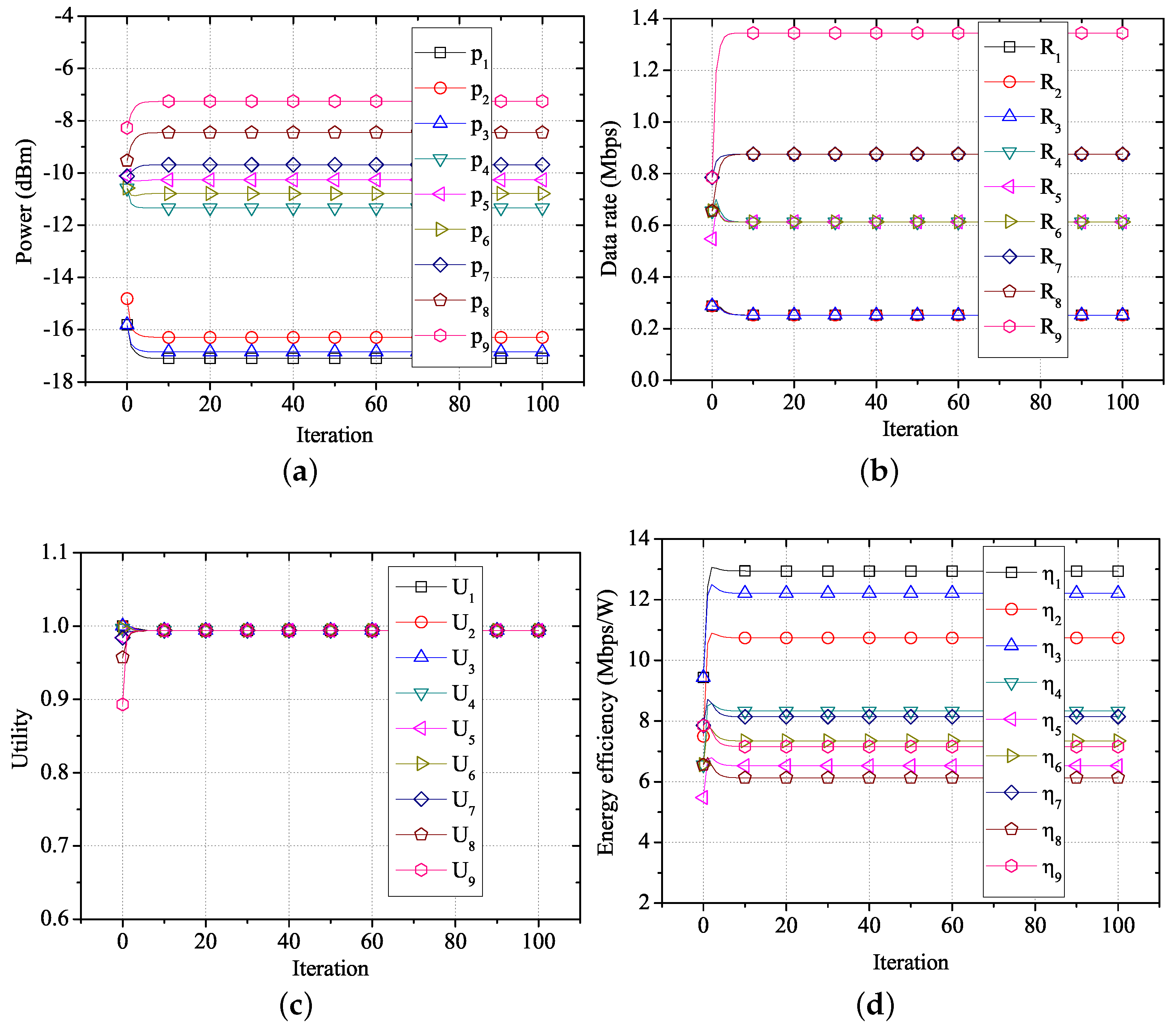
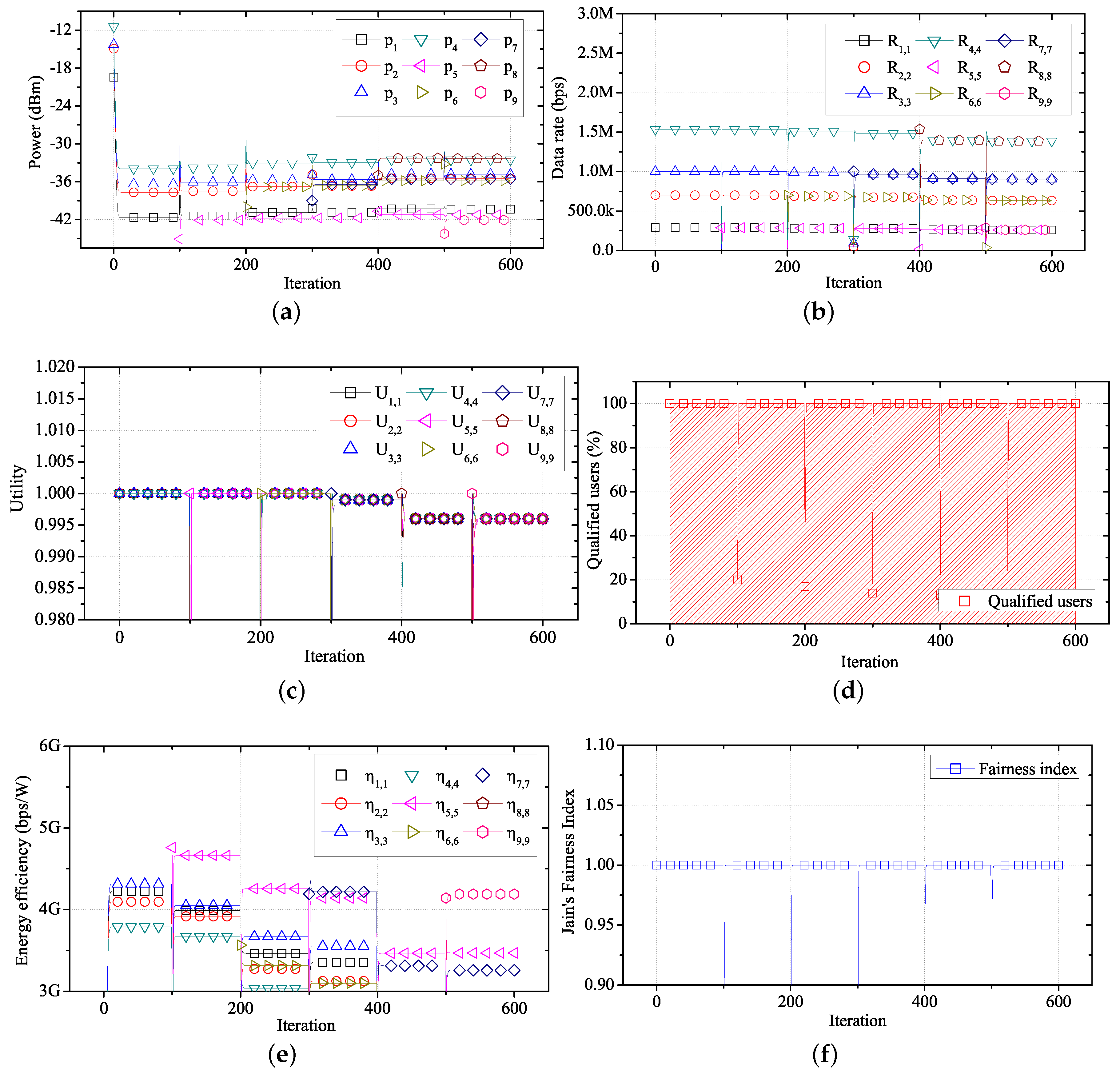
Figure 9 shows the changes in performance for each user over time, using the proposed algorithm in the network environment shown in
Figure 8 and
Table 4. As shown in
Figure 9a,
,
, and
have a low required data rate (288 kbps). Thus, each coordinator reduces the transmission power of the corresponding sensor nodes, which do not require a large transmission power. In the case of
, the coordinator increases the transmission power of the sensor node, which has a high required data rate (1.536 Mbps). By adjusting the transmission power, the data rate of each WBASN converges to a specific value, based on the required data rate, as shown in
Figure 9b. As shown in
Figure 9c, the utility of each user converges to the same value. As shown in
Figure 9d, when the proposed algorithm is applied, only the transmission power needed for data transfer at the required data rate is consumed. Hence, it shows that transmission using the proposed algorithm has a high energy-efficiency.
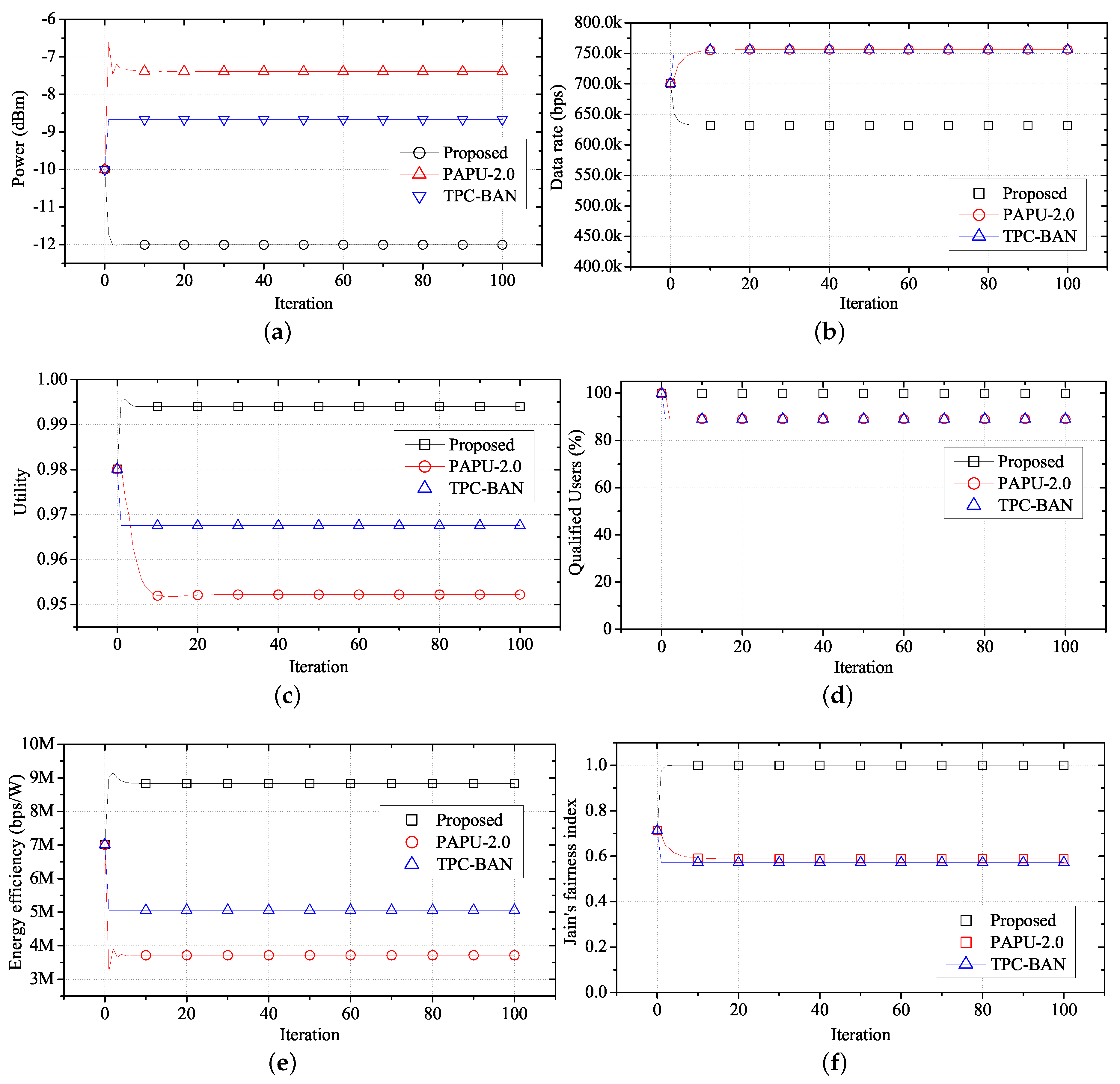
Figure 10 compares the performance of the proposed algorithm with PAPU and TPC-BAN. With the distribution of locations and applications as shown in
Figure 8 and
Table 4, we conduct simulations to obtain an average performance value of each WBASN over time when the proposed algorithm, PAPU, and TPC-BAN are employed. The purposes of PAPU and TPC-BAN are to increase the overall data rate of the entire node and to satisfy global target RSSI value, respectively, while the proposed scheme aims to increase the fairness of the QoS, and decrease the transmission power of each user, simultaneously. Therefore, when using the proposed scheme, lower transmission powers and average data rates are observed as shown in
Figure 10a,b, and a higher utility value is observed as shown in
Figure 10c. Since with the proposed algorithm each user has a high average utility, the number of users with a satisfactory QoS is greater than when PAPU or TPC-BAN is used, as shown in
Figure 10d. In addition, since the proposed scheme requires a lower transmission power on average, energy efficiency is high, as shown in
Figure 10e.
To evaluate the QoS fairness of network users, we use Jain’s fairness index [
49], defined as follows:
where
. Jain’s fairness index defines a variable
that indicates how close the current data rate
is to the required data rate
for each of the
N users in the network. As the difference in
is reduced, the QoS for each user is satisfied fairly, and the value of Jain’s fairness index approaches one.
Figure 10f is a graph comparing the Jain’s fairness index of the proposed method with the index obtained using PAPU and TPC-BAN. Since the proposed algorithm synchronizes the utility, higher QoS fairness is observed than with PAPU and TPC-BAN.
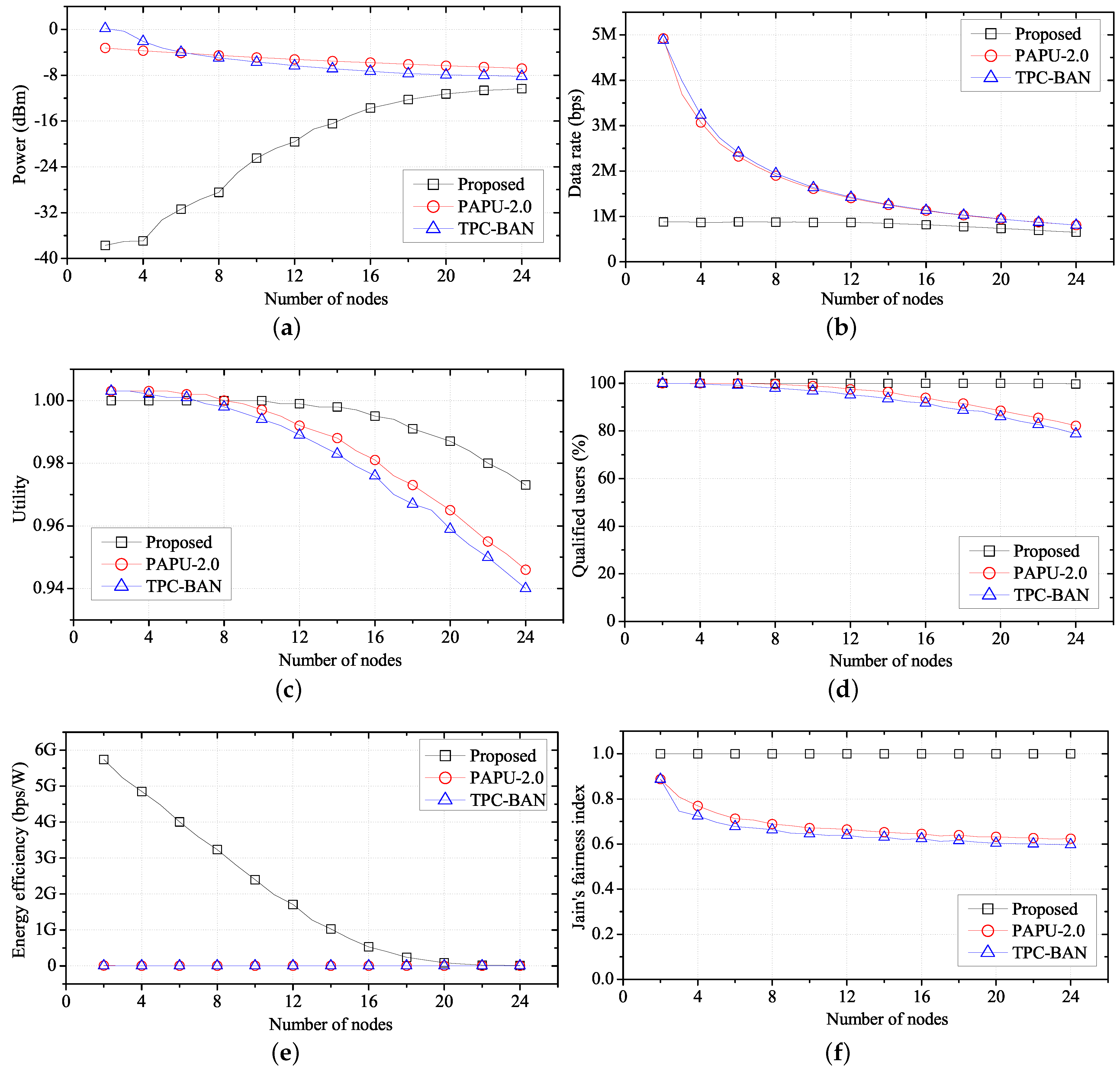
Figure 11 shows the average performance of FTPC-U, PAPU, and TPC-BAN according to the number of nodes. We change the number of nodes from 2–24, placing each node in a 14 m × 4 m space, as shown in
Figure 7. Each node is randomly assigned one of the applications listed in
Table 2.
Figure 11a shows the transmission power according to the number of nodes. In this case, the overall interference increases as the number of nodes increases. With PAPU and TPC-BAN, the hub tries to reduce the transmission power of the sensor node as the interference increases. However, with FTPC-U, the hub adjusts the transmission power of each sensor node using Equation (16), for synchronization of the utilities. In this case, if a decrease in SINR caused by the increase in interference from Equation (16) occurs, the transmission power of the sensor node is increased.
Figure 11b is a graph showing the data rate according to the number of nodes. When the number of nodes is small, we observe a high data rate, which decreases as the number of nodes increases, using PAPU or TPC-BAN. In contrast, with FTPC-U, we observe a low data rate when the number of nodes is small, because the required data rate can be achieved without a high transmission power. We note that
Figure 11c shows an average utility of one, until the number of nodes is about 12. This shows that the actual data rate is close to the required data rate. Therefore, even though the data rate observed in
Figure 11b is low, the user does not perceive a deterioration in performance. We note from
Figure 11c that the effect of the number of nodes on performance is less prevalent using FTPC-U, which controls the transmission power considering the interference caused by the increase in the number of nodes, and the data rate of each user, than it is with PAPU or TPC-BAN. Therefore, as shown in
Figure 11d, the number of users with a satisfactory QoS is kept high with FTPC-U, but decreases gradually with PAPU and TPC-BAN. Since the minimum power required for a satisfactory QoS is used with the proposed algorithm, the energy efficiency is high as shown in
Figure 11e.
Figure 11f shows the QoS fairness according to the number of nodes. FTPC-U shows higher QoS fairness than PAPU and TPC-BAN because it adapts the synchronization of utilities.
Figure 12 shows the order that each WBASN arrives to the network environment, and its corresponding location information. In the initial stage, we assume that only four WBASNs,
–
, exist. Then, one WBASN sequentially enters when the number of iterations increases by a 100, so that up to nine WBASNs are in the network environment. To evaluate performance in dense situations, an arriving WBASN is placed in a location adjacent to an existing WBASN.
Table 5 shows the application information of each WBASN in this environment.
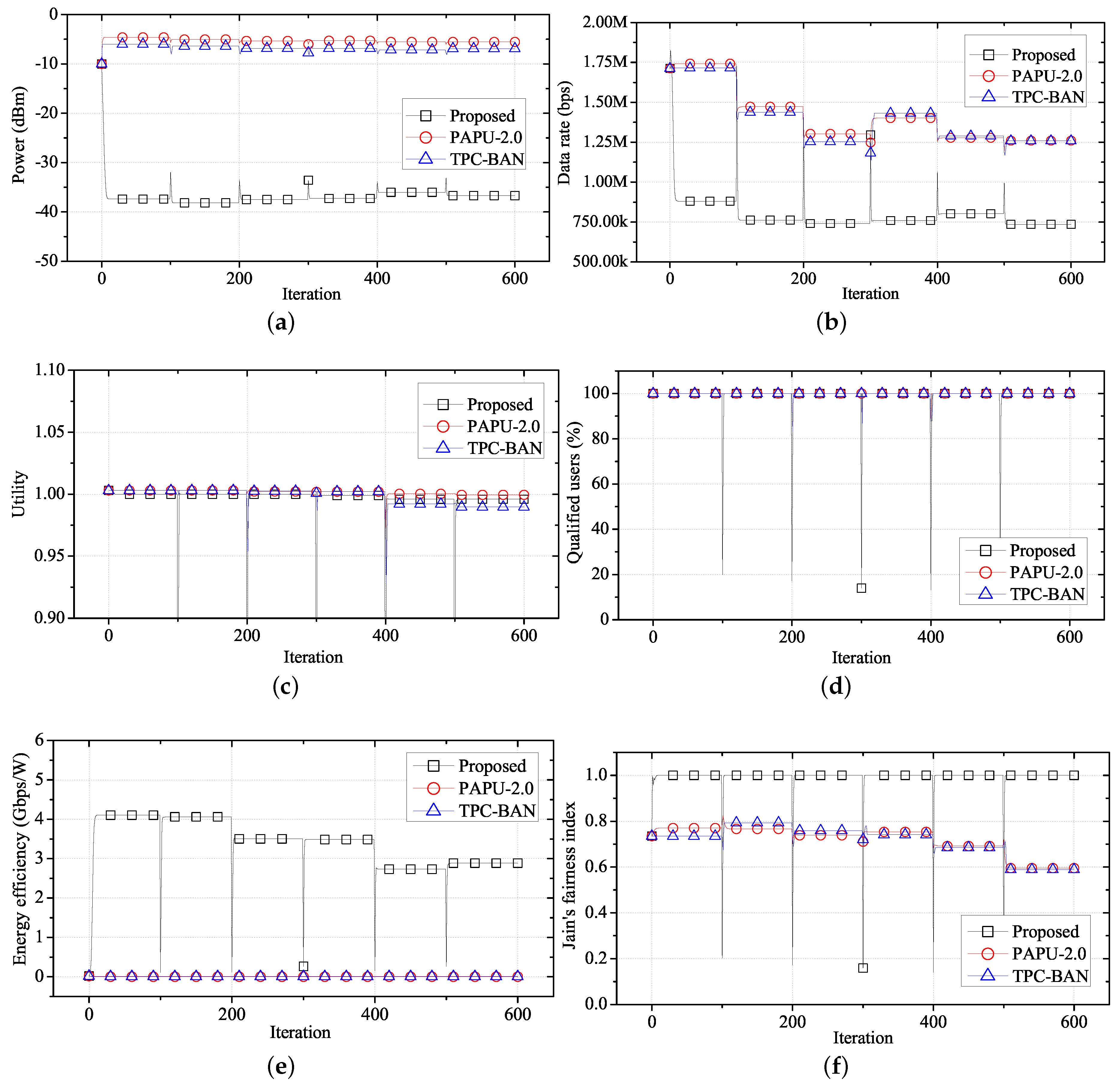
Figure 13 shows the change in performance according to the entry of WBASNs, when the network environment detailed in
Figure 12 and
Table 5 is applied.
Figure 13a,b shows the changes in transmission power and data rate when a new WBASN enters an existing network environment. Here, when the new WBASN enters, a temporary change in interference may cause a temporary change to the transmission power, and a decrease in the data rate. In addition, the utility of each WBASN can be reduced temporarily, as shown in
Figure 13c. Due to the instantaneous change in utility, the number of users with a satisfactory QoS temporarily decreases, as shown in
Figure 13d. As shown in
Figure 13e, high energy efficiency is observed using the proposed algorithm, because only as much transmission power as required is consumed.
Figure 13f shows the QoS fairness in the entry environment, indicating that the proposed scheme achieves high QoS fairness through utility synchronization.
Figure 14 shows the average performance of FTPC-U, PAPU, and TPC-BAN when a new WBASN enters an existing network environment. With the entry model and applications as shown in
Figure 12 and
Table 5, we evaluate the average performance value of each WBASN with FTPC-U, PAPU, and TPC-BAN. As shown in
Figure 14a, transmission power is not consumed unnecessarily with FTPC-U, as the influence of interference and required data rate are considered, whereas PAPU and TPC-BAN controls the transmission power to maximize the data rate and to satisfy global target RSSI, respectively. Therefore, as shown in
Figure 14c, although a lower data rate is observed using FTPC-U than with PAPU or TPC-BAN, the converged utility value is almost the same in both cases. Moreover, since all of algorithms maintain a utility close to one, the number of users with a satisfactory QoS is also maintained at about
as shown in
Figure 14d.
Figure 14e shows the energy efficiency in the WBASN entry environment. FTPC-U has a significantly higher energy efficiency than PAPU or TPC-BAN, because it operates at low power.
Figure 14f shows the QoS fairness for users in the WBASN entry environment. When PAPU or TPC-BAN is used, the QoS fairness of the users is reduced each time a new WBASN enters the network environment. However, if FTPC-U is used, Jain’s fairness index is maintained at about one. In the entry environment, the performance temporarily decreases, because interference increases at the moment of entry. The overall performance degradation at this moment is larger with FTPC-U than with PAPU or TPC-BAN. This is because, with PAPU or TPC-BAN, the transmission power of most of the sensor nodes is adjusted to a relatively high level, however, with FTPC-U, many sensor nodes are adjusted to use a low transmission power, and sensor nodes with low transmission powers are more seriously affected by interference caused by a newly entering WBASN. Nevertheless, using FTPC-U, we observe high performance in the converged state.