Research on the Sensing Performance of the Tuning Fork-Probe as a Micro Interaction Sensor
Abstract
:1. Introduction
2. Resonance Properties Measurement
2.1. Geometric and Material Parameters of the TF

| No. | Total Length Lt (mm) | Prong Length Lp (mm) | Prong Width Wp (mm) | Prong Height Hp (mm) | Gap Width Wg (mm) |
|---|---|---|---|---|---|
| 1 | 6.104 | 3.887 | 0.618 | 0.355 | 0.303 |
| 2 | 6.026 | 3.781 | 0.592 | 0.339 | 0.299 |
| 3 | 6.037 | 3.793 | 0.592 | 0.334 | 0.281 |
| 4 | 6.017 | 3.743 | 0.617 | 0.337 | 0.289 |
| 5 | 5.983 | 3.760 | 0.586 | 0.342 | 0.297 |
| 6 | 6.077 | 3.778 | 0.621 | 0.342 | 0.299 |
| 7 | 6.005 | 3.739 | 0.593 | 0.358 | 0.298 |
| 8 | 6.017 | 3.744 | 0.604 | 0.348 | 0.299 |
| 9 | 5.991 | 3.752 | 0.615 | 0.350 | 0.282 |
| Mean | 6.037 | 3.787 | 0.608 | 0.359 | 0.297 |
2.2. Frequency Spectrum of a TF
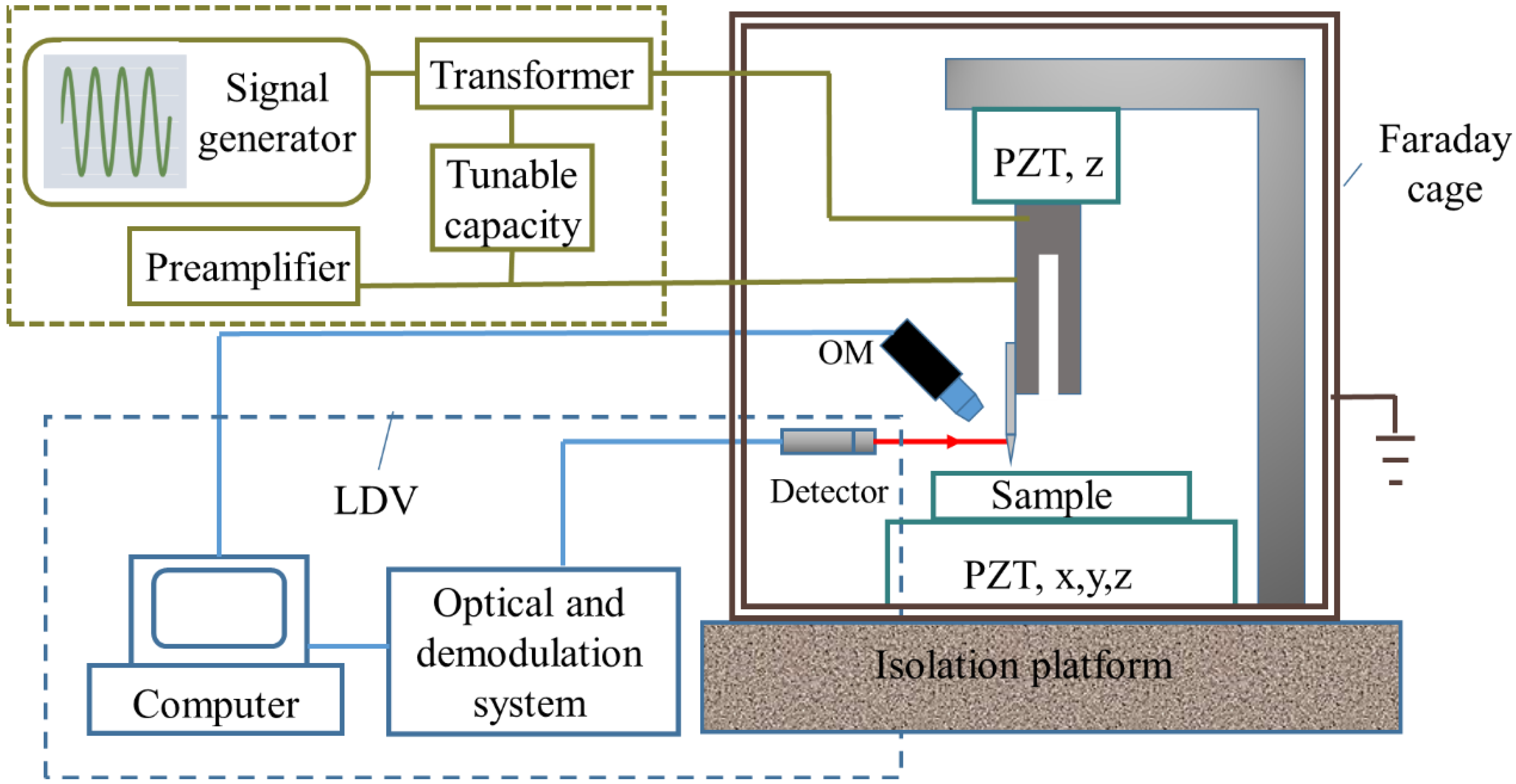
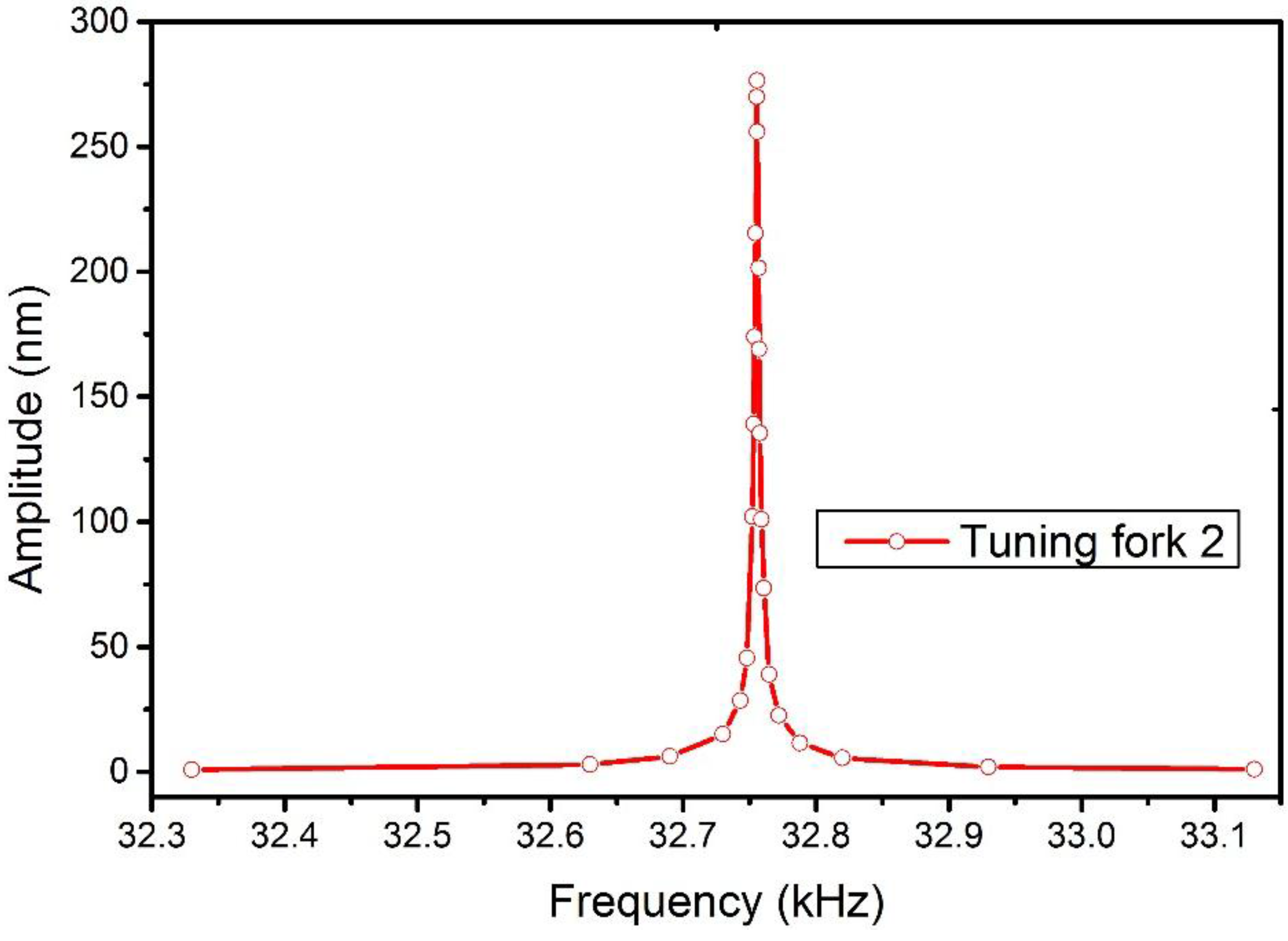
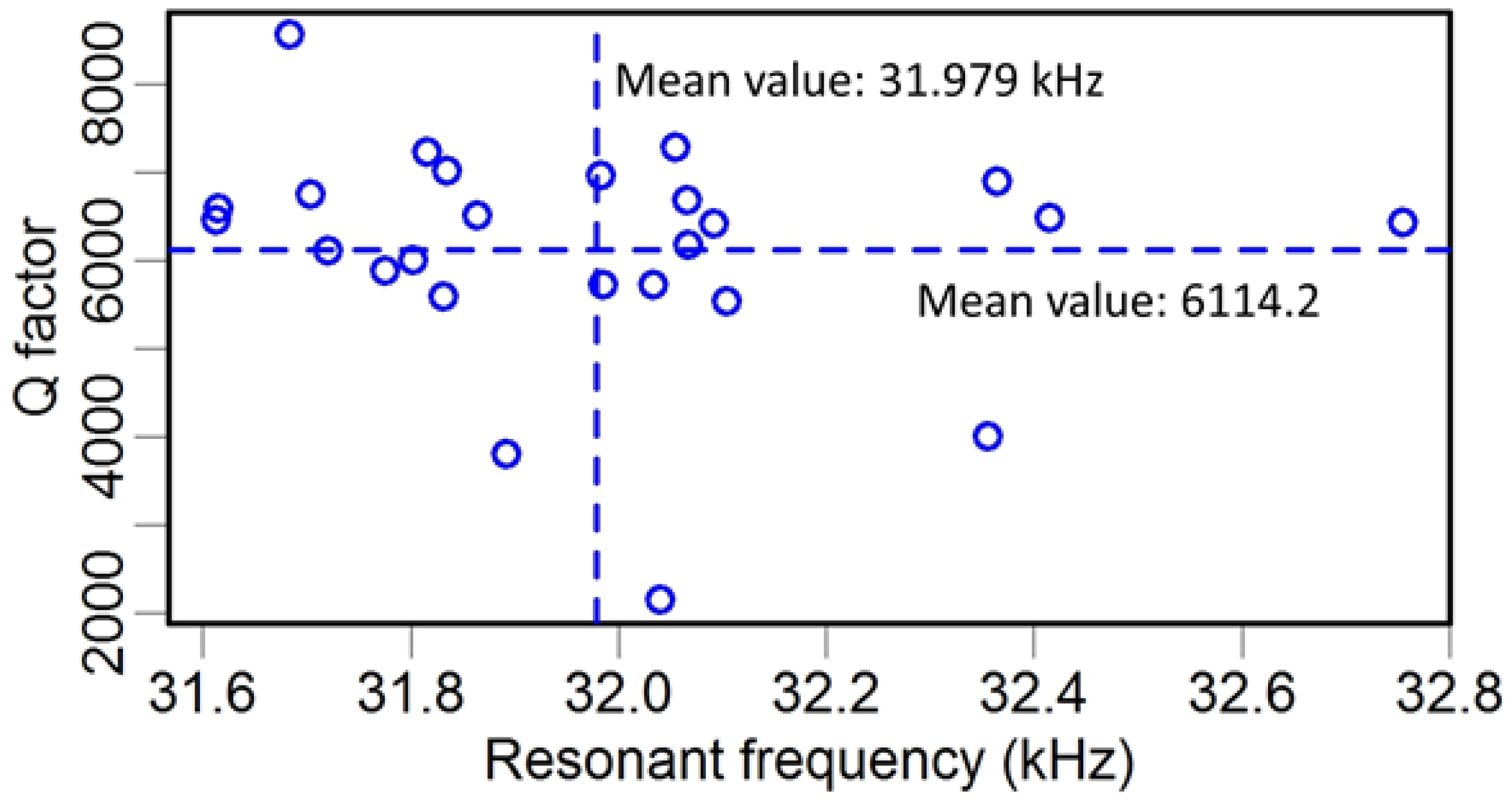
| No. | fR of TF(kHz) | Q Factor of TF | fR of TF-Probe (kHz) | Q Factor of TF-Probe |
|---|---|---|---|---|
| 23 | 32.755 | 6422 | 32.472 | 1353 |
| 24 | 31.684 | 8563 | 31.099 | 2962 |
| 25 | 31.835 | 7014 | 31.455 | 1430 |
2.3. Effect of Air Pressure on the Q Factor
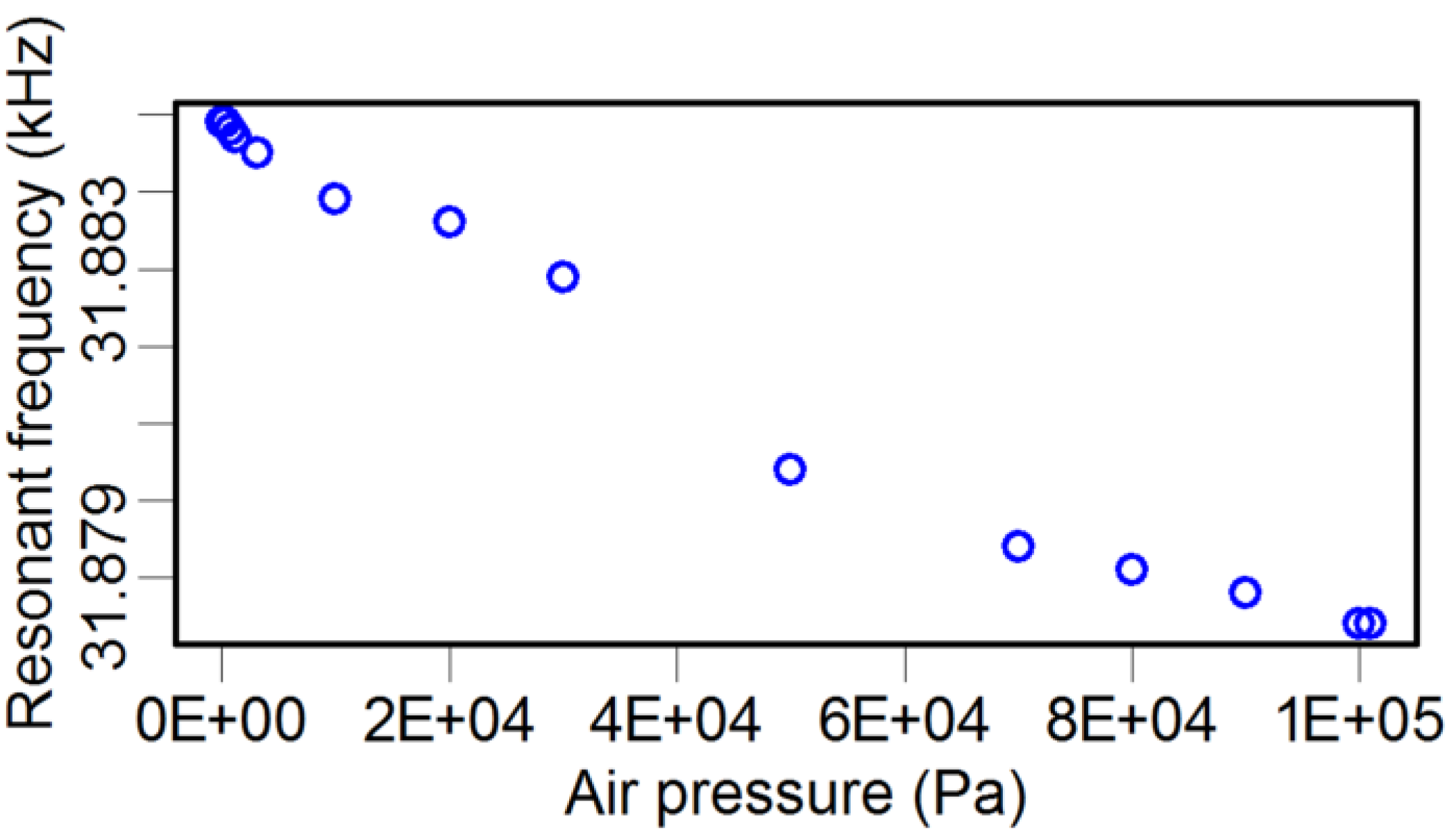
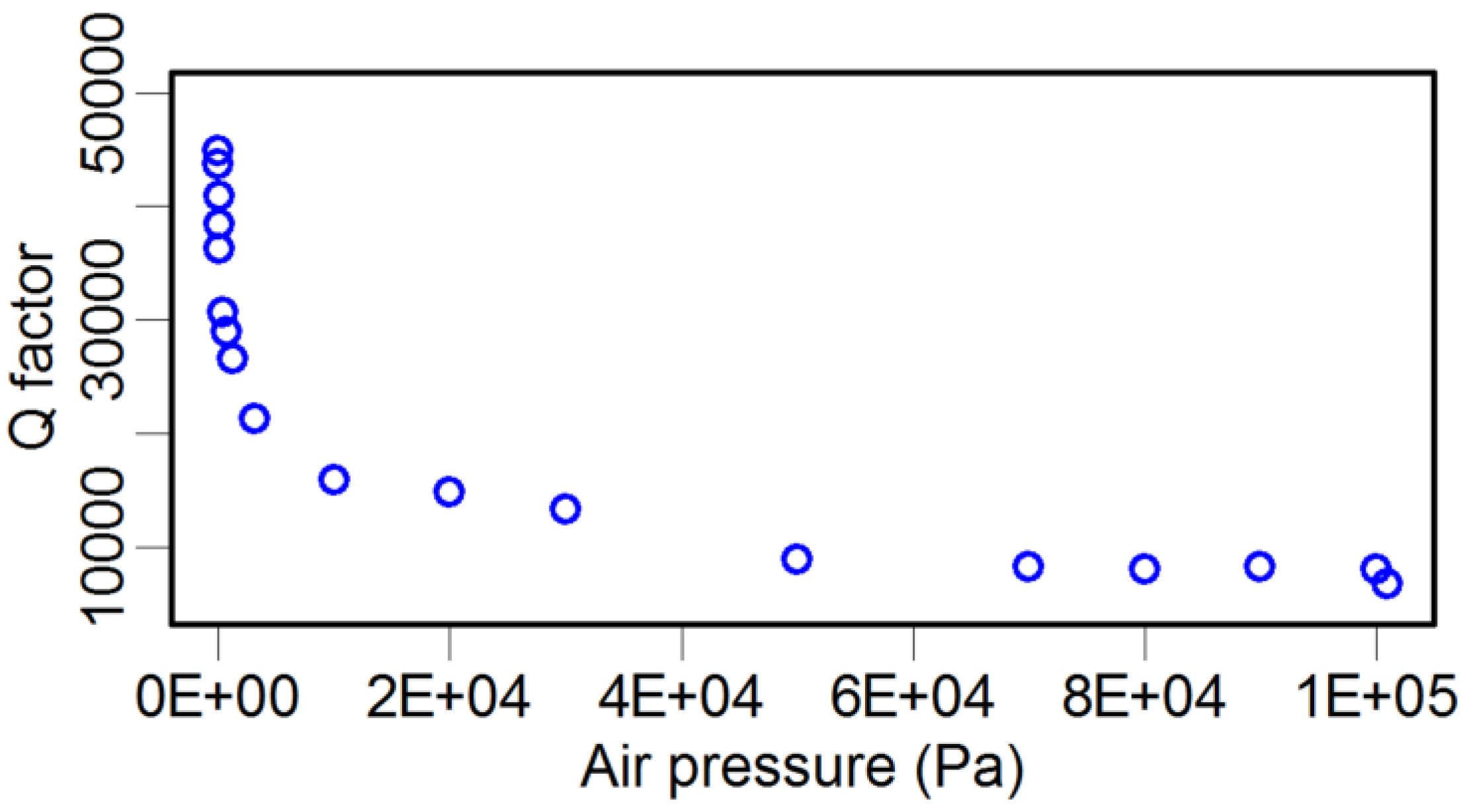
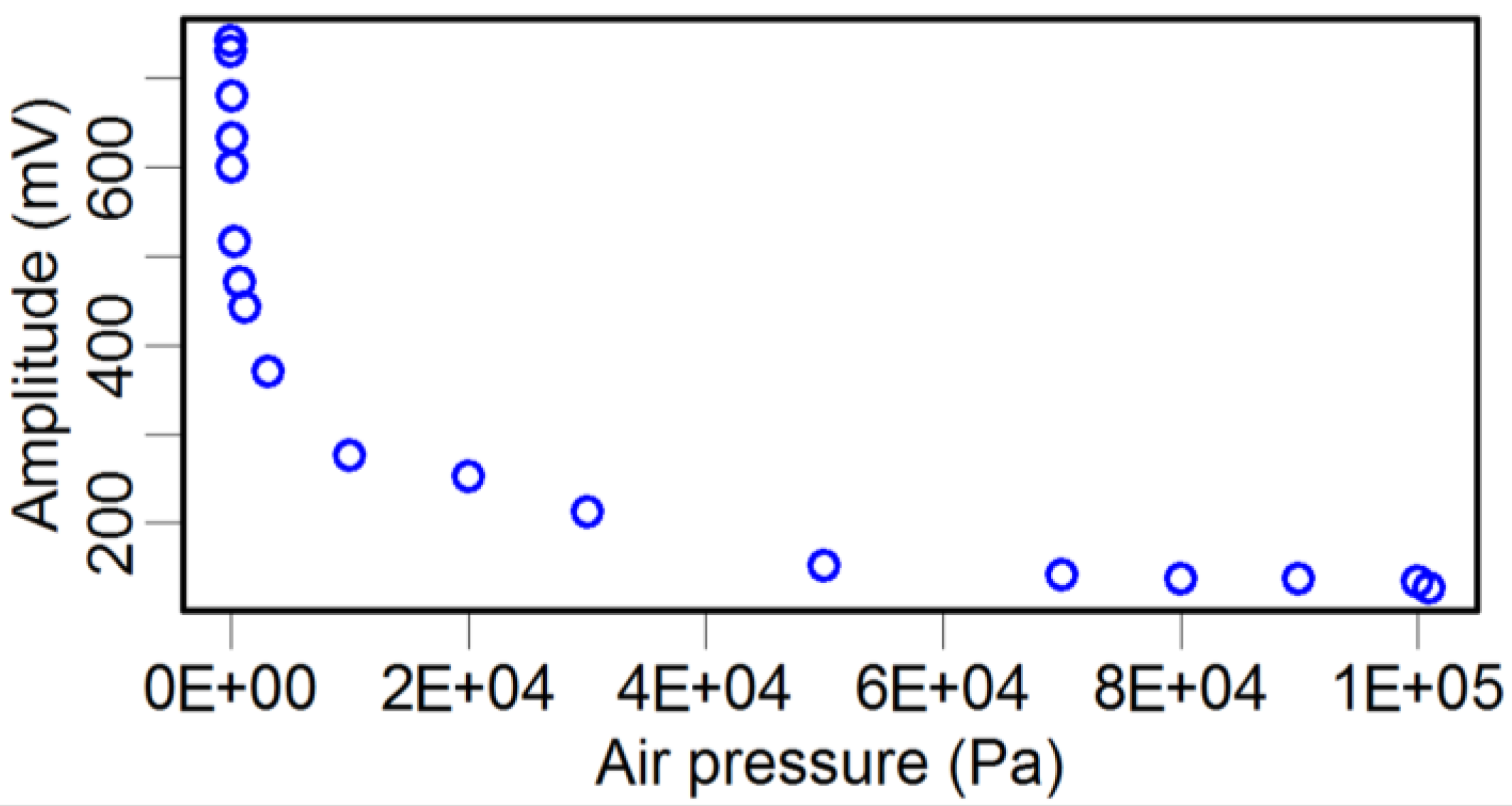
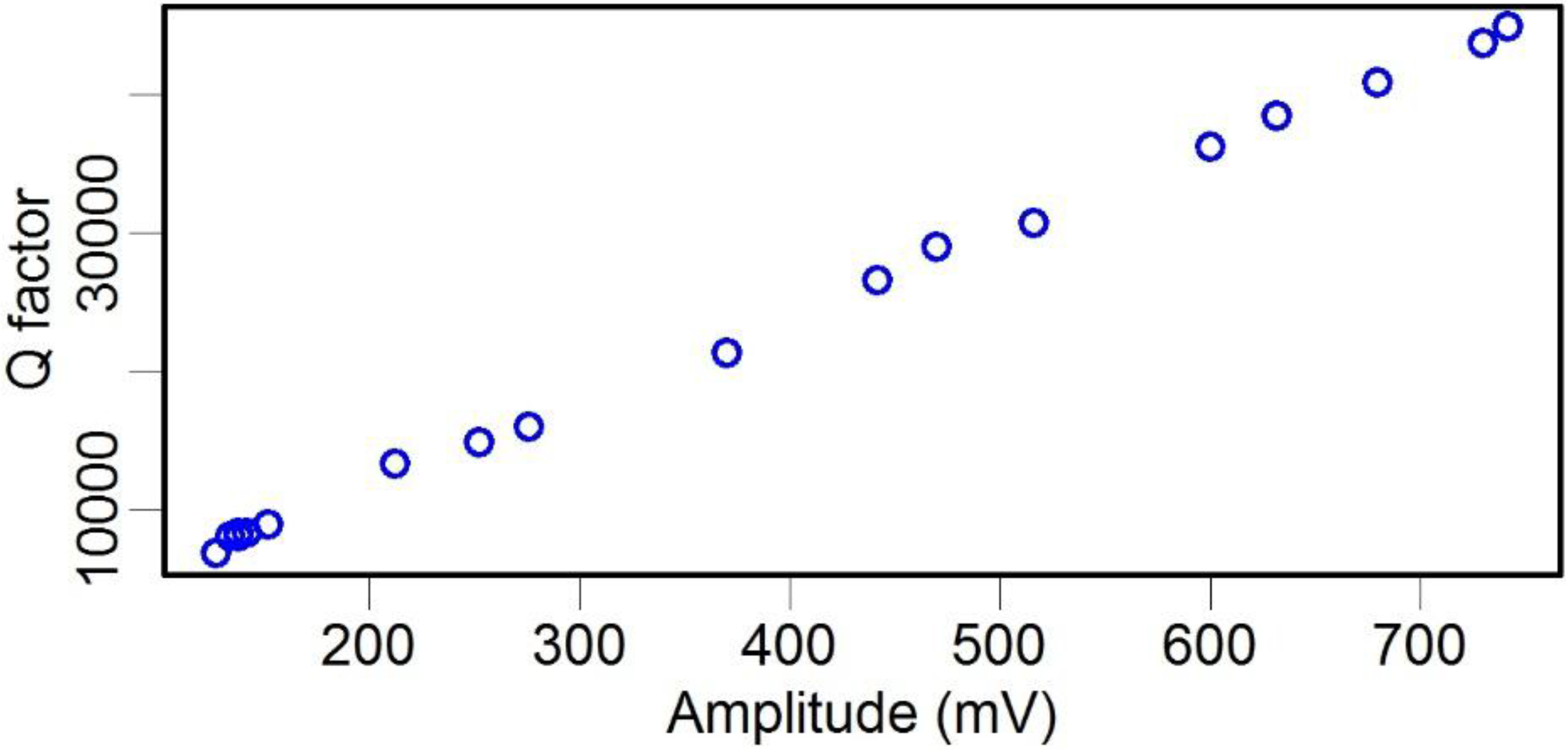
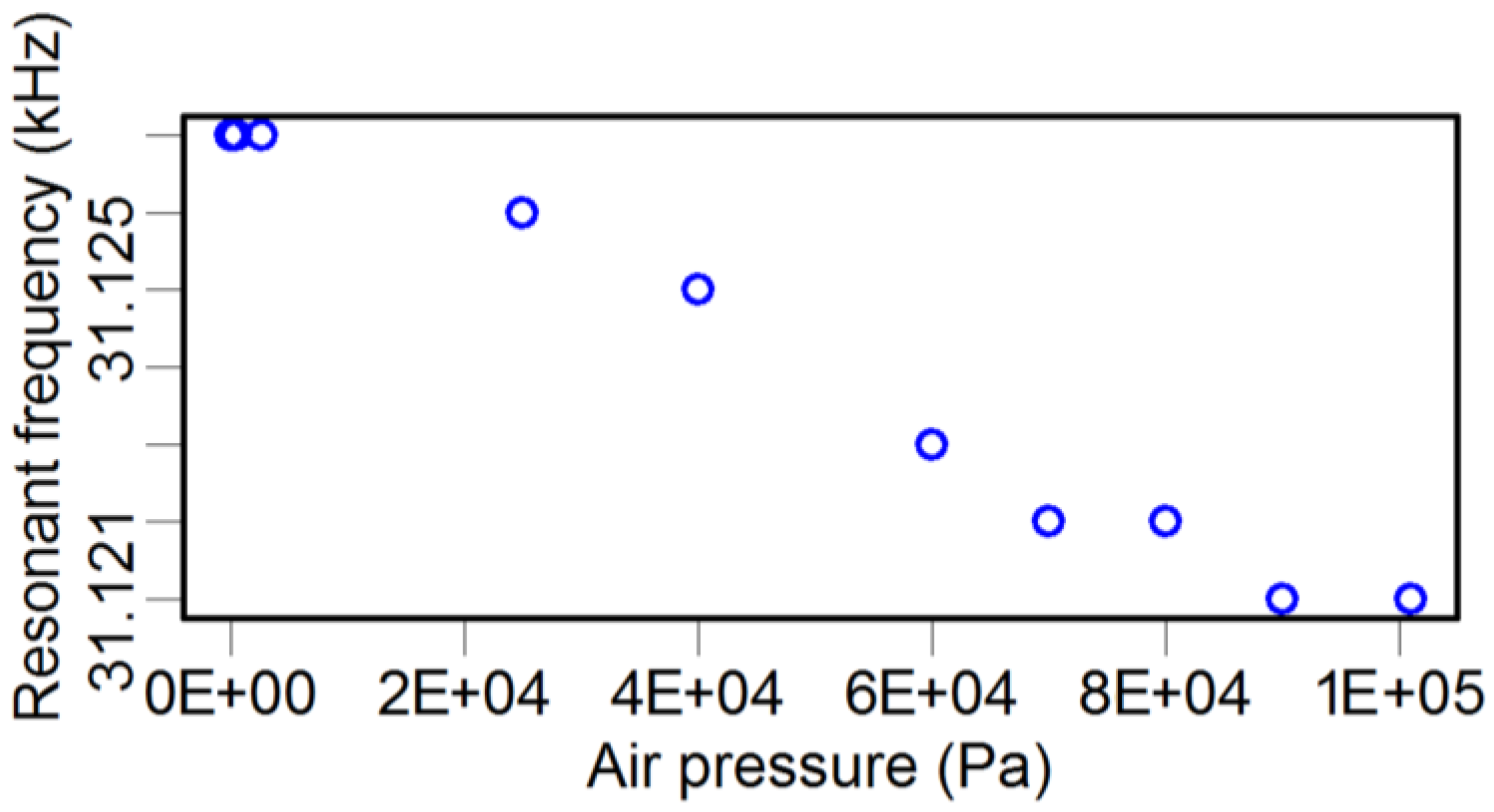
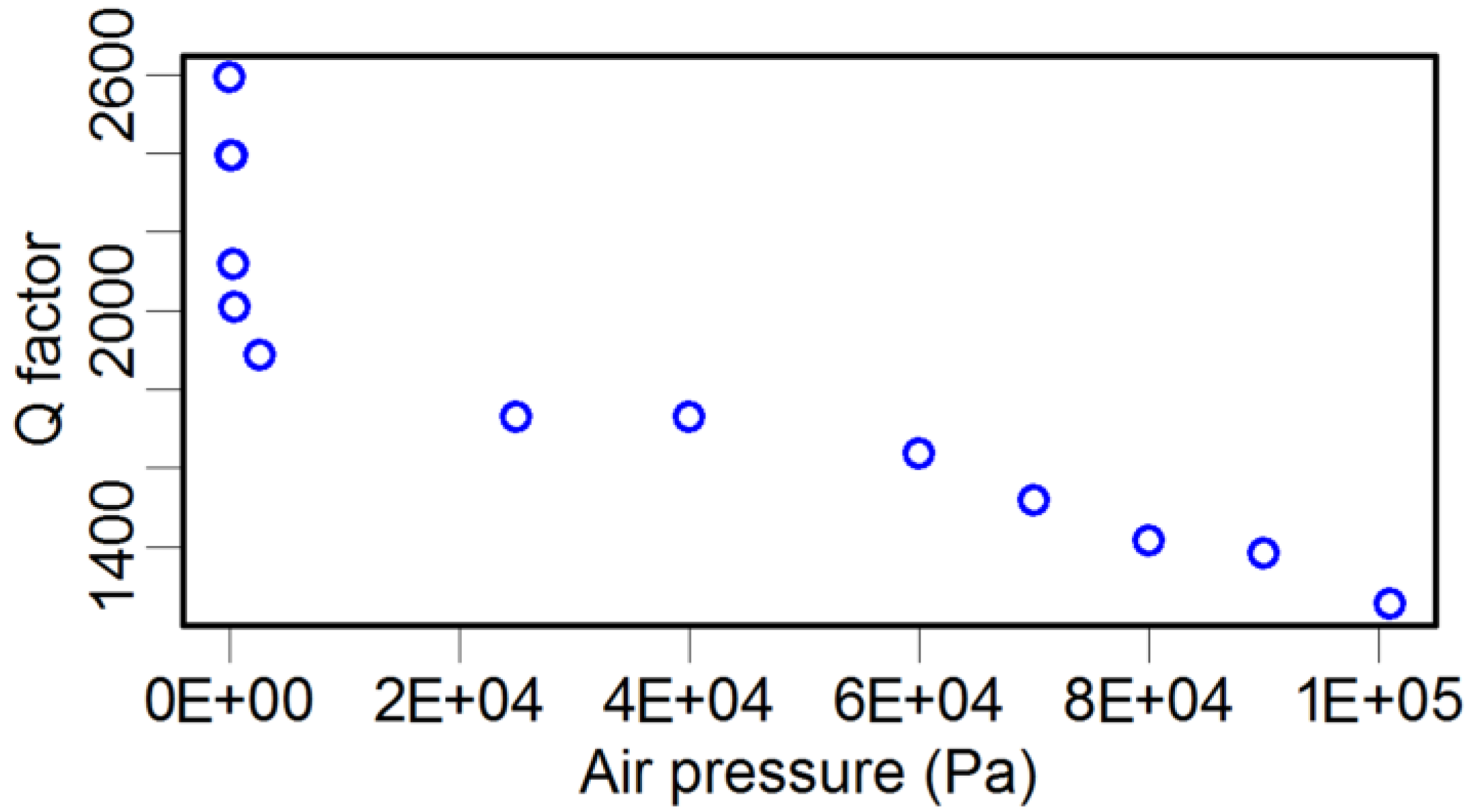
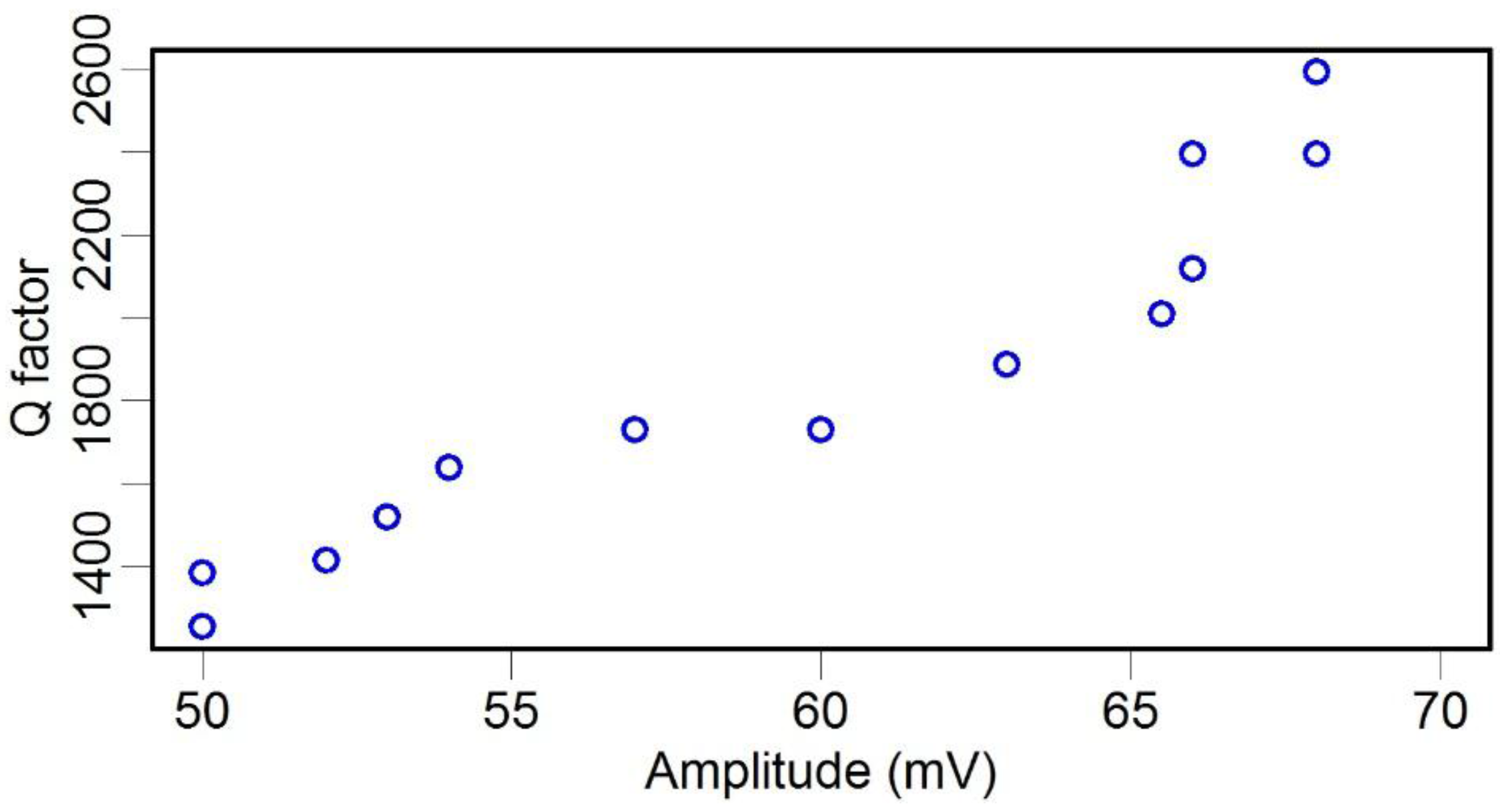
3. Dynamic Property Optimization of the TF Sensor and Its Application in Force Detection
3.1. Optimization of the Q Factor
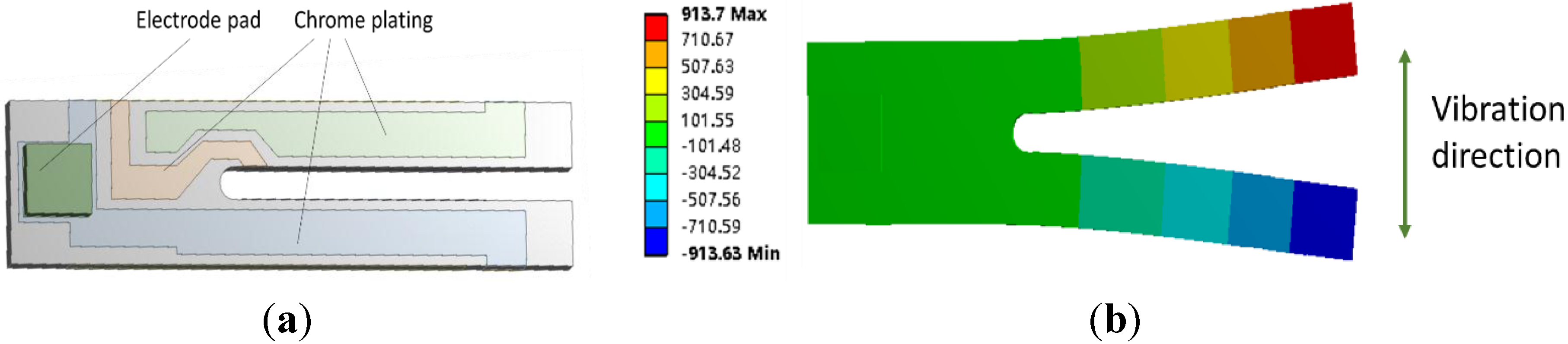
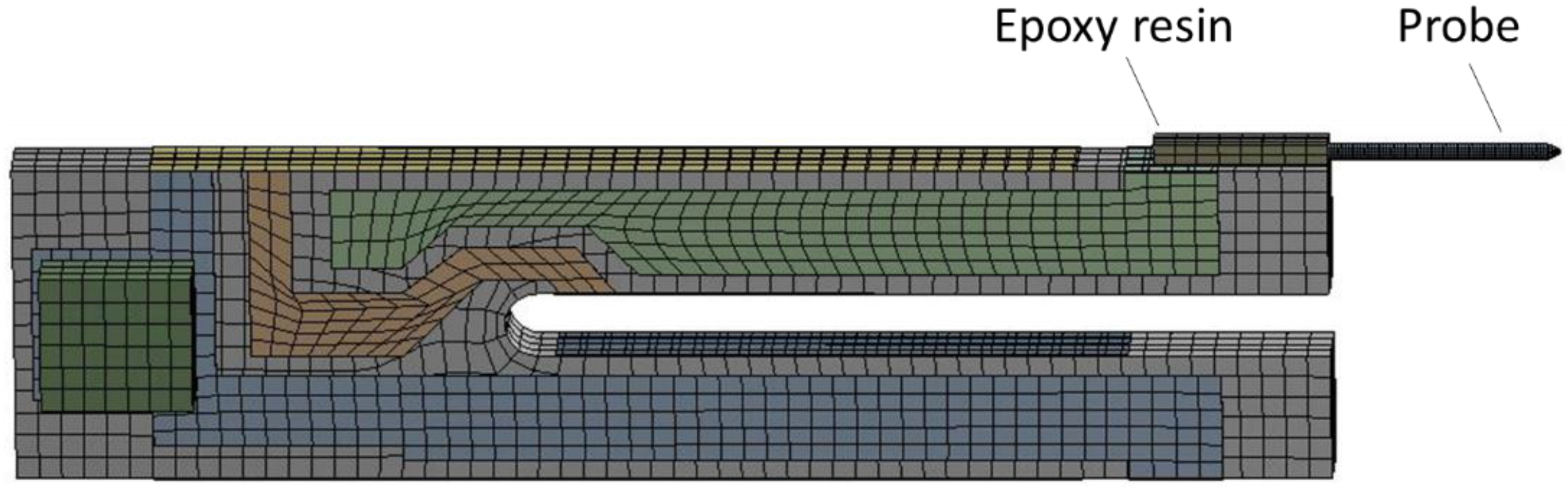
| Damping Coefficient of the Probe (Ns/m) * | Q Factor | Damping Coefficient of the Epoxy Resin (Ns/m) # | Q Factor |
|---|---|---|---|
| 0.05 | 3037 | 0.6 | 1431 |
| 0.005 | 4025 | 0.2 | 4025 |
| 0.0005 | 4182 | 0.06 | 10,063 |
| 0.00005 | 4182 | 0.02 | 17,889 |
| Young’s Modulus of the Probe (GPa) * | Q Factor | Young’s Modulus of the Epoxy Resin (GPa) # | Q Factor |
|---|---|---|---|
| 411 | 4025 | 20 | 2106 |
| 200 | 3926 | 10 | 4025 |
| 78 | 3350 | 6 | 6311 |
| 10 | 1516 | 2 | 13,691 |
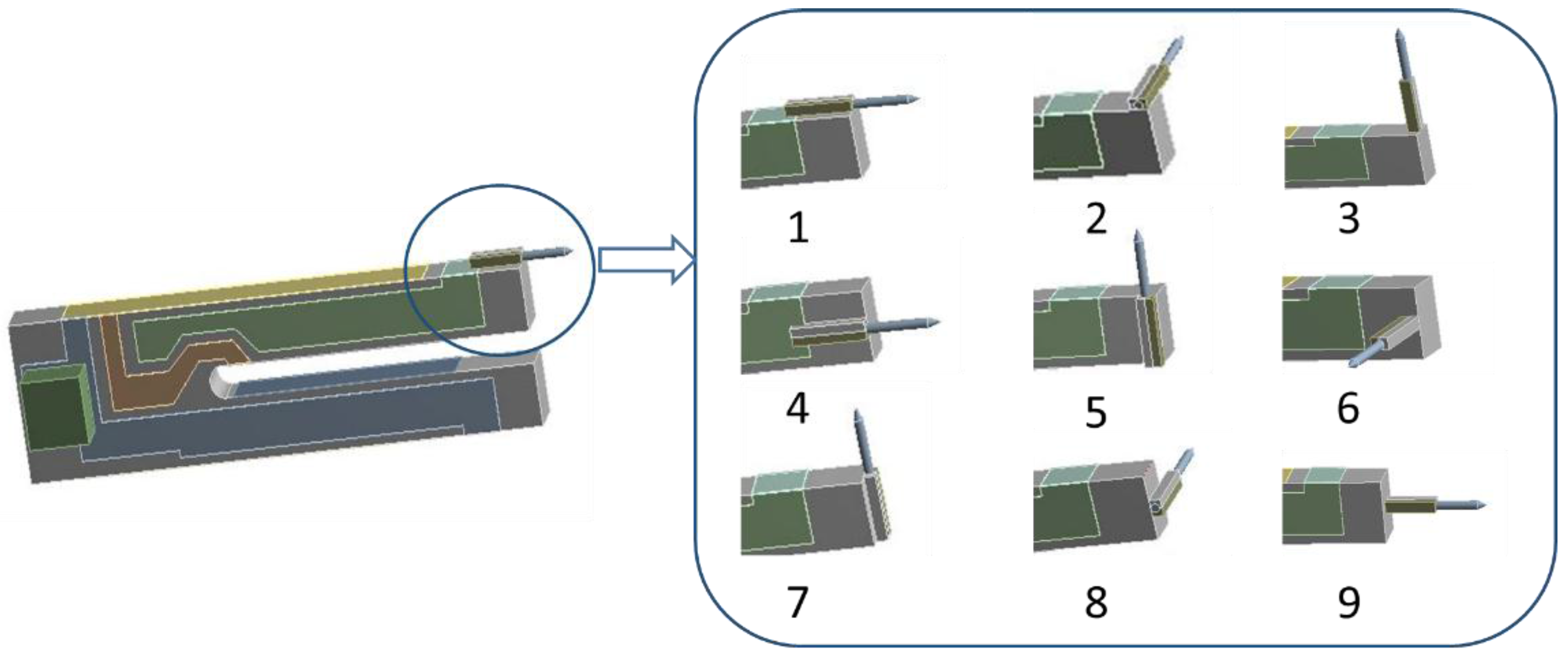
| Type | Q Factor |
|---|---|
| 1 | 12,913 |
| 2 | 22,253 |
| 3 | 29,306 |
| 4 | 20,821 |
| 5 | 40,337 |
| 6 | 17,922 |
| 7 | 37,934 |
| 8 | 22,241 |
| 9 | 6844 |
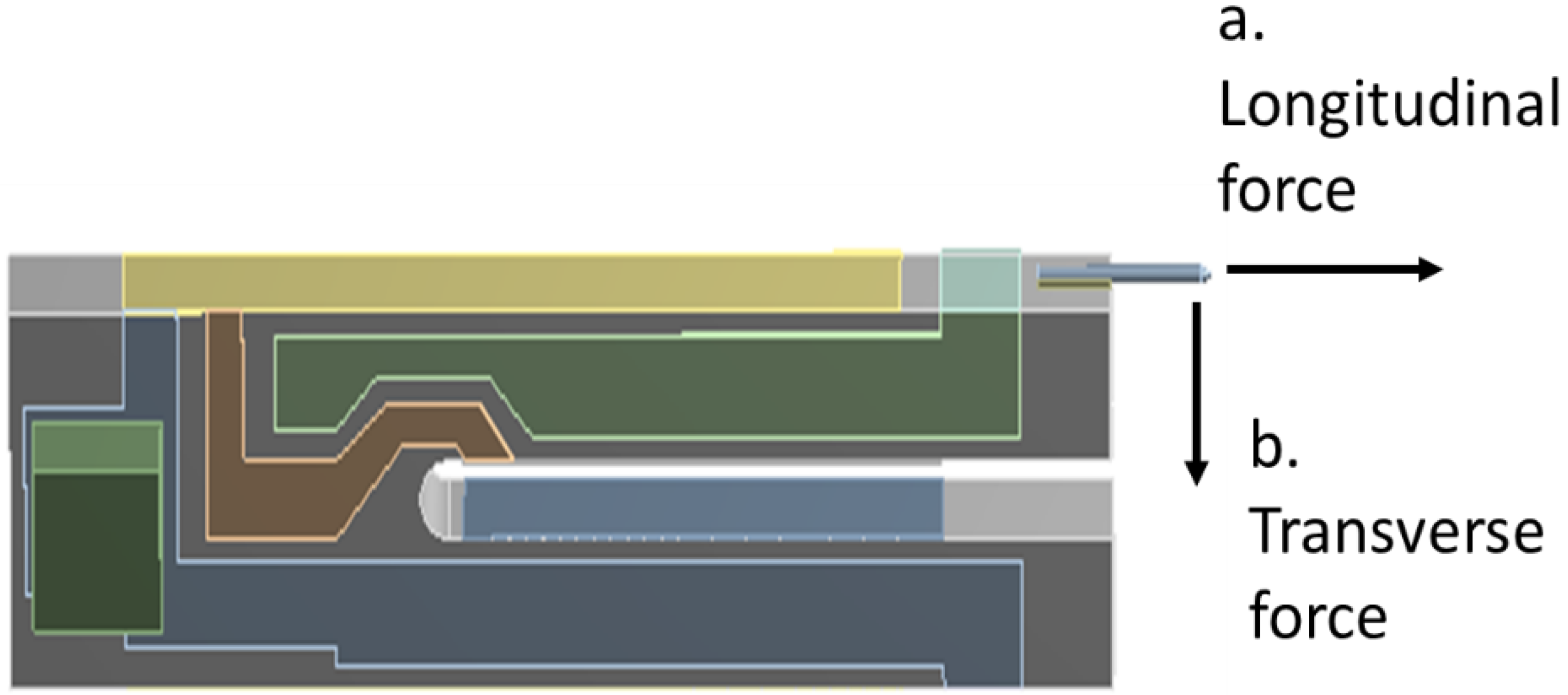
3.2. Dynamic Response of the TF Sensor under Longitudinal and Transverse Interactions
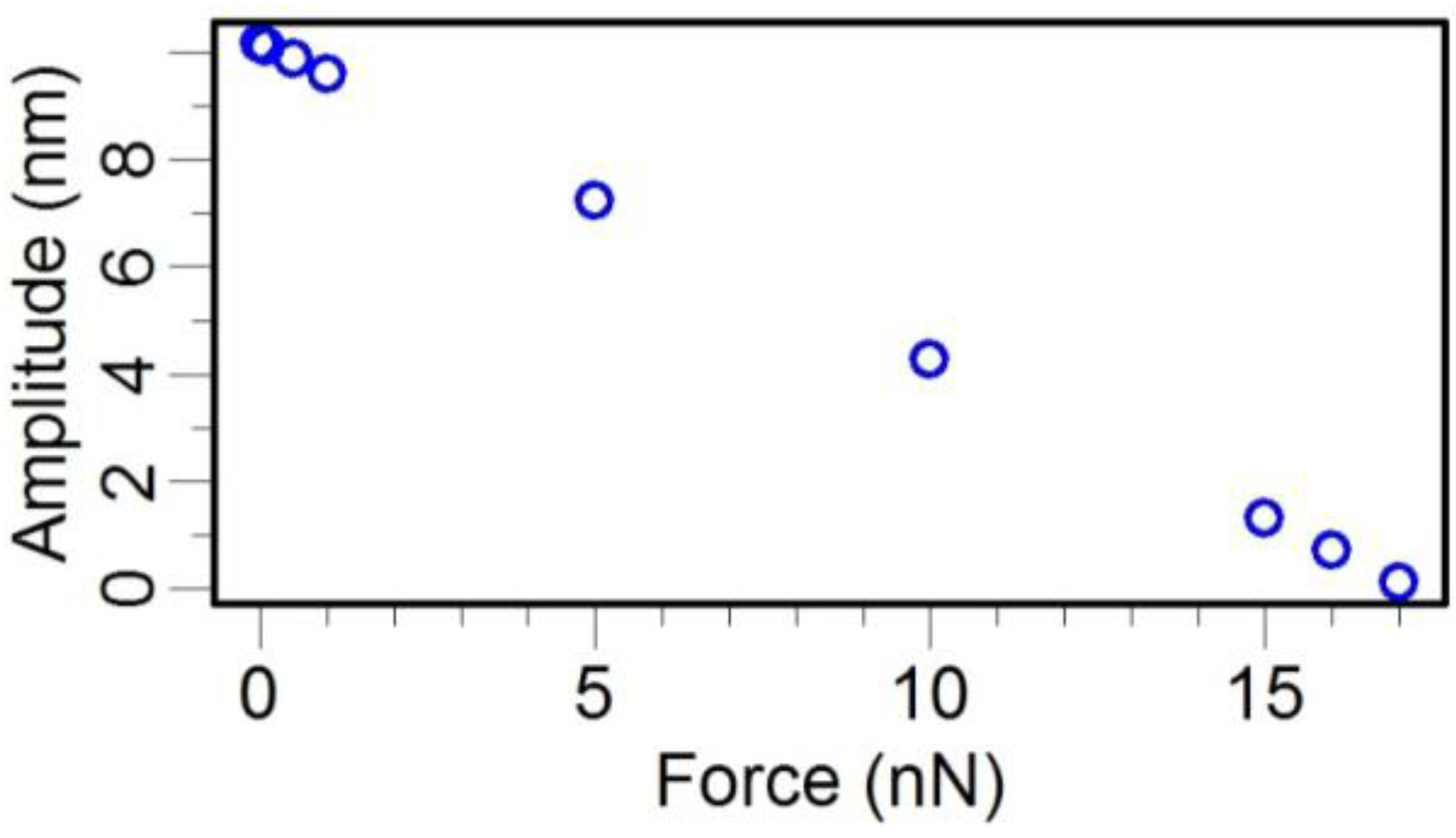
| Force (mN) | Resonance Frequency (Hz) | Probe Tip Oscillation Amplitude ( nm) | Phase Angle (°) |
|---|---|---|---|
| 1E−13 | 32,375 | 10.11 | 91.11 |
| 0.001 | 32,375 | 10.11 | 91.11 |
| 0.01 | 32,375 | 10.11 | 91.14 |
| 0.1 | 32,375 | 10.11 | 91.36 |
| 1 | 32,375 | 10.09 | 93.59 |
| 10 | 32,376 | 9.21 | 114.34 |
| 20 | 32,377 | 7.57 | 131.51 |
| 30 | 32,378 | 6.11 | 142.79 |
| 50 | 32,380 | 4.21 | 155.36 |
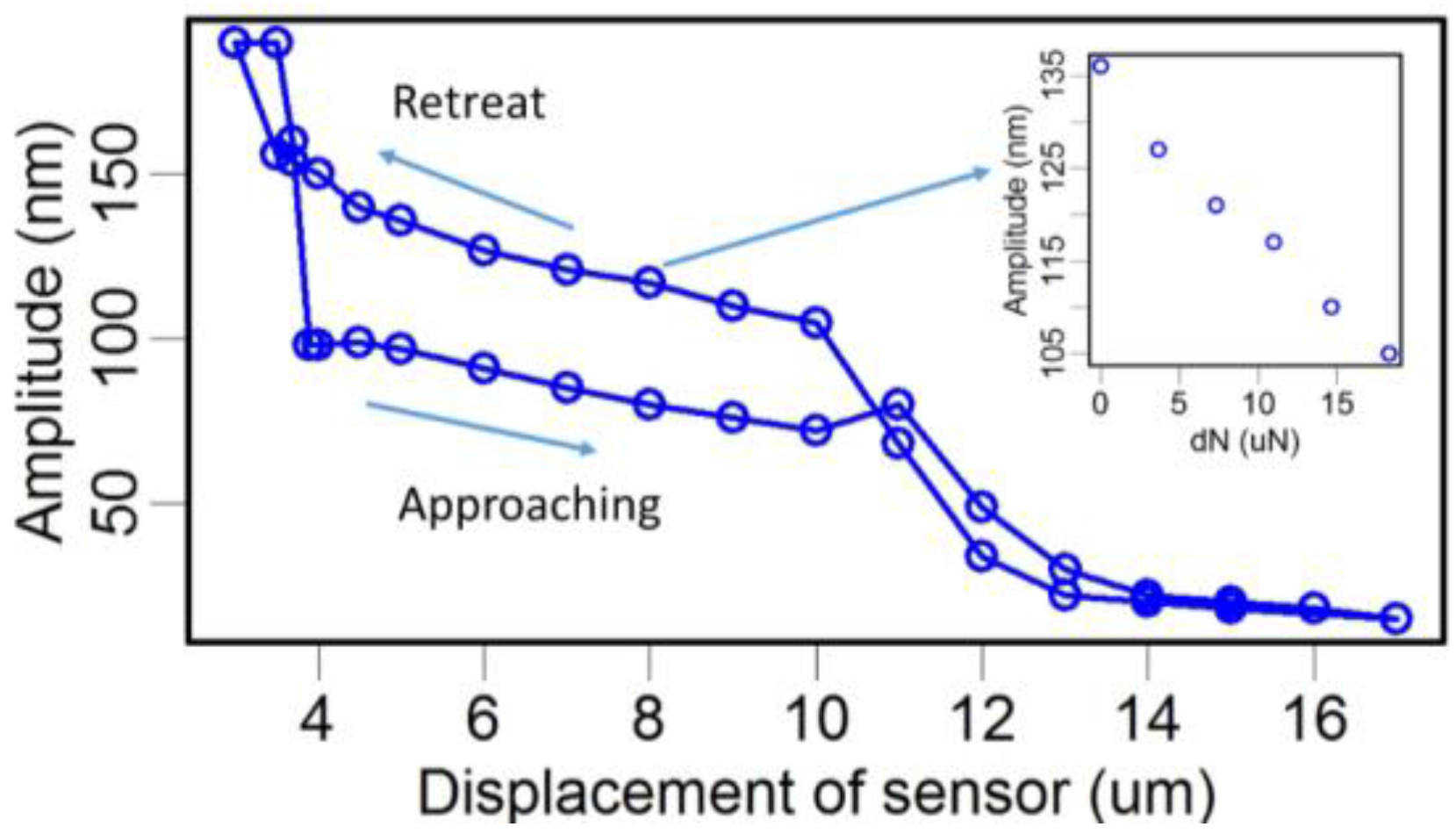
4. Drag Force Measurement
5. Discussion
5.1. Parameters Affecting the Resonance Frequency of the TF-Probe
| Probe Length (mm) | Resonance Frequency (Hz) |
|---|---|
| 0.5 | 32,426 |
| 1.0 | 32,102 |
| 1.5 | 31,598 |
| 2.0 | 30,830 |
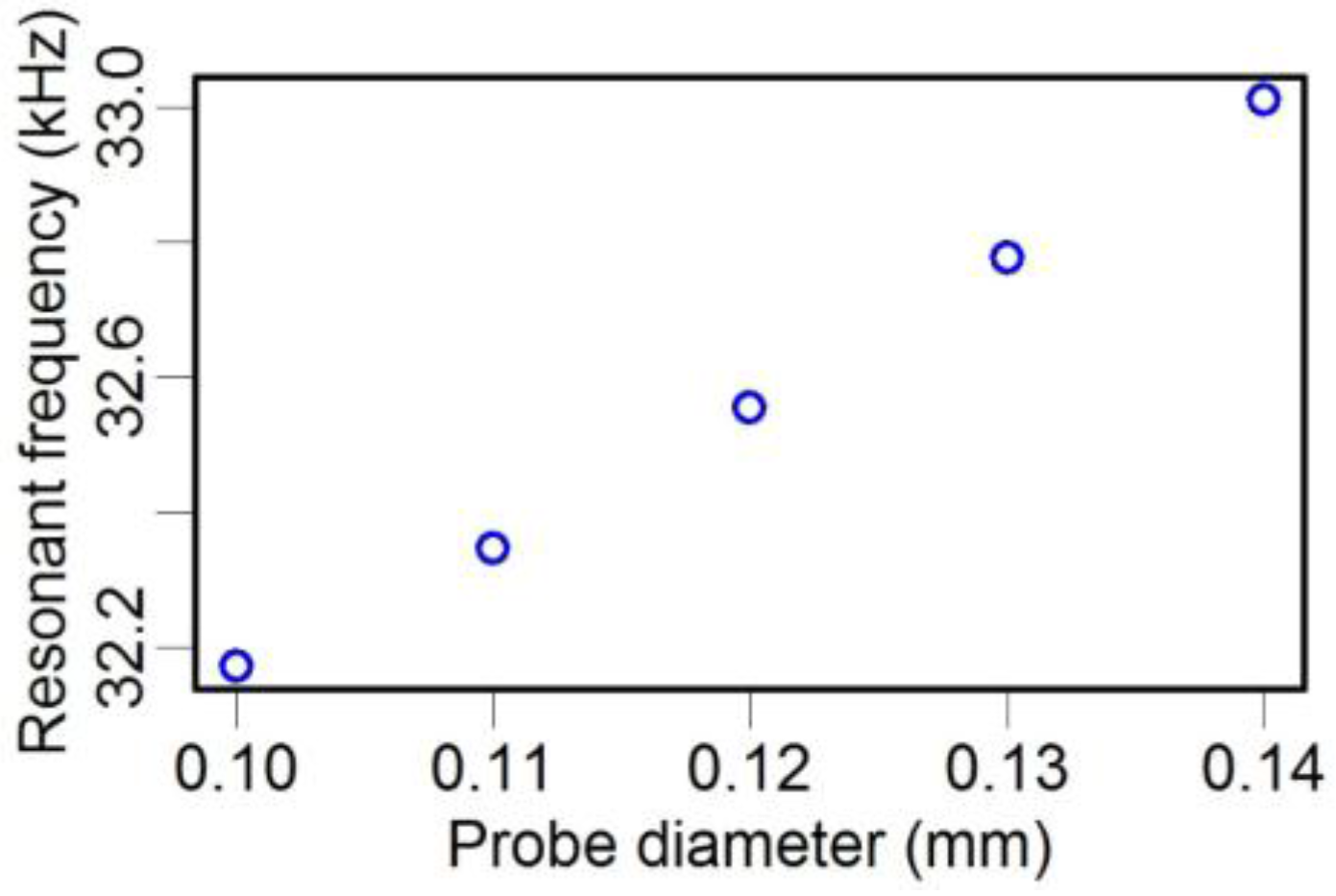
| Young’s Modulus of the Probe (GPa) * | Resonance Frequency (Hz) | Young’s Modulus of the Epoxy Resin (GPa) # | Resonance Frequency (Hz) |
|---|---|---|---|
| 411 | 32,200 | 20 | 32,214 |
| 200 | 32,192 | 10 | 32,200 |
| 78 | 32,113 | 6 | 32,186 |
| 10 | 32,056 | 2 | 32,175 |
5.2. Parameters Affecting the Spatial and the Force Resolutions of the TF-Probe
| Probe Radii (nm) | Force Range (nm) | Probe Length (mm) | Force Range (nm) | Q Factor | Force Range (nm) |
|---|---|---|---|---|---|
| 100 | 0.4 | 0.5 | 6.0 | 100 | 2.0 |
| 500 | 1.3 | 1.0 | 7.0 | 500 | 4.0 |
| 1000 | 2.0 | 1.5 | 10.5 | 3000 | 7.0 |
| 5025 | 6.0 | - | - | - | - |
| Probe Length (mm) | Oscillation Amplitude Ratio |
|---|---|
| 0.5 | 1.2 |
| 1.0 | 1.5 |
| 1.5 | 3.8 |
| 2.0 | 4.9 |
5.3. Comparison between FEM and Beam Theory
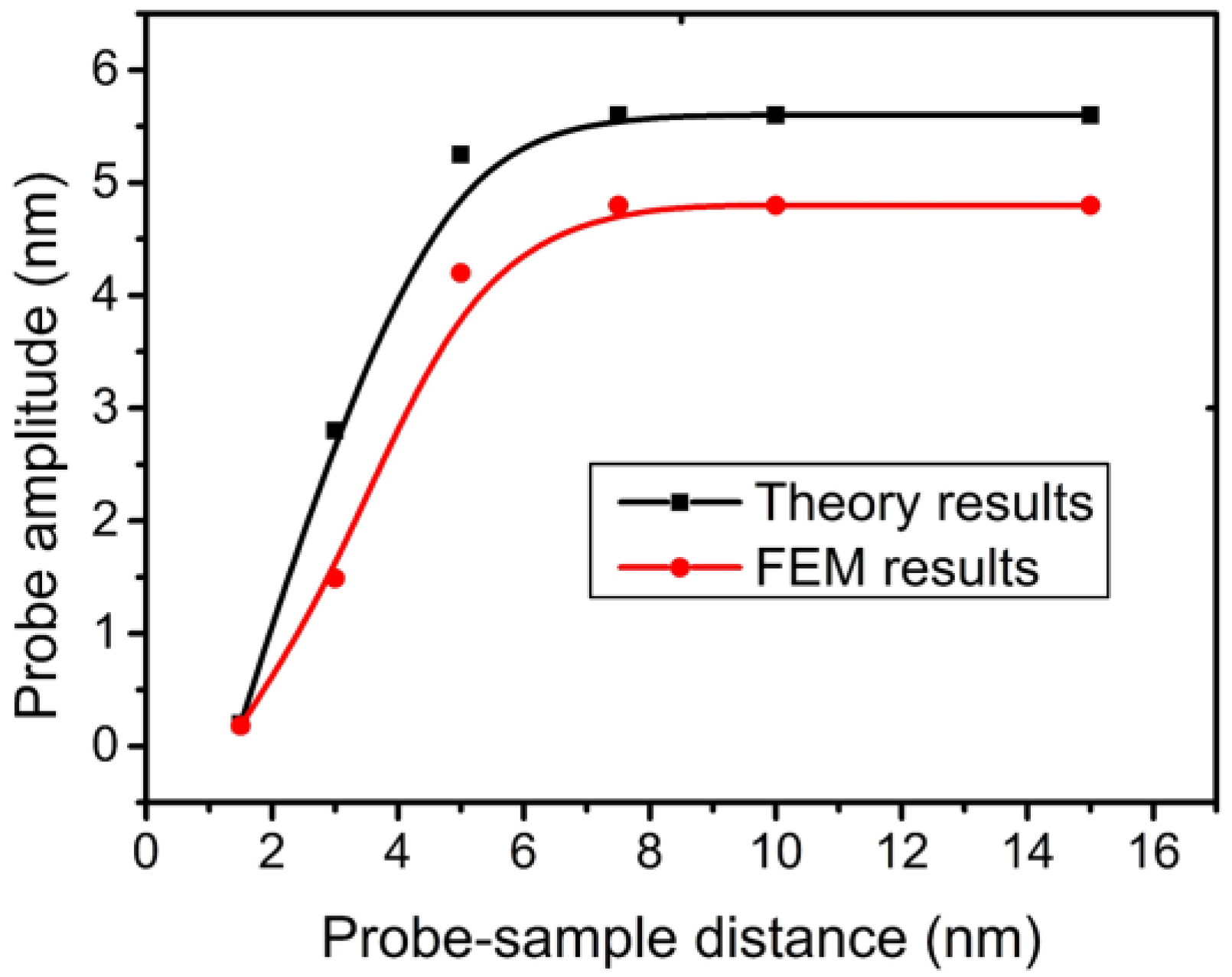
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ash, E.; Nicholls, G. Super-resolution aperture scanning microscope. Nature 1972, 237, 510–512. [Google Scholar] [CrossRef] [PubMed]
- Pohl, D.W.; Denk, W.; Lanz, M. Optical stethoscopy: Image recording with resolution λ/20. Appl. Phys. Lett. 1984, 44, 651–653. [Google Scholar] [CrossRef]
- Tarun, A.; Hayazawa, N.; Kawata, S. Tip-enhanced Raman spectroscopy for nanoscale strain characterization. Anal. Bioanal. Chem. 2009, 394, 1775–1785. [Google Scholar] [CrossRef] [PubMed]
- Webster, S.; Batchelder, D.; Smith, D. Submicron resolution measurement of stress in silicon by near-field Raman spectroscopy. Appl. Phys. Lett. 1998, 72, 1478–1480. [Google Scholar] [CrossRef]
- Gouadec, G.; Colomban, P. Raman Spectroscopy of nanomaterials: How spectra relate to disorder, particle size and mechanical properties. Prog. Cryst. Growth Charact. Mater. 2007, 53, 1–56. [Google Scholar] [CrossRef]
- Pezzotti, G. In situ study of fracture mechanisms in advanced ceramics using fluorescence and Raman microprobe spectroscopy. J. Raman Spectros. 1999, 30, 867–875. [Google Scholar] [CrossRef]
- Wermelinger, T.; Charpentier, C.; Yüksek, M.D.; Spolenak, R. Measuring stresses in thin metal films by means of Raman microscopy using silicon as a strain gage material. J. Raman Spectrosc. 2009, 40, 1849–1857. [Google Scholar] [CrossRef]
- Hecht, B.; Bielefeldt, H.; Inouye, Y.; Pohl, D.W.; Novotny, L. Facts and artifacts in near-field optical microscopy. J. Appl. Phys. 1997, 81, 2492–2498. [Google Scholar] [CrossRef]
- Cen, H.; Kang, Y.; Lei, Z.; Qin, Q.; Qiu, W. Micromechanics analysis of Kevlar-29 aramid fiber and epoxy resin microdroplet composite by Micro-Raman spectroscopy. Compos. Struct. 2006, 75, 532–538. [Google Scholar] [CrossRef]
- Rasmussen, A.; Deckert, V. New dimension in nano-imaging: breaking through the diffraction limit with scanning near-field optical microscopy. Anal. Bioanal. Chem. 2005, 381, 165–172. [Google Scholar] [CrossRef] [PubMed]
- Longo, G.; Girasole, M.; Cricenti, A. Implementation of a bimorph-based aperture tapping-SNOM with an incubator to study the evolution of cultured living cells. J. Microsc. 2008, 229, 433–439. [Google Scholar] [CrossRef] [PubMed]
- Zweyer, M.; Troian, B.; Spreafico, V.; Prato, S. SNOM on cell thin sections: observation of Jurkat and MDAMB453 cells. J. Micros. 2008, 229, 440–446. [Google Scholar] [CrossRef] [PubMed]
- Reddick, R.C.; Warmack, R.J.; Ferrell, T.L. New form of scanning optical microscopy. Phys. Rev. B 1989, 39, 767–770. [Google Scholar] [CrossRef]
- Moerner, E.; Plakhotnik, T.; Irngartner, T.; Wild, U.P.; Pohl, D.W.; Hecht, B. Near-field optical spectroscopy of individual molecules in solids. Phys. Rev. Lett. 1994, 73, 2764–2767. [Google Scholar] [CrossRef] [PubMed]
- Betzig, E.; Finn, P.L.; Weiner, J.S. Combined shear force and near-field scanning optical microscopy. Appl. Phys. Lett. 1992, 60, 2484–2486. [Google Scholar] [CrossRef]
- Toledo-Crow, R.; Yang, P.C.; Chen, Y.; Vaez-lravani, M. Near-field differential scanning optical microscope with atomic force regulation. Appl. Phys. Lett. 1992, 60, 2957–2959. [Google Scholar] [CrossRef]
- Shelimov, K.B.; Davydov, D.N.; Moskovits, M. Dynamics of a piezoelectric tuning fork/optical fiber assembly in a near-field scanning optical microscope. Rev. Sci. Instrum. 2000, 71, 437–443. [Google Scholar] [CrossRef]
- Karrai, K.; Grober, R.D. Piezoelectric tip-sample distance control for near-field optical microscopes. Appl. Phys. Lett. 1995, 66, 1842–1844. [Google Scholar] [CrossRef]
- Ruiter, A.G.T.; Veerman, J.A.; van der Werf, K.O.; van Hulst, N.F. Dynamic behavior of tuning fork shear-force feedback. Appl. Phys. Lett. 1997, 71, 28–30. [Google Scholar] [CrossRef]
- Okajima, T.; Hirotsu, S. Study of shear force between glass microscope and mica surface under controlled humidity. Appl. Phys. Lett. 1997, 71, 545–548. [Google Scholar] [CrossRef]
- Atia, W.A.; Davis, C.C. A phase-locked shear-force microscope for distance regulation in near-field optical microscopy. Appl. Phys. Lett. 1997, 70, 405–410. [Google Scholar] [CrossRef]
- Schmidt, J.U.; Bergander, H.; Eng, L.M. Shear force interaction in the viscous damping regime studied at 100 pN force resolution. J. Appl. Phys. 2000, 87, 3108–3112. [Google Scholar] [CrossRef]
- Karrai, K.; Tiemann, I. Interfacial shear force microscopy. Phys. Rev. B 2000, 62, 13174–13181. [Google Scholar] [CrossRef]
- Froehlich, F.F.; Milster, T.D. Minimum detectable displacement in near-field scanning optical microscopy. Appl. Phys. Lett. 1994, 65, 2254–2256. [Google Scholar] [CrossRef]
- Wei, C.; Chun, X.; Wei, P.K.; Fann, W. Direct measurements of the true vibrational amplitudes in shear force microscopy. Appl. Phys. Lett. 1995, 67, 3835–3837. [Google Scholar] [CrossRef]
- Gregor, M.J.; Blome, P.G.; Schofer, J.; Ulbrich, R.G. Probe-surface interaction in near-field optical microscopy: The nonlinear bending force mechanism. Appl. Phys. Lett. 1996, 68, 307–309. [Google Scholar] [CrossRef]
- Gao, F.; Li, X.; Wang, J.; Fu, Y. Dynamic behavior of tuning fork shear-force structures in a SNOM system. Ultramicroscopy 2014, 142, 10–23. [Google Scholar] [CrossRef] [PubMed]
- Yoo, J.H.; Lee, J.H.; Yim, S.Y.; Park, S.H.; Ro, M.D.; Kim, J.H.; Park, I.S.; Cho, K. Enhancement of shear-force sensitivity using asymmetric response of tuning forks for nearfield scanning optical microscopy. Opt. Express 2004, 12, 4467–4475. [Google Scholar] [CrossRef] [PubMed]
- Durkan, C.; Shvets, I.V. Investigation of the physical mechanisms of shear-force imaging. J. Appl. Phys. 1996, 80, 5659–5664. [Google Scholar] [CrossRef]
- Davy, S.; Spajer, M.; Courjon, D. Influence of the water layer on the shear force damping in near-field microscopy. Appl. Phys. Lett. 1998, 73, 2594–2596. [Google Scholar] [CrossRef]
- Brunner, R.; Marti, O.; Hollricher, O. Influence of environmental conditions on shear—force distance control in near-field optical microscopy. J. Appl. Phys. 1999, 86, 7100–7106. [Google Scholar] [CrossRef]
- Bernal, M.P.; Weible, F.M.; Boillat, P.Y.; Lambelet, P. Theoretical and experimental study of the forces between different SNOM probes and chemically treated AFM cantilevers. IEEE Proc. 2000, 88, 1460–1470. [Google Scholar] [CrossRef]
- Naber, A.; Maas, H.J.; Razavi, K.; Fischer, U.C. Dynamic force distance control suited to various probes for scanning near-field optical microscopy. Rev. Sci. Instrum. 1999, 70, 3955–3961. [Google Scholar] [CrossRef]
- Ohkubo, S.; Yamazaki, S.; Takayanagi, A.; Otani, Y.; Umeda, N. Shear-force detection by reusable quartz tuning fork without external vibration. Opt. Rev. 2003, 10, 128–130. [Google Scholar] [CrossRef]
- Giaccari, P.; Sqalli, O.; Limberger, H.G. Sub-pico-Newton shear-force feedback system in air and liquid for scanning probe microscopy. Rev. Sci. Instrum. 2004, 75, 3031–3033. [Google Scholar] [CrossRef]
- Lee, S.; Moon, Y.; Yoon, J.; Chung, H. Analytical and finite element method design of quartz tuning fork resonators and experimental test of samples manufactured using photolithography 1—Significant design parameters affecting static capacitance C0. Vacuum 2004, 75, 57–69. [Google Scholar] [CrossRef]
- Friedt, J.M.; Carry, É.; Sadani, Z.; Serio, B.; Wilm, M.; Ballandras, S. Quartz tuning fork oscillation amplitude as a limitation of spatial resolution of shear force microscopes. In Proceedings of the 19th EFTF, Besançon, France, 21–24 March, 2005; pp. 615–620.
- Vlassov, S.; Polyakov, B.; Dorogin, L.M.; Lohmus, A.; Romanov, A.E.; Kink, I.; Gnecco, E.; Lohmus, R. Real-time manipulation of gold nanoparticles inside a scanning electron microscope. Sol. State Comm. 2011, 151, 688–692. [Google Scholar] [CrossRef]
- Dorogin, L.M.; Vlassov, S.; Polykov, B.; Antsov, M.; Lohmus, R.; Kink, I.; Romanov, A.E. Real-time manipulation of ZnO nanowires on a flat surface employed for tribological measurements: Experimental methods and modeling. Phys. Status Solidi B 2013, 250, 305–317. [Google Scholar] [CrossRef]
- Andzane, J.; Poplausks, R.; Prikulis, J.; Lohmus, R.; Vlassov, S.; Kubatkin, S.; Erts, D. Application of tuning fork sensors for in-situ studies of dynamic force interactions inside scanning and transmission electron microscopes. Mater. Sci. 2012, 18, 197–201. [Google Scholar] [CrossRef]
- Kosmaca, J.; Andzane, J.; Prikulis, J.; Biswas, S.; Holmes, J.D.; Erts, D. Application of a nanoelectromechanical mass sensor for the manipulation and characterissation graphene and graphite flakes. Sci. Adv. Mater. 2014, 6, 1–6. [Google Scholar]
- Fu, Y.; Pedrini, G.; Li, X. Interferometric dynamic measurement: techniques based on high-speed imaging or a single photodetector. Sci. World J. 2014, 2014, 1–14. [Google Scholar]
- Rice, J.A.; Rice, A.C. Young’s modulus and thermal expansion of filled cyanate ester and epoxy resins. IEEE Trans. Appl. Supercond. 2009, 19, 2371–2374. [Google Scholar] [CrossRef]
- Kabir, A. Vibration Damping Property and Flexural Fatigue Behavior of Glass/Epoxy/Nanoclay Composites. Masters Thesis, Concordia University, Quebec, 15 September 2013. [Google Scholar]
- Karrai, K. Lecture notes on shear and friction force detection with quartz tuning forks. In Proceedings of the Work presented at the “Ecole Thématique du CNRS” on near-field optics, La Londe les Maures, France, March 2000; pp. 1–23.
- Zhang, W.; Turner, K.L. Pressure-Dependent Damping Characteristics of Micro Silicon Beam Resonators for Different Resonant Modes. In Proceedings of the IEEE Sensors Conference, Irvine, CA, 31 October–3 November 2005; pp. 357–360.
- Engineer’s Handbook. Available online: http://www.engineershandbook.com/Tables/ frictioncoefficients.htm (accessed on 20 July 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, F.; Li, X. Research on the Sensing Performance of the Tuning Fork-Probe as a Micro Interaction Sensor. Sensors 2015, 15, 24530-24552. https://doi.org/10.3390/s150924530
Gao F, Li X. Research on the Sensing Performance of the Tuning Fork-Probe as a Micro Interaction Sensor. Sensors. 2015; 15(9):24530-24552. https://doi.org/10.3390/s150924530
Chicago/Turabian StyleGao, Fengli, and Xide Li. 2015. "Research on the Sensing Performance of the Tuning Fork-Probe as a Micro Interaction Sensor" Sensors 15, no. 9: 24530-24552. https://doi.org/10.3390/s150924530
APA StyleGao, F., & Li, X. (2015). Research on the Sensing Performance of the Tuning Fork-Probe as a Micro Interaction Sensor. Sensors, 15(9), 24530-24552. https://doi.org/10.3390/s150924530





