Optimizing the De-Noise Neural Network Model for GPS Time-Series Monitoring of Structures
Abstract
:1. Introduction
2. Identification Models
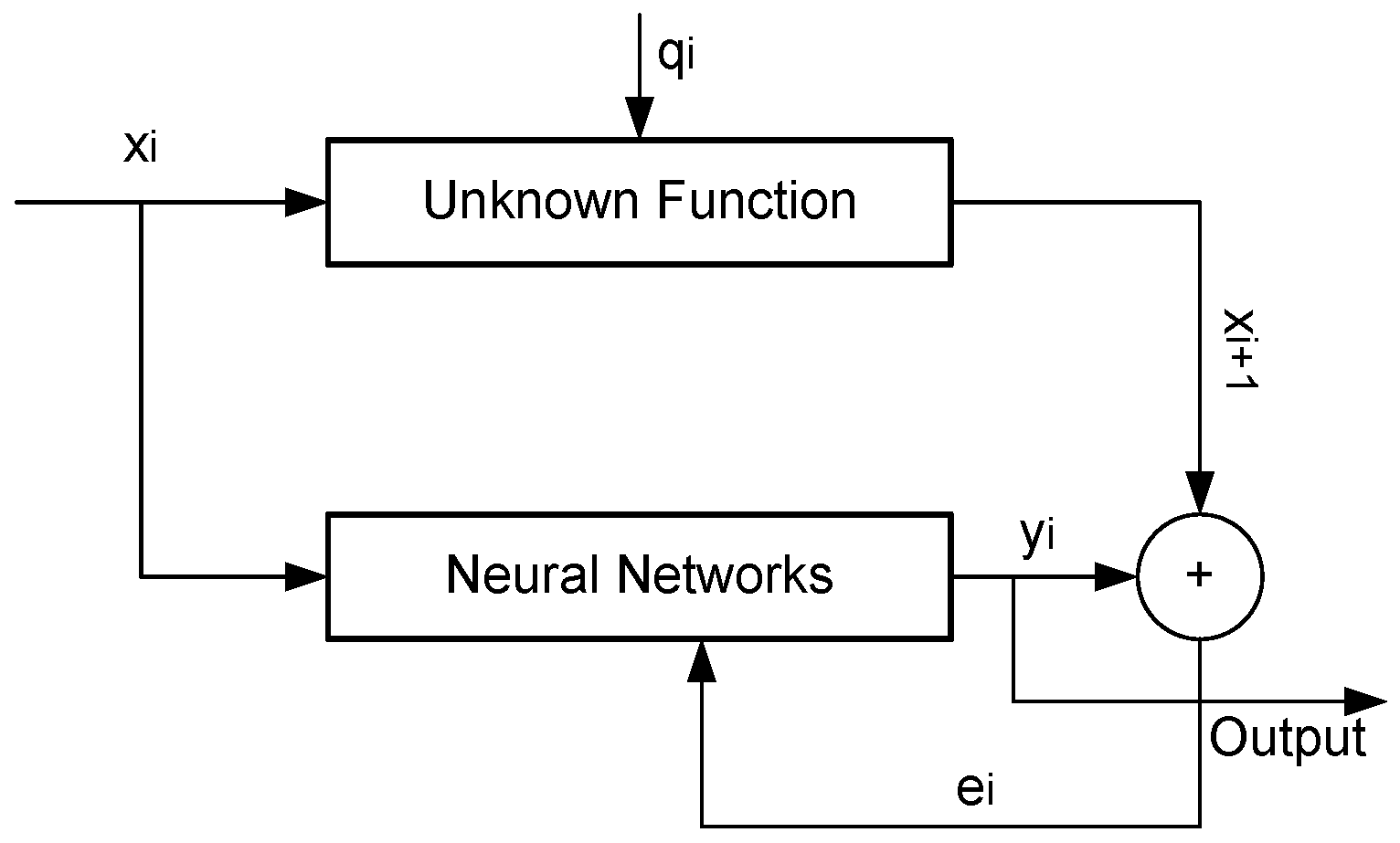
2.1. Back-Propagation Neural Networks (BPN)
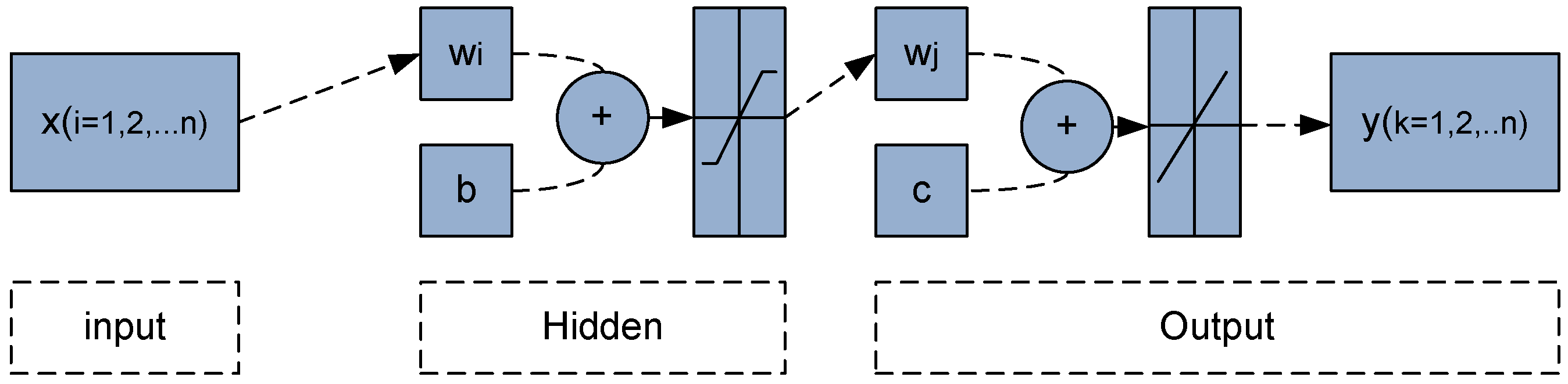
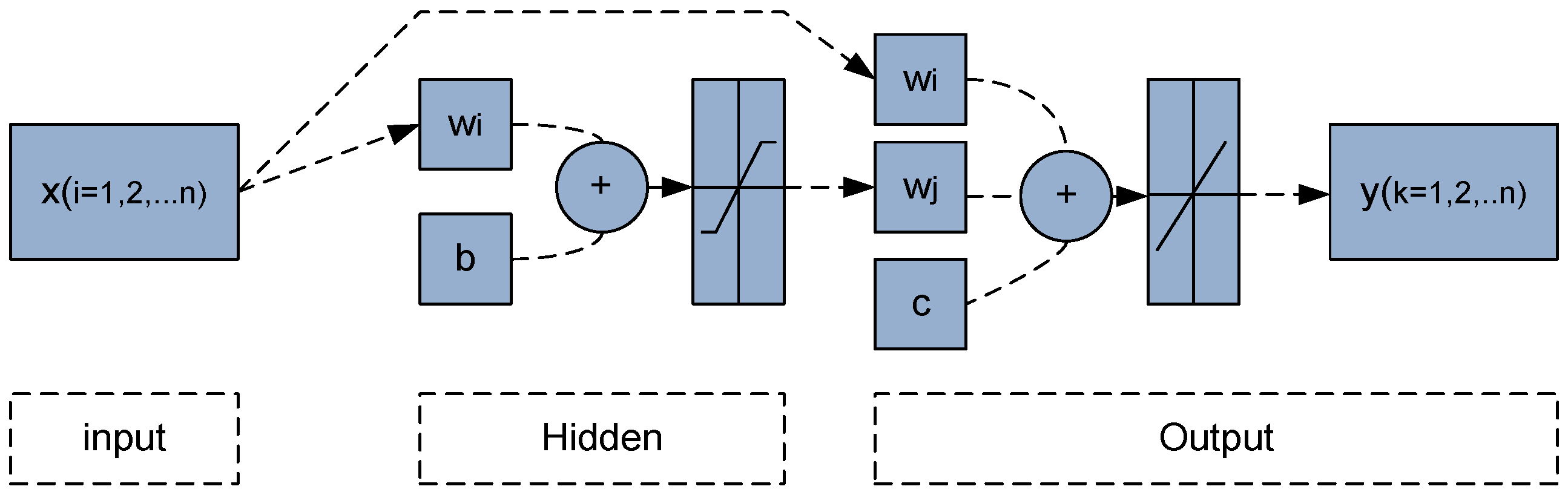
2.2. Cascade- Forward Back-Propagation Neural Network (CFN)
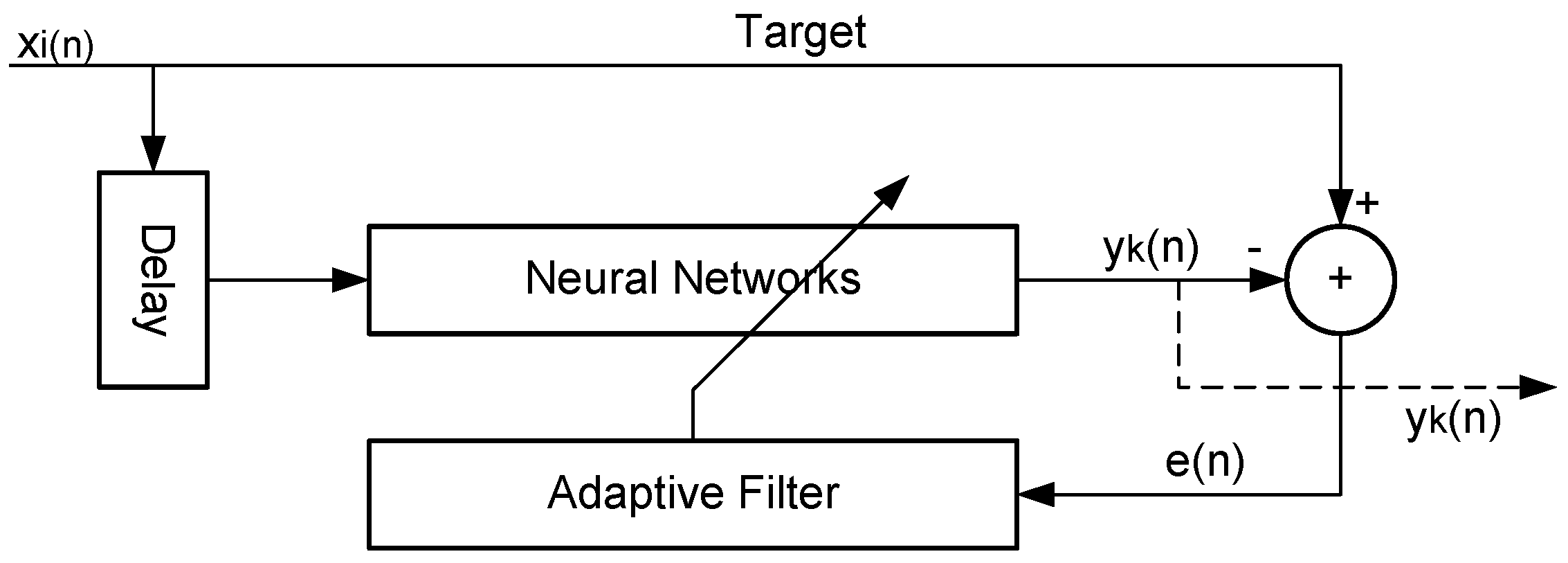
2.3. Adaptive Filter Neural Network (ADFN)
2.4. Extended Kalman Filter Neural Network (EKFN)
3. Results and Discussions
3.1. Simulation Noise Results
| Models | BPN | CFN | ADFN | EKFN |
|---|---|---|---|---|
| MAE | 0.0093 | 8.65 × 10−4 | 0.0024 | 0.0037 |
| MSE | 1.22 × 10−4 | 1.206 × 10−5 | 7.98 × 10−6 | 3.174 × 10−5 |
| R-Square | 0.987 | 0.986 | 0.997 | 0.992 |
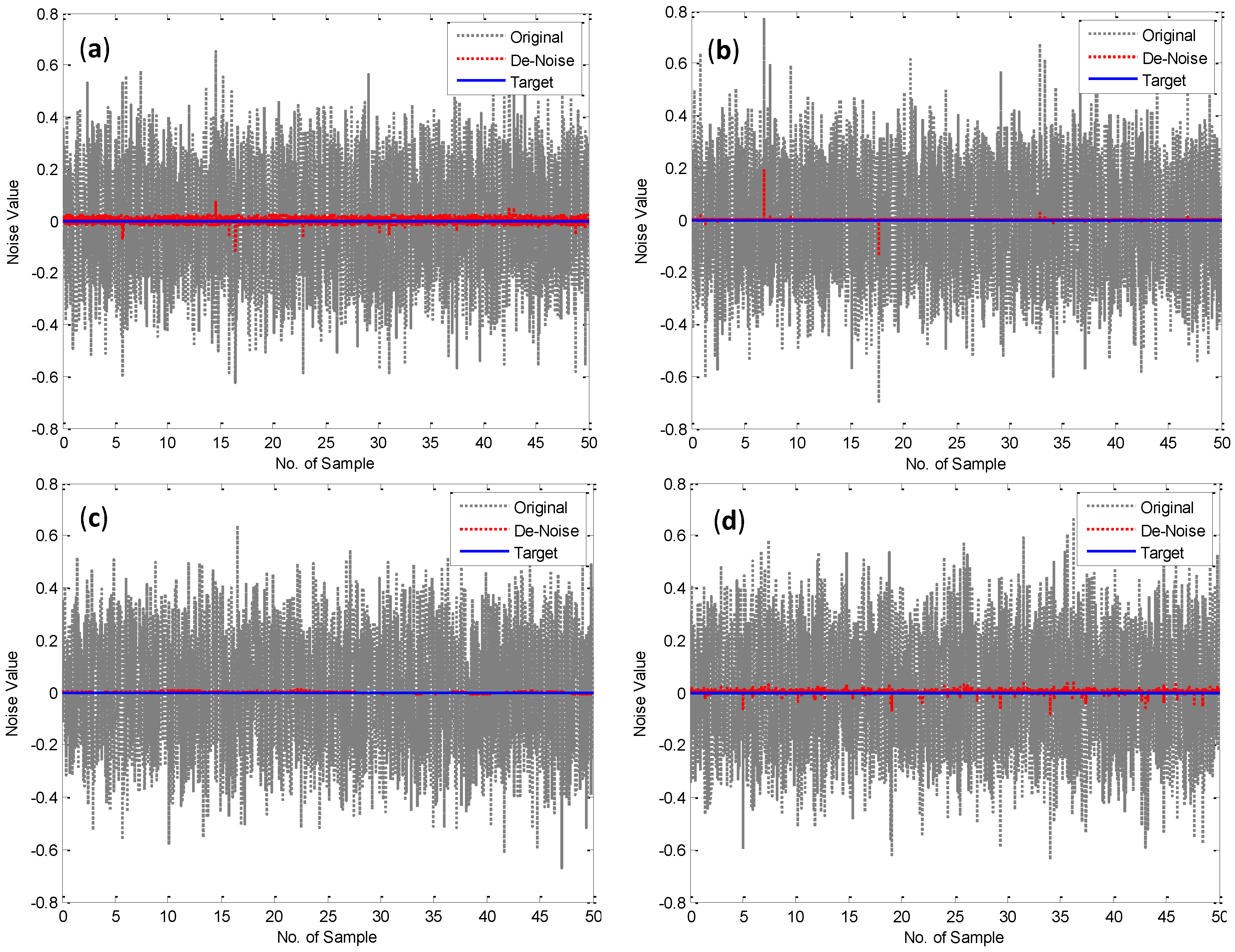
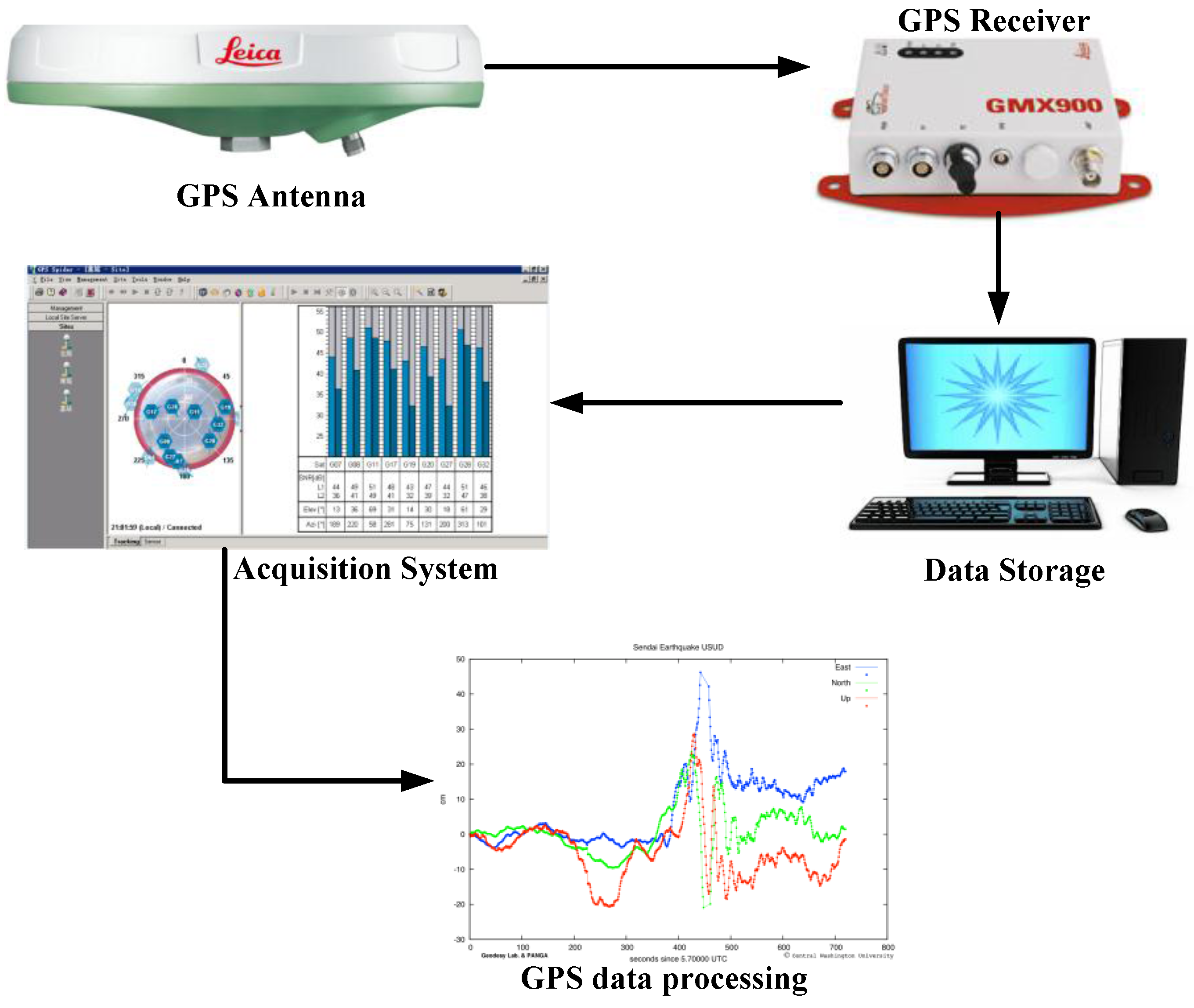
3.2. GPS-Bridge Movement Application: Case Study

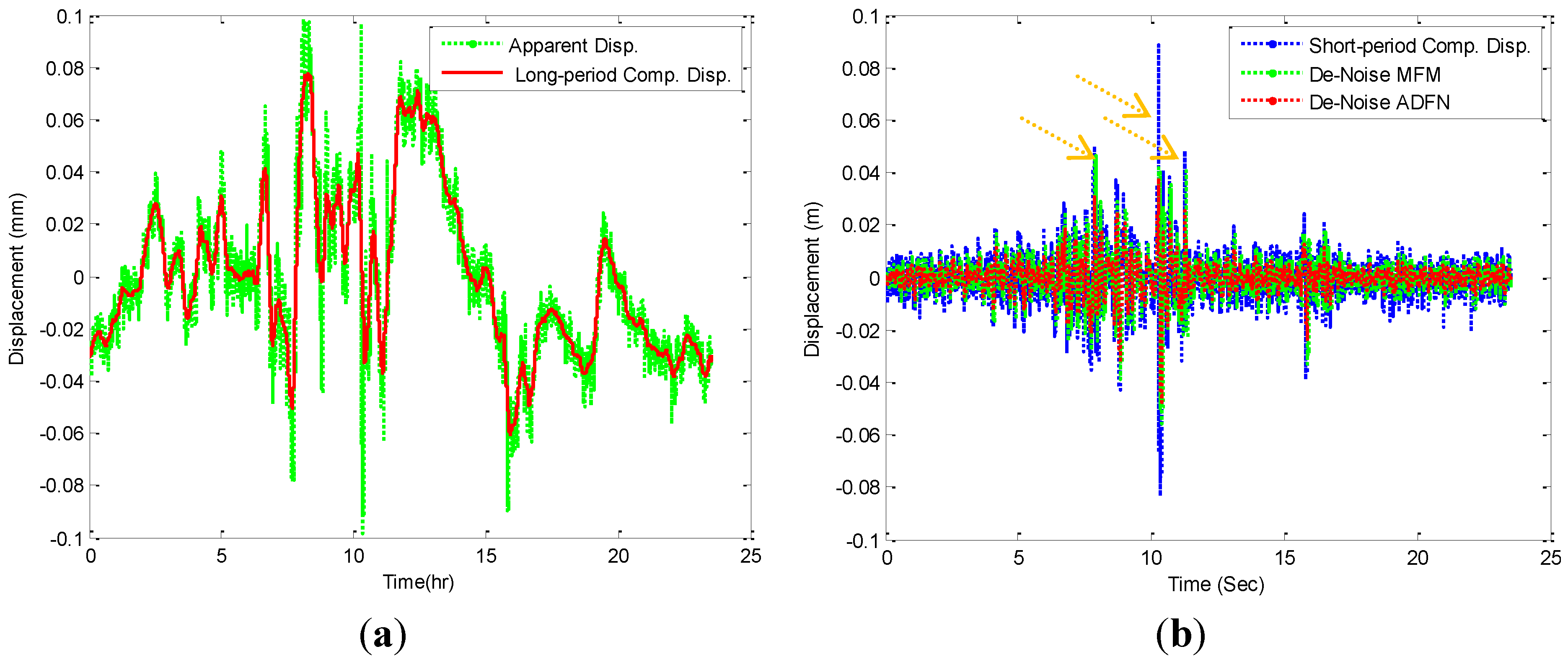
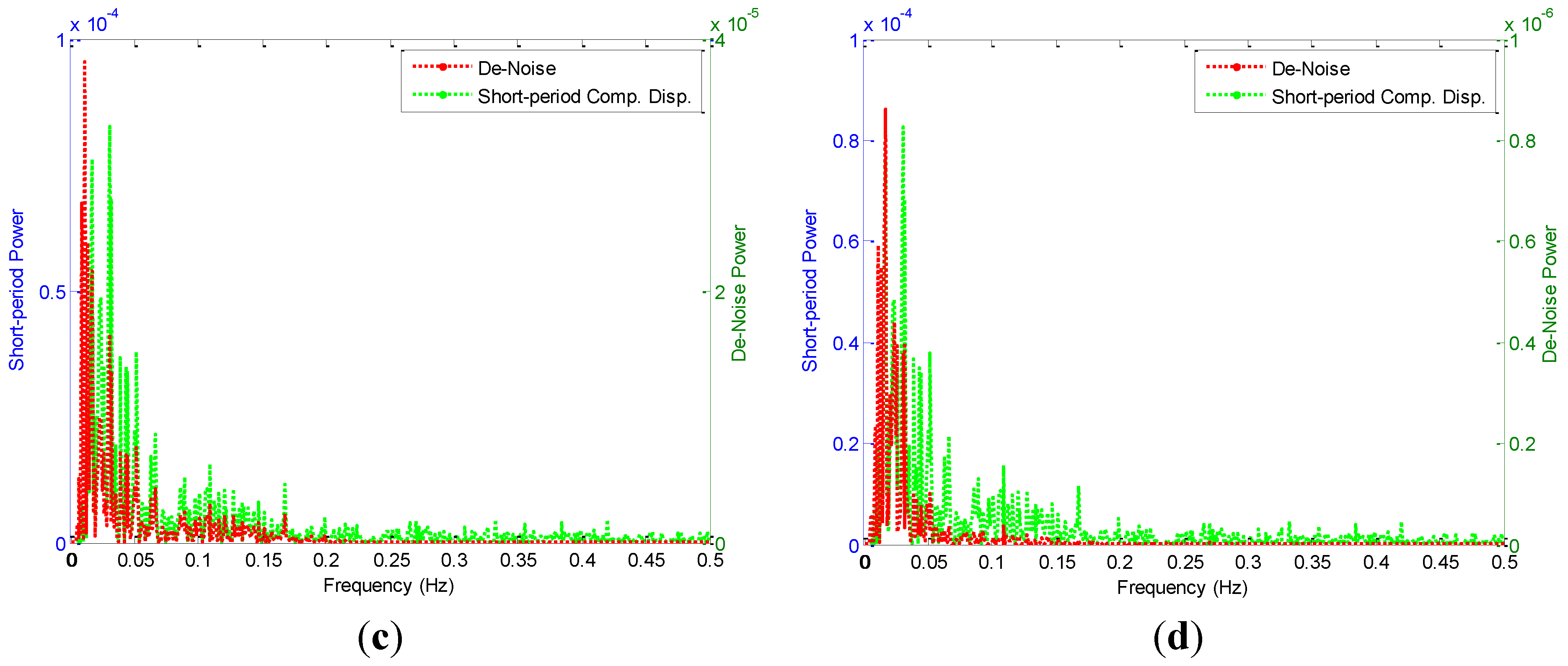
| Parameter | Original Signal | MFM Model | ADFN Model |
|---|---|---|---|
| MAE (mm) | 5.789 × 10−3 | 5.119 × 10−3 | 4.018 × 10−3 |
| MSE (mm) | 7.575 × 10−5 | 5.872 × 10−5 | 3.742 × 10−5 |
| STD (mm) | 8.703 × 10−3 | 7.663 × 10−3 | 6.117 × 10−3 |
| Absolute Max (mm) | 8.861 × 10−2 | 5.611 × 10−2 | 4.773 × 10−2 |
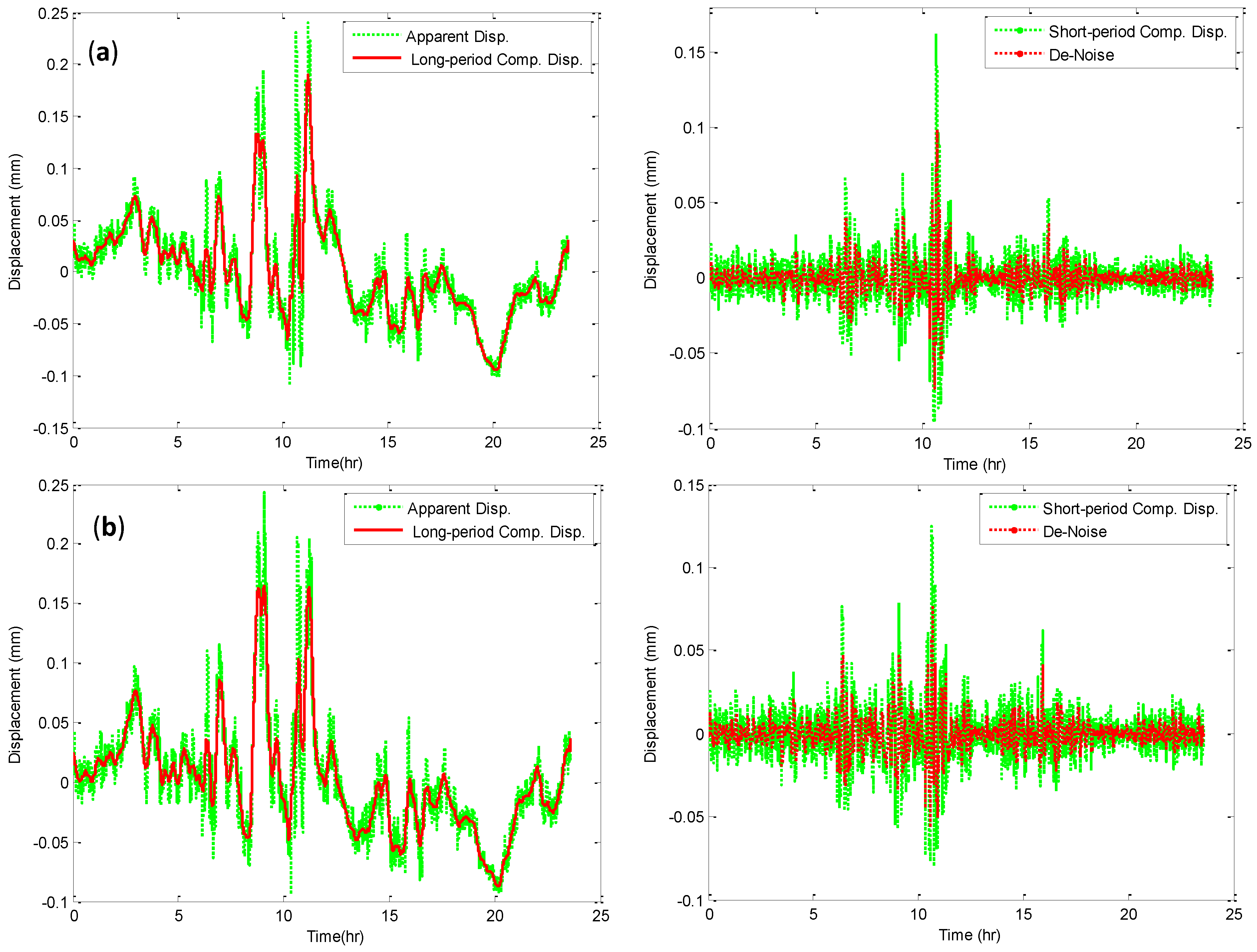
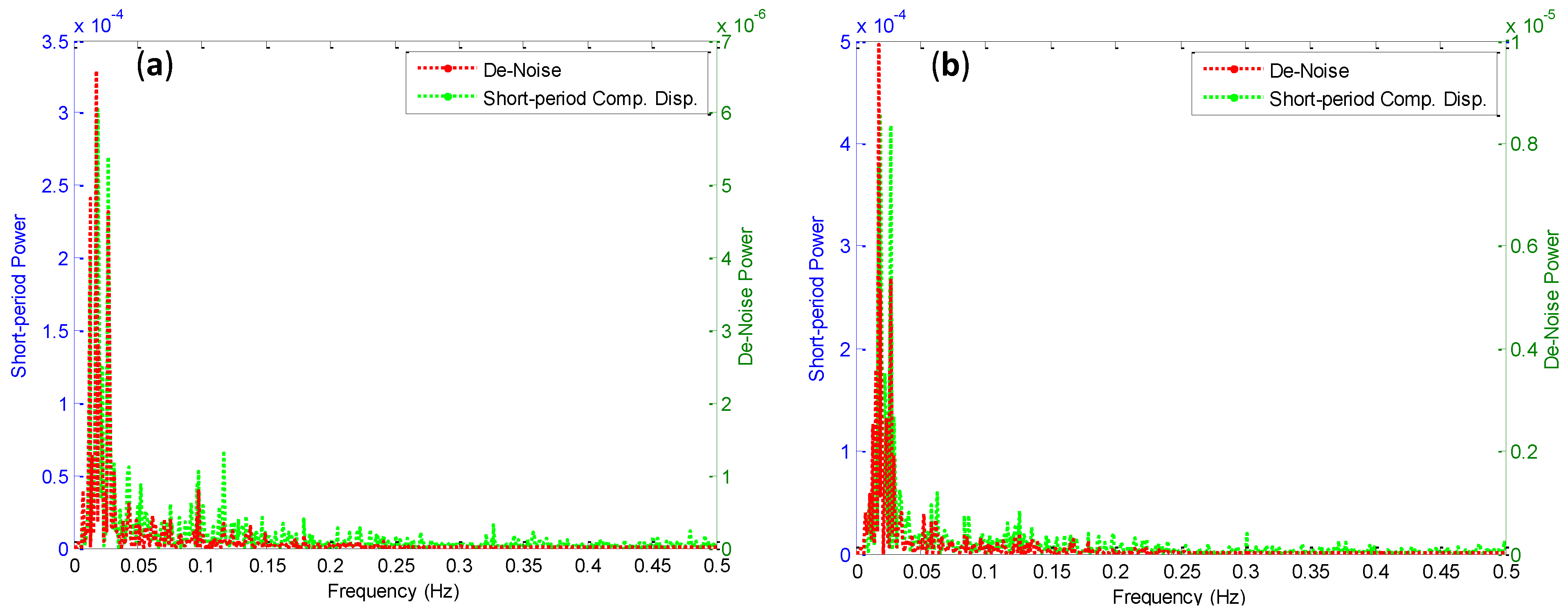
4. Conclusions
- (1)
- The multi-step filtering procedure can be constrained to de-noise the noisy measurements of the oscillations of structures, and to determine its oscillation amplitude and modal frequency. In addition, it is concluded that the ADFN is the best model and thus suggested for use to de-noise the GPS measurements. In addition, the ADFN model is observed to be more effective and accurate than MFM model for de-noising short-period components of displacements of GPS real monitoring data in time and frequency domains.
- (2)
- The apparent displacement measurements contain noises that can be considered as vibration and background noises. Moreover, the ADFN model increased the accuracy of short-period displacement by 83.3% in the x and y directions and by 93.8% in the z direction.
- (3)
- The de-noised short-period displacement component of the measurements has decreased the power spectrum density to 98%. This means that the noise has high effect on the high and low frequency vibration modes of structures. From the frequency modes calculations, it is assumed that the low frequency modes of the short-period displacement component values are between 0–0.2 Hz.
- (4)
- The GPS measurements with a sampling rate of 1.0 Hz may in fact underestimate the amplitude of displacement components, this problem, however, can be expected to overcome with the modern high-frequency GPS.
- (5)
- The de-noised short-period displacement component based on NN predictive models is expected to have significant implications in the SHM and the design of structures in the low-frequency content.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Moschas, F.; Stiros, S. Measurement of the dynamic displacements and of the modal frequencies of a short-span pedestrian bridge using GPS and an accelerometer. Eng. Struct. 2011, 33, 10–17. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Noise characteristics of high-frequency, short-duration GPS records from analysis of identical, collocated instruments. Measurement 2013, 46, 1488–1506. [Google Scholar] [CrossRef]
- Gorski, P. Investigation of dynamic characteristic of tall industrial chimney based on GPS measurements using random decrement method. Eng. Struct. 2015, 83, 30–49. [Google Scholar] [CrossRef]
- Yia, T.H.; Lia, H.N.; Gub, M. Experimental assessment of high-rate GPS receivers for deformation monitoring of bridge. Measurement 2013, 46, 420–432. [Google Scholar] [CrossRef]
- Jeon, H.; Shin, J.U.; Myung, H. The displacement estimation error back-propagation (DEEP) method for a multiple structural displacement monitoring system. Meas. Sci. Technol. 2013. [Google Scholar] [CrossRef]
- Psimoulis, P.; Ghilardi, M.; Fouache, E.; Stiros, S. Subsidence and evolution of the Thessaloniki plain, Greece, based on historical leveling and GPS data. Eng. Geol. 2007, 90, 55–70. [Google Scholar] [CrossRef]
- Gikas, V. Three-dimensional laser scanning for geometry documentation and construction management of highway tunnel during excavation. Sensors 2012, 12, 11249–11270. [Google Scholar] [CrossRef] [PubMed]
- Kaloop, M.; Kim, D. De-noising of GPS structural monitoring observation error using wavelet analysis. Geomat. Nat. Hazard. Risk 2014. [Google Scholar] [CrossRef]
- Oludolapo, O.A.; Jimoh, A.A.; Kholopane, P.A. Comparing performance of MLP and RBF neural network models for predicting South Africa’s energy consumption. J. Energ. South. Afr. 2012, 23, 40–46. [Google Scholar]
- Binti-Idris, A.; Bin-Rahim, R.F.; Ali, D. The effect of additive white gaussian noise and multipath rayleigh fading on ber statistic in digital cellular network. In Proceedings of the International RF and Microwave Conference, Putrajaya, Malaysia, 12–14 September 2006.
- Haykin, S. Kalman Filtering and Neural Networks; John Wiley & Sons, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Wang, J.W.; Wang, J.; Sinclair, D.; Watts, L. Designing a neural network for GPS/INS/PL integration. In Proceedings of the International Global Navigation Satellite System Society IGNSS Symposium, Sydney, Australia, 17–21 July 2006.
- Zhang, X.; Liu, Y.; Yang, M.; Zhang, T.; Young, A.; Li, X. Comparative study of four time series methods in forecasting typhoid fever incidence in China. PLoS ONE 2013. [Google Scholar] [CrossRef] [PubMed]
- Jwo, D.; Huang, H. Neural network aided adaptive extended Kalman filtering approach for DGPS positioning. J. Navig. 2004, 57, 449–463. [Google Scholar] [CrossRef]
- Kaloop, M.; Kim, D. GPS-structural health monitoring of a long span bridge using neural network adaptive filter. Surv. Rev. 2014, 46, 7–14. [Google Scholar] [CrossRef]
- Akyılmaz, O.; Çelik, R.N.; Apaydın, N.; Ayan, T. GPS monitoring of the Fatih Sultan Mehmet suspension bridge by using assessment methods of neural network. Spat. Inf. Sci. 2004, 34, 702–707. [Google Scholar]
- Kaloop, M.R.; Hu, J.W. Stayed-cable bridge damage detection and localization based on accelerometer health monitoring measurements. Shock Vib. 2015, in press. [Google Scholar]
- Pantazis, G.; Alevizakou, E.G. The use of artificial neural networks in predicting vertical displacements of structures. Int. J. Appl. Sci. Technol. 2013, 3, 1–8. [Google Scholar]
- Chen, Y.; Akutagawa, M.; Katayama, M.; Zhang, Q.; Kinouchi, Y. Neural network based EEG denoising. In Proceedings of the 30th Annual International IEEE EMBS Conference, Vancouver, BC, Canada, 20–24 August 2008.
- El-Rabbany, A.; El-Diasty, M. An efficient neural network model for de-noising of MEMS-based inertial data. J. Navig. 2004, 57, 407–415. [Google Scholar] [CrossRef]
- Malleswarana, M.; Vaidehib, V.; Sivasankari, N. A novel approach to the integration of GPS and INS using recurrent neural networks with evolutionary optimization techniques. Aerosp. Sci. Technol. 2014, 32, 169–179. [Google Scholar] [CrossRef]
- Chen, X.; Shena, C.; Zhang, W.; Tomizuka, M.; Xu, Y.; Chiu, K. Novel hybrid of strong tracking Kalman filter and wavelet neural network for GPS/INS during GPS outages. Measurement 2013, 46, 3847–3854. [Google Scholar] [CrossRef]
- Roy, N.; Ganguli, R. Filter design using radial basis function neural network and genetic algorithm for improved operational health monitoring. Appl. Soft Comput. 2006, 6, 154–169. [Google Scholar] [CrossRef]
- Oliveira, M.A. An application of neural networks trained with kalman filter variants (ekf and ukf) to heteroscedastic time series forecasting. Appl. Math. Sci. 2012, 6, 3675–3686. [Google Scholar]
- Bachir, G.; Habib, M.; Amar, K.; Youcef, L. The GRNN and the RBF Neural Networks for 2D Displacement Field Modelling. Case study: GPS Auscultation Network of LNG reservoir (GL4/Z industrial complex—Arzew, Algeria). Available online: http://www.fig.net/resources/proceedings/fig_proceedings/fig2012/papers/ts01f/TS01F_gourine_mahi_et_al_5684.pdf (accessed on 18 September 2015).
- Goyal, S.; Goyal, G.K. Cascade and feed-forward back-propagation artificial neural network models for prediction of sensory quality of instant coffee flavoured sterilized drink. Can. J. Artif. Intell. Mach. Pattern Recognit. 2011, 2, 78–82. [Google Scholar]
- Mistry, D.; Kulkarni, A.V. Noise cancellation using adaptive filter base on neural networks. ITSI Trans. Electron. Electron. Eng. 2013, 1, 87–91. [Google Scholar]
- Chang, C.L.; Juang, J.C. An adaptive multipath mitigation filter for gnss applications. EURASIP J. Adv. Signal Proc. 2008. [Google Scholar] [CrossRef]
- Alessandri, A.; Cuneo, M.; Pagnan, S.; Sanguineti, M. On the convergence of EKF-based parameters optimization for neural networks. In Proceedings of the 42nd IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003.
- Kaloop, M. Bridge safety monitoring based-GPS technique: Case study Zhujiang Huangpu Bridge. Smart Struct. Syst. 2012, 9, 473–487. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaloop, M.R.; Hu, J.W. Optimizing the De-Noise Neural Network Model for GPS Time-Series Monitoring of Structures. Sensors 2015, 15, 24428-24444. https://doi.org/10.3390/s150924428
Kaloop MR, Hu JW. Optimizing the De-Noise Neural Network Model for GPS Time-Series Monitoring of Structures. Sensors. 2015; 15(9):24428-24444. https://doi.org/10.3390/s150924428
Chicago/Turabian StyleKaloop, Mosbeh R., and Jong Wan Hu. 2015. "Optimizing the De-Noise Neural Network Model for GPS Time-Series Monitoring of Structures" Sensors 15, no. 9: 24428-24444. https://doi.org/10.3390/s150924428
APA StyleKaloop, M. R., & Hu, J. W. (2015). Optimizing the De-Noise Neural Network Model for GPS Time-Series Monitoring of Structures. Sensors, 15(9), 24428-24444. https://doi.org/10.3390/s150924428







