Evaluation of Content-Matched Range Monitoring Queries over Moving Objects in Mobile Computing Environments
Abstract
:1. Introduction
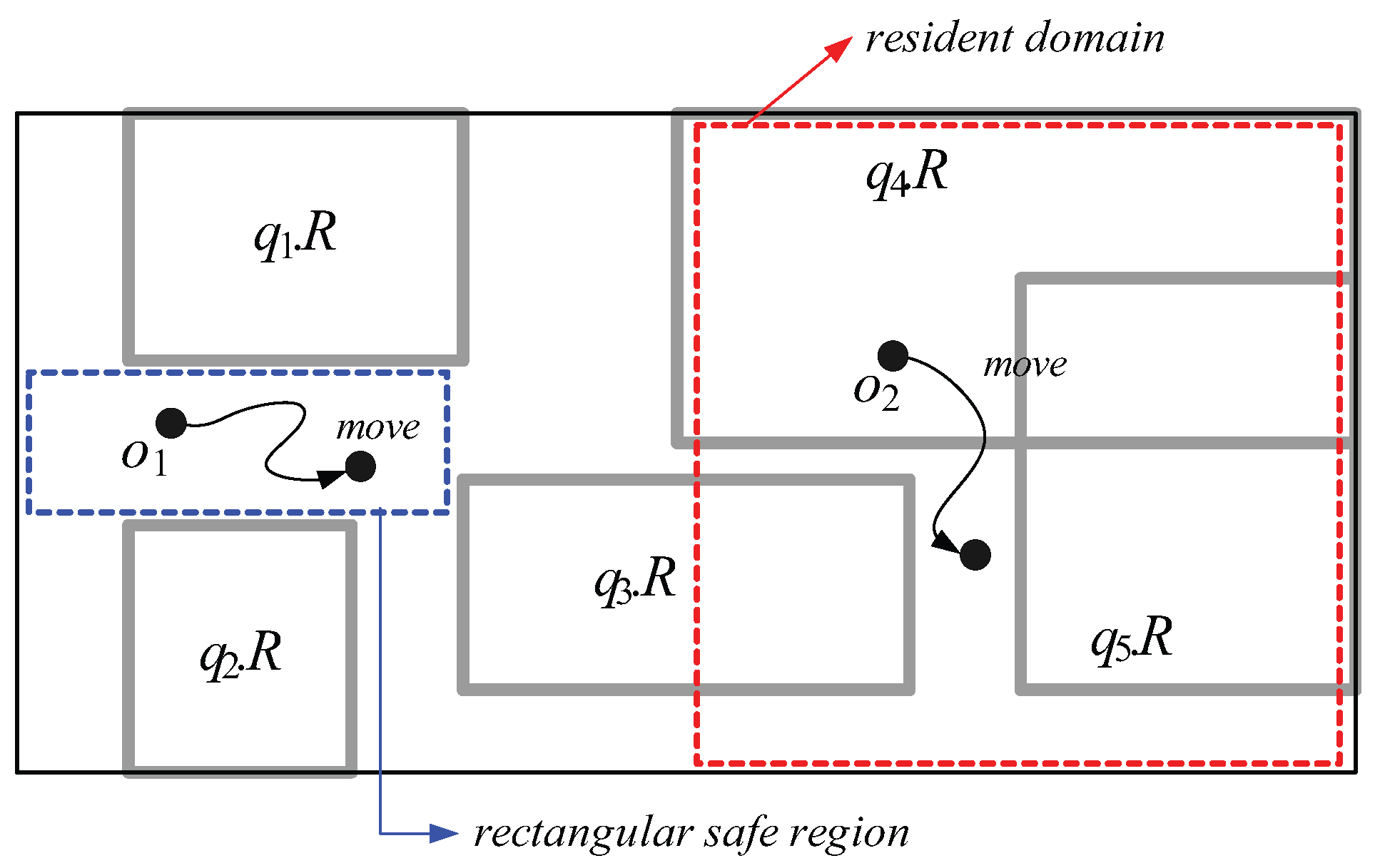
2. Related Work
3. System Overview
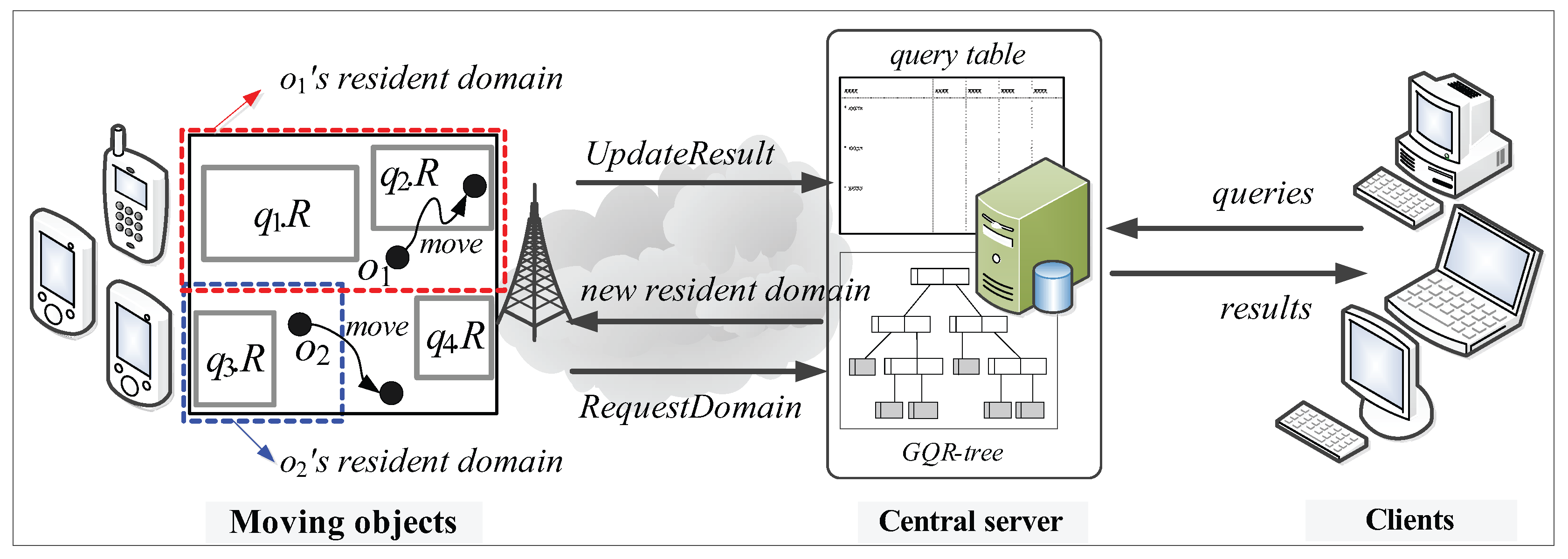
- Moving objects: Each moving object o, which is registered at the server (with its non-spatial attribute values) and is identified by its unique identifier, is capable of sensing its current location (e.g., equipped with a GPS receiver) and has some available (memory and computational) capability . We assume that each moving object o has heterogeneous capability , which indicates the maximum number of (qualified) spatial query ranges it can load and process at a time, and that ≥ θ, where θ is a system parameter that indicates the minimum number of spatial query ranges o should be able to process; thus, a moving object with more powerful capability is assigned a larger resident domain together with a greater number of spatial query ranges. There are two types of location-update messages sent from moving objects to the server: and . The former is for the purpose of receiving a new resident domain, whereas the latter is to let the server update the query result. For example, assuming the moving object in Figure 2 is assigned the blue-dotted rectangle as its resident domain together with spatial query range , it sends the message to the server because it exits its resident domain. On the other hand, assuming the moving object in Figure 2 is assigned the red-dotted rectangle as its resident domain together with spatial query ranges and , it sends the message to the server because it crosses the boundary of .
- Clients: Each geographically distributed client is able to issue multiple CM range monitoring queries over the moving objects registered at the server, and continually receives the up-to-date results of these queries from the server via wireless or high-speed wired connections. Clients do not directly communicate with moving objects; instead, they use the server as an intermediary. Each query q issued by a client is identified by its unique identifier and its spatial query range is assumed to be stationary or quasi-stationary.
- Central server: The server maintains mainly two data structures: a query table (hashed on query identifiers) and the GQR-tree. The query table stores, for each query q, an identifier, a spatial query range , a set of non-spatial values , and the result. The following three main tasks are performed by the server.
- -
- Query registration (or de-registration): When a new query q is issued (or q is terminated) by a client, the task of query registration (or de-registration) is performed, which consists of inserting q into (or deleting q from) the query table, updating the GQR-tree, and broadcasting the message ( message or message) to all the moving objects to notify them of these changes.
- -
- Domain assignment: The task of domain assignment is performed in response to the message sent by a moving object o that exits its resident domain. The server searches o’s new resident domain by traversing the GQR-tree. Then, the server assigns o’s new resident domain (together with several spatial query ranges) to o. It is important to note that the main purpose of the GQR-tree is to assign the largest possible resident domain (together with as many spatial query ranges as possible) to o.
- -
- Query result update: The task of query result update is performed mainly in response to the message sent by a moving object o that crosses any of the boundary of its assigned spatial query ranges . When receiving the message from o, the server updates the result of the corresponding query q. For example, the server updates the result of in response to the message sent by the moving object in Figure 2. As we will describe later, this task may also be performed when the server receives the message from o.
4. Problem Definition and Motivation
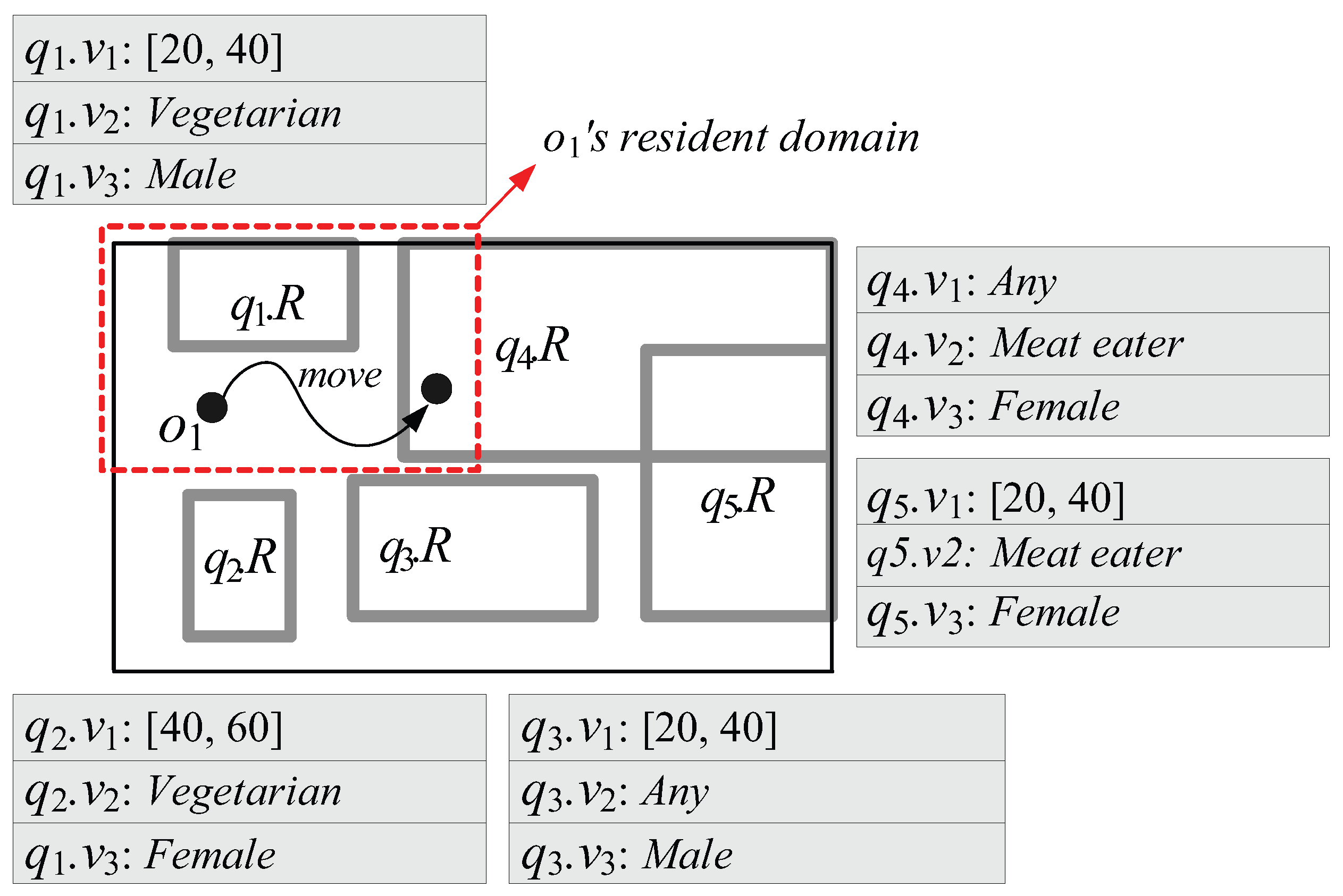
- First, because in MQM and QRT, the capability of each moving object o is measured by the number of spatial query ranges without any consideration of non-spatial query values (or intervals), o’s resident domain tends to be small. This leads o to frequently send messages to the server for receiving new resident domains. For example, let us assume that the moving object with in Figure 3 is associated with three non-spatial attributes A = {: Age, : Dietary preference, : Gender} and = { }. Suppose the queries involve non-spatial values (or intervals) specified on a subset of A, as shown in Figure 3. In MQM and QRT, the server assigns the red-dotted rectangle as ’s resident domain together with two spatial query ranges and . However, because is matched to only (i.e., , , and ) and (i.e., and ), ’s movement only affects the results of the corresponding queries and . So, when determining the size of ’s resident domain, the server can ignore the spatial query ranges , , and ; thus the server can assign much larger resident domain (i.e., entire space) together with the qualified spatial query ranges and .
- Second, due to the same reason of the first drawback, each moving object o has to send unnecessary messages to the server. For example, when in Figure 3 crosses the boundary of as depicted in the figure, it sends the message to the server. However, because is not matched to (i.e., and ), ’s movement does not affect the result of the corresponding query ; hence, can ignore , and check its movement against only (because is matched to ) and send the message if necessary.
| Notation | Explanation |
|---|---|
| o | A moving object |
| The current location of o | |
| The non-spatial attribute values of o | |
| The object bit-vector of o | |
| q | A CM range monitoring query |
| The spatial query range q specifies | |
| A set of non-spatial query values (or intervals) q specifies | |
| The query bit-vector of q | |
| A query group | |
| The group bit-vector of | |
| N | A GQR-tree node or its corresponding subspace of the entire workspace |
| A set of ’s elements (queries) whose spatial query ranges are covered by or partially intersect N | |
| The cardinality of |
5. The Group-Aware Query Region Tree (GQR-Tree)
5.1. Description
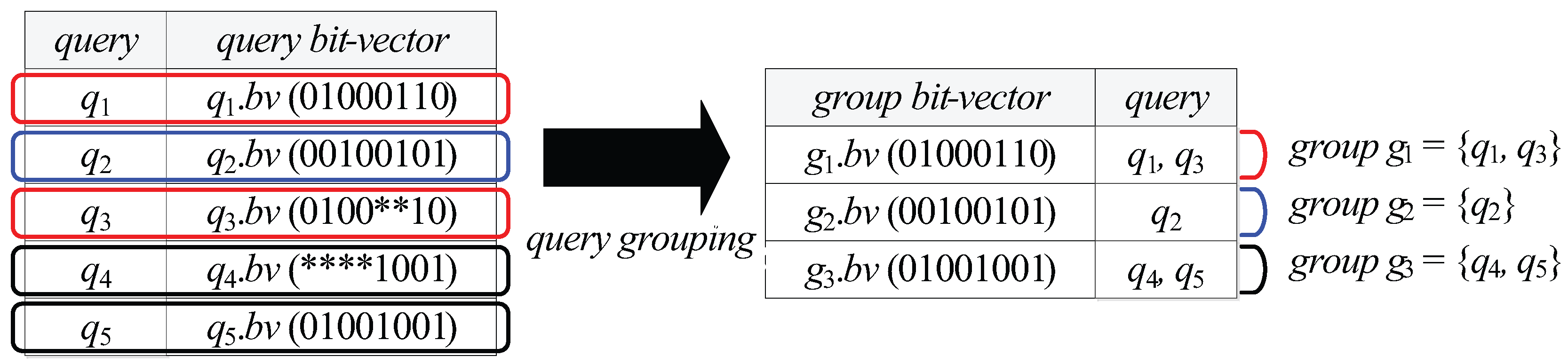
- Cover relationship (See Figure 5a): We say that covers N if () () (), where − denotes difference.
- Covered by relationship (See Figure 5b): We say that is covered by N if () () ().
- Partially intersect relationship (See Figure 5c): We say that partially intersects N if () () ().
- Equal relationship (See Figure 5d): We say that equals N if () () ().
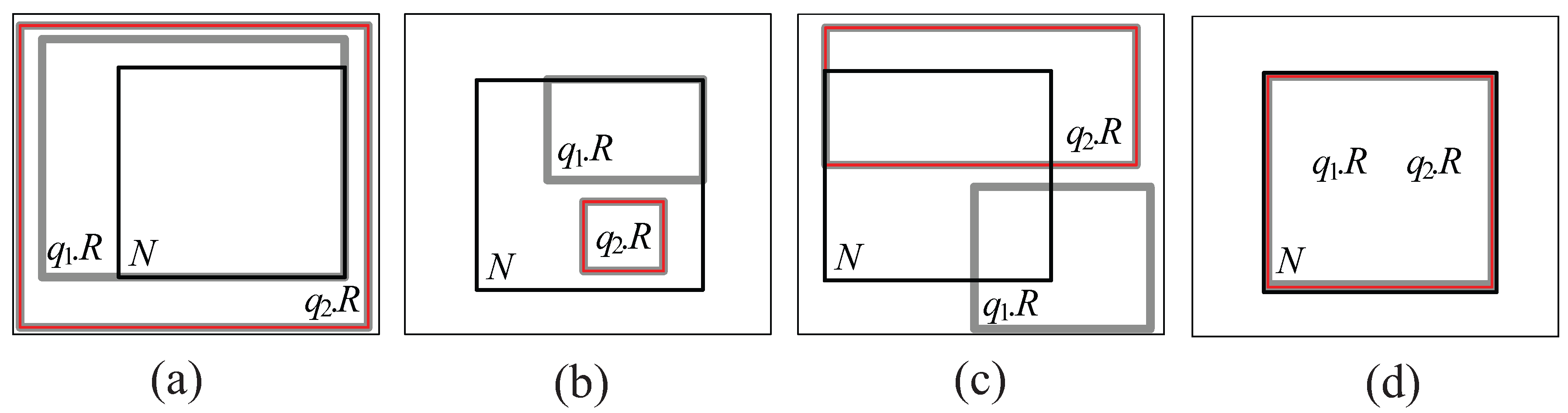
- A tuple for each query group can be stored in a leaf node N only if there exists at least one element (query) whose spatial query range is covered by or partially intersects N (i.e., ).
- A tuple for each query group can be redundantly stored in several leaf nodes if there exists an element whose spatial query range partially intersects all of these leaf nodes.
- For each entry stored in a non-leaf node N, represents one of the equal halves of N’s space.
- Each (non-leaf or leaf) node N stores, for each query group , the cardinality of (i.e., the total number of ’s elements whose spatial query ranges are covered by or partially intersect N). In case that N is a non-leaf node, N additionally stores, for each query group , a single bit flag , which is set to if 0 ≤ ≤ θ and set to otherwise.
- Each (non-leaf or leaf) node N is associated with a data structure , which is a set of tuples of the form , where is a group bit-vector of a query group and (See Definition 5 below) is a list that contains arbitrary number of query identifiers.
- A tuple for a query group can be maintained in only if there exists at least one element whose spatial query range covers or equals N.
- Each non-leaf node N is associated with another data structure , which is a set of tuples of the form , where and are defined as in the case of a leaf node.
- For each non-leaf node N, if a flag for a query group is set to , N is considered as the leaf node from the viewpoint of , and only if ≥ 1, a tuple for can be maintained in .
- For each non-leaf node N, if N is considered as the leaf node from the viewpoint of , no information about is stored in N’s descendant nodes and their associated s (if exist) and s.
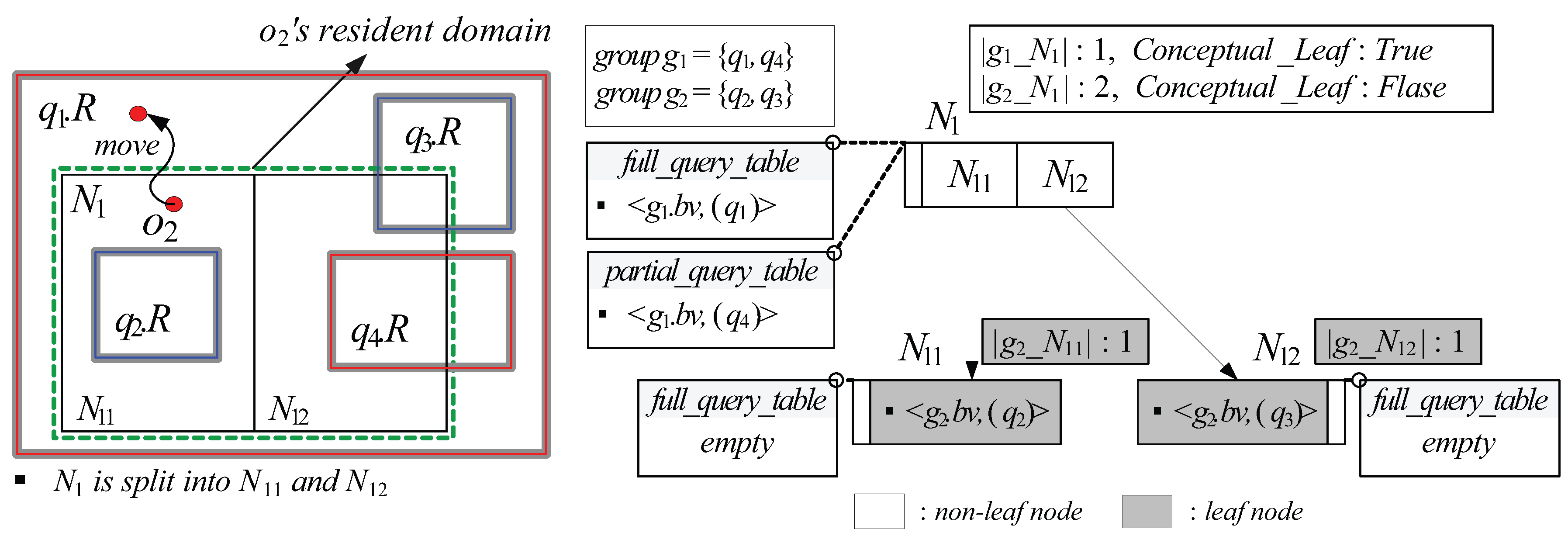
5.2. Resident Domain Search
| Algorithm 1 Search(N, o) |
| Input N: a GQR-tree node initially set to the root, o: a moving object Output R: o’s resident domain, : a set of (distinct) query identifiers 1: map to ; 2: initialize an empty set ; 3: identify the query group such that ∧ = ; 4: for each entry stored in N do 5: if contains then 6: if then 7: set R to ; 8: set to ; // one-bit flag 9: FindQueryID ; 10: return R and ; 11: else 12: Search(, o); |
- Case (1): If is a non-leaf node and stored in for is set to , FindQueryID visits and , after which it retrieves all the distinct query identifiers contained in of the tuple and of the tuple (Lines 19–25).
- Case (2): If is a leaf node, FindQueryID retrieves all the distinct query identifiers contained in of the tuple (stored in ), after which it visits and retrieves all the distinct query identifiers contained in of the tuple (Lines 29–34).
| Algorithm 2 FindQueryID() |
| Input N: a GQR-tree node, : an object bit-vector, : a bit flag initially set to Output : a set of (distinct) query identifiers 1: initialize an empty set ; 2: if = then 3: identify the query group such that ∧ = ; 4: if N is a non-leaf node then 5: if stored in N for is then 6: visit and get the tuple ; 7: retrieve all the query identifiers contained in and insert them into ; 8: return ; 9: else // stored in N for is 10: set to ; 11: for each entry stored in N do 12: FindQueryID(); 13: else // N is a leaf node 14: get the tuple stored in N; 15: retrieve all the query identifiers contained in and insert them into ; 16: return ; 17: else // = 18: identify the query group such that ∧ = ; 19: if N is a non-leaf node then 20: if stored in N for is then 21: visit and get the tuple ; 22: retrieve all the query identifiers contained in and insert them into ; 23: visit and get the tuple ; 24: retrieve all the query identifiers contained in and insert them into ; 25: return ; 26: else // stored in N for is 27: for each entry stored in N do 28: FindQueryID(); 29: else // N is a leaf node 30: get the tuple stored in N; 31: retrieve all the query identifiers contained in and insert them into ; 32: visit and get the tuple ; 33: retrieve all the query identifiers contained in and insert them into ; 34: return ; |
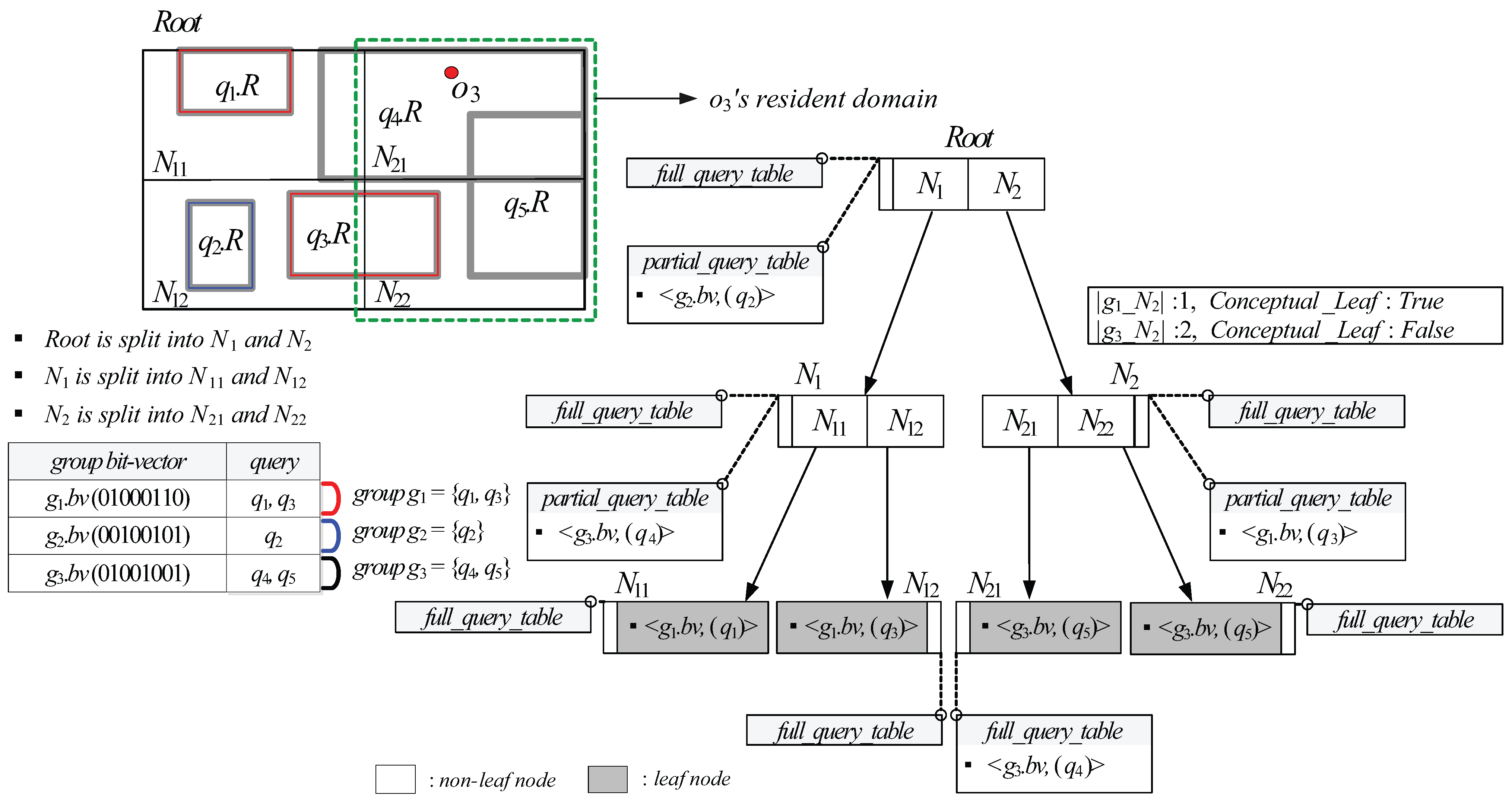
5.3. GQR-Tree Manipulations
| Algorithm 3 Insert(N, q) |
| Input N: a GQR-tree node initially set to the root, q: a newly issued query 1: map to ; 2: identify the query group whose group bit-vector is same as ; 3: if N is a non-leaf node then 4: if covers or equals N then 5: insert the query identifier of q into of the tuple maintained in ; 6: else // is covered by or partially intersects N 7: increase by 1; 8: if stored in N for is then 9: insert the query identifier of q into of the tuple maintained in ; 10: SplitNonLeaf() in case that ; 11: else // for is 12: for each entry stored in N do 13: if overlaps with then 14: Insert(, q); 15: else // N is a leaf node 16: if covers or equals N then 17: insert the query identifier of q into of the tuple maintained in ; 18: else // is covered by or partially intersects N 19: increase by 1; 20: insert the query identifier of q into of the tuple stored in N; 21: SplitLeaf() in case that ; |
- Case (1): If N’s children are non-leaf, SplitNonLeaf copies the tuple maintained in and pastes it into s of N’s children. (Line 4). Next, given the tuple maintained in , for each query q referred to by each query identifier contained in , SplitNonLeaf checks for each child node if covers or equals . If so, it inserts the query identifier of q into of the tuple maintained in (Lines 5–9). On the other hand, if is covered by or partially intersects , SplitNonLeaf increases by 1, creates a new tuple for in (if it does not exist), and inserts the query identifier of q into (Lines 10-13). Then, SplitNonLeaf deletes the tuple from (Line 14). Finally, for each N’s child node , SplitNonLeaf checks if . If so, it sets stored in for to (Lines 15–17). Otherwise, SplitNonLeaf invokes itself with and as an input (Lines 18–19).
- Case (2): If N’s children are leaf, similarly to the case (1), SplitNonLeaf copies the tuple maintained in and and pastes it into s of N’s children (Line 21). Next, given maintained in , for each q referred to by each query identifier contained in , SplitNonLeaf checks for each child node if covers or equals . If so, it inserts the query identifier of q into of the tuple maintained in (Lines 22–26). On the other hand, if is covered by or partially intersects , SplitNonLeaf increases by 1, inserts a new tuple for into (if it does not exist), and inserts the query identifier of q into (Lines 27–30). Then, SplitNonLeaf deletes the tuple from (Line 31). In case that each N’s child node overflows (i.e., ), SplitNonLeaf invokes SplitLeaf with and as an input (Lines 32–34).
| Algorithm 4 SplitNonLeaf() |
| Input N: an overflowed non-leaf node, : a group bit-vector 1: identify the query group , which causes N to be overflowed, using ; 2: set stored in N for to ; 3: if N’s children are non-leaf nodes then 4: copy the tuple maintained in and paste it into s of N’s children; 5: visit and get the tuple ; 6: for each query q referred to by each query identifier contained in do 7: for each N’s child node do 8: if covers or equals then 9: insert the query identifier of q into of the tuple maintained in ; 10: else if is covered by or partially intersects then 11: increase by 1; 12: create a new tuple for in (if it does not exist); 13: insert the query identifier of q into ; 14: delete the tuple from ; 15: for each N’s child node do 16: if then 17: set stored in for to ; 18: else 19: SplitNonLeaf(); 20: else // N’s children are leaf nodes 21: copy the tuple maintained in and paste it into s of N’s children; 22: visit and get the tuple ; 23: for each query q referred to by each query identifier contained in do 24: for each N’s child node do 25: if covers or equals then 26: insert the query identifier of q into of the tuple maintained in ; 27: else if is covered by or partially intersects then 28: increase by 1; 29: insert a new tuple for into (if it does not exist); 30: insert the query identifier of q into ; 31: delete the tuple from ; 32: for each N’s child node do 33: if then 34: SplitLeaf(); |
| Algorithm 5 SplitLeaf() |
| Input N: an overflowed leaf node, : a group bit-vector 1: identify the query group , which causes N to be overflowed, using ; 2: create two new empty leaf nodes and ; 3: create a new empty non-leaf node ; 4: insert entries and into ; 5: copy the tuple maintained in and paste it into , , and ; 6: for each group such that do 7: copy the tuple stored in N and paste it into ; 8: set and created in for to and ; 9: set and created in for to || and ; 10: find the entry stored in N’s parent and redirect to point to ; 11: get the tuple from N; 12: for each query q referred to by each query identifier contained in do 13: for each ’s child node do // we use to denote or 14: if covers or equals then 15: insert the query identifier of q into of the tuple maintained in ; 16: else if is covered by or partially intersects then 17: increase by 1; 18: insert a new tuple for into (if it does not exist); 19: insert the query identifier of q into ; 20: discard N; 21: for each ’s child node do 22: if then 23: SplitLeaf(); |
| Algorithm 6 Delete(N, q) |
| Input N: a GQR-tree node initially set to the root, q: a terminated query 1: map to ; 2: identify the query group whose group bit-vector is same as ; 3: if N is a non-leaf node then 4: if covers or equals N then 5: delete the query identifier of q from of the tuple maintained in ; 6: else // is covered by or partially intersects N 7: decrease by 1; 8: if stored in N for is then 9: delete the query identifier of q from of the tuple maintained in ; 10: MergeNonLeaf(N’s parent, ); 11: else // for is 12: for each entry stored in N do 13: if overlaps with then 14: Delete(, q); 15: else // N is a leaf node 16: if covers or equals N then 17: delete the query identifier of q from of the tuple maintained in ; 18: else // is covered by or partially intersects N 19: decrease by 1; 20: delete the query identifier of q from of the tuple stored in N; 21: MergeLeaf(N’s parent, ); |
| Algorithm 7 MergeNonLeaf() |
| Input N: a non-leaf node, which is a parent of non-leaf nodes, : a group bit-vector 1: identify the query group using ; 2: if then 3: set stored in N for to ; 4: create a new tuple for in ; 5: for each N’s child node do 6: if stored in for is then 7: visit and get the tuple ; 8: insert all the query identifiers contained in into of the tuple ; 9: visit and get the tuple ; 10: for each query q referred to by each query identifier contained in do 11: if is covered by or partially intersects N then 12: insert the query identifier of q into of the tuple ; 13: delete the information about stored in all N’s descendant nodes and their associated s (if exist) and s; 14: MergeNonLeaf(N’s parent, ); |
| Algorithm 8 MergeLeaf() |
| Input N: a non-leaf node, which is a parent of leaf nodes, : a group bit-vector 1: identify the query group using ; 2: if then 3: if every stored in N for every query group is then 4: create a new empty leaf node ; 5: copy all the tuples maintained in and , and paste them into and ; 6: set to ; 7: insert a new tuple for into ; 8: set to ; 9: find the entry stored in N’s parent and redirect to point to ; 10: for each N’s child node do; 11: get the tuple from ; 12: insert all the query identifiers contained in into of the tuple ; 13: visit and get the tuple ; 14: for each query q referred to by each query identifier contained in do 15: if is covered by or partially intersects then 16: insert the query identifier of q into of the tuple ; 17: discard N and N’s children; 18: MergeLeaf(’s parent, ); 19: else // if there exists some query group such that stored in N for is 20: set stored in N for to ; 21: create a new tuple for in ; 22: for each N’s child node do 23: get the tuple from ; 24: insert all the query identifiers contained in into of the tuple ; 25: visit and get the tuple ; 26: for each query q referred to by each query identifier contained in do 27: if is covered by or partially intersects N then 28: insert the query identifier of q into of the tuple ; 29: delete the tuples and from and ; 30: MergeNonLeaf(N’s parent, ); |
5.4. Cooperative Evaluation of CM Range Monitoring Queries
5.4.1. Server-Side Tasks
5.4.2. Object-Side Tasks
- : When receives the message from the server, given the query , it checks if (i) contains and (ii) it is matched to , i.e., or ∈ (assuming a set of non-spatial attributes A=). If this is the case, o sends the ) message to the server in order to let the server insert o into the result of q. Next, o checks if is covered by or partially intersects its current resident domain N. If so, it inserts and into the local query table. It should be noted that if the number of query identifier and spatial query range pairs stored in the local query table becomes greater than the capability of o due to the insertion, o sends the message to the server in order to receive a new resident domain (together with new query identifier and spatial query range pairs).
- : When o receives the message from the server, it just deletes the pair of and from the local query table if the pair is stored in the local query table.
6. Performance Evaluation
6.1. Simulation Setup
| Simulation Parameter | Value Used (Default) |
|---|---|
| Cardinality of Uniform/Skewed | 1000 ∼ 10,000 (5000) |
| Side length of spatial query ranges | 500 m ∼ 5000 m (2500 m) |
| Number of moving objects | 10,000 ∼ 100,000 (50,000) |
| Number of non-spatial attributes | 1 ∼ 10 (5) |
6.2. Simulation Results
6.2.1. Effect of the Number of Queries
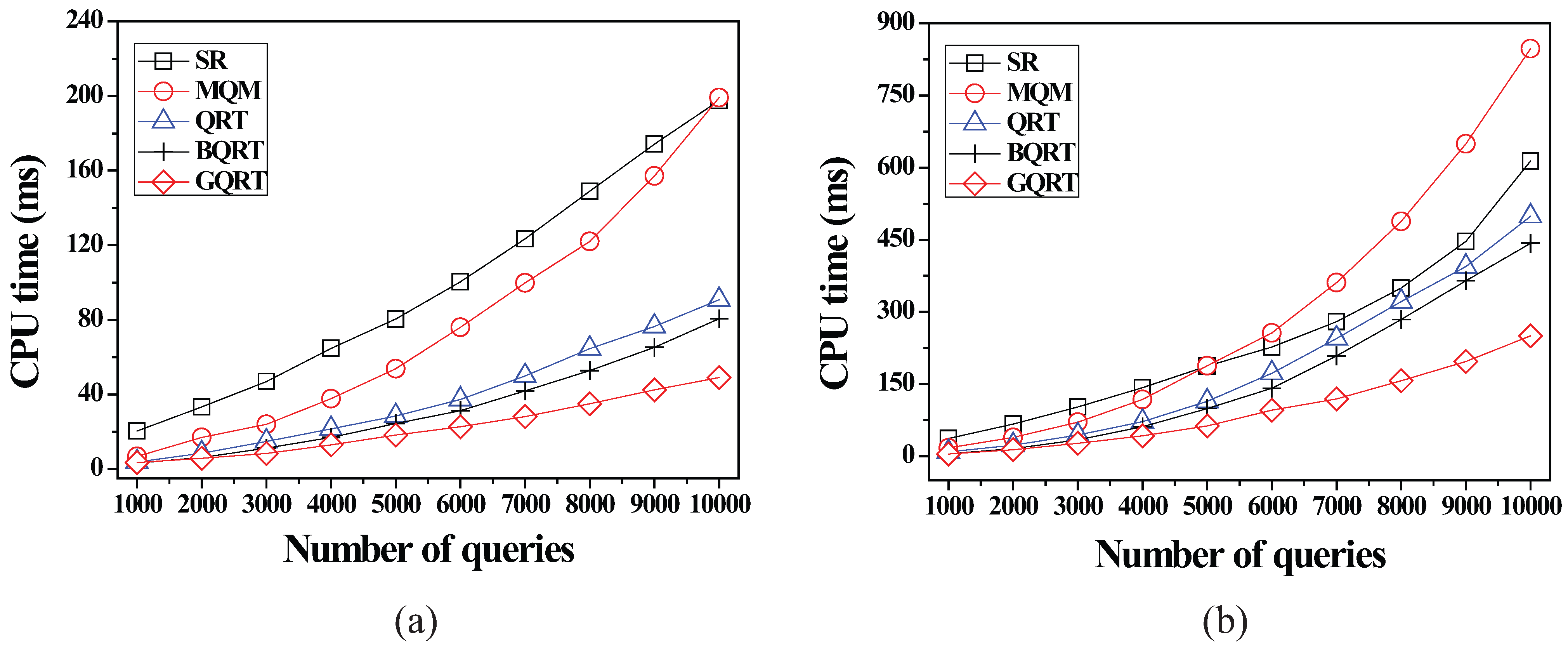
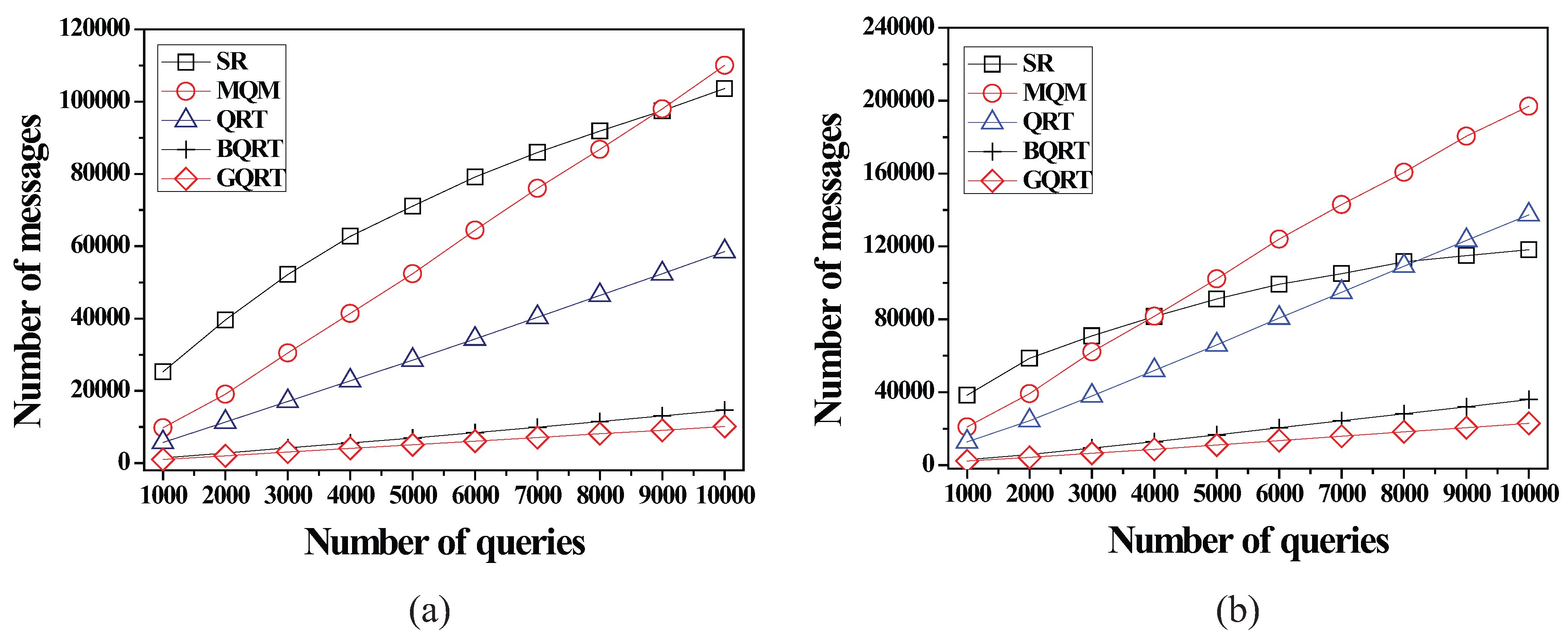
6.2.2. Effect of the Size of Spatial Query Ranges
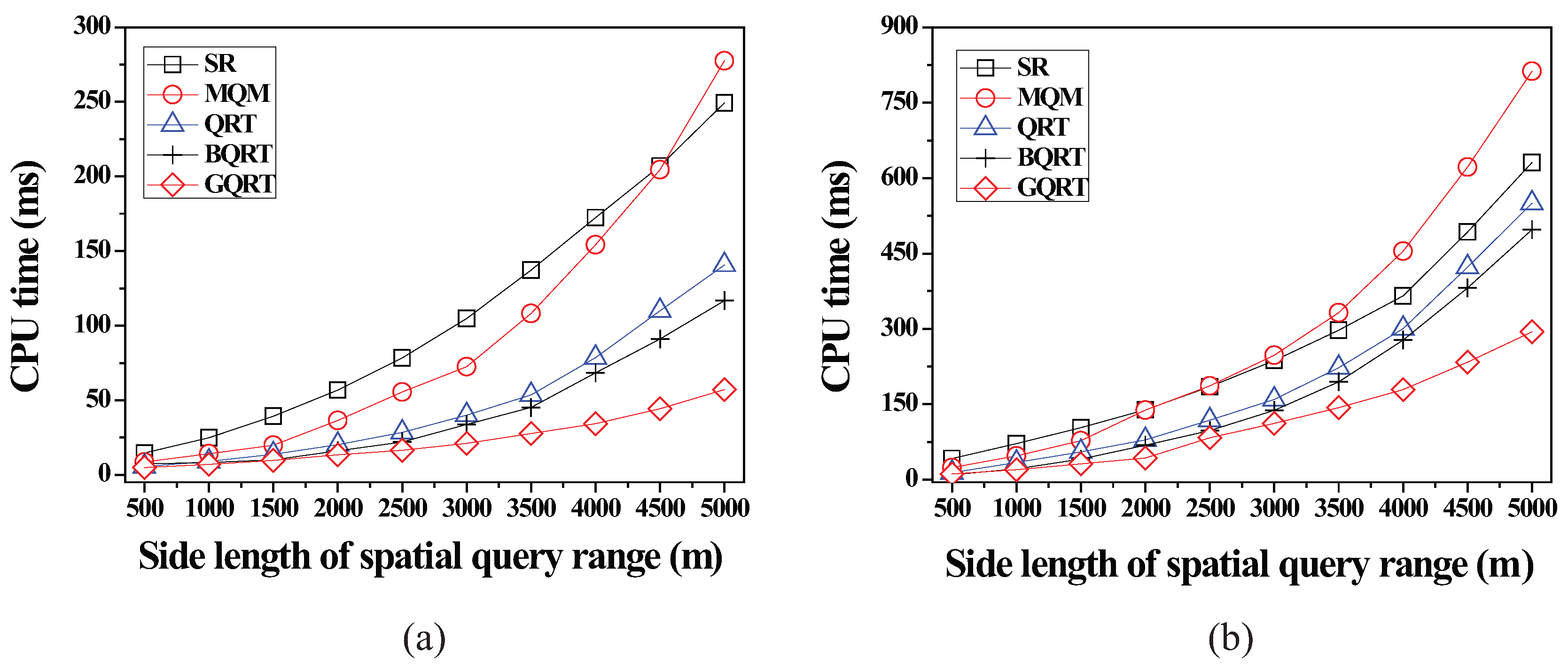
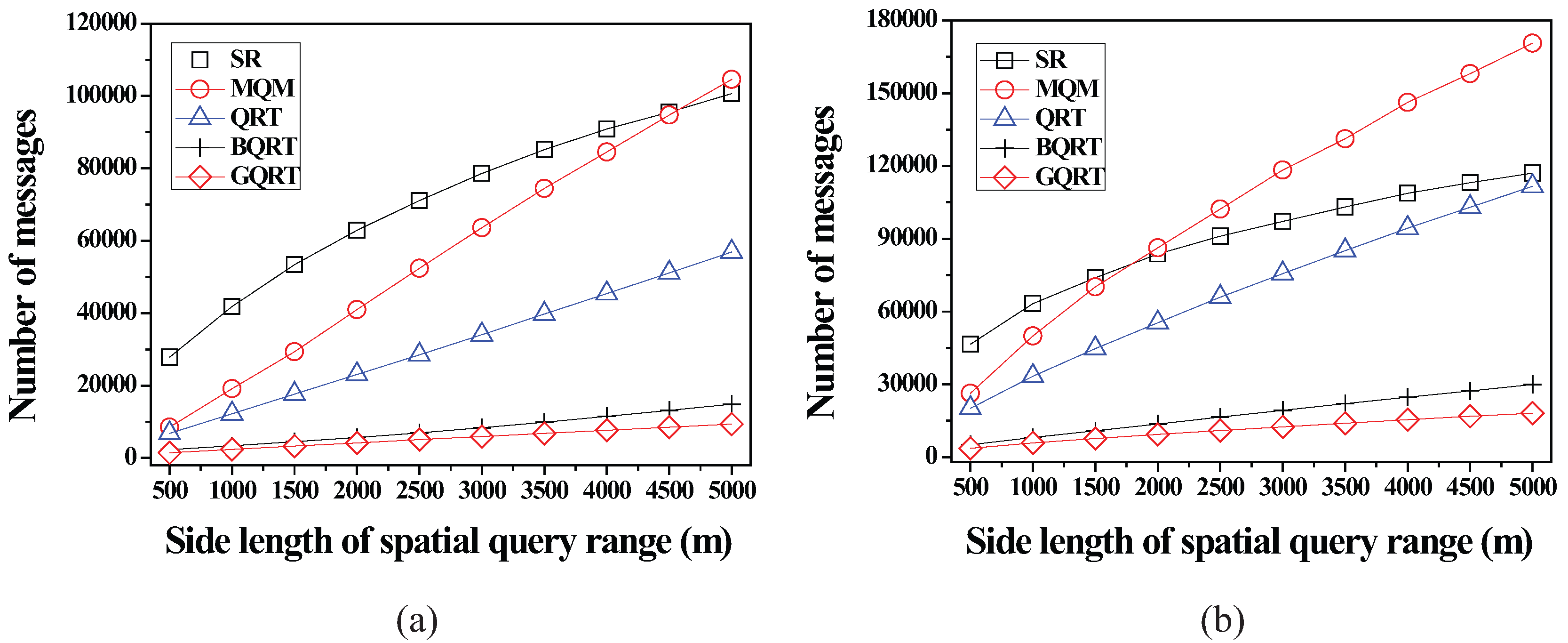
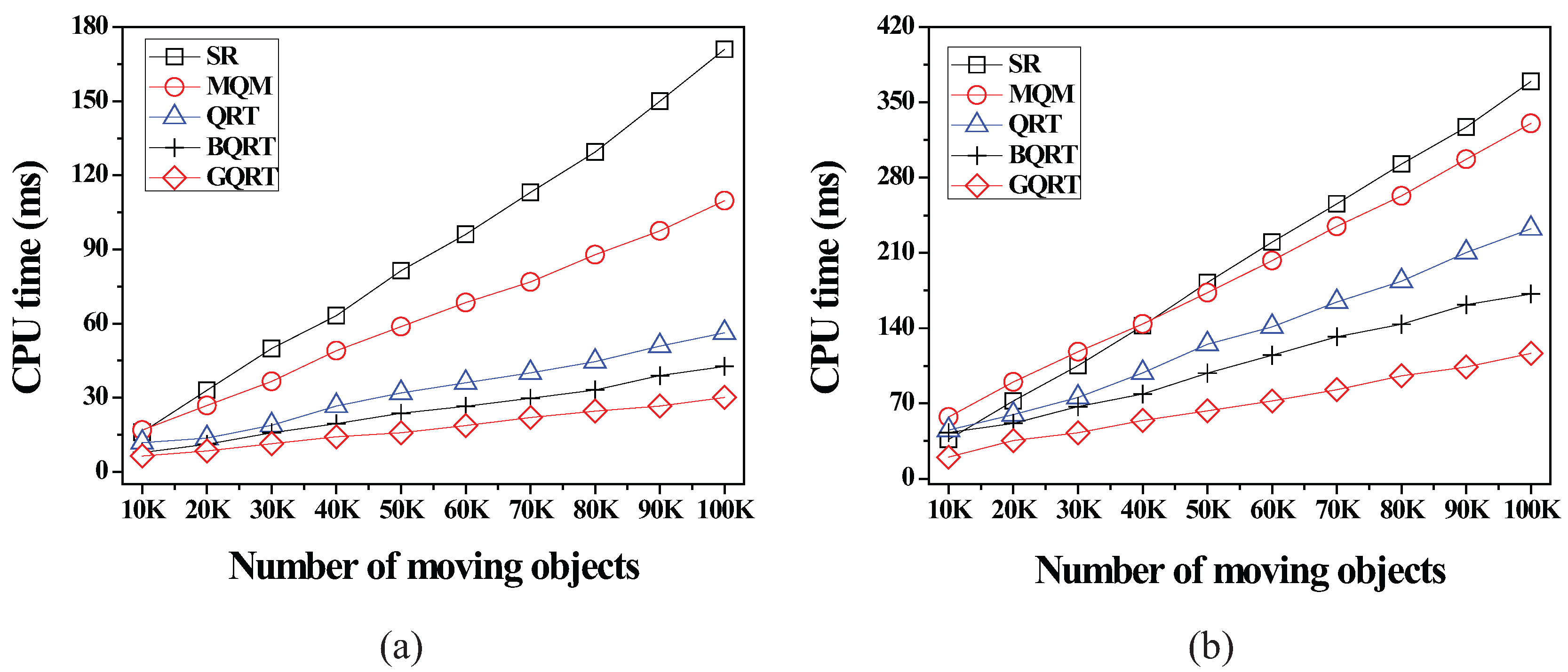
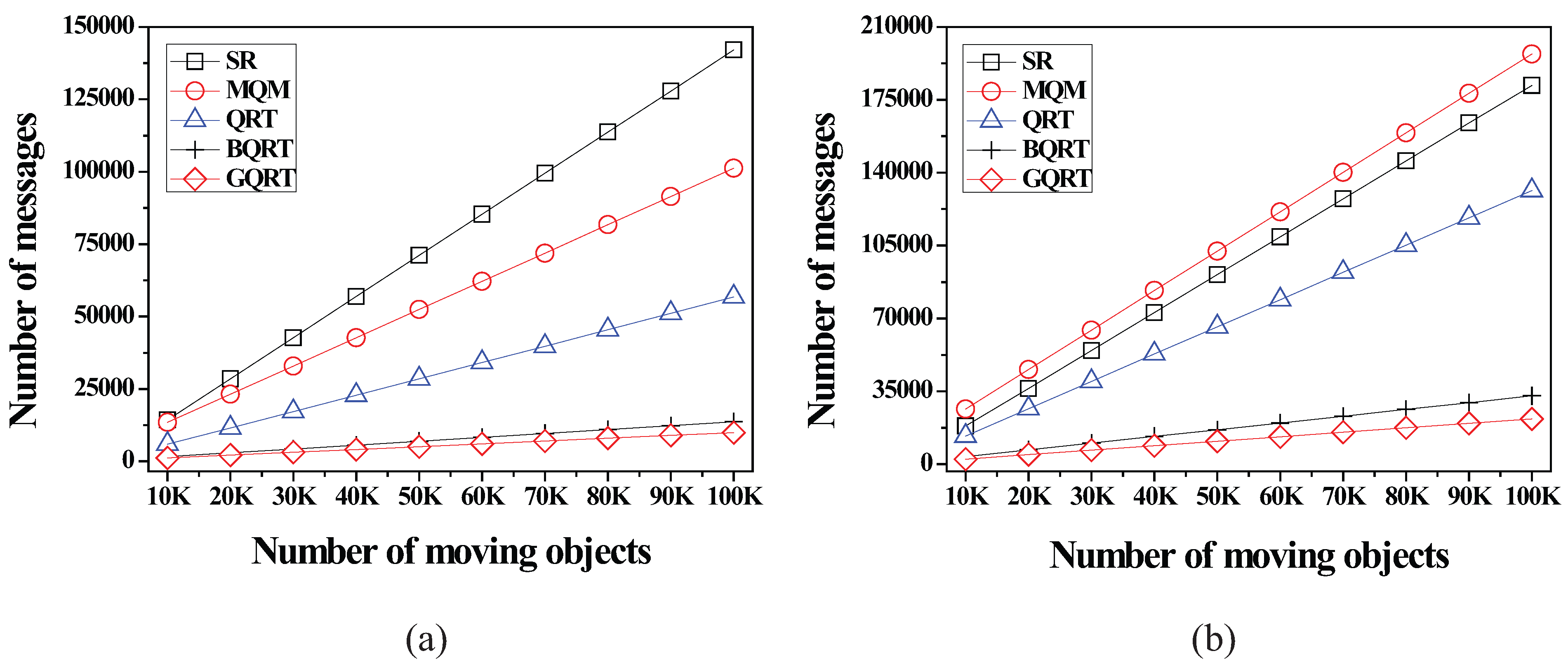
6.2.3. Effect of the Number of Moving Objects
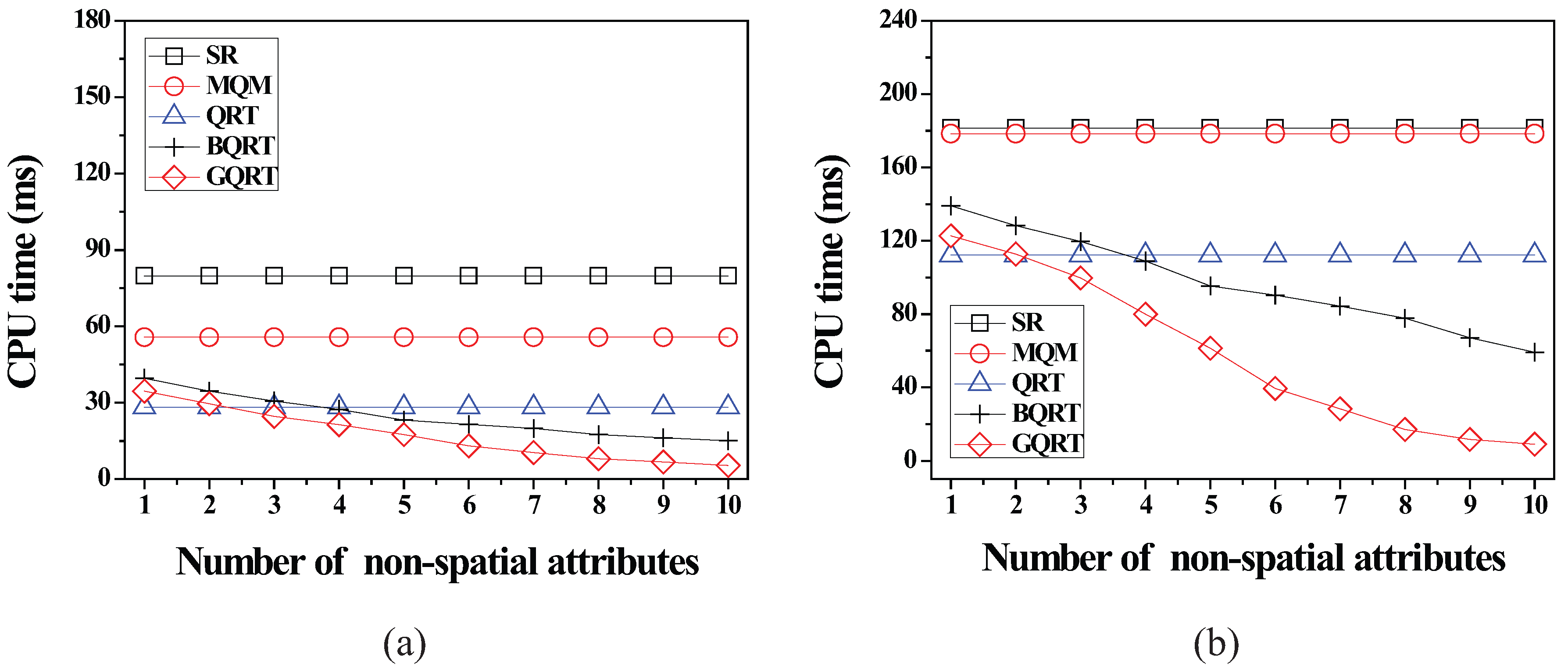
6.2.4. Effect of the Number of Non-Spatial Attributes
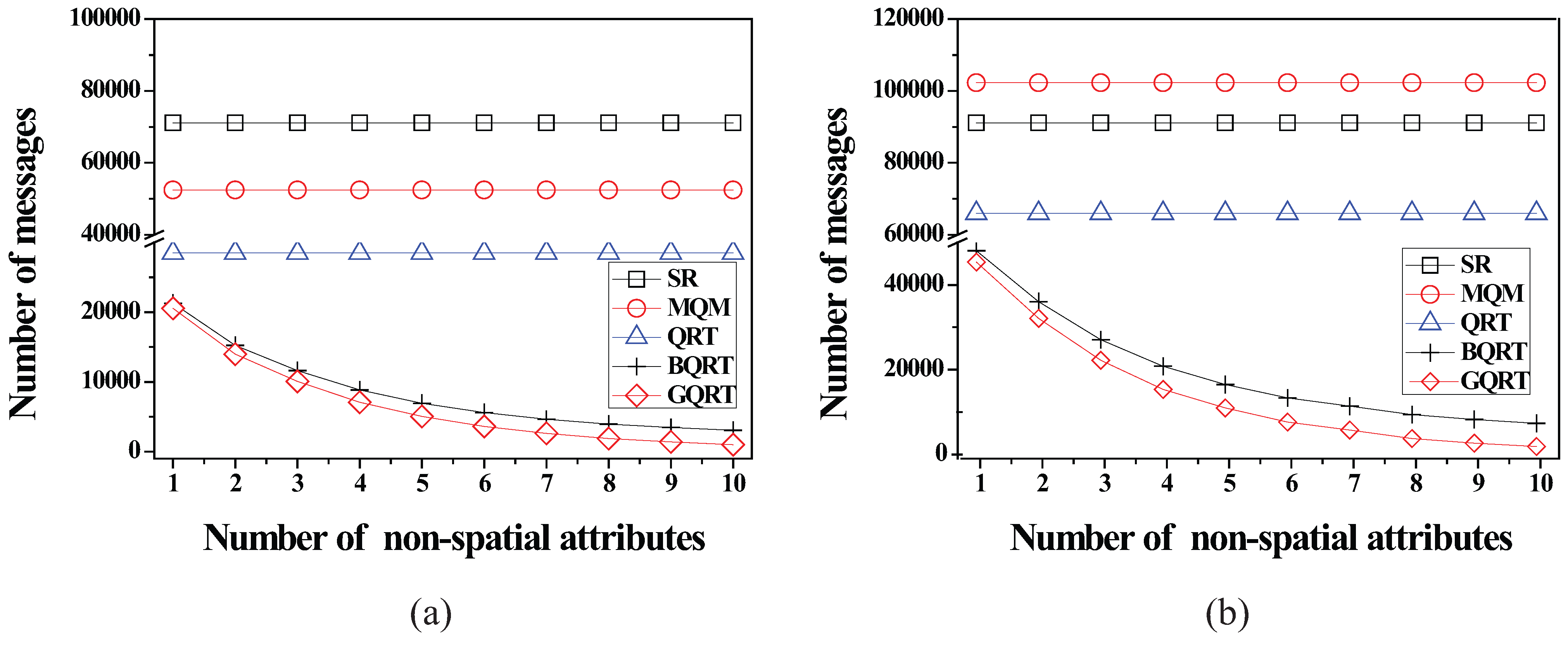
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jung, H.; Kim, Y.S.; Chung, Y.D. QR-tree: An efficient and scalable method for evaluation of continuous range queries. Inf. Sci. 2014, 274, 156–176. [Google Scholar]
- Cai, Y.; Hua, K.A.; Cao, G.; Xu, T. Real-time processing of range-monitoring queries in heterogeneous mobile databases. IEEE Trans. Mobile Comput. 2006, 5, 931–942. [Google Scholar]
- Cheema, M.A.; Brankovic, L.; Lin, X.; Zhang, W.; Wang, W. Continuous monitoring of distance-based range queries. IEEE Trans. Knowl. Data Eng. 2011, 23, 1182–1199. [Google Scholar] [CrossRef]
- Chen, X.A.; Pang, J.; Xue, R. Constructing and comparing user mobility profiles for location-based services. In Proceedings of the 28th Annual ACM Symposium on Applied Computing, Coimbra, Portugal, 18–22 March 2013.
- Gedik, B.; Liu, L. Mobieyes: A distributed location monitoring service using moving location queries. IEEE Trans. Mobile Comput. 2006, 5, 1384–1402. [Google Scholar] [CrossRef]
- Hu, H.; Xu, J.; Lee, D.L. A generic framework for monitoring continuous spatial queries over moving objects. In Proceedings of the 2005 ACM SIGMOD International Conference on Management of Data, Chicago, IL, USA, 13–16 June 2005.
- Huang, J.L.; Huang, C.C. A proxy-based approach to continuous location-based spatial queries in mobile environments. IEEE Trans. Knowl. Data Eng. 2013, 25, 260–273. [Google Scholar] [CrossRef]
- Ilarri, S.; Mena, E.; Illarramendi, A. Location-dependent query processing: Where we are and where we are heading. ACM Comput. Surv. 2010, 42, 1–73. [Google Scholar] [CrossRef]
- Jung, H.; Kim, Y.S.; Chung, Y.D. SPQI: An Efficient Index for Continuous Range Queries in Mobile Environments. J. Inf. Sci. Eng. 2013, 29, 557–578. [Google Scholar]
- Jung, H.; Cho, B.K.; Chung, Y.D.; Liu, L. On processing location based Top-k queries in the wireless broadcasting system. In Proceedings of the 2010 ACM Symposium on Applied Computing, Sierre, Switzerland, 22–26 March 2010.
- Jung, H.; Chung, Y.D.; Liu, L. Processing generalized k-nearest neighbor queries on a wireless broadcast stream. Inf. Sci. 2012, 188, 64–79. [Google Scholar] [CrossRef]
- Kalashnkov, D.V.; Prabhakar, S.; Hambrusch, S.E. Main memory evaluation of monitoring queries over moving objects. Disrtib. Parallel Database 2004, 15, 117–135. [Google Scholar] [CrossRef]
- Lee, K.C.K.; Zheng, B.; Chen, C.; Chow, C.Y. Efficient index-based approaches for skyline queries in location-based applications. IEEE Trans. Knowl. Data Eng. 2013, 25, 2507–2520. [Google Scholar] [CrossRef]
- Liu, F.; Hua, K.A.; Xie, F. A hybrid communication solution to distributed moving query monitoring systems. Electron. Commer. Res. Appl. 2011, 10, 214–228. [Google Scholar] [CrossRef]
- Mokbel, M.F.; Xiong, X.; Aref, W.G. SINA: Scalable incremental processing of continuous queries in spatio-temporal databases. In Proceedings of the 2004 ACM SIGMOD International Conference on Management of Data, Paris, France, 13–18 June 2004.
- Mouratidis, K.; Bakiras, S.; Papadias, D. Continuous monitoring of spatial queries in wireless broadcast environments. IEEE Trans. Mob. Comput. 2009, 8, 1297–1311. [Google Scholar] [CrossRef]
- Prabhakar, S.; Xia, Y.; Aref, W.G.; Hambrusch, S. Query indexing and velocity constrained indexing: Scalable techniques for continuous queries on moving objects. IEEE Trans. Comput. 2002, 51, 1124–1140. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, D.; Li, G.; Tan, K.; Bao, Z. Location-Aware Pub/Sub System: When Continuous Moving Queries Meet Dynamic Event Streams. In Proceedings of the ACM SIGMOD 2015, Melbourne, VIC, Australia, 31 May–4 June, 2015.
- Wu, K.L.; Chen, S.-K.; Yu, P.S. Efficient processing of continual range queries for location-aware mobile services. Inf. Syst. Front. 2005, 7, 435–448. [Google Scholar] [CrossRef]
- Wu, K.L.; Chen, S.-K.; Yu, P.S. On incremental processing of continual range queries for location-aware services and applications. In Proceedings of the Second Annual International Conference on Mobile and Ubiquitous Systems: Networking and Services, San Jose, CA, USA, 17–21 July 2005.
- Ding, X.; Lian, X.; Chen, L.; Jin, H. Continuous monitoring of skylines over uncertain data streams. Inf. Sci. 2012, 184, 196–214. [Google Scholar] [CrossRef]
- Guttman, A. R-trees: A dynamic index structure for spatial searching. In Proceedings of the 1984 ACM SIGMOD International Conference on Management of Data, Boston, MA, USA, 18–21 June 1984.
- Beckmann, N.; Kriegel, H.-P.; Schneider, R.; Seeger, B. The R*-tree: An efficient and robust access method for points and rectangles. In Proceedings of the 1990 ACM SIGMOD International Conference on Management of Data, Atlantic City, NJ, USA, 23–25 May 1990.
- Roussopoulos, N.; Faloutsos, C. The R+-tree: A dynamic index for multi-dimensional objects. In Proceedings of the 13th International Conference on Very Large Data Bases, Brighton, UK, 1–4 September 1987.
- Saltenis, S.; Jensen, C.; Leutenegger, S.; Lopez, M.A. Indexing the positions of continuously moving objects. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000.
- Tao, Y.; Papadias, D.; Sun, J. The TPR*-tree: An optimized spatio-temporal access method for predictive queries. In Proceedings of the 29th International Conference on Very Large Data, Berlin, Germany, 9–12 September 2003.
- Patel, J.M.; Chen, Y.; Chakka, V.P. STRIPES: An efficient index for predicted trajectories. In Proceedings of the 2004 ACM SIGMOD International Conference on Management of Data, Paris, France, 13–18 June 2004.
- Jensen, C.S.; Lin, D.; Ooi, B.C. Query and update efficient B+-tree based indexing of moving objects. In Proceedings of Thirtieth International Conference on Very Large Data Bases, Toronto, ON, Canada, 29 August–3 September 2004.
- Lee, M.L.; Hsu, W.; Jensen, C.S.; Cui, B.; Teo, K.L. Supporting frequent updates in R-trees: A bottom-up approach. In Proceedings of the 29th International Conference on Very Large Data Bases, Berlin, Germany, 9–12 September 2003.
- Song, M.; Kitagawa, H. Managing frequent updates in R-trees for update-intensive applications. IEEE Trans. Knowl. Data Eng. 2009, 21, 1573–1589. [Google Scholar]
- Song, M.; Choo, H.; Kim, W. Spatial indexing for massively update intensive applications. Inf. Sci. 2012, 203, 1–23. [Google Scholar] [CrossRef]
- Al-Khalidi, H.; Taniar, D.; Betts, J.; Alamri, S. Monitoring moving queries inside a safe region. Sci. World J. 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
- Hariharan, R.; Hore, B.; Li, C.; Mehrotra, S. Processing spatial-keyword (SK) queries in geographic information retrieval (GIR) systems. In Proceedings of the 19th International Conference on Scientific and Statistical Database Management, Banff, AB, Canada, 9–11 July 2007.
- Cong, G.; Jensen, C.S.; Wu, D. Efficient retrieval of the top-k most relevant spatial web objects. PVLDB 2009, 2, 337–348. [Google Scholar] [CrossRef]
- Zhang, D.; Chee, Y.; Mondal, A.; Tung, A.; Kitsuregawa, M. Keyword search in spatial databases: Towards searching by document. In Proceedings of the IEEE 25th International Conference on Data Engineering, Shanghai, China, 29 March–2 April 2009.
- Guo, T.; Cao, X.; Cong, G. Efficient algorithms for answering the m-Closest keywords query. In Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data, Melbourne, Australia, 31 May–4 June 2015.
- Cao, X.; Cong, G.; Jensen, C.S.; Yiu, M.L. Retrieving regions of interest for user exploration. PVLDB 2014, 7, 733–744. [Google Scholar] [CrossRef]
- Broch, J.; Maltz, D.A.; Johnson, D.; Hu, Y.-C.; Jetcheva, J. A performance comparison of multi-hop wireless ad hoc network routing protocols. In Proceedings of the 4th Annual ACM/IEEE International Conference on Mobile Computing and Networking, Dallas, TX, USA, 25–30 October 1998.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, H.; Song, M.; Youn, H.Y.; Kim, U.M. Evaluation of Content-Matched Range Monitoring Queries over Moving Objects in Mobile Computing Environments. Sensors 2015, 15, 24143-24177. https://doi.org/10.3390/s150924143
Jung H, Song M, Youn HY, Kim UM. Evaluation of Content-Matched Range Monitoring Queries over Moving Objects in Mobile Computing Environments. Sensors. 2015; 15(9):24143-24177. https://doi.org/10.3390/s150924143
Chicago/Turabian StyleJung, HaRim, MoonBae Song, Hee Yong Youn, and Ung Mo Kim. 2015. "Evaluation of Content-Matched Range Monitoring Queries over Moving Objects in Mobile Computing Environments" Sensors 15, no. 9: 24143-24177. https://doi.org/10.3390/s150924143
APA StyleJung, H., Song, M., Youn, H. Y., & Kim, U. M. (2015). Evaluation of Content-Matched Range Monitoring Queries over Moving Objects in Mobile Computing Environments. Sensors, 15(9), 24143-24177. https://doi.org/10.3390/s150924143






