Automatic Spiral Analysis for Objective Assessment of Motor Symptoms in Parkinson’s Disease
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subjects
| PD Patients | HE Subjects | |
|---|---|---|
| Patients (n, gender) | 65 (43 m, 22 f) | 10 (5 m; 5 f) |
| Age (years) | 65 ± 11 | 61 ± 7 |
| Years with levodopa | 13 ± 7 | NA |
| Hoehn and Yahr stage at present | 2.5 ± 1 * | NA |
| Total UPDRS | 49 ± 20.5 * | NA |
2.2. Experimental Setup
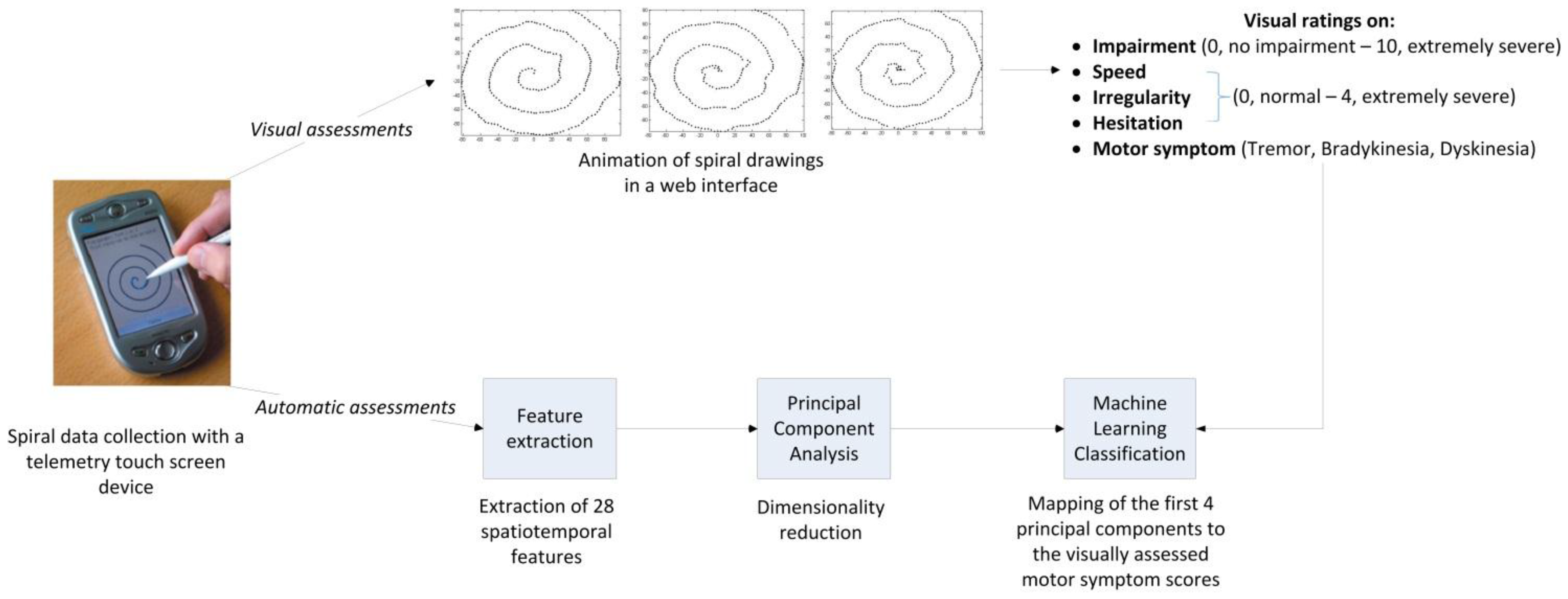
2.3. Digital Spiral Data Collection
2.4. Visual/Clinical Assessments of Motor Symptoms
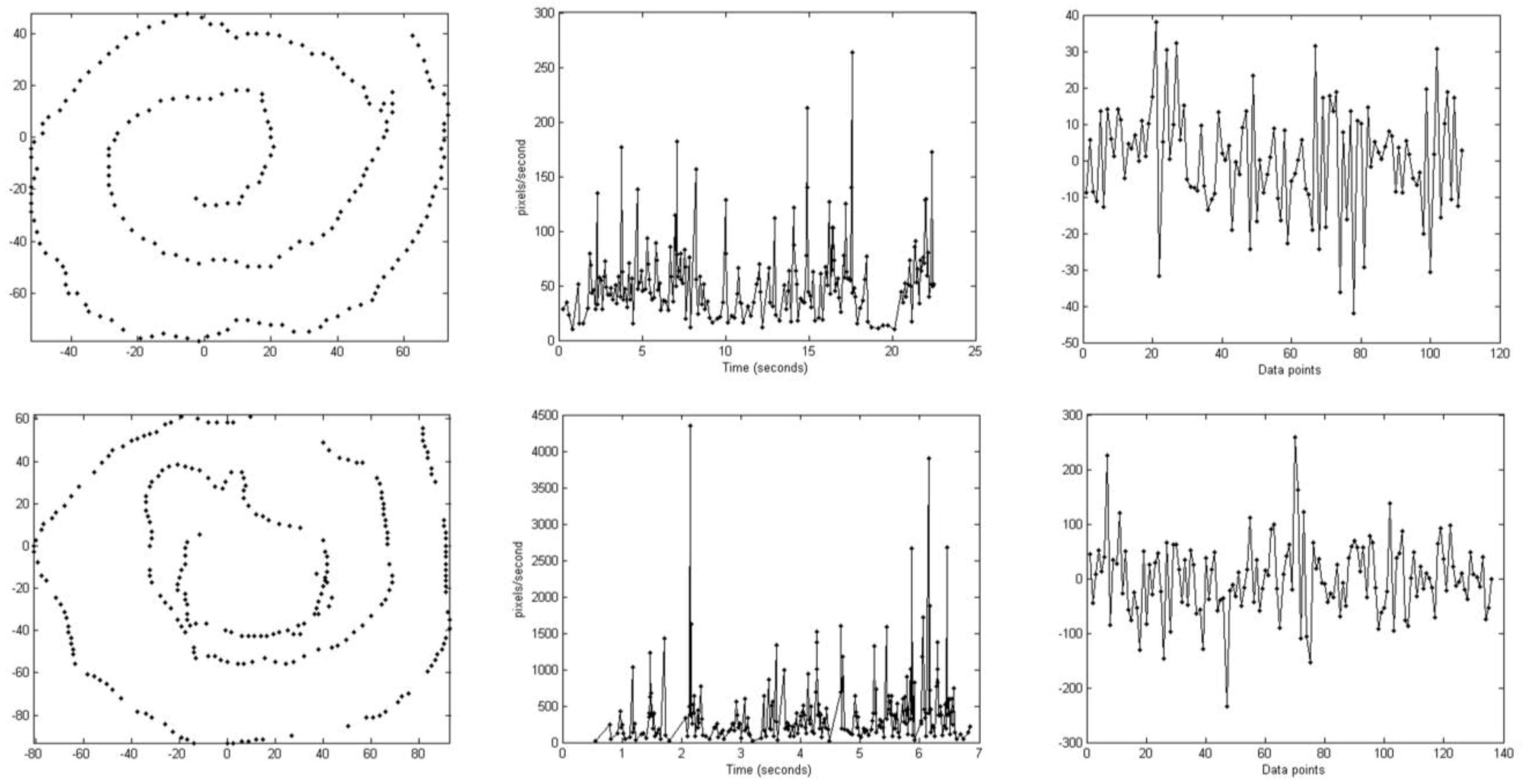
2.5. Automatic Scoring of Motor Symptoms
2.5.1. Feature Extraction
2.5.2. Principal Component Analysis
2.5.3. Classification
2.5.4. Statistical Analysis
3. Results
3.1. Inter-Rater Agreements
| Rater 1 | Rater 2 | Rater 3 | |
|---|---|---|---|
| Rater 2 | 0.52; 76.1; 25; 22.5 | ||
| Rater 3 | 0.43; 71.8; 1.9; 56 | 0.48; 76.7; 3.3; 51 | |
| Rater 4 | 0.23; 62.4; 42.3; 0 | 0.26; 66.4; 42.3; 0 | 0.63; 89.3; 12.1; 0 |
3.2. Correlations/Agreements between Computed and Visual/Clinical Scores
| PC1 | PC2 | PC3 | PC4 | |
|---|---|---|---|---|
| Impairment | 0.56 | 0.03 | 0.1 | 0.17 |
| Speed | 0.58 | 0.53 | 0.51 | 0.43 |
| Irregularity | 0.69 | 0.24 | 0.03 | 0.03 |
| Hesitation | 0.08 | 0.34 | 0.29 | 0.33 |
| MLP | RF | SVM (Radial Basis Function Kernel) | SVM (Linear) | LR | |
|---|---|---|---|---|---|
| Accuracy | 84 | 83 | 79 | 76 | 76 |
| Weighted Kappa | 0.65 | 0.60 | 0.50 | 0.47 | 0.47 |
| AUC | 0.86 | 0.85 | 0.74 | 0.74 | 0.83 |
| MLP Classifier | ||||
|---|---|---|---|---|
| Bradykinesia | Dyskinesia | Total | ||
| Raters | Bradykinesia | 28 | 8 | 36 |
| Dyskinesia | 9 | 64 | 73 | |
| Total | 37 | 72 | 109 | |
| Accuracy | 84% | |||
| Sensitivity | 75.7% (CI: 58.8%–88.2%) | |||
| Specificity | 88.9% (CI: 79.3%–95.1%) | |||
| Weighted Kappa/AUC | 0.65/0.86 | |||
3.3. Test-Retest Reliability of the Computed Scores
3.4. Separation of Healthy Elderly Subjects from PD Patients
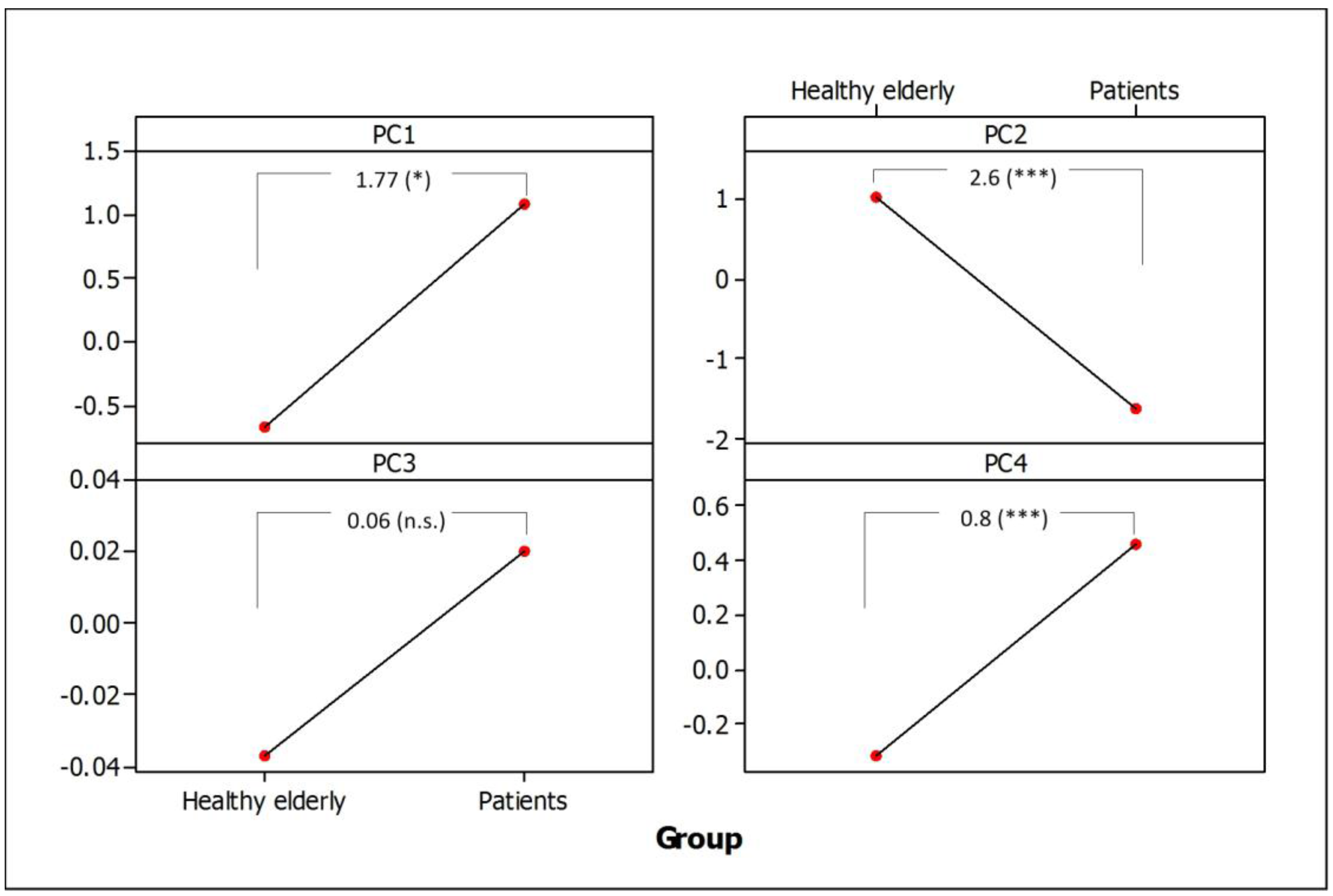
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
References
- LeWitt, P.A. Levodopa therapy for Parkinson’s disease: Pharmacokinetics and pharmacodynamics. Mov. Disord. 2005, 30, 64–72. [Google Scholar] [CrossRef] [PubMed]
- Vitale, C.; Pellecchia, M.T.; Grossi, D.; Frakassi, N.; Cuomo, T.; di Maio, L.; Barone, P. Unawareness of dyskinesia in Parkinson’s and Hunington’s diseases. Neurol. Sci. 2001, 22, 105–106. [Google Scholar] [CrossRef] [PubMed]
- Nyholm, D.; Kowalski, J.; Aquilonius, S.M. Wireless real-time electronic data capture for self-assessment of motor function and quality of life in Parkinson’s disease. Mov. Disord. 2004, 19, 446–451. [Google Scholar] [CrossRef] [PubMed]
- Goetz, C.G.; Tilley, B.C.; Shaftman, S.R.; Stebbins, G.T.; Fahn, S.; Martinez-Martin, P.; Poewe, W.; Sampaio, C.; Stern, MB.; Dodel, R.; et al. Movement Disorder Society-sponsored revision of the Unified Parkinson’s Disease Rating Scale (MDS-UPDRS): Scale presentation and clinimetric testing results. Mov. Disord. 2008, 23, 2129–2170. [Google Scholar] [CrossRef] [PubMed]
- Goetz, C.G.; Poewe, W.; Rascol, O.; Sampaio, C.; Stebbins, G.T.; Counsell, C.; Giladi, N.; Holloway, R.G.; Moore, C.G.; Wenning, G.K.; et al. Movement Disorder Society Task Force report on the Hoehn and Yahr staging scale: Status and recommendations. Mov. Disord. 2004, 19, 1020–1028. [Google Scholar] [CrossRef] [PubMed]
- Maetzler, W.; Domingos, J.; Srulijes, K.; Ferreira, J.J.; Bloem, B.R. Quantitative wearable sensors for objective assessment of Parkinson’s disease. Mov. Disord. 2013, 28, 1628–2637. [Google Scholar] [CrossRef] [PubMed]
- Memedi, M.; Khan, T.; Grenholm, P.; Nyholm, D.; Westin, J. Automatic and objective assessment of alternating tapping performance in Parkinson’s disease. Sensors 2013, 13, 16965–16984. [Google Scholar] [CrossRef] [PubMed]
- Zackrisson, T.; Bergquist, F.; Eklund, M.; Holmberg, B.; Thorlin, T. The discriminating properties of an optoelectronic movement analysis method in patients with Parkinsonism. J. Mot. Behav. 2013, 45, 415–422. [Google Scholar] [CrossRef] [PubMed]
- Tzallas, A.T.; Tsipouras, M.G.; Rigas, G.; Tsalikakis, D.G.; Karvounis, E.C.; Chondrogiorgi, M.; Psomadellis, F.; Cancela, J.; Pastorino, M.; Waldmeyer, M.T.; et al. PERFORM: A system for monitoring, assessment and management of patients with Parkinson’s disease. Sensors 2014, 14, 21329–21357. [Google Scholar] [CrossRef] [PubMed]
- Cancela, J.; Pastorino, M.; Tzallas, A.T.; Tsipouras, M.G.; Rigas, G.; Arredondo, M.T.; Fotiadis, D.I. Wearability assessment of a wearable system for Parkinson’s disease remote monitoring based on a body area network of sensors. Sensors 2014, 14, 17235–17255. [Google Scholar] [CrossRef] [PubMed]
- Djuric-Jovicic, M.D.; Jovicic, N.S.; Radovanovic, S.M.; Stankovic, I.D.; Popovic, M.B.; Kostic, V.S. Automatic identification and classification of freezing of gait episodes in Parkinson’s disease patients. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 685–694. [Google Scholar] [CrossRef] [PubMed]
- Tripoliti, E.E.; Tzallas, A.T.; Tsipouras, M.G.; Rigas, G.; Bougia, P.; Leontiou, M.; Konitsiotis, S.; Chondrogiorgi, M.; Tsouli, S.; Fotiadis, D.I. Automatic detection of freezing of gait events in patients with Parkinson’s disease. Comput. Methods Programs Biomed. 2013, 110, 12–26. [Google Scholar] [CrossRef] [PubMed]
- Tsanas, A.; Little, M.A.; McSharry, P.E.; Ramig, L.O. Accurate telemonitoring of Parkinson’s disease progression by noninvasive speech tests. IEEE Trans. Biomed. Eng. 2010, 57, 884–893. [Google Scholar] [CrossRef] [PubMed]
- Mellone, S.; Palmerini, L.; Cappello, A.; Chiari, L. Hilbert-Huang-based tremor removal to assess postural properties from accelerometers. IEEE Trans. Biomed. Eng. 2011, 58, 1752–1761. [Google Scholar] [PubMed]
- Heldman, D.A.; Espay, A.J.; LeWitt, P.A.; Giuffrida, J.P. Clinician versus machine: Reliability and responsiveness of motor endpoints in Parkinson’s disease. Parkinsonism Rel. Disord. 2014, 20, 590–595. [Google Scholar] [CrossRef] [PubMed]
- Rigas, G.; Tzallas, A.T.; Tsipouras, M.G.; Bougia, P.; Tripoliti, E.E.; Baga, D.; Fotiadis, D.I.; Tsouli, S.G.; Konitsiotis, S. Assessment of tremor activity in the Parkinson’s disease using a set of wearable sensors. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 478–487. [Google Scholar] [CrossRef] [PubMed]
- Salarian, A.; Russmann, H.; Wider, C.; Burkhards, P.R.; Vingerhoets, F.J.; Aminian, K. Quantification of tremor and bradykinesia in Parkinson’s disease using a novel ambulatory monitoring system. IEEE Trans. Biomed. Eng. 2007, 54, 313–322. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, R.I.; Kotschet, K.; Arfon, S.; Ming Xu, Z.; Johnson, W.; Drago, J.; Evans, A.; Kempster, P.; Raghav, S.; Horne, M.K. Automated assessment of bradykinesia and dyskinesia in Parkinson’s disease. J. Parkinson’s Dis. 2012, 2, 47–55. [Google Scholar]
- Dai, H.; Lin, H.; Lueth, T.C. Quantitative assessment of parkinsonian bradykinesia based on an inertial measurement unit. Biomed. Eng. Online 2015, 14. [Google Scholar] [CrossRef] [PubMed]
- Keijsers, N.L.; Horstnik, M.W.; Gielen, S.C. Automatic assessment of levodopa-induced dyskinesia in daily life by neural networks. Mov. Disord. 2003, 18, 70–80. [Google Scholar] [CrossRef] [PubMed]
- Lopane, G.; Mellone, S.; Cortelli, P.; Calandra-Buonaura, G.; Contin, M. Dyskinesia detection and monitoring by a single sensor in patients with Parkinson’s disease. Mov. Disord. 2015. [Google Scholar] [CrossRef]
- Saunders-Pullman, R.; Derby, C.; Stanley, K.; Floyd, A.; Bressman, S.; Lipton, R.B.; Deligtisch, A.; Severt, L.; Yu, Q.; Kurtis, M.; et al. Validity of spiral analysis in early Parkinson’s disease. Mov. Disord. 2008, 23, 531–537. [Google Scholar] [CrossRef] [PubMed]
- Westin, J.; Ghiamati, S.; Memedi, M.; Nyholm, D.; Johansson, A.; Dougherty, M.; Groth, T. A new computer method for assessing drawing impairment in Parkinson’s disease. J. Neurosci. Methods 2010, 190, 143–148. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Carroll, C.B.; Wang, S.Y.; Zajicek, J.; Bain, P.G. Quantifying drug-induced dyskinesia in the arms using digitized spiral-drawing tasks. J. Neurosci. Methods 2005, 144, 47–52. [Google Scholar] [CrossRef] [PubMed]
- Bain, P.G.; Findley, L.J.; Atchison, P.; Behari, M.; Vidailhet, M.; Gresty, M.; Rothwell, J.C.; Thompson, P.D.; Marsden, C.D. Assesing tremor severity. J. Neurol. Neurosur. Psychiatry 1993, 56, 868–873. [Google Scholar] [CrossRef]
- Haubenberger, D.; Kalowitz, D.; Nahab, F.B.; Toro, C.; Ippolito, D.; Luckenbaugh, D.A.; Wittevrongel, L.; Hallett, M. Validation of digital spiral analysis as outcome parameter for clinical trials in Essential Tremor. Mov. Disord. 2011, 26, 2073–2080. [Google Scholar] [CrossRef]
- Pålhagen, S.E.; Dizdar, N.; Hauge, T.; Holmberg, B.; Jansson, R.; Linder, J.; Nyholm, D.; Sydow, O.; Wainwright, M.; Widner, H.; et al. Interim analysis of long-term intraduodenal levodopa infusion in advanced Parkinson disease. Acta Neurol. Scand. 2012, 126, e29–e33. [Google Scholar] [CrossRef] [PubMed]
- Westin, J.; Dougherty, M.; Nyholm, D.; Groth, T. A home environment test battery for status assessment in patients with advanced Parkinson’s disease. Comput. Methods Programs Biomed. 2010, 98, 27–35. [Google Scholar] [CrossRef] [PubMed]
- Memedi, M.; Bergqvist, U.; Westin, J.; Grenholm, P.; Nyholm, D. A web-based system for visualizing upper limb motor performance of Parkinson’s disease patients. Mov. Disord. 2013, 28, S112–S113. [Google Scholar]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Sadikov, A.; Groznik, V.; Žabkar, J.; Možina, M.; Georgiev, D.; Pirtošek, Z.; Bratko, I. ParkinsonCheck smartphone App. In Proceedings of the European Conference on Artificial Intelligence, Prague, Czech Republic, 17–22 August 2014; pp. 1213–1214.
- Sadikov, A.; Žabkar, J.; Možina, M.; Groznik, V.; Georgiev, D.; Bratko, I. PARKINSONCHECK: A Decision Support System for Spirographic Testing. University of Ljubljana, Faculty of Computer and Information Science, Ljubljana, Slovenia, Technical Report, 2014. Available online: http://www.ailab.si/parkinsoncheck/pc-tr.pdf (accessed on 14 September 2015).
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutmann, P.; Witten, I.H. The WEKA data mining software: An update. SIGKDD Explor. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Memedi, M.; Westin, J.; Nyholm, D. Spiral drawing during self-rated dyskinesia is more impaired than during self-rated off. Parkinsonism Rel. Disord. 2013, 19, 553–556. [Google Scholar] [CrossRef] [PubMed]
- Cnaan, A.; Laird, N.M.; Slasor, P. Tutorial in biostatistics: Using the general linear mixed model to analyse unbalanced repeated measures and longitudinal data. Stat. Med. 1997, 16, 2349–2380. [Google Scholar] [CrossRef]
- Westin, J.; Schiavella, M.; Memedi, M.; Nyholm, D.; Dougherty, D.; Antonini, A. Validation of a home environment test battery for assessments in advanced Parkinson’s disease. Neurol. Sci. 2012, 33, 831–838. [Google Scholar] [CrossRef] [PubMed]
- Available online: http://users.du.se/~mmi/brad/brad.swf.html (accessed on 14 September 2015).
- Available online: http://users.du.se/~mmi/dys/dys_case.swf.html (accessed on 14 September 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Memedi, M.; Sadikov, A.; Groznik, V.; Žabkar, J.; Možina, M.; Bergquist, F.; Johansson, A.; Haubenberger, D.; Nyholm, D. Automatic Spiral Analysis for Objective Assessment of Motor Symptoms in Parkinson’s Disease. Sensors 2015, 15, 23727-23744. https://doi.org/10.3390/s150923727
Memedi M, Sadikov A, Groznik V, Žabkar J, Možina M, Bergquist F, Johansson A, Haubenberger D, Nyholm D. Automatic Spiral Analysis for Objective Assessment of Motor Symptoms in Parkinson’s Disease. Sensors. 2015; 15(9):23727-23744. https://doi.org/10.3390/s150923727
Chicago/Turabian StyleMemedi, Mevludin, Aleksander Sadikov, Vida Groznik, Jure Žabkar, Martin Možina, Filip Bergquist, Anders Johansson, Dietrich Haubenberger, and Dag Nyholm. 2015. "Automatic Spiral Analysis for Objective Assessment of Motor Symptoms in Parkinson’s Disease" Sensors 15, no. 9: 23727-23744. https://doi.org/10.3390/s150923727
APA StyleMemedi, M., Sadikov, A., Groznik, V., Žabkar, J., Možina, M., Bergquist, F., Johansson, A., Haubenberger, D., & Nyholm, D. (2015). Automatic Spiral Analysis for Objective Assessment of Motor Symptoms in Parkinson’s Disease. Sensors, 15(9), 23727-23744. https://doi.org/10.3390/s150923727









