Error Model and Compensation of Bell-Shaped Vibratory Gyro
Abstract
:1. Introduction
2. Working Concept of the Bell-Shaped Vibratory Gyro

2.1. Working Principle

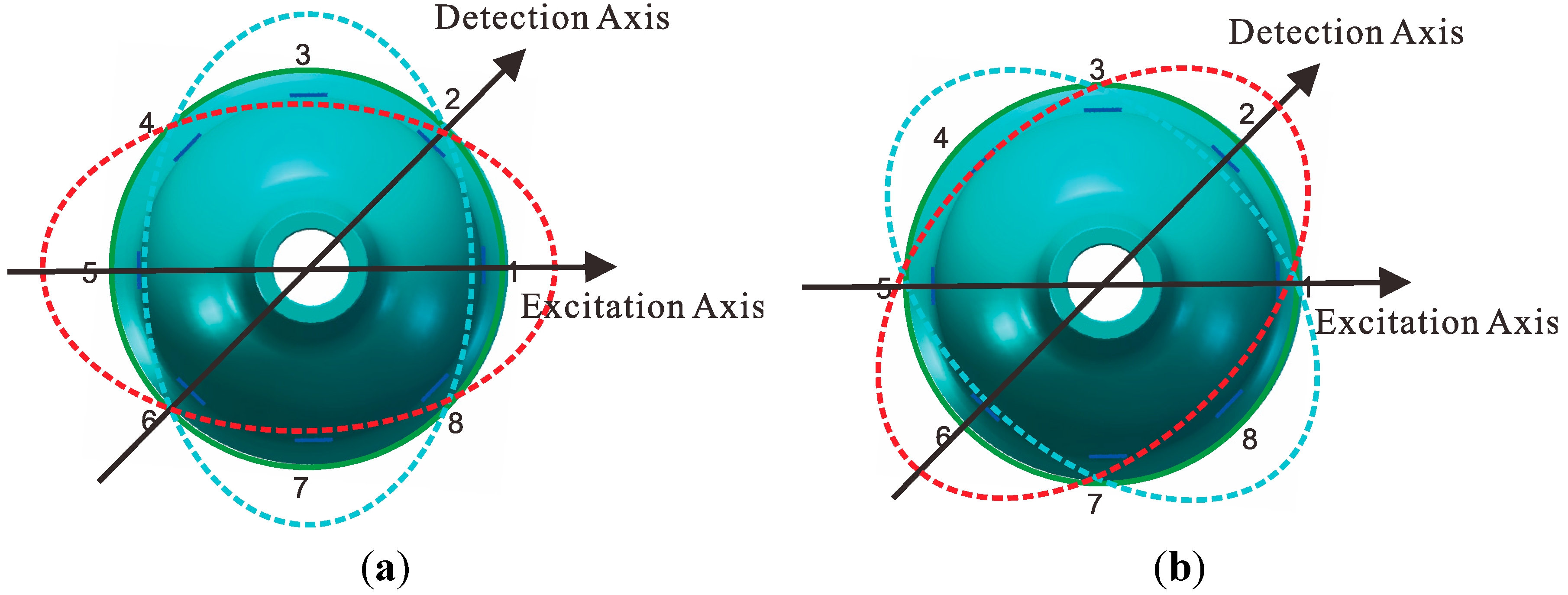
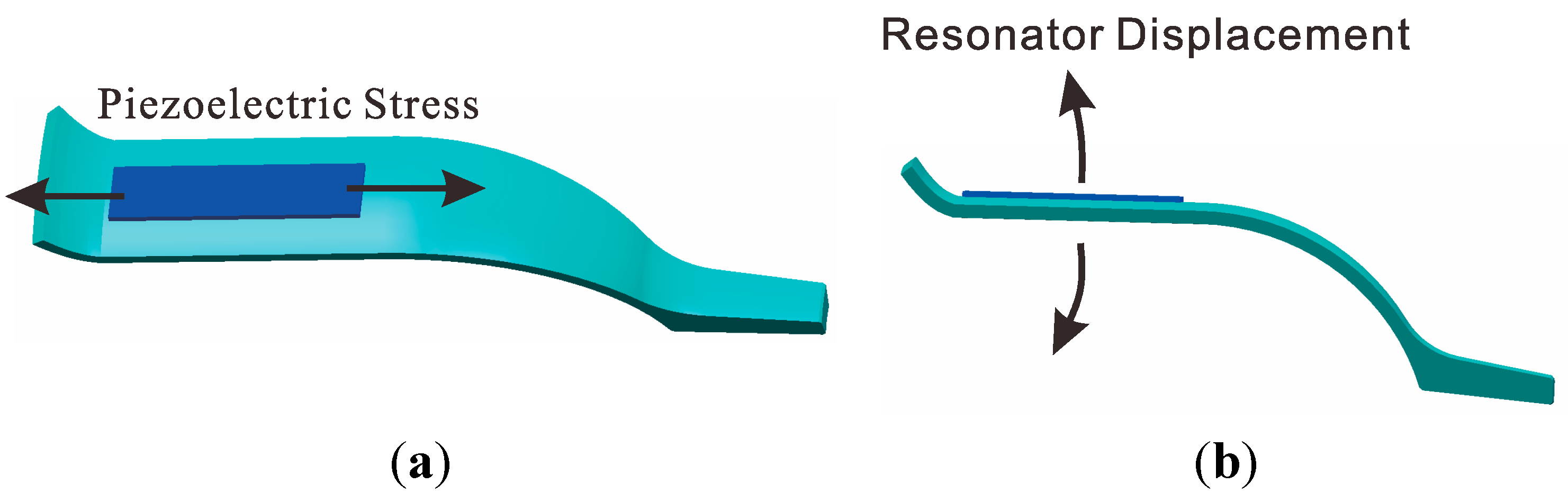
2.2. Excitation and Detection of Piezoelectricity
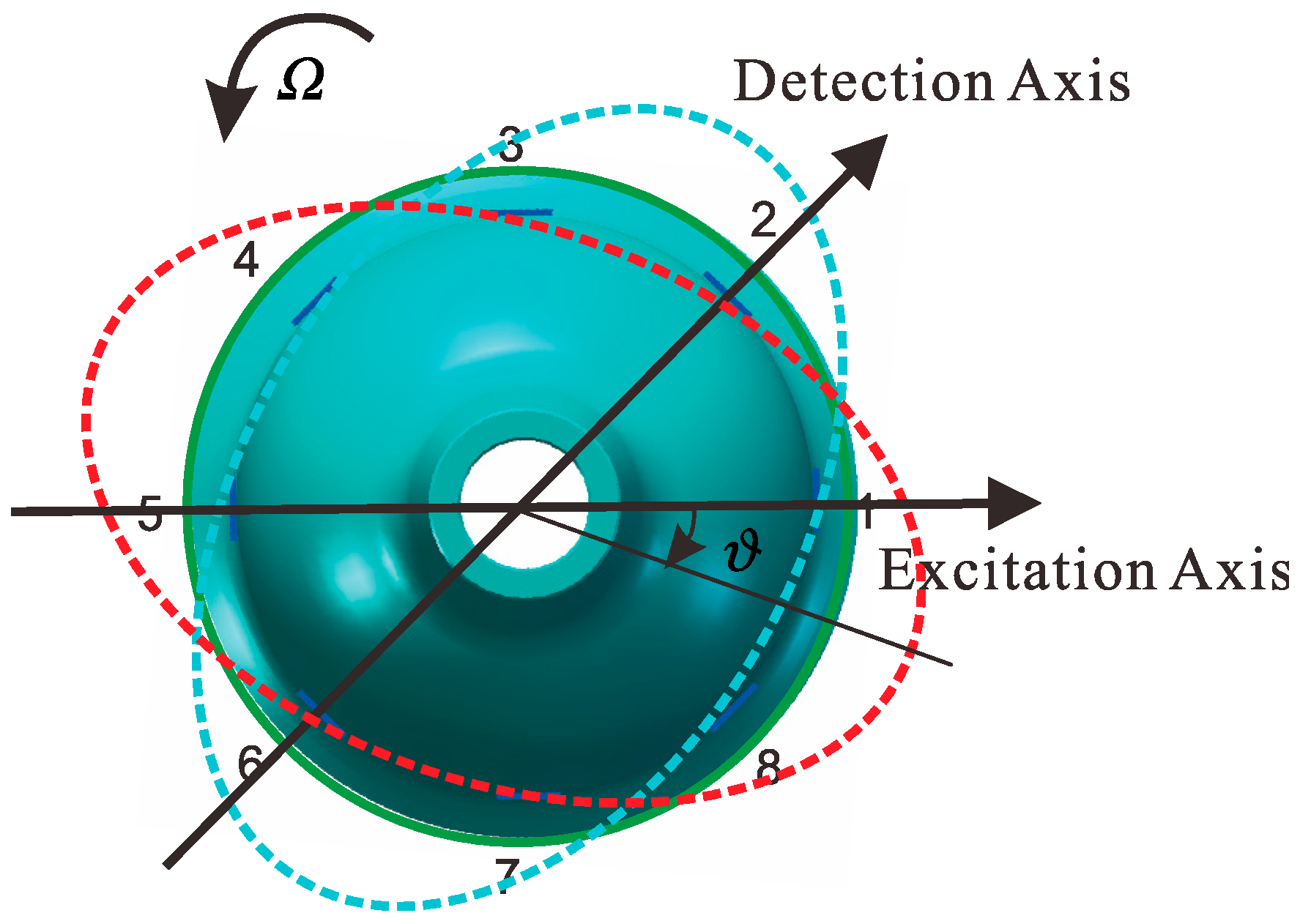
3. Error Model of Bell-Shaped Vibratory Gyro
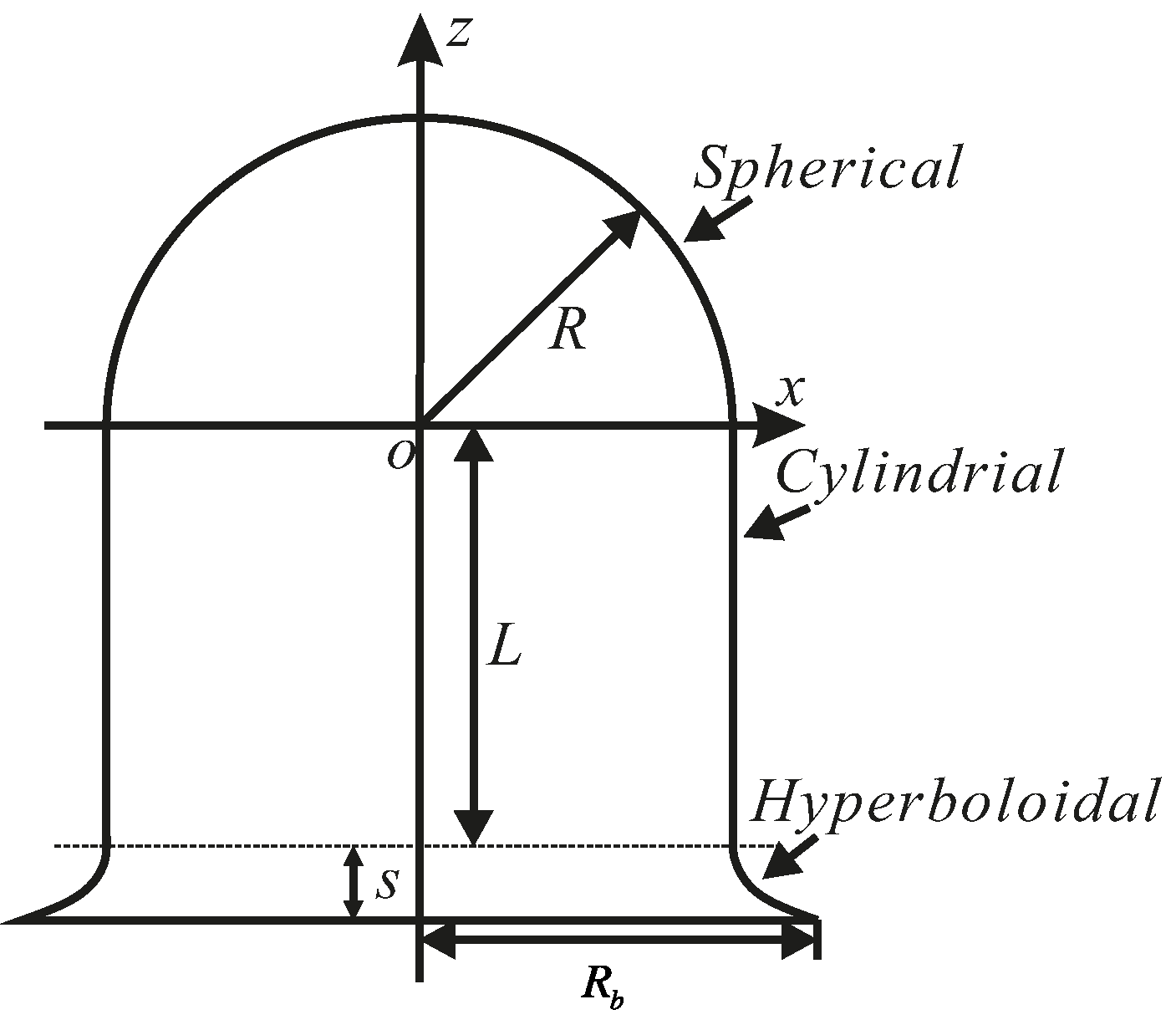
3.1. Dynamic Equation of Resonator’s Bottom Edge
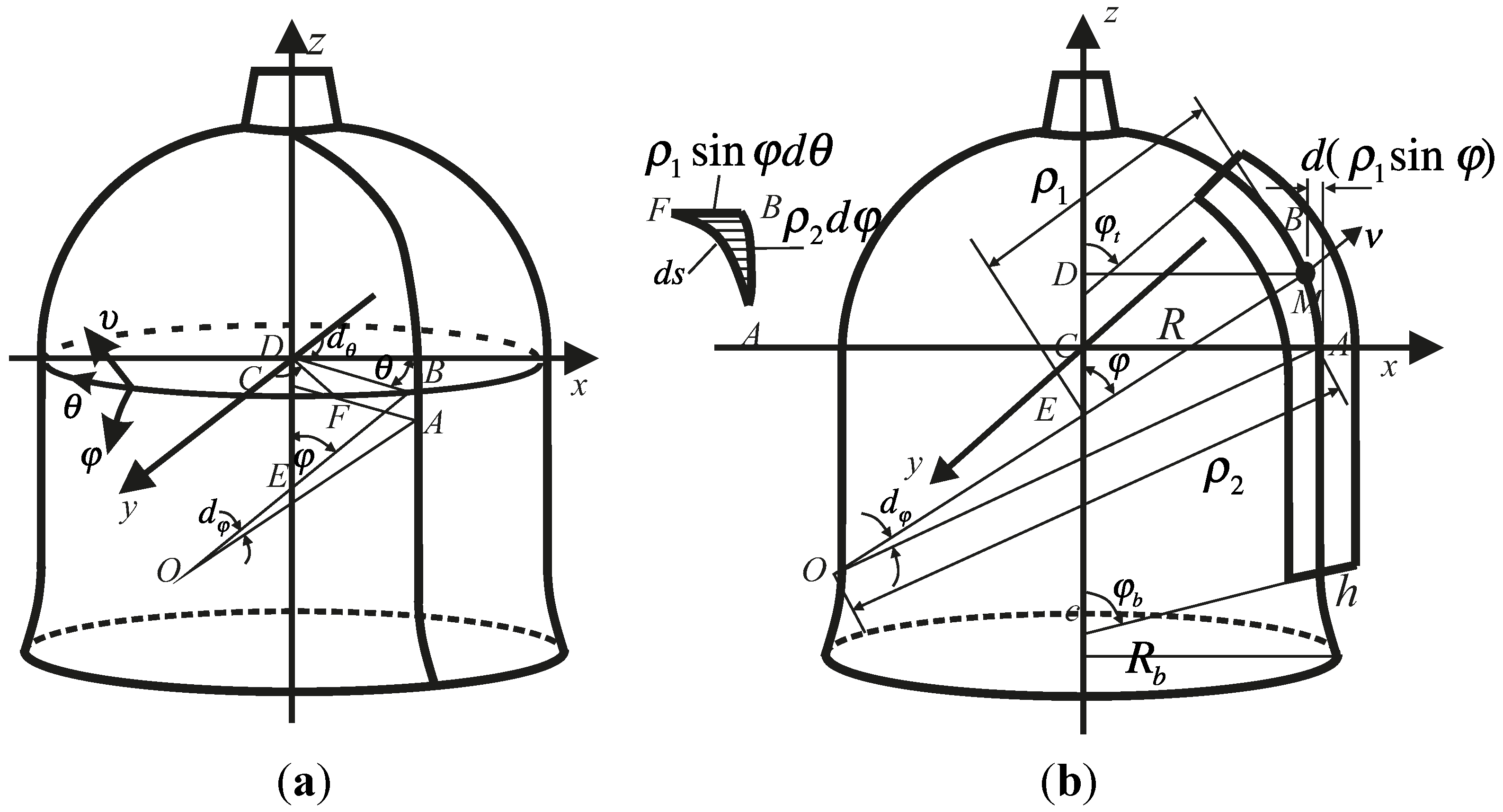
3.2. Angular Velocity Measurement
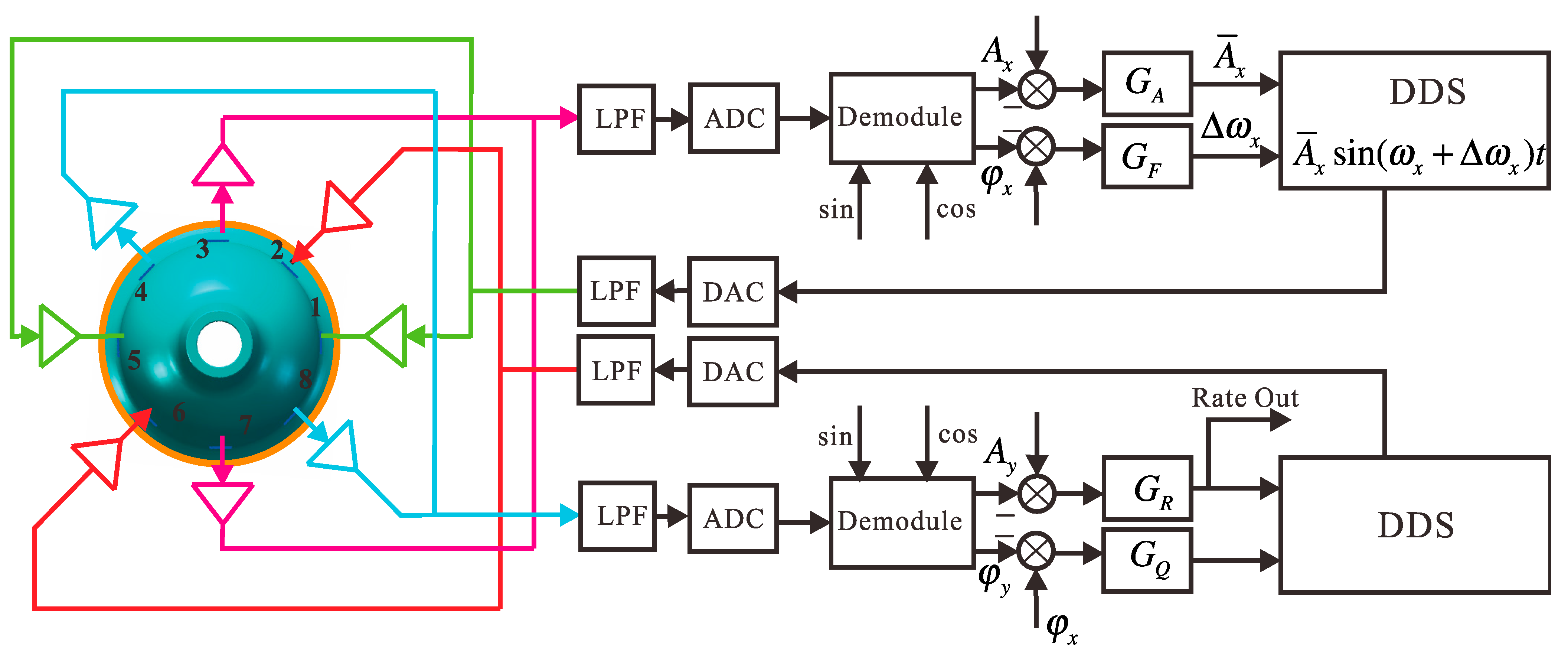
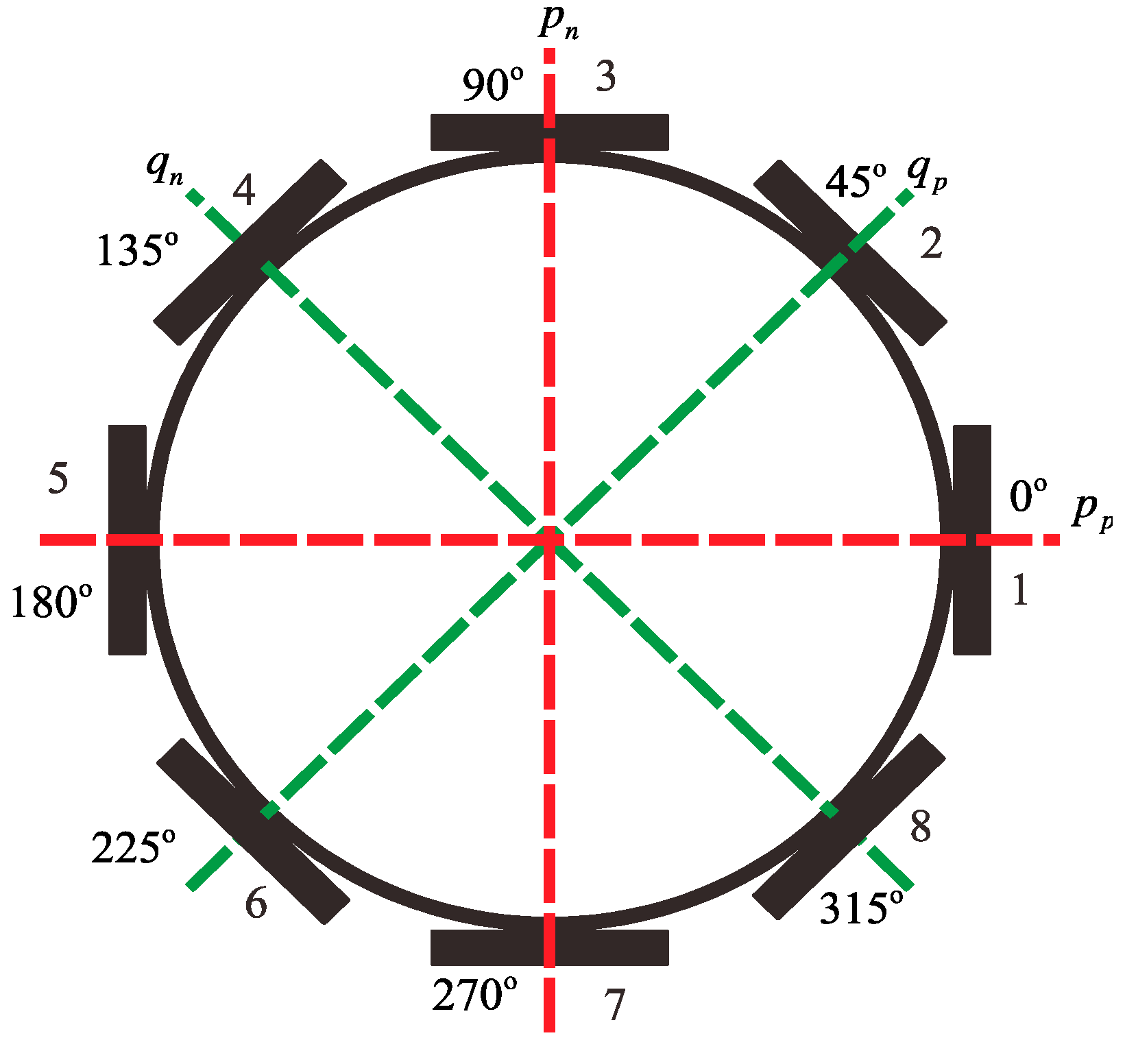
3.3. Error Model
4. Compensation Principle
4.1. Rough Compensation

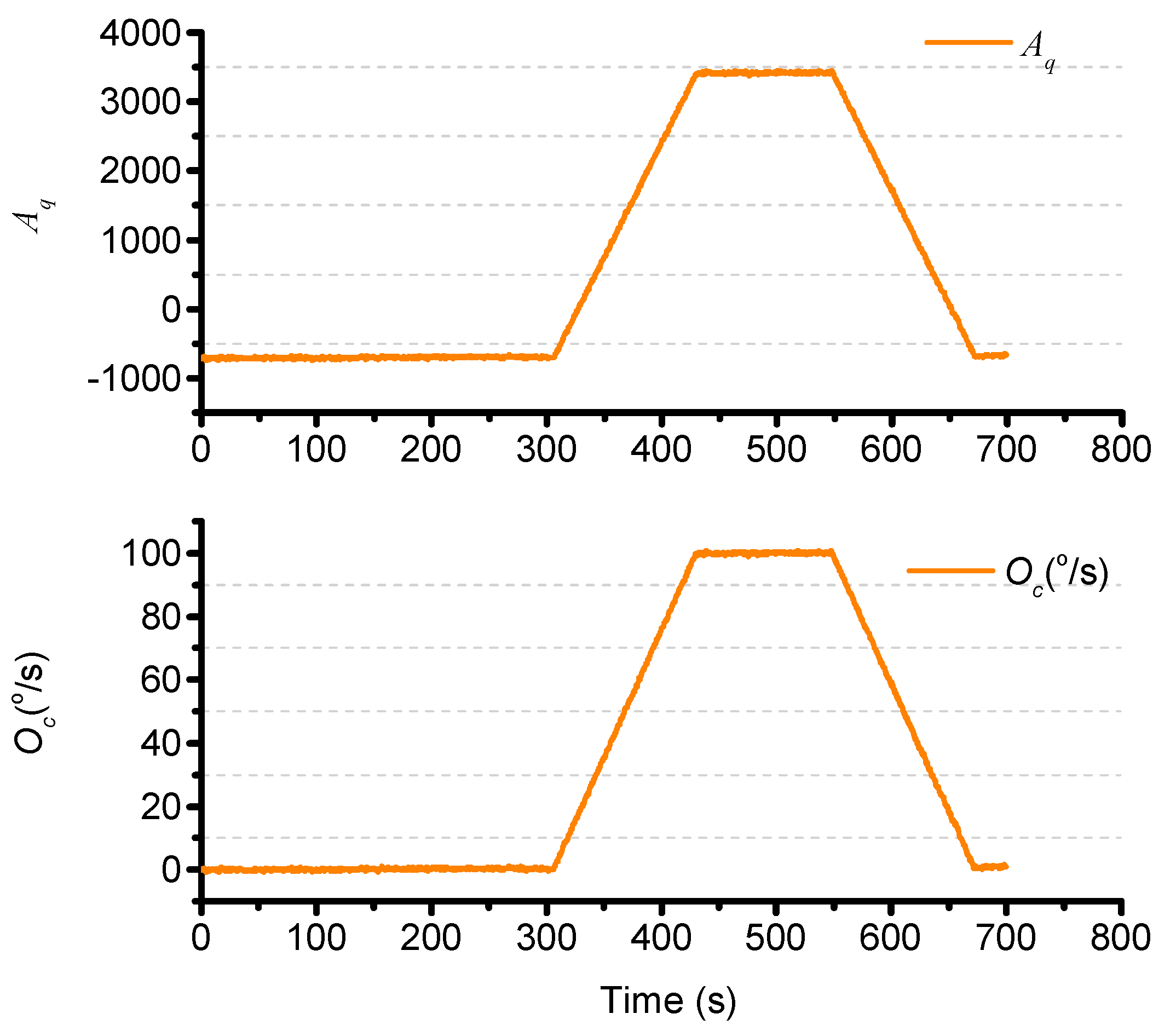
4.2. Bias Compensation
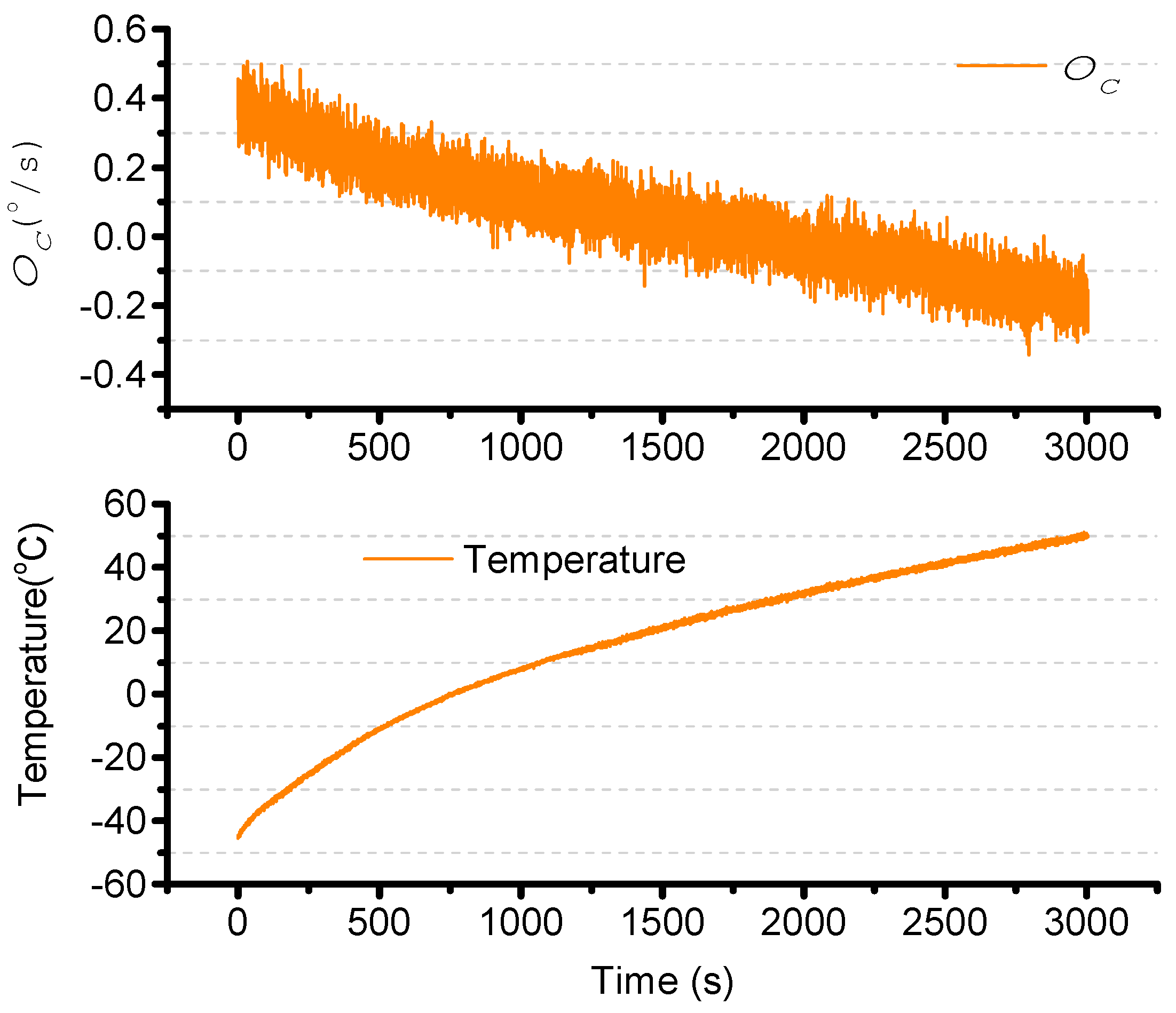
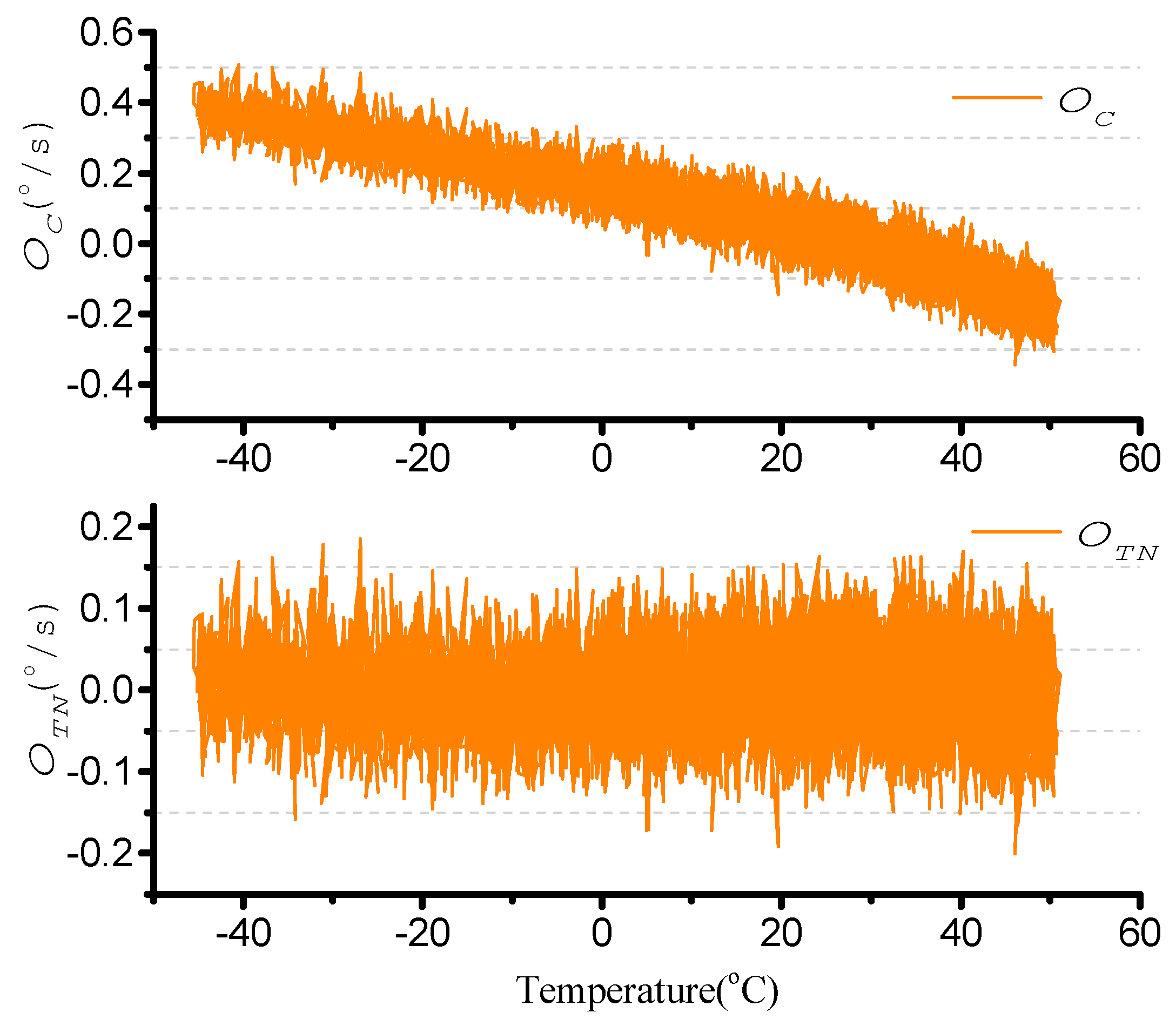
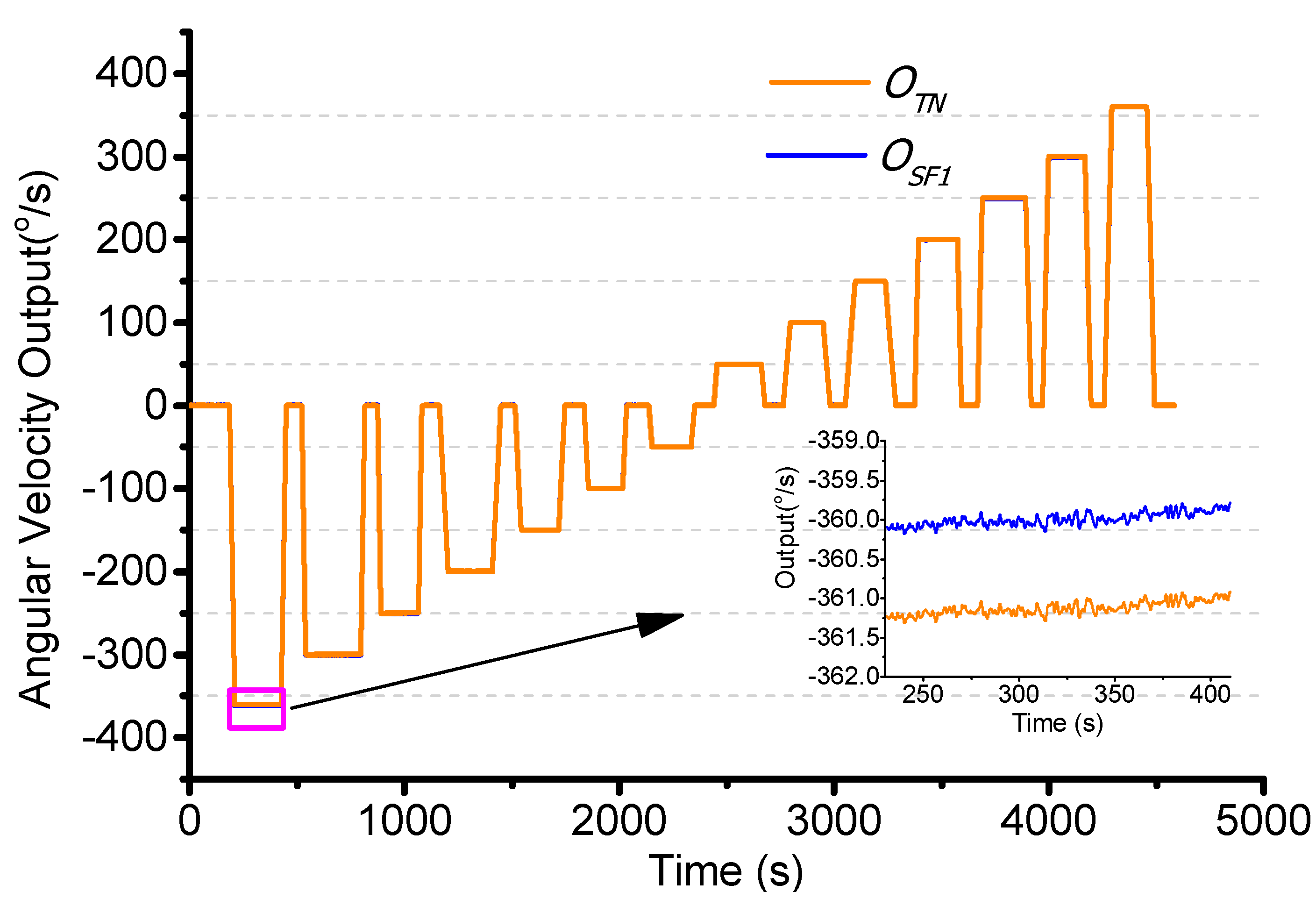
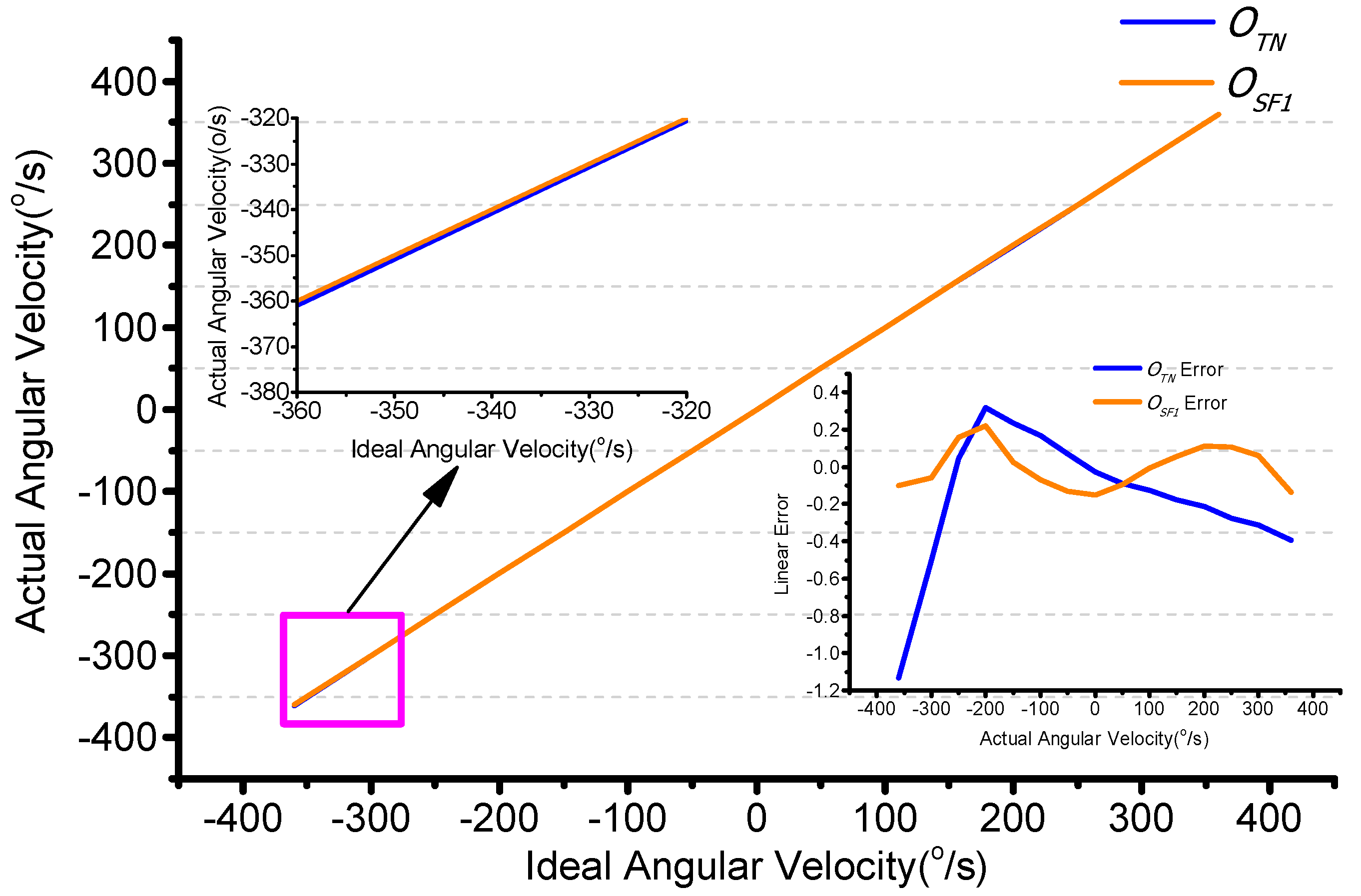
4.3. Scale Factor Compensation
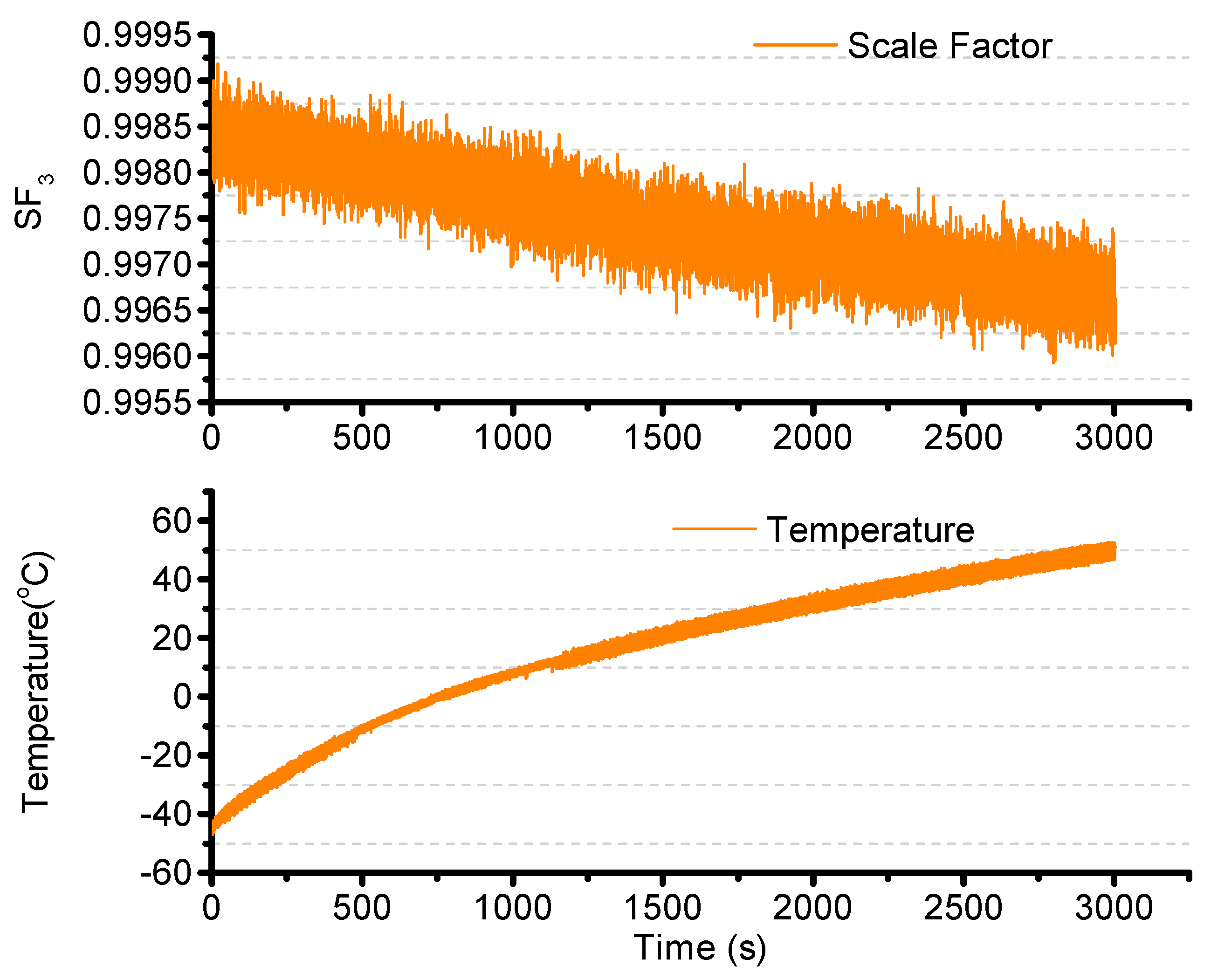
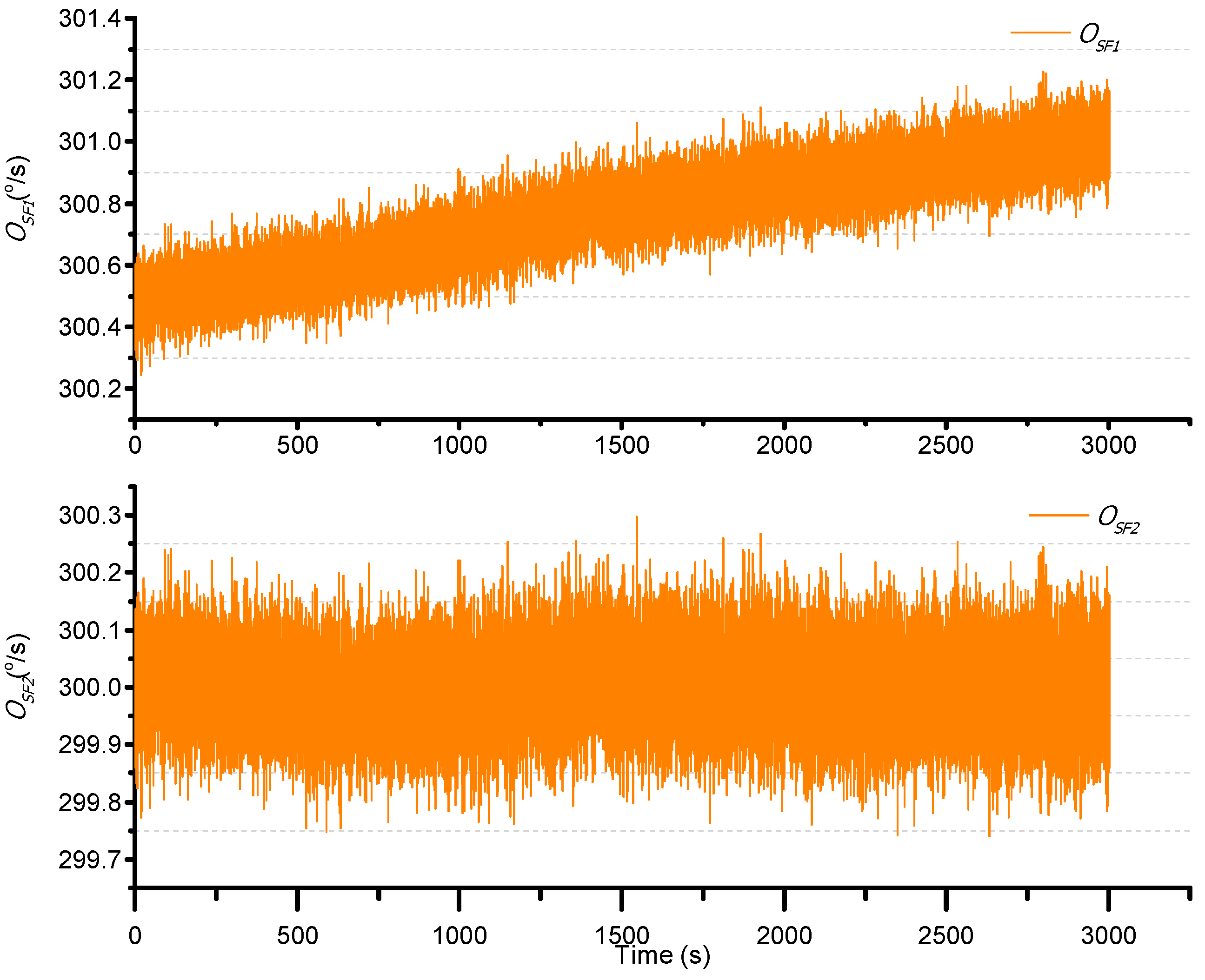
4.4. Noise Filter

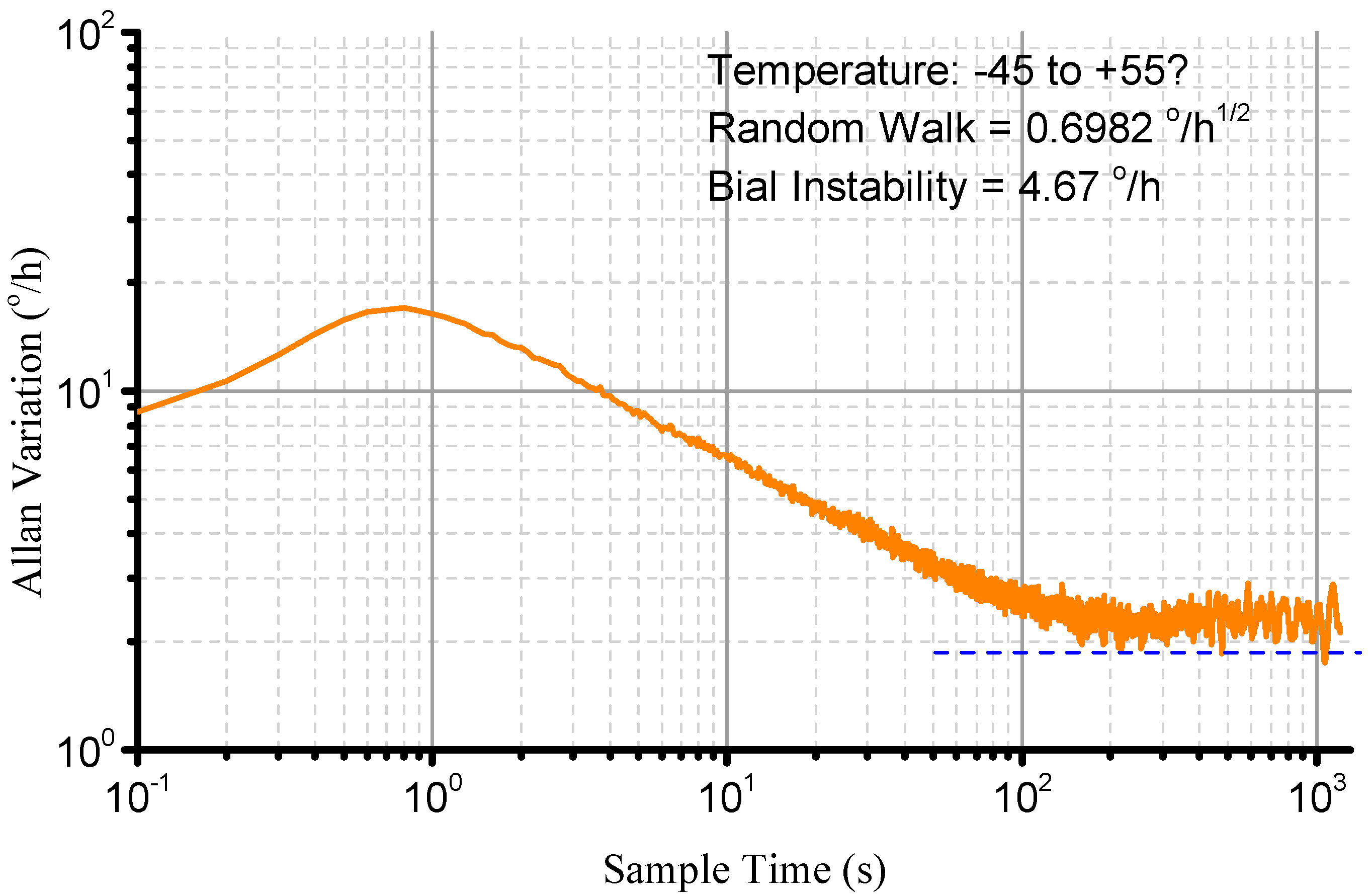
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Curey, R.K. Gyro and accelerometer panel: 50 years of service to the inertial community. IEEE Aerosp. Electron. Syst. Mag. 2013, 28, 23–29. [Google Scholar] [CrossRef]
- Armenise, M.N.; Ciminelli, C.; Dell’Olio, F.; Passaro, V.M.N. Advances in Gyroscope Technologies; Springer-Verlag: Berlin, Germany, 2011. [Google Scholar]
- Fan, Sh. Axisymmetric Shell Resonator Gyroscopes; National Defense Industry Press: Beijing, China, 2013. [Google Scholar]
- Matveev, V.A.; Basarab, M.A.; Alekin, A.V. Solid State Wave Gyro; National Defense Industry Press: Beijing, China, 2009. [Google Scholar]
- Liu, Y. Technology of Solid Wave Gyro and Navigation; China Aerospace Press: Beijing, China, 2010. [Google Scholar]
- Su, Z.; Fu, M.Y.; Li, Q.; Deng, Z.H.; Fan, J.F.; Liu, N.; Liu, H. Novel Bell-Shaped Vibrator Type Angular Rate Gyro. U.S. Patent 20140360266 A1, 11 December 2014. [Google Scholar]
- Su, Z.; Fu, M.; Li, Q.; Liu, N.; Liu, H. Research on bell-shaped vibratory angular rate gyro’s character of resonator. Sensors 2013, 13, 4724–4741. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Su, Z.; Li, Q.; Yin, F.; Hong, L.; Fang, F. Characterization of the bell-shaped vibratory angular rate gyro. Sensors 2013, 13, 10123–10150. [Google Scholar] [PubMed]
- Su, Z.; Liu, N.; Li, Q.; Fu, M.; Liu, H.; Fan, J. Research on the signal process of a bell-shaped vibratory angular Rate Gyro. Sensors 2014, 14, 5254–5277. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Su, Z.; Liu, H.; Fan, J. Adaptive sliding mode controller for bell-shaped vibratory angular rate gyro. In Proceedings of the 2014 33rd Chinese Control Conference (CCC), Nanjing, China, 28–30 July 2014; pp. 3521–3527.
- Ma, X.; Su, Z.; Li, Q.; Liu, H.; Liu, N. Quadrature drift mechanism and control of bell-shaped vibratory angular rate gyro. In Proceedings of the 2014 33rd Chinese Control Conference (CCC), Nanjing, China, 28–30 July 2014; pp. 593–597.
- Ma, X.; Su, Z. Analysis and compensation of mass imperfection effects on 3-D sensitive structure of bell-shaped vibratory gyro. Sens. Actuators A Phys. 2015, 224, 14–23. [Google Scholar] [CrossRef]
- Pi, J.; Bang, H. Imperfection parameter observer and drift compensation controller design of hemispherical resonator gyros. Int. J. Aeronaut. Space Sci. 2013, 14, 379–386. [Google Scholar] [CrossRef]
- Wang, X.; Wu, W.; Fang, Z.; Luo, B.; Li, Y.; Jiang, Q. Temperature drift compensation for hemispherical resonator gyro based on natural frequency. Sensors 2012, 12, 6434–6446. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Yi, G.; Jia, Y.; Wang, C. Realization on identification and compensation methods for the temperature model of hemispherical resonator gyro (HRG). In Proceedings of the 2011 International Conference on Electronic and Mechanical Engineering and Information Technology (EMEIT), Harbin, China, 12–14 August 2011.
- Peng, H.; Fang, Z.; Lin, K.; Zhou, Q.; Jiang, C. Error analysis of hemispherical resonator gyro drift data. In Proceedings of the 2nd International Symposium on Systems and Control in Aerospace and Astronautics, Harbin, China, 10–12 December 2008.
- Li, B.; Wu, Y.; Wang, C. The identification and compensation of temperature model for Hemispherical resonator gyro signal. In Proceedings of the 2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics (ISSCAA), Harbin, China, 8–10 June 2010.
- Wang, X.; Wu, W.; Luo, B.; Fang, Z.; Li, Y.; Jiang, Q. Force to rebalance control of HRG and suppression of its errors on the basis of FPGA. Sensors 2011, 11, 11761–11773. [Google Scholar] [CrossRef] [PubMed]
- Chikovani, V.V.; Yatsenko, Y.A.; Barabashov, A.S.; Marusyk, P.I.; Umakhanov, E.O.; Taturin, V.N. Improved accuracy metallic resonator CVG. IEEE Aerosp. Electron. Syst. Mag. 2009, 24, 40–43. [Google Scholar] [CrossRef]
- Watson, W.S. Vibratory gyro skewed pick-off and driver geometry. In Proceedings of the 2010 IEEE/ION Position Location and Navigation Symposium (PLANS), Indian Wells, CA, USA, 4–6 May 2010.
- Loveday, P.W. Analysis and Compensation of Imperfection Effects in Piezoelectric Vibratory Gyroscopes. Ph.D. Thesis, The Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 29 January 1999. [Google Scholar]
- Wu, Y.; Xi, X.; Tao, Y.; Wu, X.; Wu, X. A study of the temperature characters of vibration mode axes for vibratory cylinder gyroscopes. Sensors 2011, 11, 7665–7677. [Google Scholar] [CrossRef] [PubMed]
- Kristiansen, D.; Egeland, O. Modeling of nonlinear vibrations for analysis and control of cylinder gyroscopes. In Proceedings of the 37th IEEE Conference on Decision and Control, Tampa, FL, USA, 16–18 December 1998.
- Kang, J.H. Three-Dimensional Vibration Analysis of Thick Shells of Revolution with Arbitrary Curvature and Variable Thickness; The Ohio State University: Columbus, OH, USA, 1997. [Google Scholar]
- Shatalov, M.Y.; Joubert, S.V.; Coetzee, C.E.; Fedotov, I.A. Free vibration of rotating hollow spheres containing acoustic media. J. Sound Vib. 2009, 322, 1038–1047. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Z.; Liu, N.; Li, Q. Error Model and Compensation of Bell-Shaped Vibratory Gyro. Sensors 2015, 15, 23684-23705. https://doi.org/10.3390/s150923684
Su Z, Liu N, Li Q. Error Model and Compensation of Bell-Shaped Vibratory Gyro. Sensors. 2015; 15(9):23684-23705. https://doi.org/10.3390/s150923684
Chicago/Turabian StyleSu, Zhong, Ning Liu, and Qing Li. 2015. "Error Model and Compensation of Bell-Shaped Vibratory Gyro" Sensors 15, no. 9: 23684-23705. https://doi.org/10.3390/s150923684
APA StyleSu, Z., Liu, N., & Li, Q. (2015). Error Model and Compensation of Bell-Shaped Vibratory Gyro. Sensors, 15(9), 23684-23705. https://doi.org/10.3390/s150923684




