Optimization and Control of Cyber-Physical Vehicle Systems
Abstract
:1. Introduction

2. History of CPS

3. Cyber-Physical Vehicle Systems
3.1. Vehicle Control and Optimization Techniques
3.2. CPVS Co-Design Challenges
3.2.1. Energy Management
3.2.2. Fault Detection and Diagnosis
3.2.3. Computational Resource Management
3.2.4. Human Interaction
3.2.5. Unanticipated Scenarios
4. Control of Cyber-Physical Vehicle Systems
4.1. Anytime Control and Monitoring
4.2. Feedback Scheduling
4.3. Time-Varying Sampling and Sensor Scheduling
4.4. Event-Triggered Control
4.5. Coupled Cyber-Physical Co-Regulation
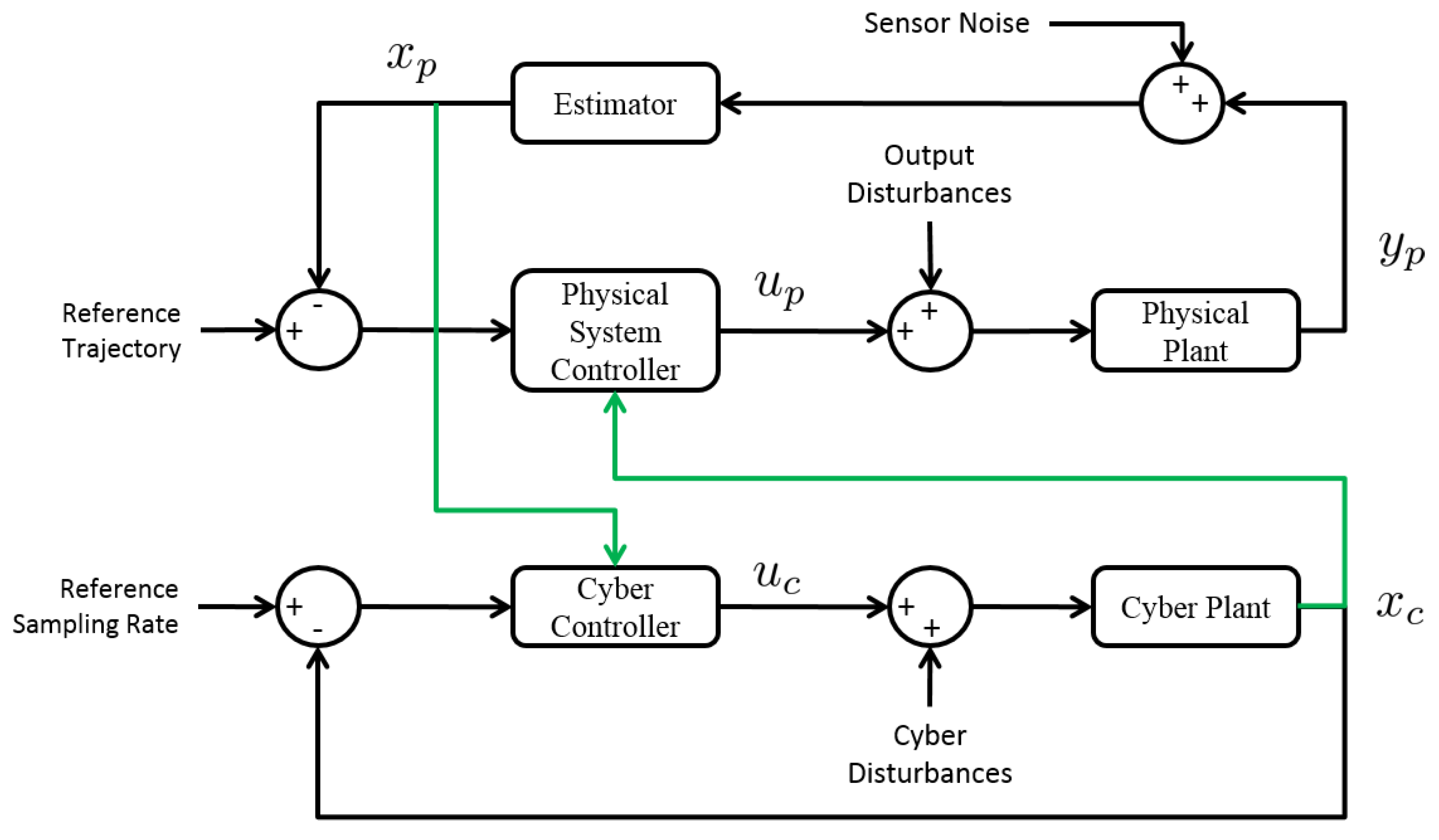
5. Trajectory and Task Optimization and Planning for Cyber-Physical Vehicle Systems
5.1. Physical Trajectory Optimization
5.2. Computing (Cyber) System Optimization
5.3. Co-Optimization
5.4. Co-Optimization Example
6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kim, K.D.; Kumar, P. Cyber–Physical Systems: A Perspective at the Centennial. IEEE Proc. 2012, 100, 1287–1308. [Google Scholar]
- Berger, C.; Rumpe, B. Autonomous Driving-5 Years after the Urban Challenge: The Anticipatory Vehicle as a Cyber-Physical System. In Proceedings of the 27th IEEE/ACM International Conference on Automated Software Engineering (ASE 2012), Essen, Germany, 3–7 September 2012.
- Kim, J.; Kim, H.; Lakshmanan, K.; Rajkumar, R.R. Parallel scheduling for cyber-physical systems: Analysis and case study on a self-driving car. In Proceedings of the ACM/IEEE 4th International Conference on Cyber-Physical Systems, Philadelphia, PA, USA, 8–11April 2013; ACM: New York, NY, USA; pp. 31–40.
- Saber, A.Y.; Venayagamoorthy, G.K. Efficient utilization of renewable energy sources by gridable vehicles in cyber-physical energy systems. IEEE Syst. J. 2010, 4, 285–294. [Google Scholar] [CrossRef]
- Zou, C.; Wan, J.; Chen, M.; Li, D. Simulation modeling of cyber-physical systems exemplified by unmanned vehicles with WSNs navigation. In Embedded and Multimedia Computing Technology and Service; Springer: New York, NY, USA, 2012; pp. 269–275. [Google Scholar]
- Abid, H.; Phuong, L.T.T.; Wang, J.; Lee, S.; Qaisar, S. V-Cloud: Vehicular cyber-physical systems and cloud computing. In Proceedings of the 4th International Symposium on Applied Sciences in Biomedical and Communication Technologies, Barcelona, Spain, 26–29 October 2011; ACM: New York, NY, USA.
- Fallah, Y.P.; Huang, C.; Sengupta, R.; Krishnan, H. Design of cooperative vehicle safety systems based on tight coupling of communication, computing and physical vehicle dynamics. In Proceedings of the 1st ACM/IEEE International Conference on Cyber-Physical Systems, Stockholm, Sweden, 12–15 April 2010; ACM: New York, NY, USA; pp. 159–167.
- Energetics Incorporated. Foundations for Innovation in Cyber-Physical Systems: Workshop Report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013. [Google Scholar]
- NSF. Cyber-Physical Systems; NSF: Ann Arbor, MI, USA, 2013; Available on line: http://www.nsf.gov/pubs/2013/nsf13502/nsf13502.htm (accessed on 31 January 2013).
- PCAST. Report to the President on Capturing Domestic Competitive Advantage in Advanced Manufacturing; Executive Office of the President, President’s Council of Advisors on Science and Technology (PCAST): Washington, DC, USA, 2012.
- PCAST. Ensuring American Leadership in Advanced Manufacturing; Executive Office of the President, President’s Council of Advisors on Science and Technology (PCAST): Washington, DC, USA, 2011.
- NITRD. High-Confidence Medical Devices: Cyber-Physical Systems for the 21st Century Health Care; Networking and Information Technology Research and Development (NITRD) Program: Arlington, VA, USA, 2009. [Google Scholar]
- PCAST. Report to the President Immediate Opportunities for Strengthening the Nation’s Cybersecurity; Executive Office of the President, President’s Council of Advisors on Science and Technology (PCAST): Washington, DC, USA, 2013.
- Kleissl, J.; Agarwal, Y. Cyber-physical energy systems: Focus on smart buildings. In Proceedings of the 47th Design Automation Conference, Anaheim, CA, USA, 13–18 June 2010; ACM: New York, NY, USA; pp. 749–754.
- Lee, I.; Sokolsky, O. Medical cyber physical systems. In Proceedings of the 2010 47th ACM/IEEE on Design Automation Conference (DAC), Anaheim, CA, USA; 2010; pp. 743–748. [Google Scholar]
- Cheng, A.M. Cyber-physical medical and medication systems. In Proceedings of the 28th International Conference on Distributed Computing Systems Workshops, Beijing, China, 17–20 June 2008; pp. 529–532.
- Jiang, Z.; Pajic, M.; Mangharam, R. Cyber–physical modeling of implantable cardiac medical devices. IEEE Proc. 2012, 100, 122–137. [Google Scholar] [CrossRef]
- Lee, I.; Sokolsky, O.; Chen, S.; Hatcliff, J.; Jee, E.; Kim, B.; King, A.; Mullen-Fortino, M.; Park, S.; Roederer, A.; et al. Challenges and research directions in medical cyber–physical systems. IEEE Proc. 2012, 100, 75–90. [Google Scholar]
- Ghorbani, M.; Bogdan, P. A cyber-physical system approach to artificial pancreas design. In Proceedings of the Ninth IEEE/ACM/IFIP International Conference on Hardware/Software Codesign and System Synthesis, Montreal, QC, Canada, 29 September–4 October 2013; IEEE Press: Piscataway, NJ, USA, 2013; p. 17. [Google Scholar]
- Bogdan, P.; Jain, S.; Goyal, K.; Marculescu, R. Implantable pacemakers control and optimization via fractional calculus approaches: A cyber-physical systems perspective. In Proceedings of the 2012 IEEE/ACM Third International Conference on Cyber-Physical Systems, Beijing, China, 17–19 April 2012; IEEE Computer Society: Washington, DC, USA, 2012; pp. 23–32. [Google Scholar]
- Karnouskos, S. Cyber-physical systems in the smartgrid. In Proceedings of the 2011 9th IEEE International Conference on Industrial Informatics (INDIN), Lisbon, Portugal, 26–29 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 20–23. [Google Scholar]
- Mo, Y.; Kim, T.H.; Brancik, K.; Dickinson, D.; Lee, H.; Perrig, A.; Sinopoli, B. Cyber–physical security of a smart grid infrastructure. IEEE Proc. 2012, 100, 195–209. [Google Scholar]
- Lee, E.A. Cyber physical systems: Design challenges. In Proceedings of the 2008 11th IEEE International Symposium on Object Oriented Real-Time Distributed Computing (ISORC), Orlando, FL, USA, 5–7 May 2008.
- Jamshidi, M. Systems of Systems Engineering: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Sztipanovits, J.; Koutsoukos, X.; Karsai, G.; Kottenstette, N.; Antsaklis, P.; Gupta, V.; Goodwine, B.; Baras, J.; Wang, S. Toward a Science of Cyber-Physical System Integration. IEEE Proc. 2012, 100, 29–44. [Google Scholar] [CrossRef]
- Bogdan, P.; Marculescu, R. Towards a science of cyber-physical systems design. In Proceedings of the 2011 IEEE/ACM International Conference on Cyber-Physical Systems (ICCPS), Chicago, IL, USA, 12–14 April 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 99–108. [Google Scholar]
- Sztipanovits, J.; Ying, S.; Cohen, I.; Corman, D.; Davis, J.; Khurana, H.; Mosterman, P.J.; Prasad, V.; Stormo, L. Strategic R&D Opportunities for 21st Century Cyber-Physical Systems; Technical Report for Steering Committee for Foundation in Innovation for Cyber-Physical Systems: Chicago, IL, USA; 13 March 2012.
- Wiener, N. Cybernetics or Control and Communication in the Animal and the Machine; MIT Press: Cambridge, MA, USA, 1965; Volume 25. [Google Scholar]
- Wikipedia. Internet-Related Prefixes. Available online: http://en.wikipedia.org/wiki/Internet-related_prefixes (accessed on 20 June 2014).
- Denyer, N. Plato: Alcibiades; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Murphy, R. Introduction to AI Robotics; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Gat, E. On Three-Layer Architectures. In Artificial Intelligence and Mobile Robots; AAAI Press: Cambridge, MA, USA, 1998; pp. 195–210. [Google Scholar]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Beard, R.W.; Kingston, D.; Quigley, M.; Snyder, D.; Christiansen, R.; Johnson, W.; McLain, T.; Goodrich, M. Autonomous vehicle technologies for small fixed-wing UAVs. J. Aerosp. Comput. Inf. Commun. 2005, 2, 92–108. [Google Scholar] [CrossRef]
- Bradley, J.M.; Atkins, E.M. A Cyber-Physical Optimization Approach to Mission Success for Unmanned Aircraft Systems. J. Aerosp. Inf. Syst. 2014, 11, 48–60. [Google Scholar]
- Bradley, J.M.; Atkins, E.M. Multi-Disciplinary Cyber-Physical Optimization for Unmanned Aircraft Systems. In Proceedings of the AIAA Infotech at Aerospace Conference and Exhibit, Garden Grove, CA, USA, 19–21 June 2012.
- Krishna, C.M.; Shin, K.G. On scheduling tasks with a quick recovery from failure. IEEE Trans. Comput. 1986, 100, 448–455. [Google Scholar] [CrossRef]
- Robust. Available online: http://www.merriam-webster.com/dictionary/robust (accessed on 1 August 2015).
- Skogestad, S.; Postlethwaite, I. Multivariable Feedback Control: Analysis and Design; Wiley: New York, NY, USA, 2007; Volume 2. [Google Scholar]
- Franklin, G.; Workman, M.; Powell, D. Digital Control of Dynamic Systems; Addison-Wesley Longman Publishing Co.: Boston, MA, USA, 1998. [Google Scholar]
- Aström, K.; Wittenmark, B. Computer-Controlled Systems: Theory and Design; Prentice-Hall: New York, NY, USA, 1984. [Google Scholar]
- Kim, J.; Lakshmanan, K.; Rajkumar, R.R. Rhythmic tasks: A new task model with continually varying periods for cyber-physical systems. In Proceedings of the 2012 IEEE/ACM Third International Conference on Cyber-Physical Systems, Beijing, China, 17–19 April 2012; IEEE Computer Society: Washington, DC, USA, 2012; pp. 55–64. [Google Scholar]
- Tabuada, P. Event-Triggered Real-Time Scheduling of Stabilizing Control Tasks. IEEE Trans. Autom. Control 2007, 52, 1680–1685. [Google Scholar] [CrossRef]
- Betts, J.T. Survey of numerical methods for trajectory optimization. AIAA J. Guid. Control Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Tomlin, C.; Lygeros, J.; Sastry, S. Synthesizing controllers for nonlinear hybrid systems. In Hybrid Systems: Computation and Control; Springer: New York, NY, USA, 1998; pp. 360–373. [Google Scholar]
- Kirk, D. Optimal Control Theory: An Introduction; Dover Publications: Mineola, NY, USA, 2004. [Google Scholar]
- Boddy, M.; Dean, T.L. Deliberation scheduling for problem solving in time-constrained environments. Artif. Intell. 1994, 67, 245–285. [Google Scholar] [CrossRef]
- Quagli, A.; Fontanelli, D.; Greco, L.; Palopoli, L.; Bicchi, A. Designing real-time embedded controllers using the anytime computing paradigm. In Proceedings of the IEEE Conference on Emerging Technologies & Factory Automation, Mallorca, Spain, 22–25 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–8. [Google Scholar]
- Arzén, K.; Cervin, A.; Eker, J.; Sha, L. An introduction to control and scheduling co-design. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 12–15 December 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 5, pp. 4865–4870. [Google Scholar]
- Cervin, A.; Eker, J.; Bernhardsson, B.; Årzén, K. Feedback–feedforward scheduling of control tasks. Real-Time Syst. 2002, 23, 25–53. [Google Scholar] [CrossRef]
- Eker, J.; Hagander, P.; Årzén, K. A Feedback Scheduler for Real-Time Control Tasks. Control Eng. Pract. 2000, 8, 1369–1378. [Google Scholar] [CrossRef]
- Branicky, M.; Phillips, S.; Zhang, W. Scheduling and Feedback Co-Design for Networked Control Systems. IEEE Trans. Autom. Control 2002, 2, 1211–1217. [Google Scholar]
- Zhang, W.; Branicky, M.; Phillips, S. Stability of Networked Control Systems. IEEE Control Syst. Mag. 2001, 21, 84–99. [Google Scholar] [CrossRef]
- Hespanha, J.; Naghshtabrizi, P.; Xu, Y. A survey of recent results in networked control systems. IEEE Proc. 2007, 95, 138–162. [Google Scholar] [CrossRef]
- Nerode, A.; Kohn, W. Models for Hybrid Systems: Automata, Topologies, Controllability, Observability. Hybrid Syst. 1993, 736, 317–356. [Google Scholar]
- Branicky, M.S. Multiple Lyapunov Functions and Other Analysis Tools for Switched and Hybrid Systems. IEEE Trans. Autom. Control 1998, 43, 475–482. [Google Scholar] [CrossRef]
- Branicky, M.; Borkar, V.; Mitter, S. A unified framework for hybrid control: Model and optimal control theory. IEEE Trans. Autom. Control 1998, 43, 31–45. [Google Scholar] [CrossRef]
- Fridman, E.; Seuret, A.; Richard, J.P. Robust sampled-data stabilization of linear systems: An input delay approach. Automatica 2004, 40, 1441–1446. [Google Scholar] [CrossRef]
- Sala, A. Computer control under time-varying sampling period: An LMI gridding approach. Automatica 2005, 41, 2077–2082. [Google Scholar] [CrossRef]
- Schinkel, M.; Chen, W.H.; Rantzer, A. Optimal control for systems with varying sampling rate. In Proceedings of the 2002 American Control Conference, Anchorage, AK, USA, 8–10 May 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 4, pp. 2979–2984. [Google Scholar]
- Gupta, V.; Chung, T.H.; Hassibi, B.; Murray, R.M. On a stochastic sensor selection algorithm with applications in sensor scheduling and sensor coverage. Automatica 2006, 42, 251–260. [Google Scholar] [CrossRef]
- Savkin, A.V.; Evans, R.J.; Skafidas, E. The problem of optimal robust sensor scheduling. Syst. Control Lett. 2001, 43, 149–157. [Google Scholar] [CrossRef]
- He, Y.; Chong, E.K. Sensor scheduling for target tracking in sensor networks. In Proceedings of the 43rd IEEE Conference on Decision and Control, Paradise Islands, The Bahamas, 14–17 December 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 1, pp. 743–748. [Google Scholar]
- Krishnamurthy, V. Algorithms for optimal scheduling and management of hidden Markov model sensors. IEEE Trans. Signal Proc. 2002, 50, 1382–1397. [Google Scholar] [CrossRef]
- Evans, J.; Krishnamurthy, V. Optimal sensor scheduling for hidden Markov model state estimation. Int. J. Control 2001, 74, 1737–1742. [Google Scholar] [CrossRef]
- Bradley, J.M. Toward Co-Design of Autonomous Aerospace Cyber-Physical Systems. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2014. [Google Scholar]
- Musardo, C.; Rizzoni, G.; Guezennec, Y.; Staccia, B. A-ECMS: An adaptive algorithm for hybrid electric vehicle energy management. Eur. J. Control 2005, 11, 509–524. [Google Scholar] [CrossRef]
- Moreno, J.; Ortúzar, M.E.; Dixon, J.W. Energy-management system for a hybrid electric vehicle, using ultracapacitors and neural networks. IEEE Trans. Ind. Electron. 2006, 53, 614–623. [Google Scholar] [CrossRef]
- Thounthong, P.; Rael, S.; Davat, B. Energy management of fuel cell/battery/supercapacitor hybrid power source for vehicle applications. J. Power Sources 2009, 193, 376–385. [Google Scholar] [CrossRef]
- Lin, X.; Wang, Y.; Bogdan, P.; Chang, N.; Pedram, M. Reinforcement learning based power management for hybrid electric vehicles. In Proceedings of the 2014 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 2–6 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 33–38. [Google Scholar]
- Lin, X.; Wang, Y.; Bogdan, P.; Chang, N.; Pedram, M. Optimizing Fuel Economy of Hybrid Electric Vehicles Using a Markov Decision Process Model. In Proceedings of the Intelligent Vehicles Symposium (IV), Dearborn, MI, USA, 8–11 June 2014; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Broderick, J.A.; Tilbury, D.M.; Atkins, E.M. Characterizing energy usage of a commercially available ground robot: Method and results. J. Field Robot. 2014, 31, 441–454. [Google Scholar] [CrossRef]
- Broderick, J.A.; Tilbury, D.M.; Atkins, E.M. Optimal coverage trajectories for a UGV with tradeoffs for energy and time. Auton. Robot. 2014, 36, 257–271. [Google Scholar] [CrossRef]
- Calise, A.J. Extended energy management methods for flight performance optimization. Aiaa J. 1977, 15, 314–321. [Google Scholar] [CrossRef]
- Corban, J.; Calise, A.; Flandro, G. Rapid near-optimal aerospace plane trajectory generation and guidance. J. Guid. Control Dyn. 1991, 14, 1181–1190. [Google Scholar] [CrossRef]
- Tsiotras, P.; Shen, H.; Hall, C. Satellite attitude control and power tracking with energy/ momentum wheels. J. Guid. Control Dyn. 2001, 24, 23–34. [Google Scholar] [CrossRef]
- Isermann, R. Fault-Diagnosis Systems: An Introduction From Fault Detection to Fault Tolerance; Springer Science & Business Media: Berlin, Germany; Heidelberg, Germany, 2006. [Google Scholar]
- Baleani, M.; Ferrari, A.; Mangeruca, L.; Sangiovanni-Vincentelli, A.; Peri, M.; Pezzini, S. Fault-tolerant platforms for automotive safety-critical applications. In Proceedings of the 2003 International Conference on Compilers, Architecture and Synthesis for Embedded Systems, San Jose, CA, USA, 30 October–1 November 2003; ACM: New York, NY, USA, 2003; pp. 170–177. [Google Scholar]
- Frank, P.M. Fault diagnosis in dynamic systems using analytical and knowledge-based redundancy: A survey and some new results. Automatica 1990, 26, 459–474. [Google Scholar] [CrossRef]
- Freddi, A.; Lanzon, A.; Longhi, S. A feedback linearization approach to fault tolerance in quadrotor vehicles. In Proceedings of the 2011 IFAC World Congress, Milan, Italy, 28 August–2 September 2011; Volume 170.
- Torres-Pomales, W. Software Fault Tolerance: A Tutorial; NASA Technical Report, NASA-2000-tm210616; NASA: Washington, DC, USA, 2000. [Google Scholar]
- Randell, B. System Structure for Software Fault Tolerance; ACM SIGPLAN Notices; ACM: New York, NY, USA, 1975; Volume 10, pp. 437–449. [Google Scholar]
- Kalbarczyk, Z.T.; Iyer, R.K.; Bagchi, S.; Whisnant, K. Chameleon: A software infrastructure for adaptive fault tolerance. IEEE Trans. Parallel Distrib. Syst. 1999, 10, 560–579. [Google Scholar] [CrossRef]
- Reis, G.A.; Chang, J.; Vachharajani, N.; Rangan, R.; August, D.I. SWIFT: Software implemented fault tolerance. In Proceedings of the International Symposium on Code Generation and Optimization, San Jose, CA, USA, 20–23 March 2005; IEEE Computer Society: Washington, DC, USA, 2005; pp. 243–254. [Google Scholar]
- Fawzi, H.; Tabuada, P.; Diggavi, S. Secure estimation and control for cyber-physical systems under adversarial attacks. IEEE Trans. Autom. Control 2014, 59, 1454–1467. [Google Scholar] [CrossRef]
- Pasqualetti, F.; Dorfler, F.; Bullo, F. Attack detection and identification in cyber-physical systems. IEEE Trans. Autom. Control 2013, 58, 2715–2729. [Google Scholar] [CrossRef]
- Xia, F. Feedback scheduling of real-time control systems with resource constraints. J. Comput. Sci. Technol. 2007, 7, 263–264. [Google Scholar]
- Salvendy, G. Handbook of Human Factors and Ergonomics; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Lamm, R.; Psarianos, B.; Mailaender, T. Highway Design and Traffic Safety Engineering Handbook; McGraw-Hill Professional Publishing: New York, NY, USA, 1999. [Google Scholar]
- Wiener, E.L.; Nagel, D.C. Human Factors in Aviation; Gulf Professional Publishing: Houston, TX, USA, 1988. [Google Scholar]
- Grech, M.; Horberry, T.; Koester, T. Human Factors in the Maritime Domain; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Shappell, S.A.; Wiegmann, D.A. A Human Error Approach to Aviation Accident Analysis: The Human Factors Analysis and Classification System; Ashgate Publishing, Ltd.: Surrey, UK, 2012. [Google Scholar]
- Li, X.; Yu, X.; Wagh, A.; Qiao, C. Human factors-aware service scheduling in vehicular cyber-physical systems. In Proceedings of the 2011 IEEE INFOCOM, Shanghai, China, 10–15 April 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 2174–2182. [Google Scholar]
- Schirner, G.; Erdogmus, D.; Chowdhury, K.; Padir, T. The future of human-in-the-loop cyber-physical systems. Computer 2013, 46, 36–45. [Google Scholar] [CrossRef]
- Poovendran, R. Cyber–Physical Systems: Close Encounters Between Two Parallel Worlds. IEEE Proc. 2010, 98, 1363–1366. [Google Scholar] [CrossRef]
- Lavretsky, E.; Wise, K. Robust and Adaptive Control: With Aerospace Applications; Springer Science & Business Media: Berlin, Germany; Heidelberg, Germany, 2012. [Google Scholar]
- Evers, L.; Dollevoet, T.; Barros, A.I.; Monsuur, H. Robust UAV mission planning. Ann. Oper. Res. 2014, 222, 293–315. [Google Scholar] [CrossRef]
- Angelov, P. Autonomous Learning Systems: From Data Streams to Knowledge in Real-Time; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Prokopenko, M.; Wang, P. On Self-referential shape replication in robust aerospace vehicles. In Proceedings of the Artificial Life IX: 9th International Conference on the Simulation and Synthesis of Living Systems, Boston, MA, USA, 12–15 September 2004; pp. 27–32.
- Aström, K.J.; Murray, R.M. Feedback Systems: An Introduction for Scientists and Engineers; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Hellerstein, J.L.; Diao, Y.; Parekh, S.; Tilbury, D.M. Feedback Control of Computing Systems; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Zilberstein, S.; Russell, S.J. Anytime Sensing, Planning and Action: A Practical Model for Robot Control. In Proceedings of the International Joint Conferences on Artificial Intelligence, Chambéry, France, 28 August–3 September 1993; Volume 93, pp. 1402–1407.
- Gupta, V. On an anytime algorithm for control. In Proceedings of the 48th IEEE Conference on Decision and Control, Shanghai, China, 15–18 December 2009; IEEE: Piscataway, NJ, USA, 2010; pp. 6218–6223. [Google Scholar]
- Michalska, H.; Mayne, D.Q. Robust receding horizon control of constrained nonlinear systems. IEEE Trans. Autom. Control 1993, 38, 1623–1633. [Google Scholar] [CrossRef]
- Henriksson, D.; Åkesson, J. Flexible Implementation of Model Predictive Control Using Sub-Optimal Solutions; Lund University: Lund, Sweden, 2004. [Google Scholar]
- McGovern, L.K.; Feron, E. Closed-loop stability of systems driven by real-time, dynamic optimization algorithms. In Proceedings of the 38th IEEE Conference on Decision and Control, Phoenix, AZ, USA, 7–10 December 1999; IEEE: Piscataway, NJ, USA, 1999; Volume 4, pp. 3690–3696. [Google Scholar]
- Bradley, J.M.; Atkins, E.M. Computational-Physical State Co-Regulation in Cyber-Physical Systems. In Proceedings of the 2011 ACM/IEEE Conference on Cyber-Physical Systems, Chicago, IL, USA, 12–14 April 2011.
- Bradley, J.M.; Atkins, E.M. Toward Continuous State-Space Regulation of Coupled Cyber-Physical Systems. IEEE Proc. 2012, 100, 60–74. [Google Scholar] [CrossRef]
- Russell, S.J.; Zilberstein, S. Composing Real-Time Systems. In Proceedings of the International Jonit Conferences on Artificial Intelligence, Sydney, Australia, 24–30 August 1991; Volume 91, pp. 212–217.
- Zilberstein, S. Using anytime algorithms in intelligent systems. AI Mag. 1996, 17, 73. [Google Scholar]
- Hansen, E.A.; Zilberstein, S. Monitoring and control of anytime algorithms: A dynamic programming approach. Artif. Intell. 2001, 126, 139–157. [Google Scholar] [CrossRef]
- Finkelstein, L.; Markovitch, S. Optimal schedules for monitoring anytime algorithms. Artif. Intell. 2001, 126, 63–108. [Google Scholar] [CrossRef]
- Samad, T.; Cofer, D.; Ha, V.; Binns, P. High-confidence control: Ensuring reliability in high-performance real-time systems. Int. J. Intell. Syst. 2004, 19, 315–326. [Google Scholar] [CrossRef]
- Sha, L.; Abdelzaher, T.; Årzén, K.; Cervin, A.; Baker, T.; Burns, A.; Buttazzo, G.; Caccamo, M.; Lehoczky, J.; Mok, A. Real-time Scheduling Theory: A Historical Perspective. Real-time Syst. 2004, 28, 101–155. [Google Scholar] [CrossRef]
- Cervin, A. Integrated Control and Real-Time Scheduling. Ph.D. Thesis, Lund University, Lund, Sweden, 2003. [Google Scholar]
- Eker, J.; Cervin, A. A Matlab toolbox for real-time and control systems co-design. In Proceedings of the Sixth International Conference on Real-Time Computing Systems and Applications, Hong Kong, China, 13–15 December 1999; IEEE: Piscataway, NJ, USA, 1999; pp. 320–327. [Google Scholar]
- Lincoln, B.; Cervin, A. JITTERBUG: A tool for analysis of real-time control performance. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 2, pp. 1319–1324. [Google Scholar]
- Henriksson, D.; Cervin, A.; Årzén, K.E. TrueTime: Real-time control system simulation with MATLAB/Simulink. In Proceedings of the Nordic Matlab Conference, Copenhagen, Denmark, 21–22 October 2003.
- Henriksson, D.; Cervin, A.; Årzén, K.E. TrueTime: Simulation of control loops under shared computer resources. In Proceedings of the 15th IFAC World Congress on Automatic Control, Barcelona, Spain, 21–26 July 2002.
- Aström, K.J.; Bernhardsson, B.M. Comparison of Riemann and Lebesgue sampling for first order stochastic systems. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; IEEE: Piscataway, NJ, USA, 2002; Volume 2, pp. 2011–2016. [Google Scholar]
- Heemels, W.; Johansson, K.H.; Tabuada, P. An introduction to event-triggered and self-triggered control. In Proceedings of the 2012 IEEE 51st Annual Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 3270–3285. [Google Scholar]
- Velasco, M.; Martí, P.; Bini, E. On Lyapunov Sampling for Event-Driven Controllers. In Proceedings of the 48th IEEE Conference on Decision and Control, 2009 Held Jointly with the 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 6238–6243. [Google Scholar]
- Lunze, J.; Lehmann, D. A state-feedback approach to event-based control. Automatica 2010, 46, 211–215. [Google Scholar] [CrossRef]
- Heemels, W.; Sandee, J.; van den Bosch, P. Analysis of event-driven controllers for linear systems. Int. J. Control 2008, 81, 571–590. [Google Scholar] [CrossRef]
- Lemmon, M.; Chantem, T.; Hu, X.S.; Zyskowski, M. On self-triggered Full-Information H-Infinity Controllers. In Hybrid Systems: Computation and Control; Springer: New York, NY, USA, 2007; pp. 371–384. [Google Scholar]
- Bradley, J.M.; Atkins, E.M. Coupled Cyber-Physical System Modeling and Coregulation of a CubeSat. IEEE Trans. Robot. 2015, 31, 443–456. [Google Scholar] [CrossRef]
- Rao, S.S.; Rao, S. Engineering Optimization: Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Venkataraman, P. Applied Optimization with MATLAB Programming; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Wolf, W.H. Hardware-software co-design of embedded systems [and prolog]. IEEE Proc. 1994, 82, 967–989. [Google Scholar] [CrossRef]
- Chiodo, M.; Engels, D.; Giusto, P.; Hsieh, H.; Jurecska, A.; Lavagno, L.; Suzuki, K.; Sangiovanni-Vincentelli, A. A case study in computer-aided co-design of embedded controllers. Des. Autom. Embed. Syst. 1996, 1, 51–67. [Google Scholar] [CrossRef]
- Cassandras, C.G.; Li, W. Sensor networks and cooperative control. Eur. J. Control 2005, 11, 436–463. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W.; Atkins, E.M. Information consensus in multivehicle cooperative control. IEEE Control Syst. 2007, 27, 71–82. [Google Scholar] [CrossRef]
- Cao, X.; Cheng, P.; Chen, J.; Sun, Y. An online optimization approach for control and communication codesign in networked cyber-physical systems. IEEE Trans. Ind. Inform. 2013, 9, 439–450. [Google Scholar] [CrossRef]
- Song, Z.; Chen, Y.; Sastry, C.R.; Tas, N.C. Optimal Observation for Cyber-Physical Systems: A Fisher-Information-Matrix-Based Approach; Springer Science & Business Media: Berlin, Germany; Heidelberg, Germany, 2009. [Google Scholar]
- Dubins, L.E. On curves of minimal length with a constraint on average curvature, and with prescribed initial and terminal positions and tangents. Am. J. Math. 1957, 79, 497–516. [Google Scholar] [CrossRef]
- Shanmugavel, M.; Tsourdos, A.; White, B.; Żbikowski, R. Co-operative path planning of multiple UAVs using Dubins paths with clothoid arcs. Control Eng. Pract. 2010, 18, 1084–1092. [Google Scholar] [CrossRef]
- Savla, K.; Frazzoli, E.; Bullo, F. On the point-to-point and traveling salesperson problems for Dubins’ vehicle. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 786–791. [Google Scholar]
- Reeds, J.; Shepp, L. Optimal paths for a car that goes both forwards and backwards. Pac. J. Math. 1990, 145, 367–393. [Google Scholar] [CrossRef]
- Chitsaz, H.; LaValle, S.M. Time-optimal paths for a Dubins airplane. In Proceedings of the 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 2379–2384. [Google Scholar]
- Bryson, A.E. Applied Optimal Control: Optimization, Estimation and Control; CRC Press: Boca Raton, FL, USA, 1975. [Google Scholar]
- Pontryagin, L.S. Mathematical Theory of Optimal Processes; CRC Press: Boca Raton, FL, USA, 1987. [Google Scholar]
- Pontryagin, L.; Boltyanskii, V.; Gamkredidze, R.; Mishchenko, E. The Mathematical Theory of Optimal Processes; Interscience: New York, NY, USA, 1961. [Google Scholar]
- Tsiotras, P. Stabilization and optimality results for the attitude control problem. J. Guid. Control Dyn. 1996, 19, 772–779. [Google Scholar] [CrossRef]
- Lennon, J.A.; Atkins, E.M. Multi-objective spacecraft trajectory optimization with synthetic agent oversight. J. Aerosp. Comput. Inf. Commun. 2005, 2, 4–24. [Google Scholar] [CrossRef]
- Bortoff, S.A. Path planning for UAVs. In Proceedings of the American Control Conference, Chicago, IL, USA, 28–30 June 2000; IEEE: Piscataway, NJ, USA, 2000; Volume 1, pp. 364–368. [Google Scholar]
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming; Siam: Philadelphia, PA, USA; Volume 19.
- Kurina, G.A.; März, R. On linear-quadratic optimal control problems for time-varying descriptor systems. SIAM J. Control Optim. 2004, 42, 2062–2077. [Google Scholar] [CrossRef]
- Applegate, D.L.; Bixby, R.E.; Chvatal, V.; Cook, W.J. The Traveling Salesman Problem: A Computational Study; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Bellman, R. Dynamic programming treatment of the travelling salesman problem. J. ACM (JACM) 1962, 9, 61–63. [Google Scholar] [CrossRef]
- Bellman, R. Dynamic programming and Lagrange multipliers. Proc. Natl. Acad. Sci. USA 1956, 42, 767. [Google Scholar] [CrossRef] [PubMed]
- Bertsekas, D.P.; Bertsekas, D.P.; Bertsekas, D.P.; Bertsekas, D.P. Dynamic Programming and Optimal Control; Athena Scientific: Belmont, MA, USA, 1995; Volume 1. [Google Scholar]
- Karlin, S. A First Course in Stochastic Processes; Academic Press: Waltham, MA, USA, 2014. [Google Scholar]
- Puterman, M.L. Markov Decision Processes: Discrete Stochastic Dynamic Programming; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Buttazzo, G.C. Hard Real-Time Computing Systems: Predictable Scheduling Algorithms and Applications; Springer Science & Business Media: Berlin, Germany; Heidelberg, Germany, 2011; Volume 24. [Google Scholar]
- Liu, C.; Layland, J. Scheduling algorithms for multiprogramming in a hard-real-time environment. J. ACM (JACM) 1973, 20, 46–61. [Google Scholar] [CrossRef]
- Stankovic, J.A.; Spuri, M.; Di Natale, M.; Buttazzo, G.C. Implications of classical scheduling results for real-time systems. Computer 1995, 28, 16–25. [Google Scholar] [CrossRef]
- Davis, R.I.; Burns, A. A survey of hard real-time scheduling for multiprocessor systems. ACM Comput. Surv. (CSUR) 2011, 43, 35. [Google Scholar] [CrossRef]
- Kato, S.; Lakshmanan, K.; Rajkumar, R.; Ishikawa, Y. TimeGraph: GPU scheduling for real-time multi-tasking environments. In Proceedings of the 2011 USENIX Annual Technical Conference, Portland, OR, USA, 15–17 June 2011; pp. 17–30.
- Marculescu, R.; Bogdan, P. Cyberphysical systems: workload modeling and design optimization. IEEE Des. Test Comput. 2010, 28, 78–87. [Google Scholar] [CrossRef]
- Tricaud, C.; Chen, Y.Q. Optimal mobile actuator/sensor network motion strategy for parameter estimation in a class of cyber physical systems. In Proceedings of the American Control Conference, Saint Louis, MI, USA, 10–12 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 367–372. [Google Scholar]
- Wolf, M. High-Performance Embedded Computing: Applications in Cyber-Physical Systems and Mobile Computing; Morgan Kaufmann: Burlington, MA, USA, 2014. [Google Scholar]
- Unsal, O.S.; Koren, I. System-level power-aware design techniques in real-time systems. IEEE Proc. 2003, 91, 1055–1069. [Google Scholar] [CrossRef]
- Koren, I.; Krishna, C. Temperature-aware computing. Sustain. Comput. Inform. Syst. 2011, 1, 46–56. [Google Scholar] [CrossRef]
- Krishna, C. Fault-tolerant scheduling in homogeneous real-time systems. ACM Comput. Surv. (CSUR) 2014, 46, 48. [Google Scholar] [CrossRef]
- Longuski, J.M.; Guzman, J.J.; Prussing, J.E. Optimal Control with Aerospace Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- Techy, L.; Woolsey, C.A. Minimum-Time Path Planning for Unmanned Aerial Vehicles in Steady Uniform Winds. J. Guid. Control Dyn. 2009, 32, 1736–1746. [Google Scholar] [CrossRef]
- Chakrabarty, A.; Langelaan, J.W. Energy-Based Long-Range Path Planning for Soaring-Capable Unmanned Aerial Vehicles. J. Guid. Control Dyn. 2011, 34, 1002–1015. [Google Scholar] [CrossRef]
- Aydin, H.; Melhem, R.; Mosse, D.; Mejia-Alvarez, P. Power-aware scheduling for periodic real-time tasks. IEEE Trans. Comput. 2004, 53, 584–600. [Google Scholar] [CrossRef]
- Mutapcic, A.; Boyd, S.; Murali, S.; Atienza, D.; De Micheli, G.; Gupta, R. Processor Speed Control With Thermal Constraints. IEEE Trans. Circ. Syst. I 2009, 56, 1994–2008. [Google Scholar] [CrossRef]
- Shin, D.; Chung, S.W.; Chung, E.Y.; Chang, N. Energy-Optimal Dynamic Thermal Management: Computation and Cooling Power Co-Optimization. IEEE Trans. Ind. Inform. 2010, 6, 340–351. [Google Scholar] [CrossRef]
- Coloe, B.; Atkins, E. Cyber-Physical Optimization of an Unmanned Aircraft System with Thermal Consideration. In Proceedings of the 54th IEEE Conference on Decision and Control, Osaka, Japan, 15–18 December 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Bini, E.; Buttazzo, G. The Optimal Sampling Pattern for Linear Control Systems. IEEE Trans. Autom. Control 2014, 59, 78–90. [Google Scholar] [CrossRef]
- Kowalska, K.; Mohrenschildt, M. An approach to variable time receding horizon control. Optim. Control Appl. Methods 2012, 33, 401–414. [Google Scholar] [CrossRef]
- Bradley, J.M.; Atkins, E.M. Cyber–Physical Optimization for Unmanned Aircraft Systems. J. Aerosp. Inf. Syst. 2014, 11, 48–60. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bradley, J.M.; Atkins, E.M. Optimization and Control of Cyber-Physical Vehicle Systems. Sensors 2015, 15, 23020-23049. https://doi.org/10.3390/s150923020
Bradley JM, Atkins EM. Optimization and Control of Cyber-Physical Vehicle Systems. Sensors. 2015; 15(9):23020-23049. https://doi.org/10.3390/s150923020
Chicago/Turabian StyleBradley, Justin M., and Ella M. Atkins. 2015. "Optimization and Control of Cyber-Physical Vehicle Systems" Sensors 15, no. 9: 23020-23049. https://doi.org/10.3390/s150923020
APA StyleBradley, J. M., & Atkins, E. M. (2015). Optimization and Control of Cyber-Physical Vehicle Systems. Sensors, 15(9), 23020-23049. https://doi.org/10.3390/s150923020




