Inspection of Pole-Like Structures Using a Visual-Inertial Aided VTOL Platform with Shared Autonomy
Abstract
:1. Introduction

1.1. Related Work
1.1.1. Climbing Robots for Inspection Tasks
1.1.2. Flying Robots for Inspection Tasks
1.2. Contributions and Overview
- The development of onboard flight controllers using monocular visual features (lines) and inertial sensing for visual servoing (PBVS and IBVS) to enable VTOL MAV close quarters manoeuvring.
- The use of shared autonomy to permit an un-skilled operator to easily and safely perform MAV-based pole inspections in outdoor environments, with wind, and at night.
- Significant experimental evaluation of state estimation and control performance for indoor and outdoor (day and night) flight tests, using a motion capture device and a laser tracker for ground truth. Video demonstration [22].
- A performance evaluation of the proposed systems in comparison to skilled pilots for a pole inspection task.
2. Coordinate Systems and Image Processing
2.1. Coordinate Systems
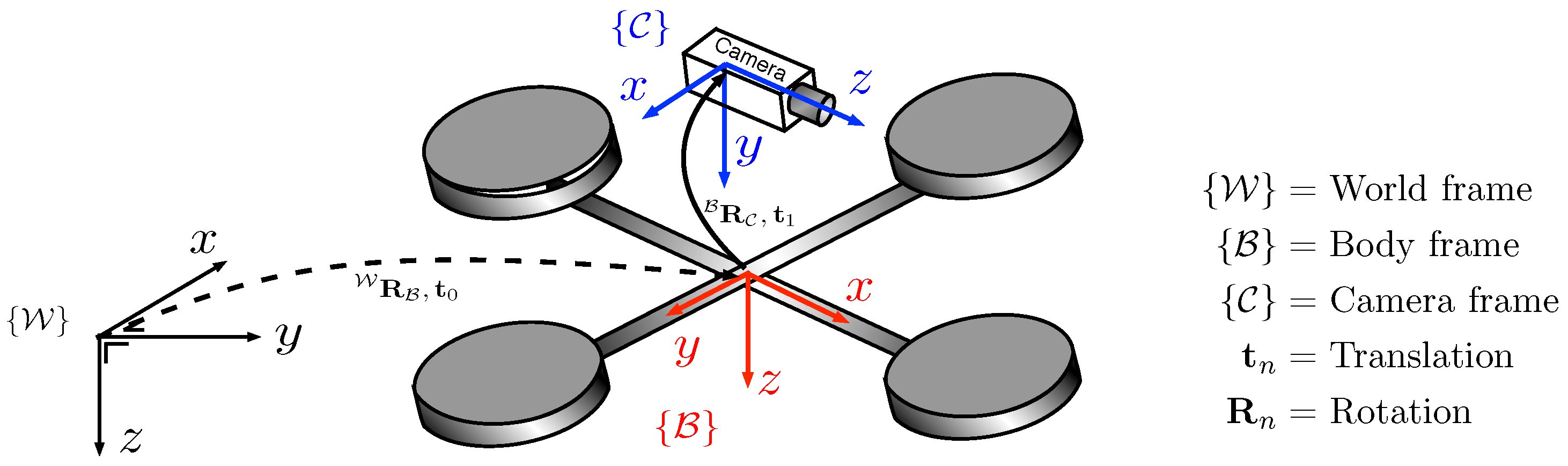
2.2. Image Processing for Fast Line Tracking
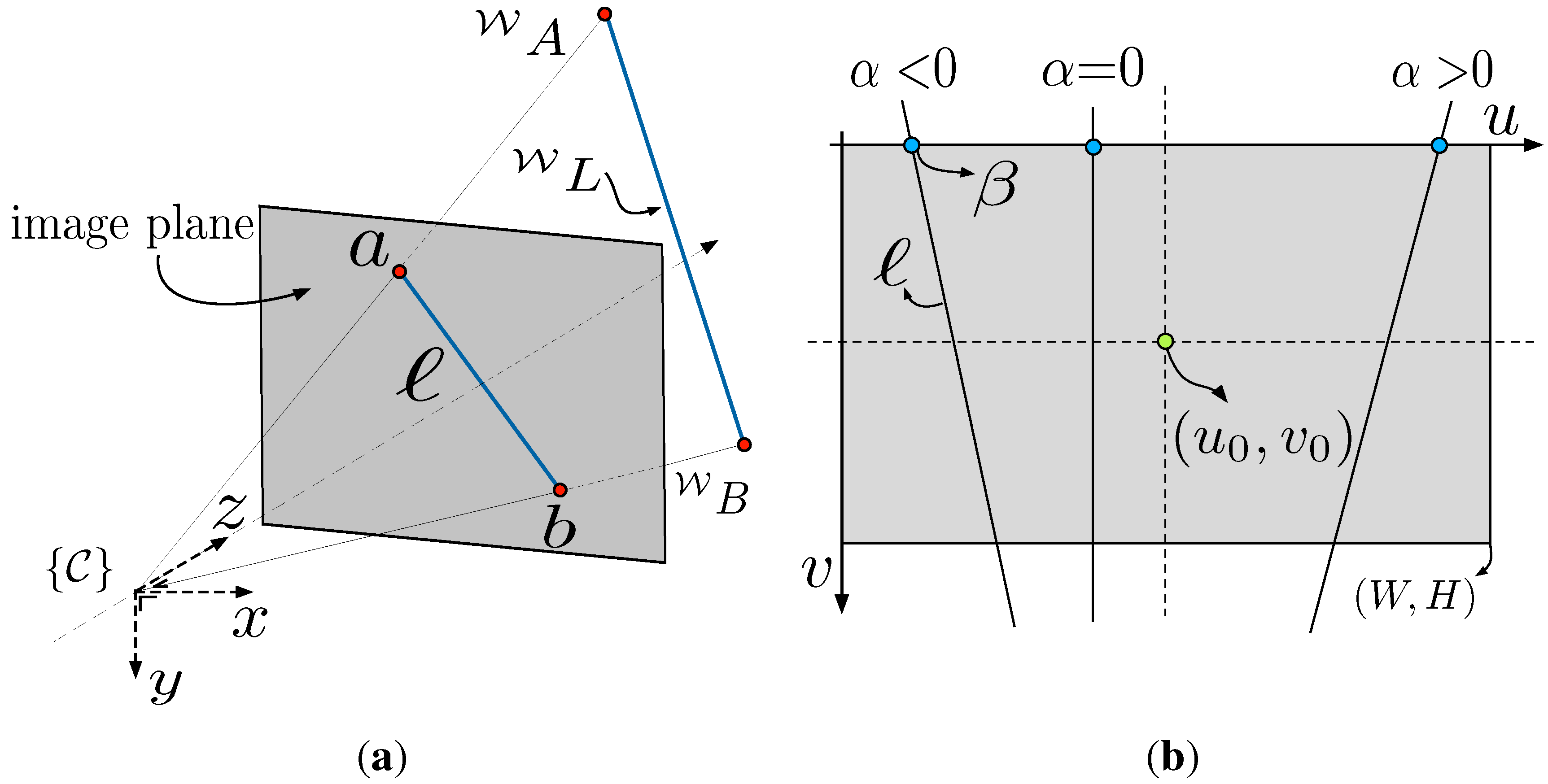
2.2.1. 2D and 3D Line Models
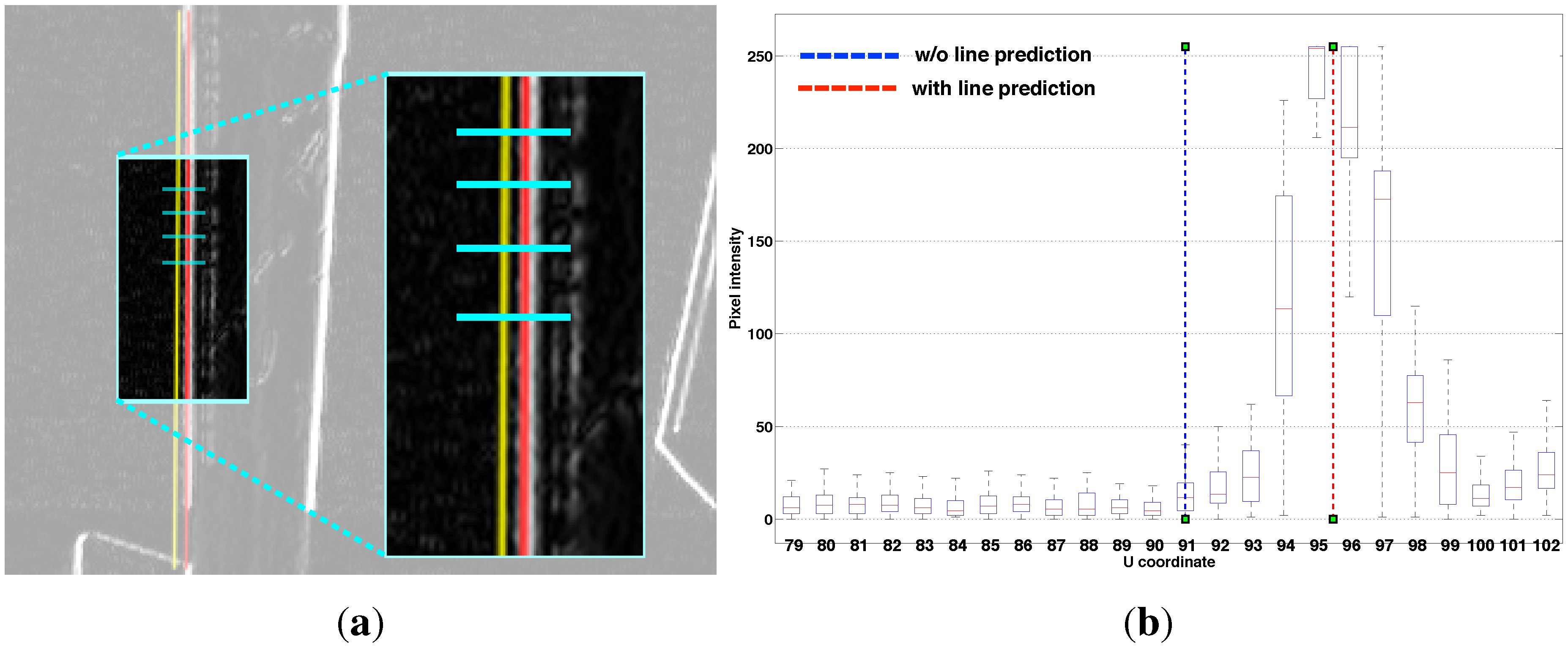
2.2.2. Line Prediction and Tracking
3. Position Based Visual Servoing (PBVS)


3.1. Horizontal Plane EKF
3.1.1. Process Model
3.1.2. Measurement Model
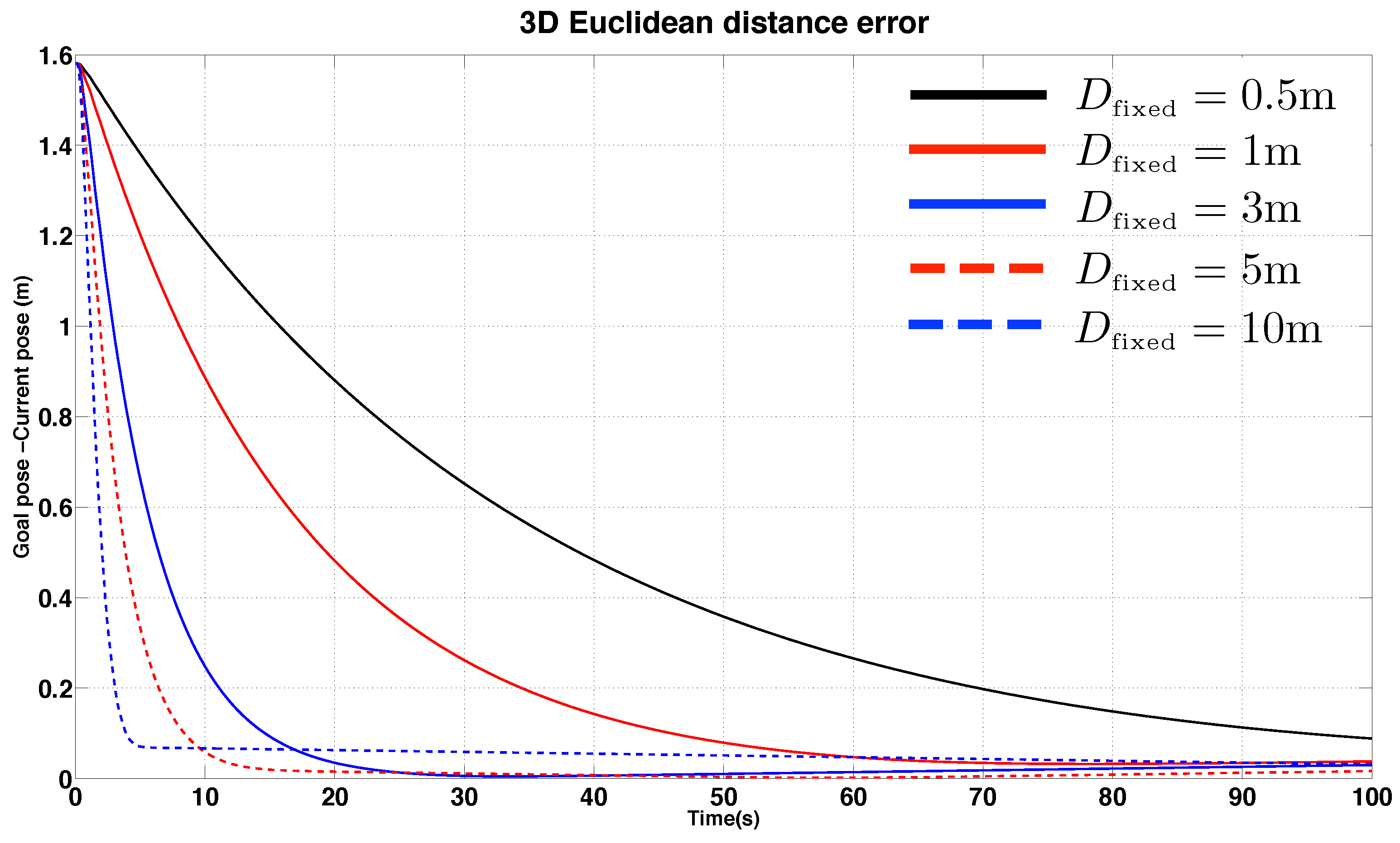
3.1.3. Simulation Results
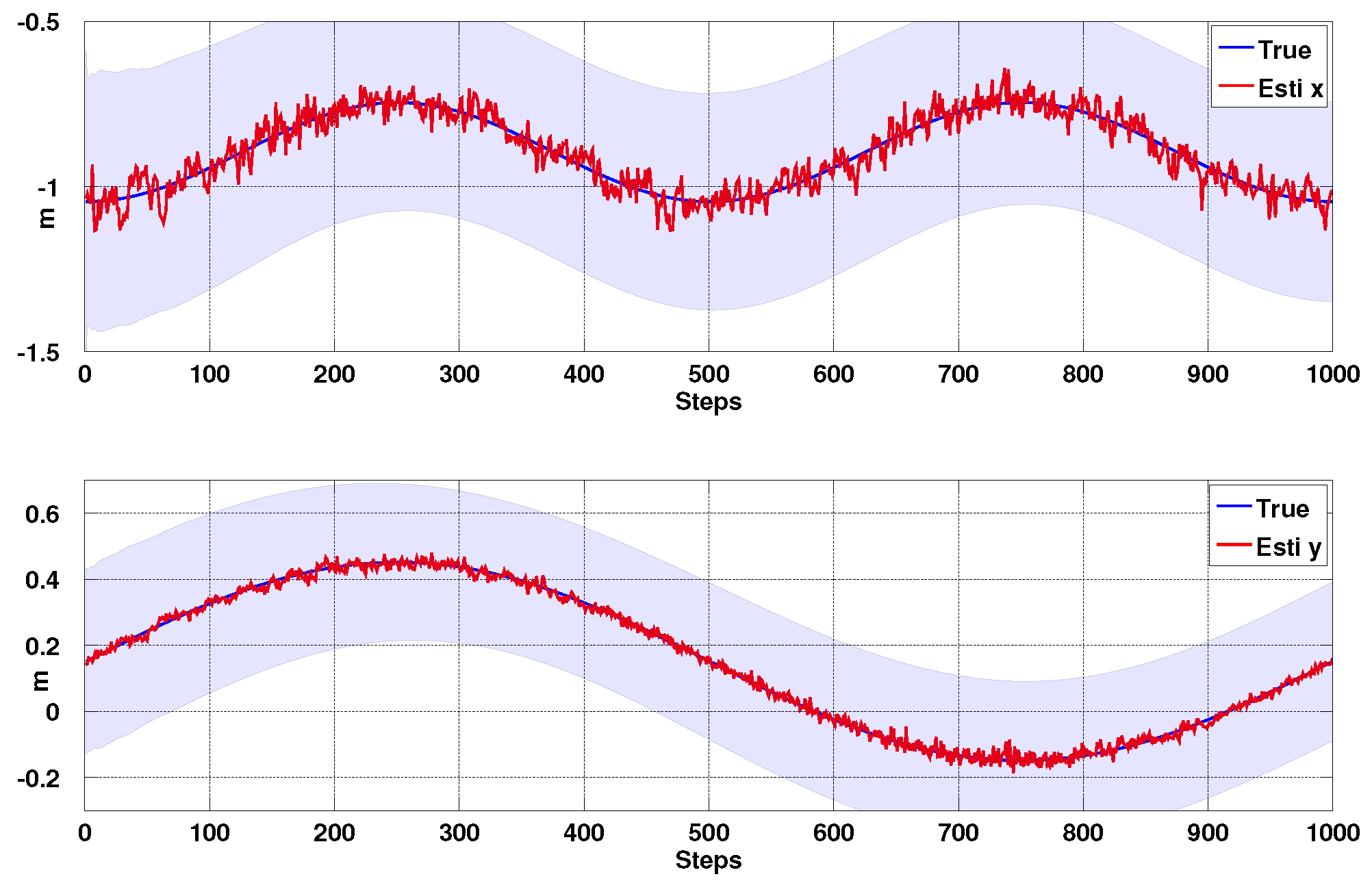
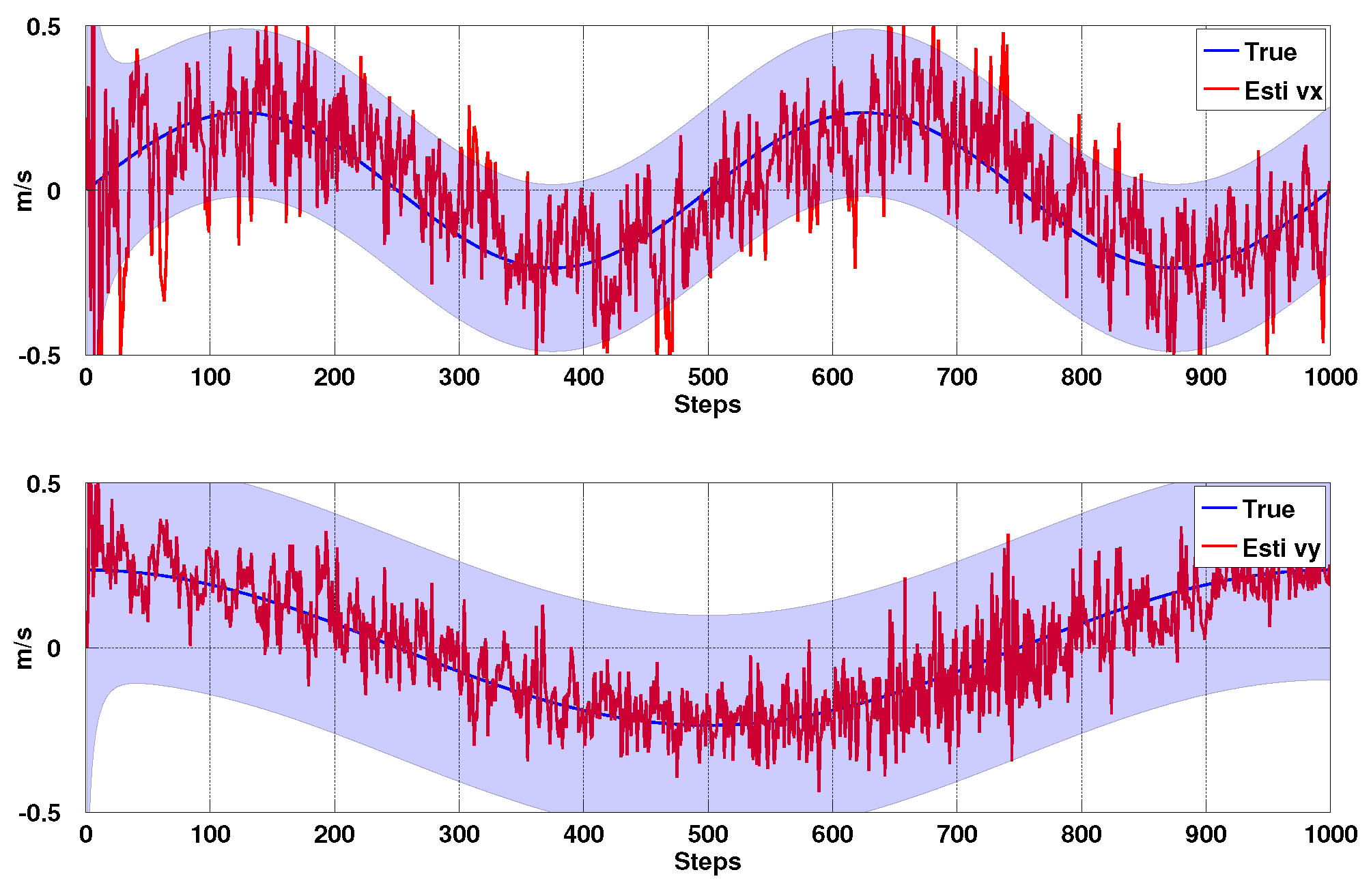

3.2. Kalman Filter-Based Vertical State Estimation
4. Image Based Visual Servoing (IBVS)

4.1. Line-Feature-Based IBVS
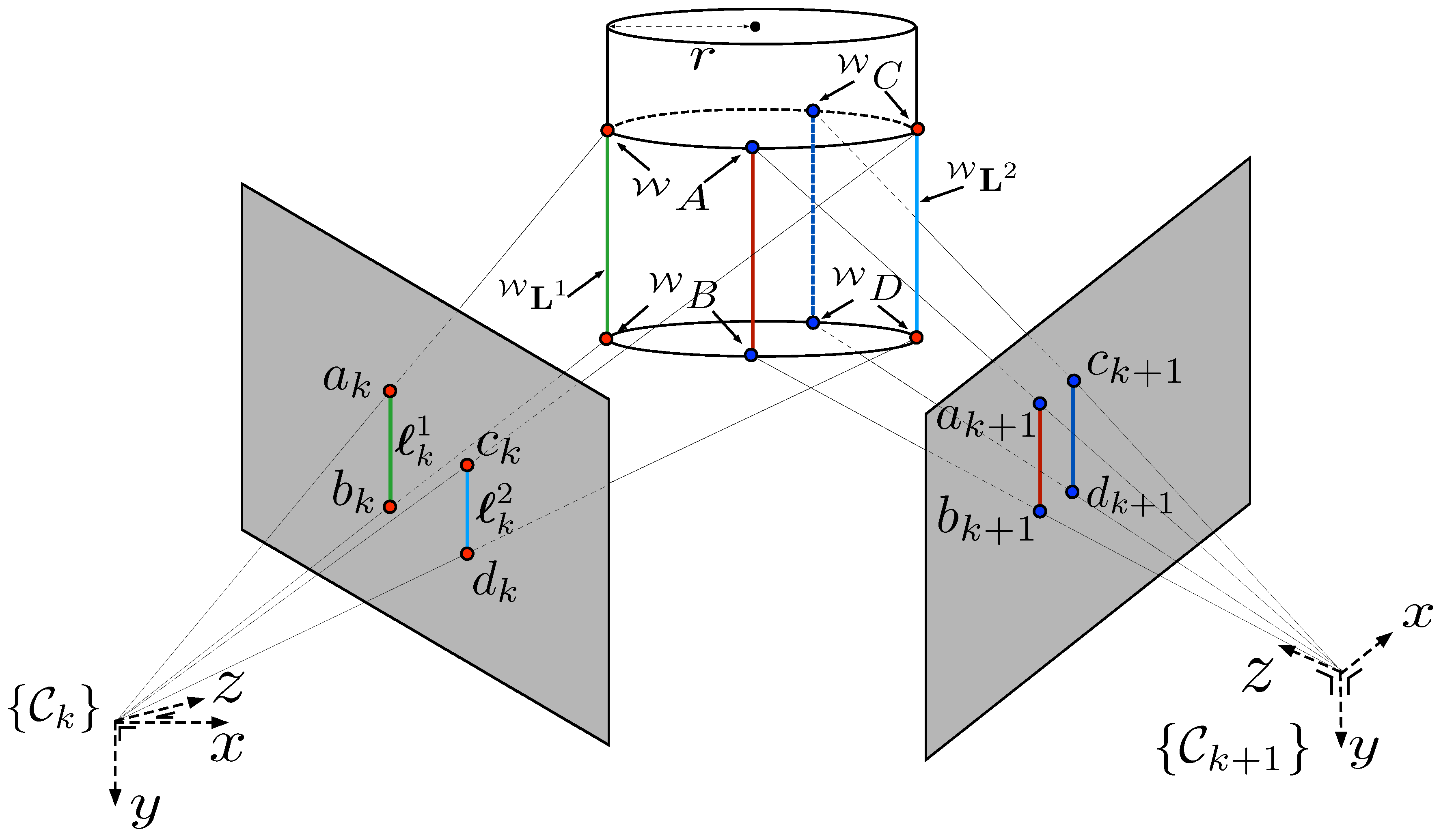
4.1.1. Image Jacobian for Line Features

4.1.2. Unobservable and Ambiguous States with Line Features
| # of lines | Rank | Unobservable | Ambiguities | Condition |
|---|---|---|---|---|
| 1 | 2 | vy | vx ∼ vz ∼ ωy, ωx ∼ ωz | Line not on the optical axis |
| 2 | 4 | vy | vx ∼ ωy | — |
| 3 | 6 (Full) | — | Lines are not parallel |
4.1.3. De-Rotation Using an IMU
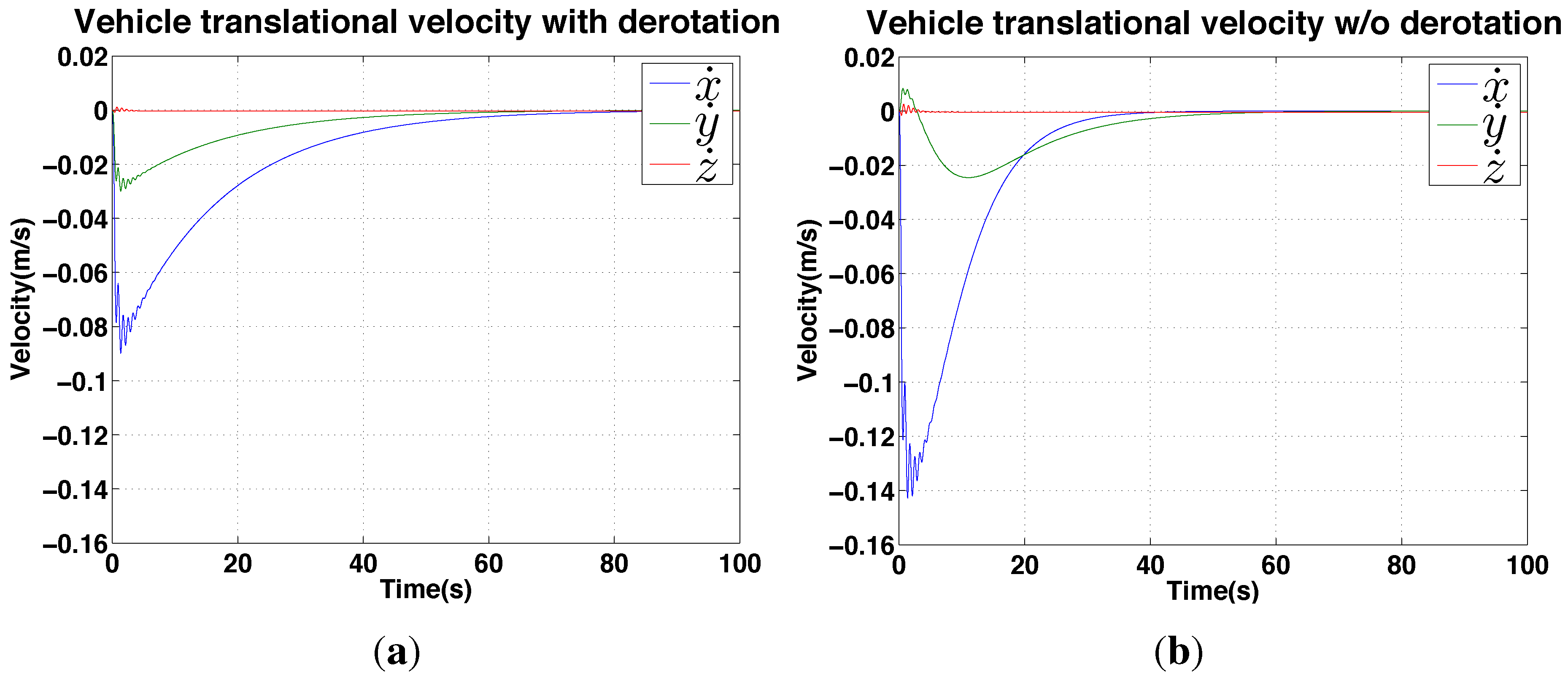
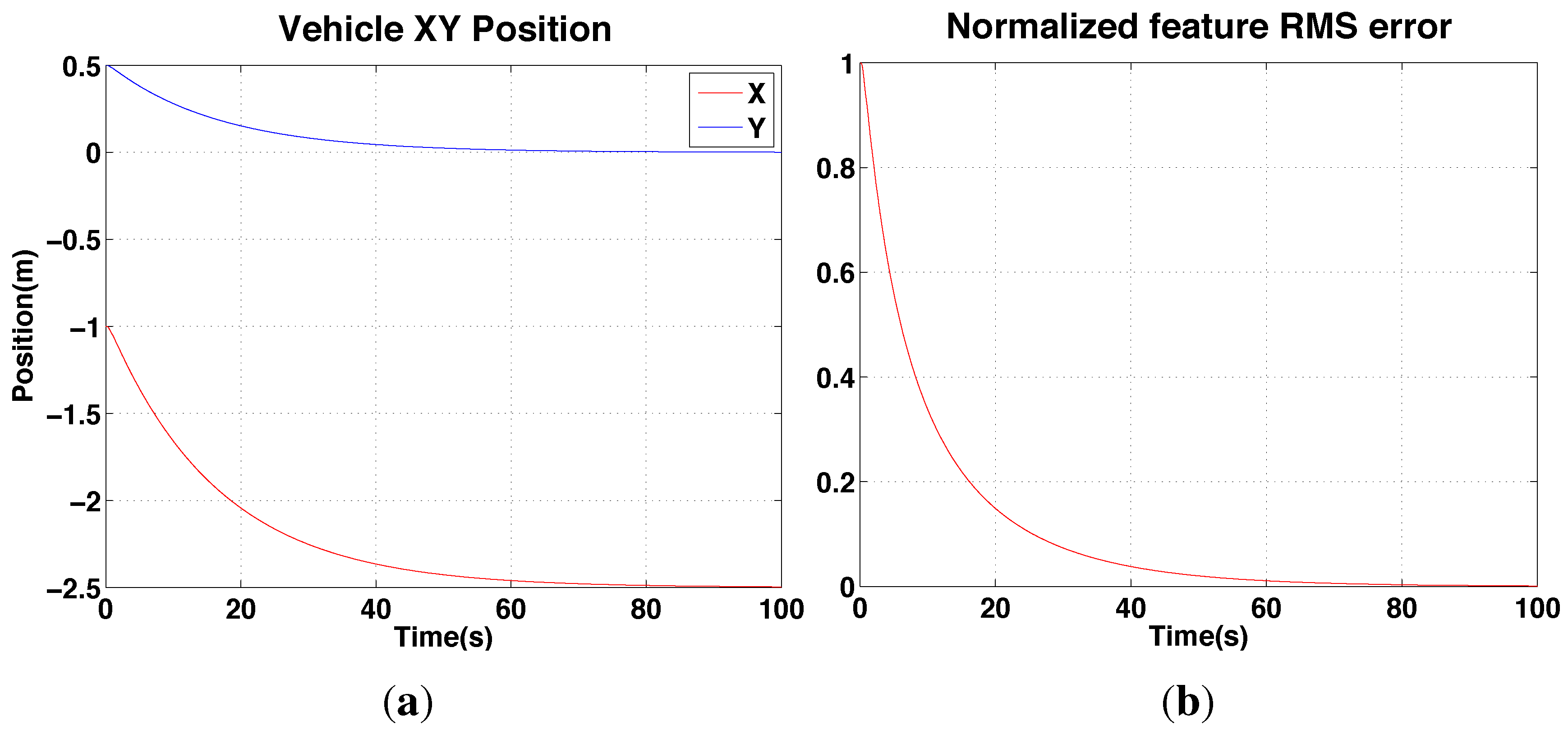
4.2. IBVS Simulation Results
5. Shared Autonomy

6. Experimental Results
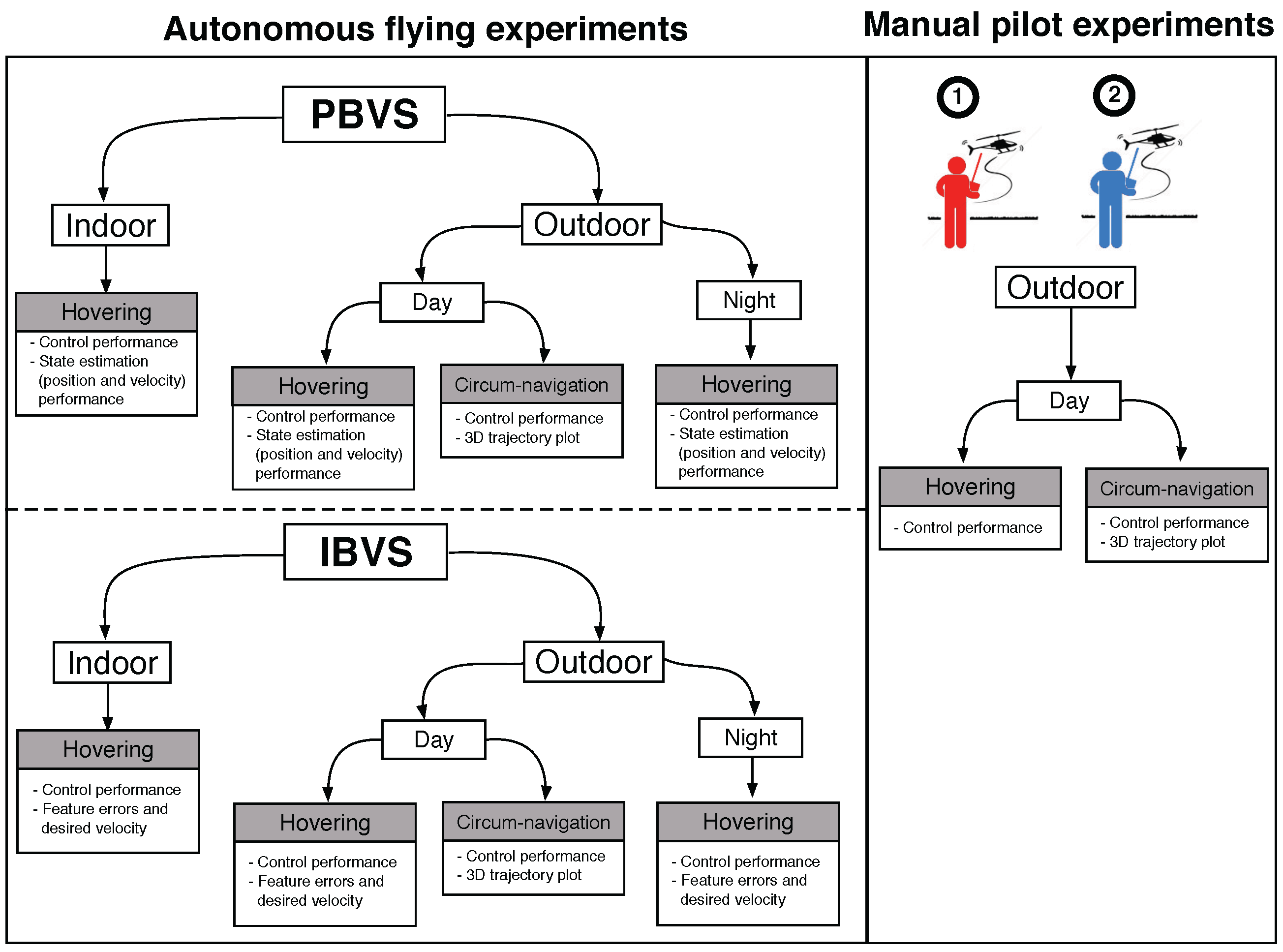

6.1. Hardware Configuration

Software Configuration
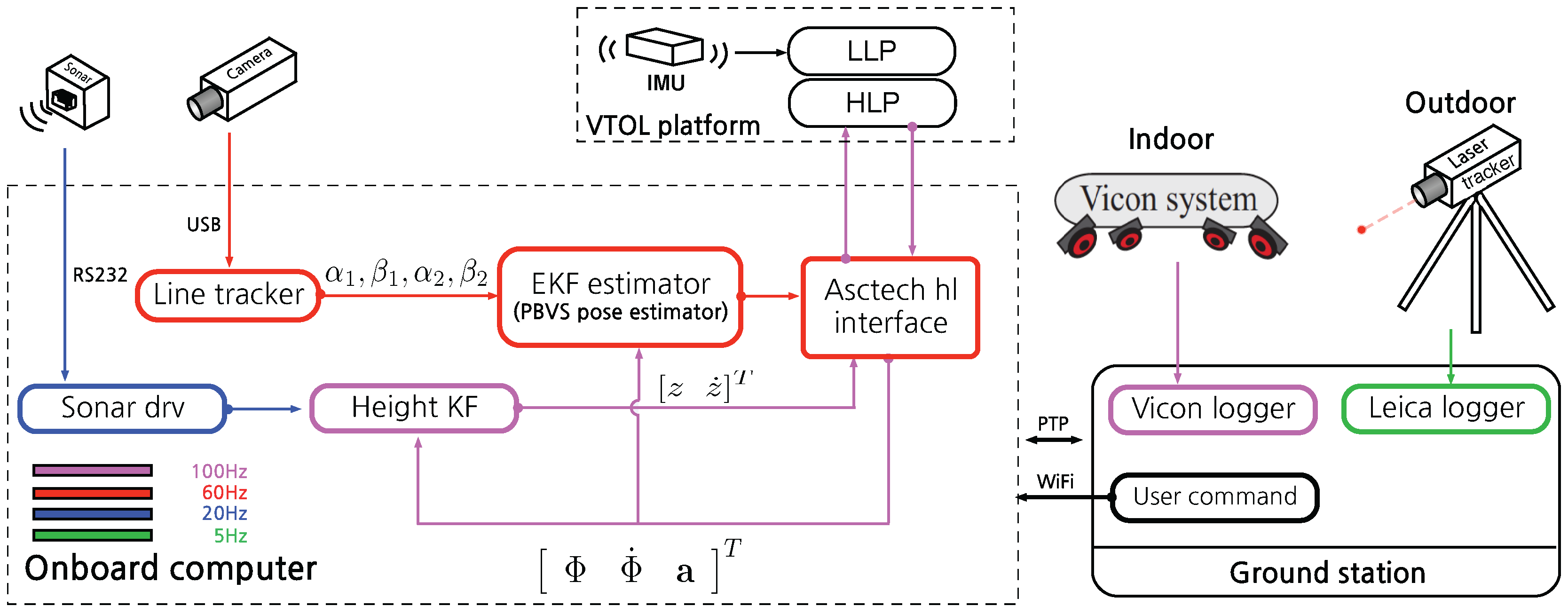
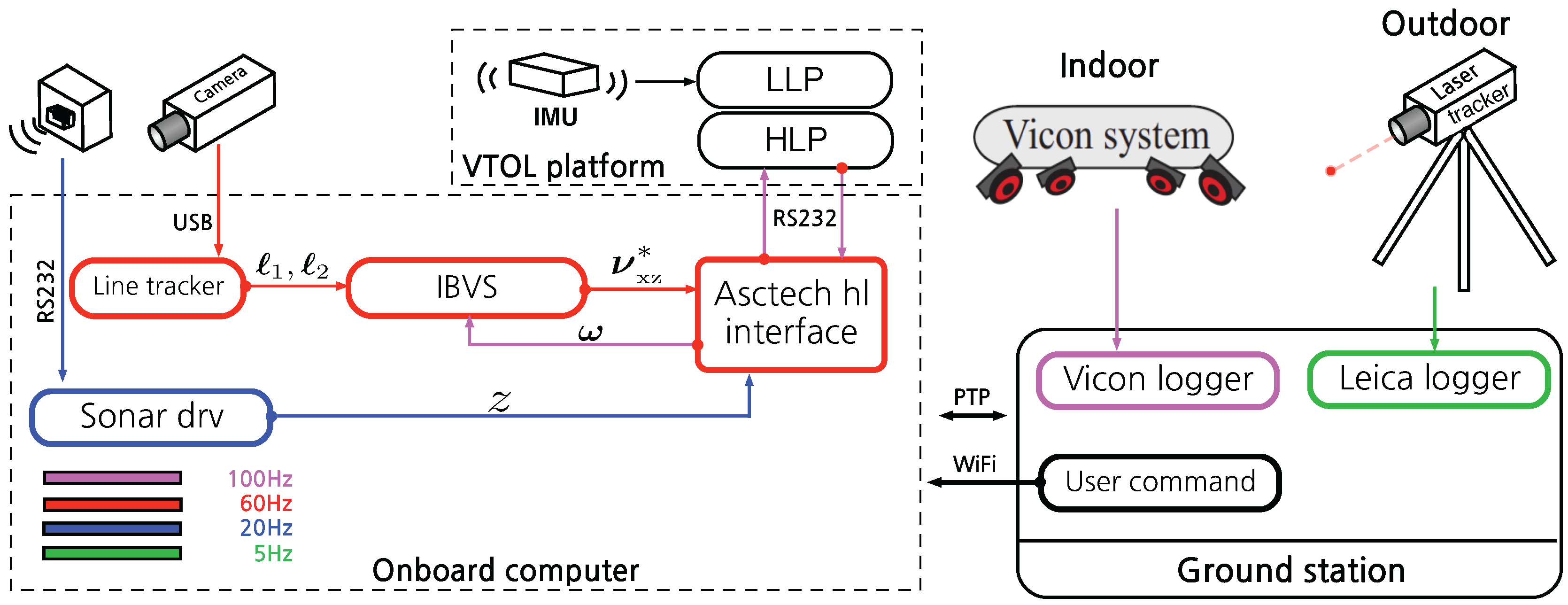
6.2. Position-Based Visual Servoing (PBVS)
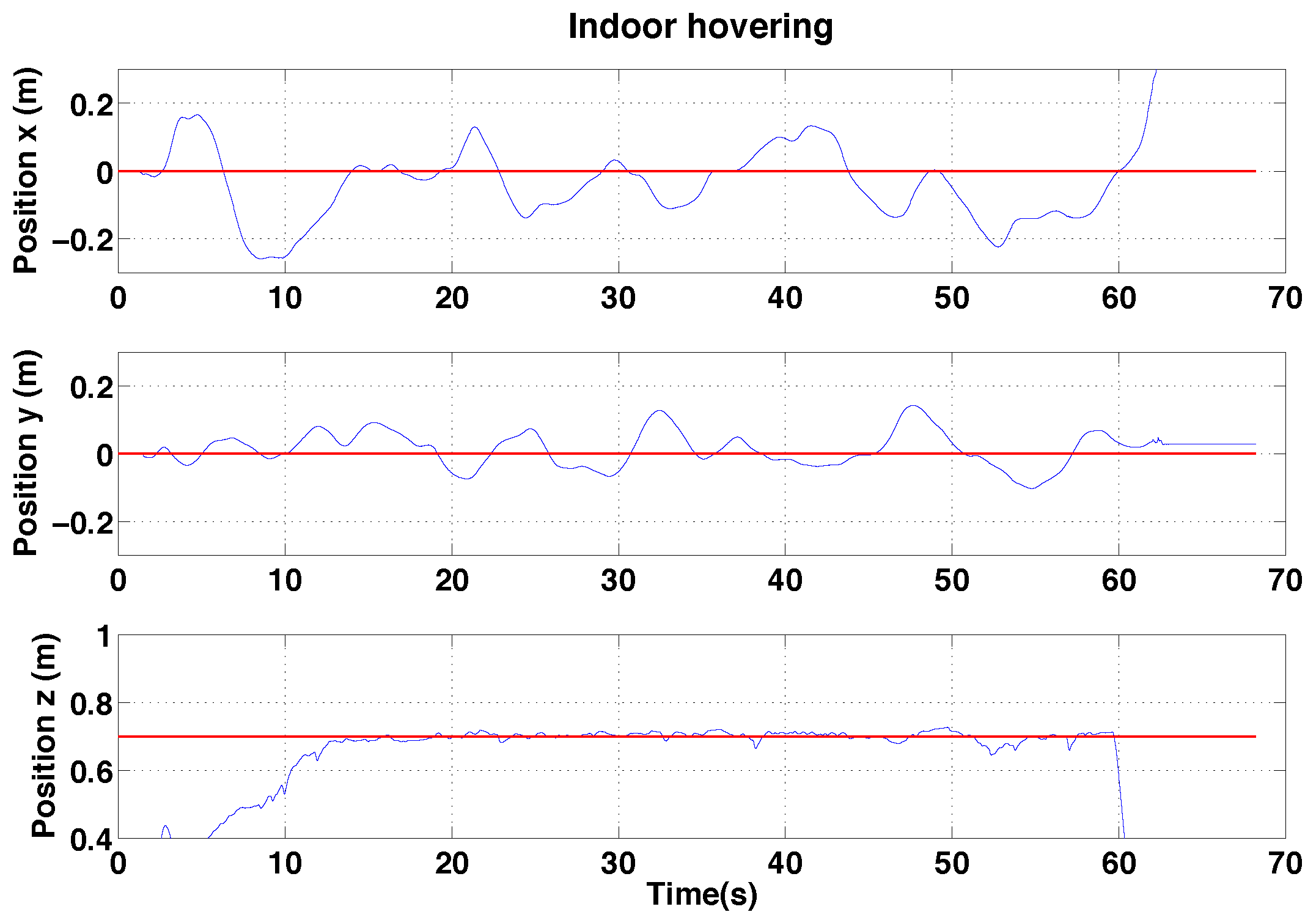
6.2.1. PBVS Indoor Hovering
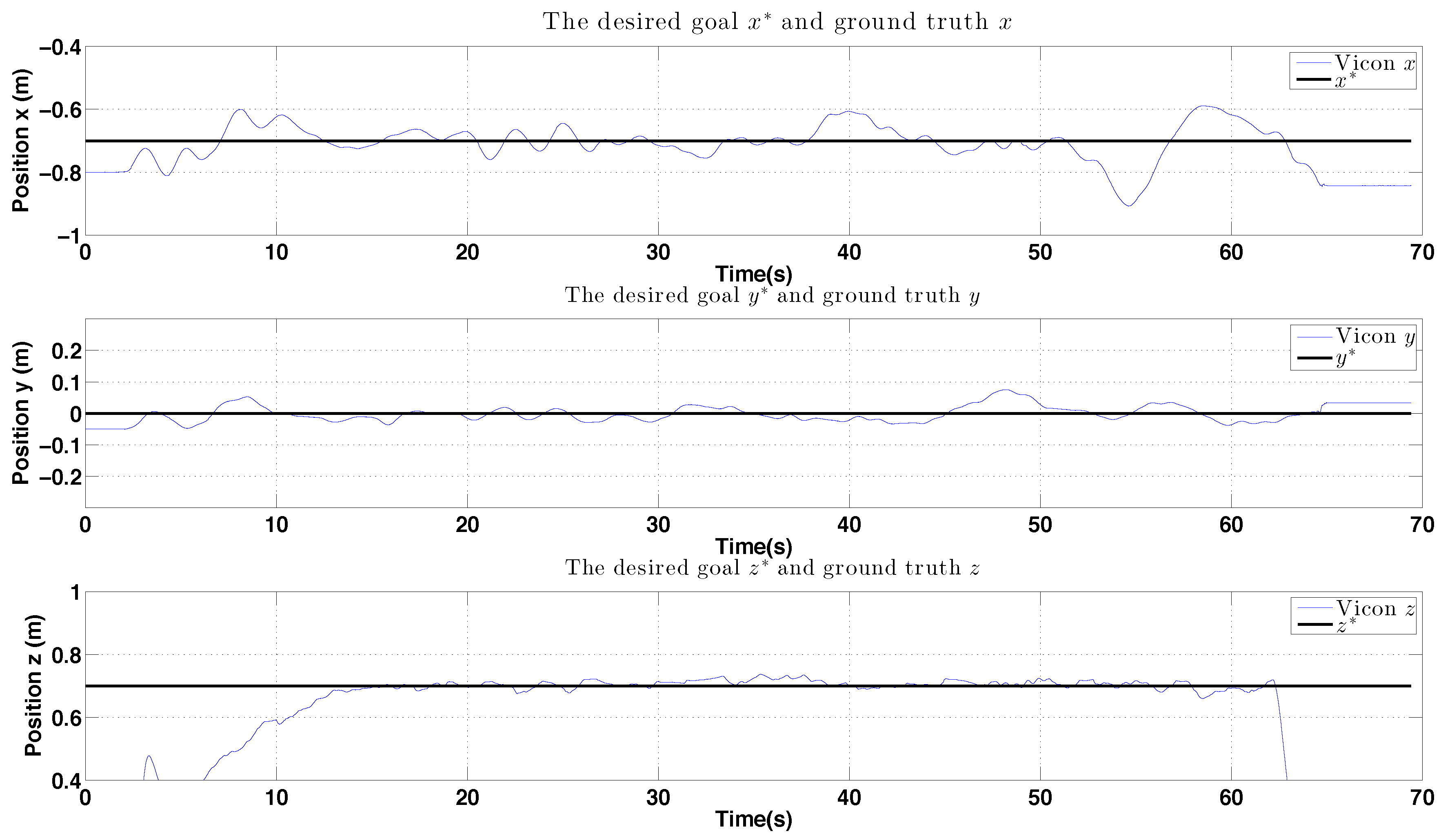
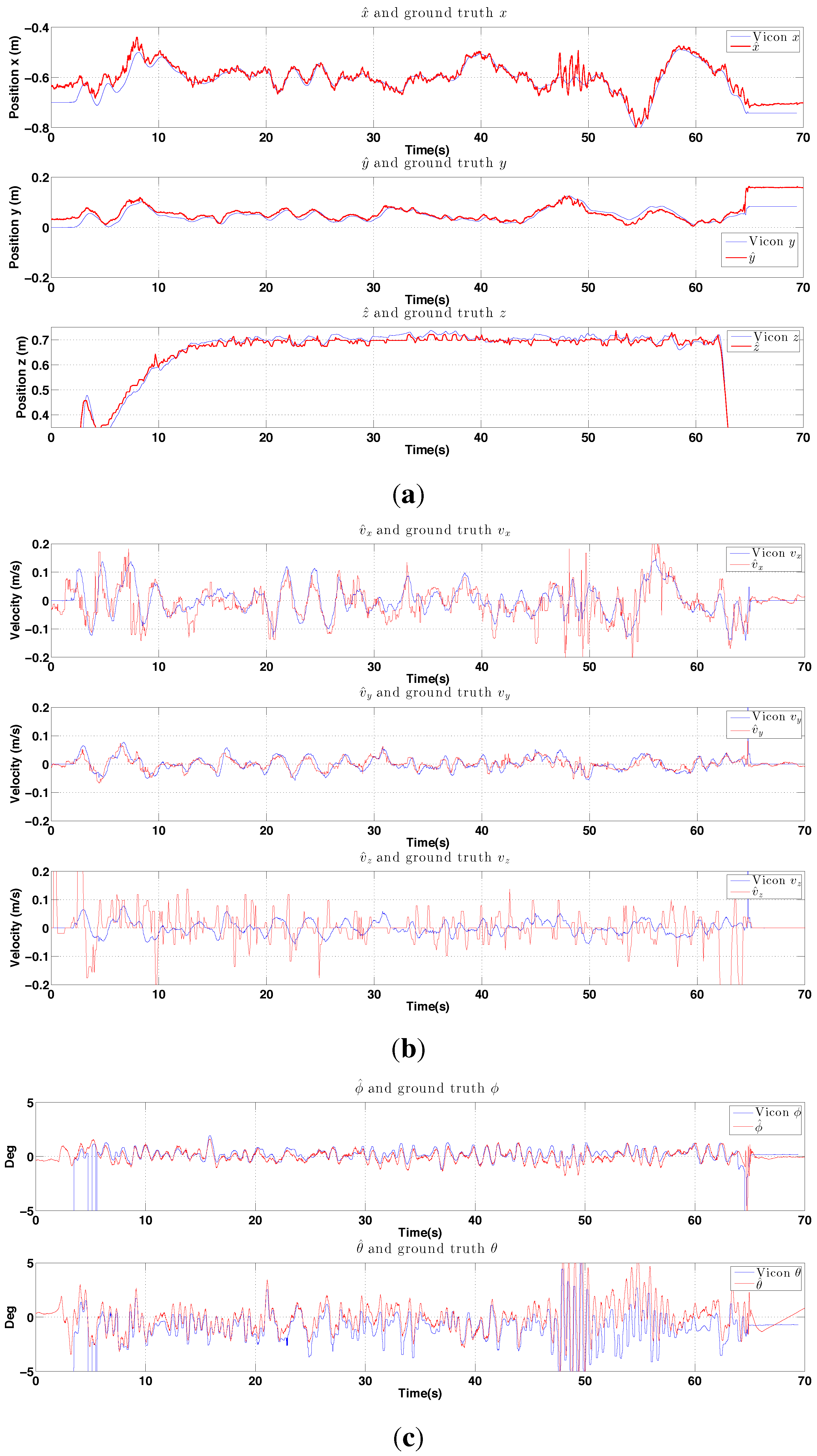
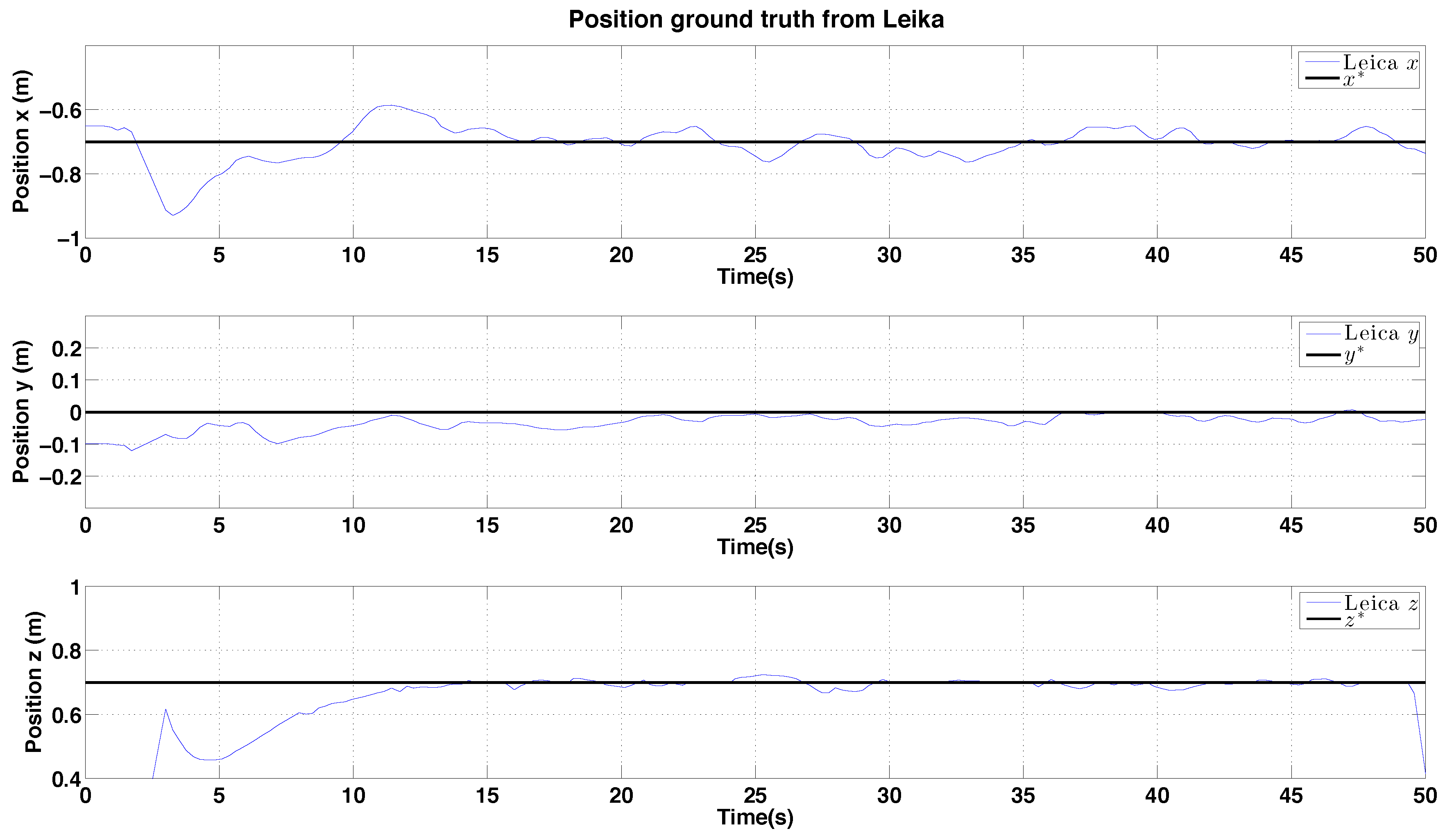
6.2.2. PBVS Day-Time Outdoor Hovering
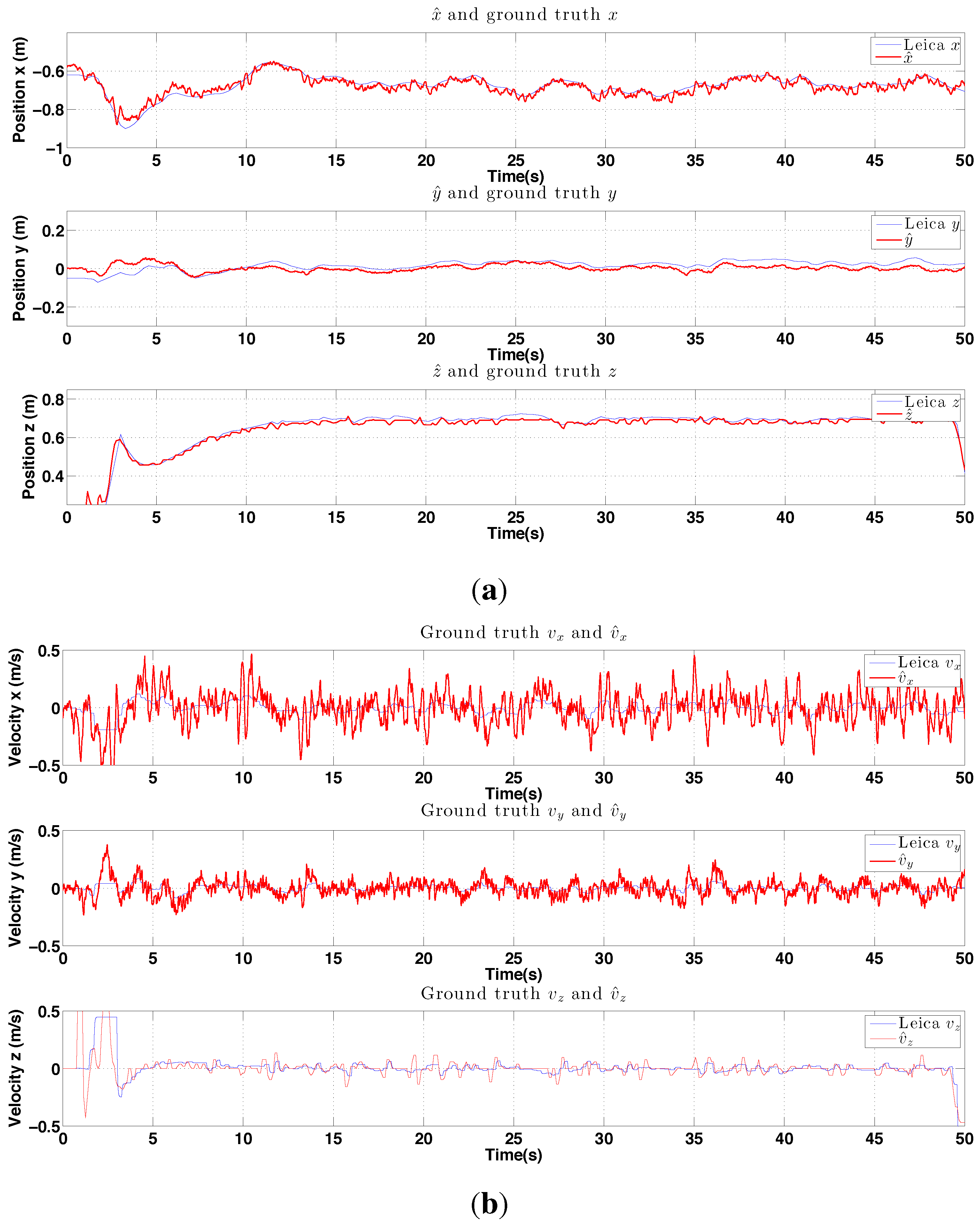
6.2.3. PBVS Night-Time Outdoor Hovering
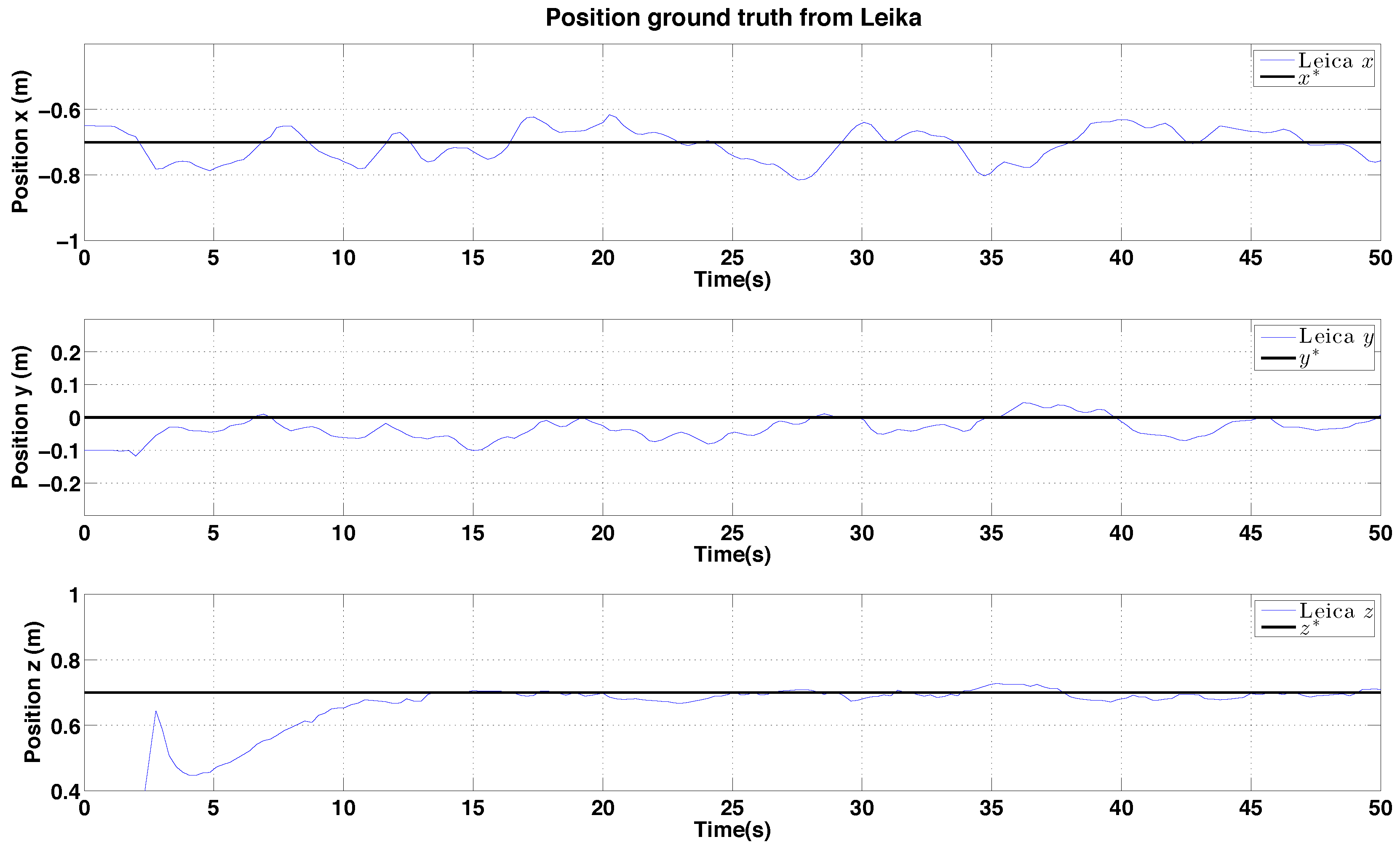
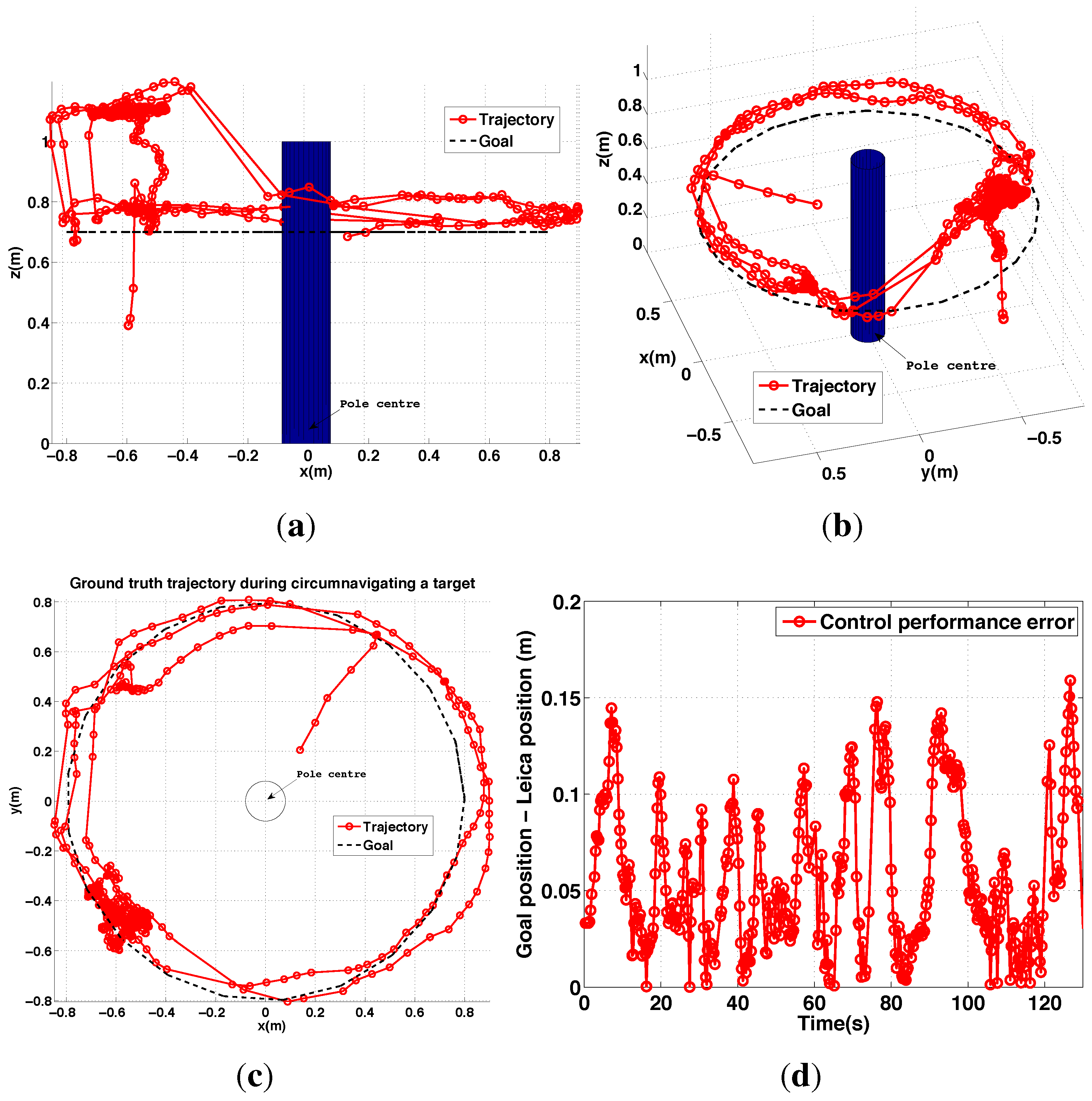
6.2.4. PBVS Day-Time Outdoor Circumnavigation

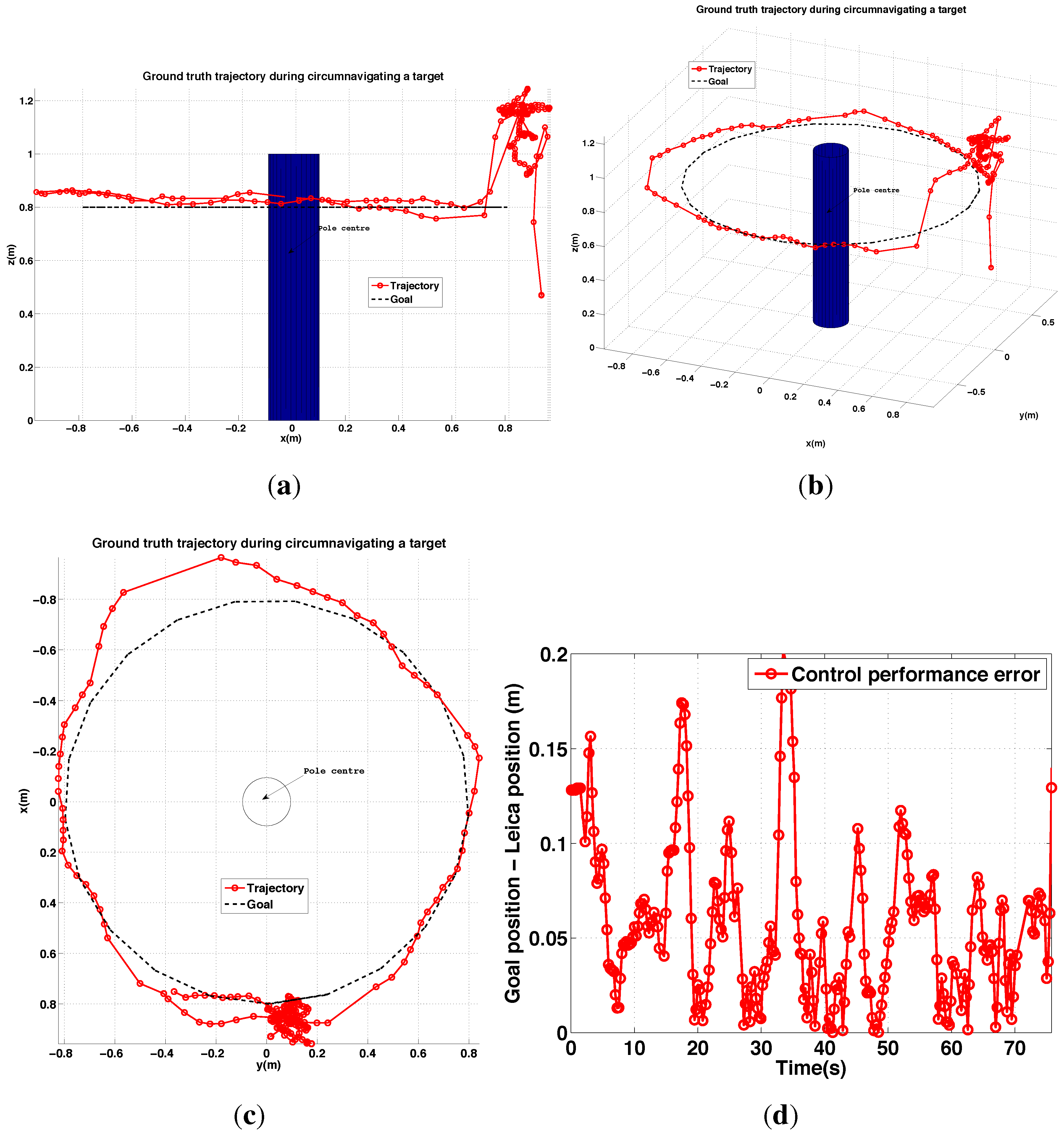
6.3. Imaged-Based Visual Servoing (IBVS)
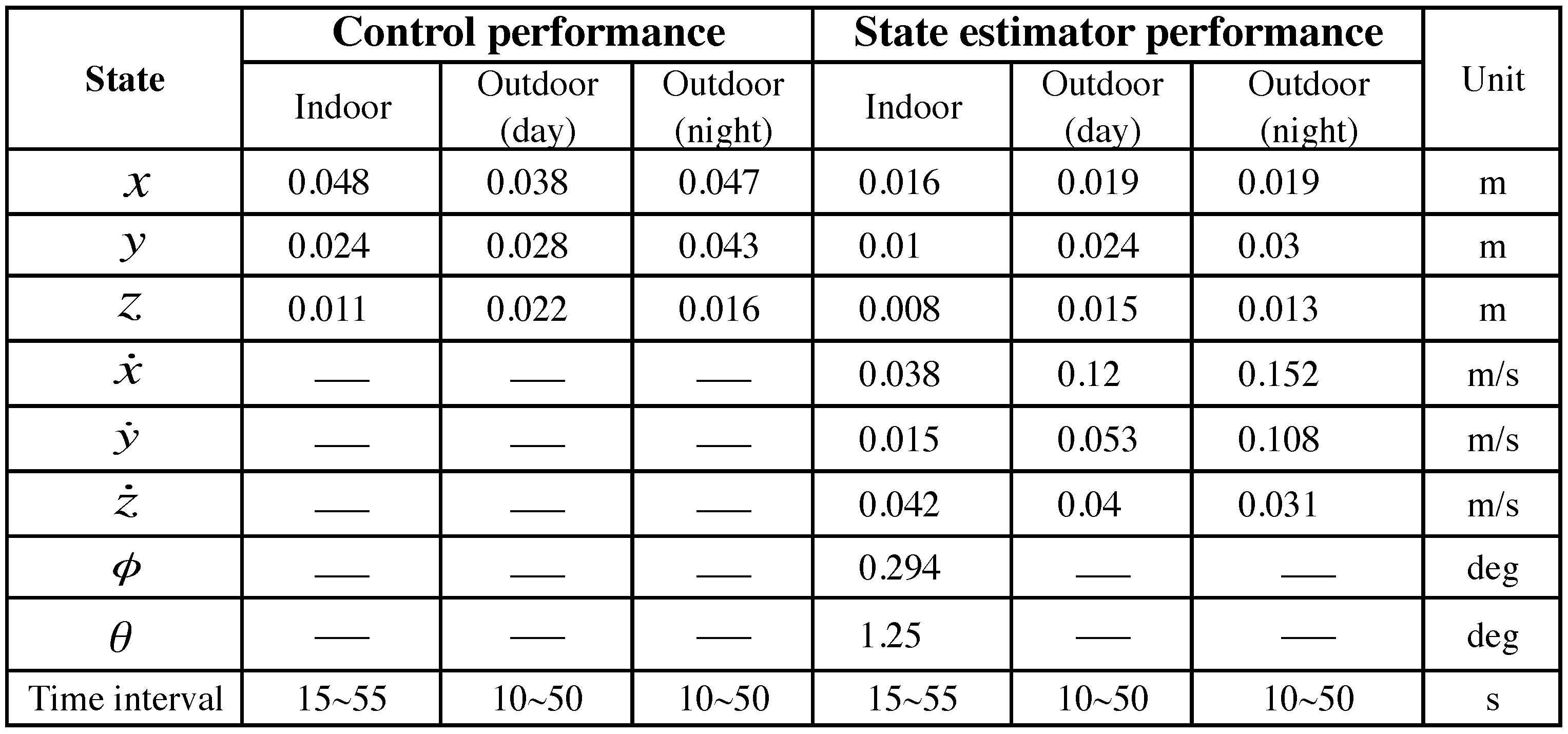
| State w.r.t { W} | Indoor | Outdoor (Day) | Outdoor (Night) | Unit |
|---|---|---|---|---|
| x | 0.084 | 0.068 | 0.033 | m |
| y | 0.057 | 0.076 | 0.050 | m |
| z | 0.013 | 0.013 | 0.013 | m |
| Duration | 15∼60 | 15∼55 | 15∼70 | s |
| Wind speed | — | 1.8∼2.5 | less than 1 | m/s |
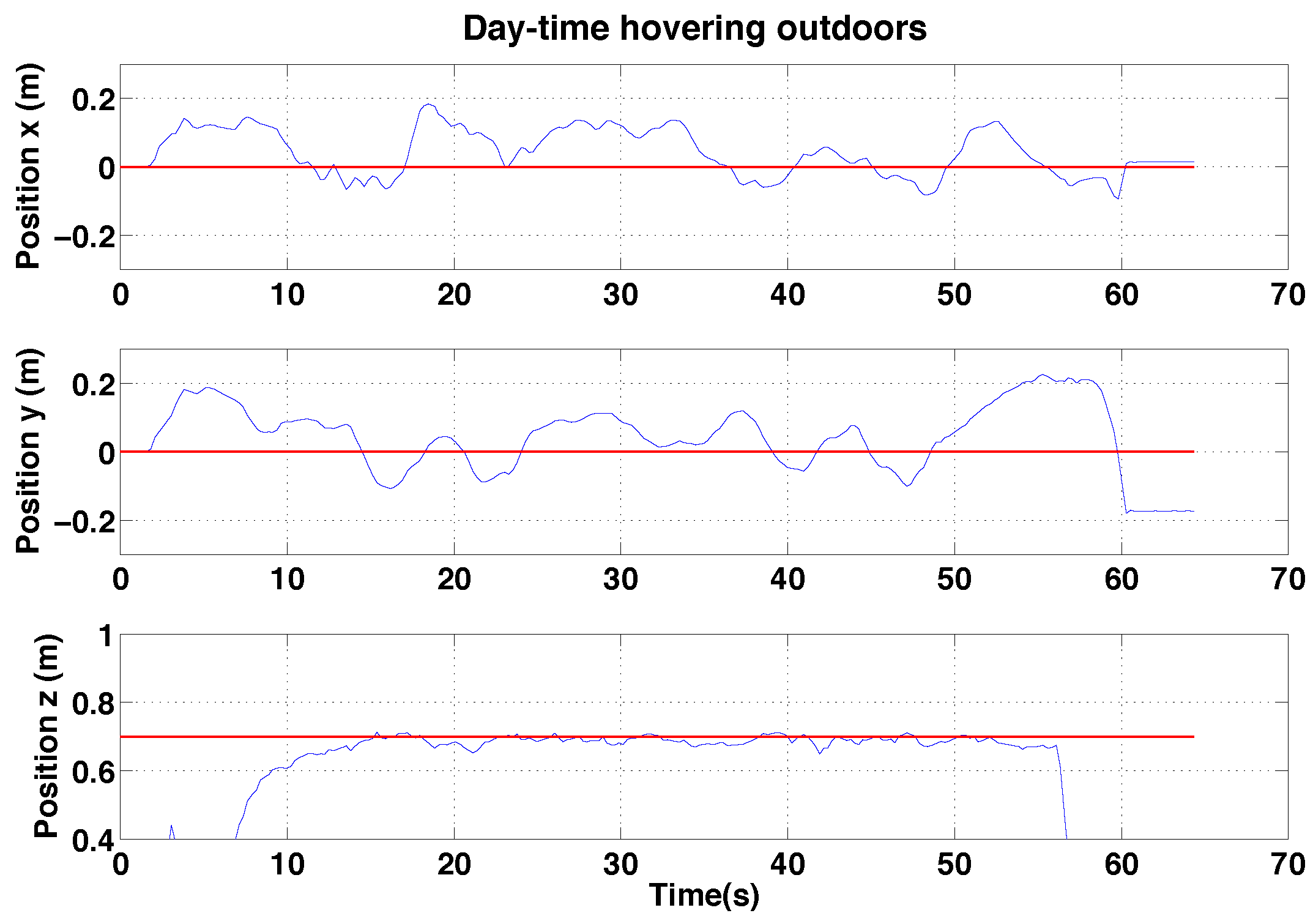

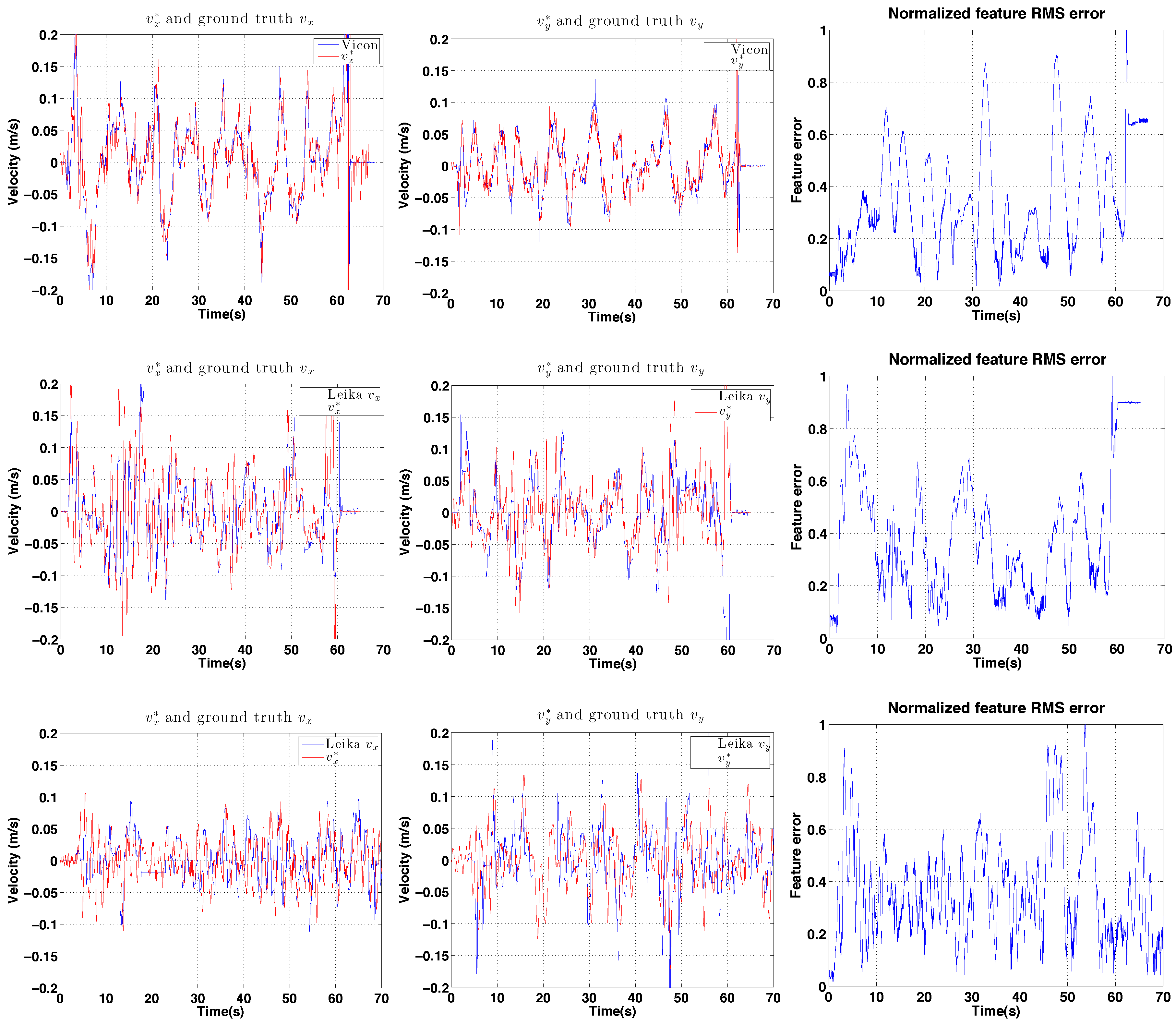
6.3.1. IBVS-Based Hovering
6.3.2. IBVS Day-Time Outdoor Circumnavigation
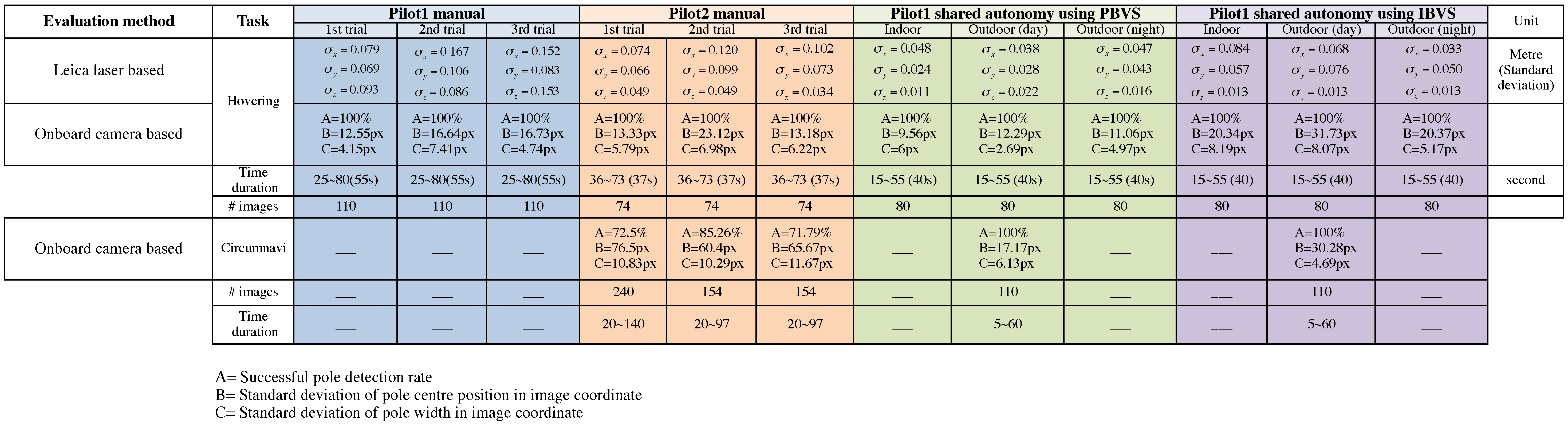
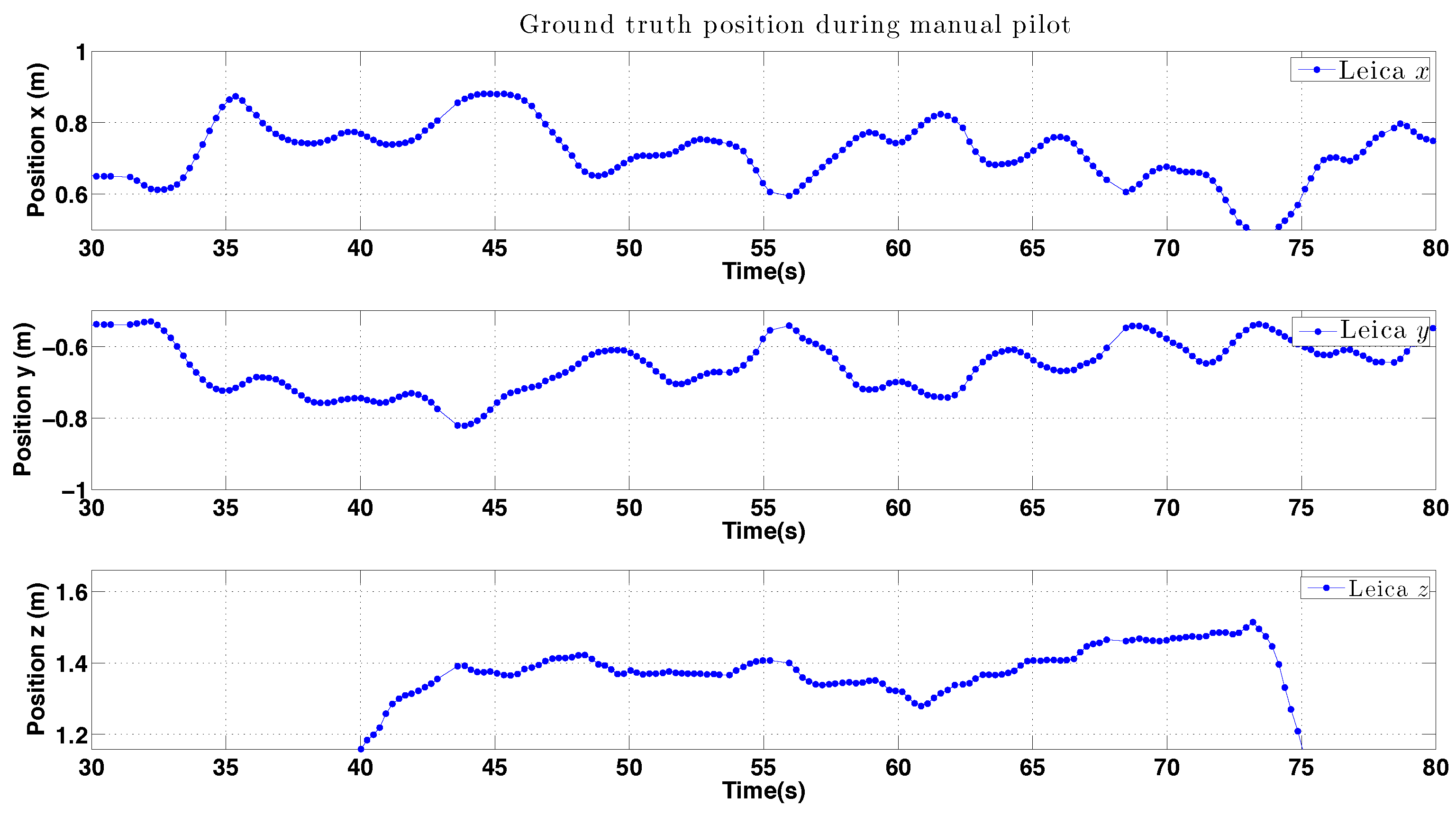
6.4. Manually Piloted Experiments
| PBVS | IBVS | Unit | |
|---|---|---|---|
| Max error margin | 0.024 | 0.017 | m |
| Standard deviation | 0.038 | 0.034 | m |
| Duration | 0∼75 | 0∼125 | s |
- [A] is the percentage pole detection rate in the onboard camera images. If the task is performed correctly the pole will be visible in 100% of the images.
- [B] is the standard deviation of the horizontal pole centre position (pixels) in the onboard camera images. This is a more graduated performance measure than A, and says something about the quality of the translational and heading angle control of the vehicle. If the task is performed well this should be 0. Note this statistic is computed over the frames in which the pole is visible.
- [C] is the standard deviation of the pole width (pixels) in the onboard camera images. It says something about the quality of the control of the vehicle position in the standoff direction, and if the task is performed well this should be 0. Note this statistic is computed over the frames in which the pole is visible.

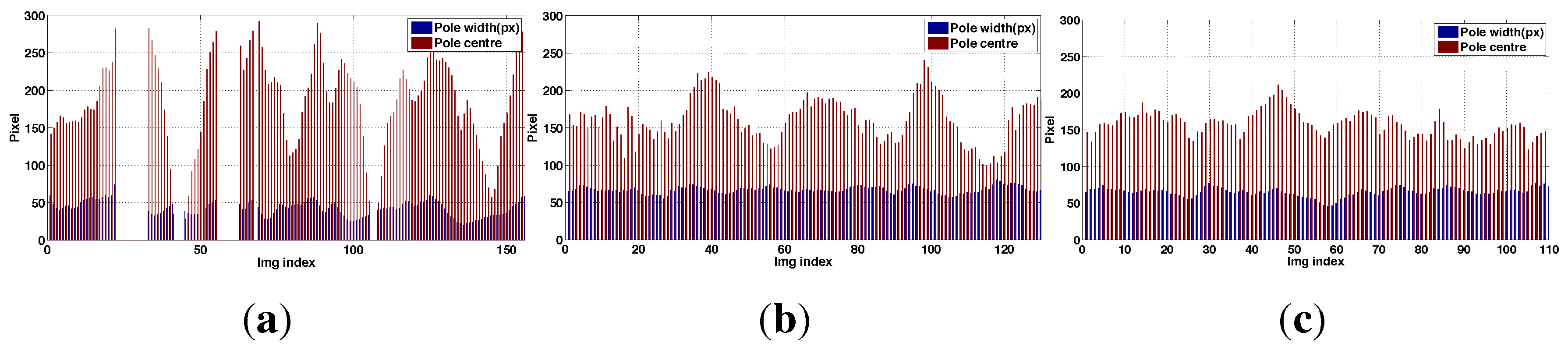


6.5. Limitations and Failure Cases


7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Echelon. Monitored Outdoor Lighting. Available online: http://info.echelon.com/Whitepaper-Monitored-Outdoor-Lighting.html (accessed on 27 August 2015).
- Pratt, K.S.; Murphy, R.R.; Stover, S.; Griffin, C. CONOPS and autonomy recommendations for VTOL small unmanned aerial system based on Hurricane Katrina operations. J. Field Robot. 2009, 26, 636–650. [Google Scholar] [CrossRef]
- Consumer Reports Magazine. Available online: http://www.consumerreports.org/cro/magazine-archive/may-2009/may-2009-toc.htm (accessed on 27 August 2015).
- Balaguer, C.; Gimenez, A.; Jardon, A. Climbing Robots’ Mobility for Inspection and Maintenance of 3D Complex Environments. Auton. Robot. 2005, 18, 157–169. [Google Scholar] [CrossRef]
- Kim, S.; Spenko, M.; Trujillo, S.; Heyneman, B.; Santos, D.; Cutkosky, M. Smooth Vertical Surface Climbing With Directional Adhesion. IEEE Trans. Robot. 2008, 24, 65–74. [Google Scholar]
- Xu, F.; Wang, X.; Wang, L. Cable inspection robot for cable-stayed bridges: Design, analysis, and application. J. Field Robot. 2011, 28, 441–459. [Google Scholar] [CrossRef]
- Haynes, G.C.; Khripin, A.; Lynch, G.; Amory, J.; Saunders, A.; Rizzi, A.A.; Koditschek, D.E. Rapid Pole Climbing with a Quadrupedal Robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 2767–2772.
- Parness, A.; Frost, M.; King, J.; Thatte, N. Demonstrations of gravity-independent mobility and drilling on natural rock using microspines. In Proceedings of the IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 3547–3548.
- Ahmadabadi, M.; Moradi, H.; Sadeghi, A.; Madani, A.; Farahnak, M. The evolution of UT pole climbing robots. In Proceedings of the 2010 1st International Conference on Applied Robotics for the Power Industry (CARPI), Montreal, QC, Canada, 5–7 October 2010; pp. 1–6.
- Kendoul, F. Survey of advances in guidance, navigation, and control of unmanned rotorcraft systems. J. Field Robot. 2012, 29, 315–378. [Google Scholar] [CrossRef]
- Voigt, R.; Nikolic, J.; Hurzeler, C.; Weiss, S.; Kneip, L.; Siegwart, R. Robust embedded egomotion estimation. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 2694–2699.
- Burri, M.; Nikolic, J.; Hurzeler, C.; Caprari, G.; Siegwart, R. Aerial service robots for visual inspection of thermal power plant boiler systems. In Proceedings of the International Conference on Applied Robotics for the Power Industry, Zurich, Switzerland, 11–13 September 2012; pp. 70–75.
- Nikolic, J.; Burri, M.; Rehder, J.; Leutenegger, S.; Huerzeler, C.; Siegwart, R. A UAV system for inspection of industrial facilities. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; pp. 1–8.
- Ortiz, A.; Bonnin-Pascual, F.; Garcia-Fidalgo, E. Vessel Inspection: A Micro-Aerial Vehicle-based Approach. J. Intell. Robot. Syst. 2013, 76, 151–167. [Google Scholar] [CrossRef]
- Eich, M.; Bonnin-Pascual, F.; Garcia-Fidalgo, E.; Ortiz, A.; Bruzzone, G.; Koveos, Y.; Kirchner, F. A Robot Application for Marine Vessel Inspection. J. Field Robot. 2014, 31, 319–341. [Google Scholar] [CrossRef]
- Bachrach, A.; Prentice, S.; He, R.; Roy, N. RANGE–Robust autonomous navigation in GPS-denied environments. J. Field Robot. 2011, 28, 644–666. [Google Scholar] [CrossRef]
- Shen, S.; Michael, N.; Kumar, V. Autonomous Multi-Floor Indoor Navigation with a Computationally Constrained MAV. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 20–25.
- Sa, I.; Corke, P. Improved line tracking using IMU and Vision for visual servoing. In Proceedings of the Australasian Conference on Robotics and Automation, University of New South Wales, Sydney, Australia, 2–4 December 2013.
- Sa, I.; Hrabar, S.; Corke, P. Outdoor Flight Testing of a Pole Inspection UAV Incorporating High-Speed Vision. In Proceedings of the International Conference on Field and Service Robotics, Brisbane, Australia, 9–11 December 2013.
- Sa, I.; Hrabar, S.; Corke, P. Inspection of Pole-Like Structures Using a Vision-Controlled VTOL UAV and Shared Autonomy. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014; pp. 4819–4826.
- Sa, I.; Corke, P. Close-quarters Quadrotor flying for a pole inspection with position based visual servoing and high-speed vision. In Proceedings of the IEEE International Conference on Unmanned Aircraft Systems, Orlando, FL, USA, 27–30 May 2014; pp. 623–631.
- Video demonstration. Available online: http://youtu.be/ccS85_EDl9A (accessed on 27 August 2015).
- Hough, P. Machine Analysis of Bubble Chamber Pictures. In Proceedings of the International Conference on High Energy Accelerators and Instrumentation, Geneva, Switzerland, 14–19 September 1959.
- Shi, D.; Zheng, L.; Liu., J. Advanced Hough Transform Using A Multilayer Fractional Fourier Method. IEEE Trans. Image Process. 2010. [Google Scholar] [CrossRef]
- Hager, G.; Toyama, K. X vision: A portable substrate for real-time vision applications. Comput. Vis. Image Understand. 1998, 69, 23–37. [Google Scholar] [CrossRef]
- Bartoli, A.; Sturm, P. The 3D line motion matrix and alignment of line reconstructions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Kauai, USA, 8–14 December 2001; Volume 1, pp. 1–287.
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Bartoli, A.; Sturm, P. Structure-from-motion using lines: Representation, triangulation, and bundle adjustment. Comput. Vis. Image Understand. 2005, 100, 416–441. [Google Scholar] [CrossRef]
- Mahony, R.; Hamel, T. Image-based visual servo control of aerial robotic systems using linear image features. IEEE Trans. Robot. 2005, 21, 227–239. [Google Scholar] [CrossRef]
- Solà, J.; Vidal-Calleja, T.; Civera, J.; Montiel, J.M. Impact of Landmark Parametrization on Monocular EKF-SLAM with Points and Lines. Int. J. Comput. Vis. 2012, 97, 339–368. [Google Scholar] [CrossRef]
- Chaumette, F.; Hutchinson, S. Visual servo control. I. Basic approaches. IEEE Robot. Autom. Mag. 2006, 13, 82–90. [Google Scholar] [CrossRef]
- Fischler, M.; Bolles, R. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Durrant-Whyte, H. Introduction to Estimation and the Kalman Filter; Technical Report; The University of Sydney: Sydney, Australia, 2001. [Google Scholar]
- Mahony, R.; Kumar, V.; Corke, P. Modeling, Estimation and Control of Quadrotor Aerial Vehicles. IEEE Robot. Autom. Mag. 2012. [Google Scholar] [CrossRef]
- Leishman, R.; Macdonald, J.; Beard, R.; McLain, T. Quadrotors and Accelerometers: State Estimation with an Improved Dynamic Model. IEEE Control Syst. 2014, 34, 28–41. [Google Scholar] [CrossRef]
- Corke, P. Robotics, Vision & Control: Fundamental Algorithms in MATLAB; Springer: Brisbane, Australia, 2011; ISBN 978-3-642-20143-1. [Google Scholar]
- Corke, P.; Hutchinson, S. A new partitioned approach to image-based visual servo control. IEEE Trans. Robot. Autom. 2001, 17, 507–515. [Google Scholar] [CrossRef]
- Malis, E.; Rives, P. Robustness of image-based visual servoing with respect to depth distribution errors. In Proceedings of the IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; pp. 1056–1061.
- Espiau, B.; Chaumette, F.; Rives, P. A new approach to visual servoing in robotics. IEEE Trans. Robot. Autom. 1992, 8, 313–326. [Google Scholar] [CrossRef]
- Pissard-Gibollet, R.; Rives, P. Applying visual servoing techniques to control a mobile hand-eye system. In Proceedings of the IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995; pp. 166–171.
- Briod, A.; Zufferey, J.C.; Floreano, D. Automatically calibrating the viewing direction of optic-flow sensors. In Proceedings of the IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; pp. 3956–3961.
- Corke, P.; Hutchinson, S. Real-time vision, tracking and control. In Proceedings of the IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 622–629.
- Feddema, J.; Mitchell, O.R. Vision-guided servoing with feature-based trajectory generation [for robots]. IEEE Trans. Robot. Autom. 1989, 5, 691–700. [Google Scholar] [CrossRef]
- Hosoda, K.; Asada, M. Versatile visual servoing without knowledge of true Jacobian. In Proceedings of the IEEE International Conference on Intelligent Robot Systems, Munich, Germany, 12–16 September 1994; pp. 186–193.
- Omari, S.; Ducard, G. Metric Visual-Inertial Navigation System Using Single Optical Flow Feature. In Proceedings of the European Contol Conference, Zurich, Switzerland, 17–19 July 2013.
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.B.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In Proceedings of the IEEE International Conference on Robotics and Automation Workshop on Open Source Software, Kobe, Japan, 12–17 May 2009; pp. 5–11.
- O’Sullivan, L.; Corke, P. Empirical Modelling of Rolling Shutter Effect. In Proceedings of the IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014.
- Achtelik, M.; Achtelik, M.; Weiss, S.; Siegwar, R. Onboard IMU and Monocular Vision Based Control for MAVs in Unknown In- and Outdoor Environments. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011.
- Leica TS30. Available online: http://www.leica-geosystems.com/en/Engineering-Monitoring-TPS-Leica-TS30_77093.htm (accessed on 27 August 2015).
- Bachrach, A.G. Autonomous Flight in Unstructured and Unknown Indoor Environments. Master’s Thesis, MIT, Cambridge, MA, USA, 2009. [Google Scholar]
- Abbeel, P.; Coates, A.; Montemerlo, M.; Ng, A.Y.; Thrun, S. Discriminative Training of Kalman Filters. In Proceedings of the Robotics: Science and Systems, Cambridge, MA, USA, 8–11 June 2005; pp. 289–296.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sa, I.; Hrabar, S.; Corke, P. Inspection of Pole-Like Structures Using a Visual-Inertial Aided VTOL Platform with Shared Autonomy. Sensors 2015, 15, 22003-22048. https://doi.org/10.3390/s150922003
Sa I, Hrabar S, Corke P. Inspection of Pole-Like Structures Using a Visual-Inertial Aided VTOL Platform with Shared Autonomy. Sensors. 2015; 15(9):22003-22048. https://doi.org/10.3390/s150922003
Chicago/Turabian StyleSa, Inkyu, Stefan Hrabar, and Peter Corke. 2015. "Inspection of Pole-Like Structures Using a Visual-Inertial Aided VTOL Platform with Shared Autonomy" Sensors 15, no. 9: 22003-22048. https://doi.org/10.3390/s150922003
APA StyleSa, I., Hrabar, S., & Corke, P. (2015). Inspection of Pole-Like Structures Using a Visual-Inertial Aided VTOL Platform with Shared Autonomy. Sensors, 15(9), 22003-22048. https://doi.org/10.3390/s150922003





