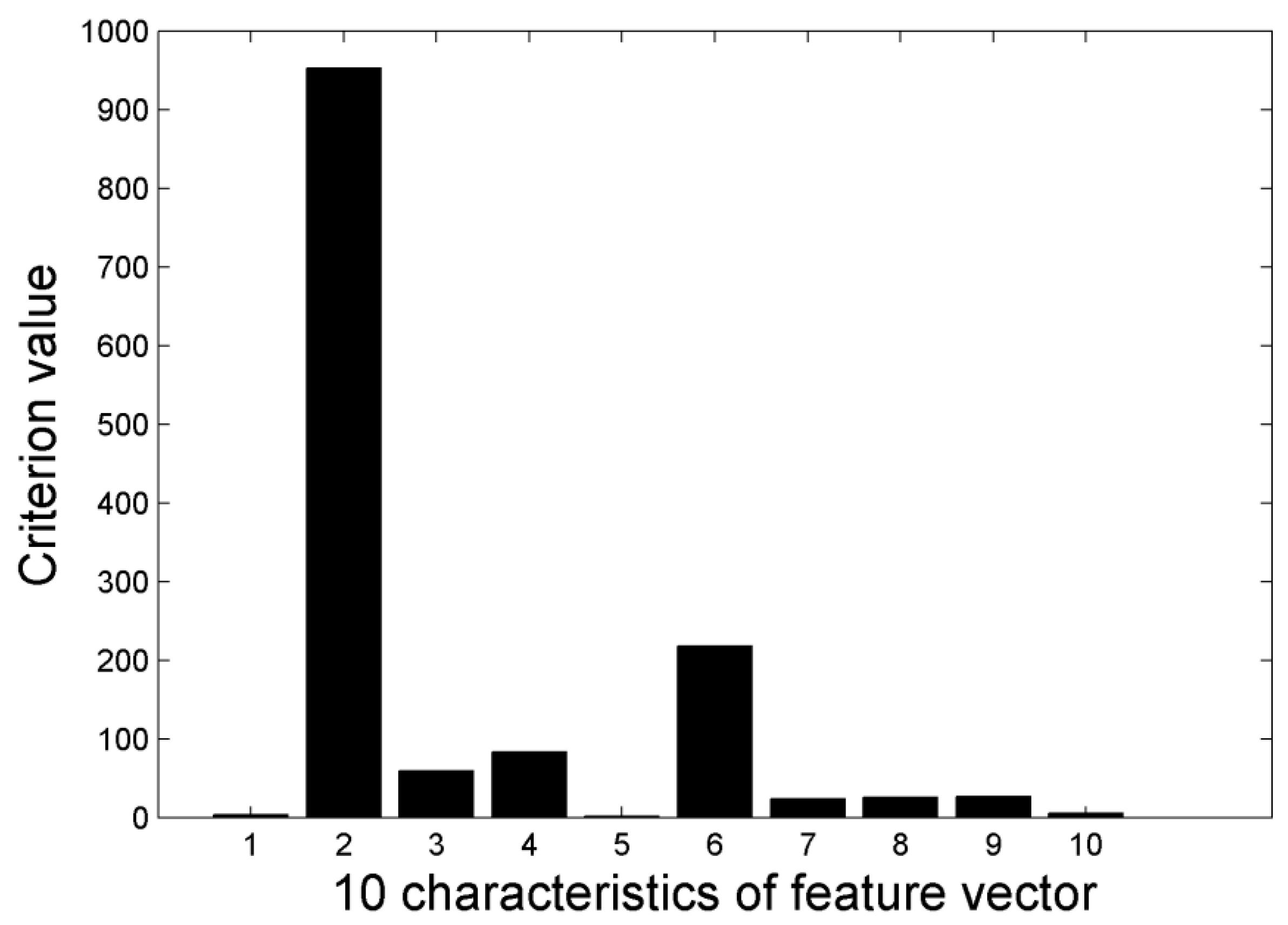
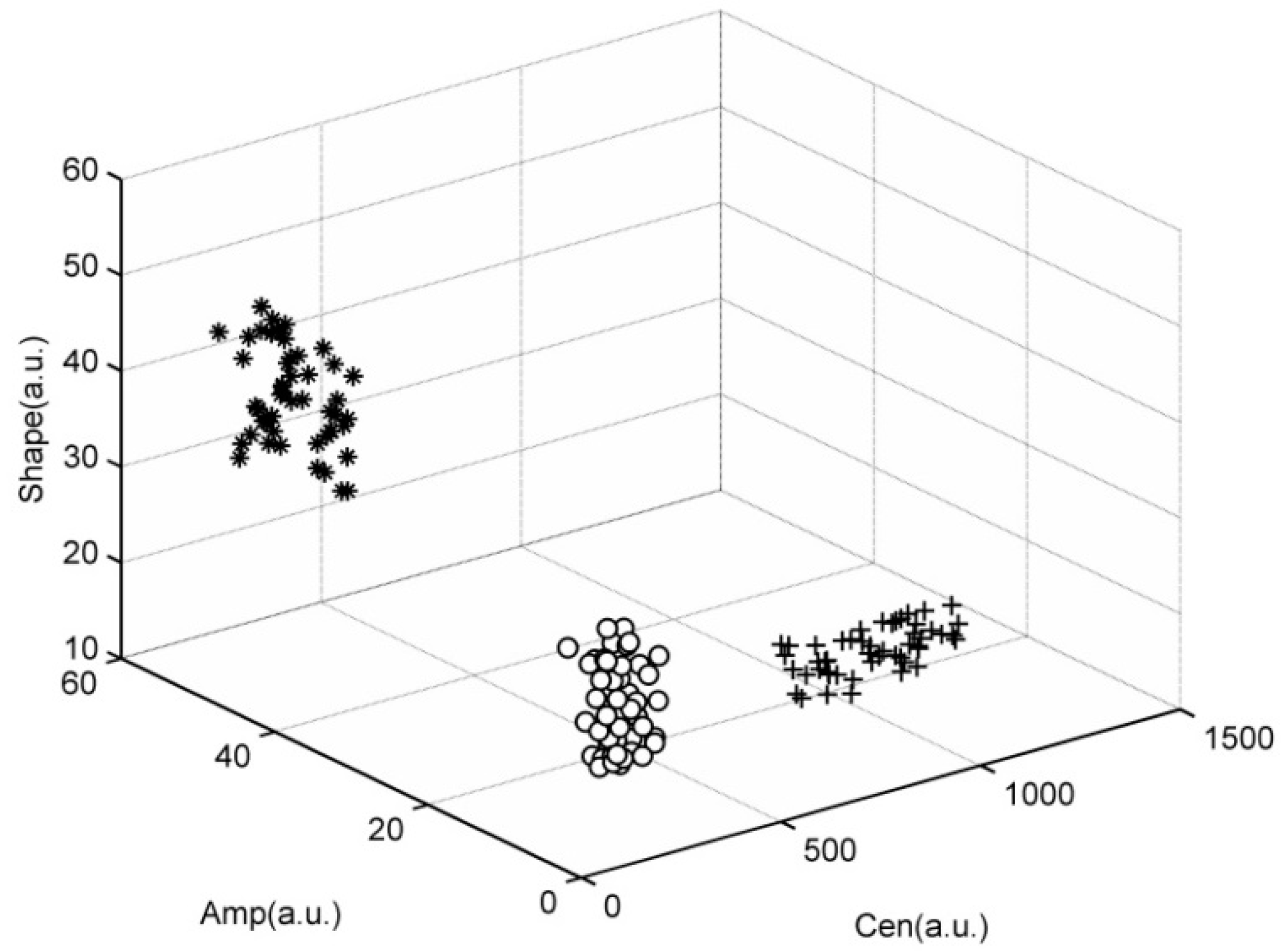
1. Introduction
Optical fiber vibration sensing systems based on phase-sensitive optical time-domain reflectometer (Φ-OTDR) devices can detect and locate vibration signals by measuring the backscatter light scattered across the entire optical spectrum. A Φ-OTDR uses a single mode fiber for optical transmission and sensing, and can be used for real-time monitoring and accurate positioning across long distances [
1,
2]. It has been used for monitoring the health of engineering structures, optical fiber perimeter protection and gas or oil pipeline safety pre-warning systems [
3,
4,
5,
6]. Accurate recognition of different vibration signals is crucial in a Φ-OTDR pre-warning system. False positives will be an inefficient use of resources and more seriously, delays in processing time may threaten people’s lives and property, therefore, there is a lot of attention is being given in Φ-OTDR research to techniques to accurately recognize the event type, ensure warnings are given in sufficient time and reduce the false positive rate.
Due to the nonlinear, dynamic nature of the signal acquired by a Φ-OTDR vibration sensing system, a location scheme based on the wavelet packet transform (WPT) is proposed to reduce the number of false alarms [
7]. Previous studies have used the short-time Fourier transform (STFT) and the continuous wavelet transform (CWT) for recognition of Φ-OTDR systems [
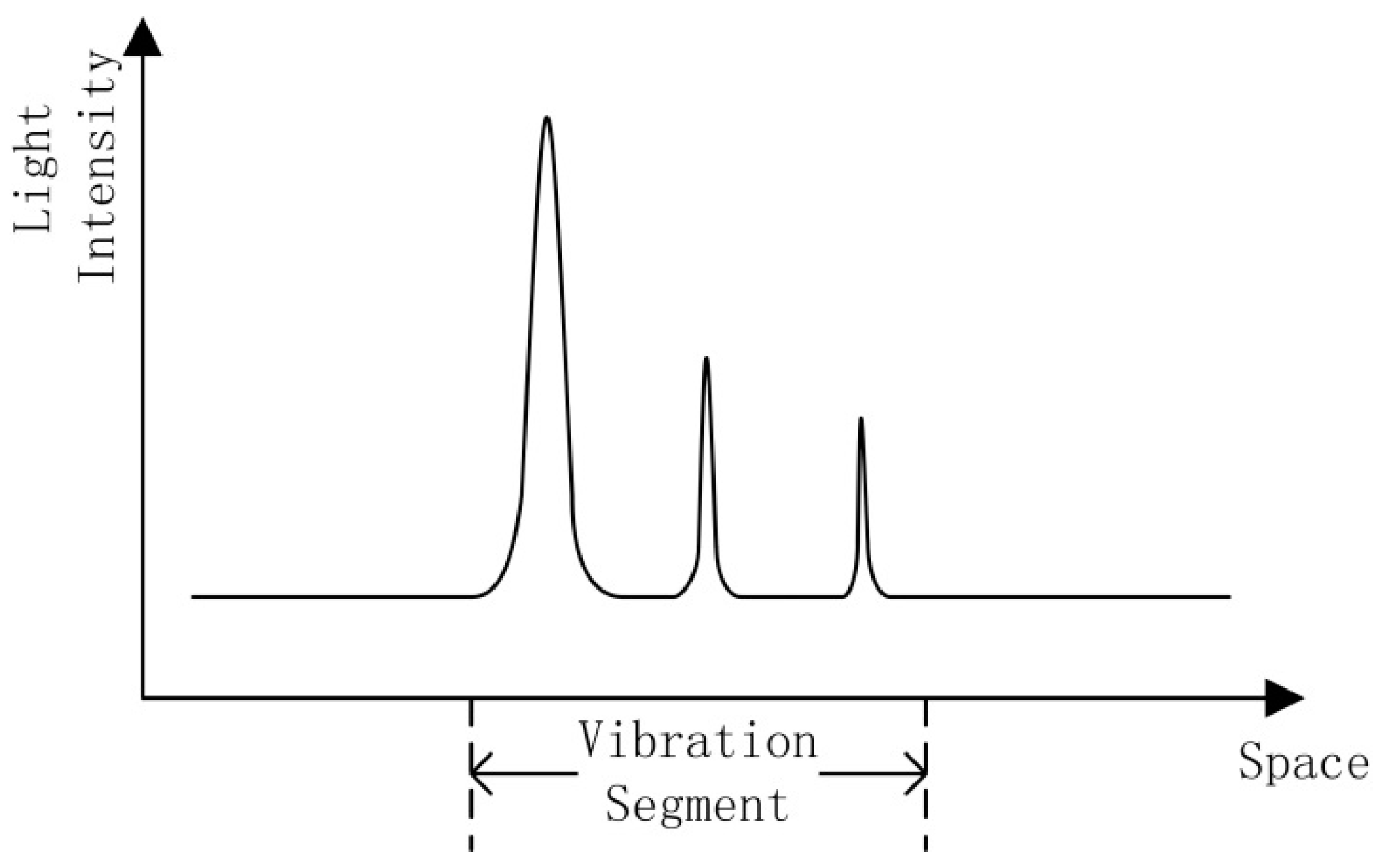
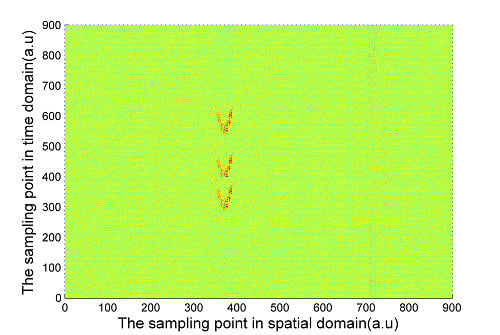
8]. These traditional methods focus on finding and locating the intrusion events. If the features of the time domain signal can be extracted after the event has been located, different event types can be classified based on these signal features. However, this method is time consuming, due to the requirement to firstly pinpoint the location in the recognition process. If multiple events occur simultaneously, the recognition time will increase significantly. The intrusion signal of an Φ-OTDR system is not a single point in the space domain; it occurs across a range, since the attenuation will continue for a period along the optic fiber. Within the attenuation range, each scattered light signal contains the vibration response, but since the initial phase of each interference signal is different, the amplitudes of the vibration responses are different within the attenuation range, as shown in
Figure 1. The peaks are due to backscattering when an intrusion event occurs. However, the maximum point may not be the location of the intrusion. If the event location is identified as the point with the maximum light intensity, then an error in location will occur.
Figure 1.
Figure 1. Scattering curve of intrusion signal.
Figure 1.
Figure 1. Scattering curve of intrusion signal.
Once there is an error in locating the event, the time domain signal of that location will not be the real signal corresponding to the intrusion event. Therefore the features of the event cannot be extracted correctly, which will lead to a recognition error. This conventional method is inadequate for a Φ-OTDR system and thus a highly efficient and precise method is necessary for recognition of intrusion events. In this paper, after a brief presentation of the Φ-OTDR signal characteristics in
Section 2, a method based on time-space domain signals is proposed. The algorithm is evaluated in this paper using the criteria of recognition accuracy and speed. The recognition accuracy is the percentage of correct recognition events of all events. Recognition speed is the time calculated from feature extraction to recognition. The method proposed in this paper improves both the speed and accuracy of the recognition method, and is therefore a very suitable method to recognize different events within a Φ-OTDR sensing system. In
Section 3, a feature extraction method based on morphology is proposed. The classifier design and performance evaluation are demonstrated in
Section 4, and the final section provides the conclusions.
2. Φ-OTDR Signal Characteristics
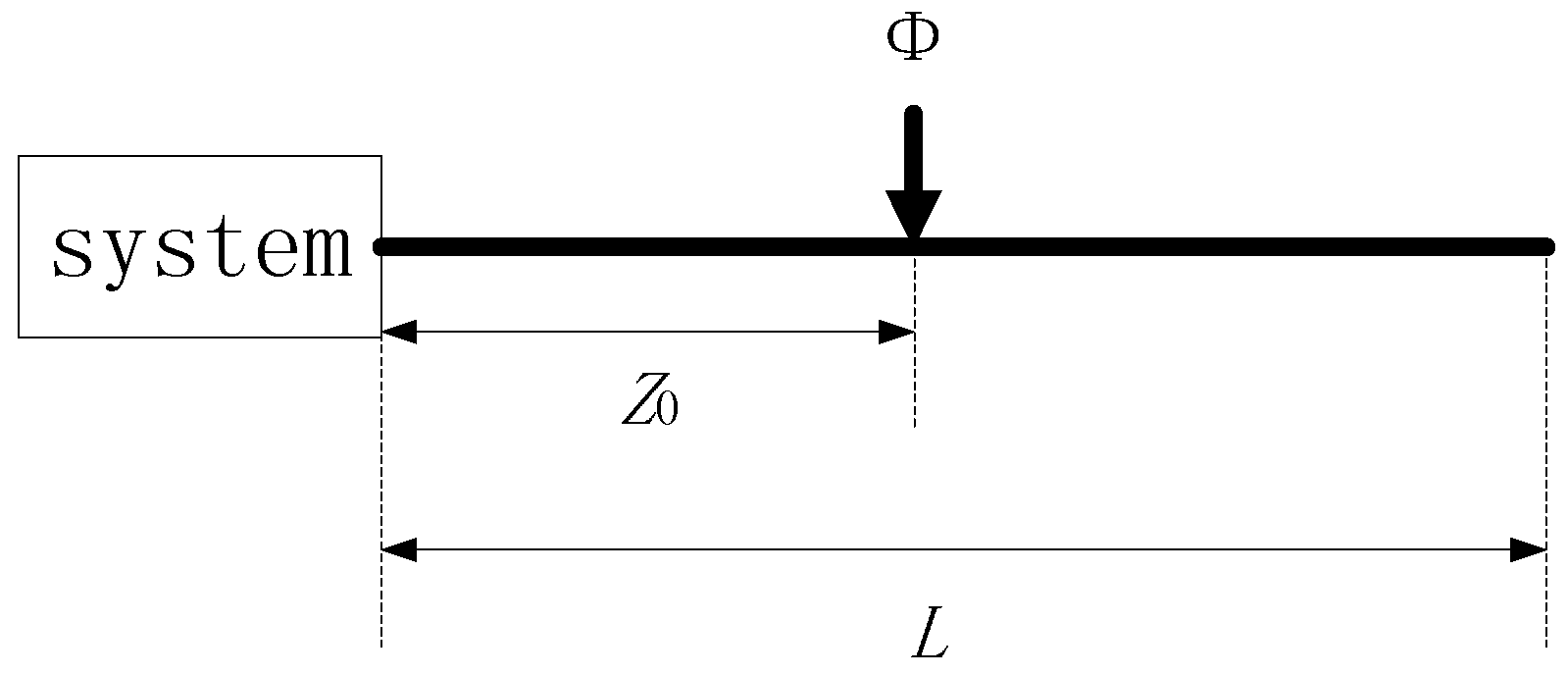
The Φ-OTDR system has unique signal characteristics compared with other optic fiber sensing systems. Rayleigh Scattering (RS) light traveling within a fiber is phase modulated by vibrations that are applied to the fiber to acquire a RS curve for the pulse duration. The time-space domain signal is acquired by clustering all RS curves. It can reflect the characteristics in the space and time domain simultaneously. The propagation distance of vibrations in the space domain reflects the energy of the intrusion signal and the signal characteristics in the time domain reflect the duration of the intrusion event. A simplified construction of an Φ-OTDR system is shown in
Figure 2. It can be assumed that that
ε(
t) is the optical pulse and
L is the length of optical fiber. The vibration occurs at position
z0 and the optical phase is therefore modulated by the vibration, with variation Φ.
Figure 2.
Simplified construction of a Φ-OTDR system.
Figure 2.
Simplified construction of a Φ-OTDR system.
The Rayleigh scattering field intensity can be expressed as follows:
where
n is the number of optical pulses. If the optical pulse period is
,
s ∈ (
nT,
nL/
c+
nT).
can also be regarded as the abscissa of any point in the optical fiber.
is the velocity of light, β is the transmission constant, 2
z/
c is the optical pulse delay and 2β
z is the optical phase delay.
E1 and
E2 are the Rayleigh scattering field intensities before and after the intrusion event, respectively.
The interference intensity can be expressed as:
where
ϕ0 is the initial phase of the Φ-OTDR system. The value of
ϕ in Equation (4) not only changes in the time domain but also in the spatial domain. The attenuation of
ϕ in the spatial domain can be expressed as:
In Equation (6), α is the phase attenuation coefficient,
s0 is the position of the intrusion event and
d is the range of the intrusion force.
is the phase variation in the time domain. The schematic diagram is shown in
Figure 3.
Figure 3.
Parameters of Equation (6).
Figure 3.
Parameters of Equation (6).
The length and refractive index of the optical fiber will be modified when there is an intrusion force on the optical fiber.
can be calculated as follows:
where
β is the propagation constant of the optical wave,
L is the length of the optical fiber and
n is the refractive index. The
βL(Δ
L/
L) term is the effect due to strain, which can be regarded as being due to the phase variation along with the optical length variation. The
term is the photoelastic effect, due to the phase variation along with the refractive index variation. Δ
L and Δ
n are determined by the characteristics of the intrusion force and edatope, which are calculated in detail in the literature [
9].
A Φ-OTDR pipeline safety pre-warning system was used as the case study in this paper. Common events which threaten pipeline safety are a vehicle passing over the pipeline, soil digging above the pipeline, and walking over the pipeline. Experiments were done using the Dagang-Zaozhuang product oil pipeline. The sensing cable used is a GYTA six-core single mode communication optical fiber, which was buried 30 cm above the pipeline and 1.5 m underground. Twenty km of optical fiber was used in the experiment. The laser pulse repetition frequency is 500 Hz and the sampling frequency is 50 MHz. Two seconds of data are used to constitute an image. For this particular application, the recognition accuracy must be as high as possible.
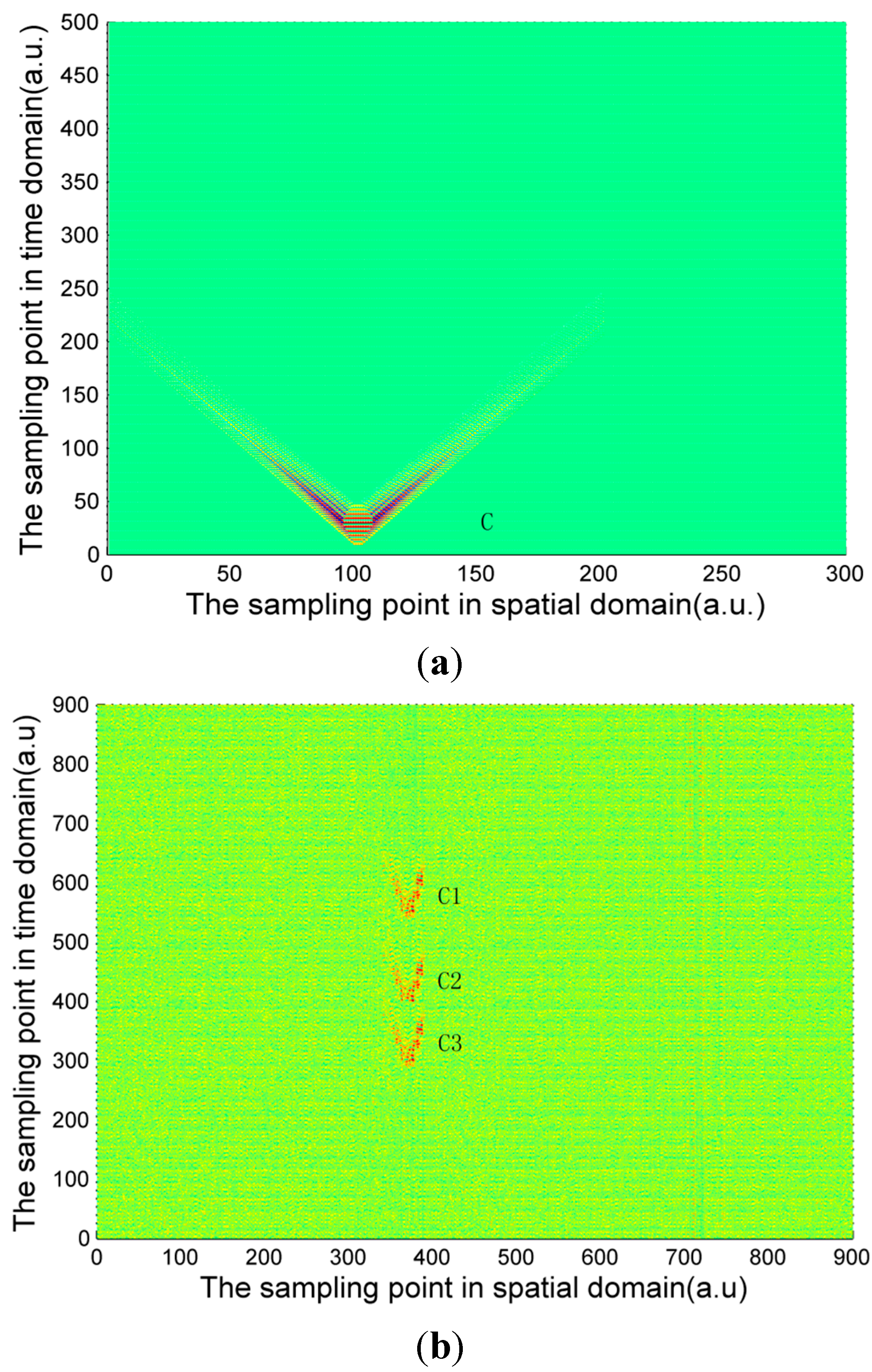
The signal calculated by Equation (4) and the experimentally measured signals of three pipeline safety events are shown in
Figure 4,
Figure 5 and
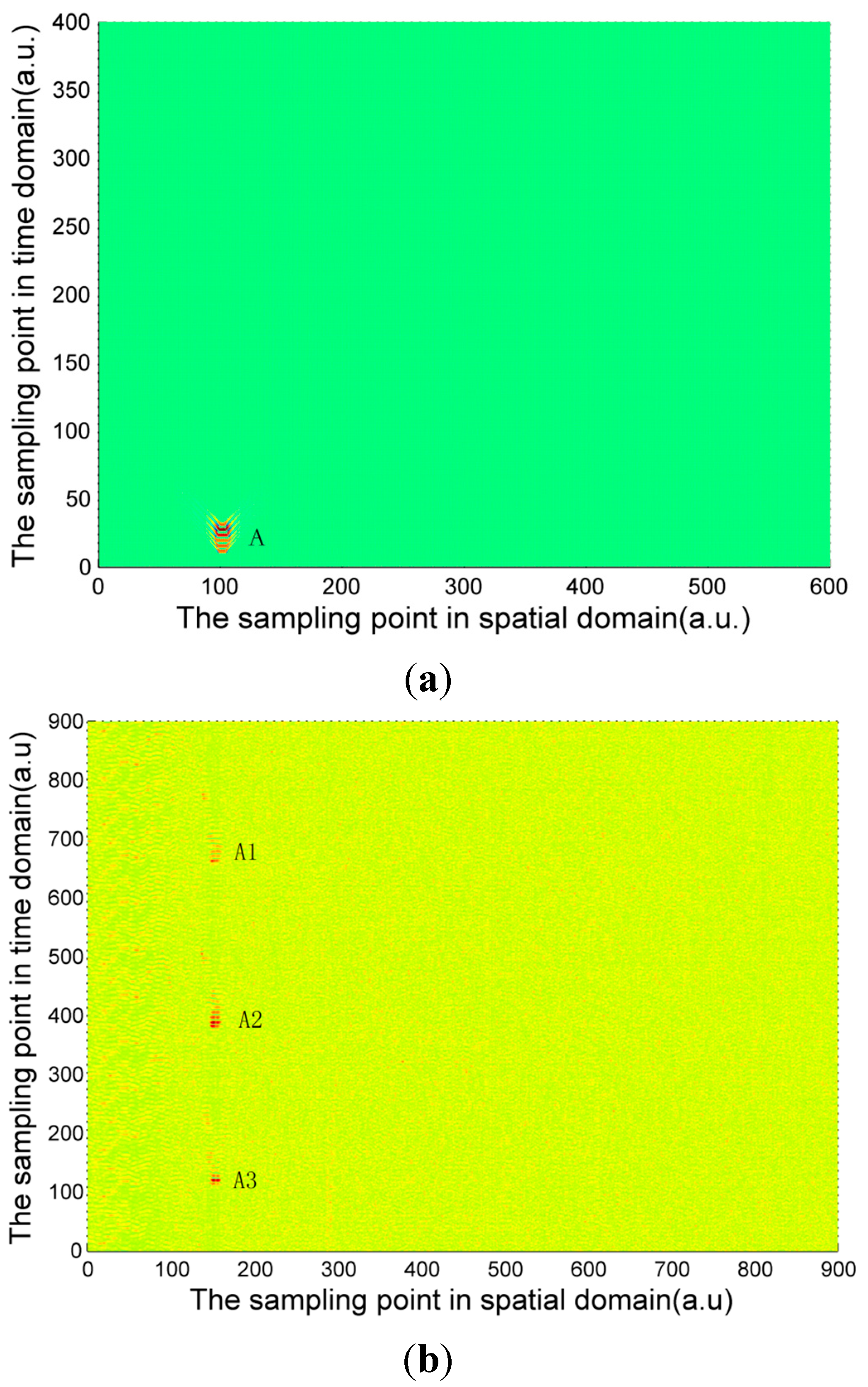
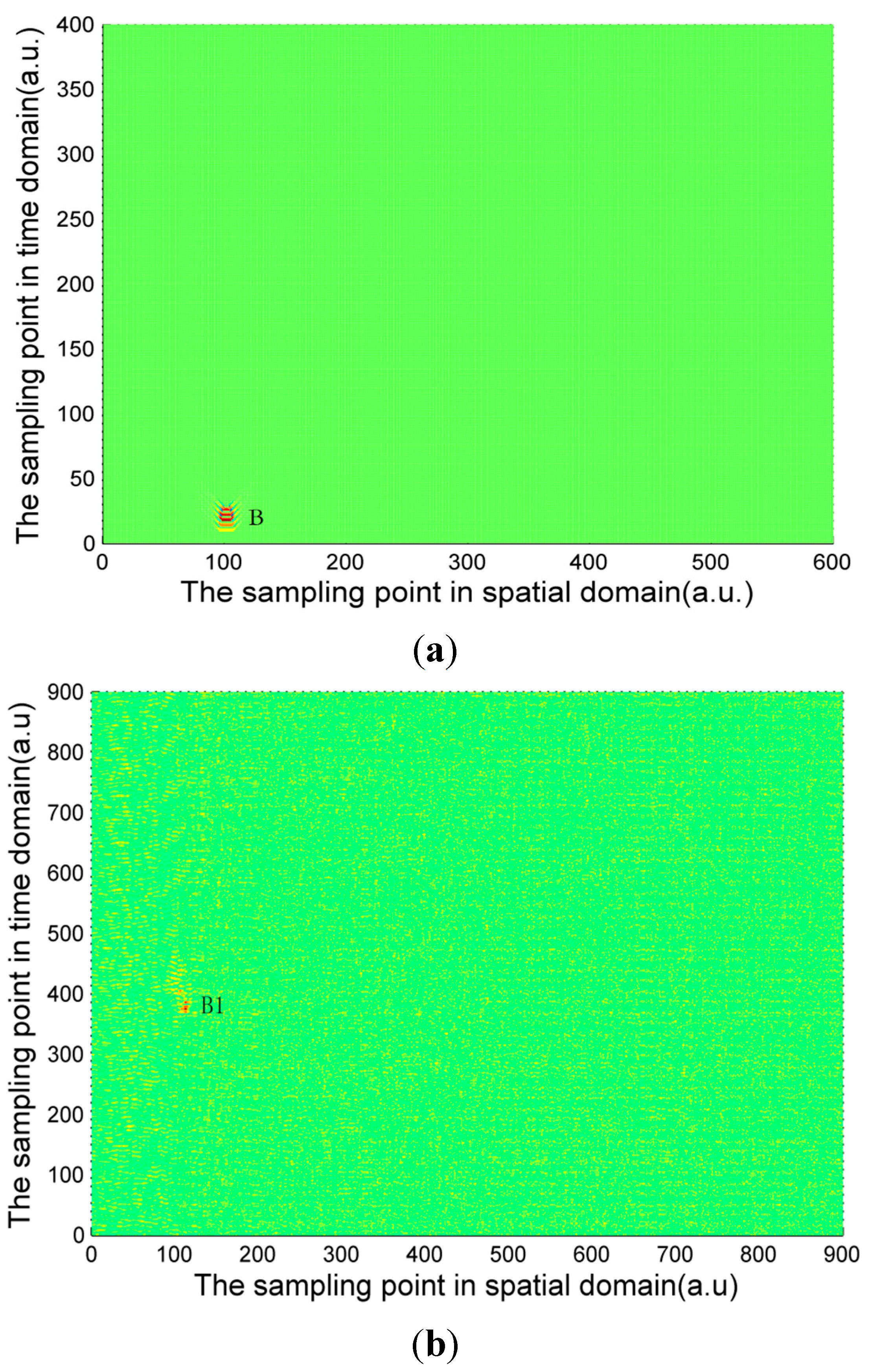
Figure 6. Due to the long distance of the Φ-OTDR system monitoring, the vibration range is relatively small. An intrusion event is usually a fleck in the time-space domain image. The intrusion event occurs continuously in practice, so there are not only one event region in general in time-space signal image. Usually, walking frequency is three steps within 2 s, the interval between the wheels of the vehicle pressing the deceleration strip is about 0.25 s, and the interval due to digging is much larger than 2 s in the experiment. There are three event regions A1, A2, A3 in the experimental walking event, A2, A3 are repetition of A1. There are only one event region B1 in the experimental digging event, and three event regions C1, C2, C3 in the vehicle passing event. Therefore events are calculated only once for simulation signal, marked as region A, region B and region C in
Figure 4,
Figure 5 and
Figure 6. In
Figure 4,
Figure 5 and
Figure 6, the graphs in (a) are the simulation signals calculated by Equation (4) and the graphs in (b) are the experimentally measured signals. In order to illustrate the problem more clearly, the simulation signals are appropriately amplified. In the simulation process, for calculation convenience, many environmental factors were ignored. Soil is idealized as elastic half-space [
10], and intrusion events are idealized as single frequency signals. Although there are some differences between the simulation and experimental signal images, they are basically the same.
Figure 4.
(a) Calculated walking signal; (b) Experimentally measured walking signal.
Figure 4.
(a) Calculated walking signal; (b) Experimentally measured walking signal.
Figure 5.
(a) Calculated digging signal (b) Experimentally measured digging signal.
Figure 5.
(a) Calculated digging signal (b) Experimentally measured digging signal.
The characteristic differences of the three types of events are obvious both in the simulation and experimental signals images. When a vehicle passes over the optical fiber, a vibration signal is produced by the wheels pressing on the deceleration strip on the ground. The duration of this event is very short but the energy is large, so the force can be considered ideally as an instantaneous force. Since the propagation distance is relatively high, a “V”-like shape will be formed. The forces due to walking and digging change relatively slowly with time and energy; the propagation distance is short. The energy and force variation of walking and digging are both different, so the size and the shape of the regions in the image are different. Based on the different image characteristics of each of the three different events, image processing technology can be used for image segmentation, and then a feature extraction method based on morphology proposed in this paper is used for event classification.
Figure 6.
(a) Calculated signal of vehicle passing; (b) Experimentally measured signal of vehicle passing.
Figure 6.
(a) Calculated signal of vehicle passing; (b) Experimentally measured signal of vehicle passing.
4. Experiments
The event samples acquired using the Φ-OTDR pre-warning system are multiclass and the number of samples is small, so the Relevance Vector Machine (RVM) technique is used in this paper. RVM is a machine learning method based on the Bayesian framework. It is sparser than the Support Vector Machine (SVM) technique; hence it has a shorter recognition time and a higher accuracy [
18]. This makes it more suitable for use for recognition for an optical fiber pre-warning system [
19,
20,
21]. The Gauss kernel function is used in this paper because of its widely usability and excellent performance. The kernel parameter is usually set between 0 and 1 [
22]. Through experimental analysis, it was found that the highest accuracy was obtained when the parameter of the kernel function was set to 0.6. The RVM technique was designed for two-class classification problems; therefore a one-to-one multi-category method is used for recognition of the three events [
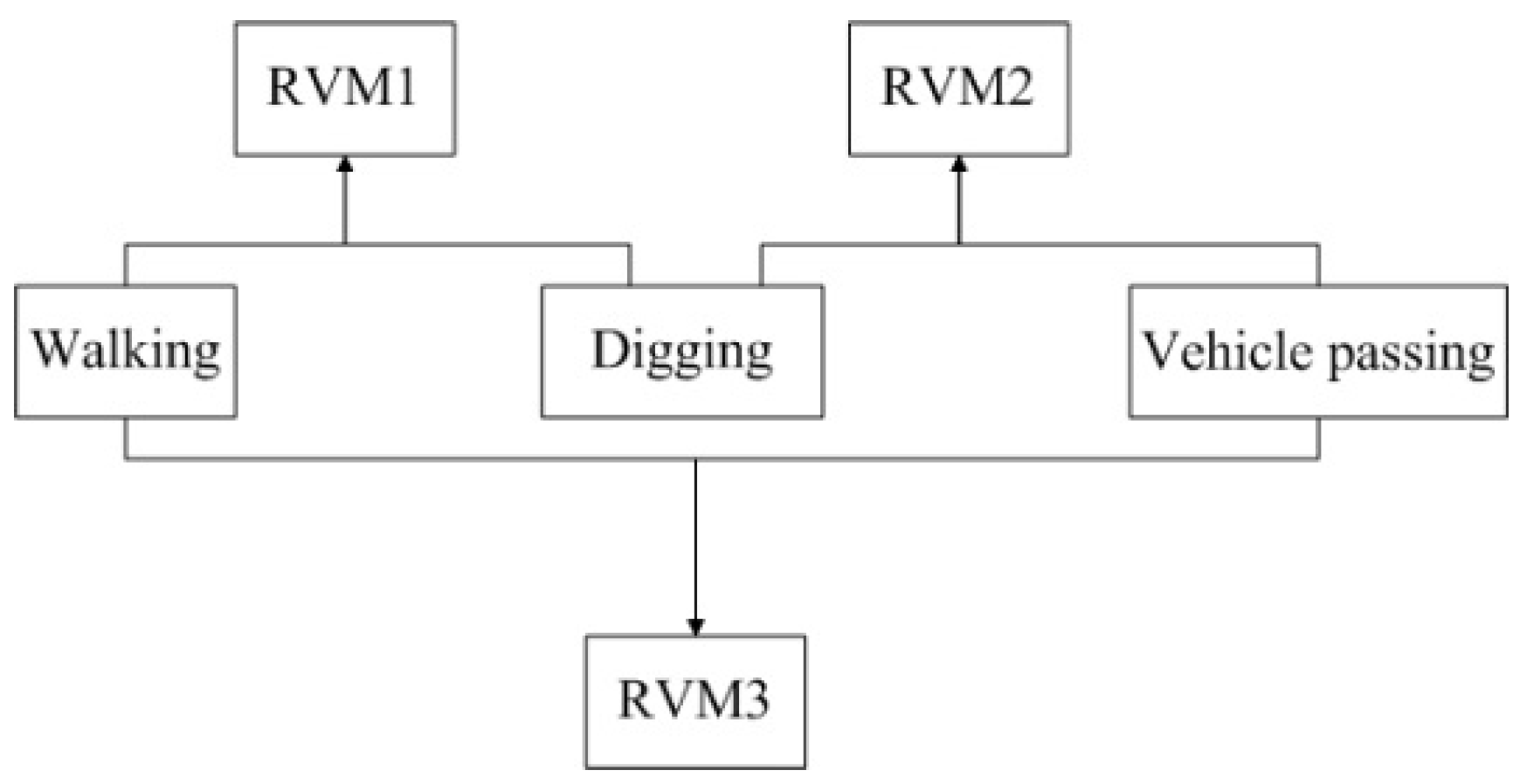
23]. Each classifier recognizes two classes, so there are three classifiers for recognition of the three intrusion events. Each classifier is trained with two events and the training process is shown in
Figure 14.
Figure 14.
Training process of the three classifiers.
Figure 14.
Training process of the three classifiers.
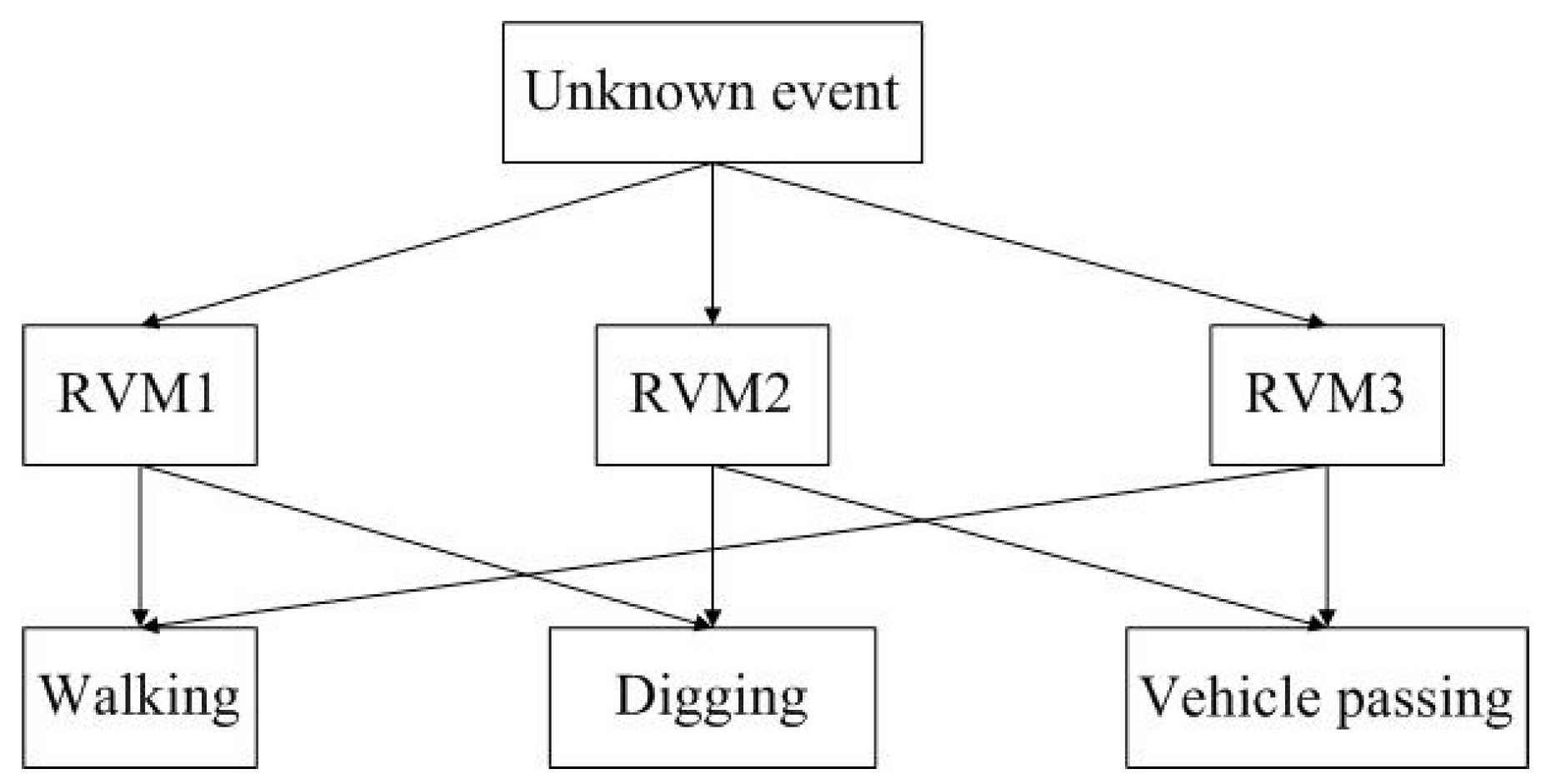
During the recognition process, an unknown event is recognized by the three classifiers. If two classifiers have the same results, the event will belong to that class. The recognition process is shown in
Figure 15.
Figure 15.
Recognition process of three classifiers.
Figure 15.
Recognition process of three classifiers.
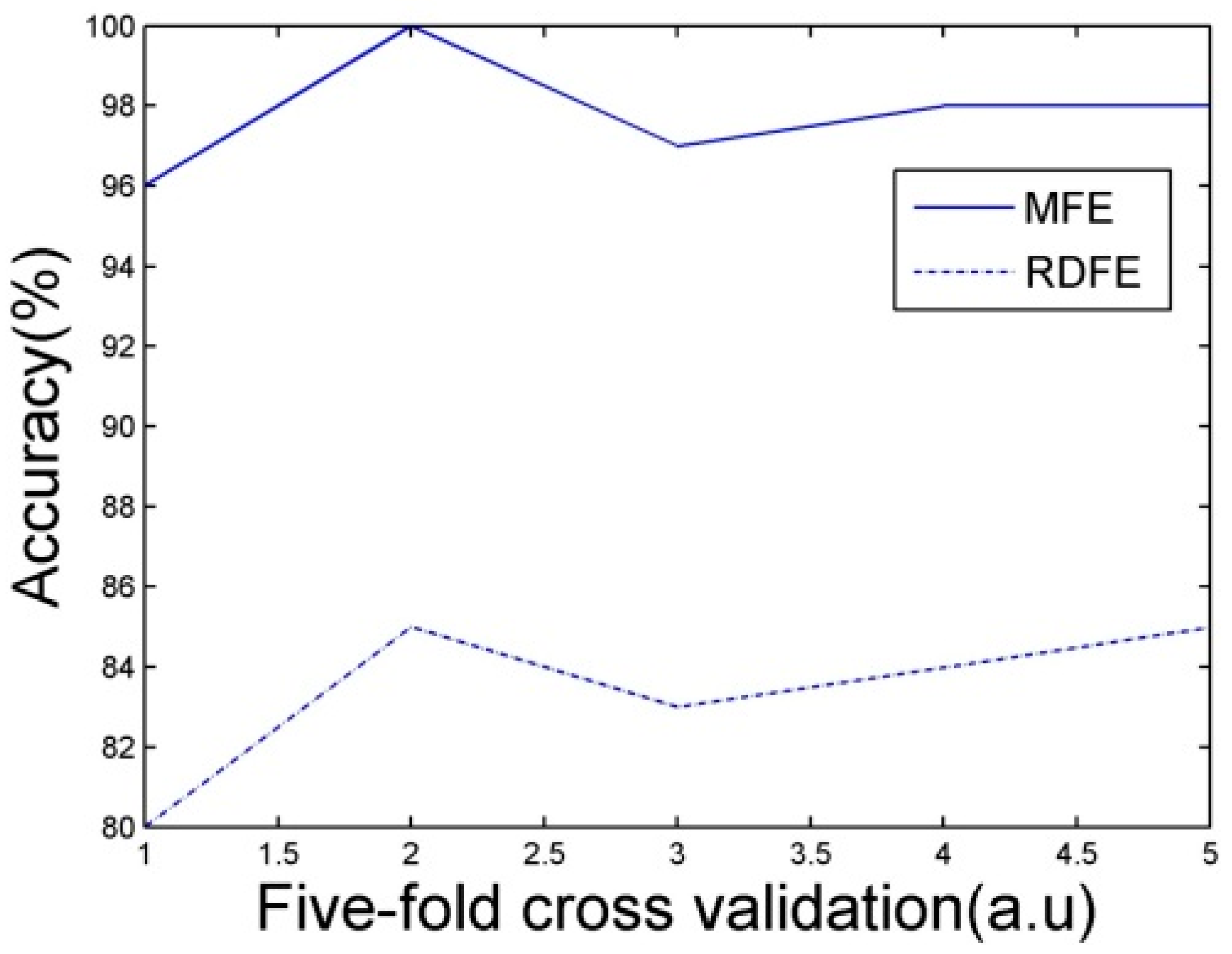
The performance of the classifiers must be evaluated before recognition. Classifiers are evaluated by a five-fold cross validation. 20 samples from each set of 100 samples of each event are selected for training the classifiers. The accuracy of five-fold cross validation is shown in
Figure 16.
Figure 16.
Accuracy of five-fold cross validation.
Figure 16.
Accuracy of five-fold cross validation.
In
Figure 16, the recognition accuracy of Morphological Feature Extraction (MFE) method with feature selection proposed in this paper is much higher than Region Descriptor Feature Extraction (RDFE) without feature selection. The recognition accuracy can reach over 95%. A single cross validation result is shown in
Table 4.
Table 4.
A single cross validation result.
Table 4.
A single cross validation result.
| Sample Model | Walking | Digging | Vehicle Passing |
|---|
| Sample size | 20 | 20 | 20 |
| Walking | 20 | 1 | 0 |
| Digging | 0 | 19 | 0 |
| Vehicle passing | 0 | 0 | 20 |
| Accuracy (%) | 100 | 95 | 100 |
As seen from
Table 4, the recognition accuracy of each event also reaches over 95%. This result contains the case where multiple events happen at the same time. There is a recognition error for the digging since the walking signal is mixed with the digging signal due to environmental disturbance. The category of the test sample is known in the test processing, so the classifiers sort the signal into the wrong class. This mistake can be avoided when this method is used in online monitoring, since the class that the signal belongs to is unknown. Traditionally, an event was located in the space domain by a moving average method, and then the event signal was extracted in the time domain. The wavelet method was used for extracting the features [
24]. RVM was also used as classifier, and five-fold cross validation was used for evaluating the recognition accuracy. The results of the one dimension signal were shown in
Table 4. Identification of the location of the event in the time domain is time-consuming, and since the position accuracy is easily affected by noises, the recognition performance is unsatisfactory. The mean accuracy and recognition time of different methods are shown also in
Table 5. When Φ-OTDR is used for safety online monitoring, the algorithm computation time is the recognition time
i.e., the time calculated from feature extraction to recognition. When an event occurs, the real-time monitoring system firstly acquires the event signal, then extracts the features proposed in this paper, and finally recognizes the event using the RVM classifiers. The training process was performed before real-time monitoring. In this paper, the recognition time must be within one second.
Table 5.
Performance comparison of different methods.
Table 5.
Performance comparison of different methods.
| Method | Average Precision (%) | Recognition Time (s) |
|---|
| WFE-RVM | 80 | 10.526 |
| RDFE-RVM | 85.4 | 2.169 |
| MFE-RVM | 97.8 | 0.7028 |
In
Table 5, Wavelet Feature Extraction RVM (WFE-RVM) is the traditional recognition method. Region Descriptor Feature Extraction RVM (RDFE-RVM) is the recognition method without feature selection. Morphological Feature Extraction RVM (MFE-RVM) is the recognition method proposed in this paper. Compared with WFE and RDFE, the MFE method proposed in this paper can greatly improve the recognition accuracy. There are only four features after feature selection; therefore the speed of the algorithm also can be increased significantly. The recognition accuracy can reach 97.87%, and the recognition time is within one second, so it meets the requirement of Φ-OTDR online monitoring.