Design of a Thermoacoustic Sensor for Low Intensity Ultrasound Measurements Based on an Artificial Neural Network
Abstract
:1. Introduction
2. Sensor Design and Simulation
2.1. Sensor Design

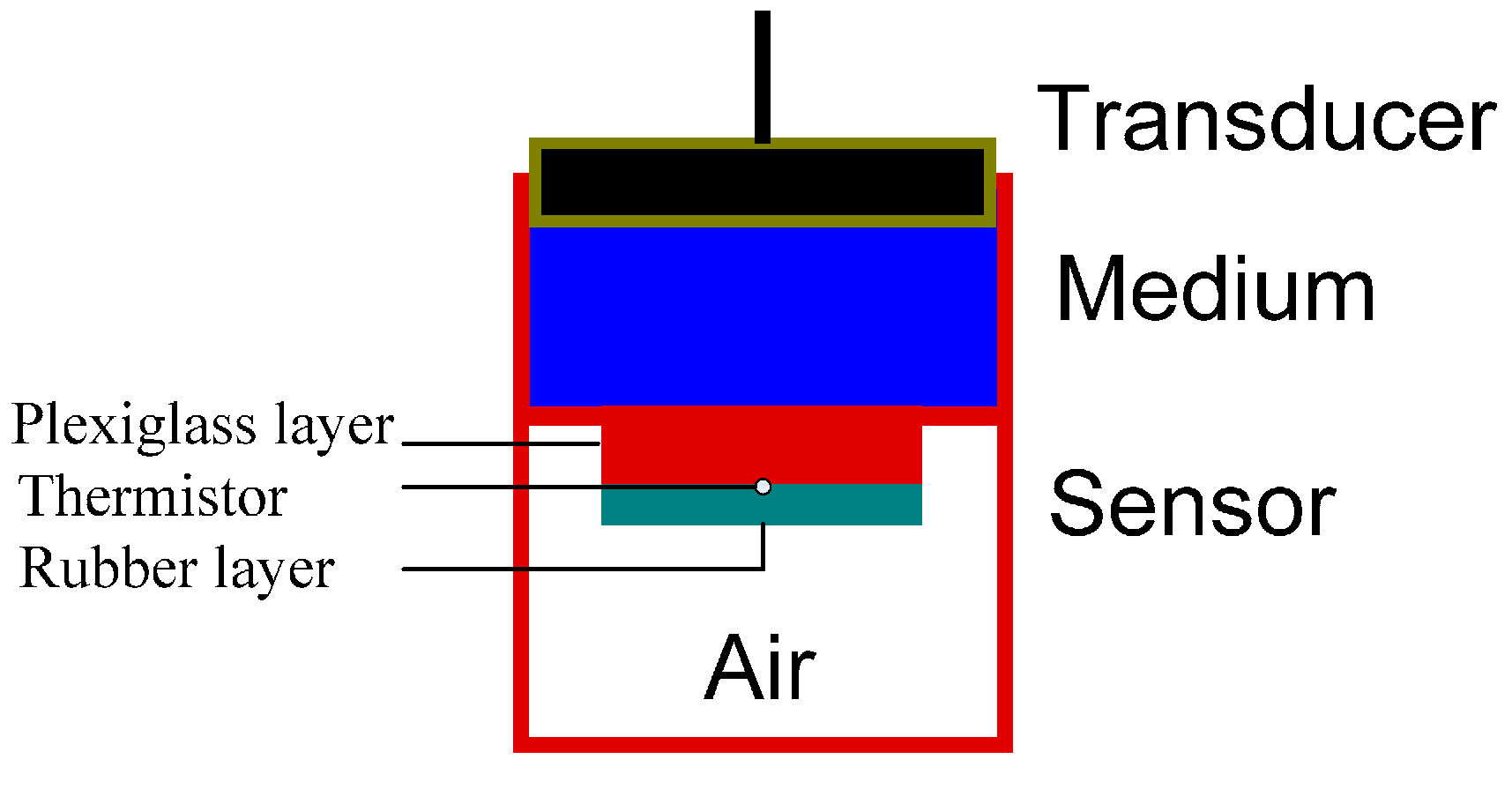
2.2. Simulation of Ultrasound Propagation in Sensor
| Material | Attenuation Coefficient (dB·cm−1 MHz−1) | Density (kg/m3) | Speed of Sound in Media (m/s) |
|---|---|---|---|
| Ultrasound Medium | 0.002 | 1000 | 1481 |
| Air | 1.64 | 1.204 | 343 |
| Plexiglass | 1.13 | 1180 | 2730 |
| Polyurethane Rubber | 30 | 1010 | 1500 |
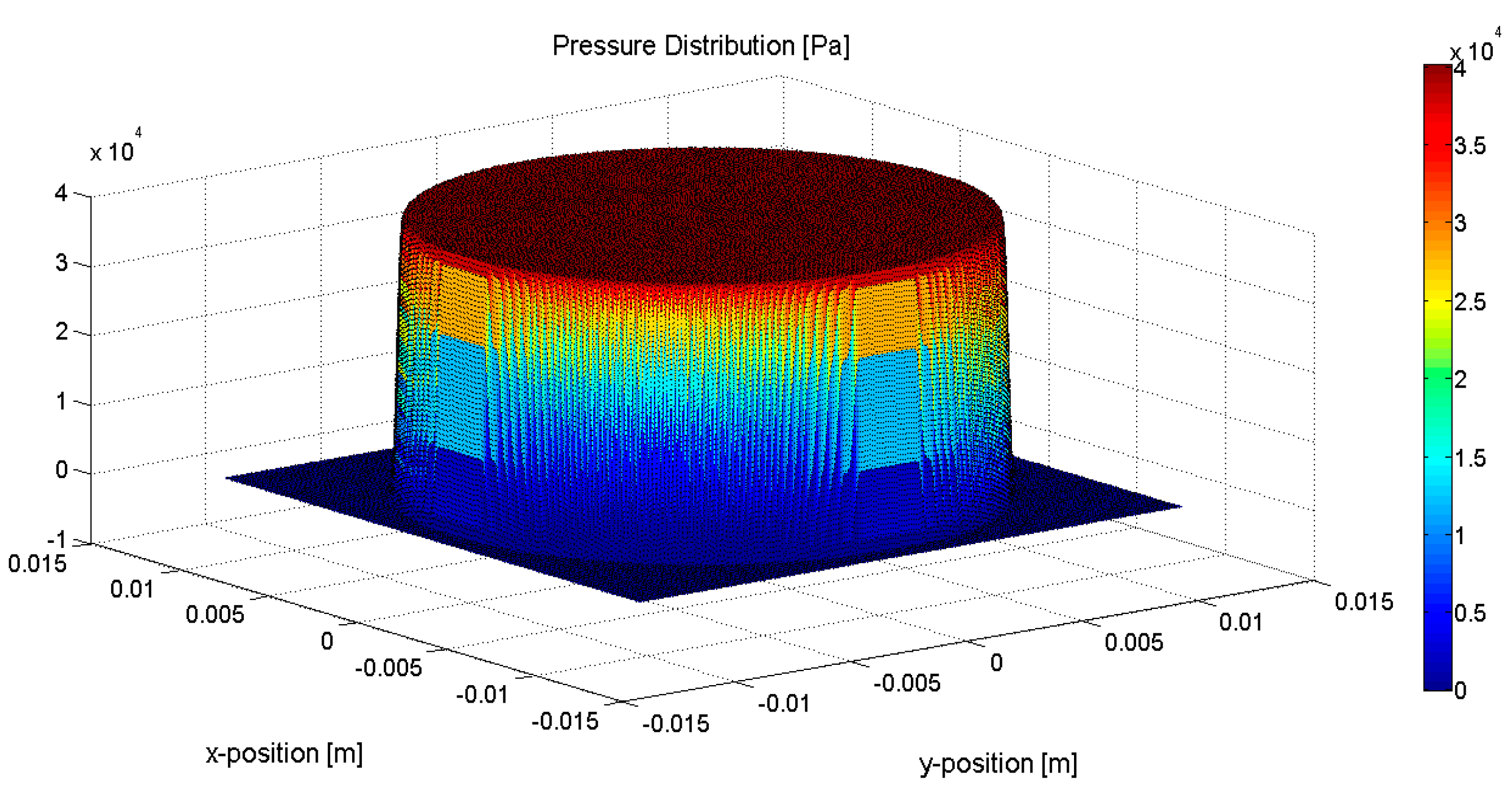
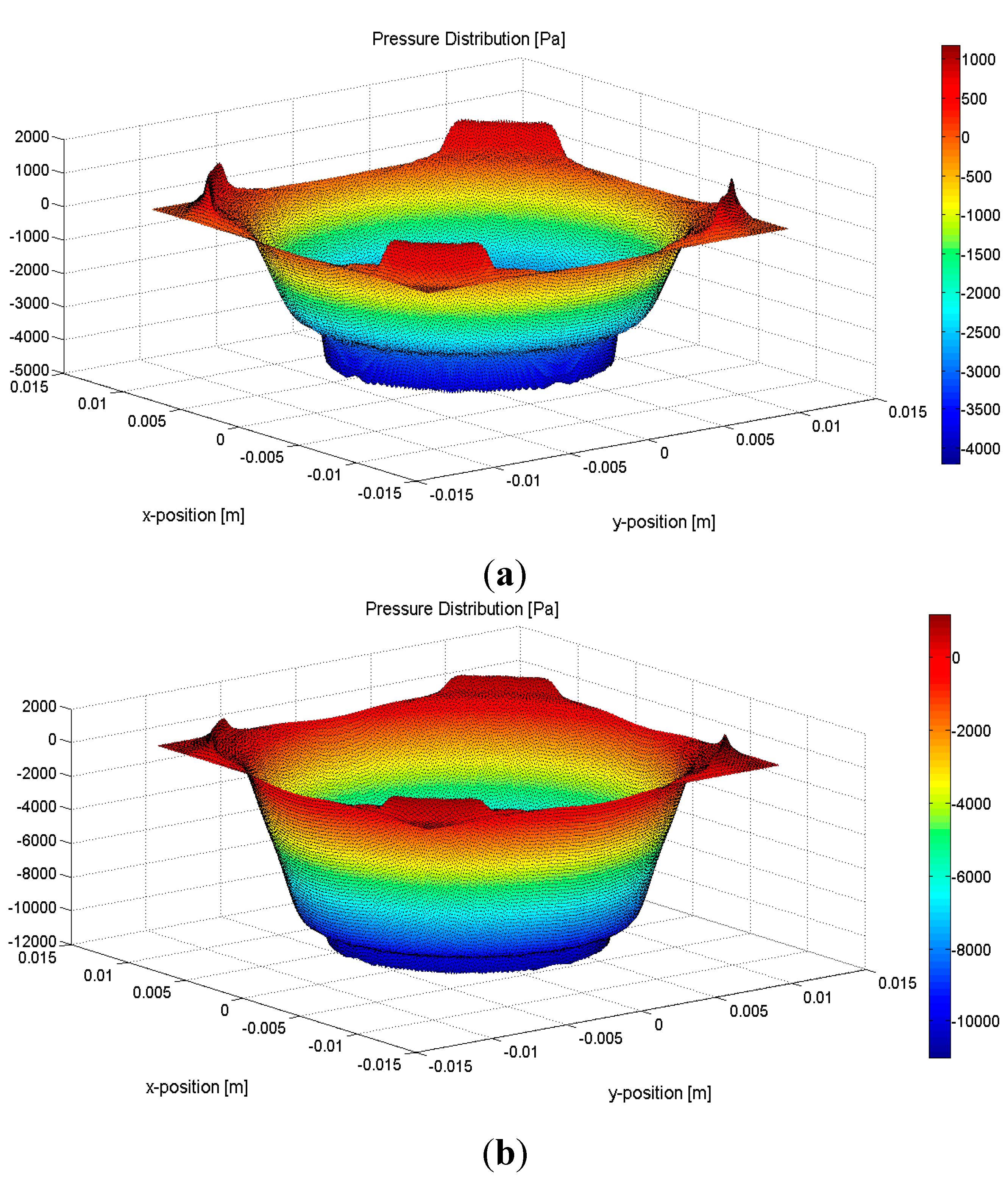
3. Sensor Calibration
3.1. Calibration for Thermistor Data
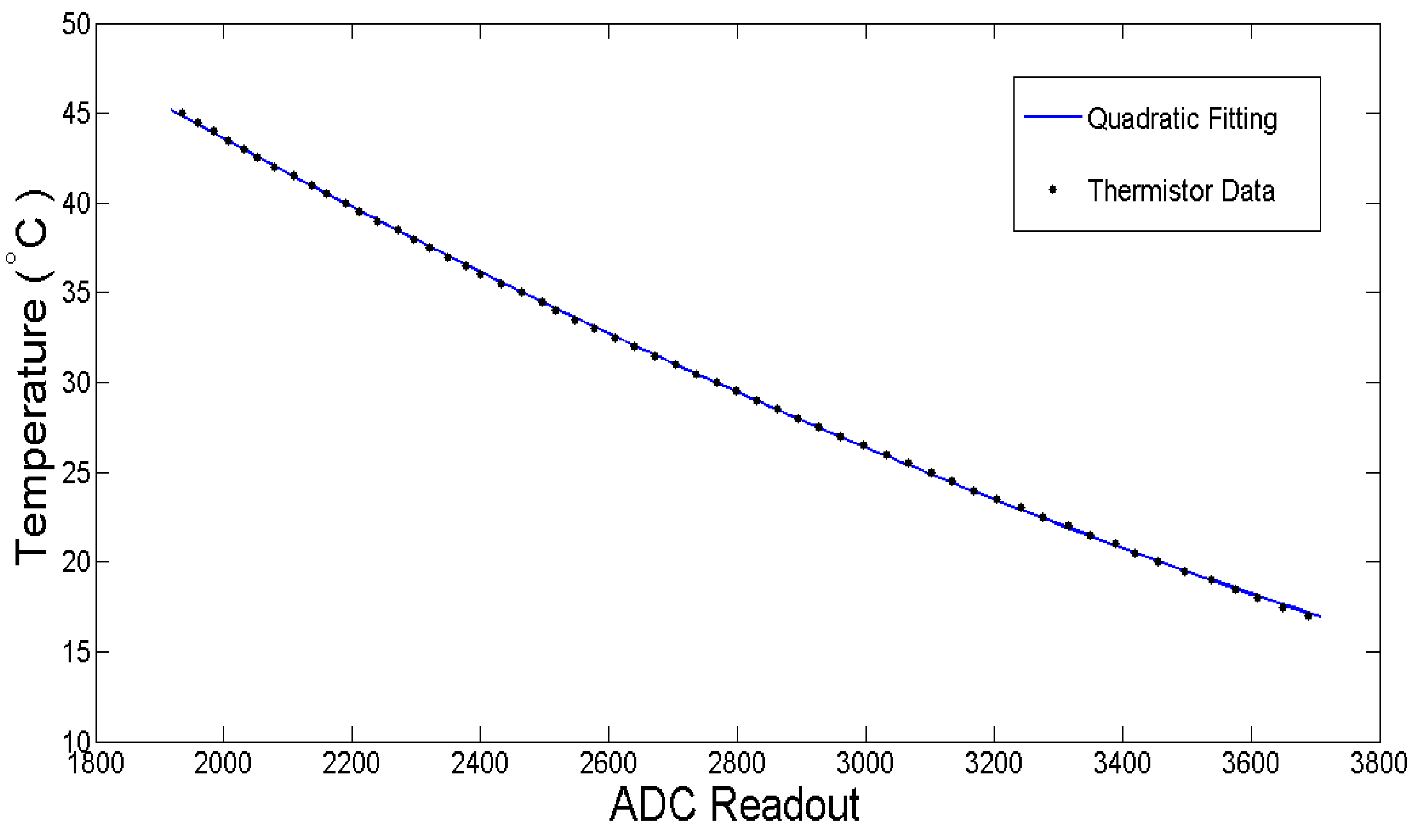
| SSE | R-squared | RMSE | |
|---|---|---|---|
| Quadratic Model | 0.3335 | 0.9999 | 0.07859 |
3.2. Approach for Relating Temperature Rise to Ultrasound Intensity
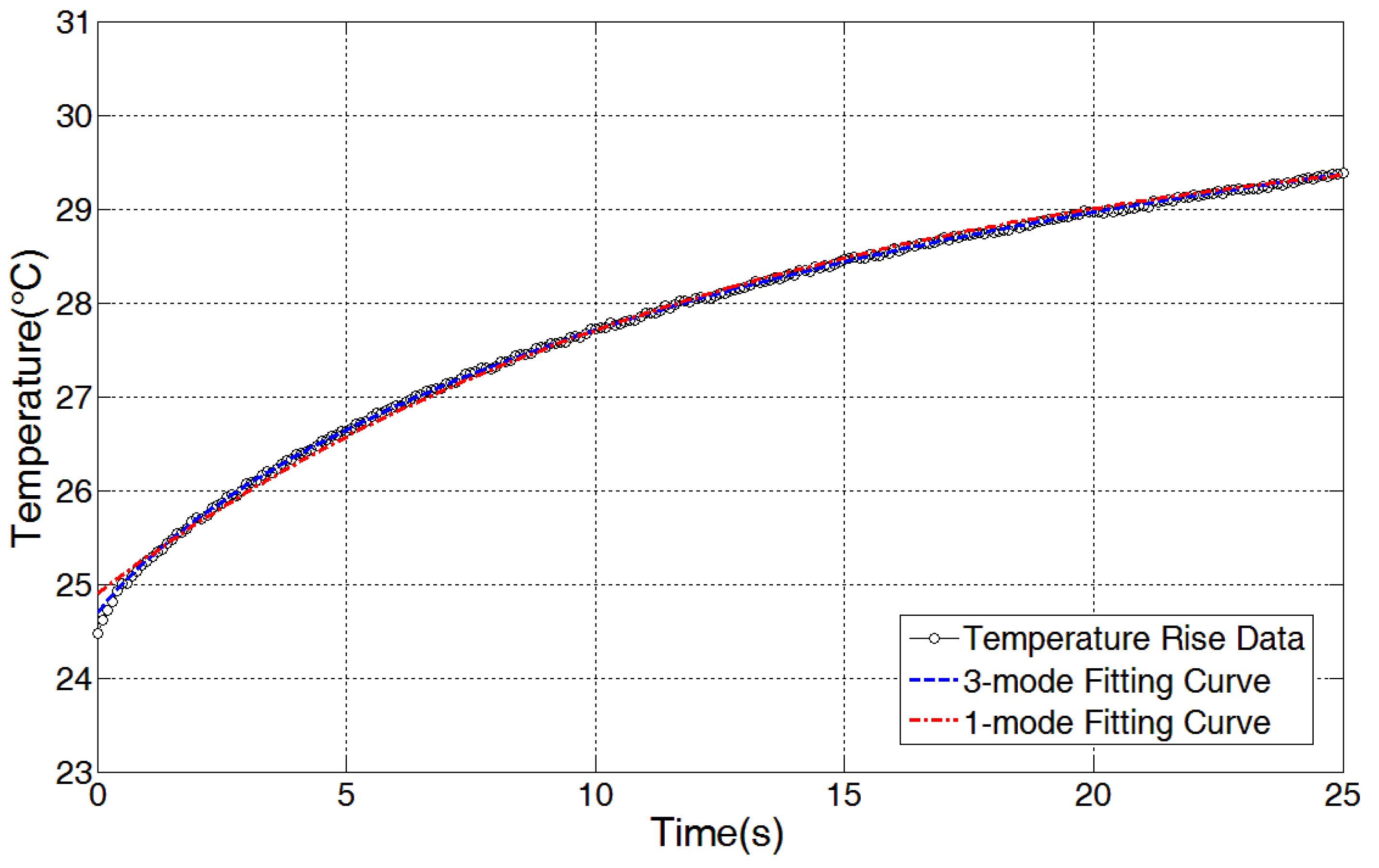
| Ultrasound Intensity (mW/cm2) | Coefficient C (°C) | Coefficient τ (s) | Coefficient T0 (°C) |
|---|---|---|---|
| 60 | 4.847 (4.798,4.895) | 10.75 (10.46,11.04) | 24.9 (24.88, 24.93) |
| SSE | R-square | RMSE |
|---|---|---|
| 0.4923 | 0.9982 | 0.04999 |
4. Artificial Neural Network in Sensor Design
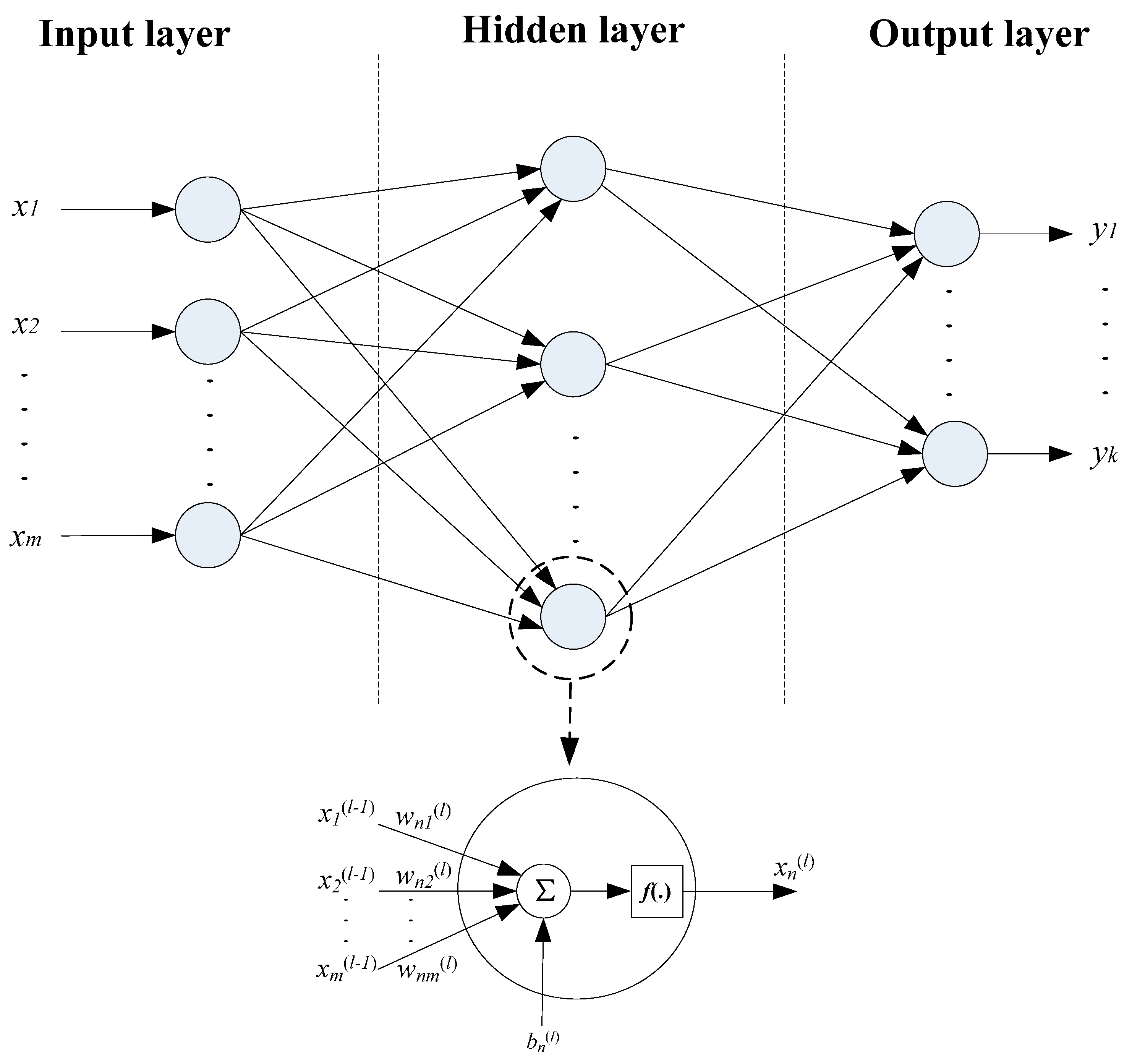
4.1. Artificial Neural Network Model in Sensor Design
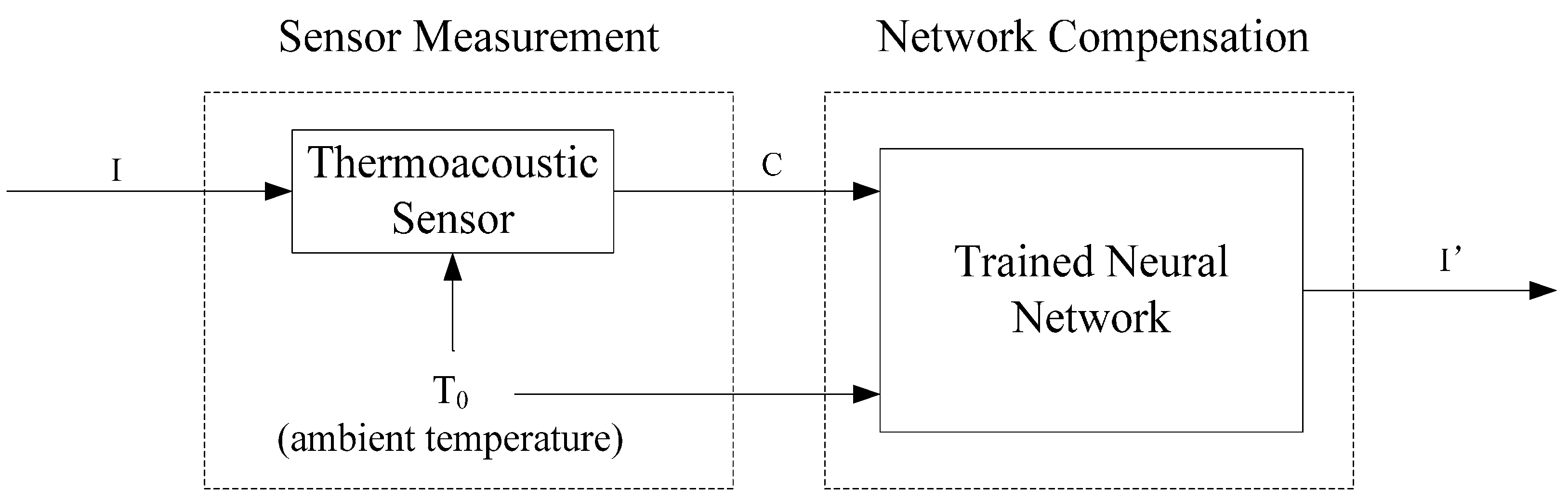
4.2. Artificial Neural Network Training
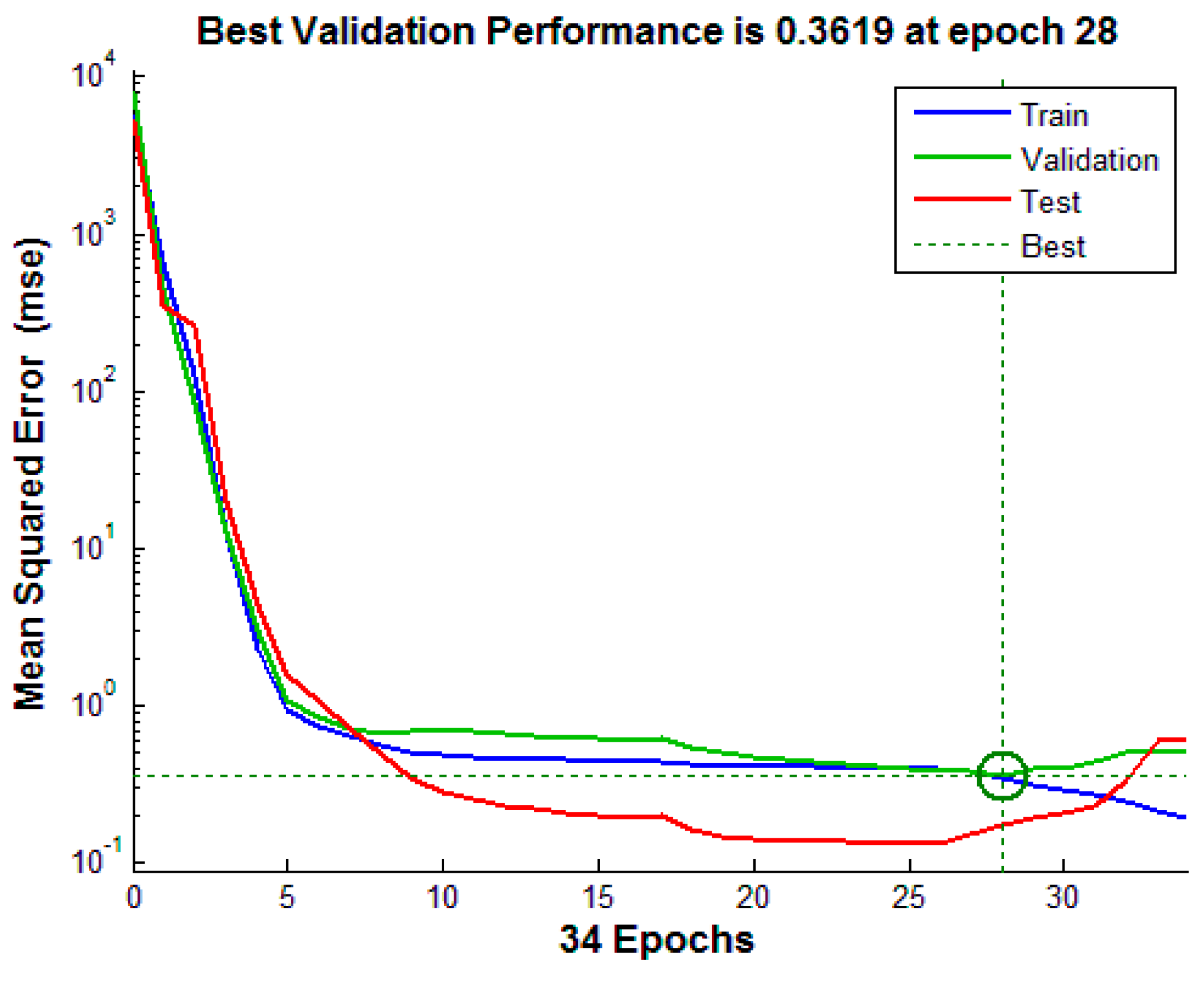

5. Sensor Performance Evaluation
5.1. Neural Network Evaluation with Untrained Data Sets
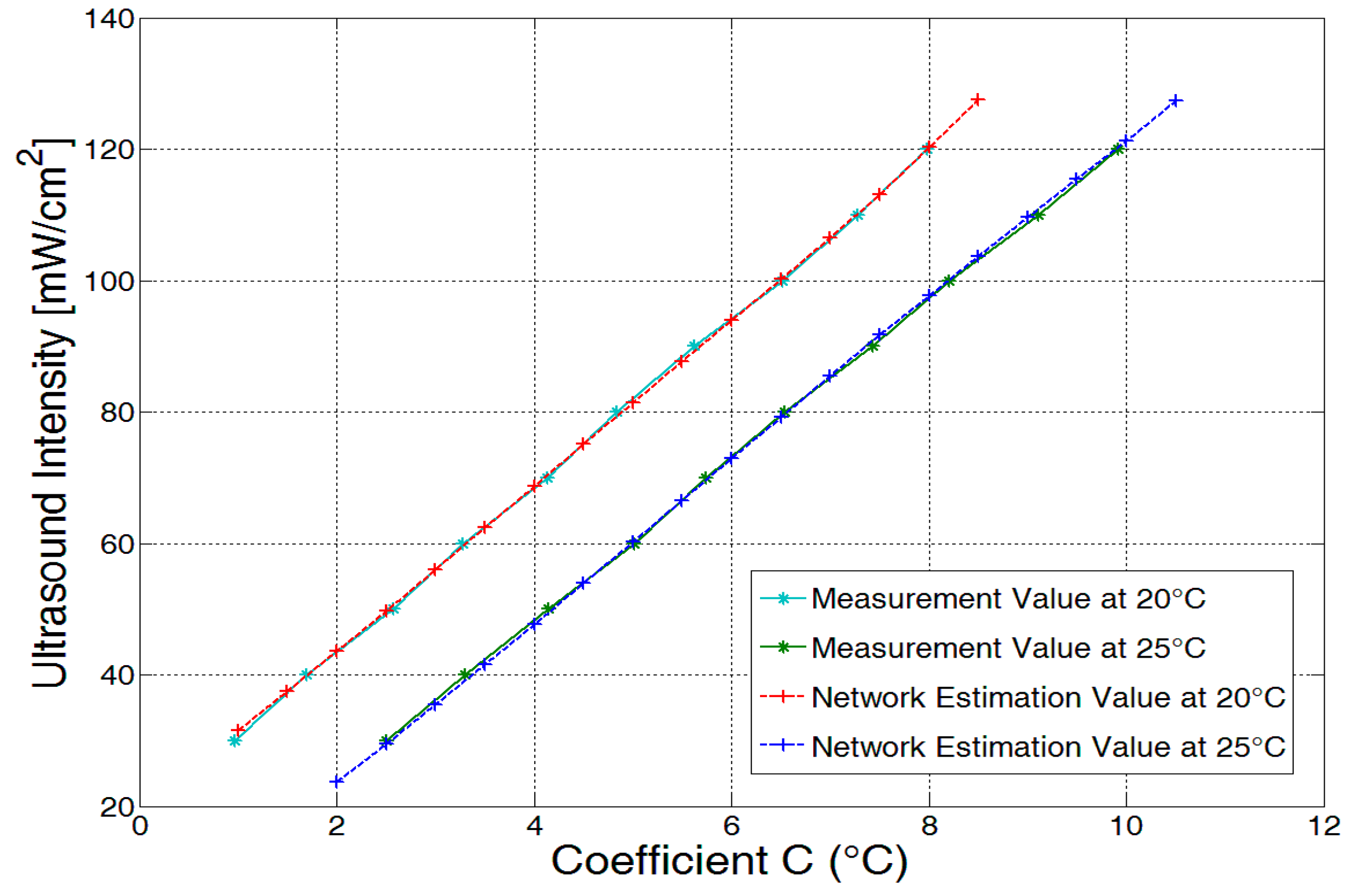
5.2. Network Temperature Compensation Performance
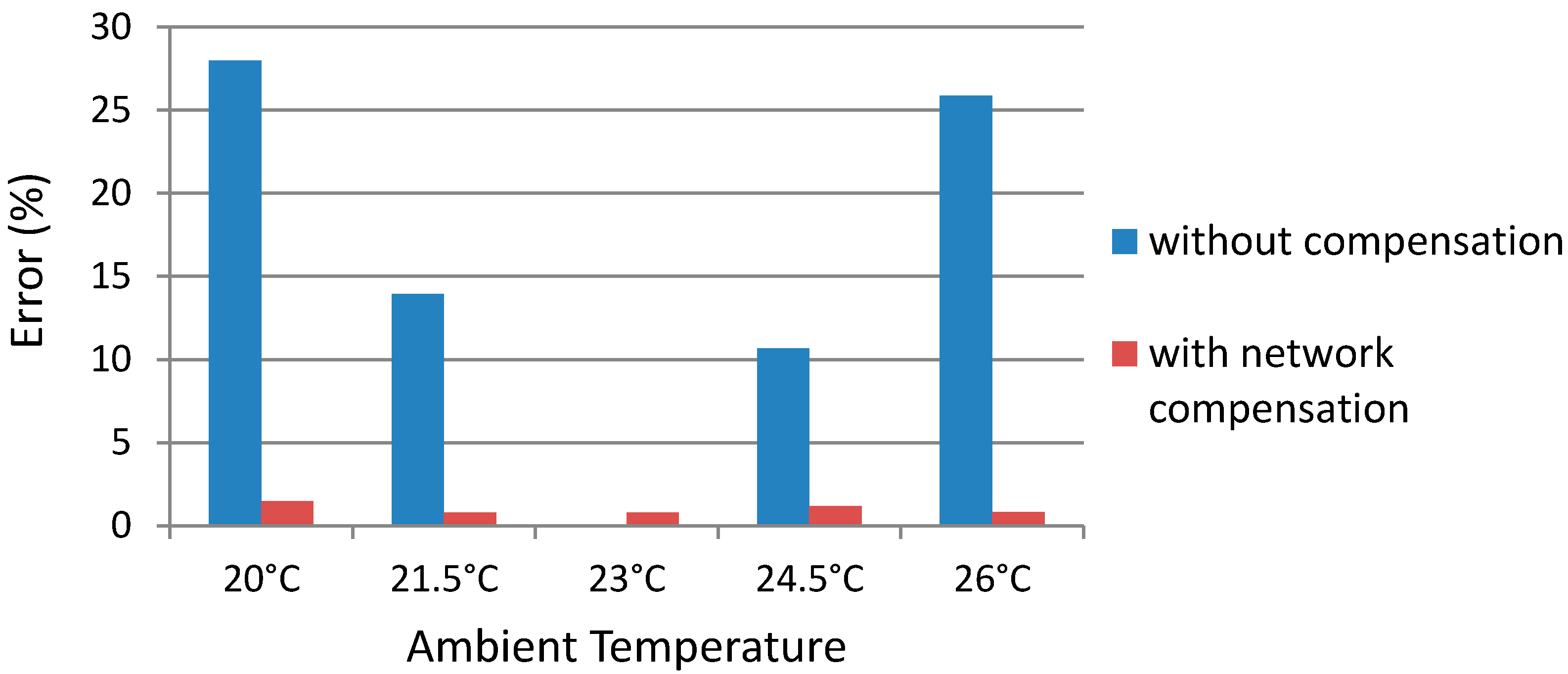
5.3. Sensor Response Time
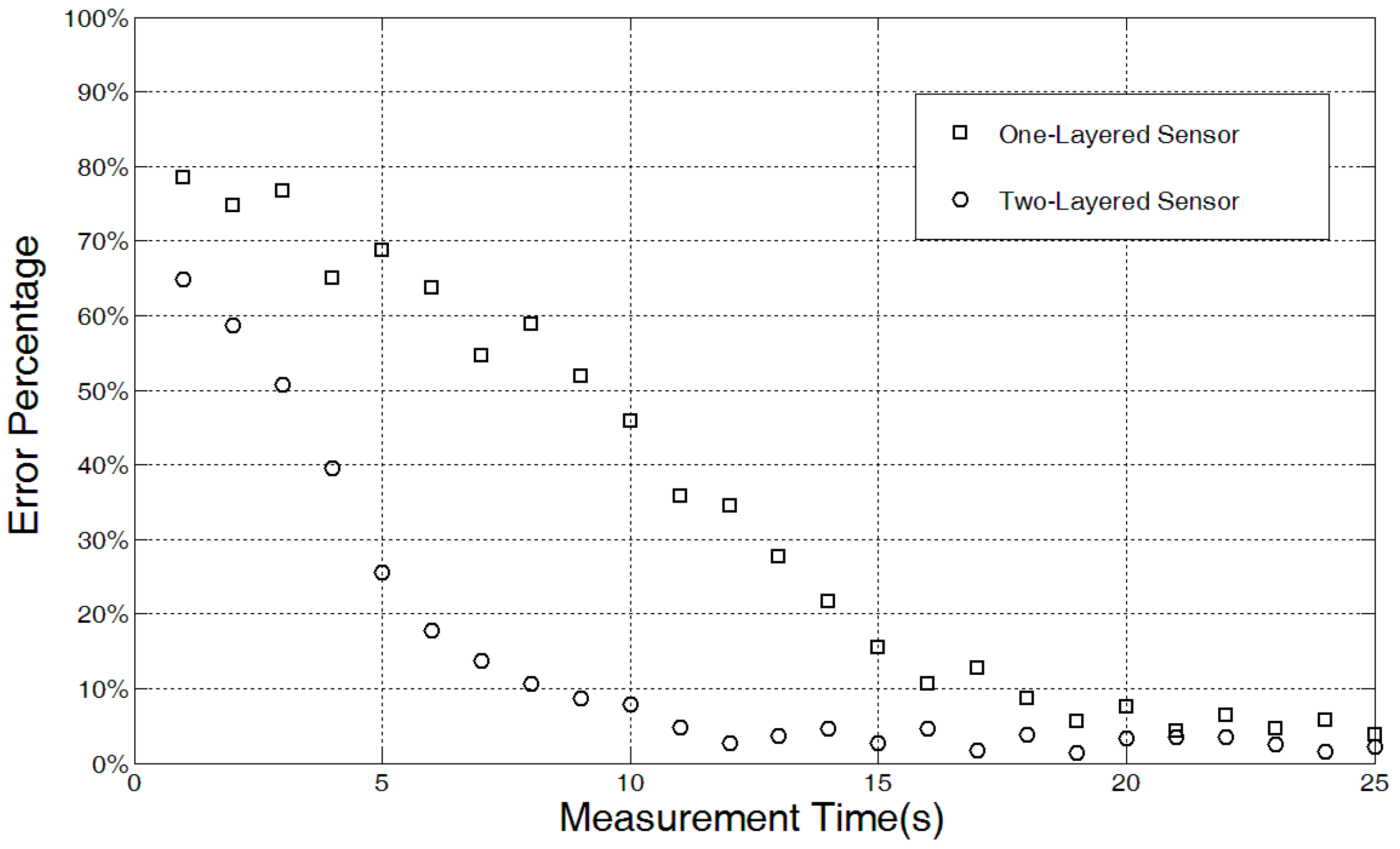
5.4. Measurement Comparison with Our Previous Design
| Target I (mW/cm2) | Thermoacoustic Sensor I (mW/cm2) | ||
|---|---|---|---|
| #1 | #2 | #3 | |
| 30 | 28.85 | 30.74 | 29.68 |
| 40 | 40.33 | 39.42 | 39.06 |
| 60 | 61.66 | 60.37 | 59.82 |
| 80 | 77.33 | 80.22 | 83.03 |
| 100 | 101.78 | 99.12 | 101.9 |
| 120 | 123.26 | 118.86 | 122.43 |
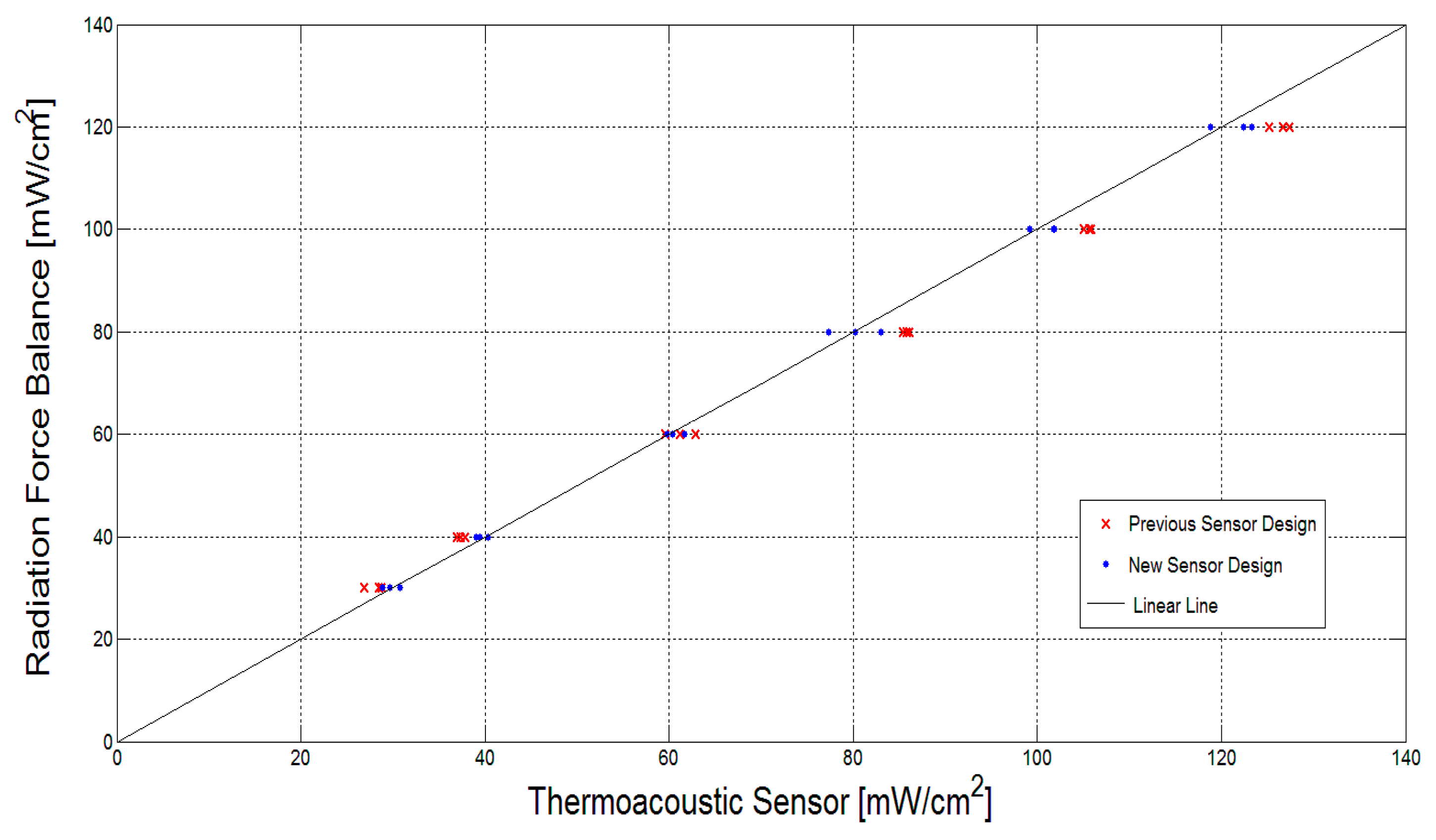
6. Discussion
| Advantages | Disadvantages | |
|---|---|---|
| Radiation Force Balance |
|
|
| Thermoacoustic Sensor |
|
|
7. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Malizos, K.N.; Hantes, M.E.; Protopappas, V.; Papachristos, A. Low-intensity pulsed ultrasound for bone healing: An overview. Injury 2006, 37, S56–S62. [Google Scholar] [CrossRef] [PubMed]
- Khanna, A.; Nelmes, R.T.; Gougoulias, N.; Maffulli, N.; Gray, J. The effects of lipus on soft-tissue healing: A review of literature. Br. Med. Bull. 2009, 89, 169–182. [Google Scholar] [CrossRef] [PubMed]
- El-Bialy, T.; El-Shamy, I.; Graber, T.M. Repair of orthodontically induced root resorption by ultrasound in humans. Am. J. Orthod. Dentofac. Orthop. 2004, 126, 186–193. [Google Scholar] [CrossRef]
- Al-Daghreer, S.; Doschak, M.; Sloan, A.J.; Major, P.W.; Heo, G.; Scurtescu, C.; Tsui, Y.Y.; El-Bialy, T. Long term effect of low intensity pulsed ultrasound on a human tooth slice organ culture. Arch. Oral Biol. 2012, 57, 760–768. [Google Scholar] [CrossRef] [PubMed]
- Marvel, S.; Okrasinski, S.; Bernacki, S.H.; Loboa, E.; Dayton, P.A. The development and validation of a lipus system with preliminary observations of ultrasonic effects on human adult stem cells. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 1977–1984. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Gul-Uludag, H.; Ang, W.T.; Yang, X.; Huang, M.; Marquez-Curtis, L.; McGann, L.; Janowska-Wieczorek, A.; Xing, J.; Swanson, E.; Chen, J. Low-intensity pulsed ultrasound-mediated stimulation of hematopoietic stem/progenitor cell viability, proliferation and differentiation in vitro. Biotechnol. Lett. 2012, 34, 1965–1973. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Ang, W.T.; Xing, J.; Zhang, J.; Chen, J. Applications of ultrasound to enhance mycophenolic acid production. Ultrasound Med. Biol. 2012, 38, 1582–1588. [Google Scholar] [CrossRef] [PubMed]
- Xing, J.Z.; Yang, X.; Xu, P.; Ang, W.T.; Chen, J. Ultrasound-enhanced monoclonal antibody production. Ultrasound Med. Biol. 2012, 38, 1949–1957. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Xing, J.; Xing, J.Z.; Ang, W.T.; Chen, J. Applications of low-intensity pulsed ultrasound to increase monoclonal antibody production in cho cells using shake flasks or wavebags. Ultrasonics 2014, 54, 1439–1447. [Google Scholar] [CrossRef] [PubMed]
- Artho, P.A.; Thyne, J.G.; Warring, B.P.; Willis, C.D.; Brismee, J.M.; Latman, N.S. A calibration study of therapeutic ultrasound units. Phys. Ther. 2002, 82, 257–263. [Google Scholar] [PubMed]
- Shaw, A.; Hodnett, M. Calibration and measurement issues for therapeutic ultrasound. Ultrasonics 2008, 48, 234–252. [Google Scholar] [CrossRef] [PubMed]
- Zeqiri, B.; Gelat, P.N.; Barrie, J.; Bickley, C.J. A novel pyroelectric method of determining ultrasonic transducer output power: Device concept, modeling, and preliminary studies. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 2318–2330. [Google Scholar] [CrossRef] [PubMed]
- Wilkens, V. A thermal technique for local ultrasound intensity measurement: Part 1. Sensor concept and prototype calibration. Meas. Sci. Technol. 2010, 21. [Google Scholar] [CrossRef]
- Wilkens, V. A thermal technique for local ultrasound intensity measurement: Part 2. Application to exposimetry on a medical diagnostic device. Meas. Sci. Technol. 2010, 21. [Google Scholar] [CrossRef]
- Wilkens, V.; Reiman, H. Output intensity measurements on a diagnostic ultrasound machine using a calibrated thermoacoustic sensor. J. Phys. Conf. Ser. 1 2004. [Google Scholar] [CrossRef]
- Ter Haar, G. Therapeutic applications of ultrasound. Prog. Biophys. Mol. Biol. 2007, 93, 111–129. [Google Scholar] [CrossRef] [PubMed]
- Myers, M.R.; Herman, B.A. A theoretical assessment of a thermal technique to measure acoustic power radiated by ultrasound transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 565–572. [Google Scholar] [CrossRef] [PubMed]
- Wilkens, V. Thermoacoustic ultrasound power measurement using evaluation of transient temperature profiles. Proc. IEEE Ultrason. Symp. 2002, 2, 1399–1402. [Google Scholar]
- Xing, J.D.; Choi, M.; Ang, W.; Yu, X.J.; Chen, J. Design and characterization of a close-proximity thermoacoustic sensor. Ultrasound Med. Biol. 2013, 39, 1613–1622. [Google Scholar] [CrossRef] [PubMed]
- Hagan, M.T.; Demuth, H.B.; Beale, M.H. Neural Network Design, 1st ed.; PWS Pub.: Boston, MA, USA, 1996. [Google Scholar]
- Noriega, J.R.; Wang, H. A direct adaptive neural-network control for unknown nonlinear systems and its application. IEEE Trans. Neural Netw. 1998, 9, 27–34. [Google Scholar] [CrossRef] [PubMed]
- Hafiane, M.L.; Dibi, Z.; Manck, O. On the capability of artificial neural networks to compensate nonlinearities in wavelength sensing. Sensors 2009, 9, 2884–2894. [Google Scholar] [CrossRef] [PubMed]
- Baha, H.; Dibi, Z. A Novel Neural Network-Based Technique for Smart Gas Sensors Operating in a Dynamic Environment. Sensors 2009, 9, 8944–8960. [Google Scholar] [CrossRef] [PubMed]
- Patra, J.C.; van den Bos, A.; Kot, A.C. An ann-based smart capacitive pressure sensor in dynamic environment. Sens. Actuators A Phys. 2000, 86, 26–38. [Google Scholar] [CrossRef]
- Wilson, J. Thermal Diffusivity. Available online: http://www.electronics-cooling.com/2007/08/thermal-diffusivity (accessed on 24 April 2015).
- Culjat, M.O.; Goldenberg, D.; Tewari, P.; Singh, R.S. A Review of Tissue Substitutes for Ultrasound Imaging. Ultrasound Med. Biol. 2010, 36, 861–873. [Google Scholar] [CrossRef] [PubMed]
- Wikipedia. Speed of Sound. Available online: http://en.wikipedia.org/wiki/Speed_of_sound (accessed on 27 April 2015).
- NDT Resource Center. Material Properties Tables Acoustic Properties. Available online: https://www.nde-ed.org/GeneralResources/MaterialProperties/UT/ut_matlprop_index.htm (accessed on 27 April 2015).
- AptFlex F28. Available online: http://acoustics.co.uk/wp-content/uploads/2014/01/Apflex-F28.pdf (accessed on 27 April 2015).
- Treeby, B.E.; Cox, B.T. K-wave: Matlab toolbox for the simulation and reconstruction of photoacoustic wave fields. J. Biomed. Opt. 2010, 15. [Google Scholar] [CrossRef] [PubMed]
- Treeby, B.E.; Jaros, J.; Rendell, A.P.; Cox, B.T. Modeling nonlinear ultrasound propagation in heterogeneous media with power law absorption using a k-space pseudospectral method. J. Acoust. Soc. Am. 2012, 131, 4324–4336. [Google Scholar] [CrossRef] [PubMed]
- Needle-hydrophones. Available online: http://acoustics.co.uk/products/pressure-intensity-measurements/needle-hydrphones (accessed on 2 June 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, J.; Chen, J. Design of a Thermoacoustic Sensor for Low Intensity Ultrasound Measurements Based on an Artificial Neural Network. Sensors 2015, 15, 14788-14808. https://doi.org/10.3390/s150614788
Xing J, Chen J. Design of a Thermoacoustic Sensor for Low Intensity Ultrasound Measurements Based on an Artificial Neural Network. Sensors. 2015; 15(6):14788-14808. https://doi.org/10.3390/s150614788
Chicago/Turabian StyleXing, Jida, and Jie Chen. 2015. "Design of a Thermoacoustic Sensor for Low Intensity Ultrasound Measurements Based on an Artificial Neural Network" Sensors 15, no. 6: 14788-14808. https://doi.org/10.3390/s150614788
APA StyleXing, J., & Chen, J. (2015). Design of a Thermoacoustic Sensor for Low Intensity Ultrasound Measurements Based on an Artificial Neural Network. Sensors, 15(6), 14788-14808. https://doi.org/10.3390/s150614788






