1. Introduction
Multiprocessor systems can achieve higher performance by thread-level parallelism with a lower clock frequency, which have advantages over highly superscalar uniprocessor architectures [
1]. Multiprocessor systems can be classified into homogeneous and heterogeneous ones. The use of Heterogeneous Multiprocessor Systems (HMS) can sometimes dramatically improve performance and energy consumption relative to homogeneous ones [
2]. More and more real-time applications are ported to HMS, such as gaming for Xbox360 and aerospace applications for QorIQ from FreeScale [
3,
4].
Task scheduling is challenging and complex for real-time applications especially on HMS. Recently, reducing energy consumption is becoming more and more important in order to lower cooling requirement and overall operational costs. Also, minimizing the energy consumption can help to prolong the battery lifetime for battery-driven embedded systems and guarantee the real-time constraints. Thus, there is a need to shift the focus from solely optimizing multiprocessor resource management without violating task deadlines to optimizing them for energy efficiency.
The problem of scheduling independent, periodic real-time tasks on HMS without energy consideration is already NP-hard in the strong case [
5]. The additional objective for saving energy further complicates the problem.
A classical solution for energy-aware real-time task scheduling is to formulate it as an Integer Linear Programming (ILP) problem [
6,
7]. Then, a linear relaxation heuristic is introduced to solve the equivalent ILP problem. Besides, some approximate algorithms are proposed in [
8,
9], which are (
m + 2)-approximation and 0.5-approximation, respectively, where
m is the number of the available processor types. A dynamic programming method is also proposed to provide certain worst-case performance guarantee [
10]. However, these approximate or heuristic algorithms cannot efficiently work in practice for large size problems, although these studies enlighten the way. Recently, swarm intelligence algorithms such as Ant Colony Optimization (ACO) and Genetic Algorithm (GA) heuristics [
11] are introduced. Comparing to the ILP and approximation algorithms, ACO and GA are more efficient while they are still time-consuming for large-scale problems. Thus, new quick meta-heuristics for energy-aware real time scheduling need further research.
A meta-heuristic designates a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. A particularly successful meta-heuristic, the Shuffled Frog Leaping Algorithm (SFLA) [
12,
13] is inspired by the behavior of the evolution of frog foraging. The frogs are divided into subgroups named as memeplexes, which have different cultures. Each memeplex performs a local search. The frogs in each memeplex can exchange ideas. After several evolution steps, memeplexes exchange the ideas in a shuffled process. Until the convergence criteria are satisfied, the algorithm does not stop. In essence, SFLA combines the benefits of Particle Swarm Optimization (PSO) and Memetic Algorithm (MA) for mixing information from parallel local searches to move toward a global solution.
The main objective of this work is to design novel real-time scheduling algorithms based on SFLA, which can quickly find an optimal solution not only satisfying hard task deadlines but also reducing energy consumption.
Specifically, our work aims to:
Formulate the energy-aware real-time taskscheduling problem for HMS by incorporating the energy consumption into the constraints and optimization objectives.
Develop SFLA-based energy-aware real-time scheduling algorithms that improve the energy efficiency of a real-time system without violating the task deadlines under a short decision time.
Perform extensive experiments comparing our approach with traditional and other swarm intelligence algorithms.
The rest of the paper is organized as follows.
Section 2 discusses related work, followed by the formulation of the energy-aware real-time scheduling problem for HMS presented in
Section 3.
Section 4 describes the overview and prototype of the shuffled frog leaping algorithm. The proposed energy-aware real-time scheduling algorithms based on SFLA are discussed in
Section 5. A performance analysis of the proposed energy-aware task scheduling algorithms is presented in
Section 6.
Section 7 concludes the paper with summary and future research directions.
3. Formulation
This section first provides the models of the real-time tasks and HMS to ease further discussion. After that, a DVFS-enabled energy model is given. Then, the energy-aware real-time tasks scheduling problem and its linear programming formulation are presented. Finally, we prove the equivalency of this problem and its ILP formulation.
3.1. Real-Time Task and Processor Models
Let T = {T1, T2, ..., Tn} denote a real-time task set with n tasks Ti (i = 1, 2, ..., n). Each task Ti is independent, periodic and indivisible with hard deadlines. A real-time task Ti is described by a 4-tuple (ai, ci,j, di, pi), where ai denotes its initial arrival time, ci,j denotes the worst case execution time (WCET) of Ti when it is assigned to processor Mj, di denotes its relative deadline, and pi denotes its arrival interval between two consecutive instances of the task. We assume that all of the tasks are released at the same time 0, which means ai = 0. The deadlines of tasks are considered to be implicit, which means the relative deadline of task Ti is assumed to be equal to its period, i.e., di = pi. Each task can only be assigned to a unique processor and task migration is forbidden. After the task, Ti is assigned to a processor, we simply use the earliest-deadline-first (EDF) policy for task scheduling because it is an optimal uniprocessor scheduling policy for independent real-time tasks.
Let M = {M1, M2, …, Mk} denote a heterogeneous platform, where each Mj (j = 1, 2, …, k) is a preemptive processor. Mj executes only one instruction in a clock cycle. We use fj to denote the clock frequency and ci,j to denote the running time for Ti on processor Mj. If we define cyclei as the number of clock cycles for Ti, ci,j and fj can be formulated as follows: ci,j = cyclei/fj. The utilization of task Ti assigned to processor Mj is denoted by ui,j, which is a real number in . If ci,j > di, we set ui,j to , which means Ti cannot execute on Mj. Otherwise, ui,j = ci,j/di. Let the utility matrix Un×k denote the computing costs when n tasks run on k processors. Each element ui,j in Un×k indicates the computing costs when Ti runs on Mj.
Let matrix Xn×k denote a scheduling (mapping) of n tasks to k processors. Each element xi,j in the matrix denotes whether Ti is assigned to Mj. As the tasks are indivisible, each xi,j has only two kinds of values, either 0 or 1. xi,j = 1 indicates that Ti is assigned to Mj and xi,j = 0 indicates that Ti is not assigned to Mj.
3.2. Energy Model
The HMS is DVFS-enabled, where processors can run at different power settings. The energy consumption of a processor is mainly contributed by the dynamic energy consumption resulting from the charging and discharging of gates on the DVS CMOS circuits [
8].
Let
Ei,j denote the energy consumption of
Ti on
Mj in one period. The energy consumption accounts for the energy consumption of the CPUs, which dominates the overall energy consumption including the memory access, I/O,
etc. It can be formulated as follows:
where
Cef and
l are constants [
34,
35].
Let
Energy denote the total energy consumption of
n tasks on
k processors, which is formulated as follows:
Let
Max_Energy denote the theoretical maximum energy consumption of
n tasks on
k processors, formulated as follows:
Note that the tasks have different periods, their total energy consumption is calculated based on the least common multiple of periods of all tasks, denoted by LCM.
3.4. Equivalency of e-RTSP and Its ILP Formulation
The problem of e-RTSP is formulated as an ILP problem. In this section, we will prove (Theorem 1) the equivalency of the two problems.
Lemma 1. If the ILP problem in Definition 1 has a feasible solution when U = 1, then the feasible solution is mapped to a feasible schedule of the e-RTSP problem.
Proof. If the linear programming problem in Definition 1 has a feasible solution when
U = 1, then every constraint is satisfied. Constraints (1) and (2) mean that each task in
T = {
T1,
T2, ...,
Tn} is assigned to a processor completely without decomposition and migration, which correspond to the restricted conditions in our task scheduling model. Constraint (4) indicates that the hard deadline of each task
Ti must be met on the heterogeneous platform. Constraint (3) means that for each processor
Mj (
j = 1, 2, …,
k) we have
. Therefore, if a task set {
Tj1,
Tj2, ...,
Tjl} is assigned to
Mj, then
can be set up. If a uniprocessor has
, a proper scheduling algorithm can find a feasible schedule, which meets the deadlines of all the periodic tasks’ instances, which is proven in [
36]. We complete the proof of Lemma 1. □
Lemma 2. If the e-RTSP problem has a feasible schedule, then the ILP problem in Definition 1 has a feasible solution when U = 1.
Proof. According to the task model, processor model, scheduling model and utility model described earlier, if the problem of assigning real-time tasks onto HMS has a feasible schedule, it is obvious that the constraints (1), (2) and (4) in Definition 1 are satisfied. Next, we will show that the constraint (3) is satisfied as well. It is assumed that every instance of each task arrives instantly.
For a feasible schedule, a uniprocessor Pj is selected, and it is assumed that h tasks Ti (i = 1, 2, ..., h) are assigned to Mj in the scheme, without loss of generality. For all these h tasks Ti (i = 1, 2, ..., h), let D denote the least common multiple of their periods. Let ni denote the number of the instances of each task Ti (i = 1, 2, ..., h) arriving in the time interval [0, D). Since the schedule is feasible, it can be seen that the total execution time is not more than D, namely . Because we have ni × di = D for each task Ti (i = 1, 2, ..., h), so the following derivation is tenable and the constraint (3) in Definition 1 is satisfied. We complete the proof of Lemma 2. □
Theorem 1. The e-RTSP problem is equivalent to its ILP problem in Definition 1.
Proof. Lemma 1 and Lemma 2 have proved the necessity and sufficiency. Thus, Theorem 1 is proven. □
4. Overview of Shuffled Frog Leaping Algorithm
The Shuffled Frog Leaping Algorithm (SFLA) was proposed by Eusuff
et al. in 2003 [
12]. SFLA is a novel meta-heuristic algorithm for combinatorial optimization problems. It paves a new way to solve the energy-aware real-time task scheduling problems.
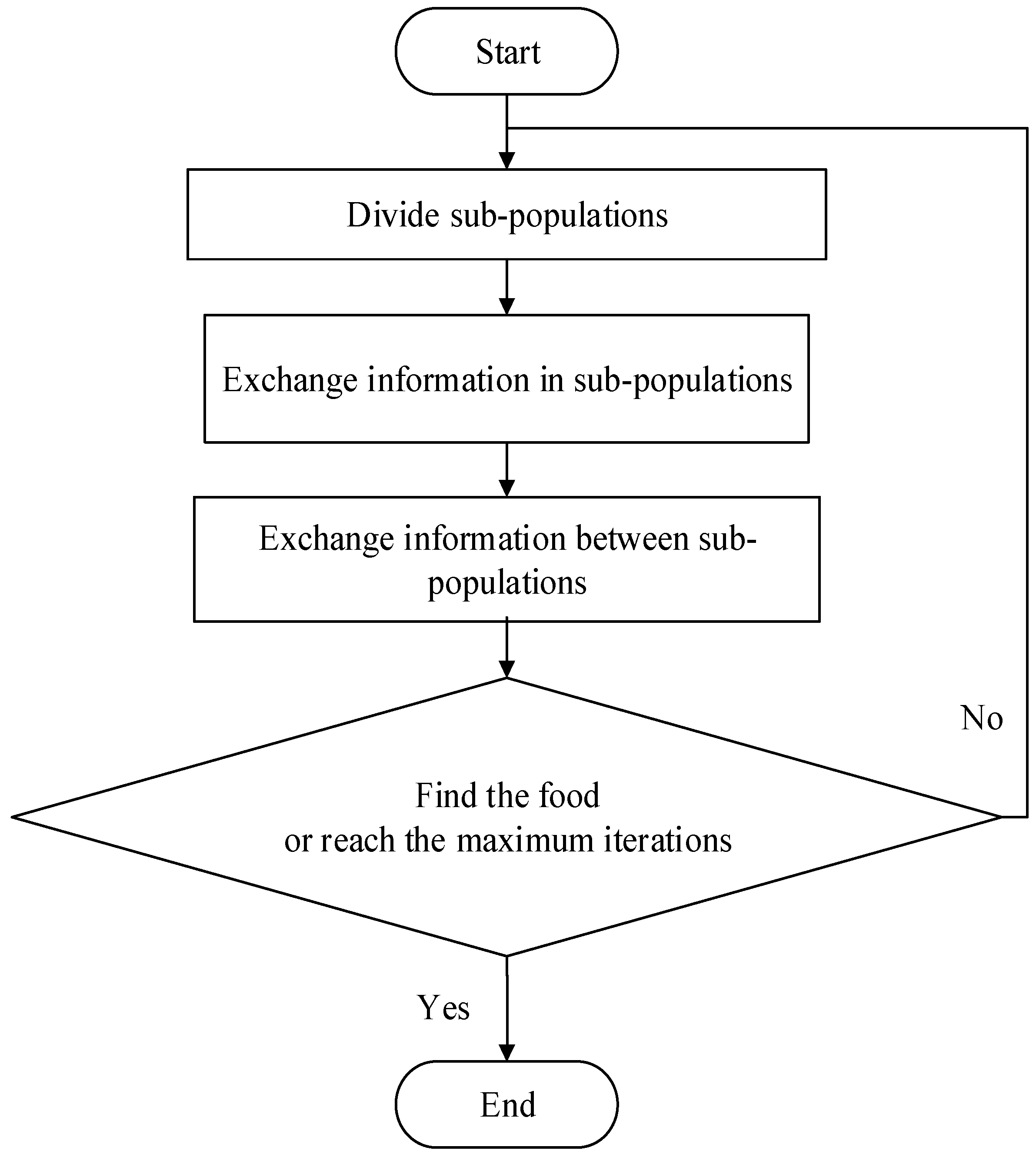
The basic idea of SFLA is inspired by the frog foraging behavior. A lot of frogs live in the wetlands where many stones are discretely placed. The frogs try to find a place with more food by jumping to different stones. Every frog has its own culture, and the frogs in the same population can exchange their food information through communication. The frogs in the wetlands are divided into several sub-populations according to a certain strategy and each sub-population has its own culture. The sub-population conducts a local search. When the sub-populations’ local search is satisfied, the information exchange between different sub-populations will begin to complete the global search. The local search and the global search will be conducted alternately until a frog finds the food or the alternating times reach the maximum.
Figure 1 shows the process of SFLA. The parameters of SFLA are shown in
Table 1.
Figure 1.
Flow chart of shuffled frog leaping algorithm.
Figure 1.
Flow chart of shuffled frog leaping algorithm.
Table 1.
The parameters of Shuffled Frog Leaping Algorithm (SFLA).
Table 1.
The parameters of Shuffled Frog Leaping Algorithm (SFLA).
| Number | Parameter | Description |
|---|
| 1 | F | The total number of the frogs in the population |
| 2 | m | The number of sub-populations |
| 3 | n | The number of the frogs in a sub-population |
| 4 | Px | The global best frog |
| 5 | Pb | The local best frog |
| 6 | Pw | The local worst frog |
| 7 | Ls | The iterations of local search |
| 8 | Sf | The iterations of global search |
| 9 | Fitness | The quality evaluation standard of frog |
| 10 | Smax | The frog’s maximum jump step |
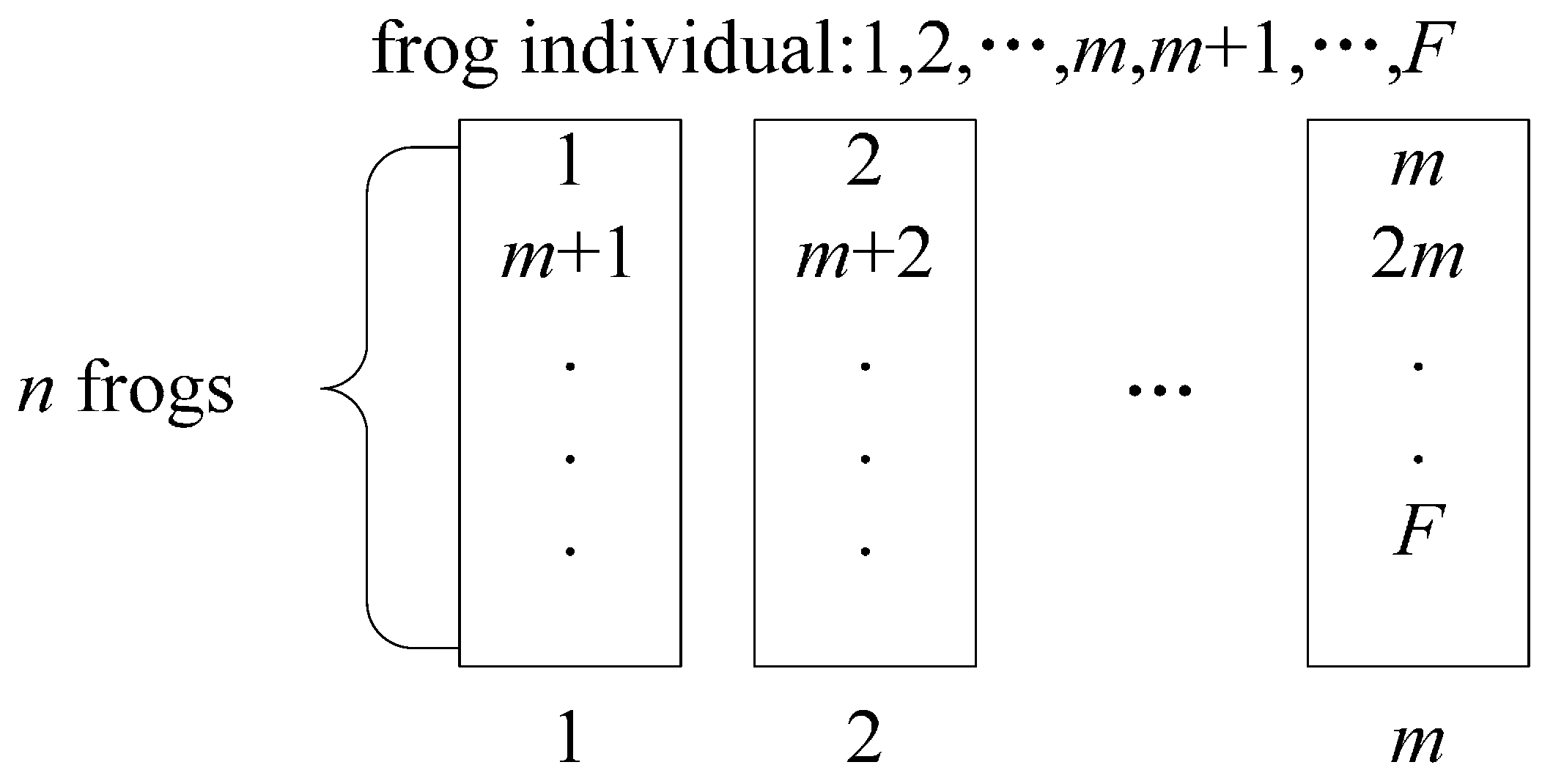
In order to balance the search ability of each sub-population, a sub-population division strategy needs to be conducted. The sub-population division strategy is: calculate the fitness value of each frog, sort them in descending (or ascending) order according to the fitness, and finally divide them into sub-populations according to the strategy shown in
Figure 2.
Figure 2.
The sub-population division strategy.
Figure 2.
The sub-population division strategy.
The information transferred in the sub-population is realized through the influence of
Pb on
Pw. It is given by:
- (1)
Calculate the jump step of
Pw- (2)
GA, ACO, PSO, MA and SFLA are all meta-heuristics. GA begins with numbers of stochastic individuals and searches the solution space through mutation and crossover between individuals. ACO is a probability-type algorithm to construct an optimal path in a graph. It begins with numbers of empty individuals and gradually constructs them by randomly choosing paths according to their pheromone; a parameter indicates the quality of each path. PSO begins with numbers of stochastic individuals just like a genetic algorithm, but it finds the global optimal solution by iteratively following the best solution it has found ever before. MA is a combination of population-based global search and individual-based local heuristic search. SFLA combines population-based global search and sub-population-based local search. During the local search stage, SFLA moves on by the influence of its local and global best solutions.
Note that SFLA combines the search strategy of PSO and MA. It conducts population-based global search like MA and sub-population-based local search by iteratively following the local and global best solutions like PSO. Therefore, SFLA has both the benefits of PSO and MA. Compared with GA, SFLA moves to the aim solution more quickly because it has higher search directivity.
As a swarm intelligent optimization algorithm, SFLA combines the advantages of the Particle Swarm Optimization and the Memetical Algorithm. It is simple and easy to realize. It has fewer parameters, fast convergence speed and a strong global search capability. The SFLA mainly focuses on continuous optimization problems, so it has fewer outcomes in the discrete combinatorial optimization problems. In [
13], a discrete SFLA is proposed to solve the Traveling Salesman Problem, but SFLA’s application in real-time task scheduling problems cannot be found currently.
5. Applying SFLA to e-RTSP
In this section, SFLA is applied to solve the energy-aware real-time task scheduling on HMS. As SFLA is originally designed for continuous optimization problems, while e-RTSP is a discrete optimization problem, thus our main aim is to redesign SFLA and apply it to discrete optimization problem. Also, the following optimization procedures are proposed to quickly obtain the feasible solution with the minimal energy consumption. First, the encoding scheme and the fitness function are defined. Then, the information transfer mode between frogs is designed. Next, the local and global search strategies of SFLA are applied to schedule real-time tasks. Finally, a novel optimization scheme is presented to avoid the premature and local optimal solution.
5.1. Encoding
Encoding is the first step to modify SFLA for e-RTSP, a discrete optimization problem. An encoding scheme is designed and it maps a scheduling scheme to a frog of SFLA. The real-time task-scheduling scheme mapped to a frog is realized by compressing the scheduling matrix Xn×k. The compression method is shown as follows: remove the elements with value 0, retain the elements with value 1 and replace these elements with their column numbers, finally a one-dimensional array (where i, j, l = 1, 2, …, k, i ≠ j ≠ l, k is the number of processors , n is the number of tasks) is attained. In the one-dimensional array, the index denotes the task number and the element denotes the processor number the task is assigned to. It can be seen that each frog is a solution of the scheduling problem. According to whether the frog satisfies the constraints (4), it may have two states, namely feasible or infeasible. The feasible frog is the target of SFLA.
Table 2 shows a scheduling matrix of assigning 10 tasks to four processors. The corresponding encoding frog is {2,1,2,0,3,3,0,1,3,0}.
Table 2.
Scheduling matrix X10×4.
Table 2.
Scheduling matrix X10×4.
| | Processors | P0 | P1 | P2 | P3 |
|---|
| Tasks | |
|---|
| T0 | 0 | 0 | 1 | 0 |
| T1 | 0 | 1 | 0 | 0 |
| T2 | 0 | 0 | 1 | 0 |
| T3 | 1 | 0 | 0 | 0 |
| T4 | 0 | 0 | 0 | 1 |
| T5 | 0 | 0 | 0 | 1 |
| T6 | 1 | 0 | 0 | 0 |
| T7 | 0 | 1 | 0 | 0 |
| T8 | 0 | 0 | 0 | 1 |
| T9 | 1 | 0 | 0 | 0 |
5.2. Fitness Function
Defining the fitness function is the second step to modify SFLA for e-RTSP. In the original SFLA, the fitness function is usually a consecutive function, which is not suitable for e-RTSP. However, a feasible choice to define the fitness function is to seek information from the effect of the fitness function. The fitness function is a specific type of objective function, which is used to summarize how close a given scheduling solution is to achieving the optimal aim. In e-RTSP, the goal is to quickly find a scheme, which is schedulable and consumes less energy. Therefore, the fitness function is designed as classical fitness and energy-aware fitness, respectively.
As for the classical real-time scheduling problem, the fitness function is defined to optimize the number of feasible solutions, which is shown as follow:
where
nSchedulable is the number of the processors whose assigned computing capacity have not exceeded its maximum computing capacity.
However, the aim of
e-
RTSP is to minimize the energy consumption. The energy-aware fitness is defined as
Fitness_Energy, whose calculation equation is:
where the definitions of
Energy and
Max_Energy are from Equations (2) and (3).
5.3. Information Transfer Modes
Designing the information transfer mode is the third step as well as the most important step to modify SFLA for e-RTSP. In this step, the core of the original SFLA is modified to realize the search in the solution space of e-RTSP. It can be seen from Equations (4) and (5) that when SFLA is applied to solve discrete combinatorial optimization problems, the information transfer mode between frogs should be changed flexibly. According to the basic idea of SFLA and Equations (4) and (5), it can be seen that the essence of SFLA’s information transfer is that the high fitness individual influences the low fitness individual’s mind. From this perspective, two kinds of discrete information transfer modes are designed.
(1) Divergent Information Transfer
A one-dimensional array R[n] is used to realize the divergent information transfer. Every element of R[n] is calculated by rand()%2. If R[i] = 1, replace Pw’s current element with Pb’s current element. Smax denotes the maximum number of the replacement elements between two frogs. Whether to set up Smax or not depends on the algorithm’s performance. We take a scheduling problem with 10 tasks and four processors as an example. In a sub-population, Pb = {1,0,0,3,2,0,1,2,1,3} and Pw = {0,1,0,1,3,2,2,3,1,0}. If R[n] = {1,0,0,1,1,0,1,0,0,0}, then the Pw’ = {1,1,0,3,2,2,1,3,1,0}.
(2) Concentrated Information Transfer
An inherited culture ration λ and a starting point r are used to realize the concentrated information transfer. r is in , where n is the number of the tasks. Smax can be described as . The concentrate information transfer can be realized by replacing Pw’s elements with Pb’s elements from index r to (r + Smax − 1). We also take a scheduling problem with 10 tasks and four processors as an example. In a sub-population, Pb = {1,0,0,3,2,0,1,2,1,3} and Pw = {0,1,0,1,3,2,2,3,1,0}. If λ = 0.40 and r = 3, then Smax = 4 and Pw’ = {0,1,0,3,2,0,1,3,1,0}.
These two information transfer modes both realize the information exchange between Pb and Pw. SFLA using a divergent information transfer mode is called D-SFLA and that using a concentrate information transfer mode is called C-SFLA.
5.4. SFLA Algorithm for e-RTSP
Having modified for discrete optimization problem e-RTSP, SFLA is ready to be applied to assign real-time tasks to heterogeneous processors. First, the whole process of applying SFLA to e-RTSP is given. Next, the sub-population information transfer process of applying SFLA to e-RTSP is described in detail.
(1) Applying SFLA’s Whole Process
According to the basic idea of SFLA, the whole process of applying SFLA to assign real-time tasks to heterogeneous processors is shown as follows:
- Step 1
Initialize parameters. Initialize the number of scheduling schemes F in the population, the number of sub-populations m, the number of the scheduling schemes n in each sub-population. Initialize the iterations of the sub-population and the maximum iterations when Px cannot be improved. Initialize the parameters of e-RTSP, include the number of tasks, the number of processors, the heterogeneity of tasks, processors and the utilization matrix.
- Step 2
Generate the original scheduling scheme set. Generate F scheduling schemes randomly in the solution space, namely generating F frogs.
- Step 3
Divide the scheduling scheme set into m sub-populations. Calculate the fitness of each frog and sort them in descending order according to their fitness. Divide them into m sub-populations. Determine Px of the population, Pb and Pw of each sub-population.
- Step 4
Transfer information in each sub-population. Conduct the information transfer mode in each sub-population according to the iterations of the sub-population. The information transfer process searches the solution space of the scheduling problem and the frogs will jump to the better scheduling schemes.
- Step 5
Transfer information between sub-populations. Combine the frogs in each sub-population back to the population and sort them in descending order according to their fitness. Update Px.
- Step 6
Check the termination conditions. If SFLA finds a feasible scheduling scheme or the iterations where Px cannot be improved to reach the maximum, then stop the operation of SFLA. Else return to Step 3.
(2) Information Transfer Process in Sub-Populations
In the whole process of SFLA, Step 4 is the core. To ensure that the frogs to jump towards the feasible scheduling schemes, the information transfer in each sub-population needs to obey a certain rule. The information transfer rule in each sub-population is: transfer information from Pb to Pw, and obtain a Pw’. If the fitness of Pw’ is better than that of Pw, replace Pw with Pw’. Else replace Pb with Px to transfer information to Pw and obtain a new Pw’. If the fitness of Pw’ is better than that of Pw, replace Pw with Pw’. Else generate a new frog randomly and replace Pw with the new frog. The pseudo code of the information transfer process in sub-population is shown in Algorithm 1.
Algorithm 1. Sub-Population Information Transfer Algorithm.
Input: an original scheduling scheme set.
Output: an updated scheduling scheme set.
1. Determine Px;
2. for each memeplex i{
3. for each iteration j{
4. Determine Pb, Pw;
5. Pw’ = Pw applies Equations (4) and (5) with Pb;
6. Evaluate the fitness of Pw’;
7. if (Pw’ is better than Pw)
8. Replace Pw with Pw’;
9. else{
10. Pw’ = Pw applies Equations (4) and (5) with Px;
11. Evaluate the fitness of Pw’;
12. if (Pw’ is better than Pw)
13. Replace Pw with Pw’;
14. else{
15. Generate a new frog Pw’;
16. Evaluate the fitness of Pw’;
17. Replace Pw with Pw’;}}}}
For a sub-population, Px and Pb influence Pw alternately, leading the frogs to jump towards the feasible scheduling schemes. If Pw cannot be improved, a new frog is generated to replace it to ensure the activeness of the population.
5.5. Precocity Remission
One of SFLA’s drawbacks applied to e-RTSP is precocity. With little diversity in the population, SFLA may become less improvable before it has fully searched the solution space of the e-RTSP problem. This phenomenon is called precocity. In the process of the sub-population information transfer, Equations (4) and (5) are applied to Pw frequently, leaving the structure of Pw similar to that of Px and Pb. We imported an algorithm to remit the precocity. Its pseudo code taking Px for example is shown in Algorithm 2.
In Algorithm 2, the structure of Px is disturbed without reducing its fitness. The diversity of the whole population is guaranteed by applying Algorithm 2. Pb is disturbed after every information transfer iteration in the sub-population and Px is disturbed after every information transfer iteration between sub-populations. Thus, it will not add much computing overhead to SFLA.
Algorithm 2. Px Disturbance Algorithm.
Input: Px.
Output: a new Px whose structure is disturbed.
1. for each task i{
2. for each processor j{
3. t = the number of the processor that task i is assigned in Px;
4. if (j is equal to t)
5. Go to Line 2;
6. else{
7. temp_solution = Px replaces t with j;
8. Evaluate the fitness of temp_solution;
9. if (the fitness of temp_solution is larger than that of Px)
10. Px = temp_solution;}}}
5.6. Local Optimal Avoidance
Another drawback of SFLA applied to
e-
RTSP is that it is easy to fall into a local optimal solution. A local optimal solution is a scheme in which tasks are assigned to processors extremely unevenly. Namely the fitness of the local optimal solution is quite high, but the assigned computing capacity of the processor exceeds its maximal computing capacity. Construction of a sub-population in each sub-population can prevent the occurrence of such a situation to a certain extent. To prevent local optimal solutions, several frogs in a sub-population will be selected into the sub-population. As the convergence speed of SFLA cannot be slowed down, the frogs with higher fitness should be assigned a higher selected probability. As in [
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32], the selected probability of each frog is defined as follows:
where
n is the number of the frogs in a sub-population.
As the frogs in a sub-population are sorted in descending order according to their fitness, so Equation (8) gives higher selected probability to the frogs with higher fitness.
5.7. Convergence Acceleration
As the original population is generated randomly when applying SFLA’s whole process to e-RTSP, the overall qualities of these scheduling schemes are low. We apply the neighborhood search to the original population to improve the fitness of each frog. It consists of two parts: (1) migrate a task from a processor to a different one if the energy consumption becomes less without lowering the fitness; and (2) exchange two tasks between two processors if the energy consumption becomes less without lowering the fitness. A frog becomes a better solution in its neighborhood by applying the neighborhood search. The overall quality of the population is improved with this preprocessing and so SFLA can find a feasible scheduling scheme more quickly.
5.8. Summary of the SFLA Applied to e-RTSP
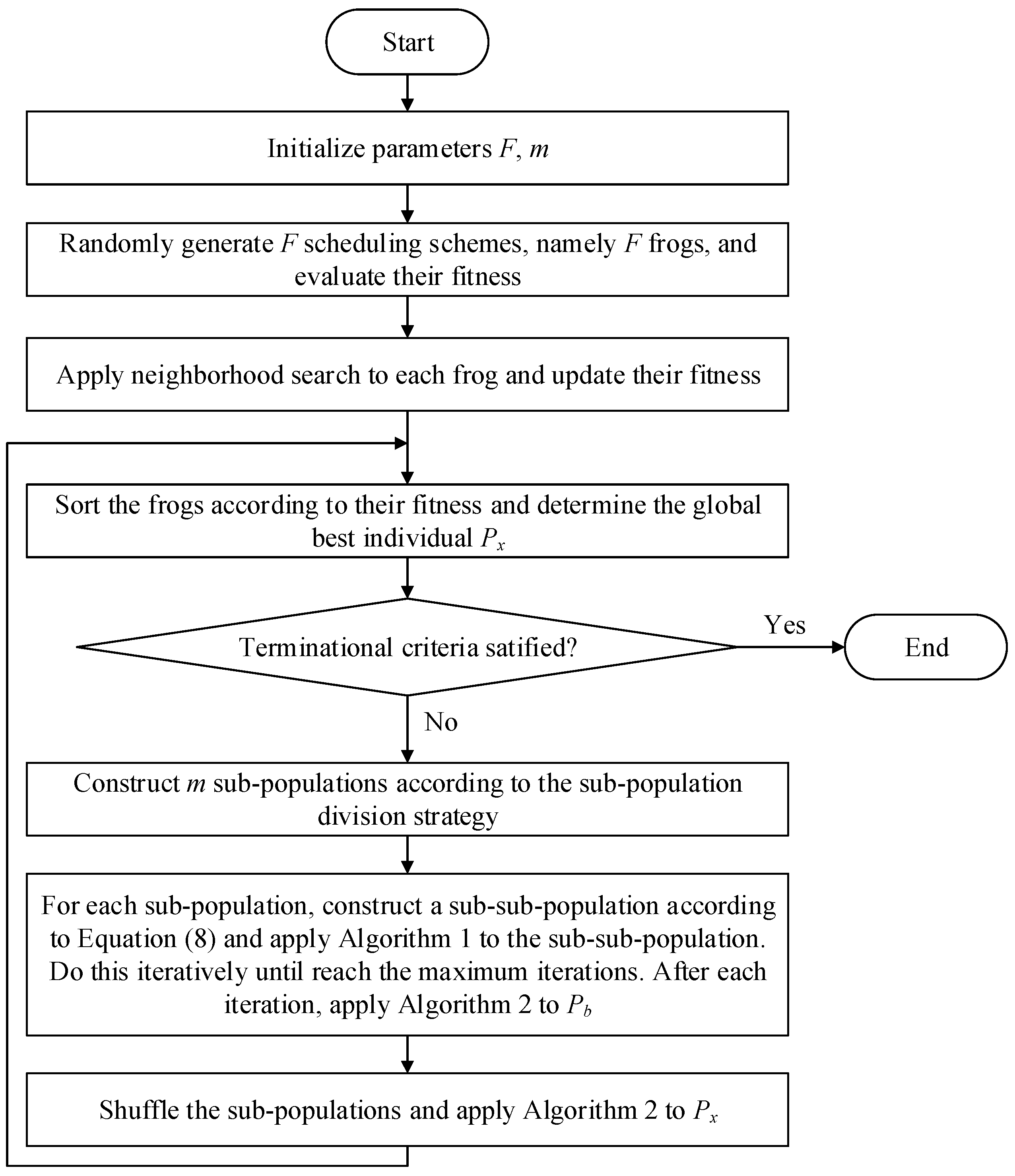
In this section,
Figure 3 concludes the above procedures.
Figure 3.
Flow chart of SFLA for e-RTSP.
Figure 3.
Flow chart of SFLA for e-RTSP.
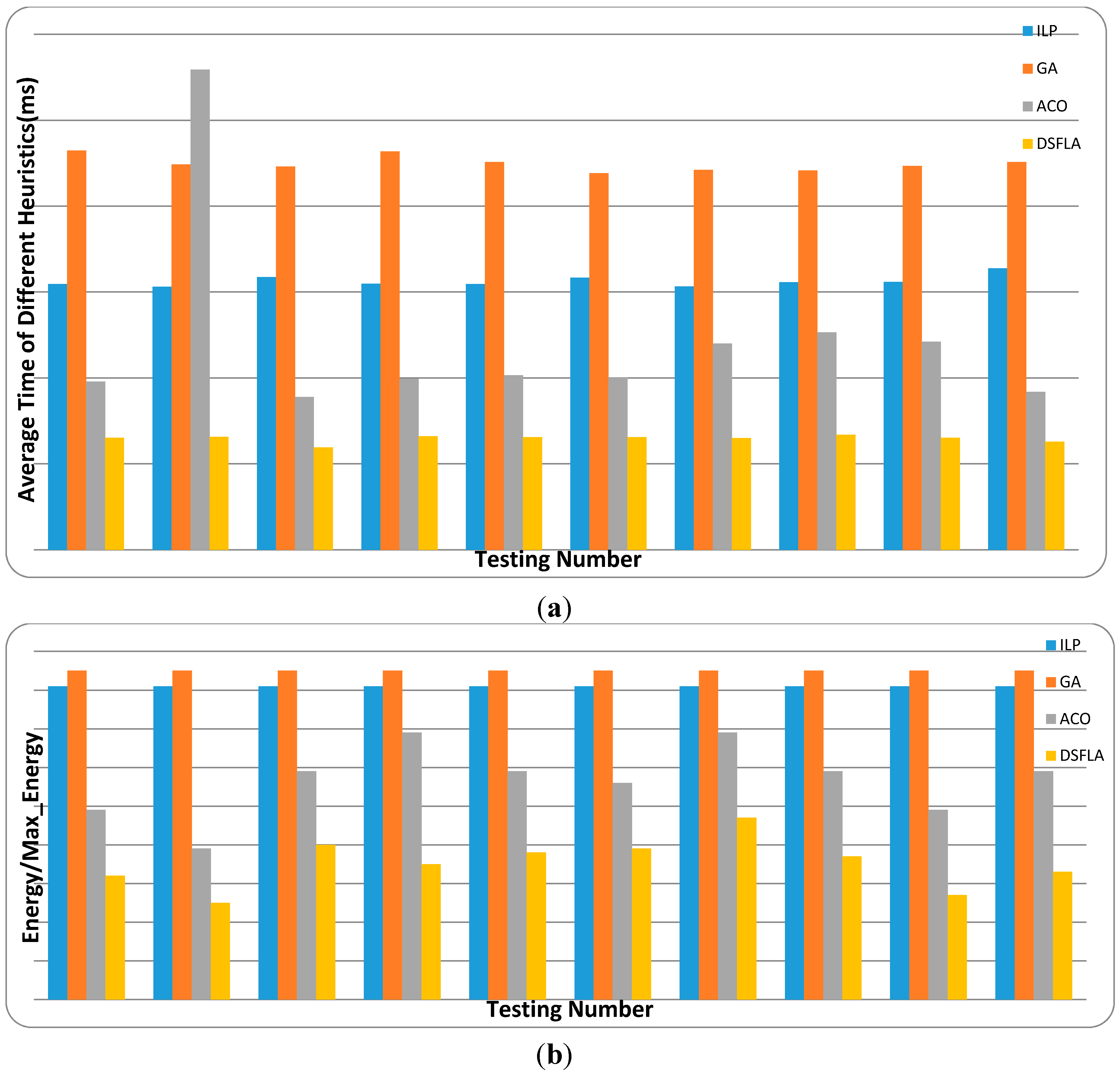
6. Experiment
Extensive experiments are conducted to estimate SFLA’s performance for the energy-aware real-time task-scheduling problem. Our task and processor sets are not only generated from
synthetic data for simulation but also from
real data of benchmarks. The
synthetic data are generated following the same setting in [
11]. The
real data are from the Embedded System Synthesis Benchmarks Suite (E3S) [
37].
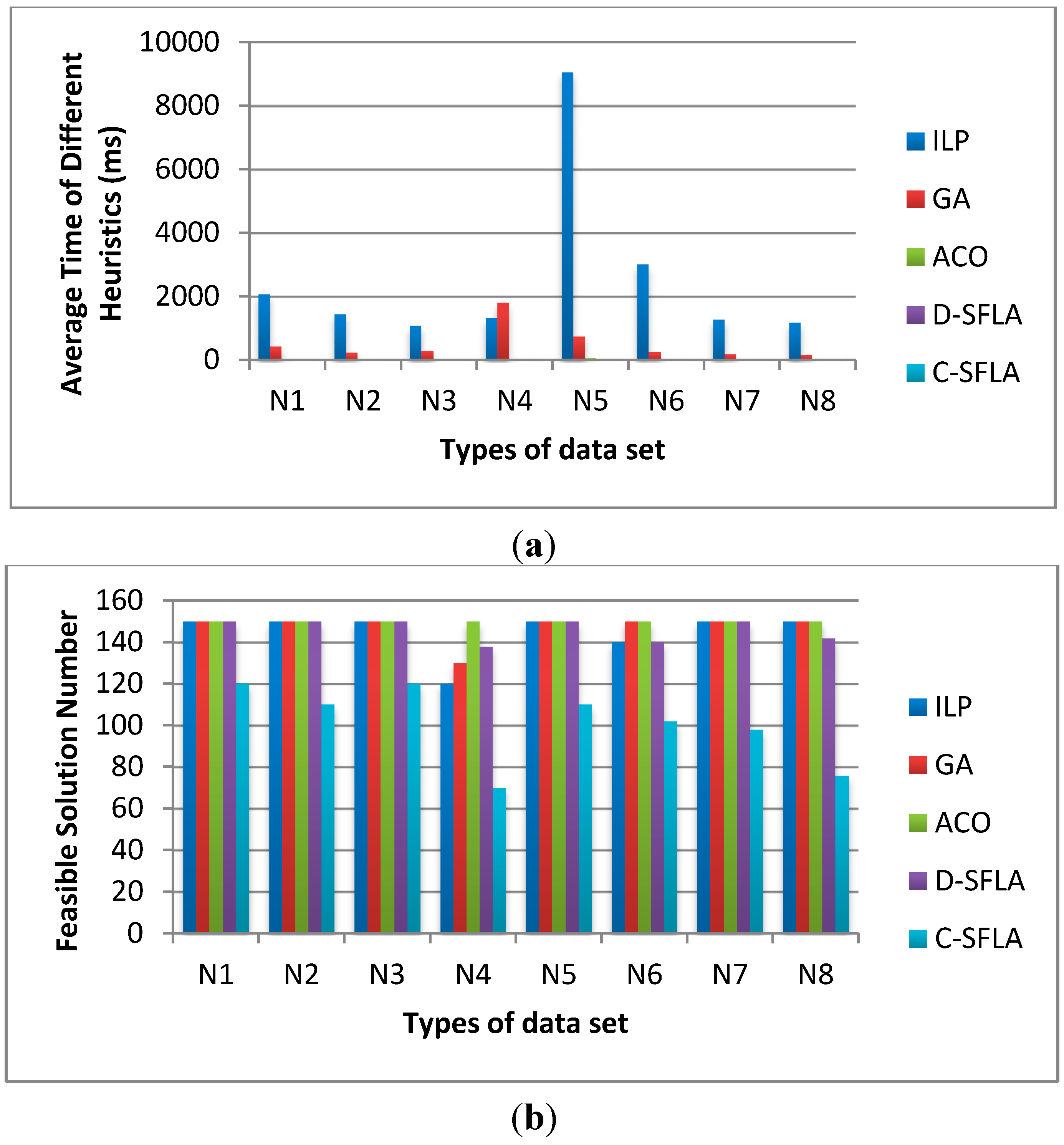
First, we generate the synthetic data sets for simulation. Then, the parameter tests are conducted to determine the optimal parameters for SFLA. After that, SFLA is compared with several familiar scheduling algorithms with synthetic and real data of benchmarks. Their performance is analyzed in detail.
6.1. Generation of Synthetic Data Sets for Simulation
First, the generating method of the utilization matrix is introduced. φ
P denotes the heterogeneity of multiprocessors
P and φ
T denotes the heterogeneity of real-time tasks
T. To make the experiment more practical, the utilization matrix must reflect φ
P and φ
T. The utilization matrix can be generated by the following steps, where
n is the number of tasks,
m is the number of processors,
i is in the interval [1,
n] and
j is in the interval [1,
m].
- Step 1
Generate a one-dimensional integer array cycle[n] randomly. Each cycle[i] is in [100, 1000] and is equal to the number of the clock cycles that Ti needs.
- Step 2
Generate a one-dimensional floating-point array TB[n] randomly. Each TB[i] is in [1, φT]. It is a task baseline vector.
- Step 3
Calculate the one-dimensional array period[n]. period[i] is the period of Ti and is calculated from cycle[i]/TB[i].
- Step 4
Generate a two-dimensional integer array speed[n][m] randomly. For each Ti, generate a one-dimensional array speed[i][m]. Each speed[i][j] is limited in [φT, φT ×φP].
- Step 5
Calculate the two-dimensional array exe[n][m]. Each exe[i][j] is equal to the executing time that Ti needs on Pj. The elements are given by cycle[i]/speed[i][j].
- Step 6
Calculate the utilization matrix Un×m. The calculation equation is given by ui,j = exe[i][j]/period[i].
Next, the generating method of the test data set is given. A utilization matrix is consistent if a task runs faster on a processor than on the other processors when the other tasks also run faster on them. This test data set contains all 8 combinations of φ
P, φ
T and the consistency, namely Consistent, High φ
T, High φ
P; Consistent, High φ
T, Low φ
P; Consistent, Low φ
T, High φ
P; Consistent, Low φ
T, Low φ
P; Inconsistent, High φ
T, High φ
P; Inconsistent, High φ
T, Low φ
P; Inconsistent, Low φ
T, High φ
P; and Inconsistent, Low φ
T, Low φ
P, where High φ
T is 100, Low φ
T is 5, High φ
P is 20, and Low φ
P is 5. They are, respectively, represented by C_HT_HP, C_HT_LP, C_LT_HP, C_LT_LP, IC_HT_HP, IC_HT_LP, IC_LT_HP, and IC_LT_LP. For each combination 15 test instances are generated, so the SFLA experiment is run on 120 test instances in total. Each test instance runs 10 times.
Table 3 shows the utilization matrix scale of SFLA’s parameter test.
Table 3.
The utilization matrix scale of SFLA’s parameter test.
Table 3.
The utilization matrix scale of SFLA’s parameter test.
| No. | Config. | Size | No. | Config. | Size |
|---|
| N1 | C_HT_HP | U90×4 | N5 | IC_HT_HP | U140×5 |
| N2 | C_HT_LP | U50×8 | N6 | IC_HT_HP | U50×8 |
| N3 | C_LT_HP | U70×4 | N7 | IC_LT_HP | U90×4 |
| N4 | C_LT_LP | U40×8 | N8 | IC_LT_LP | U50×8 |
6.2. Parameter Setting for SFLA
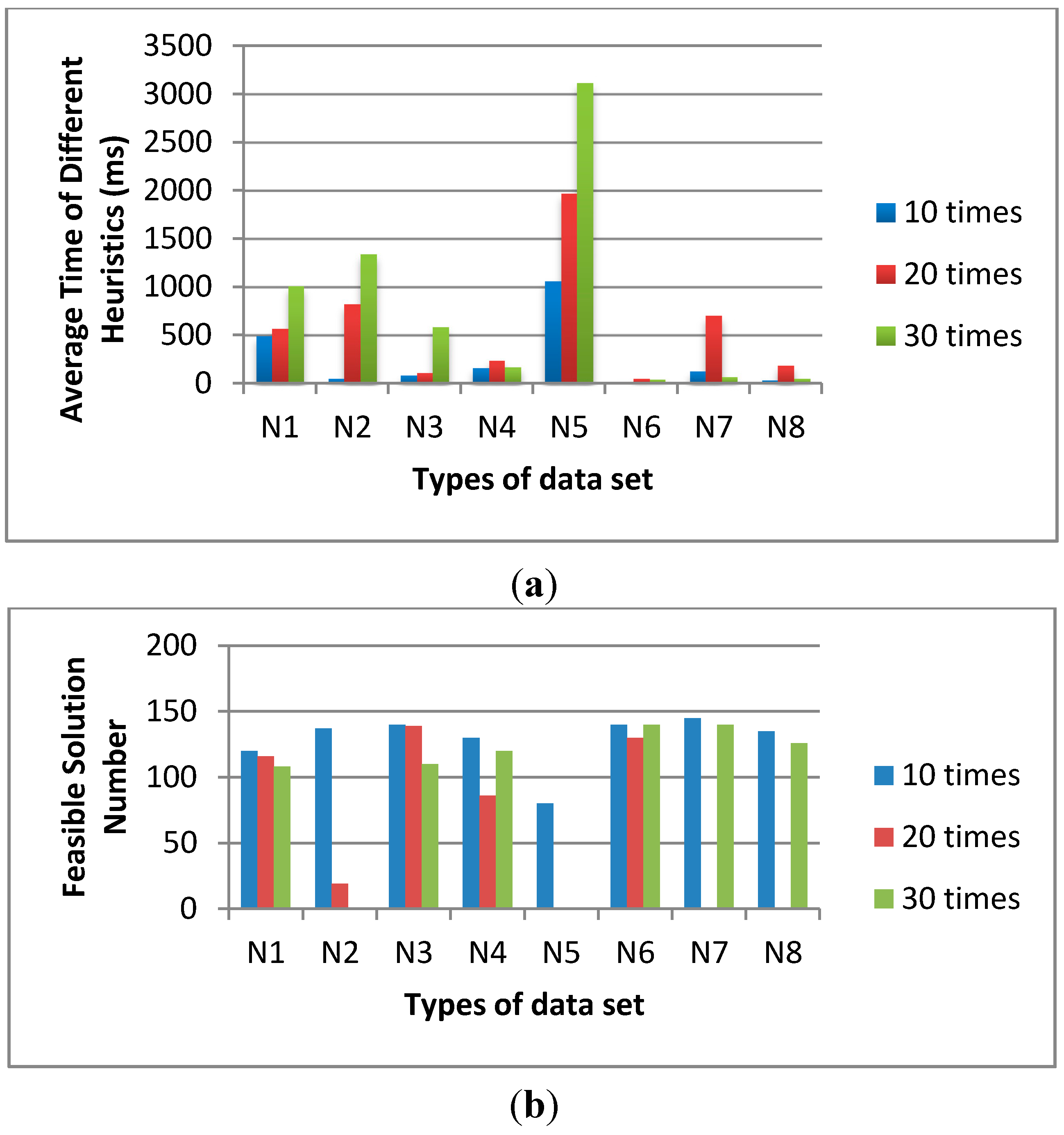
Since SFLA is a new combinatorial optimization algorithm, there are few references to determine the values of its parameters. In order to find better parameter values for SFLA, four kinds of parameter tests were conducted. The influences of three factors on D-SFLA’s performance were tested with control variants. They are the number of the sub-population iterations, the sub-populations size and the population size. The influence of λ on C-SFLA’s performance was also tested. In the experimental results, Avg. stands for the average time that D-SFLA needs to process a problem instance and Feas. stands for the times that D-SFLA can find a feasible schedule in the total 150 times running. We also provide the median for each plotted value by running every test for 20 times.
In
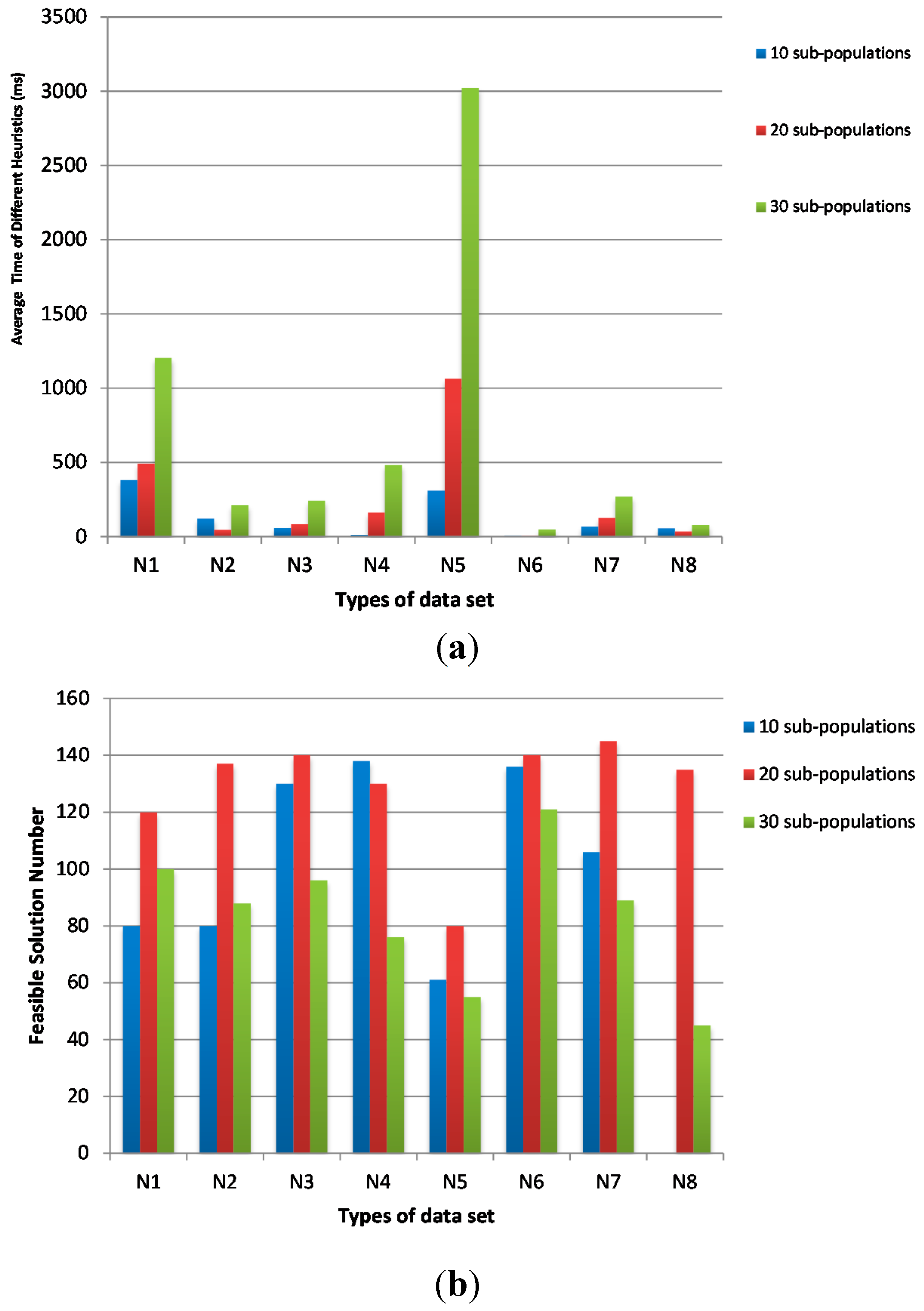
Figure 4, we fix the population size as 200 and the sub-population size as 20. The iteration number of sub-population is varied from 10, 20 to 30 times. The average time of 10 times is shorter than the others and the feasible solution numbers of 10 times are much more than the others.
Figure 4.
The influence of sub-population iterations on (a) average time and (b) feasible solution number.
Figure 4.
The influence of sub-population iterations on (a) average time and (b) feasible solution number.
In
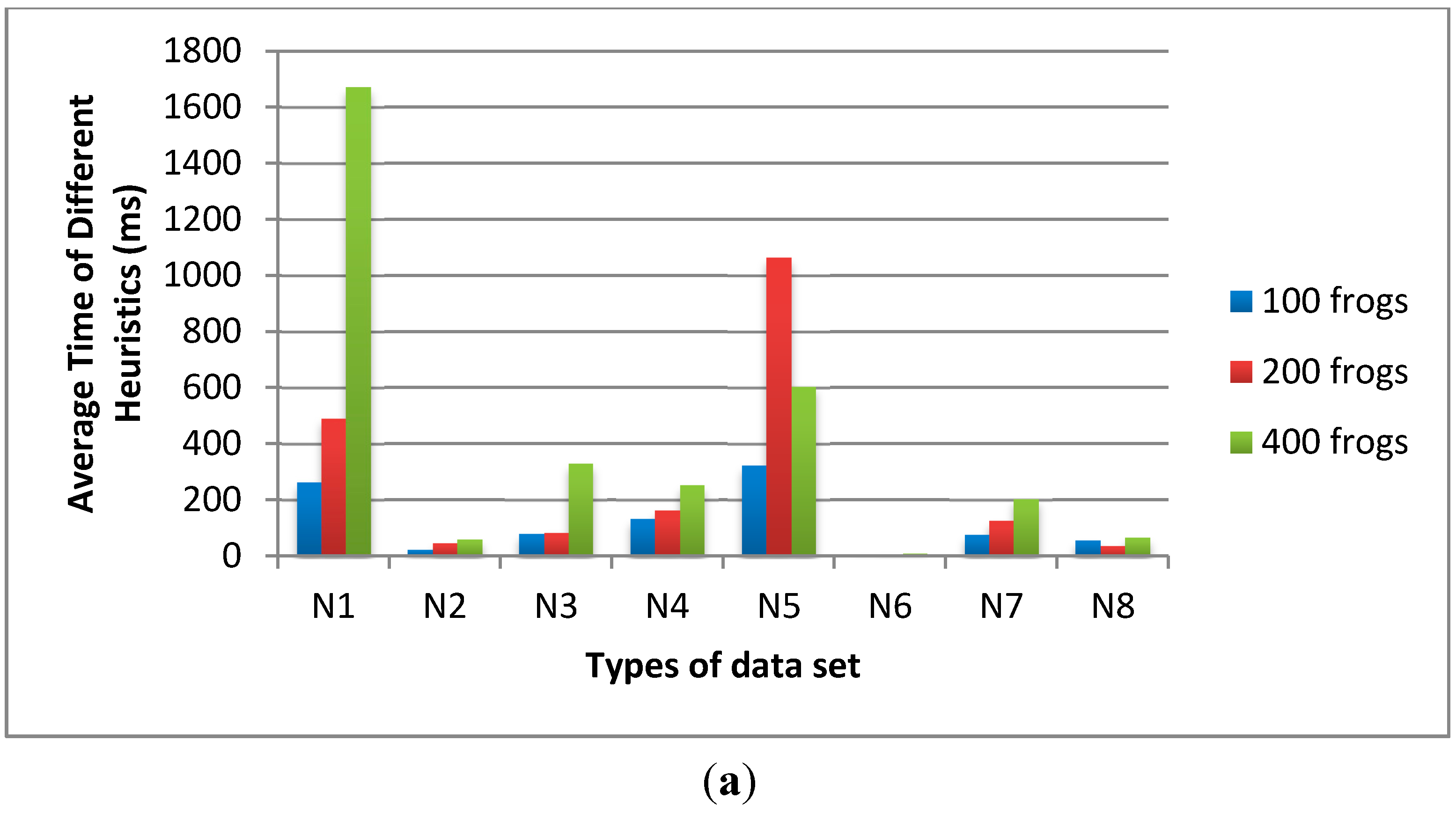
Figure 5, we fix the population size as 200 and the sub-population iteration number as 10. The sub-population size is varied from 10, 20 to 30 frogs. The average time of 20 sub-populations is shorter than that of 30 sub-populations and the feasible solution numbers of 20 sub-populations are much higher than that of 30 sub-populations. Although the average time of 10 sub-populations is slightly shorter than that of 20 sub-populations, the feasible solution numbers of 20 sub-populations are much higher than that of 10 sub-populations.
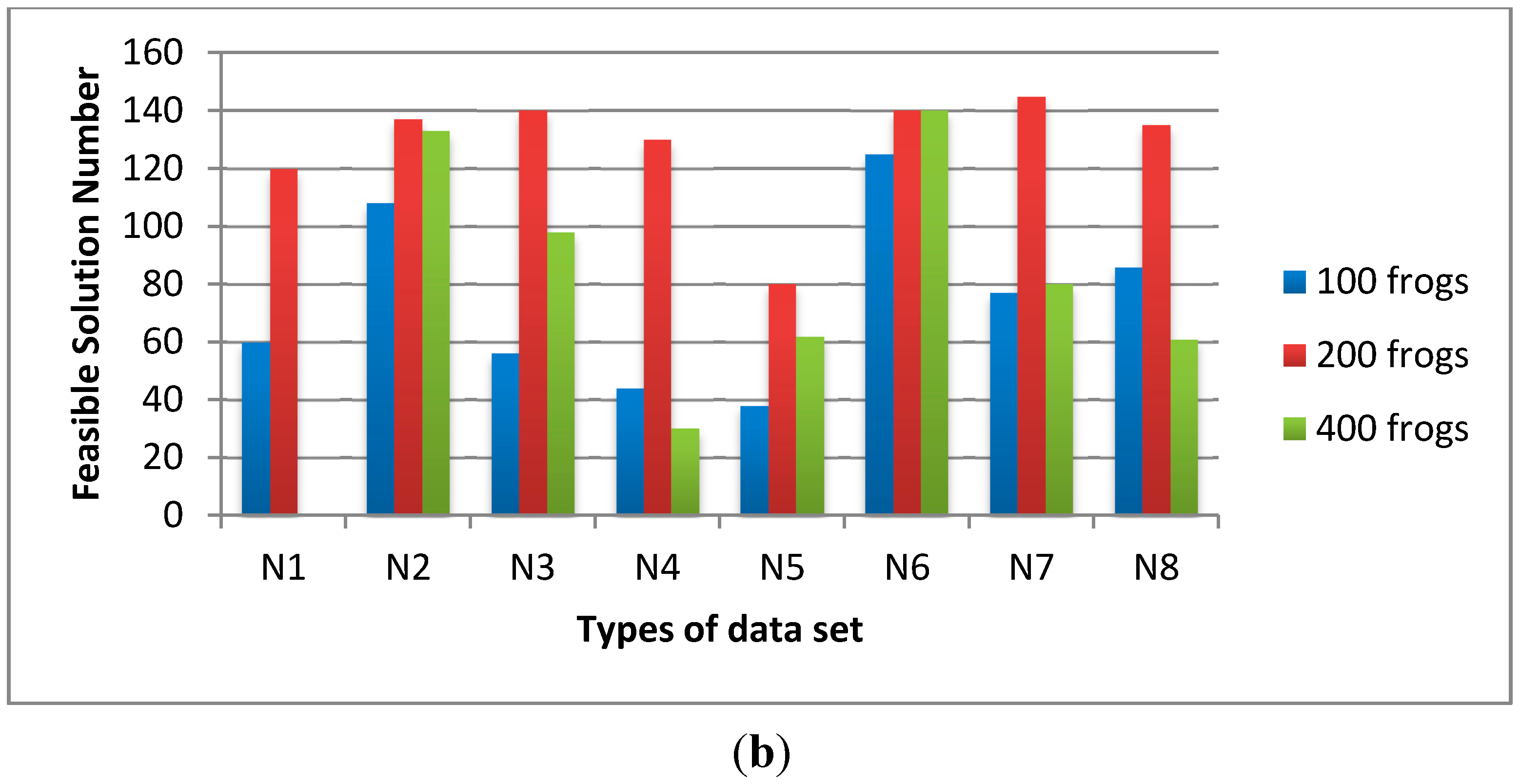
In
Figure 6, we fix the sub-population size as 20 and the iteration number of sub-population as 10 times. The population size is varied from 100, 200 to 400 frogs. The results show that the average time of population size 200 is shorter than the others and the feasible solution numbers of population size 200 are much higher than the others. Therefore, the optimal parameters of D-SFLA are set in
Table 4.
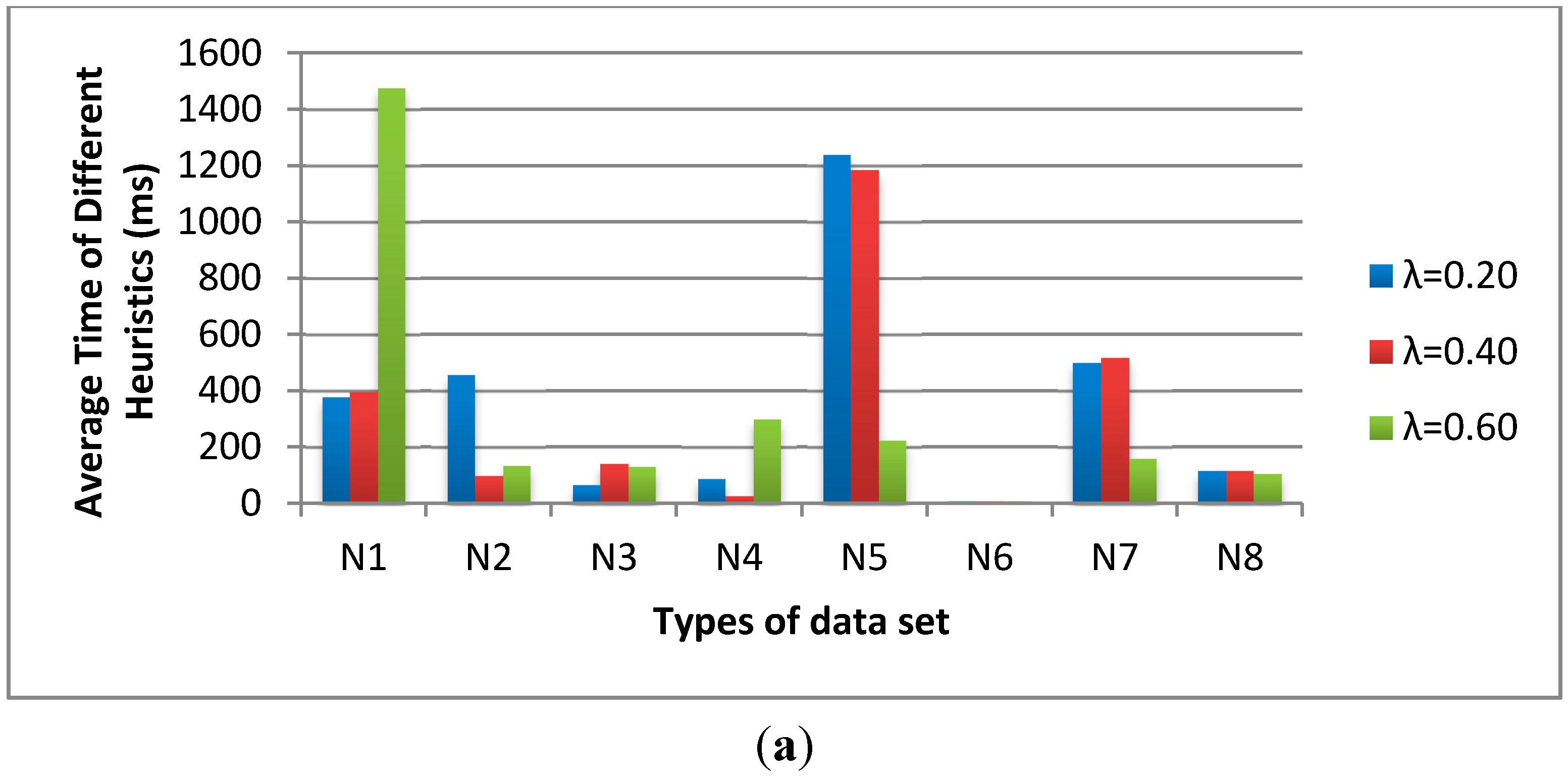
In
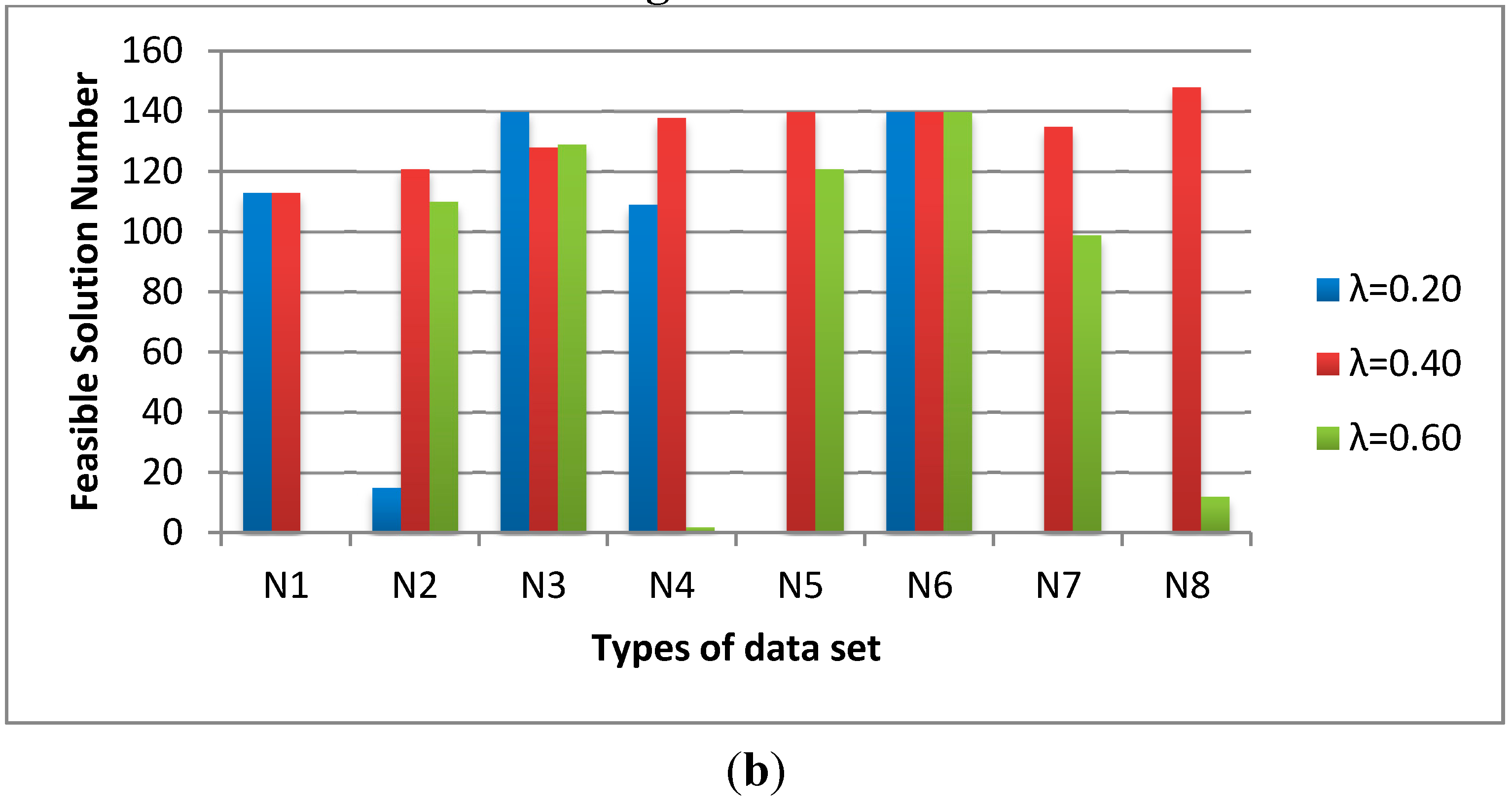
Figure 7, we fix the population size as 200, the sub-population size as 20 and the sub-population iteration number as 10. The influence of λ is varied from 0.2, 0.4 to 0.6. The average time of λ = 0.4 is shorter than the others and the feasible solution numbers of λ = 0.4 are much higher than the others. Thus, we determine the λ = 0.4 for the C-SFLA.
Figure 5.
The influence of sub-population size on (a) average time and (b) feasible solution number.
Figure 5.
The influence of sub-population size on (a) average time and (b) feasible solution number.
Figure 6.
The influence of population size on (a) average time and (b) feasible solution number.
Figure 6.
The influence of population size on (a) average time and (b) feasible solution number.
Figure 7.
The influence of λ on (a) average time and (b) feasible solution number.
Figure 7.
The influence of λ on (a) average time and (b) feasible solution number.
Table 4.
The parameters of SFLA.
Table 4.
The parameters of SFLA.
| No. | Parameter | Value |
|---|
| 1 | Population Size | 200 |
| 2 | Sub-population Size | 20 |
| 3 | Sub-population Iterations | 10 |