Color Filtering Localization for Three-Dimensional Underwater Acoustic Sensor Networks
Abstract
:1. Introduction
| Notation | Explanation |
|---|---|
| Communication range | |
| A 3D UASNs | |
| Number of anchors | |
| Number of mobile nodes | |
| Anchors or mobile nodes | |
| Set of anchors | |
| Set of mobile nodes | |
| Smaller angle of acoustic signal from the anchors received by the mobile node | |
| Euclidean distance between the node and the node | |
| The set of task anchors corresponding to the mobile node | |
| Number of task anchors in | |
| The set of task projections for | |
| RGB sequences for the projections in at time instant | |
| RGB sequences for the anchors in at time instant | |
| Task-ring for task projection | |
| Depth difference between the task anchor and the mobile node | |
| Projection of the task anchor | |
| Distance between the mobile node and the task anchor’s projection | |
| The set of the sampling area | |
| Proportion factor of distances weights | |
| The kth sample | |
| Nearness degree between the mobile node and the sample | |
| The filtered samples set | |
| Threshold for nearness degree at time instant | |
| Number of the filtered samples at time instant |
2. Background
2.1. Related Studies
2.2. Network Model
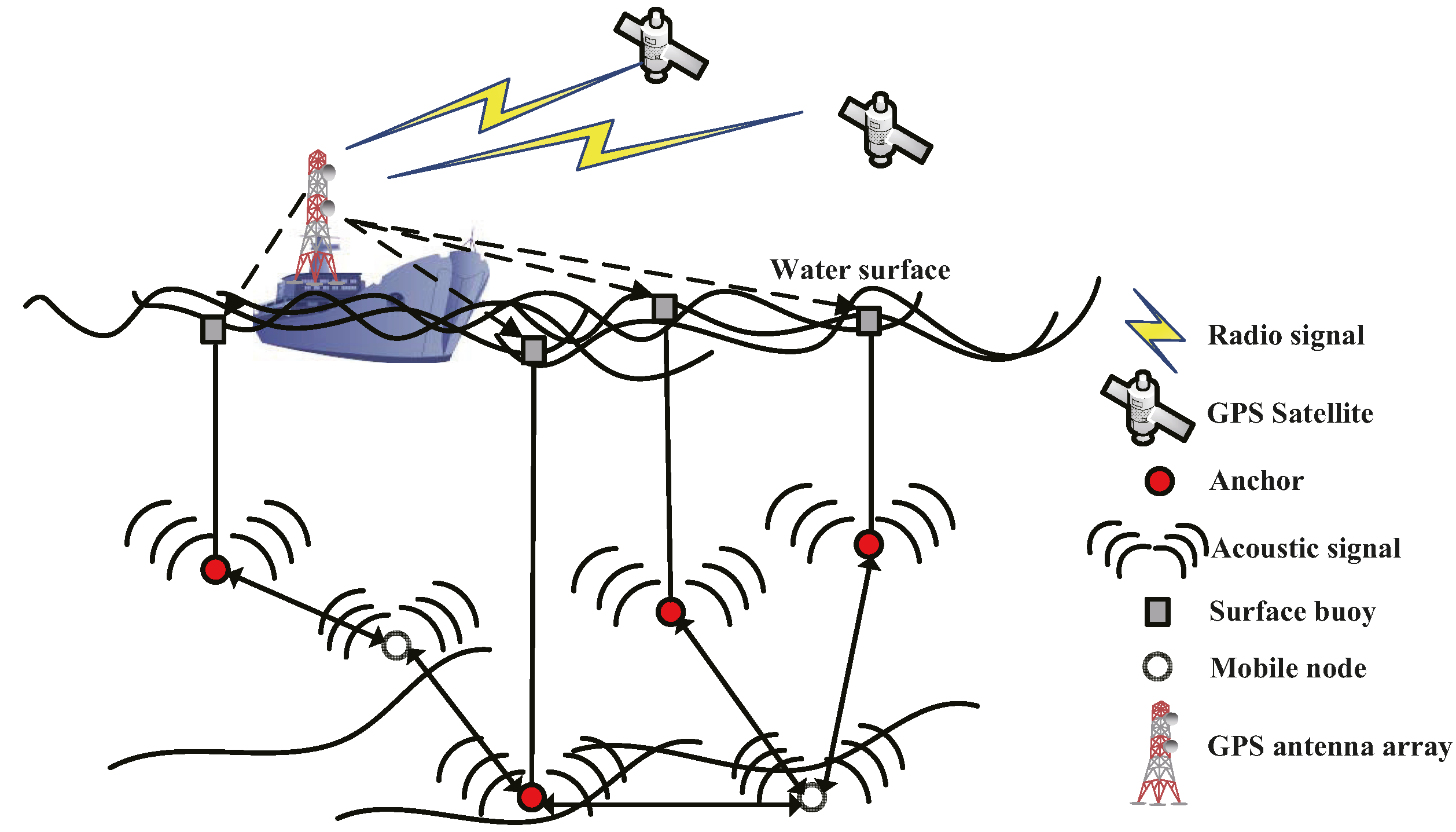
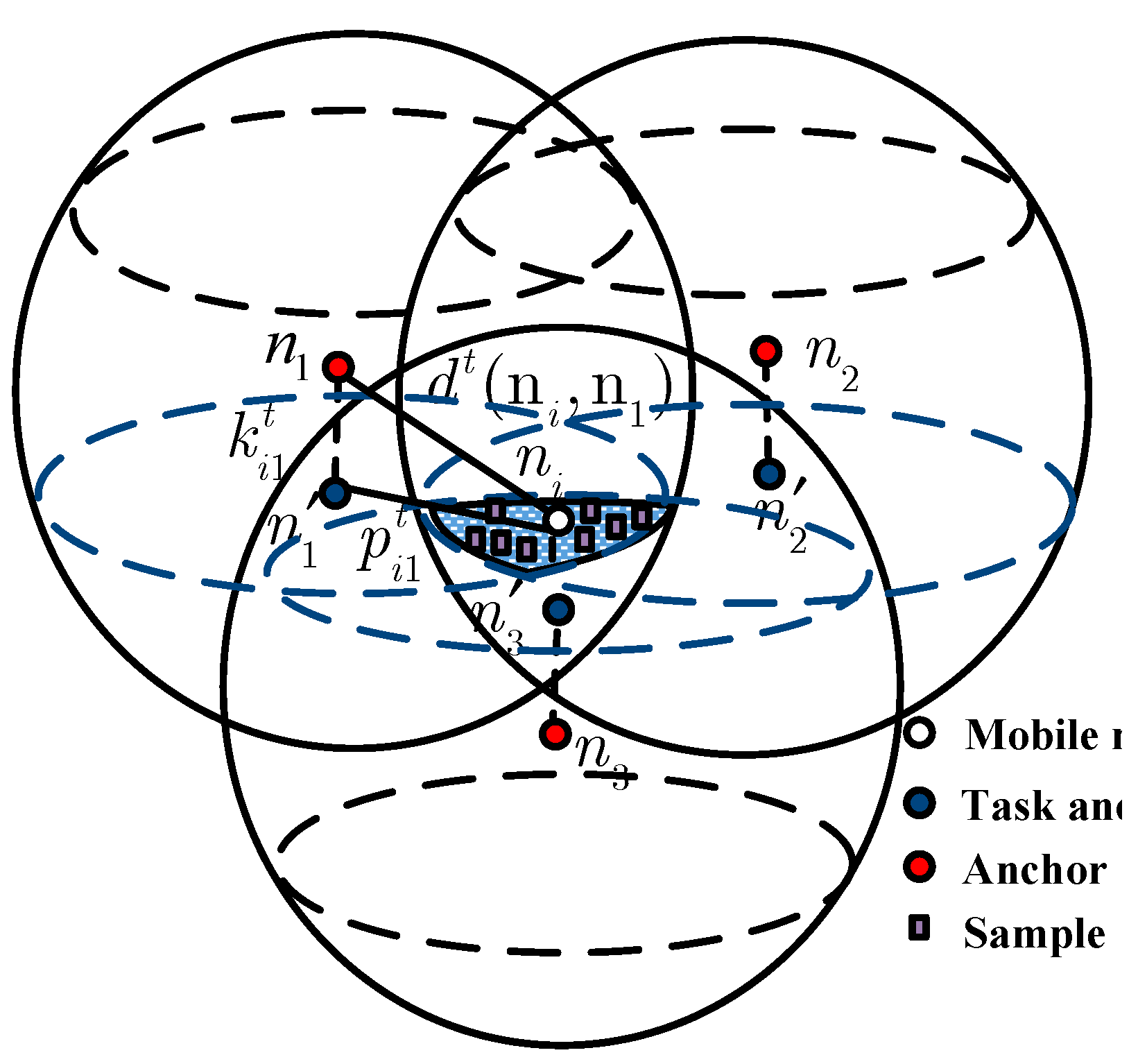
2.3. Problem Formulation
3. Algorithm Design
3.1. Hierarchical Structure Model

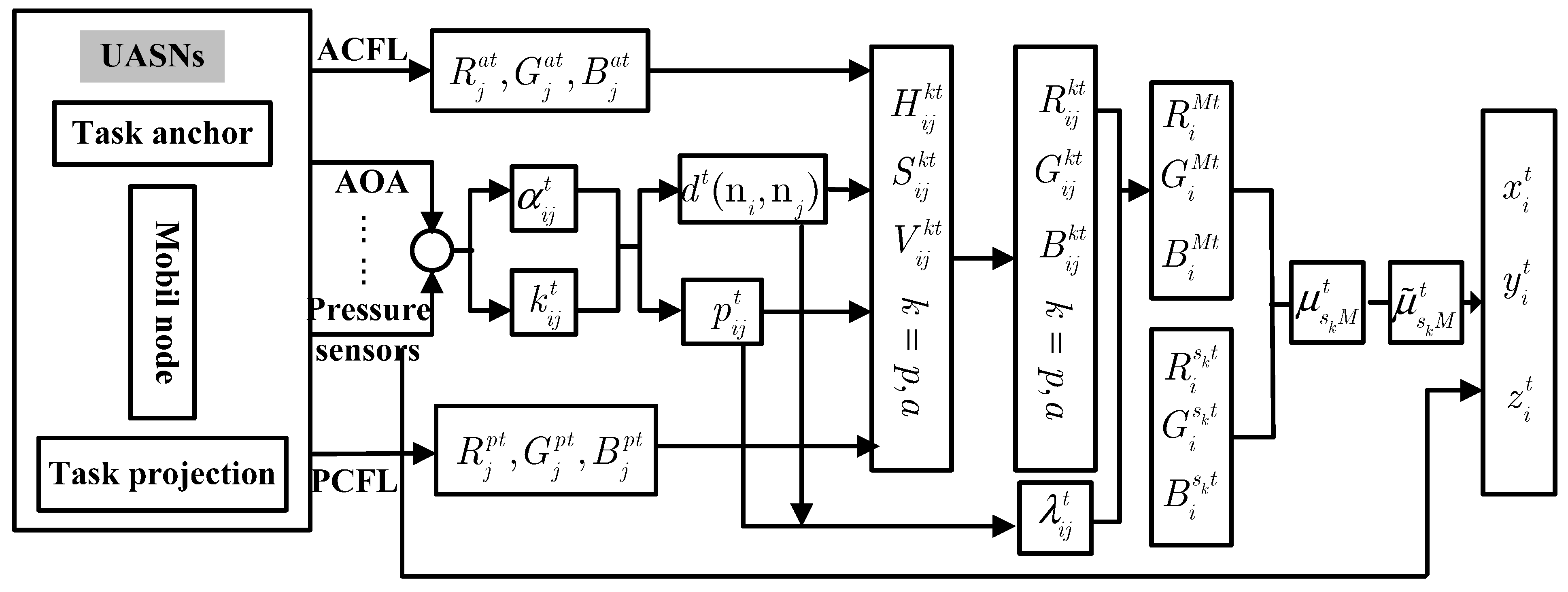
3.2. PCFL and ACFL
| Algorithm 1. The PCFL and ACFL algorithms. |
| 1: if the mobile node senses the request command of localization then |
| 2: sends the acoustic signal in the communication range |
| 3: if receives the acknowlegement signals from the task anchors then |
| 4: is named as the task anchor |
| 5: and are measured by AOA and the deployed pressure sensors respectively |
| 6: |
| 7: |
| 8: end if |
| 9: end if |
| 10: while is the RGB values for the task anchors |
| is the RGB values for the task anchors’ projections do |
| 11: |
| 12: |
| 13: |
| 14: |
| 15: |
| 16: end while |
| 17: if then |
| 18: is the set of the sampling area |
| 19: end if |
| 20: if is the RGB sequence of sample sk then |
| 21: |
| 22: |
| 23: |
| 24: |
| 25: end if |
3.3. Feasibility Analysis
| Algori-thms | PCFL/ACFL | Anchor-aid | AUV-aid | AFLA |
|---|---|---|---|---|
| Time | O(n) | O(nlogn) | O(nlogn) | O(n2) |
| Space | O(n) | O(n) | O(n) | O(n) |
4. Simulation Results
| Parameter | Value |
|---|---|
| Localization area | 1000 m × 1000 m × 20 m |
| The maximum communication radius | 100 m |
| The speed of mobile nodes | 2 m/s–20 m/s |
| Speed of sound | 1500 m/s |
| Error in speed of sound | 0.07 m/s |
| The measurement error of communication angle | 0°–10° |
| The number of samples | 50–500 |
| The density of anchors | 0.5–5 |
| The number of anchors | 5–100 |
| The number of deployed mobile nodes | 20–100 |
| Error in speed of sound | 0.07 m/s |
| The times of simulation run | 50 |
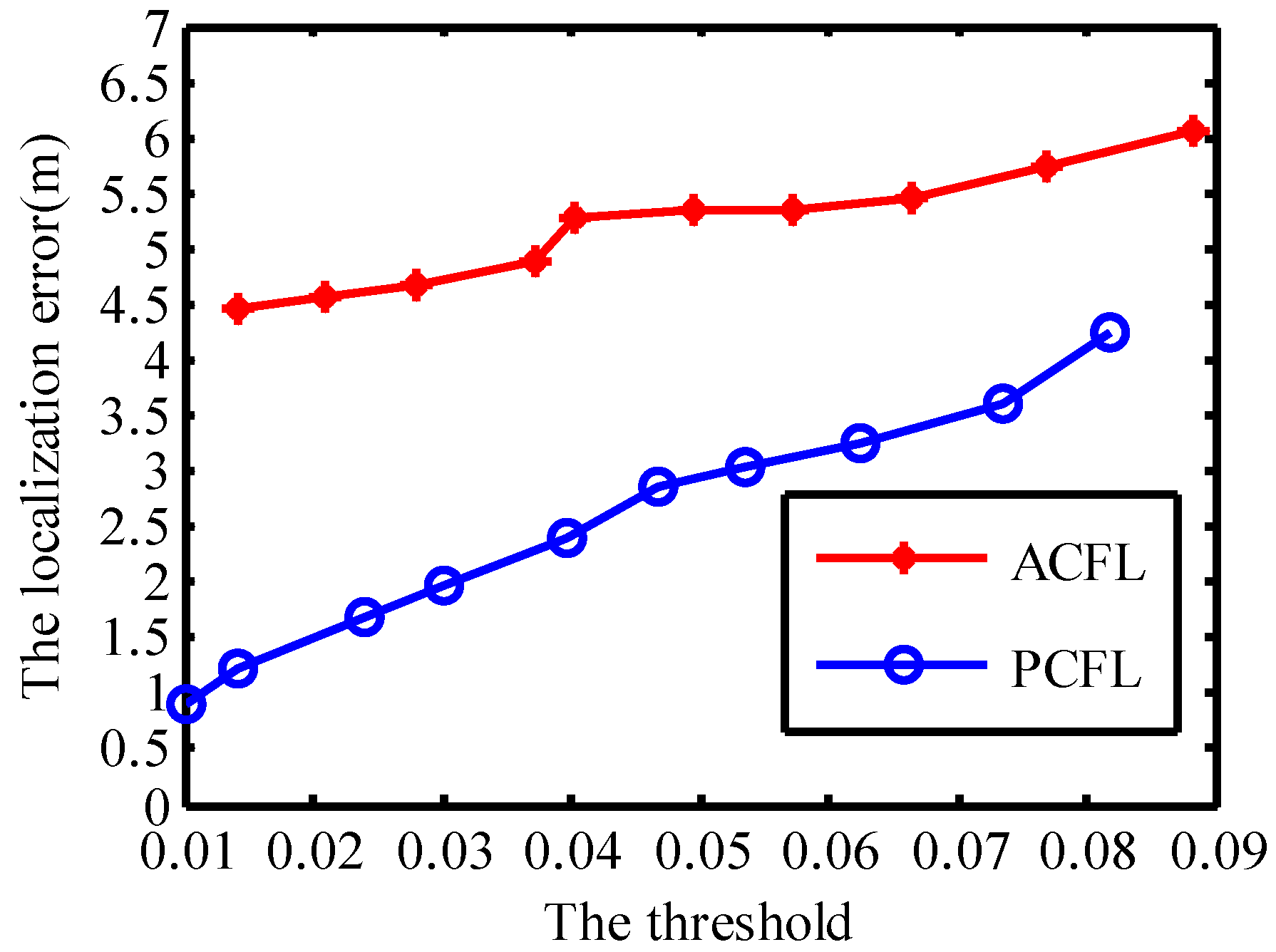
4.1. The Localization Error of ACFL and PCFL under Different Parameters
4.1.1. The Threshold ()
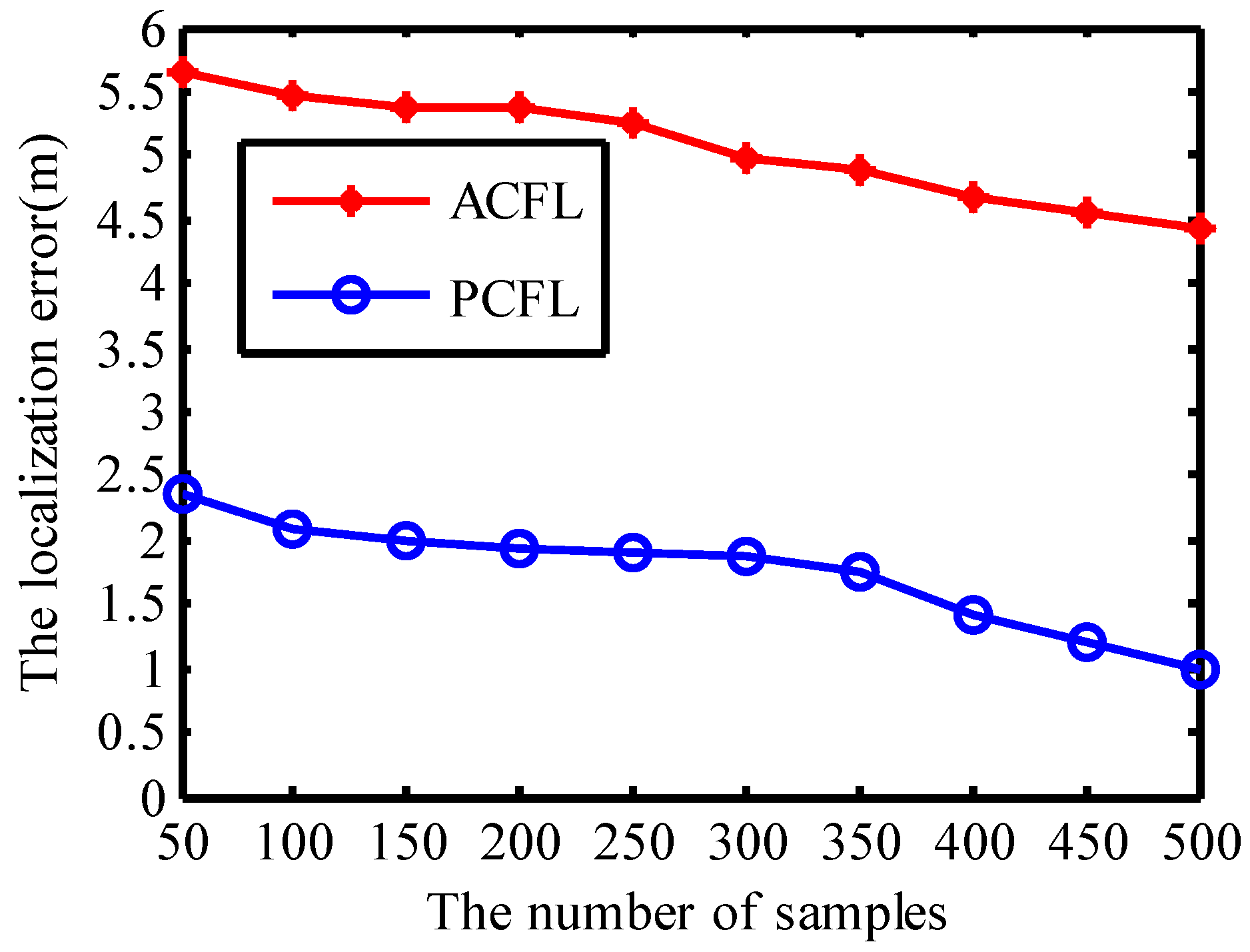
4.1.2. The Number of Samples
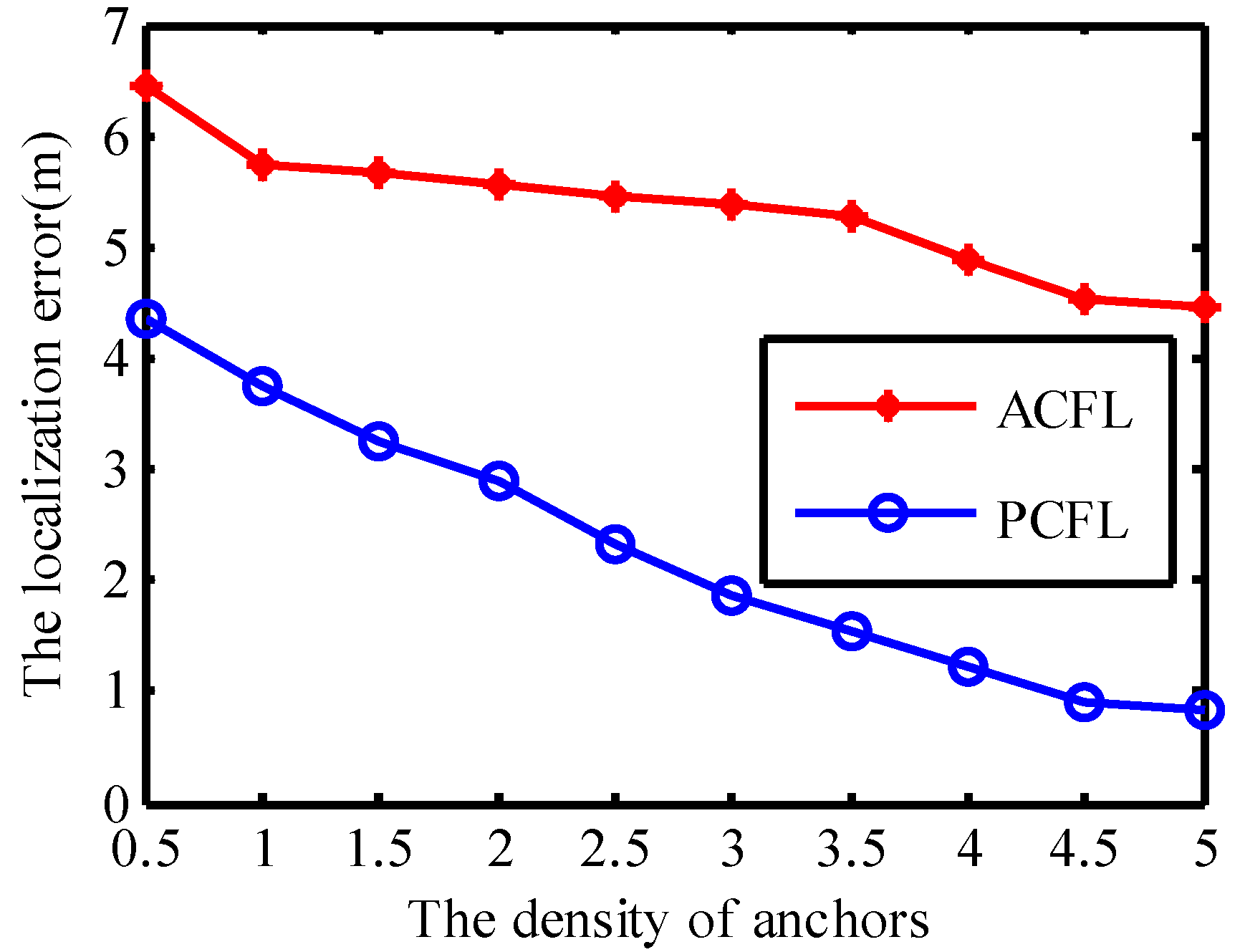
4.1.3. The Density of Anchors
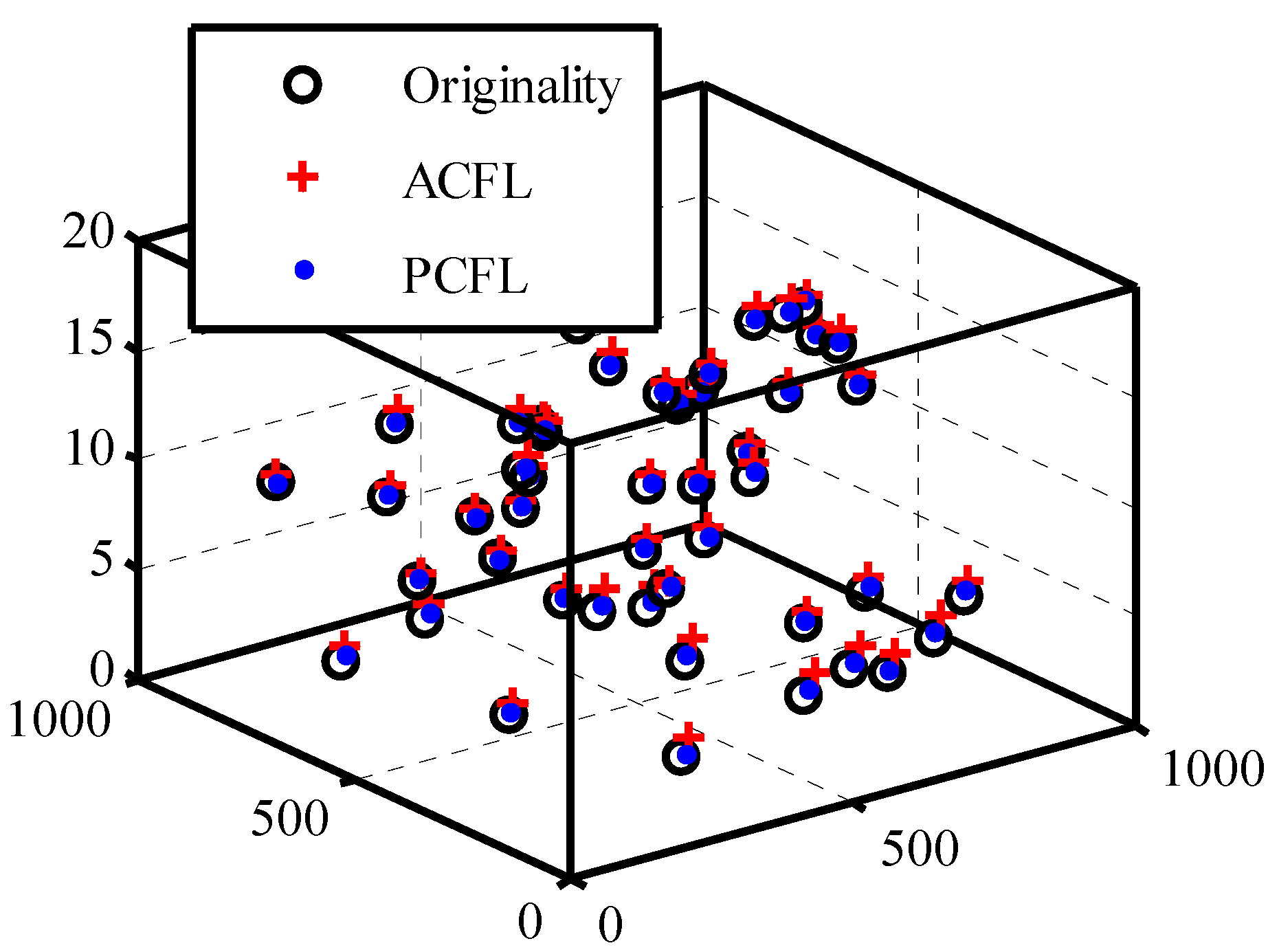
4.1.4. The Estimated and Original Location
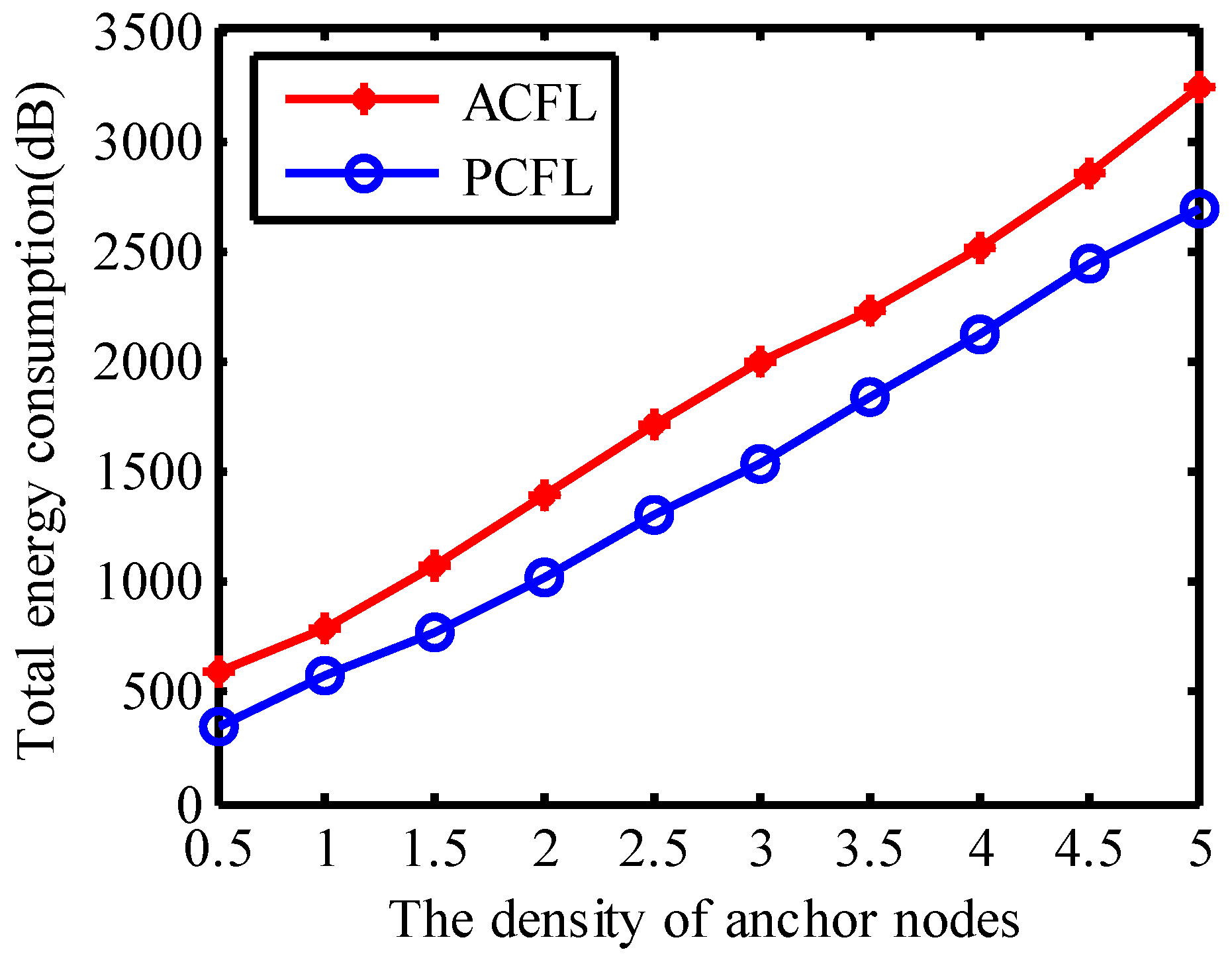
4.1.5. Total Energy Consumption
4.1.6. Runtime
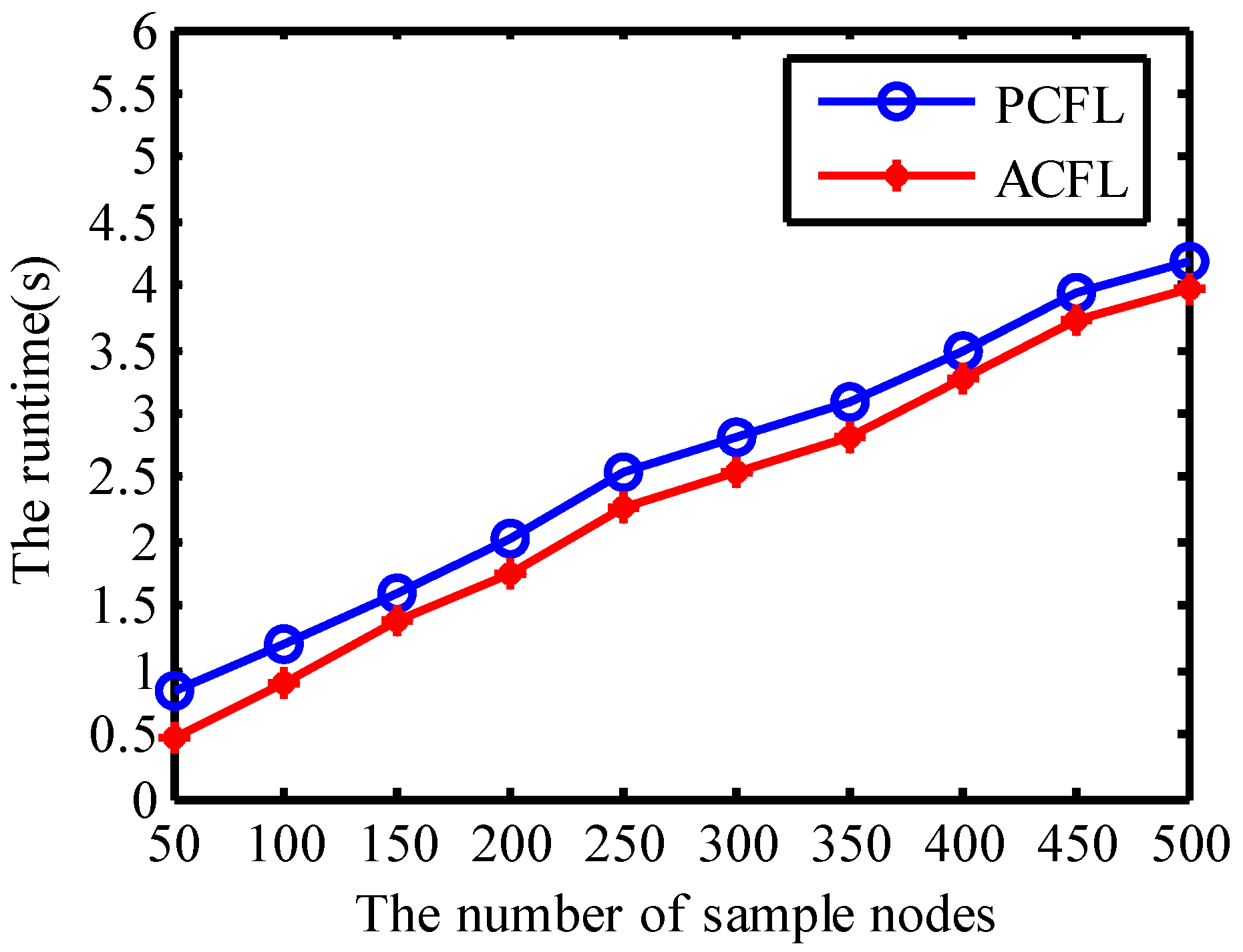
4.2. Comparison with Different Methods
| Algorithm | Average Error(m) | Max Error(m) | Min Error(m) | Standard Deviation(m) |
|---|---|---|---|---|
| Anchor-based | 5.59 | 16.86 | 2.81 | 4.06 |
| AUV-aid | 9.82 | 7.72 | 1.56 | 2.69 |
| AFLA | 2.63 | 13.89 | 0.31 | 1.8 |
| ACFL | 4.56 | 10.22 | 0.51 | 2.06 |
| PCFL | 1.83 | 5.01 | 0.14 | 0.87 |
4.3. The Percentage Distribution of the Localization Error
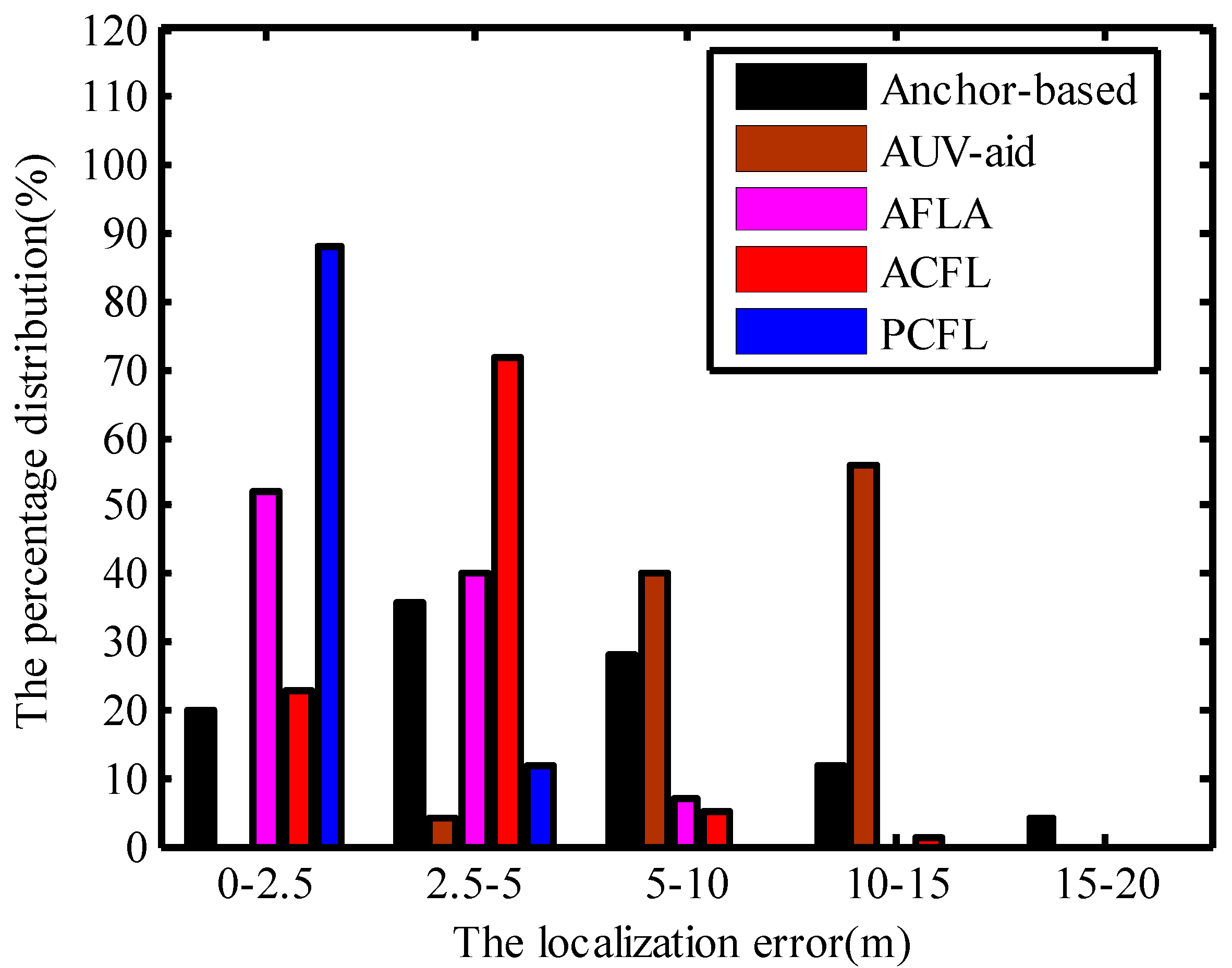
4.4. Error and the Speed of Mobile Nodes
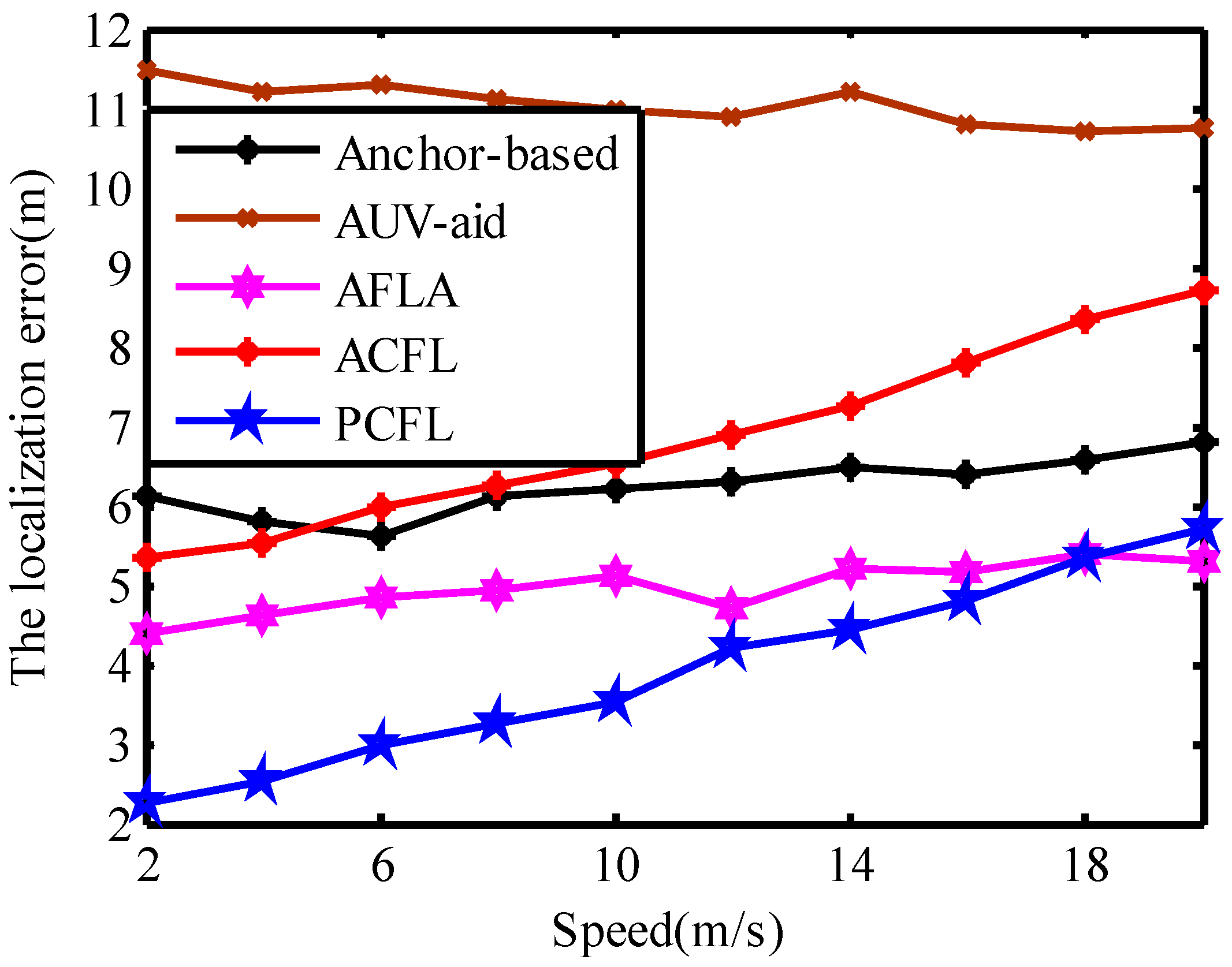
4.5. Error and the Number of Deployed Mobile Nodes
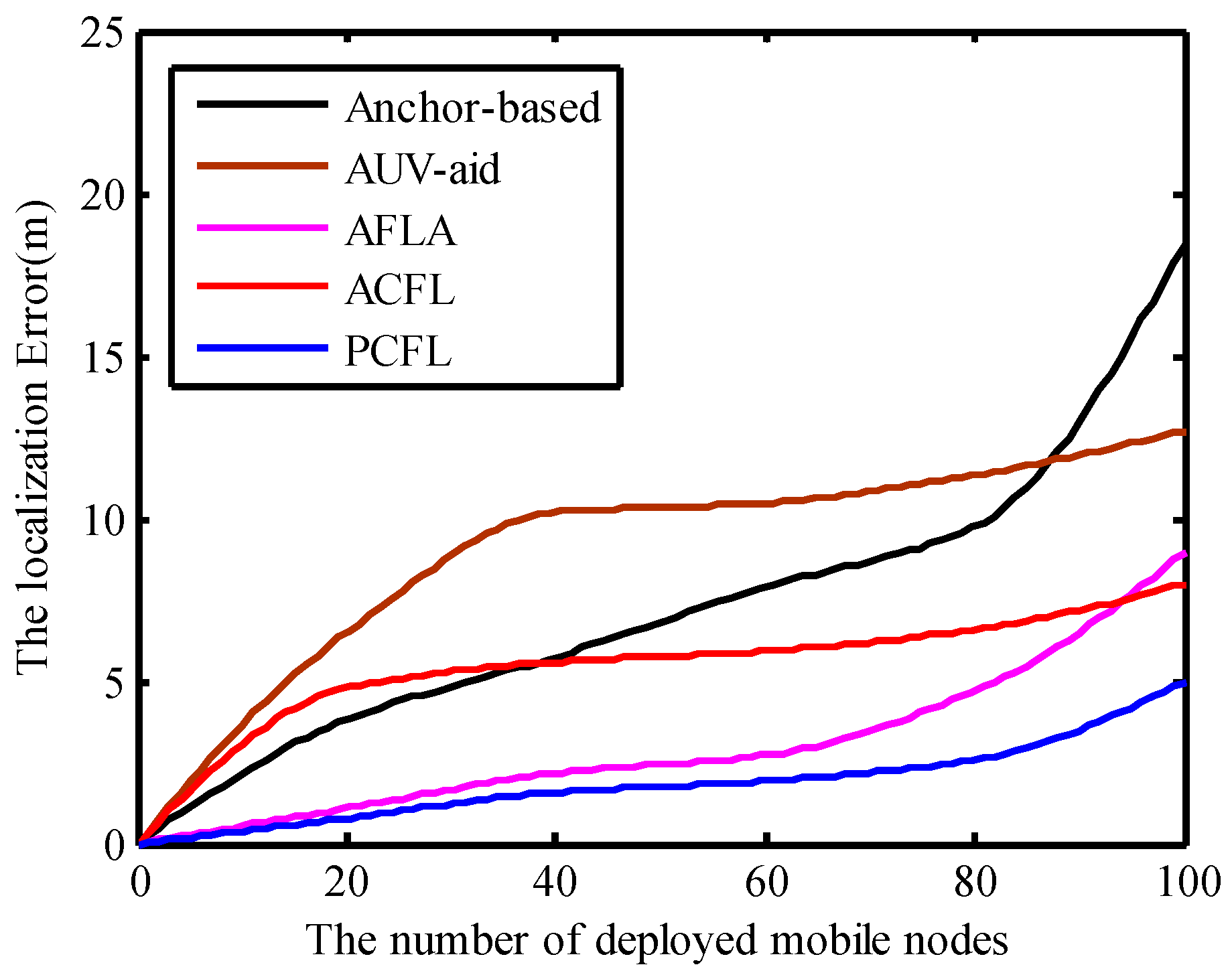
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Climent, S.; Sanchez, A.; Capella, J.V.; Meratnia, N.; Serrano, J. Underwater Acoustic Wireless Sensor Networks: Advances and Future Trends in Physical, MAC and Routing Layers. Sensors 2014, 14, 795–833. [Google Scholar] [CrossRef] [PubMed]
- Erol-Kantarci, M.; Mouftah, H.; Oktug, S. A Survey of Architectures and Localization Techniques for Underwater Acoustic Sensor Networks. IEEE Commun. Surv. Tutor. 2011, 13, 487–502. [Google Scholar] [CrossRef]
- Lloret, J. Underwater Sensor Nodes and Networks. Sensors 2013, 13, 11782–11796. [Google Scholar] [CrossRef] [PubMed]
- Isbitiren, G.; Akan, O. Three-dimensional underwater target tracking with acoustic sensor networks. IEEE Trans. Veh. Technol. 2011, 60, 3897–3906. [Google Scholar] [CrossRef]
- Ramezani, H.; Jamali-Rad, H.; Leus, G. Target localization and tracking for an isogradient sound speed profile. IEEE Trans. Signal Process. 2013, 61, 1434–1446. [Google Scholar] [CrossRef]
- Zeng, Y.; Cao, J.; Hong, J.; Zhang, S.; Xie, L. Secure localization and location verification in wireless sensor networks: A survey. J. Supercomput. 2013, 64, 685–701. [Google Scholar] [CrossRef]
- Diamant, R.; Tan, H.; Lampe, L. LOS and NLOS classification for underwater acoustic localization. IEEE Trans. Mobile Comput. 2014, 13, 311–323. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, Y. Localization for anchor-free underwater sensor networks. Comput. Electron. Eng. 2013, 39, 1812–1821. [Google Scholar] [CrossRef]
- Chen, H.; Liu, B.; Huang, P.; Liang, J.; Gu, Y. Mobility-assisted node localization based on TOA measurements without time synchronization in wireless sensor networks. Mobile Netw. Appl. 2012, 17, 90–99. [Google Scholar] [CrossRef]
- Hua-Jie, S.; Xiao-Ping, Z.; Zhi, W. Efficient closed-form algorithms for AOA based self-localization of sensor nodes using auxiliary variables. IEEE Trans. Signal Process. 2014, 62, 2580–2594. [Google Scholar] [CrossRef]
- Liang, Q.; Zhang, B.; Zhao, C.; Pi, Y. TDoA for passive localization: Underwater versus terrestrial environment. IEEE Trans. Para. Distr. 2013, 24, 2100–2108. [Google Scholar] [CrossRef]
- Shee, S.H.; Chang, T.C.; Wang, K.; Hsieh, Y.L. Efficient color-theory-based dynamic localization for mobile wireless sensor networks. Wirel. Pers. Commun. 2011, 59, 375–396. [Google Scholar] [CrossRef]
- Dai, G.; Mao, K.; Lei, Y.; Fan, C.; Shao, B.; Chen, Q. 3D Localization Algorithm Base on Layered Structure for Wireless Sensor Networks. J. Inf. Comput. Sci. 2013, 10, 1337–1343. [Google Scholar] [CrossRef]
- Gui, L.; Val, T.; Wei, A.; Dalce, R. Improvement of range-free localization technology by a novel DV-hop protocol in wireless sensor networks. Ad Hoc Netw. 2015, 24, 55–73. [Google Scholar] [CrossRef]
- Velimirovic, A.S.; Djordjevic, G.L.; Velimirovic, M.M.; Jovanovic, M.D. Fuzzy ring-overlapping range-free (FRORF) localization method for wireless sensor networks. Comput. Commun. 2012, 35, 1590–1600. [Google Scholar] [CrossRef]
- Lee, J.; Chung, W.; Kim, E. A new range-free localization method using quadratic programming. Comput. Commun. 2011, 34, 998–1010. [Google Scholar] [CrossRef]
- Zhi-hua, L.; Shuang, Z. A New Color Dynamic Localization for Mobile Nodes Based on Local Sampling and Filtering in WSN. J. Elect. Inf. Technol. 2014, 2385–2392. [Google Scholar]
- Diamant, R.; Lampe, L. Underwater Localization with Time-Synchronization and Propagation Speed Uncertainties. IEEE Trans. Mobil Comput. 2013, 12, 1257–1269. [Google Scholar] [CrossRef]
- Erol, M.; Vieira, F.; Gerla, M. AUV-Aided Localization for Underwater Sensor Networks. In International Conference on Wireless Algorithms, Systems and Applications, Chicago, IL, USA, 1–3 August 2007; pp. 44–54.
- Xiuzhen, C.; Haining, S.; Qilian, L.; Du, D. Silent Positioning in Underwater Acoustic Sensor Networks. IEEE Trans. Veh. Technol. 2008, 57, 1756–1766. [Google Scholar] [CrossRef]
- Kussat, N.H.; Chadwell, C.D.; Zimmerman, R. Absolute Positioning of an Autonomous Underwater Vehicle Using GPS and Acoustic Measurements. IEEE J. Ocean. Eng. 2005, 30, 153–164. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Y.; Liao, H.; Lin, C.; Hu, K.; Chang, T. A Power-efficient Routing Protocol for Underwater Wireless Sensor Networks. Appl. Soft Comput. 2011, 11, 2348–2355. [Google Scholar] [CrossRef]
- Domingo, M.C.; Prior, R. Energy Analysis of Routing Protocols for Underwater Wireless Sensor Networks. Comput. Commun. 2008, 31, 1227–1238. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Gao, H.; Wang, W.; Chang, S.; Chen, J. Color Filtering Localization for Three-Dimensional Underwater Acoustic Sensor Networks. Sensors 2015, 15, 6009-6032. https://doi.org/10.3390/s150306009
Liu Z, Gao H, Wang W, Chang S, Chen J. Color Filtering Localization for Three-Dimensional Underwater Acoustic Sensor Networks. Sensors. 2015; 15(3):6009-6032. https://doi.org/10.3390/s150306009
Chicago/Turabian StyleLiu, Zhihua, Han Gao, Wuling Wang, Shuai Chang, and Jiaxing Chen. 2015. "Color Filtering Localization for Three-Dimensional Underwater Acoustic Sensor Networks" Sensors 15, no. 3: 6009-6032. https://doi.org/10.3390/s150306009
APA StyleLiu, Z., Gao, H., Wang, W., Chang, S., & Chen, J. (2015). Color Filtering Localization for Three-Dimensional Underwater Acoustic Sensor Networks. Sensors, 15(3), 6009-6032. https://doi.org/10.3390/s150306009





