A Mixed Approach to Similarity Metric Selection in Affinity Propagation-Based WiFi Fingerprinting Indoor Positioning
Abstract
:1. Introduction
2. System Model
2.1. A General Model for WkNN Deterministic Algorithms
- Selection of k: Previous works showed the impact of the methodology of selecting the set of k RPs and the value of k itself on the positioning performance of deterministic WkNN algorithms [5,6,7], but no univocal and general way to select the value of k was provided. Section 2.2 presents the two selection schemes considered in this work.
- Clustering algorithm: Two-step algorithms considered in this work require the selection of a clustering algorithm to be used in the offline phase. Several works proposed the affinity propagation algorithm [13] as a viable solution to fulfill this task [12,14,15,16], and the algorithm was also adopted in this work. The affinity propagation algorithm and its application to RP clustering and coarse localization steps are discussed in Section 2.3.
- Similarity metrics: Different similarity metrics can be adopted in two-step algorithms for coarse and fine localization steps, respectively, leading to , and thus, introducing an additional degree of freedom in the algorithm design. This possibility, not yet explored in the literature, will be thoroughly addressed in Section 3.
2.2. k Selection Schemes
2.3. Affinity Propagation Clustering for Indoor Positioning
2.3.1. RP Clustering
- Responsibility : This reflects the accumulated evidence for how well-suited is to serve as the exemplar for , taking into account other potential exemplars for .
- Availability : This reflects the accumulated evidence for how appropriate it would be for to choose as its exemplar, taking into account the support from other RPs that should be an exemplar.
- Degeneracies: Degeneracies can arise, for example, if the similarity metric is commutative and two elements (RPs) are isolated from all of the others. In this case, oscillations in deciding which of the two elements should be the exemplar might appear. The solution proposed in [13] is to add a small amount of random noise to similarities values to avoid such a deadlock situation.
- Outliers: The algorithm might occasionally lead to an RP belonging to a cluster, but being physically far away from the cluster exemplar. In [12], taking advantage of the knowledge of the position of each RP, each outlier is forced to join the cluster characterized by the exemplar at the minimum distance from the outlier itself.
2.3.2. Cluster Selection
- Similarity to the exemplar fingerprints (Criterion I): the similarity between the i-th online reading and each -th exemplar fingerprint (with ) is evaluated, and clusters corresponding to exemplars with similarity values above a predefined threshold α are selected.
- Similarity to the cluster average fingerprints (Criterion II): in this case, a cluster fingerprint is computed by averaging the RP fingerprints within the cluster. The similarity between the i-th online reading and each -th cluster fingerprint (with ) is then evaluated, and the clusters with similarity values above α are selected.
2.3.3. Similarity Metric for RP Clustering and Cluster Selection Steps
3. Similarity in the Context of WiFi Fingerprinting Indoor Positioning
3.1. Offline Phase Similarity Metrics
- RP positions (with ).
- RP RSS fingerprints (with ).
3.1.1. A Spatial Distance-Based Similarity Metric
3.2. Offline/Online Phase Similarity Metrics
3.2.1. Minkowski Distance-Based Metrics: Manhattan and Euclidean
3.2.2. Inner Product-Based Metrics: Cosine Similarity and Pearson Correlation
3.2.3. A Frequentist Approach: p-values from the Pearson Correlation
3.2.4. Exploring Interdisciplinary Metrics: Shepard Similarity
3.3. A Comparative Framework for RSS-Based Similarity Metrics
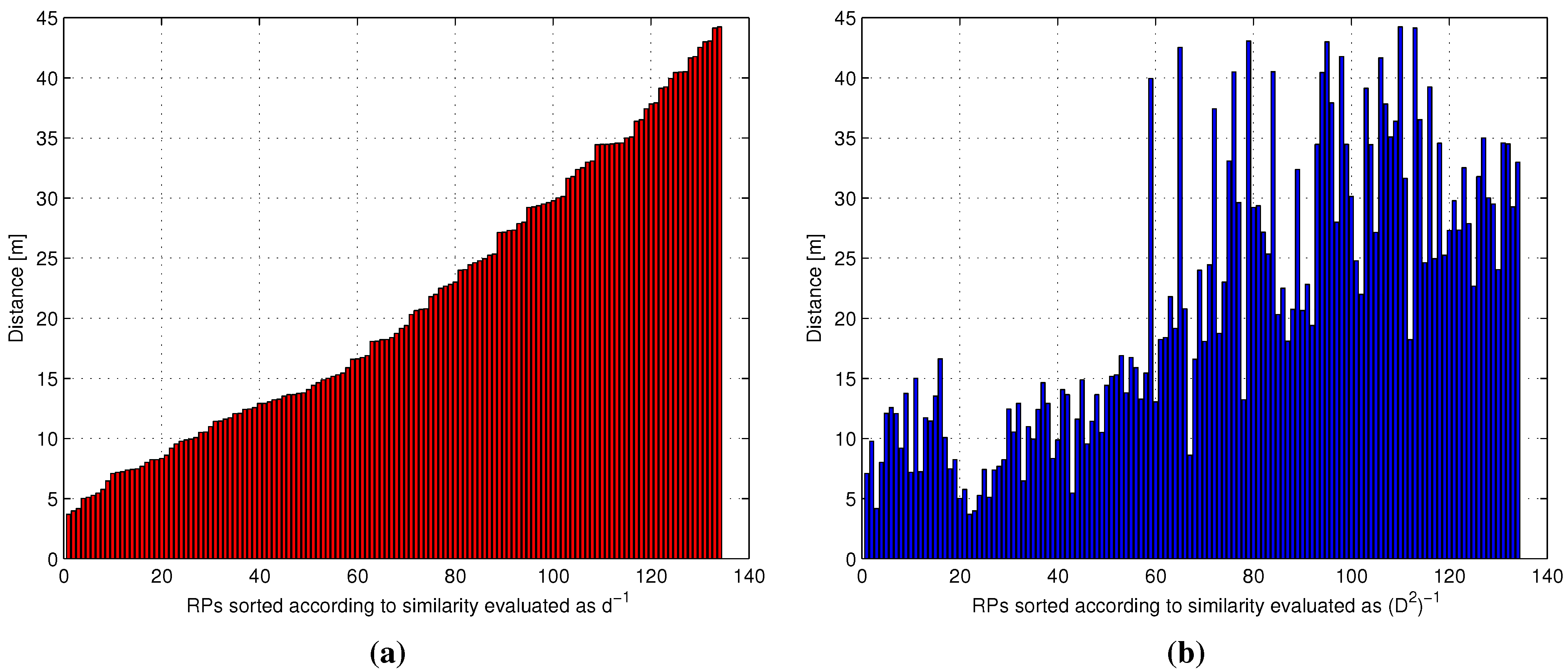
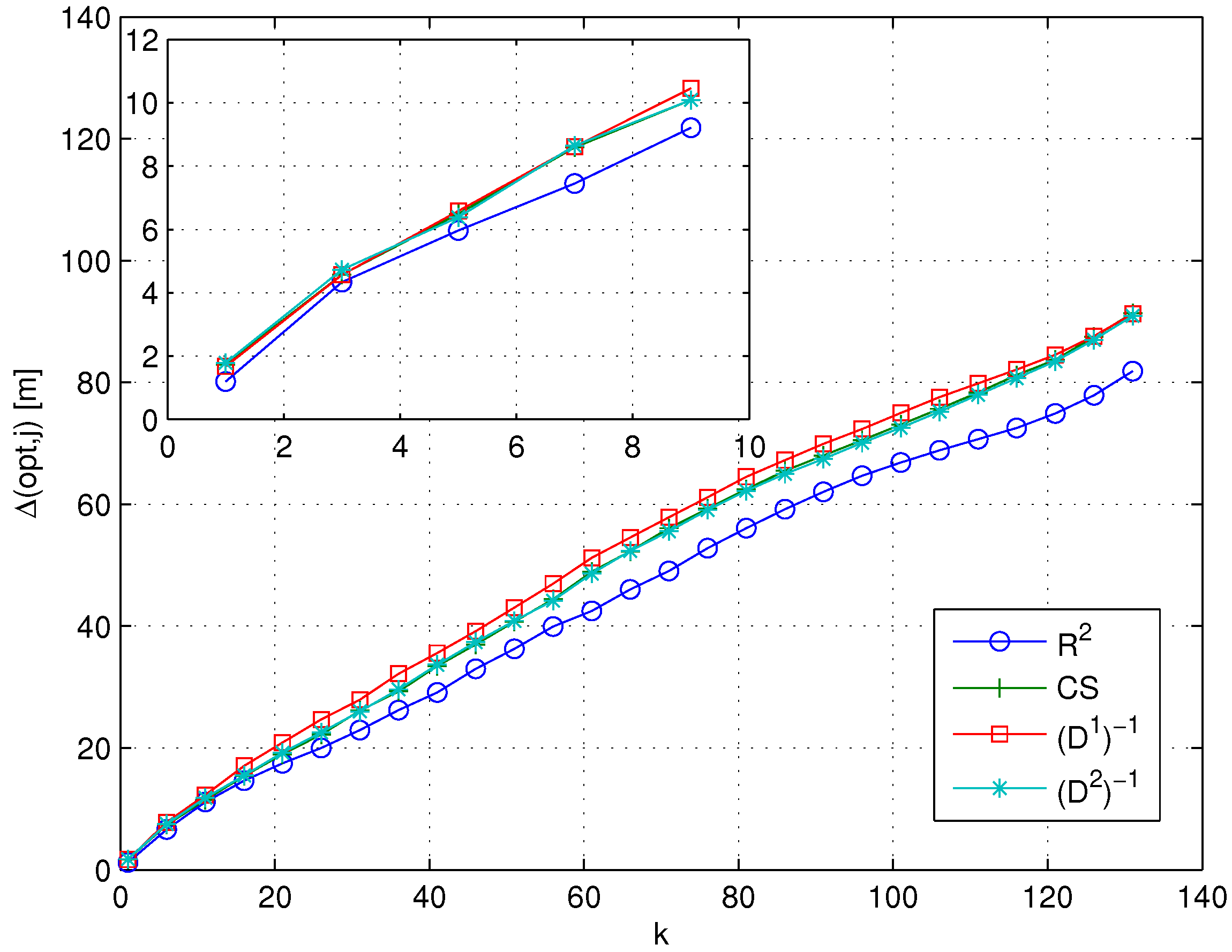
4. Experimental Results and Discussion
4.1. Testbed Implementation and Performance Indicators
4.2. Flat Algorithms
- Ideal sorting/ideal weighting (ISIW): This case corresponds to an ideal upper bound benchmark where the spatial distances between each TP and the RPs are assumed to be known and then used for both RP sorting and weighting.
- Ideal sorting/real weighting (ISRW): In this case, the spatial distances between each TP and the RPs are assumed to be known and used during the RP sorting phase. However, once the RPs are sorted, different RSS-based metrics are evaluated as RP weights, in order to isolate the impact of RSS-based metrics on the weighting phase.
- Real sorting/real weighting (RSRW): This case represents the only feasible use case, where the spatial distances between each TP and the RPs are unknown. In this case, RSS-based metrics are evaluated and then used in both RP sorting and weighting phases.
4.3. Affinity Propagation-Based Algorithms
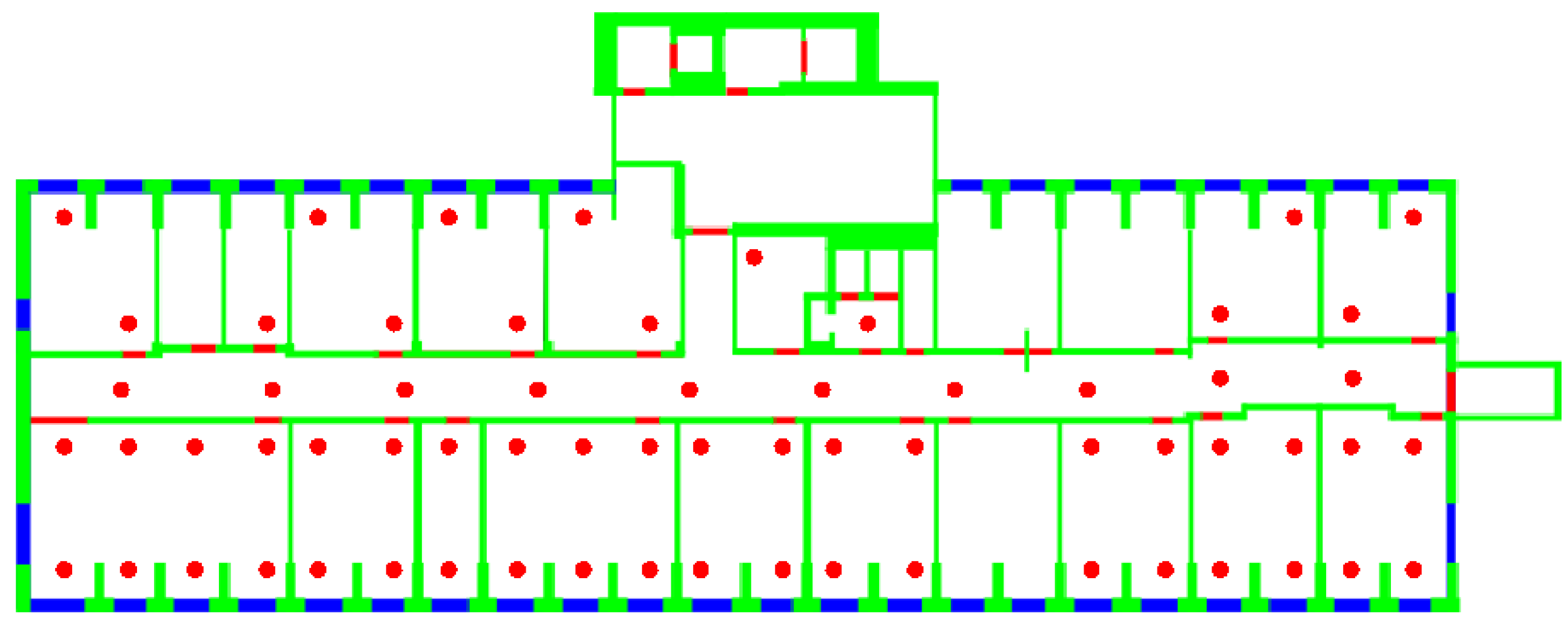
4.3.1. Topology
- Clustering was performed separately for the two floors composing the testbed, assuming the knowledge of the floor for each RP.
- With reference to the degeneracy issue identified in Section 2.3.1, the solution proposed in [13] of adding random noise to similarity values was not implemented, since different similarities are characterized by significantly different ranges of values, making it impossible to add noise with the same power to all similarity metrics.
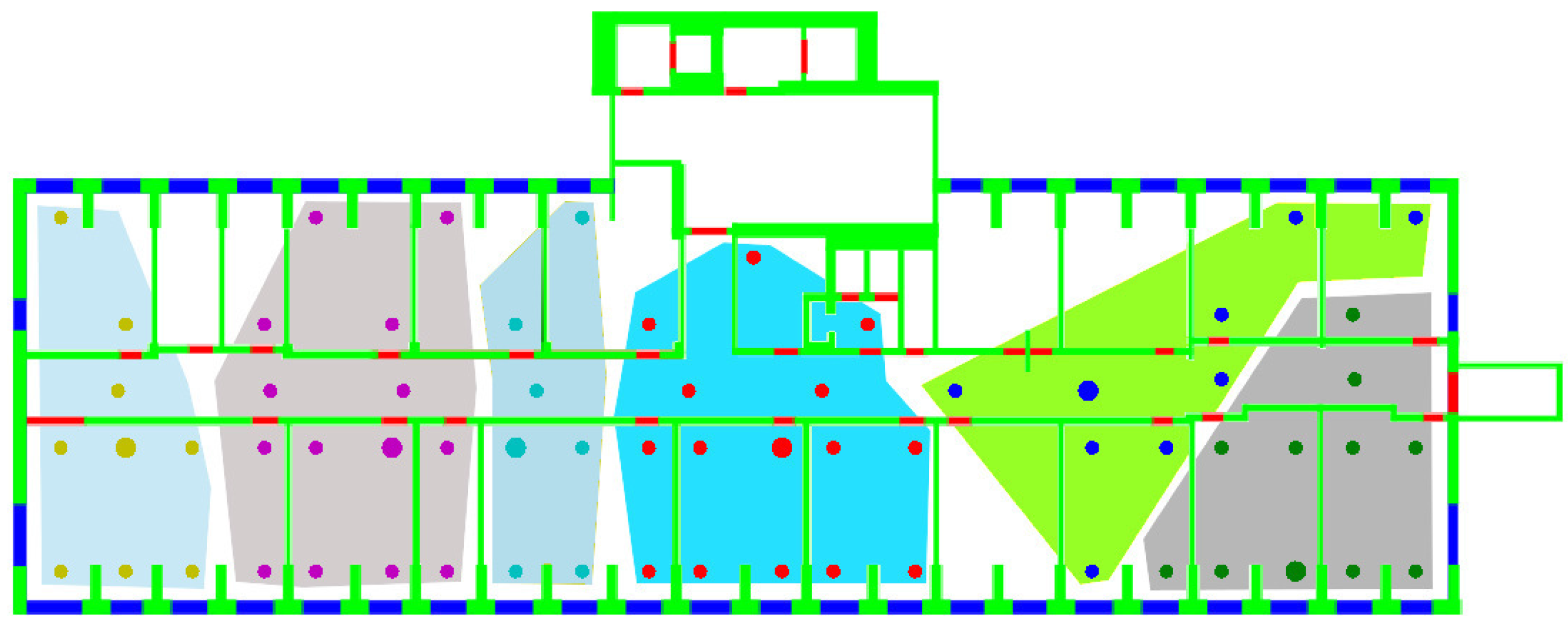
- On the other hand, the outlier issue, also identified in Section 2.3.1, was addressed by actually implementing the solution proposed in [12] to eliminate such outliers. This leads in all cases to clusters occupying convex regions on each floor. Figure 6 shows as an example the clusters obtained on the DIET first floor, using the gen metric.
| Metric | |||||
|---|---|---|---|---|---|
| 37 | 3.62 | 6 | 2 | 1.07 | |
| gen | 13 | 10.31 | 15 | 5 | 9.06 |
| 13 | 10.31 | 19 | 4 | 27.73 | |
| -value | 43 | 3.11 | 6 | 2 | 1.10 |
| 13 | 10.31 | 15 | 5 | 7.90 | |
| 29 | 4.62 | 8 | 2 | 3.17 | |
| 27 | 4.96 | 8 | 2 | 4.19 | |
| 34 | 3.94 | 7 | 2 | 2.54 | |
| 20 | 67 | 69 | 2 | 216.01 |
- The first group including gen, and metrics, leading to the creation of relatively few, large clusters, although with different variances.
- The second group, including , -value, , and metrics, leading to small clusters with low variances. -value in particular leads to the largest number of clusters with the lowest variance among all metrics.
4.3.2. Positioning Accuracy: A Backward Approach
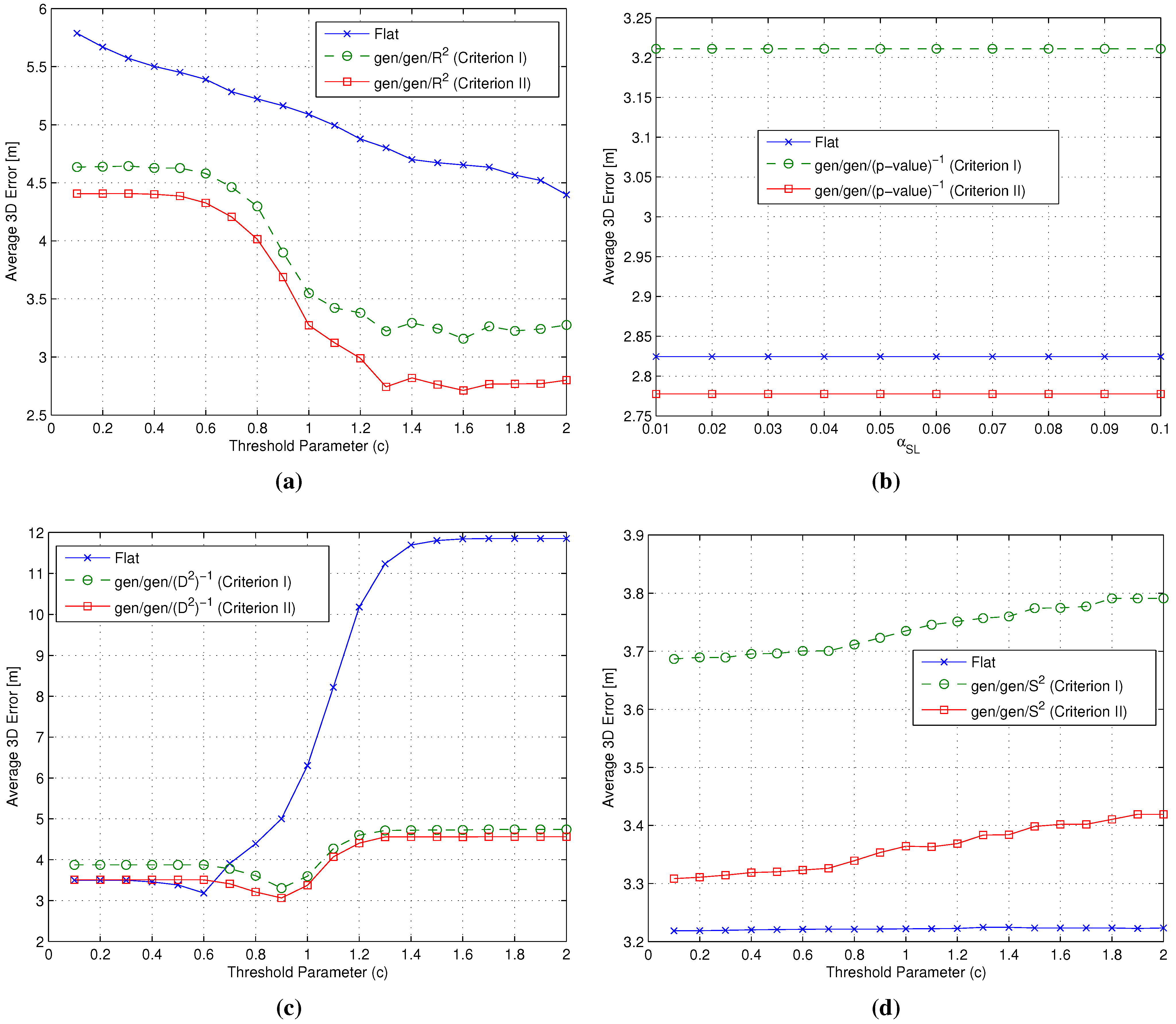
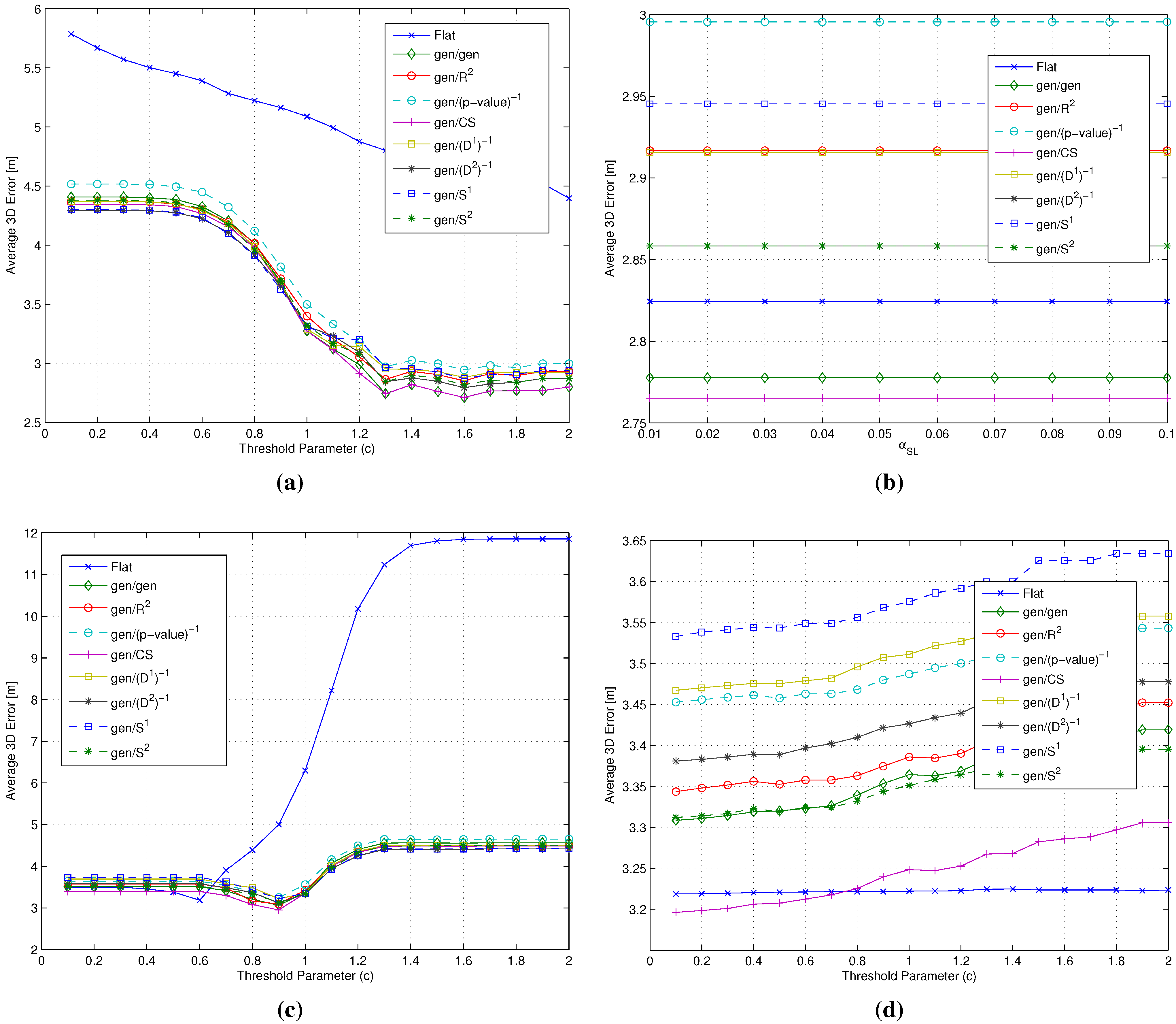
- Cluster matching criterion selection: The first step in the backward approach was the selection of one of the cluster matching criteria introduced in Section 2.3.2 in order to focus on a single criterion in the following steps of the analysis. In order to do so, both and were set equal to the gen metric, while the four metrics characterized by the smallest , already considered in the analysis of flat algorithms (see Section 3.3 and Section 4.2), were adopted as the metric, in order to identify which of the two criteria performs better under different conditions.
- selection: Having selected the best cluster matching criterion, the second step focused on the analysis and possibly the selection of the best metrics to be used during both coarse and fine localization steps. To do so, the metric was kept set to the gen metric, while and metrics were allowed to change. In particular, all of the RSS-based metrics introduced in Section 3.2 were considered as candidates for the role of the metric, while, based on the analysis already carried out in Section 3.3 and Section 4.2, candidates for the role of the metric were restricted to the four metrics with the smallest . Based on the positioning errors achieved by the different gen/ combinations, this phase concluded with a joint and selection.
- selection: The last step was the analysis of the impact of different metrics on the RP clustering step, aiming at the selection of the best one. In this case, all metrics defined in both Section 3.1 and Section 3.2 were eligible for the role of the metric, while keeping both and set to the metrics selected as a result of the selection step.
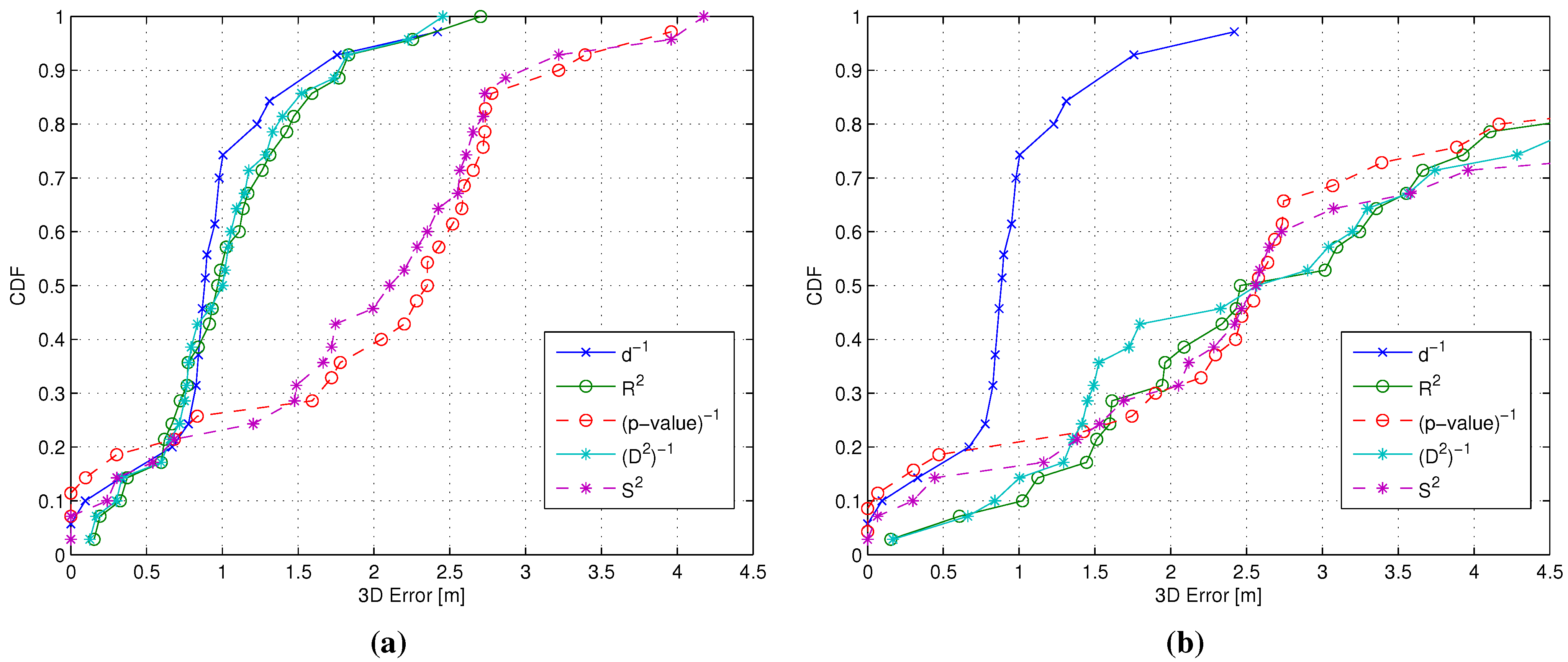
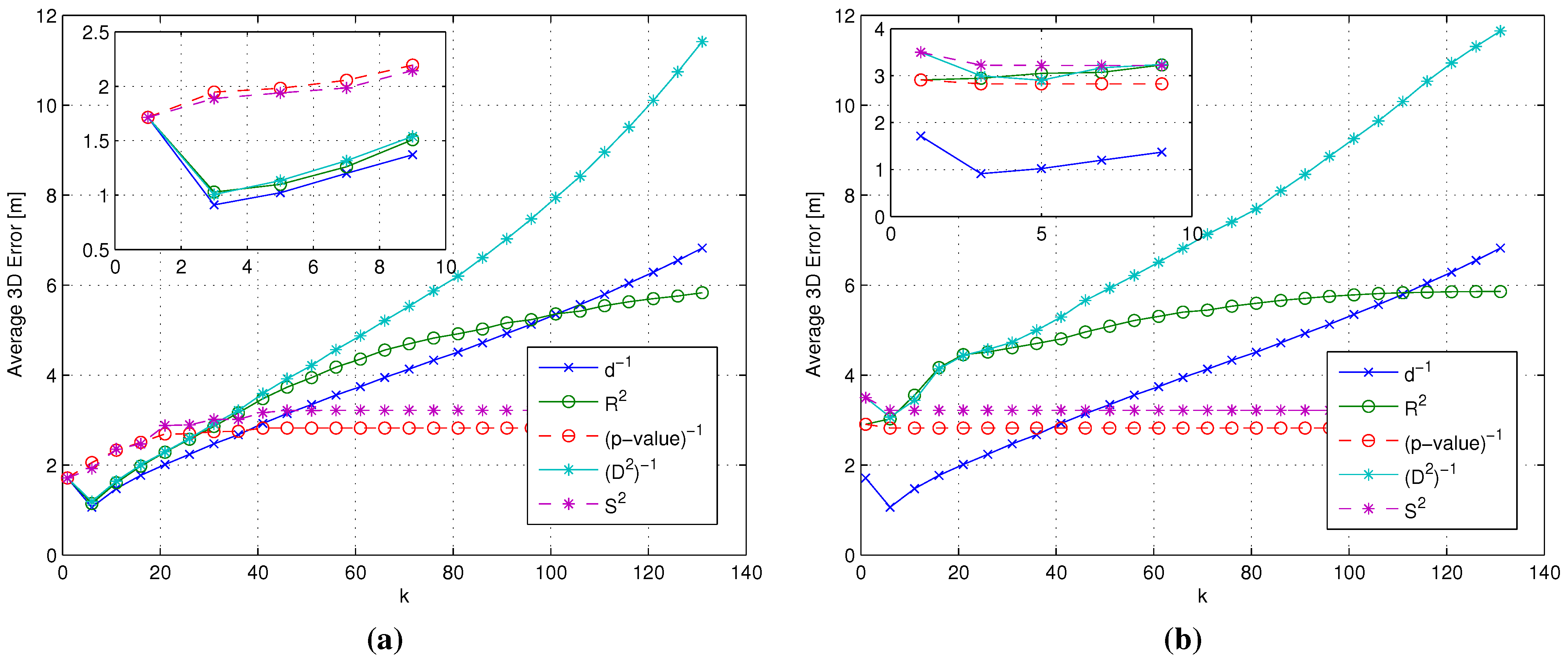
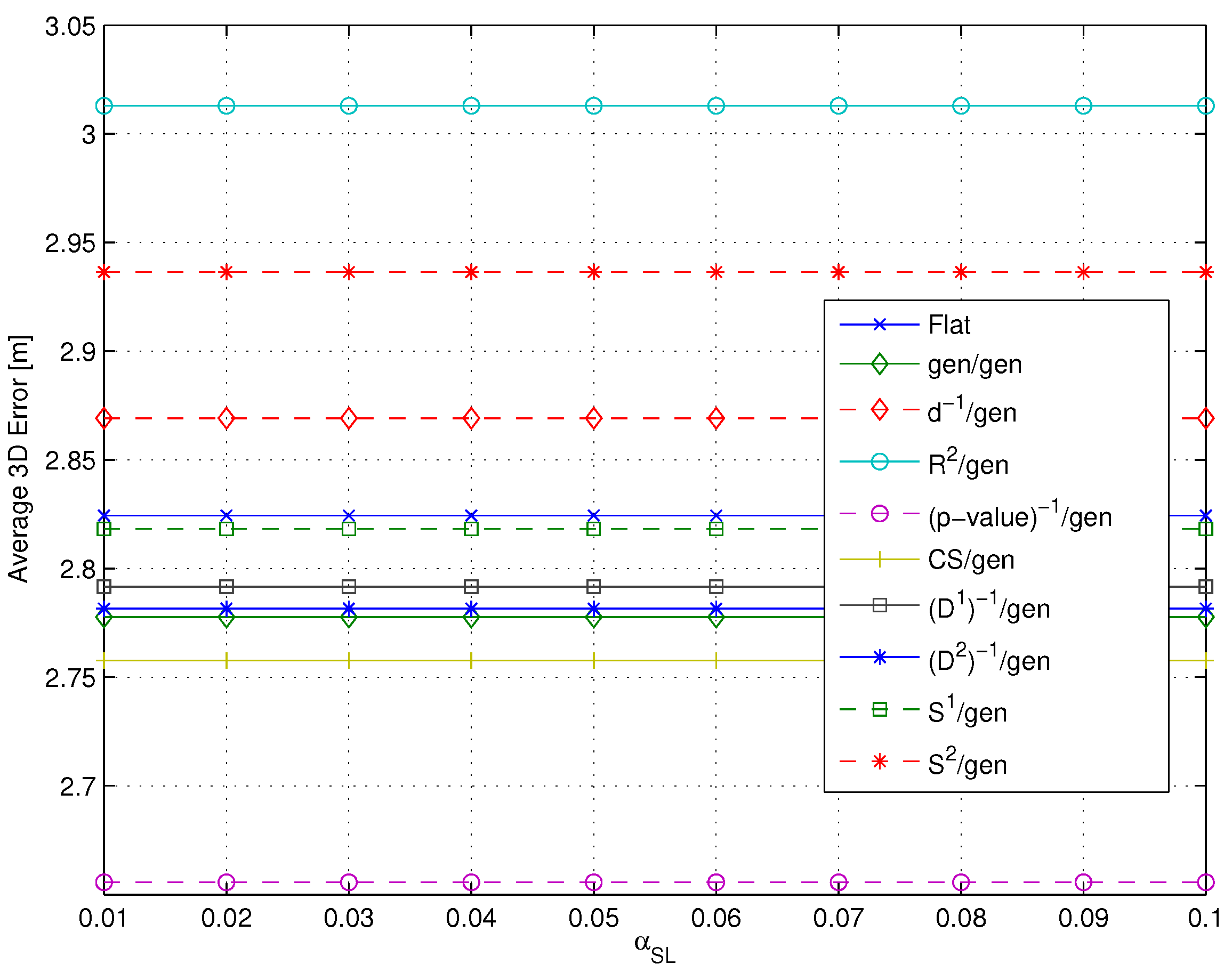
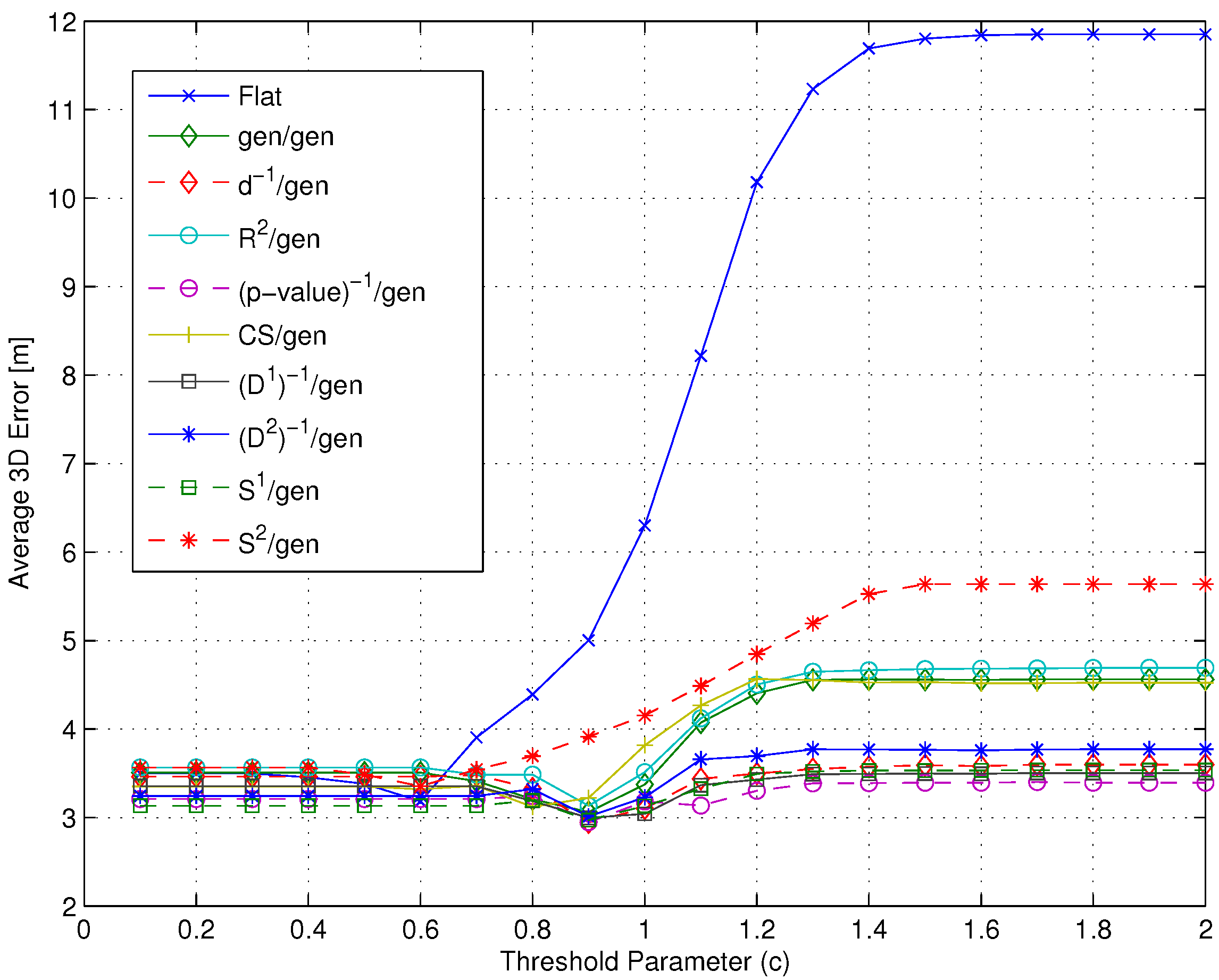
- Impact of the metric: The use of different metrics significantly affects the positioning accuracy. Among all metrics, -value emerged as the best candidate to play the role of , since at the same time, it minimizes the impact of the RP selection threshold and the positioning error, with a value around m below any other metric.
- Impact of the metric: Different metrics have a negligible effect on the positioning accuracy, with a difference in the evaluated average errors in a range of about twenty centimeters. The substantial independence of the performance from the selected metric is confirmed by Figure 9, showing the impact of metrics on the value of (defined in Section 4.1 as the average number of RPs within the clusters selected after the coarse localization step).
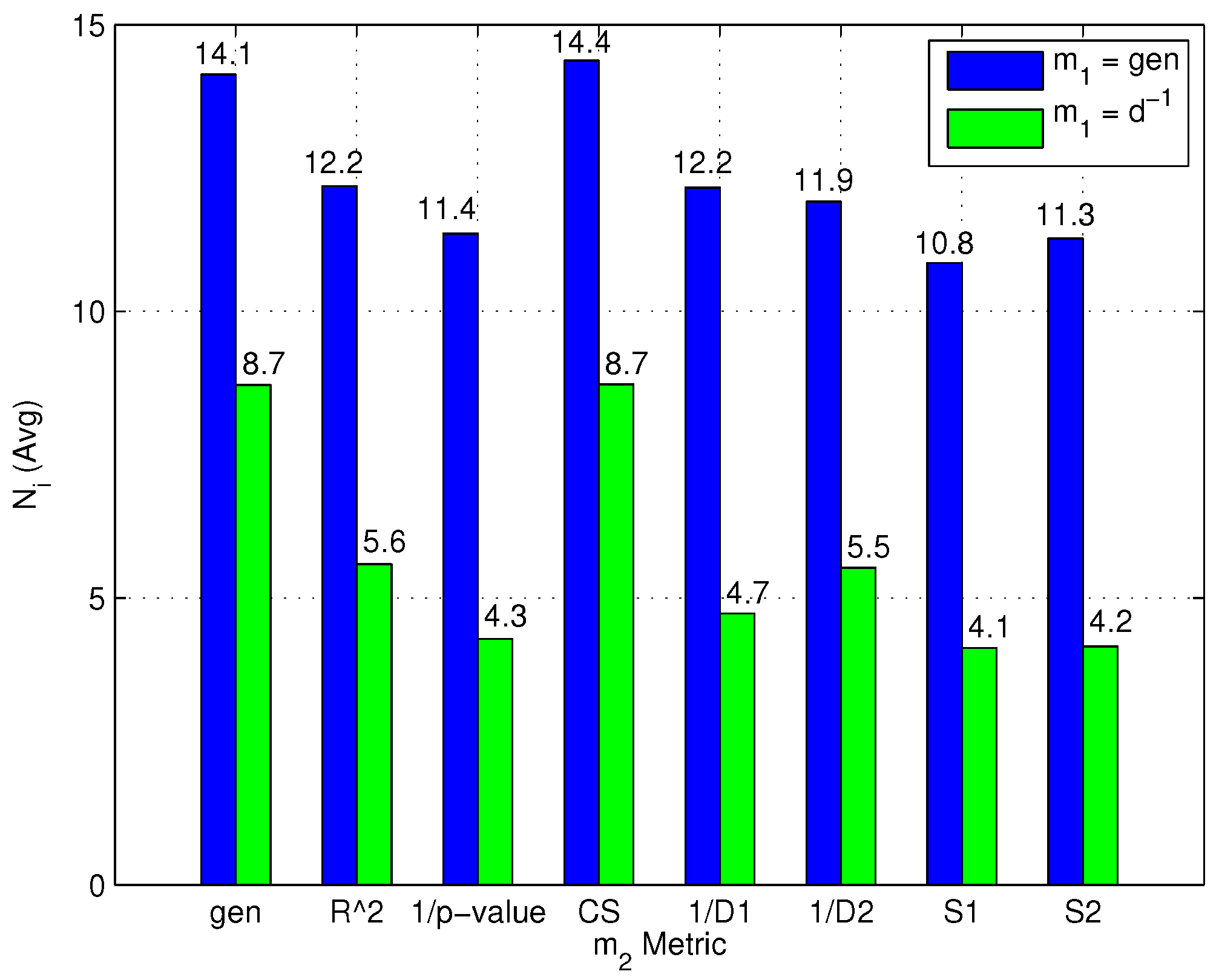
- Figure 11 shows that if a metric different from -value, characterized by a lower selectivity, is selected, the impact of can be significantly larger, especially when many RPs are selected.
4.3.3. Computational Complexity
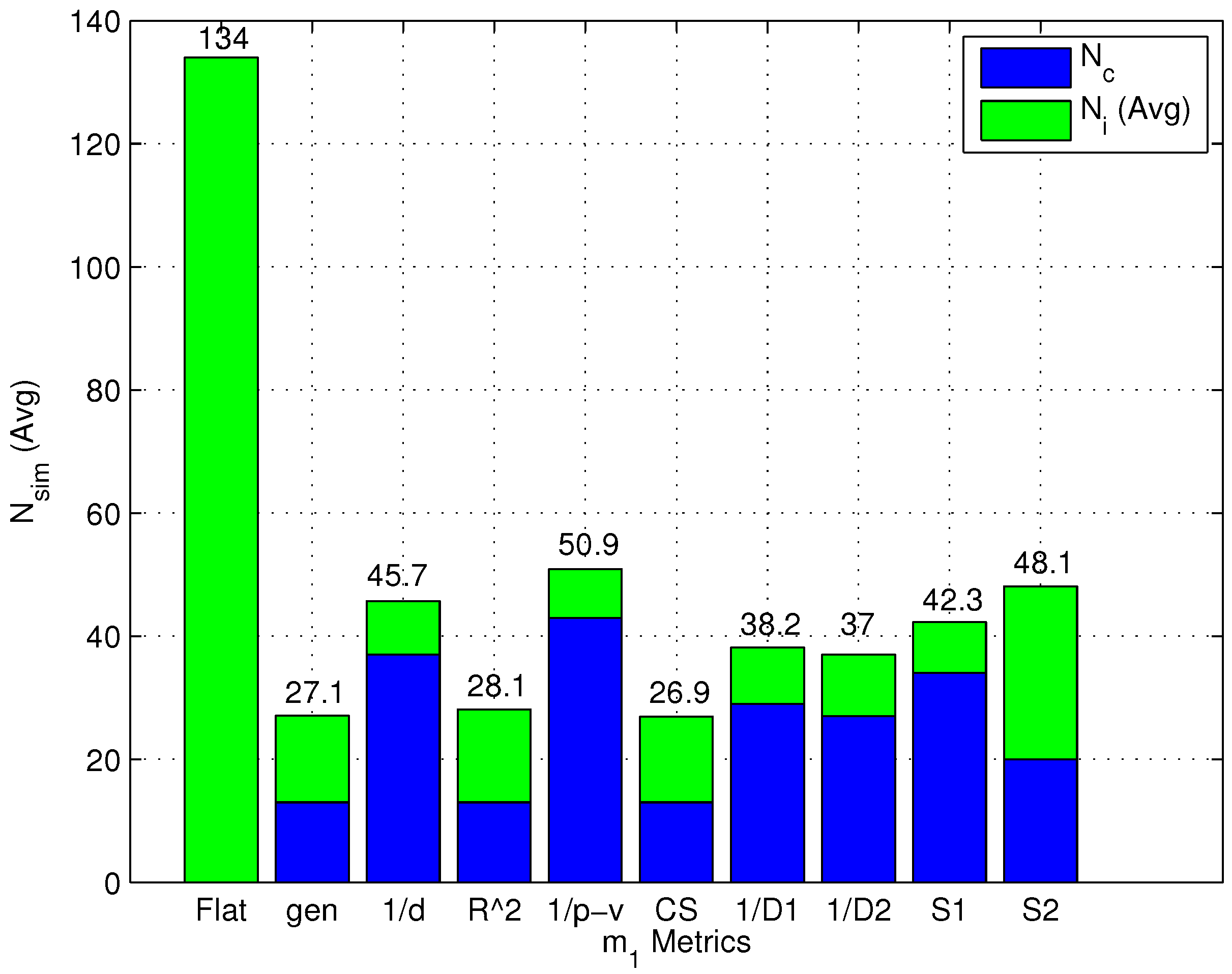
- As expected, the number of computed similarity values is always equal to N for a flat algorithm.
- Two-step algorithms significantly reduce the average computational complexity of the online phase. Moreover, metrics can be divided into two different groups: (1) metrics that minimize the number of formed clusters and conversely maximize the number of RPs selected after the coarse localization step; and (2) metrics that maximize the number of formed clusters and conversely minimize the number of RPs remaining after the coarse localization step.
- The first group of metrics shows a value slightly lower than the second group. in particular obtained the lowest computational complexity; at the same time, both groups show a value significantly lower than the flat algorithm.
- As a final note, it can be observed that the -value metric, which minimizes positioning error as found in Section 4.3.2, is not the metric minimizing .
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yuan, S.; Win, M.Z. Fundamental Limits of Wideband Localization—Part I: A General Framework. IEEE Trans. Inf. Theory 2010, 56, 4956–4980. [Google Scholar] [CrossRef]
- Liu, H.; Darabi, H.; Banerjee, P.; Jing, L. Survey of Wireless Indoor Positioning Techniques and Systems. IEEE Trans. Syst. Man Cybern. C Appl. Rev. 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- Honkavirta, V.; Perälä, T.; Ali-Löytty, S.; Piché, R. Comparative Survey of WLAN Location Fingerprinting Methods. In Proceedings of the Workshop on Positioning, Navigation and Communication (WPNC’09), Hannover, Germany, 19 March 2009; pp. 243–251.
- Bahl, P.; Padmanabhan, V.N. RADAR: An in-building RF-based user location and tracking system. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM’00), Tel Aviv, Israel, 26–30 March 2000; pp. 775–784.
- Shin, B.; Lee, J.H.; Lee, T.; Kim, H.S. Enhanced weighted K-nearest neighbor algorithm for indoor WiFi positioning systems. In Proceedings of the International Conference on Computing Technology and Information Management (ICCM’12), Seoul, Korea, 24–26 April 2012; pp. 574–577.
- Yu, F.; Jiang, M.; Liang, J.; Qin, X.; Hu, M.; Peng, T.; Hu, X. 5G WiFi Signal-Based Indoor Localization System Using Cluster k-Nearest Neighbor Algorithm. Int. J. Distrib. Sens. Netw. 2014, 2014. [Google Scholar] [CrossRef]
- Li, B.; Salter, J.; Dempster, A.G.; Rizos, C. Indoor Positioning Techniques Based on Wireless LAN; Technical Report; School of Surveying and Spatial Information Systems, UNSW: Sydney, Australia, 2006. [Google Scholar]
- Roos, T.; Myllymäki, P.; Tirri, H.; Misikangas, P.; Sievänen, J. A Probabilistic Approach to WLAN User Location Estimation. Int. J. Wirel. Inform. Netw. 2002, 9, 155–164. [Google Scholar] [CrossRef]
- Youssef, M.; Agrawala, A.; Udaya Shankar, A. WLAN location determination via clustering and probability distributions. In Proceedings of the IEEE International Conference on Pervasive Computing and Communications (PerCom’03), Dallas-Fort Worth, TX, USA, 23–26 March 2003; pp. 143–151.
- Youssef, M.; Agrawala, A. Handling samples correlation in the Horus system. In Proceedings of the IEEE International Conference on Computer Communications (INFOCOM’04), Hong Kong, China, 7–11 March 2004; pp. 1023–1031.
- Le Dortz, N.; Gain, F.; Zetterberg, P. WiFi fingerprint indoor positioning system using probability distribution comparison. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP’12), Kyoto, Japan, 25–30 March 2012; pp. 2301–2304.
- Feng, C.; Au, W.S.A.; Valaee, S.; Tan, Z. Received-Signal-Strength-Based Indoor Positioning Using Compressive Sensing. IEEE Trans. Mobile Comput. 2012, 11, 1983–1993. [Google Scholar] [CrossRef]
- Frey, B.J.; Dueck, D. Clustering by Passing Messages Between Data Points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef] [PubMed]
- Tian, Z.; Tang, X.; Zhou, M.; Tan, Z. Fingerprint indoor positioning algorithm based on affinity propagation clustering. EURASIP J. Wirel. Commun. 2013, 2013. [Google Scholar] [CrossRef]
- Ding, G.; Tan, Z.; Zhang, J.; Zhang, L. Fingerprinting localization based on affinity propagation clustering and artificial neural networks. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC’13), Shanghai, China, 7–10 April 2013; pp. 2317–2322.
- Hu, X.; Shang, J.; Gu, F.; Han, Q. Improving Wi-Fi Indoor Positioning via AP Sets Similarity and Semi-Supervised Affinity Propagation Clustering. Int. J. Distrib. Sens. Netw. 2015, 2015. [Google Scholar] [CrossRef]
- Torres-Sospedra, J.; Montoliu, R.; Trilles, S.; Belmonte, Ó.; Huerta, J. Comprehensive analysis of distance and similarity measures for Wi-Fi fingerprinting indoor positioning systems. Expert Syst. Appl. 2015, 42, 9263–9278. [Google Scholar] [CrossRef]
- Caso, G.; de Nardis, L.; di Benedetto, M.-G. Frequentist Inference for WiFi Fingerprinting 3D Indoor Positioning. In Proceedings of the International Conference on Communications (ICC’15), Workshop on Advances in Network Localization and Navigation (ANLN’15), London, UK, 8–12 June 2015.
- Philipp, M.; Kessel, M.; Werner, M. Dynamic nearest neighbors and online error estimation for SMARTPOS. Int. J. Adv. Internet Tech. 2013, 6, 1–11. [Google Scholar]
- Salton, G.; McGill, M.J. Introduction to Modern Information Retrieval; McGrw-Hill, Inc.: New York, NY, USA, 1986. [Google Scholar]
- Ali, S.F.M.; Hassan, R. Local Positioning System Performance Evaluation with Cosine Correlation Similarity Measure. In Proceedings of the International Conference on Bio-Inspired Computing: Theories and Applications (BIC-TA’11), Penang, Malaysia, 27–29 September 2011; pp. 151–156.
- Luo, Y.; Hoeber, O.; Chen, Y. Enhancing Wi-Fi fingerprinting for indoor positioning using human-centric collaborative feedback. Hum. Cent. Comput. Inf. Sci. 2013, 3. [Google Scholar] [CrossRef]
- He, S.; Chan, S.-H.G. Sectjunction: Wi-Fi indoor localization based on junction of signal sectors. In Proceedings of the IEEE International Conference on Communications (ICC’14), Sydney, Australia, 10–14 June 2014; pp. 2605–2610.
- Egghe, L.; Leydesdorff, L. The relation between Pearson’s correlation coefficient r and Salton’s cosine measure. J. Assoc. Inf. Sci. Technol. 2009, 60, 1027–1036. [Google Scholar] [CrossRef]
- Stigler, S.M. Francis Galton’s account of the invention of correlation. Stat. Sci. 1989, 4, 73–79. [Google Scholar] [CrossRef]
- Fisher, R.A. Frequency distribution of the values of the correlation coefficient in samples from an indefinitely large population. Biometrika 1915, 10, 507–521. [Google Scholar] [CrossRef]
- Tsui, A.W.; Chuang, Y.-H.; Chu, H.-H. Unsupervised learning for solving RSS hardware variance problem in WiFi localization. Mob. Net. Appl. 2009, 14, 677–691. [Google Scholar] [CrossRef]
- Popleteev, A.; Osmani, V.; Mayora, O. Investigation of indoor localization with ambient FM radio stations. In Proceedings of the IEEE International Conference on Pervasive Computing and Communications (PerCom’12), Lugano, Switzerland, 19–23 March 2012; pp. 171–179.
- Neyman, J.; Pearson, E.S. On the problems of the most efficient tests of statistical hypotheses. Philos. Trans. R. Soc. Lond. A 1933, 231, 289–337. [Google Scholar] [CrossRef]
- Ashby, F.G.; Perrin, N.A. Toward a unified theory of similarity and recognition. Psychol. Rev. 1988, 95, 124–150. [Google Scholar] [CrossRef]
- Shepard, R.N. The analysis of proximities: Multidimensional scaling with an unknown distance function. Psychometrika 1962, 27, 125–140. [Google Scholar] [CrossRef]
- Young, F.W.; Hamer, R.M. Theory and Applications of Multidimensional Scaling; Erlbaum: Hillsdale, NJ, USA, 1994. [Google Scholar]
- Shepard, R.N. Toward a universal law of generalization for psychological science. Science 1987, 237, 1317–1323. [Google Scholar] [CrossRef] [PubMed]
- Caso, G.; de Nardis, L. On the applicability of Multi-Wall Multi-Floor propagation models to WiFi Fingerprinting Indoor Positioning. In Proceedings of the EAI International Conference on Future access enablers of ubiquitous and intelligent infrastructures (Fabulous’15), Ohrid, Republic of Macedonia, 23–25 September 2015.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caso, G.; De Nardis, L.; Di Benedetto, M.-G. A Mixed Approach to Similarity Metric Selection in Affinity Propagation-Based WiFi Fingerprinting Indoor Positioning. Sensors 2015, 15, 27692-27720. https://doi.org/10.3390/s151127692
Caso G, De Nardis L, Di Benedetto M-G. A Mixed Approach to Similarity Metric Selection in Affinity Propagation-Based WiFi Fingerprinting Indoor Positioning. Sensors. 2015; 15(11):27692-27720. https://doi.org/10.3390/s151127692
Chicago/Turabian StyleCaso, Giuseppe, Luca De Nardis, and Maria-Gabriella Di Benedetto. 2015. "A Mixed Approach to Similarity Metric Selection in Affinity Propagation-Based WiFi Fingerprinting Indoor Positioning" Sensors 15, no. 11: 27692-27720. https://doi.org/10.3390/s151127692
APA StyleCaso, G., De Nardis, L., & Di Benedetto, M.-G. (2015). A Mixed Approach to Similarity Metric Selection in Affinity Propagation-Based WiFi Fingerprinting Indoor Positioning. Sensors, 15(11), 27692-27720. https://doi.org/10.3390/s151127692







