The Quasi-Biennial Vertical Oscillations at Global GPS Stations: Identification by Ensemble Empirical Mode Decomposition
Abstract
:1. Introduction
2. The Effectiveness of EEMD in Recovering Signal Components with Time-varying Amplitudes
2.1. Simulated Time Series with Components of Time-varying Amplitudes
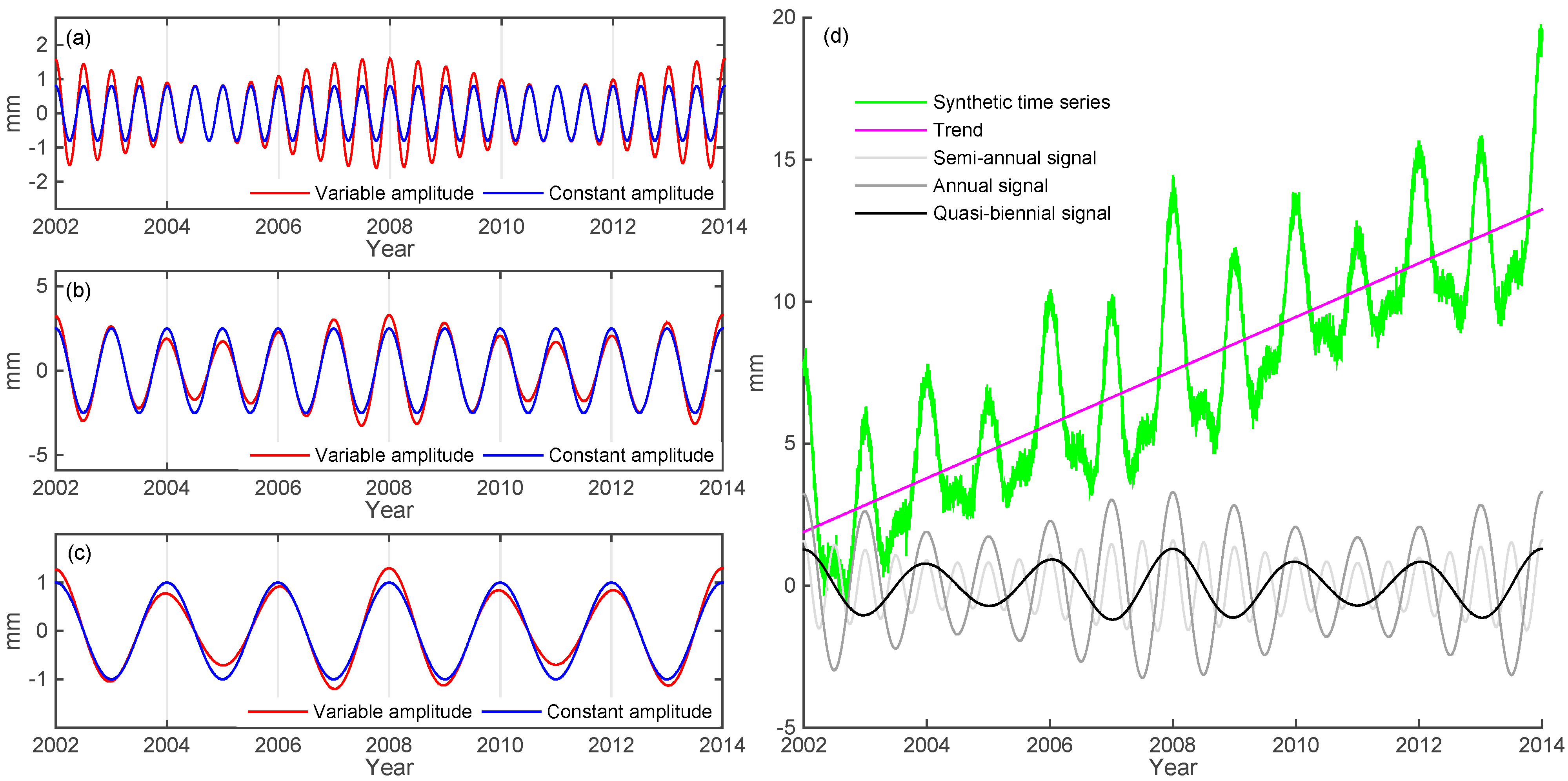
2.2. Recovering the Signal Components by EEMD
- Adding white noise sequence in the target time series;
- Decomposing the time series containing the white noises into IMFs;
- Repeating the above two steps, but with different white noise series each time;
- Taking the mean of many-times decomposed IMFs as the final result IMF.
3. GPS Data Processing Strategy for Optimized Coordinate Solutions
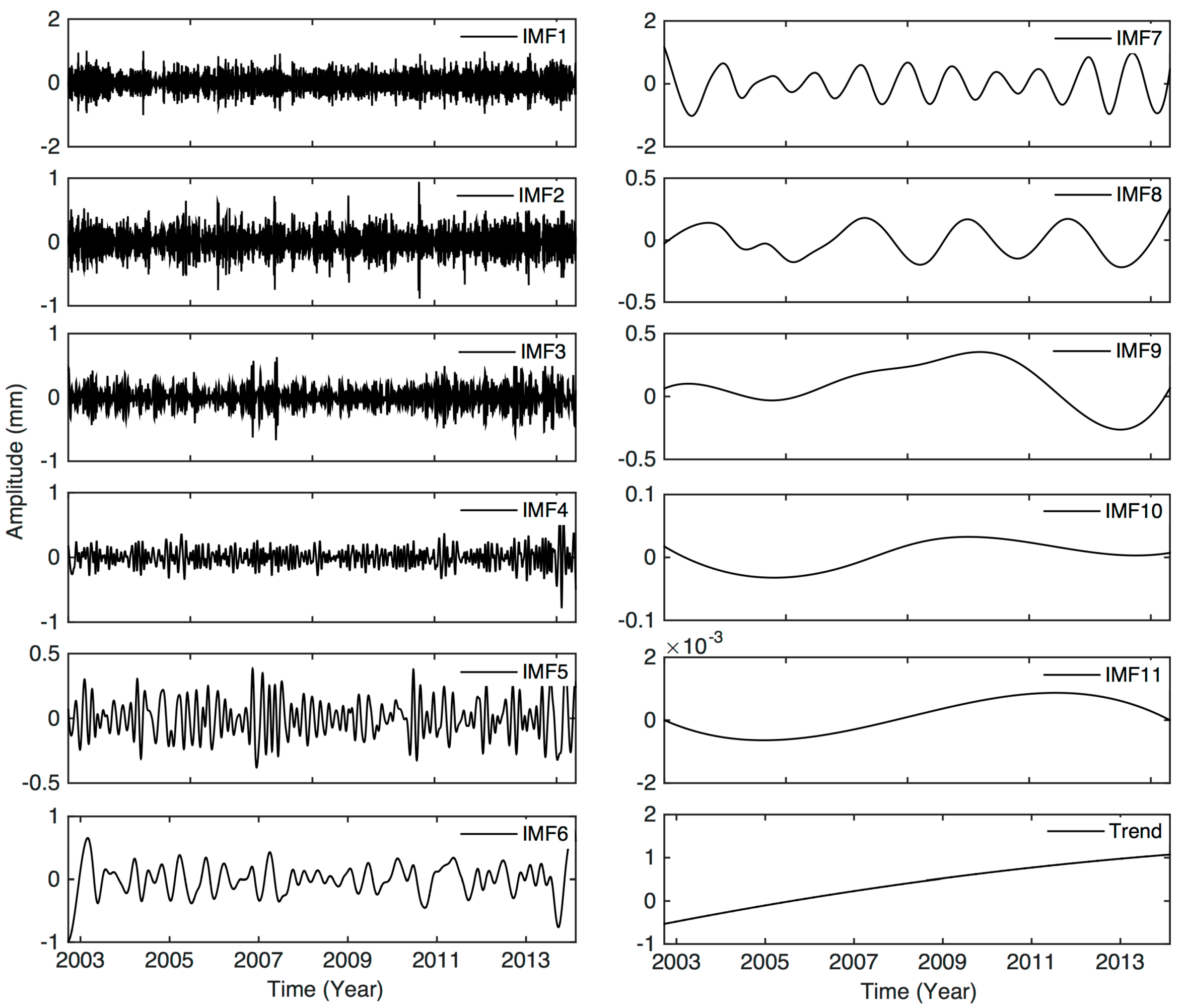
4. Results of Nonlinear Signal Identification by EEMD
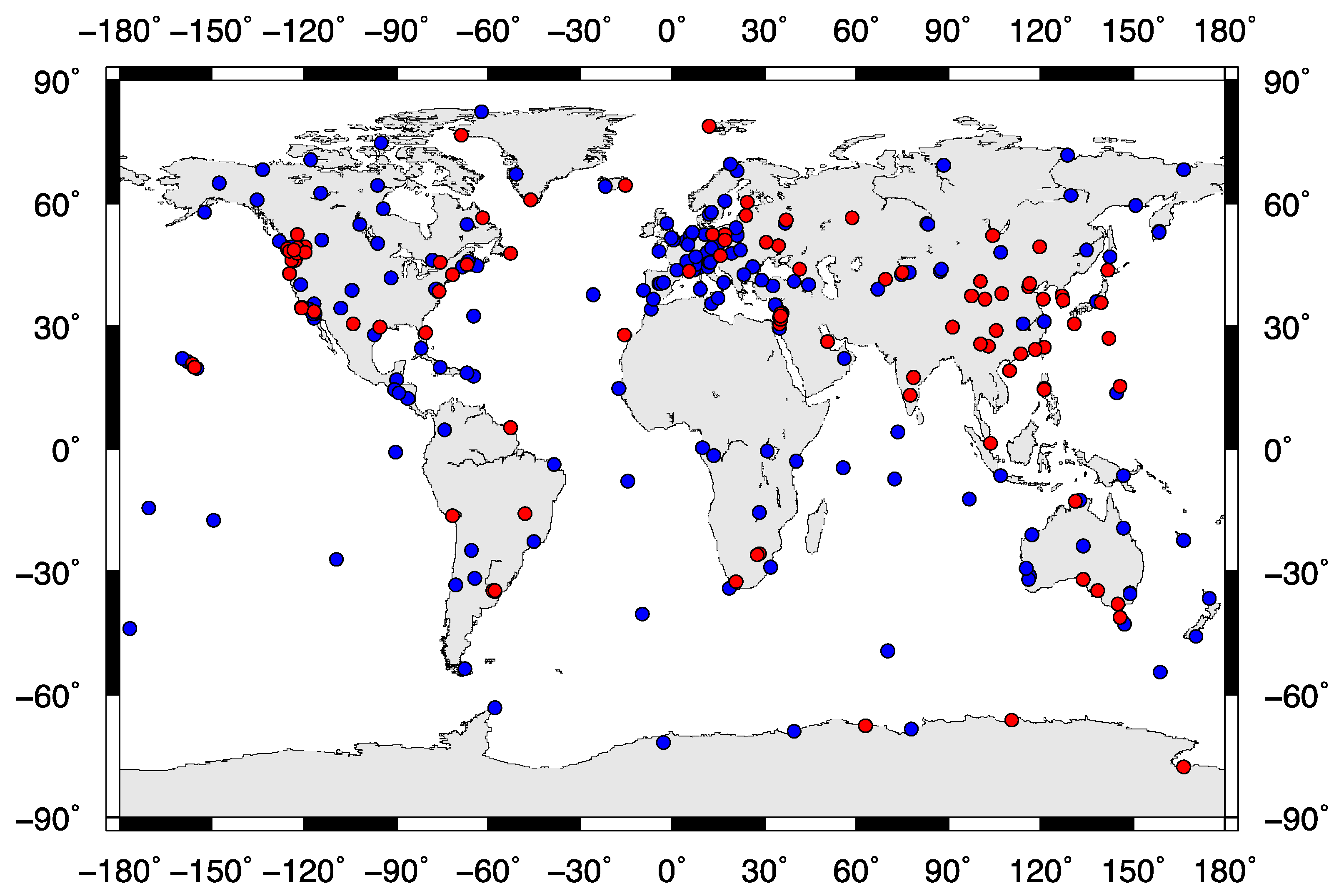
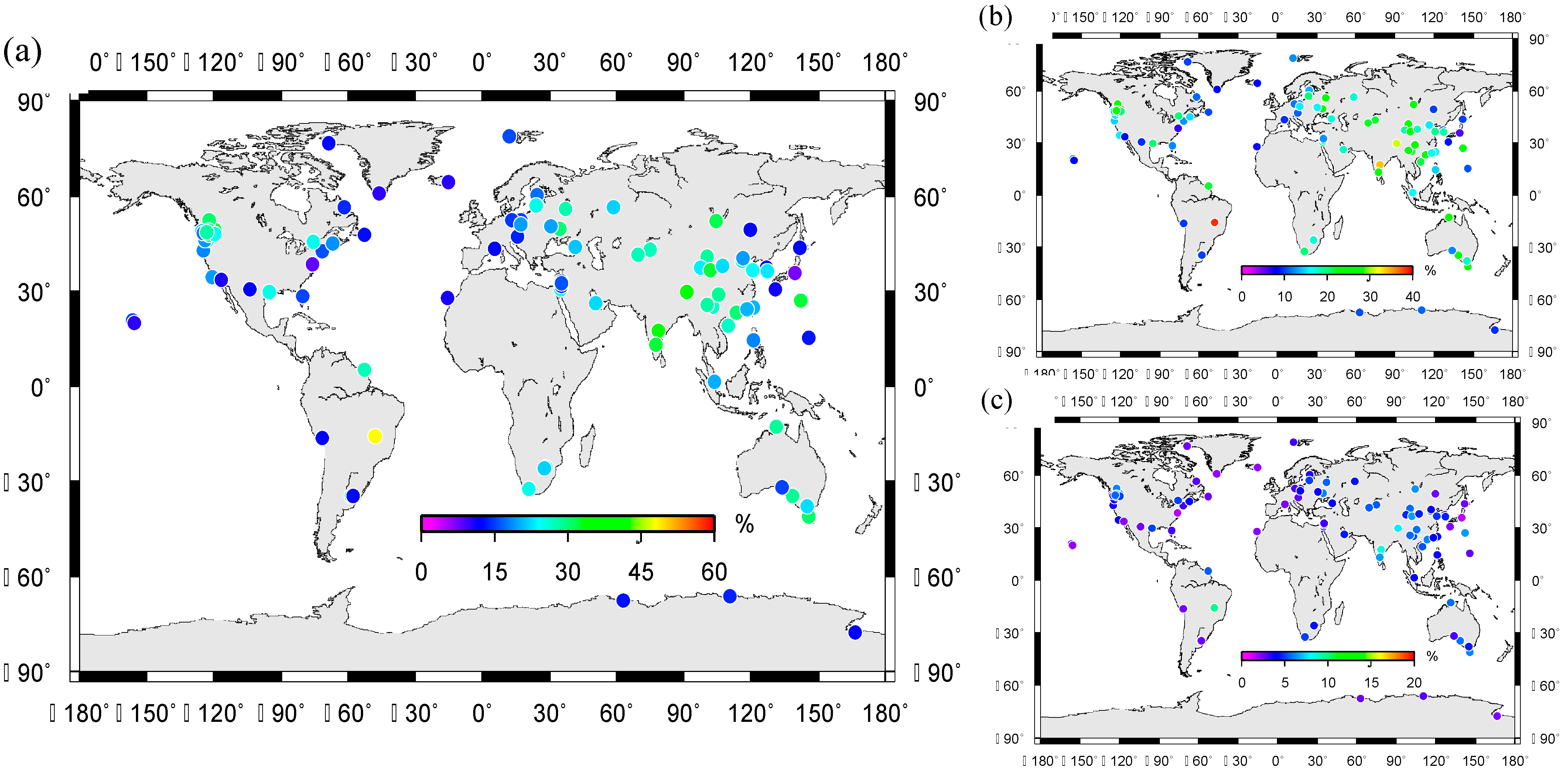
4.1. Global GPS Stations with the Quasi-Biennial Oscillation Signals
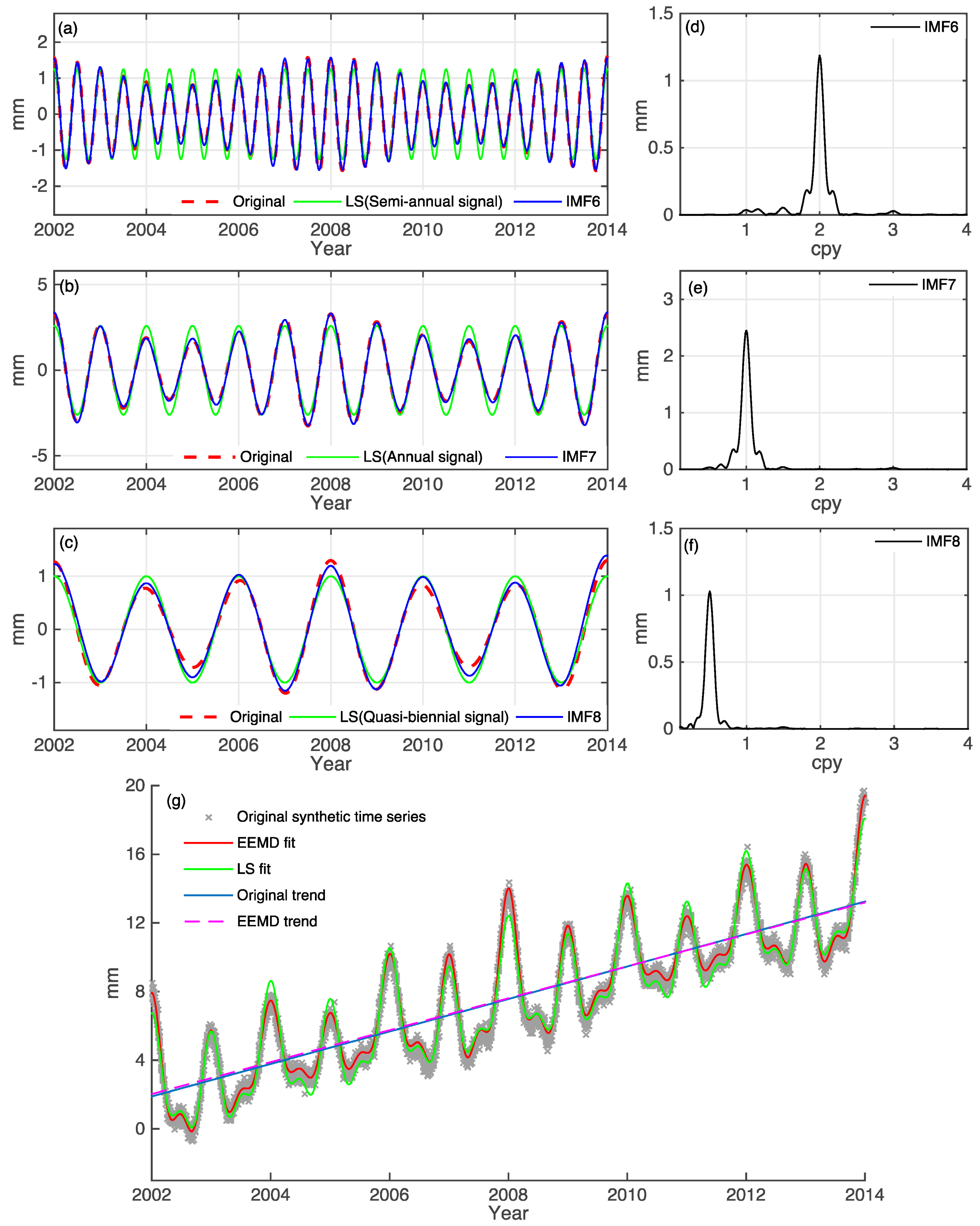
4.2. Extracting Nonlinear Signals by EEMD: Example at Lhasa and Kunming
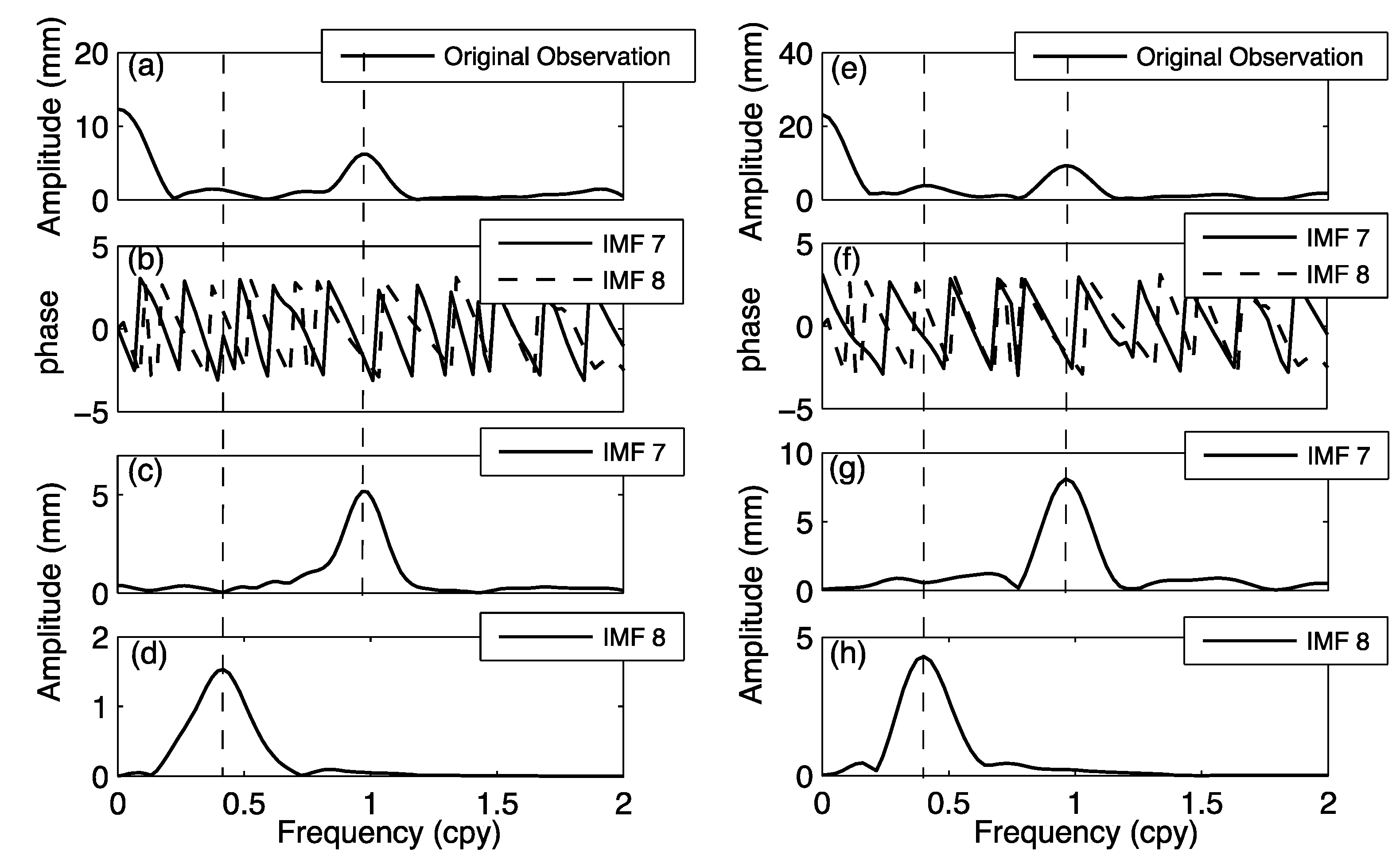
4.3. Comparison between Dominant Signals Recovered by EEMD and Least-Squares Fit
5. Discussion
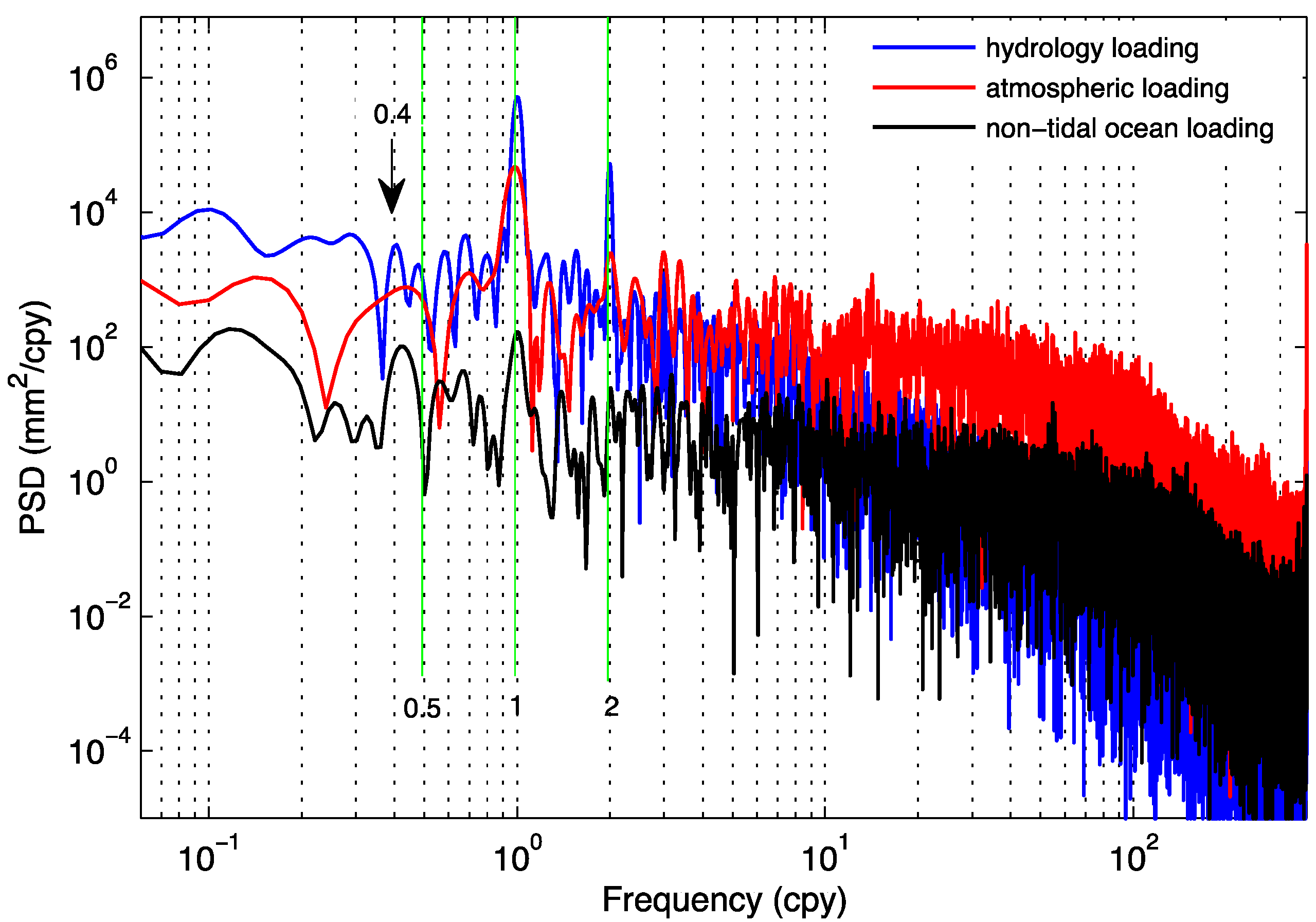
5.1. Mass Loading Contributions
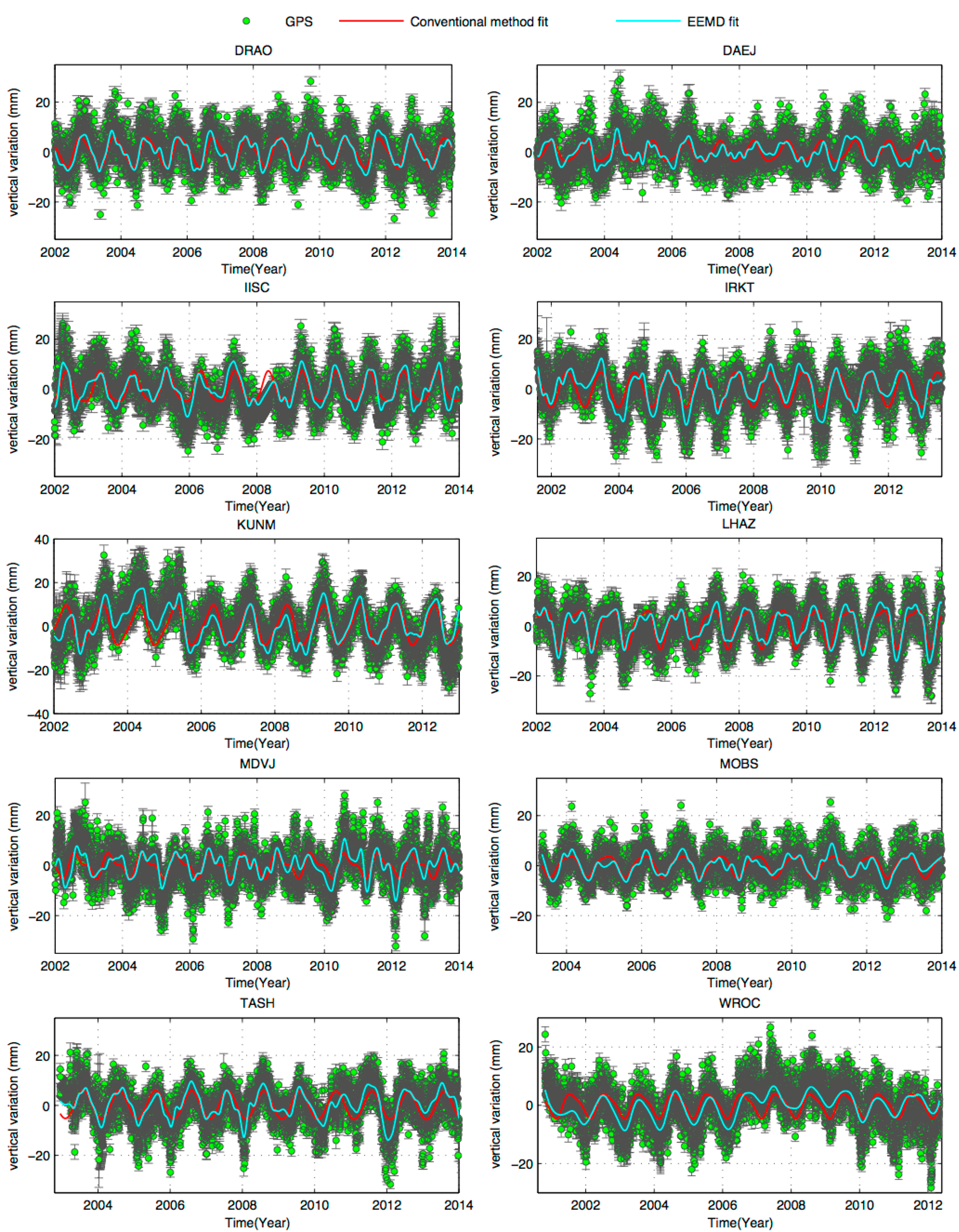
| Station | Latitude | Longitude | Frequency (cpy) | Amplitude (mm) |
|---|---|---|---|---|
| DRAO | −119.625 | 49.323 | 0.429 ± 0.015 | 0.87 ± 0.15 |
| DAEJ | 127.374 | 36.399 | 0.411 ± 0.013 | 1.46 ± 0.11 |
| IISC | 77.57 | 13.021 | 0.419 ± 0.015 | 1.97 ± 0.15 |
| IRKT | 104.316 | 52.219 | 0.468 ± 0.009 | 1.55 ± 0.13 |
| KUNM | 102.797 | 25.030 | 0.424 ± 0.019 | 4.30 ± 0.13 |
| LHAZ | 91.104 | 29.657 | 0.417 ± 0.019 | 1.53 ± 0.11 |
| MDVJ | 37.214 | 56.021 | 0.458 ± 0.019 | 1.63 ± 0.17 |
| MOBS | 144.975 | −37.829 | 0.429 ± 0.015 | 0.52 ± 0.11 |
| TASH | 75.23 | 37.77 | 0.421 ± 0.01 | 2.38 ± 0.14 |
| MROC | 17.062 | 51.113 | 0.439 ± 0.012 | 1.59 ± 0.13 |
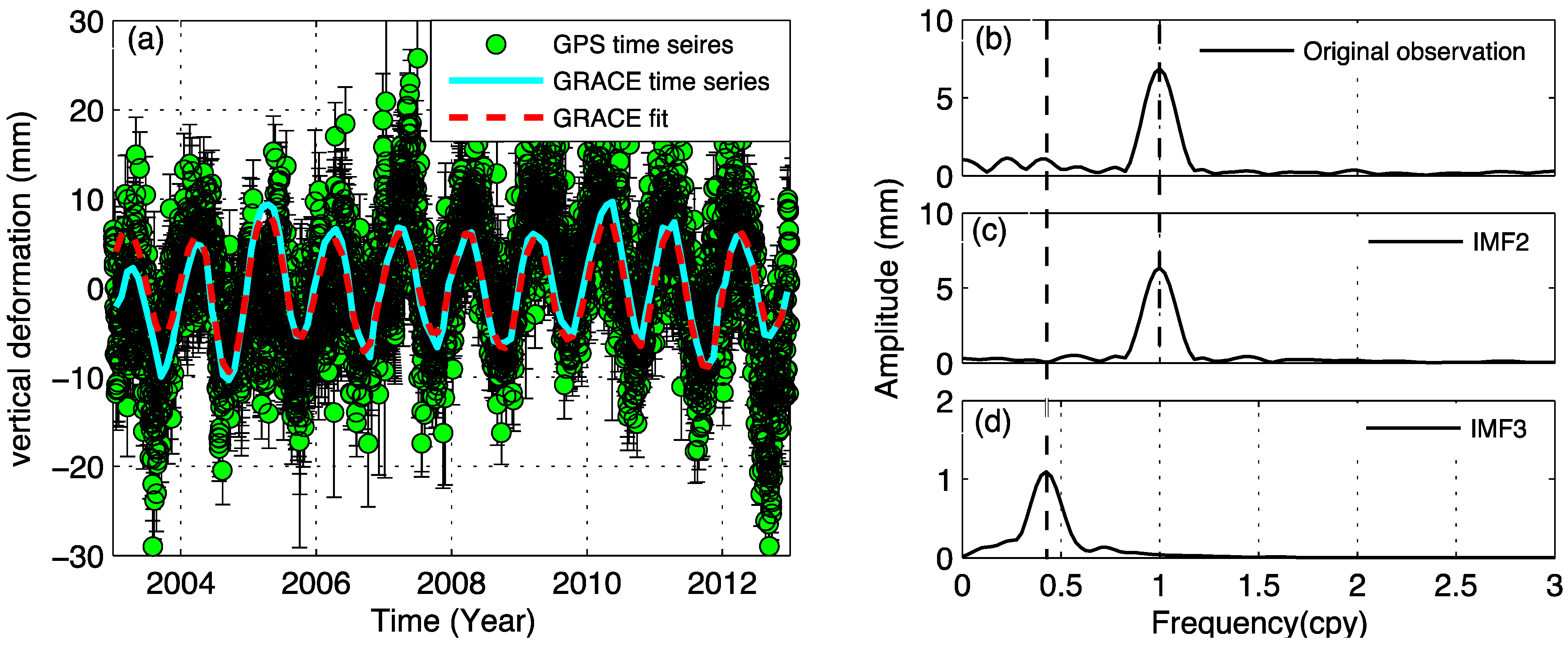
5.2. Comparison with GRACE-Derived Loading
5.3. Other Potential Causes of Quasi-Biennial Signals
5.4. Correlation Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Blewitt, G.; Lavallée, D.; Clarke, P.; Nurutdinov, K. A new global mode of earth deformation: seasonal cycle detected. Science 2001, 294, 2342–2345. [Google Scholar] [CrossRef] [PubMed]
- Blewitt, G.; Lavallée, D. Effect of annual signals on geodetic velocity. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Dong, D.; Fang, P.; Bock, Y.; Cheng, M.K.; Miyazaki, S. Anatomy of apparent seasonal variations from GPS-derived site position time series. J. Geophys. Res. 2002, 107, 2075. [Google Scholar] [CrossRef]
- van Dam, T.; Wahr, J.; Milly, P.C.D.; Shmakin, A.B.; Blewitt, G.; Lavallée, D.; Larson, K.M. Crustal displacements due to continental water loading. Geophys. Res. Lett. 2001, 28, 651–654. [Google Scholar] [CrossRef]
- van Dam, T.; Wahr, J.; Lavallée, D. A comparison of annual vertical crustal displacements from GPS and Gravity Recovery and Climate Experiment (GRACE) over Europe. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Tregoning, P.; Watson, C. Atmospheric effects and spurious signals in GPS analyses. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Fu, Y.; Freymueller, J.; Jensen, T. Seasonal hydrological loading in southern Alaska observed by GPS and GRACE. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Van Dam, T.; Ray, R. S1 and S2 Atmospheric Tide Loading Effects for Geodetic Applications. Data set/Model: Available online: http://geophy.uni.lu/ggfc-atmosphere/tide-loading-calculator.html (accessed on 2 October 2015).
- Yuan, L.G.; Ding, X.L.; Zhong, P.; Chen, W.; Huang, D.F. Estimates of ocean tide loading displacements and its impact on position time series in Hong Kong using a dense continuous GPS network. J Geod. 2009, 83, 999–1015. [Google Scholar] [CrossRef]
- Beavan, J.; Denys, P.; Denham, M.; Hager, B.; Herring, T.; Molnar, P. Distribution of present-day vertical deformation across the Southern Alps, New Zealand, from 10 years of GPS data. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, P.Z.; Freymueller, J.; Bilham, R.; Larson, K.M.; Lai, X.A.; You, X.Z.; Niu, Z.J.; Wu, J.C.; Li, Y.X.; et al. Present-day crustal deformation in China constrained by Global Positioning System measurements. Science 2001, 294, 574–577. [Google Scholar] [CrossRef] [PubMed]
- Gan, W.; Zhang, P.; Shen, Z.K.; Niu, Z.; Wang, M.; Wan, Y.; Zhou, D.; Cheng, J. Present-day crustal motion within the Tibetan Plateau inferred from GPS measurements. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Ray, J.; Altamimi, Z.; Collilieux, X.; van Dam, T. Anomalous harmonics in the spectra of GPS position estimates. GPS Solut. 2008, 12, 55–64. [Google Scholar] [CrossRef]
- Freymueller, J. Seasonal position variations and regional reference frame. In Geodetic Reference Frames—IAG Symposium Munich, Germany, 9–14 October 2006; Springer Berlin Heidelberg: Heidelberg, Germany, 2009; pp. 191–196. [Google Scholar]
- Fu, Y.; Freymueller, J. Seasonal and long-term vertical deformation in the Nepal Himalaya constrained by GPS and GRACE measurements. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Kusche, J.; Schrama, E.J.O. Surface mass redistribution inversion from global GPS deformation and Gravity Recovery and Climate Experiment (GRACE) gravity data. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Zou, R.; Freymueller, J.; Ding, K.; Yang, S.; Wang, Q. Evaluating seasonal loading models and their impact on global and regional reference frame alignment. J. Geophys. Res. 2014, 119, 1337–1358. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Roy. Soc. Lond. A 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.H.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1. [Google Scholar] [CrossRef]
- Heki, K. Seasonal modulation of interseismic strain buildup in north-eastern Japan driven by snow loads. Science 2001, 293, 89–92. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.E.; Chern, C.C.; Huang, K.; Salvino, L.W.; Long, S.R.; Fan, K.L. A new spectral representation of earth-quake data: Hilbert spectral analysis of station TCU129, Chi-Chi, Taiwan, 21 September 1999. Bull. Seismol. Soc. Am. 2004, 91, 1310–1338. [Google Scholar] [CrossRef]
- Jackson, L.P.; Mound, J.E. Geomagnetic variation on decadal time scales: What can we learn from empirical mode decomposition? Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Shen, W.B.; Ding, H. Observation of spheroidal normal mode multiplets below 1 mHz using ensemble empirical mode decomposition. Geophys. J. Int. 2014, 196, 1631–1642. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.J.M.; Watkins, M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Scripps Orbit and Permanent Array Center. Available online: http://sopac.ucsd.edu/ (accessed on 2 October 2015).
- Jet Propulsion Laboratory archive site. Available online: ftp://sideshow.jpl.nasa.gov/pub/JPL_GPS_Products/Final (accessed on 2 October 2015).
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short note: a global model of pressure and temperature for geodetic applications. J Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Ray, R.D.; Ponte, R.M. Barometeric tides from ECMWF operational analyses. Ann. Geophysicae 2003, 21, 1897–1910. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Bähr, H.; Altamimi, Z.; Heck, B. Variance Component Estimation for Combination of Terrestrial Reference Frames. Master Thesis, Kahrlsruhe University, Kahrlsruhe, Germany, 2007. [Google Scholar]
- Zhang, G.; Yao, T.; Xie, H.; Kang, S.; Lei, Y. Increased mass over the Tibetan Plateau: From lakes or glaciers? Geophys. Res. Lett. 2013, 40, 2125–2130. [Google Scholar] [CrossRef]
- Chao, B.F.; Gilbert, F. Autoregressive estimation of complex eigenfrequencies in low frequency seismic spectra. Geophys. J. R. 1980, 63, 641–657. [Google Scholar] [CrossRef]
- Ding, H.; Chao, B.F. Detecting harmonic signals in a noisy time-series: the z-domain Autoregressive (AR-z) spectrum. Geophys. J. Int. 2015, 201, 1287–1296. [Google Scholar] [CrossRef]
- Tregoning, P.; van Dam, T. Atmospheric pressure loading corrections applied to GPS data at the observation level. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- EOST/IPGS Loading Service. Available online: http://loading.u-strasbg.fr (accessed on 2 October 2015).
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Cheng, M.K.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. 2013, 118, 1–8. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Li, K.F.; Tung, K.K. Quasi-biennial oscillation and solar cycle influences on winter Arctic total ozone. J. Geophys. Res. Atmos. 2014, 119, 5823–5835. [Google Scholar] [CrossRef]
- Seo, J.; Choi, W.; Youn, D.; Park, D.S.R.; Kim, J.Y. Relationship between the stratospheric quasi-biennial oscillation and the spring rainfall in the western North Pacific. Geophys. Res. Lett. 2013, 40, 5949–5953. [Google Scholar] [CrossRef]
- Xu, X.; Manson, A.H.; Meek, C.E.; Drummond, J.R. Quasi-biennial modulation of the wintertime Arctic temperature as revealed by Aura-MLS measurements. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Scaife, A.A.; Athanassiadou, M.; Andrews, M.; Arribas, A.; Baldwin, M.; Dunstone, N.; Knight, J.; MacLachlan, C.; Manzini, E.; Müller, W.A.; et al. Predictability of the quasi-biennial oscillation and its northern winter teleconnection on seasonal to decadal timescales. Geophys. Res. Lett. 2014, 41, 1752–1758. [Google Scholar] [CrossRef]
- Inoue, M.; Takahashi, M.; Naoe, H. Relationship between the stratospheric quasi-biennial oscillation and tropospheric circulation in northern autumn. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Akilan, A.; AbdulAzeez, K.K.; Balaji, S.; Schuh, H.; Srinivas, Y. GPS derived Zenith Total Delay (ZTD) observed at tropical locations in South India during atmospheric storms and depressions. J. Atmos. Sol.-Terr. Phys. 2015, 125–126, 1–7. [Google Scholar] [CrossRef]
- Laura, I.F.; Amalia, M.M.; Ana, G.E. Quasi-biennial oscillation in GPS VTEC measurements. Adv. Space Res. 2014, 54, 161–167. [Google Scholar]
- Tang, W.; Xue, X.H.; Lei, J.; Dou, X.K. Ionospheric quasi-biennial oscillation in global TEC observations. J. Atmos. Sol.-Terr. Phys. 2014, 107, 36–41. [Google Scholar] [CrossRef]
- Abarca del Rio, R.; Gambis, D.; Salstein, D.A. Interannual signals in length of day and atmospheric angular momentum. Ann. Geophysicae 2000, 18, 347–364. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Shen, W.-B.; Ding, H.; Hwang, C.; Li, J.; Zhang, T. The Quasi-Biennial Vertical Oscillations at Global GPS Stations: Identification by Ensemble Empirical Mode Decomposition. Sensors 2015, 15, 26096-26114. https://doi.org/10.3390/s151026096
Pan Y, Shen W-B, Ding H, Hwang C, Li J, Zhang T. The Quasi-Biennial Vertical Oscillations at Global GPS Stations: Identification by Ensemble Empirical Mode Decomposition. Sensors. 2015; 15(10):26096-26114. https://doi.org/10.3390/s151026096
Chicago/Turabian StylePan, Yuanjin, Wen-Bin Shen, Hao Ding, Cheinway Hwang, Jin Li, and Tengxu Zhang. 2015. "The Quasi-Biennial Vertical Oscillations at Global GPS Stations: Identification by Ensemble Empirical Mode Decomposition" Sensors 15, no. 10: 26096-26114. https://doi.org/10.3390/s151026096
APA StylePan, Y., Shen, W.-B., Ding, H., Hwang, C., Li, J., & Zhang, T. (2015). The Quasi-Biennial Vertical Oscillations at Global GPS Stations: Identification by Ensemble Empirical Mode Decomposition. Sensors, 15(10), 26096-26114. https://doi.org/10.3390/s151026096








