Hyperbolic Positioning with Antenna Arrays and Multi-Channel Pseudolite for Indoor Localization
Abstract
:1. Introduction

2. Positioning Theory
2.1. Overview
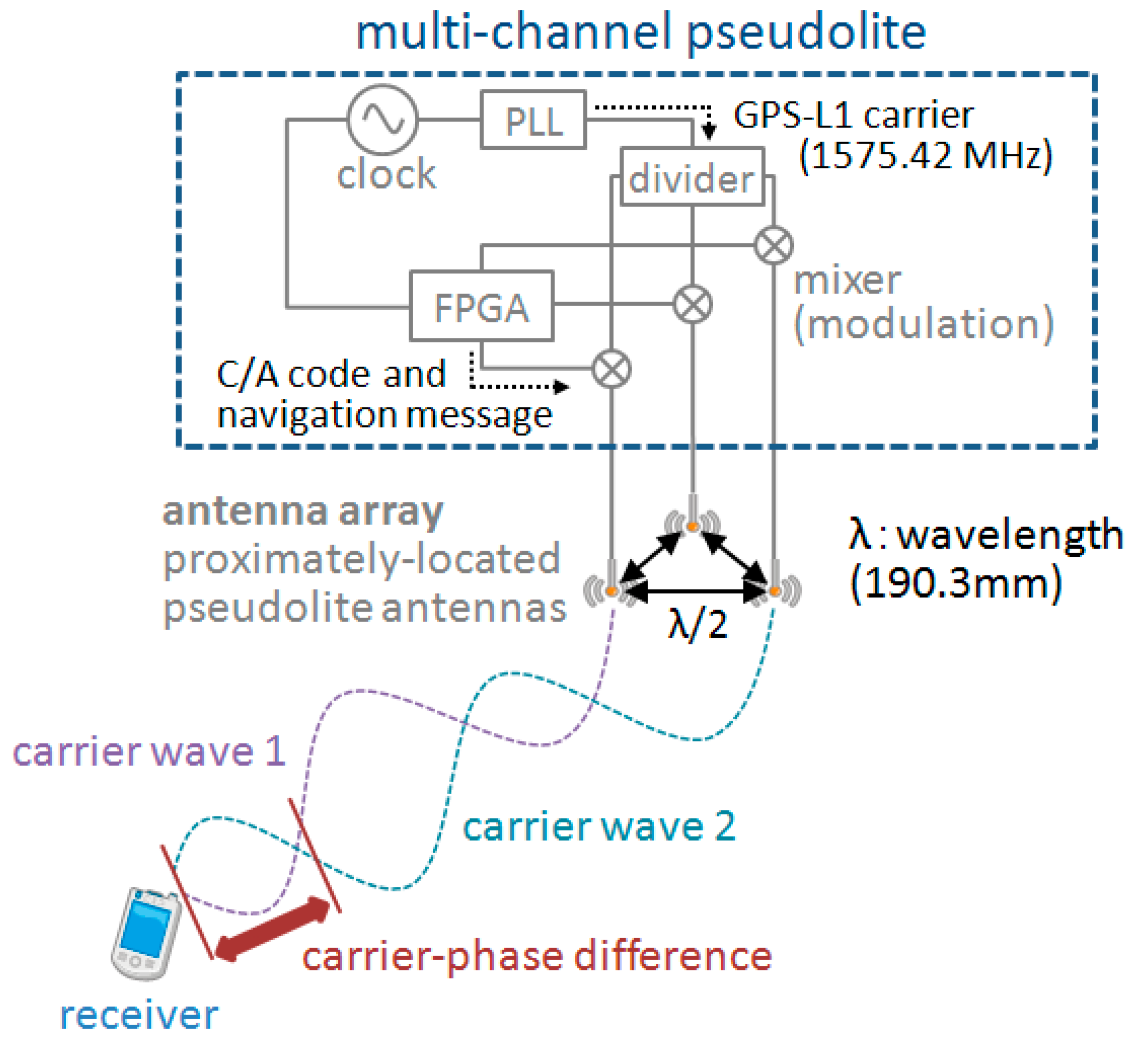
2.2. Positioning Algorithm
2.3. Dilution of Precision
3. Two-Dimensional Positioning Experiment
3.1. Devices
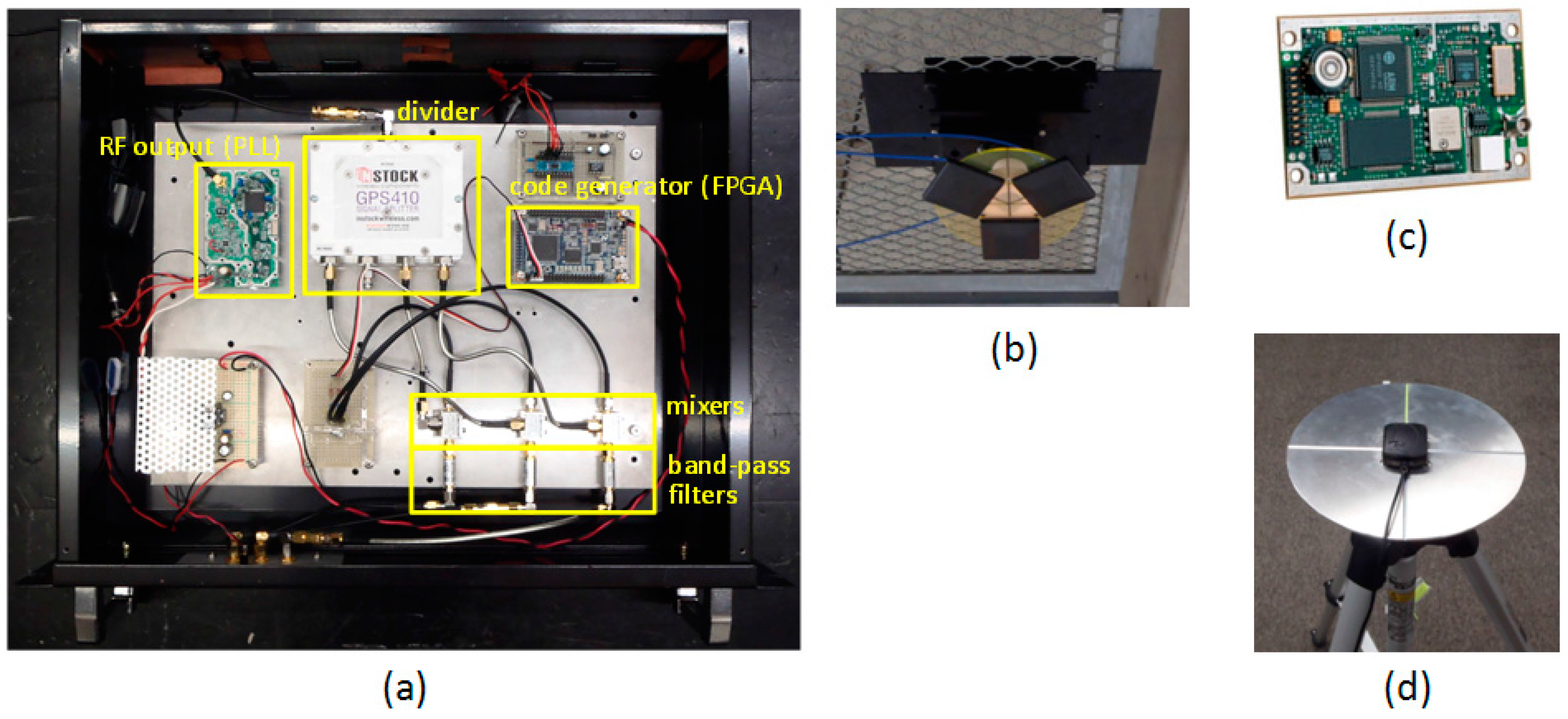
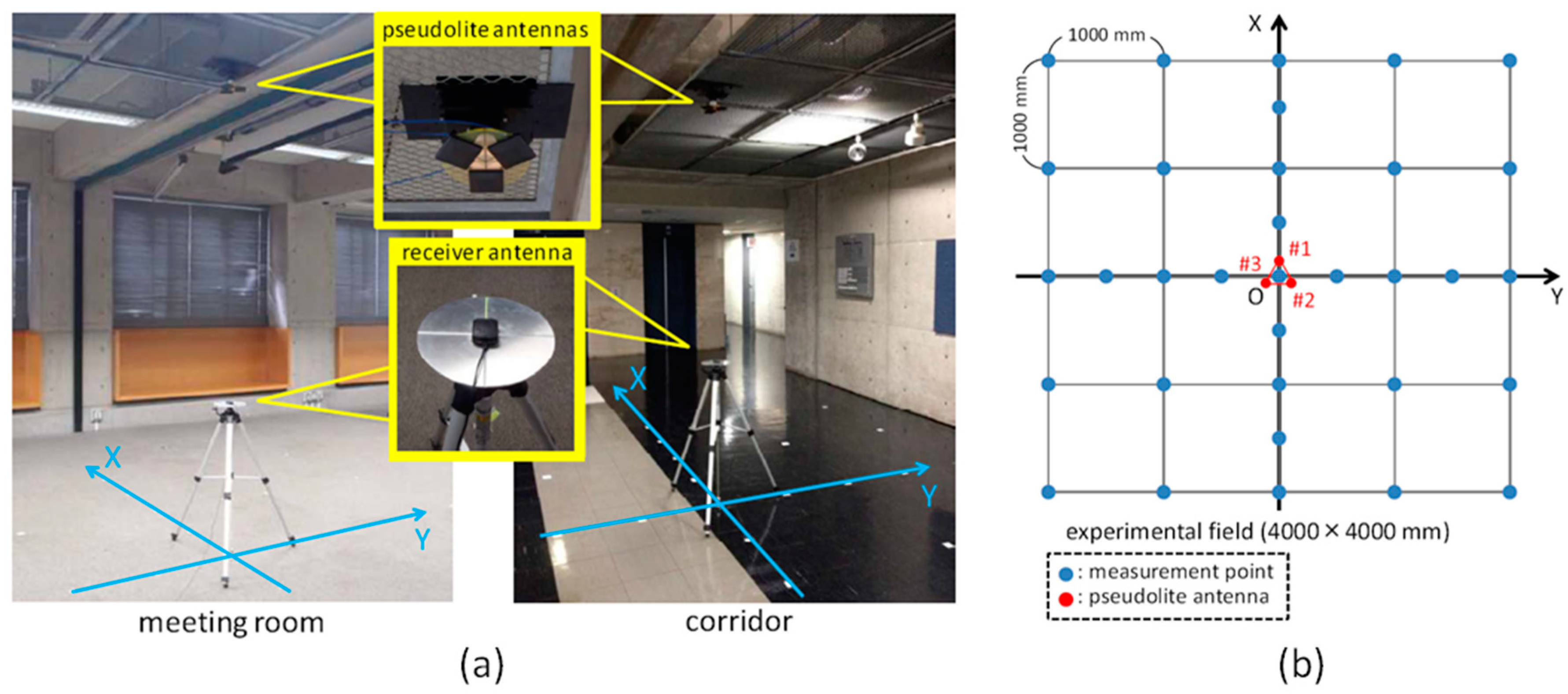
3.2. Setup and Procedure
3.3. Experimental Results
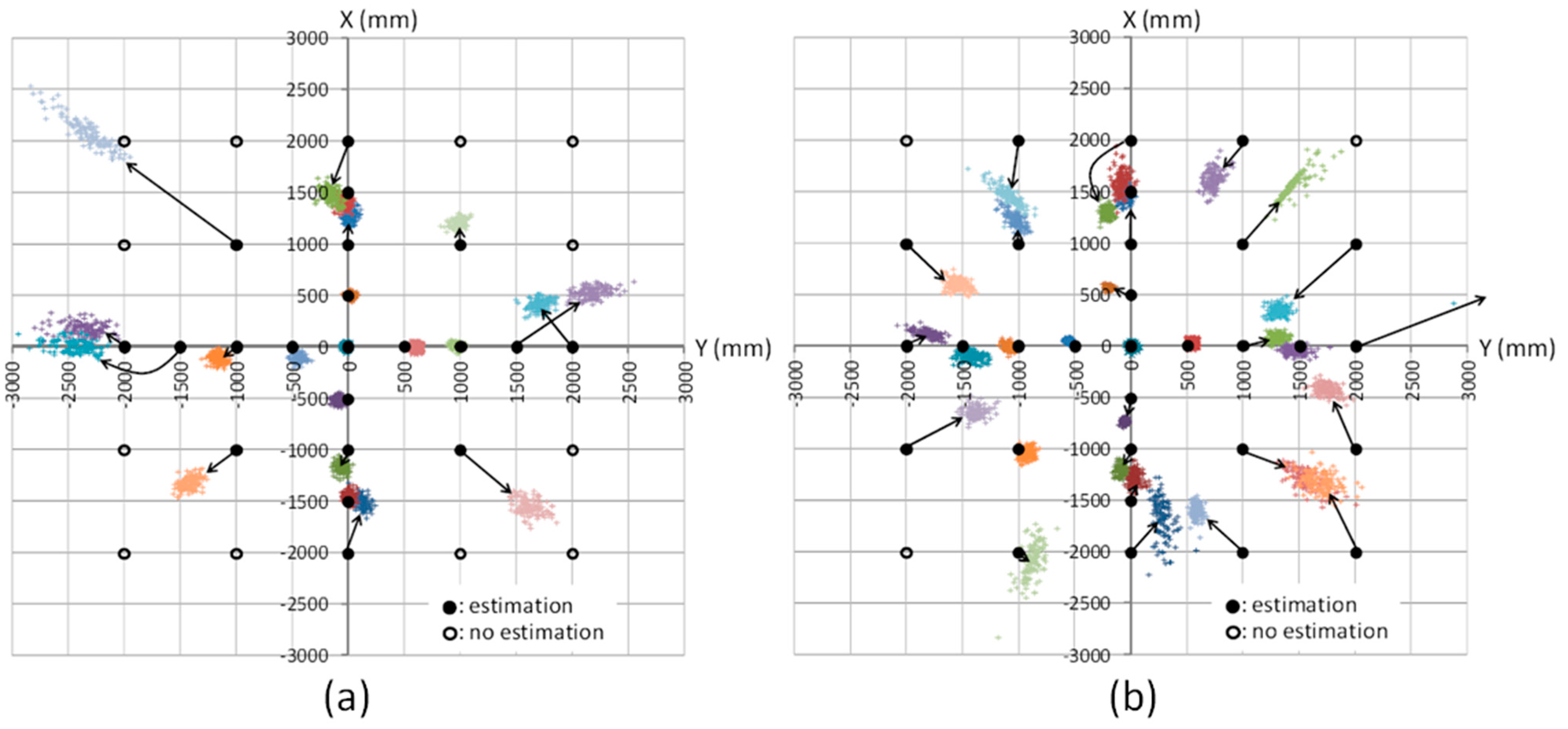
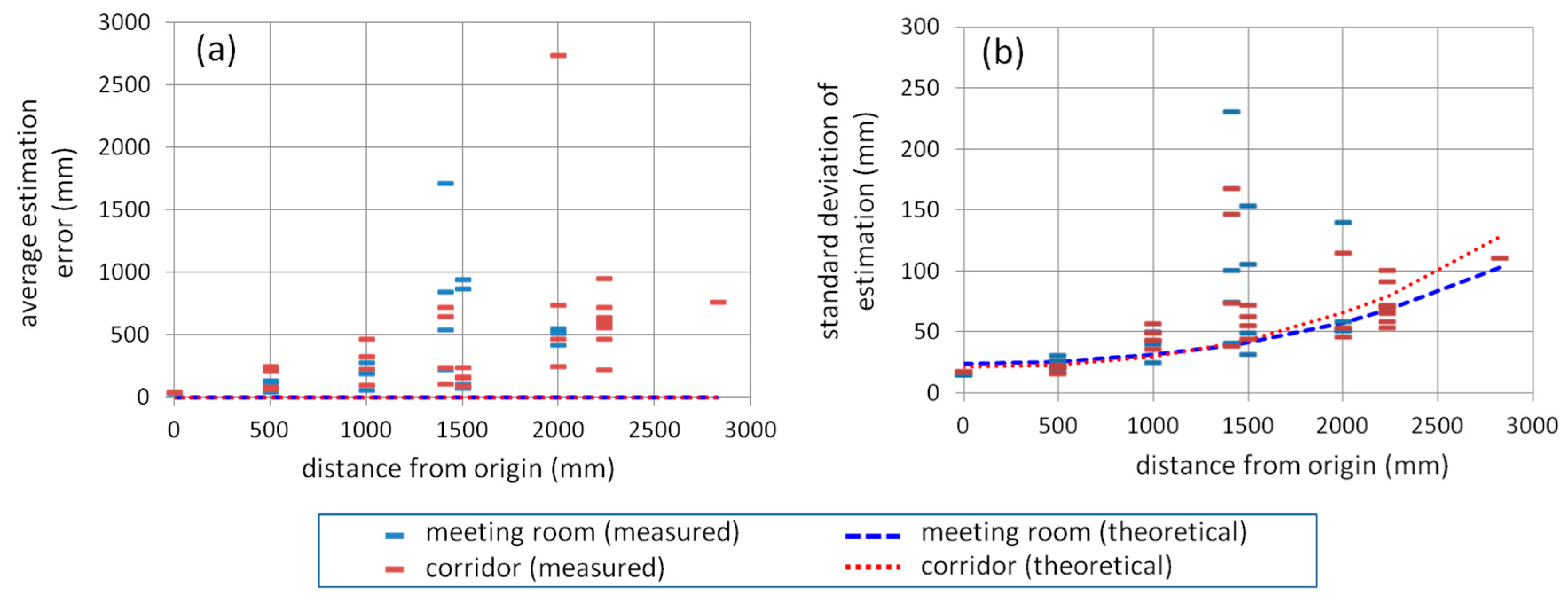
3.4. Discussion
4. Preparation for Simulation
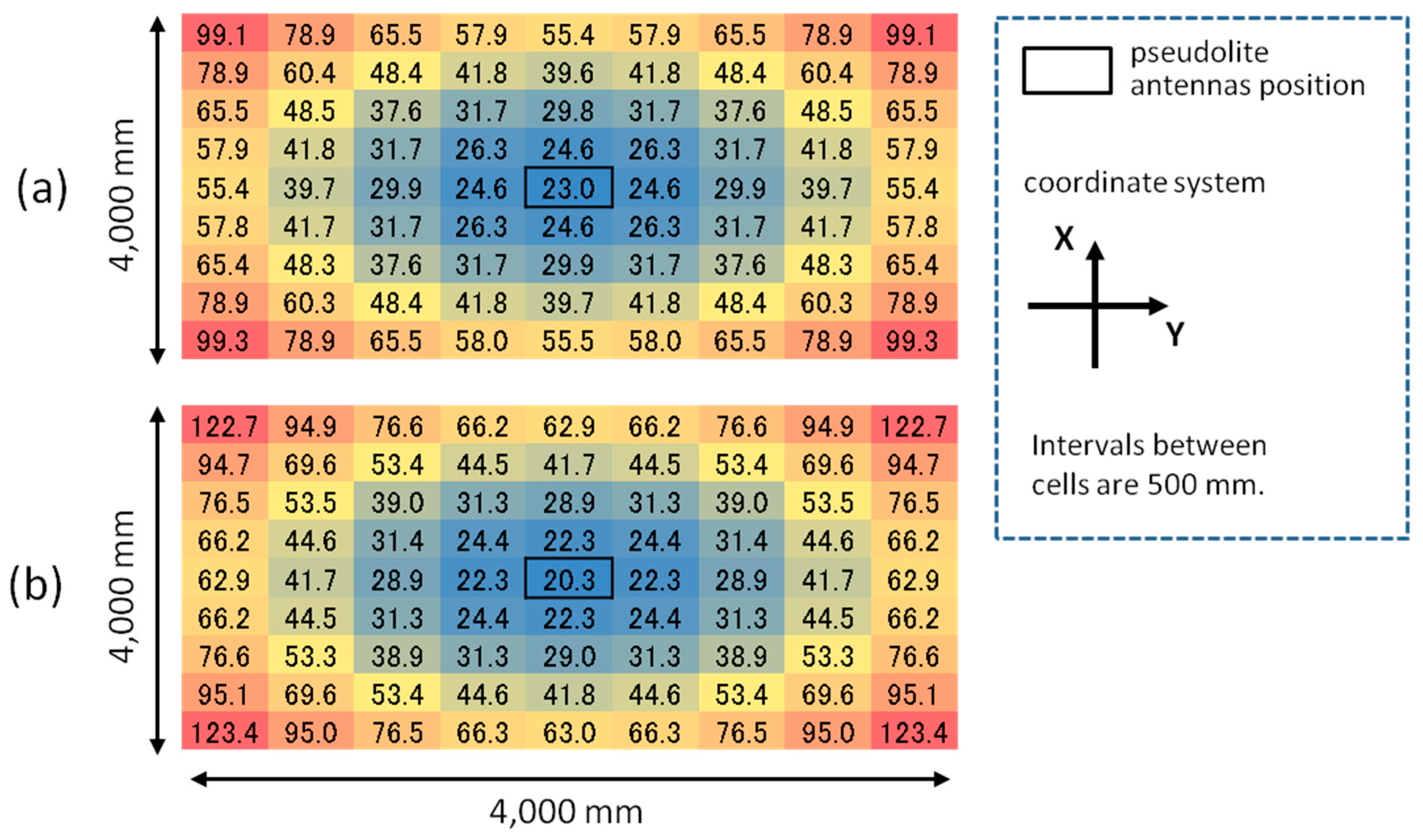


5. Simulation of Three-Dimensional Positioning
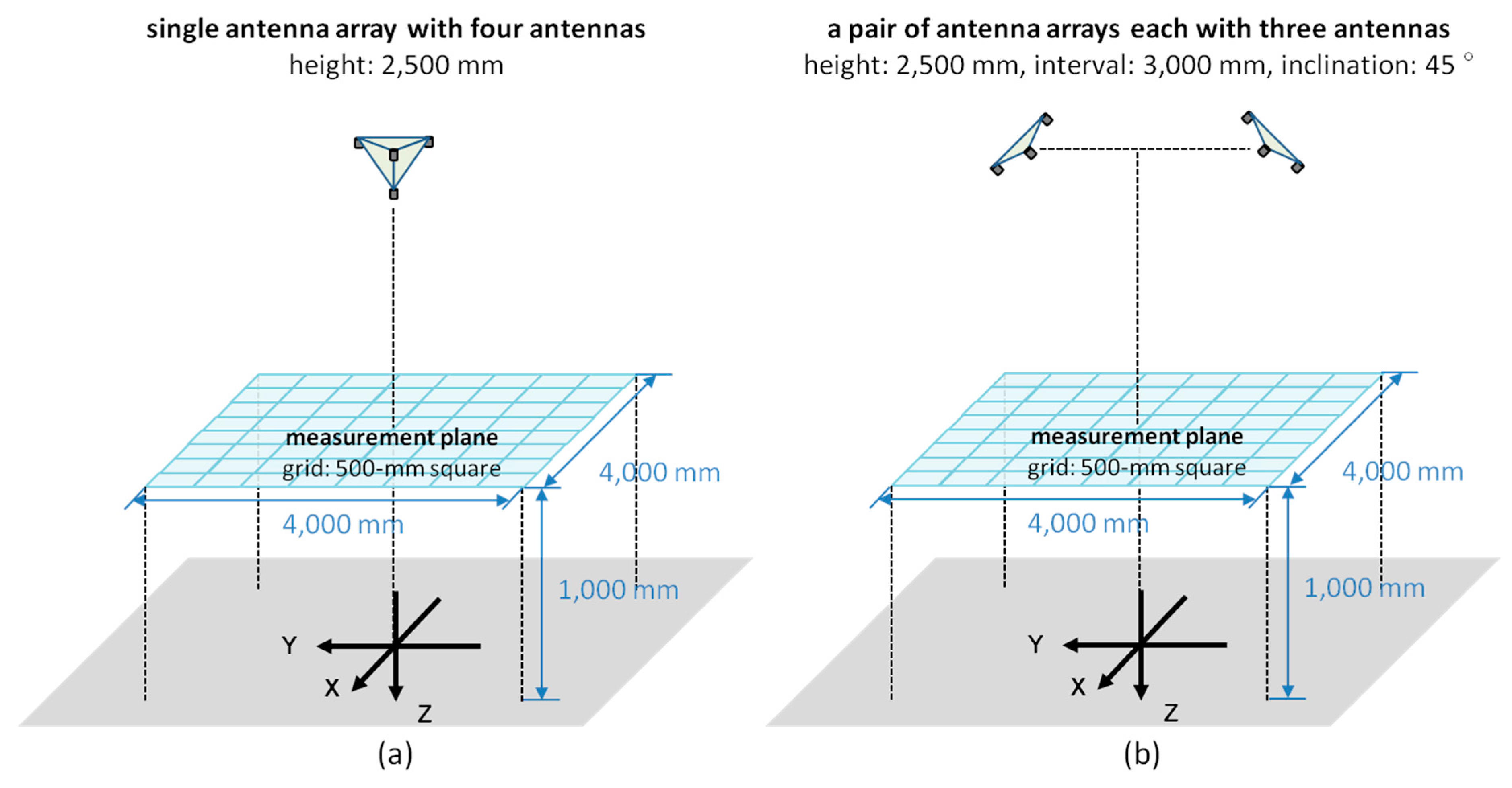
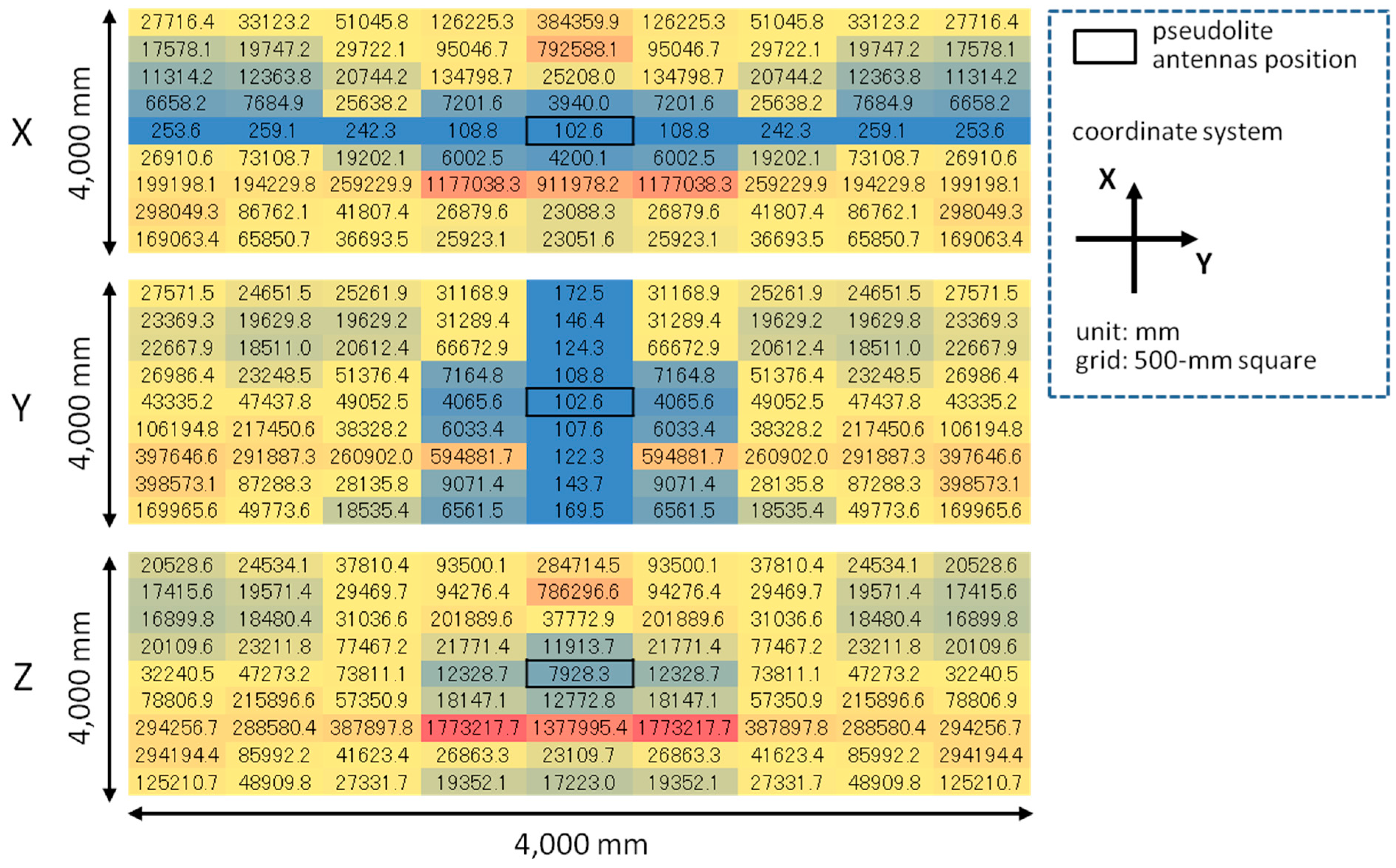
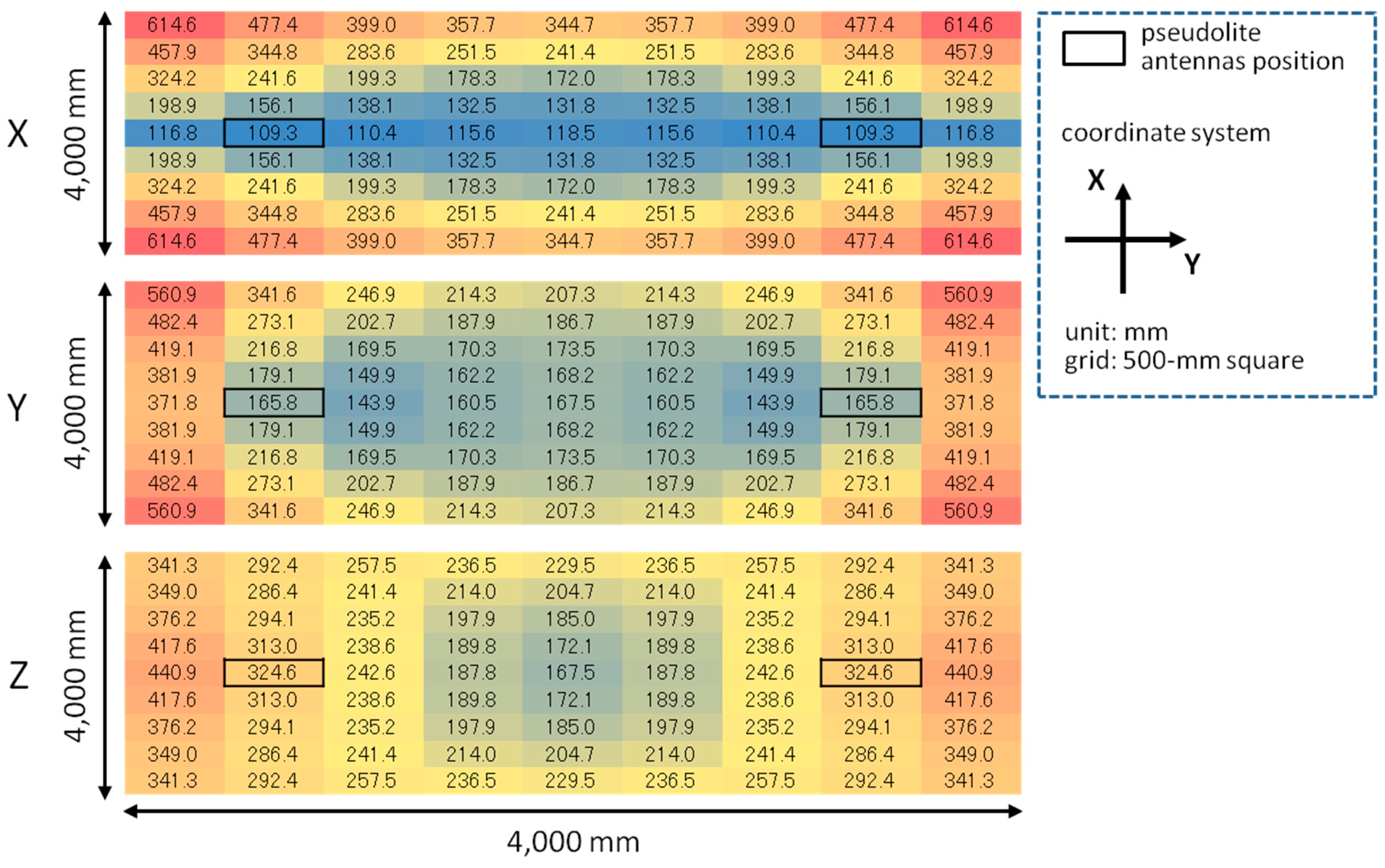
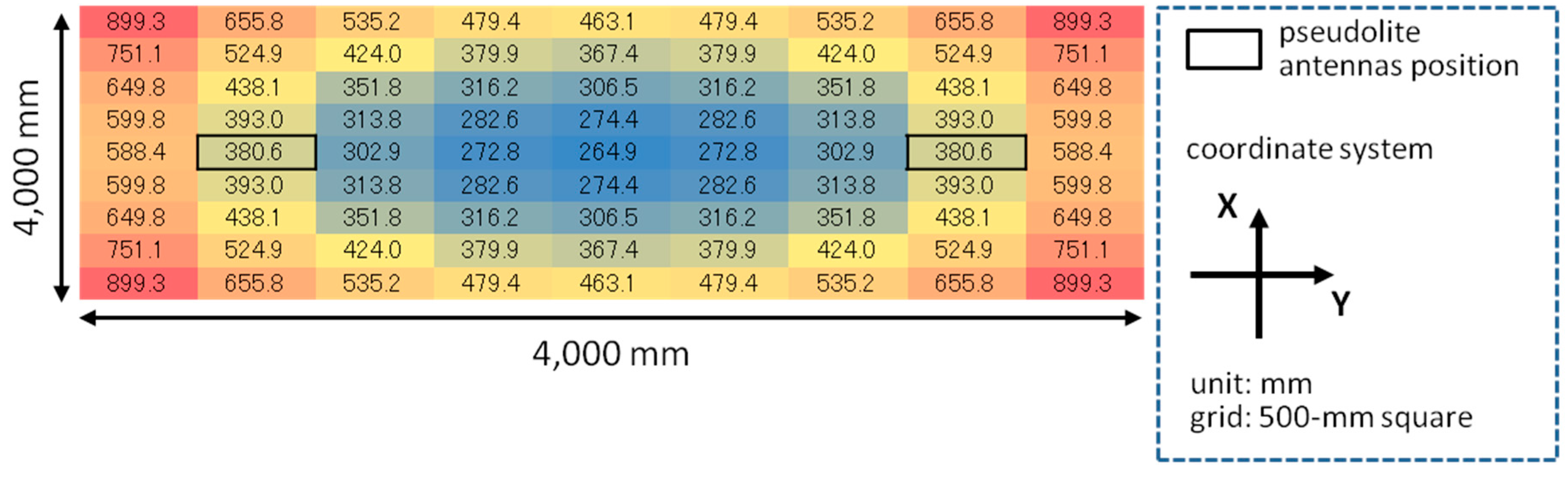
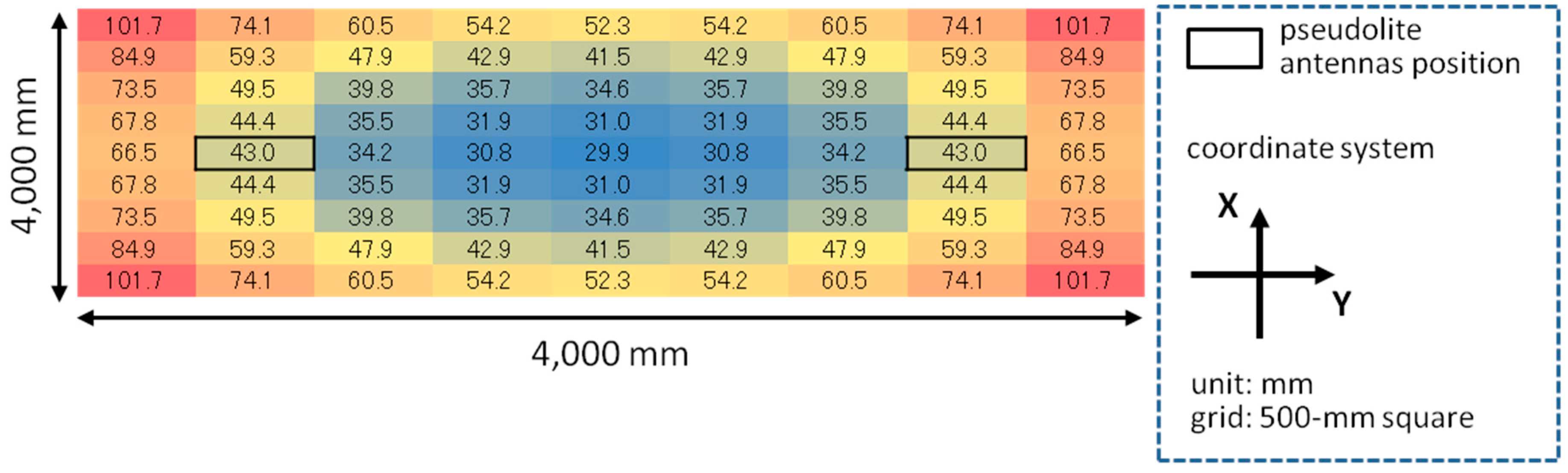
6. Initial Value Convergence Analysis
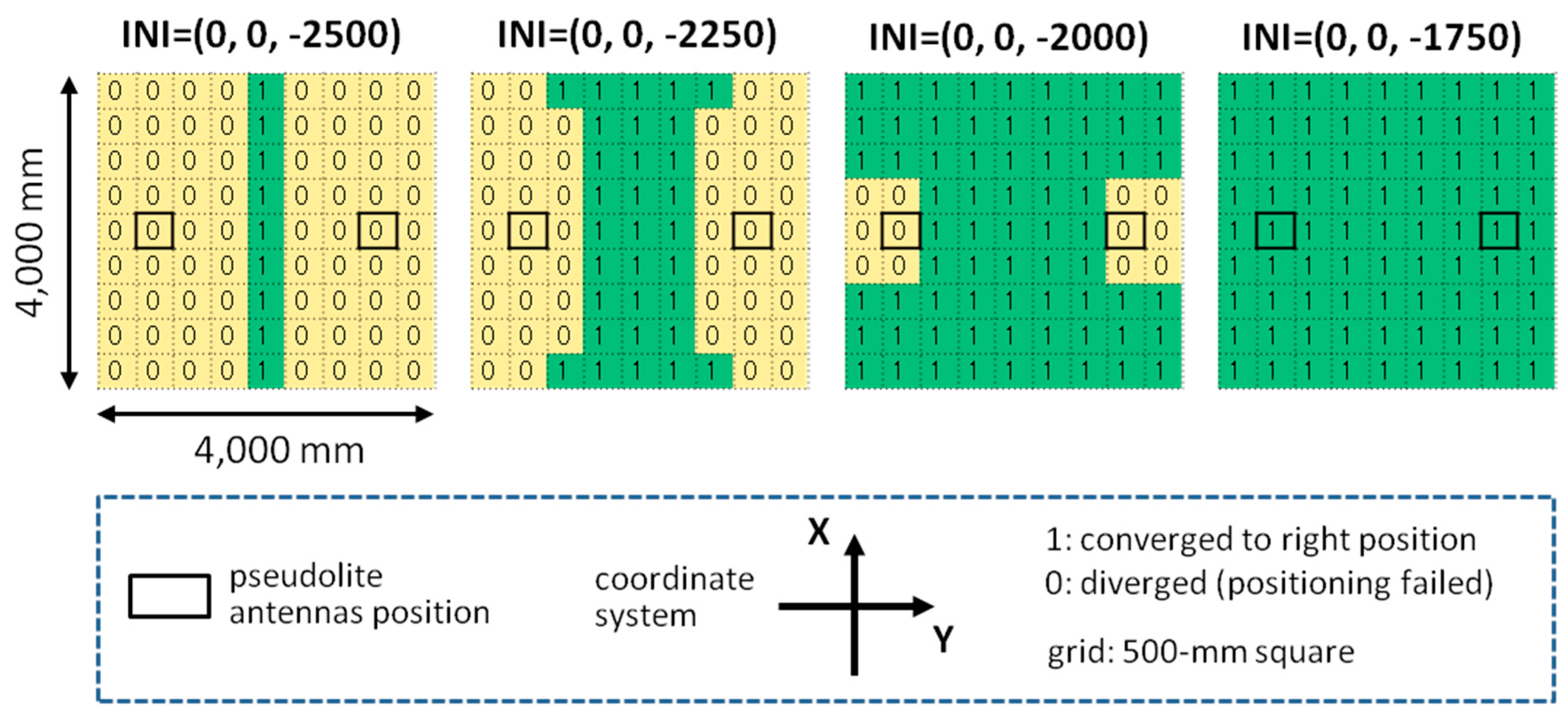
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Combain Positioning Service. Available online: https://combain.com/ (accessed on 6 July 2015).
- Navizon Inc. Available online: http://www.navizon.com/ (accessed on 6 July 2015).
- iBeacon for Developers. Available online: https://developer.apple.com/ibeacon/ (accessed on 6 July 2015).
- Bose, A.; Foh, C.H. A Practical Path Loss Model for Indoor WiFi Positioning Enhancement. In Proceedings of the 6th International Conference on Information, Communications & Signal Processing, Singapore, 10–13 December 2007; pp. 1–5.
- Moka, E.; Retscherb, G. Location determination using WiFi fingerprinting versus WiFi trilateration. J. Locat. Based Serv. 2007, 1, 145–159. [Google Scholar] [CrossRef]
- Naya, F.; Noma, H.; Ohmura, R.; Kogure, K. Bluetooth-based Indoor Proximity Sensing for Nursing Context Awareness. In Proceedings of the Ninth IEEE International Symposium on Wearable Computers, Osaka, Japan, 18–21 October 2005; pp. 212–213.
- Heissmeyer, S.; Overmeyer, L.; Müller, A. Indoor Positioning of Vehicles using an Active Optical Infrastructure. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN2012), Sydney, Australia, 13–15 November 2012; pp. 1–8.
- Gezici, S.; Tian, Z.; Biannakis, G.B.; Kobayashi, H.; Molisch, A.F.; Poor, V.; Sahinoglu, Z. Localization via Ultra-Wideband Radios. IEEE Signal Process. Mag. 2005, 22, 70–84. [Google Scholar] [CrossRef]
- Holm, S. Ultrasound positioning based on time-of-flight and signal strength. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN2012), Sydney, Australia, 13–15 November 2012; pp. 13–15.
- Mautz, R. Indoor Positioning Technologies. Habilitation Thesis, ETH Zurich, Zurich, Switzerland, February 2012. [Google Scholar]
- Kohtake, N.; Morimoto, S.; Kogure, S.; Manandhar, D. Indoor and Outdoor Seamless Positioning using Indoor Messaging System and GPS. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation (IPIN2011), Guimarães, Portugal, 21–23 September 2011.
- Interface Specifications for QZSS (IS-QZSS V1.6). Available online: http://qz-vision.jaxa.jp/USE/is-qzss/index_e.html (accessed on 6 July 2015).
- Sakamoto, Y.; Arie, H.; Ebinuma, T.; Fujii, K.; Sugano, S. Hyperbolic Positioning with Proximate Multi-channel Pseudolite for Indoor Localization. In Proceedings of the IGNSS Symposium 2013, Gold Coast, Australia, 16–18 July 2013.
- Petovello, M. Why are carrier phase ambiguities integer? Inside GNSS. Available online: http://www.insidegnss.com/node/4368 (accessed on 23 September 2015).
- Interface Specification IS-GPS-200H. Available online: http://www.gps.gov/technical/icwg/ (accessed on 6 July 2015).
- Langley, R.B. Dilution of Precision. GPS World 1999, 10, 52–59. [Google Scholar]
- Takasu, T.; Yasuda, A. Evaluation of RTK-GPS Performance with Lowcost Single-Frequency GPS Receivers. In Proceedings of the International Symposium on GPS/GNSS, Tokyo, Japan, 11–14 November 2008.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fujii, K.; Sakamoto, Y.; Wang, W.; Arie, H.; Schmitz, A.; Sugano, S. Hyperbolic Positioning with Antenna Arrays and Multi-Channel Pseudolite for Indoor Localization. Sensors 2015, 15, 25157-25175. https://doi.org/10.3390/s151025157
Fujii K, Sakamoto Y, Wang W, Arie H, Schmitz A, Sugano S. Hyperbolic Positioning with Antenna Arrays and Multi-Channel Pseudolite for Indoor Localization. Sensors. 2015; 15(10):25157-25175. https://doi.org/10.3390/s151025157
Chicago/Turabian StyleFujii, Kenjirou, Yoshihiro Sakamoto, Wei Wang, Hiroaki Arie, Alexander Schmitz, and Shigeki Sugano. 2015. "Hyperbolic Positioning with Antenna Arrays and Multi-Channel Pseudolite for Indoor Localization" Sensors 15, no. 10: 25157-25175. https://doi.org/10.3390/s151025157
APA StyleFujii, K., Sakamoto, Y., Wang, W., Arie, H., Schmitz, A., & Sugano, S. (2015). Hyperbolic Positioning with Antenna Arrays and Multi-Channel Pseudolite for Indoor Localization. Sensors, 15(10), 25157-25175. https://doi.org/10.3390/s151025157




