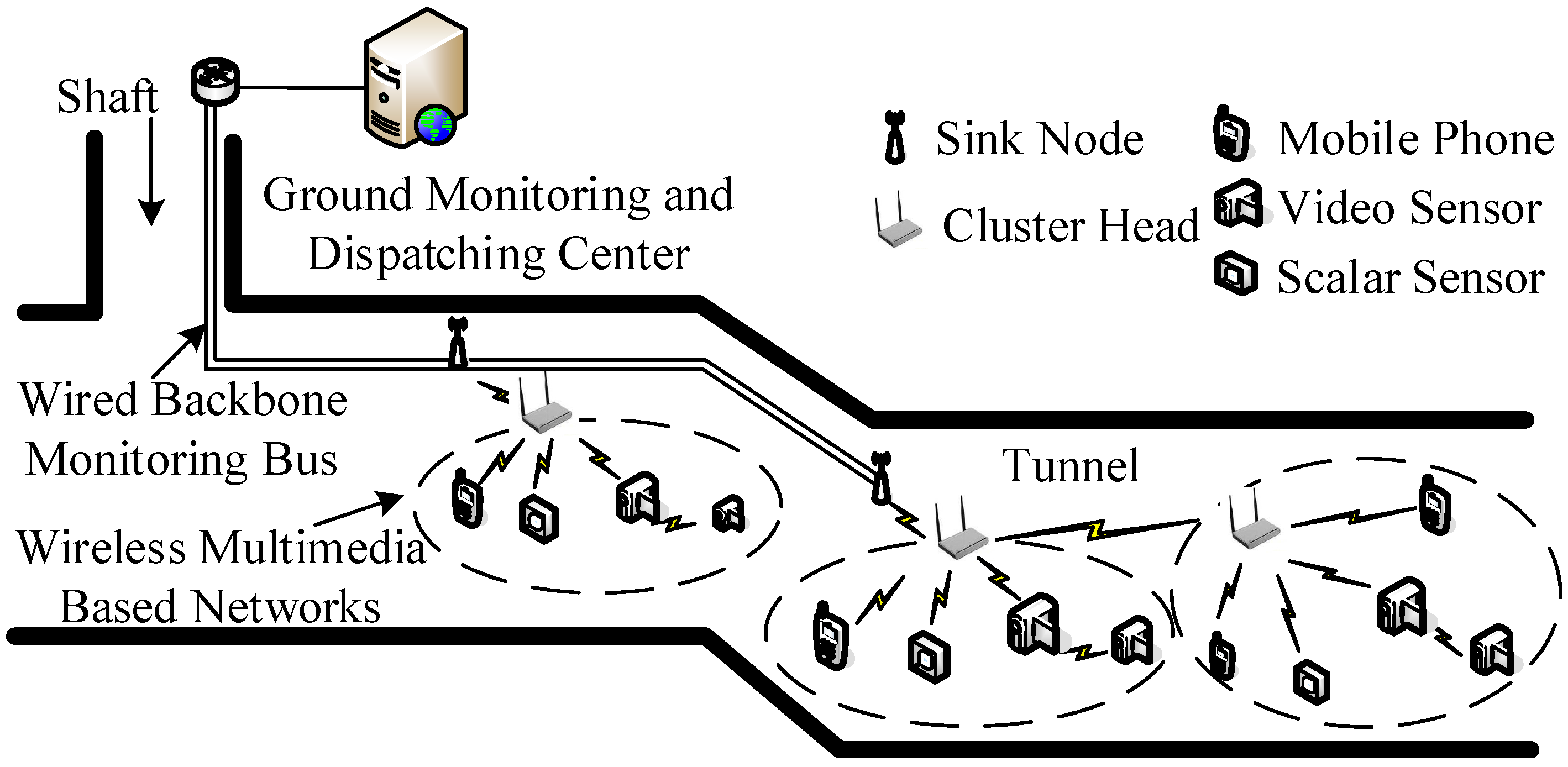
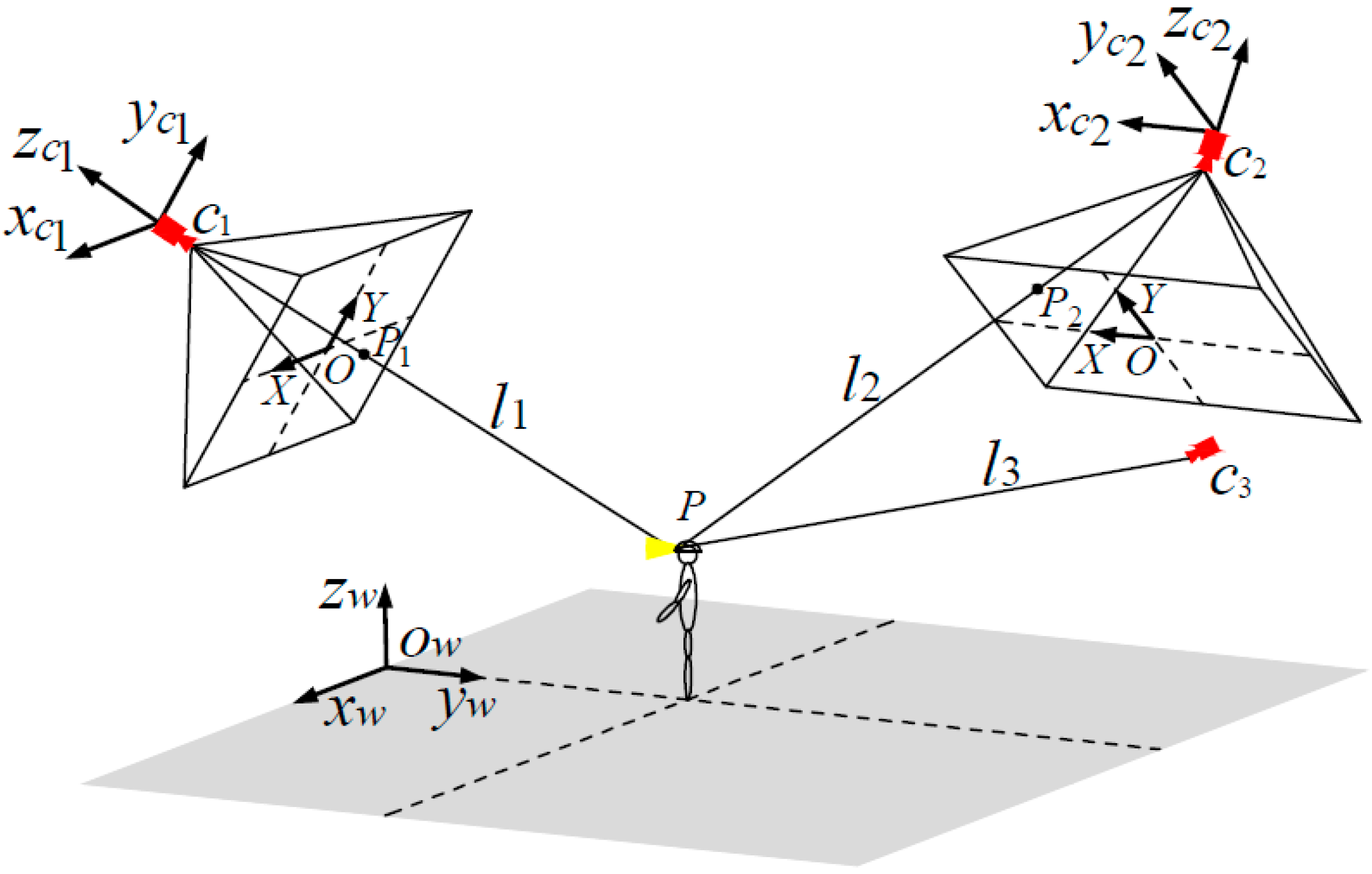
4.1. Experiment in a Corridor
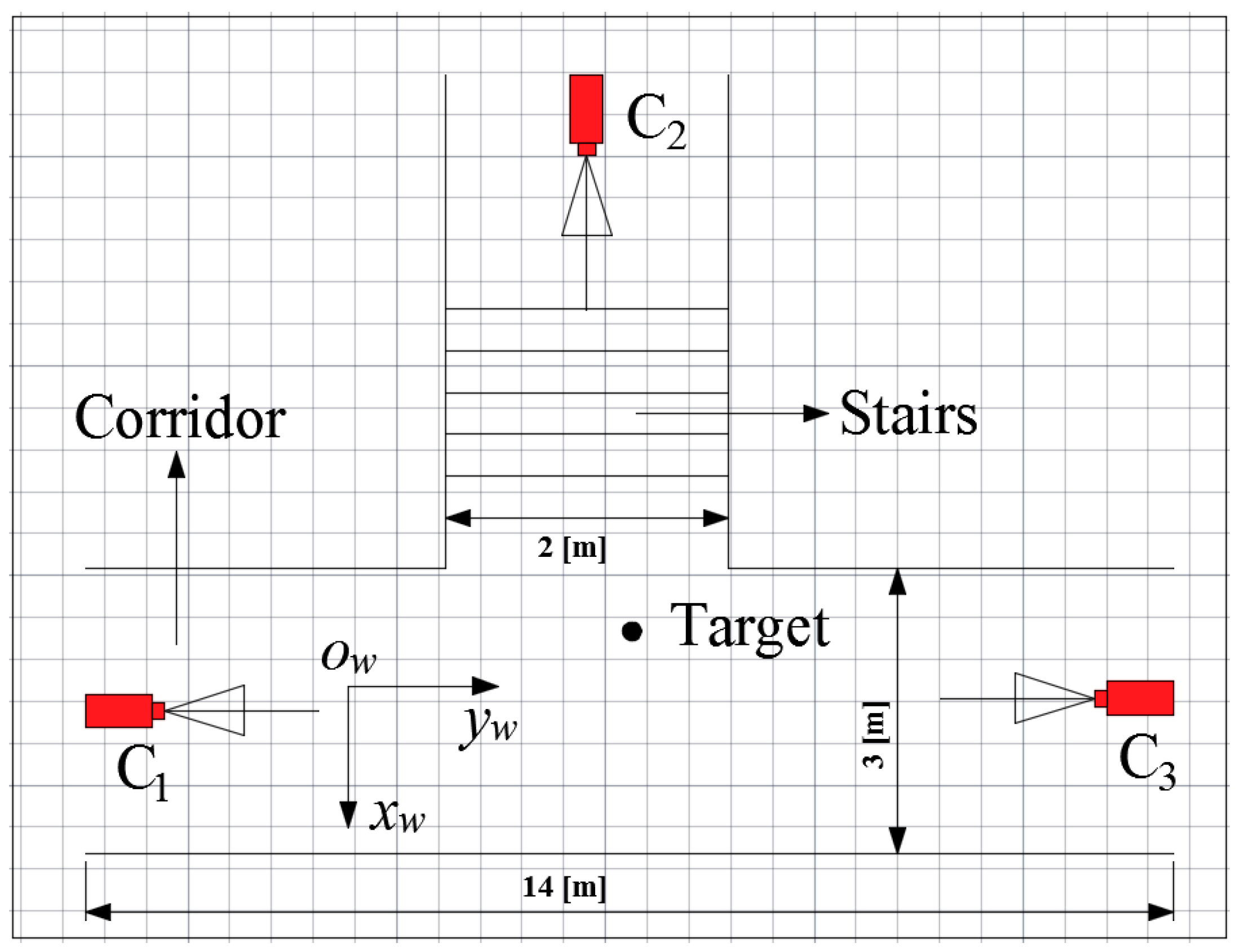
In order to evaluate the performances of the proposed miner’s lamp video collaborative localization algorithm based on underground WMSNs, a test was carried out. A corridor with stairs shown in
Figure 4 was selected to simulate the bifurcation structure of underground tunnels. Lights in the corridor were turned off to simulate the insufficient illumination tunnels. Smoke machine sprayed smoke in the corridor to simulate tunnels with great amounts of water vapor and dusts. The tester wore dark blue overalls and safety helmet with miner’s lamp turning on to simulate miners in underground tunnels. A World Coordinate System (WCS) was established at the entrance of the corridor with the transverse direction of the corridor as
xw-axis, the longitudinal direction as
yw-axis and the altitude direction as
zw-axis, respectively.
Figure 4.
(a) The image of the corridor taken by camera C1; (b) The image of the corridor taken by camera C2; (c) The image of the corridor taken by camera C3.
Figure 4.
(a) The image of the corridor taken by camera C1; (b) The image of the corridor taken by camera C2; (c) The image of the corridor taken by camera C3.
In the test, three isomorphic cameras TY803-130 were adopted manually at the top of the corridor by tripods. The cameras
C1,
C2 and
C3 were deployed according to
Figure 2, and the topology of the experiment is shown in
Figure 5. Cameras are wirelessly linked by Wi-Fi with carrier frequency 2.4 GHz and 802.11 n transmission protocol.
Table 1 lists the intrinsic parameters of three cameras, including focal length
f, image resolution
M ×
N and the physical size of the photosensitive element CMOS.
Table 2 lists the geometrical parameters of three cameras, including the world coordinates of the locations of cameras, the angle of yaw
φ between the WCS
xw-axis and the Camera Coordinate System (CCS)
xw-axis in counterclockwise direction and the
θ between the WCS
zw-axis and the CCS
zw-axis in counterclockwise direction.
Figure 5.
Topology of the experiment.
Figure 5.
Topology of the experiment.
Table 1.
Intrinsic parameters of cameras.
Table 1.
Intrinsic parameters of cameras.
| Parameter | Value |
|---|
| f/mm | 6.0 |
| M × N /pixel | 1280 × 960 |
| CMOS/mm | 4.8 × 3.6 |
Table 2.
Geometrical parameters of cameras.
Table 2.
Geometrical parameters of cameras.
| | (xw,yw,zw)/m | φ/° | θ/° |
|---|
| Camera 1 | (0.29, −2.20, 2.32) | 0 | 70 |
| Camera 2 | (−6.33, 2.86, 3.08) | −90 | 64 |
| Camera 3 | (0.15, 8.95, 2.34) | 180 | 70 |
The tester walked into the corridor at a normal pace. Cameras
C1,
C2 and
C3 worked together to monitor the corridor and collected the video information at the same time. At a certain time point, cameras
C1,
C2 and
C3 collected the images of corridor, as is shown in
Figure 4a–c, respectively.
Cameras C1, C2 and C3 detected the miner’s lamp by the difference value between the current images from their video sequences and the background images. In the experiment, 60% maximum grey value of difference image is selected as threshold. Cameras C1, C2 and C3 detected the miner’s lamp at interval of 0.5 s and calculated the pixel coordinates of mapping points of the miner’s lamp on their own imaging plane. Then, the pixel coordinates were translated to the coordinates in the WCS by applying Equations (1) and (2). Therefore, three straight lines of three-dimension (3-D) between cameras C1, C2 and C3 and their corresponding mapping points of the miner’s lamp could be established in the WCS.
By applying Equations (5) and (6) to calculate the optimum intersection of the three straight lines, the position coordinate of three-dimension (3-D) of the miner’s lamp in the WCS could be obtained which also provided both the plane coordinate of the tester in the corridor and the altitude of the miner’s lamp from the corridor ground. 10 gauge points on the ground of the corridor had been marked and measured to show the localization precision of the miner’s lamp. The tester would walk to pass these 10 gauge points and stay for one second at each gauge point. By applying the proposed algorithm, cameras C1, C2 and C3 could locate the tester’s lamp automatically at interval of 0.5 s when the tester passed each gauge point.
In order to compare the estimated localization of the tester’s lamp with the actual location of the tester’s lamp, the error of altitude localization is defined as
where
hr(
i) is the actual altitude of the tester’s lamp from the tunnel ground and
hl(
i) is the altitude of the tester’s lamp obtained by the proposed algorithm. Thus, the average error of the altitude localization is defined as
where
N is the number of gauge points in the test.
Similarly, the error of plane localization which includes errors both in
x-axis and
y-axis is defined as
where
is the actual plane location of the tester’s lamp and
is the estimated plane coordinates with the proposed algorithm. Thus, the average error of the plane localization is defined as
where
N is the number of gauge points in the test.
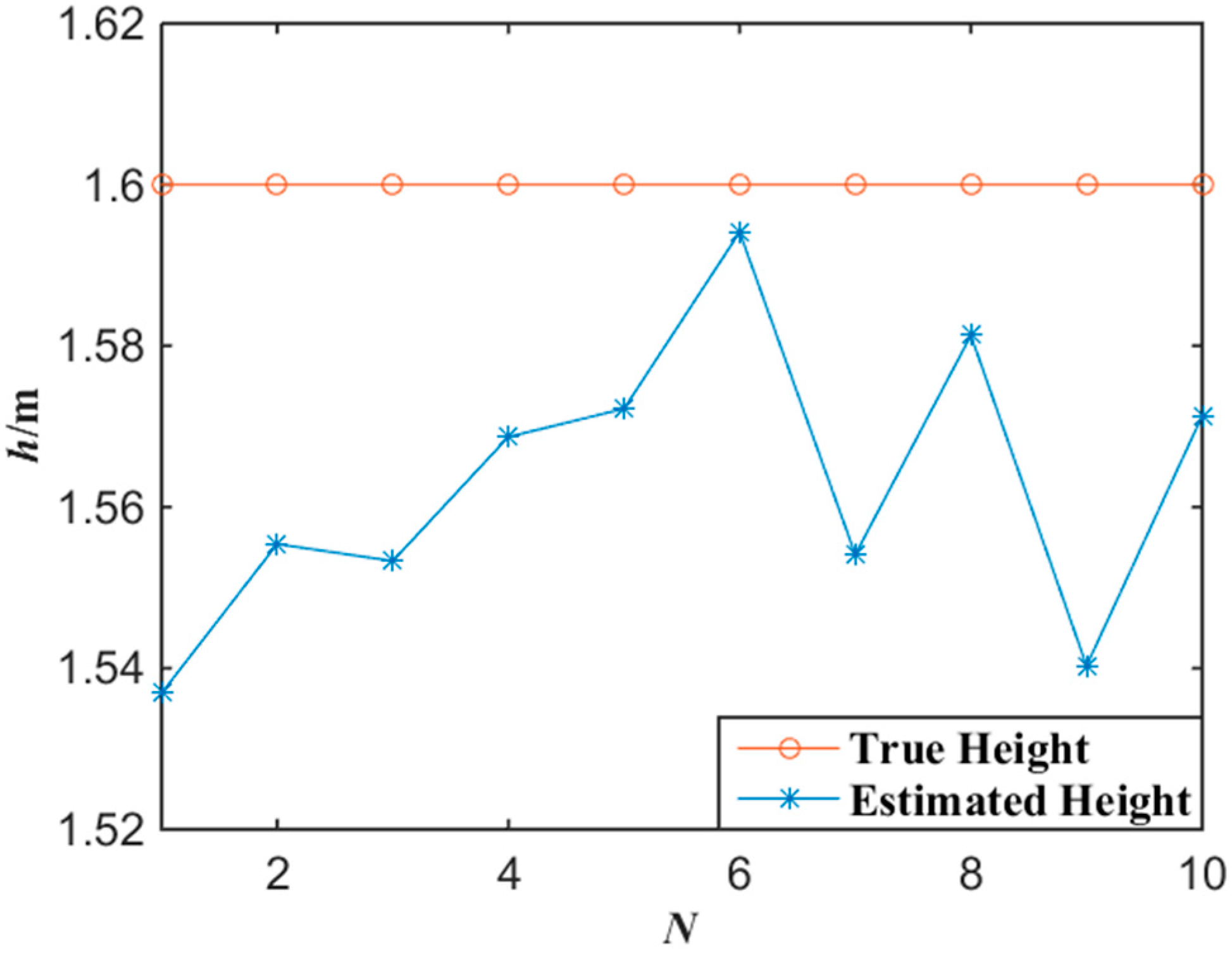
Figure 6 shows the experimental results of the altitude localization of tester’s lamp with the proposed algorithm. According to the experimental data of
Figure 6, the average error of the altitude localization of the tester is 3.7 cm by applying Equations (7) and (8).
Figure 6.
Experimental data of altitude with the miner’s lamp video collaborative localization.
Figure 6.
Experimental data of altitude with the miner’s lamp video collaborative localization.
Figure 7 shows the experimental results of the plane localization of tester’s lamp with the proposed algorithm where the tester stood at each gauge point passed. According to the experimental data of
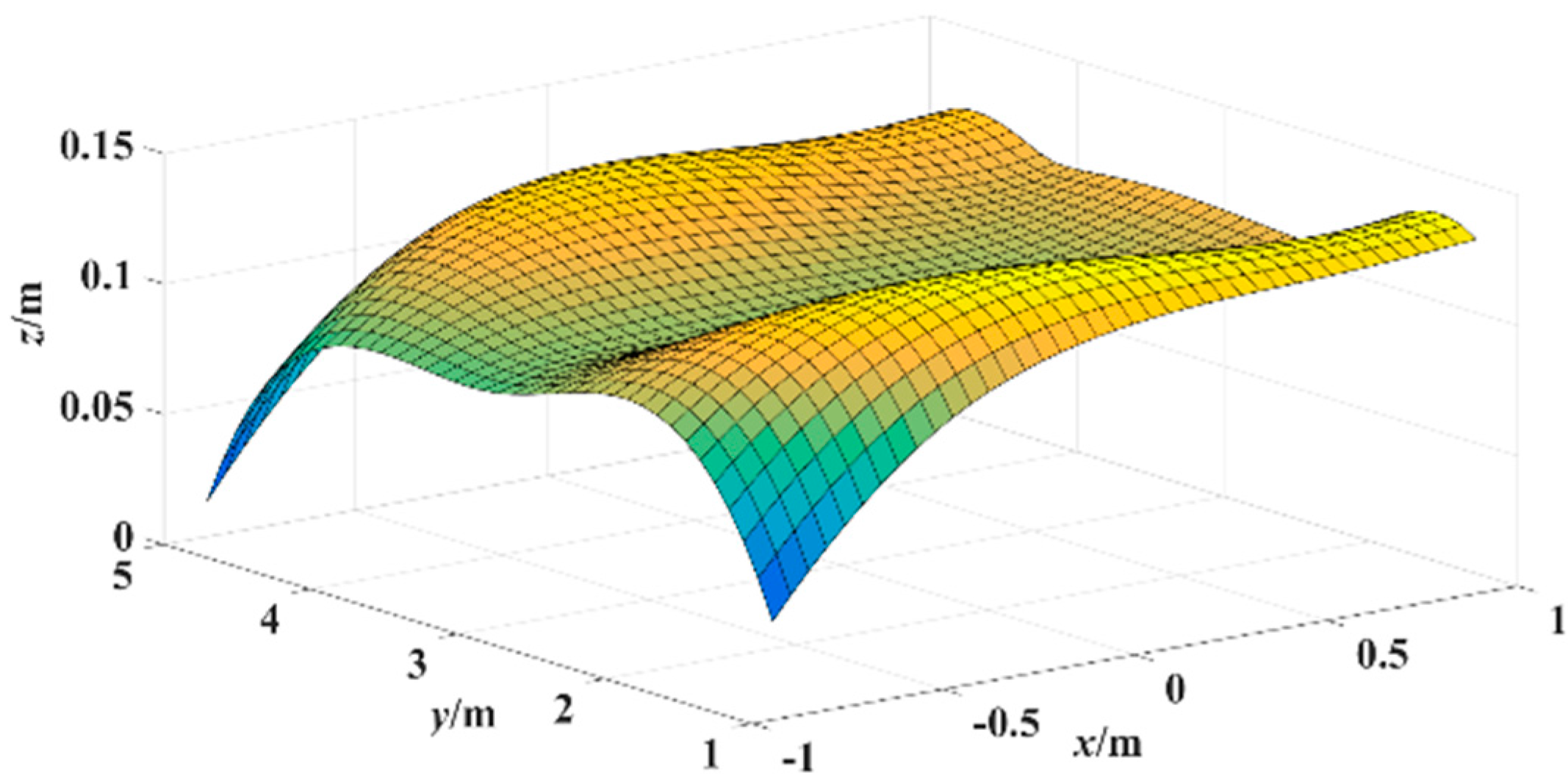
Figure 7, the error surface of plane localization is shown in
Figure 8 which applies a linear interpolation algorithm to the error of plane localization calculated with Equation (9). In
Figure 8,
x-y plane is the corridor ground, (
x,
y) coordinate represents the tester’s actual location, and coordinate
z represents the error of plane localization between the locations estimated and the actual locations. As shown in
Figure 8, the average error of the plane localization is around 10 cm with the proposed algorithm.
Figure 7.
Experimental data of plane localization with the miner’s lamp video collaborative localization.
Figure 7.
Experimental data of plane localization with the miner’s lamp video collaborative localization.
Figure 8.
Error surface of plane localization with the miner’s lamp video collaborative localization.
Figure 8.
Error surface of plane localization with the miner’s lamp video collaborative localization.
In order to evaluate the performance of the miner’s lamp collaborative localization algorithm under the condition that the miner moves continuously, cameras
C1,
C2 and
C3 were also applied to detect the movement of the tester in the corridor. The tester walked straight into the corridor from the entrance at a normal pace. Then, the tester turned about 45° at point A and walked about 1.5 m to point B. After that, the tester turned again at point B and walked toward point C.
Figure 9 shows the tester’s actual motion trajectory as well as the estimated motion trajectory with the proposed algorithm at interval of 0.5 s. In
Figure 9, the motion trajectory estimated is obtained by connecting two adjacent tester’s locations with line segments.
Figure 9.
Trajectory tracked with the miner’s lamp video collaborative localization.
Figure 9.
Trajectory tracked with the miner’s lamp video collaborative localization.
In the bottom right of
Figure 9, it can be observed that the location error is larger when the tester began to enter into the corridor. This is because when the tester began to enter into the corridor, the mapping points of tester’s cap-lamp were respectively on the edge of the imaging planes of cameras
C1,
C2 and
C3 at the same time. Due to the non-linear relationship between object and image on the imaging edge [
29], the mapping points of tester’s cap-lamp on the imaging planes will distort to some extent which will lead to larger location error. However, the maximum error for the movement orbit tracing is about 20 cm which is also acceptable to trace a miner. In contrast, the location error is smaller when the tester was around central area of the corridor. This is because the images of cameras
C1,
C2 and
C3 have a good linear relationship when the miner’s lamp is around central area which results in smaller errors.
4.2. Experiment in an Underground Tunnel
In order to evaluate the performances of the proposed algorithm in the realistic scenario of underground tunnels, a test was also carried out in the realistic scenario of an underground tunnel. The test was performed in the underground tunnel of Track Vibration Abatement and Control Laboratory at Beijing Jiaotong University, as shown in
Figure 10. The width and the altitude of the underground tunnel are 4 m with horseshoe shaped structure. In the test, six isomorphic cameras TY803-130 were deployed manually at the top of the tunnel by tripods. The cameras
C1,
C2,
C3,
C4,
C5 and
C6 were powered by lithium batteries.
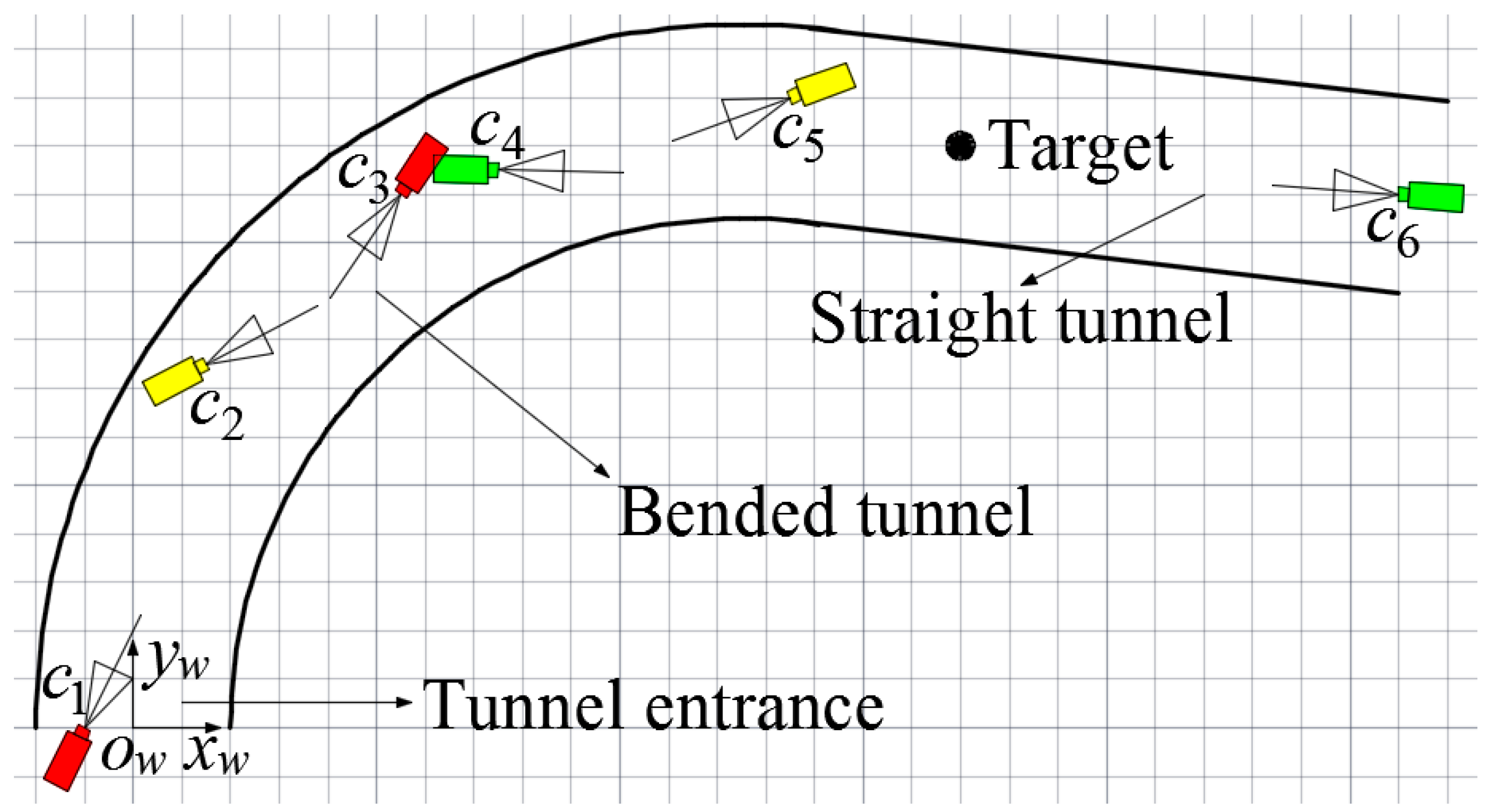
Figure 10 and
Figure 11 show the actual deployment of cameras and the topology of the experiment, respectively. A World Coordinate System (WCS) was established at the entrance of the tunnel with the transverse direction of the tunnel as
xw-axis, the longitudinal direction as
yw-axis and the altitude direction as
zw-axis, respectively. As shown in
Figure 11, the six isomorphic cameras were divided into three groups and the two cameras in the same group were deployed oppositely, with cameras
C1 and
C3 as the first group, cameras
C2 and
C5 as the second group and cameras
C4 and
C6 as the third group. Cameras
C1 and
C3 are deployed crosswise along the direction of center line of the bended tunnel to monitor the area of tunnel entrance together. In the same way, cameras
C2 and
C5 are deployed crosswise along the direction of center line of the bended tunnel to monitor the area of bended tunnel together. Similarly, cameras
C4 and
C6 are deployed crosswise along the longitudinal direction of the straight tunnel to monitor the area of straight tunnel together.
Figure 10.
(a) The actual deployment of cameras; (b) Gauge points on the ground of the tunnel.
Figure 10.
(a) The actual deployment of cameras; (b) Gauge points on the ground of the tunnel.
Figure 11.
Topology of the experiment.
Figure 11.
Topology of the experiment.
The intrinsic parameters of six cameras, including focal length
f, image resolution
M ×
N and the physical size of the photosensitive element CMOS are listed in
Table 1.
Table 3 lists the geometrical parameters of six cameras, including the world coordinates of the locations of cameras, the angle of yaw
φ between the WCS
xw-axis and the CCS
xw-axis in counterclockwise direction and the
θ between the WCS
zw-axis and the CCS
zw-axis in counterclockwise direction.
Table 3.
Geometrical parameters of cameras.
Table 3.
Geometrical parameters of cameras.
| | (xw,yw,zw)/m | φ/° | θ/° |
|---|
| Camera 1 | (−1.00, 0, 2.87) | −26.6 | 68.0 |
| Camera 2 | (1.50,7.50, 2.90) | −62.7 | 67.4 |
| Camera 3 | (5.50, 11.00, 2.88) | 146.1 | 70.6 |
| Camera 4 | (7.50, 11.50, 2.90) | −91.2 | 71.8 |
| Camera 5 | (13.50, 13.00, 2.87) | 110.1 | 71.2 |
| Camera 6 | (26.00, 11.00, 2.85) | 86.0 | 72.1 |
In the test, tester wore dark blue overalls and safety helmet with miner’s lamp turning on to simulate miners in underground tunnels. The tester walked into the tunnel at a normal pace. Cameras
C1,
C2,
C3,
C4,
C5 and
C6 worked together to monitor the tunnel and collected the video information at the same time.
Figure 12a–f showed the images of the tunnel collected by cameras
C1,
C2,
C3,
C4,
C5 and
C6 at a certain time point, respectively.
Cameras C1 and C3, cameras C2 and C5, and cameras C4 and C6 detected the miner’s lamp by the difference value between the current images from their video sequences and the background images, respectively. In the experiment, 60% maximum grey value of difference image is selected as threshold. Cameras C1, C2, C3, C4, C5 and C6 detected the miner’s lamp at interval of 0.5 s and calculated the pixel coordinates of mapping points of the miner’s lamp on their own imaging plane. Then, the pixel coordinates were translated to the coordinates in the WCS by applying Equations (1) and (2).
Therefore, when two cameras of a certain group detected the miner’s lamp simultaneously, two straight lines of three-dimension (3-D) between two cameras in the group and their corresponding mapping points of the miner’s lamp could be established in the WCS. By applying Equations (5) and (6) to calculate the optimum intersection of the two straight lines, the position coordinate of three-dimension (3-D) of the miner’s lamp in the WCS could be obtained which provided both the plane coordinate of the tester along the tunnel and the altitude of the miner’s lamp from the tunnel ground.
Figure 12.
(a) The image of the tunnel taken by camera C1; (b) The image of the tunnel taken by camera C2; (c) The image of the tunnel taken by camera C3; (d) The image of the tunnel taken by camera C4; (e) The image of the tunnel taken by camera C5; (f) The image of the tunnel taken by camera C6.
Figure 12.
(a) The image of the tunnel taken by camera C1; (b) The image of the tunnel taken by camera C2; (c) The image of the tunnel taken by camera C3; (d) The image of the tunnel taken by camera C4; (e) The image of the tunnel taken by camera C5; (f) The image of the tunnel taken by camera C6.
In order to evaluate the localization precision of the proposed algorithm when applied to the realistic scenario of underground tunnel, dozens of gauge points had been marked on the ground of the tunnel, as shown in
Figure 10b. Gauge points formed grids with horizontal and vertical spacing of one meter (1 m) on the ground of the tunnel.
In the test, the tester walked and passed these gauge points. The tester would stand and squat about one second (1 s) at each gauge point passed, respectively. The coordinates of gauge points in the WCS and the altitude of the miner’s lamp from the tunnel ground when the tester stood and squatted had been measured manually which provided actual locations of tester’s lamp. When the tester could be located by cameras of two groups simultaneously, the average value of localizations of the two groups was selected as the localization result of the tester’s lamp.
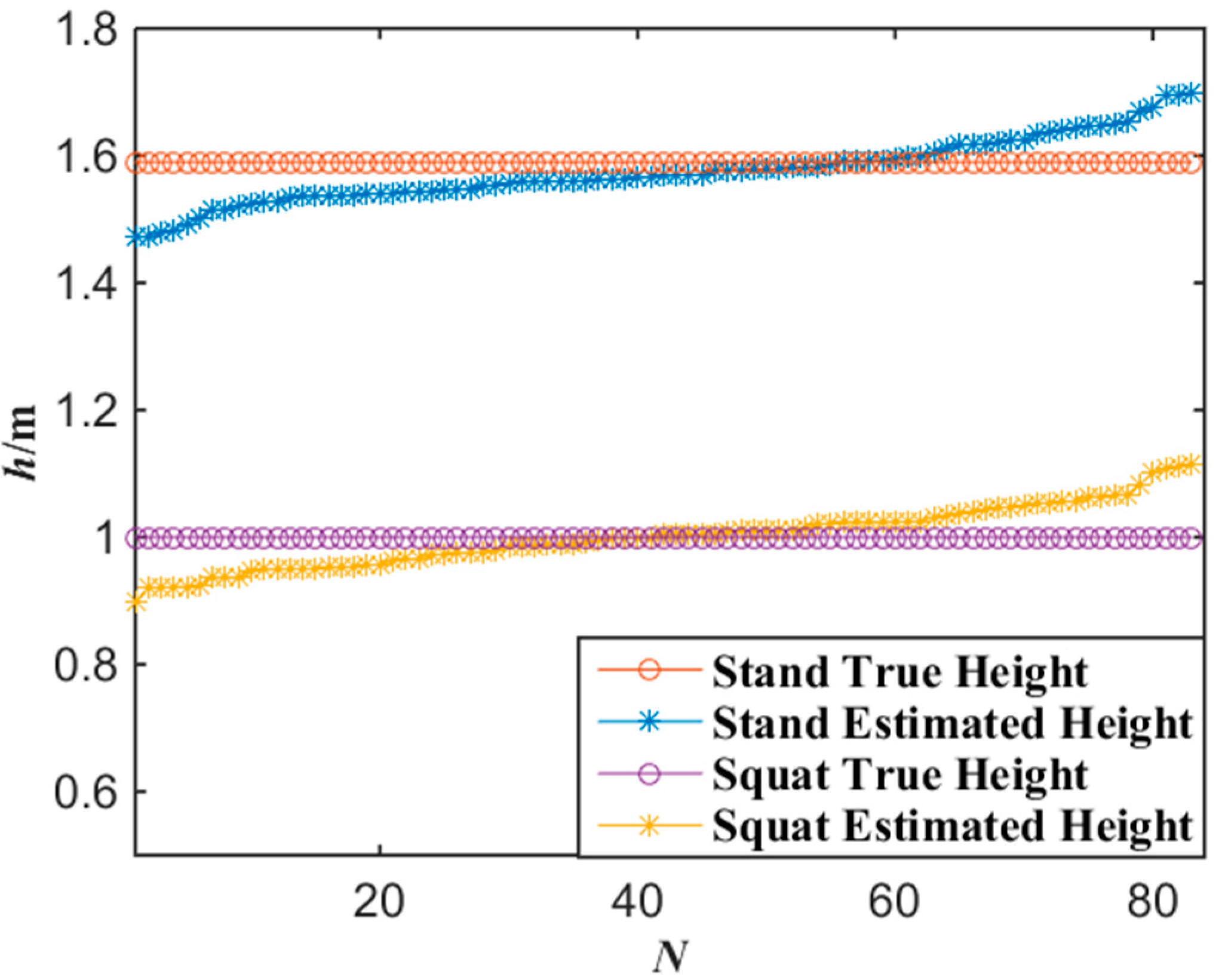
Figure 13 shows the experimental results of the altitude localization of tester’s lamp with the proposed algorithm where the tester stood and squatted at each gauge point passed, respectively. According to the experimental data of
Figure 13, when the number of gauge points is 83, the average error of the altitude localization for up-right and squat postures of the tester are 4.7 cm and 3.9 cm by applying Equations (7) and (8), respectively. Generally, when the error of altitude localization is less than 10 cm, the miners’ posture of standing or squatting can be correctly distinguished. Thus, 10 cm error of altitude localization can be accepted. If the altitude of a miner’s lamp is similar to a normal human altitude, it indicates that the miner is in the posture of walking or standing. However, if the altitude of a miner’s lamp is much lower than normal human altitude, it indicates that the miner may be in other postures, for example, in the posture of squat. No matter what posture a miner keeps, the altitude of a miner’s lamp can be obtained with the proposed miner’s lamp video collaborative localization algorithm based on WMSNs and the posture of the miner can be analyzed.
Figure 13.
Experimental data of altitude with the miner’s lamp video collaborative localization.
Figure 13.
Experimental data of altitude with the miner’s lamp video collaborative localization.
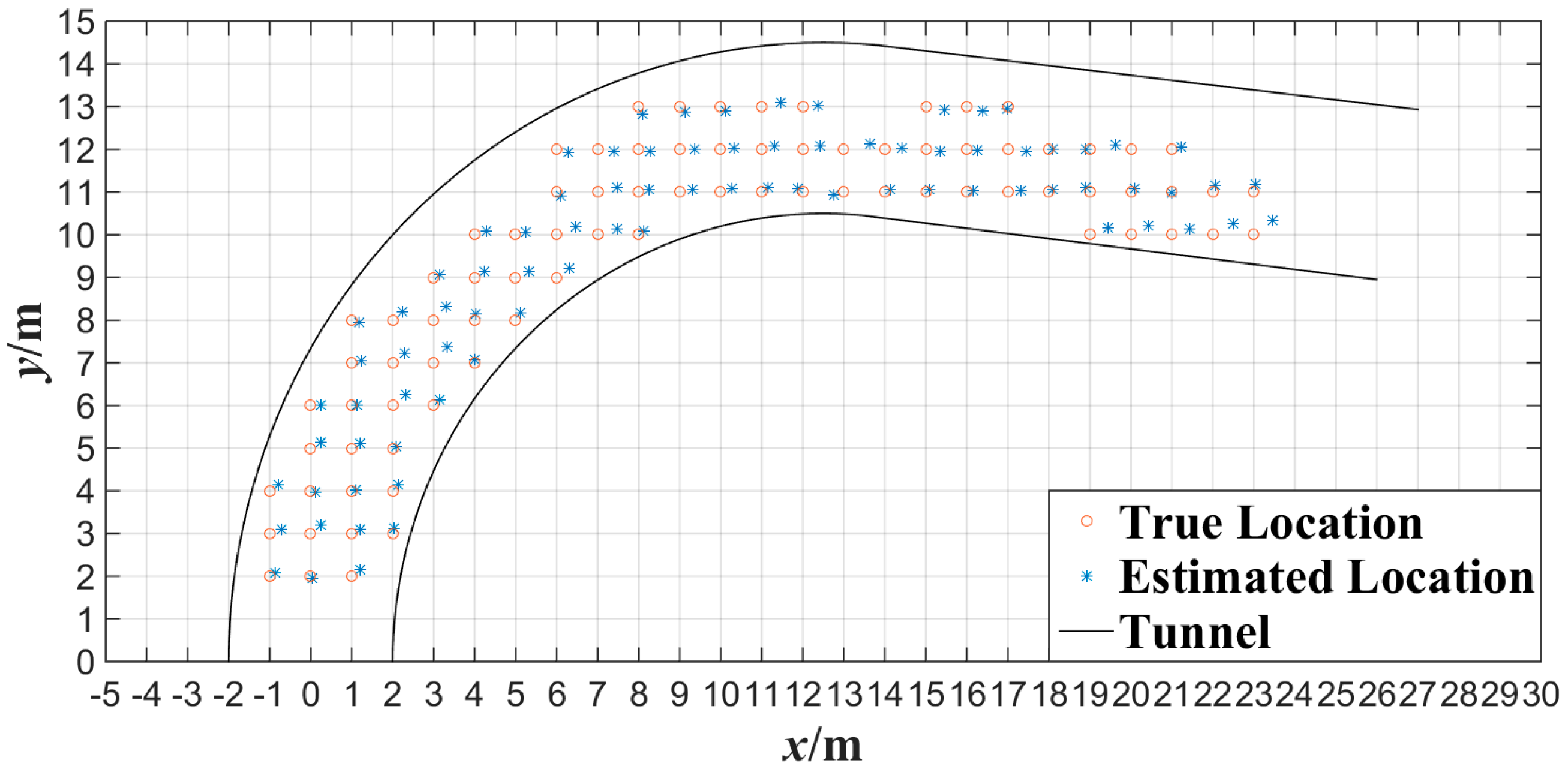
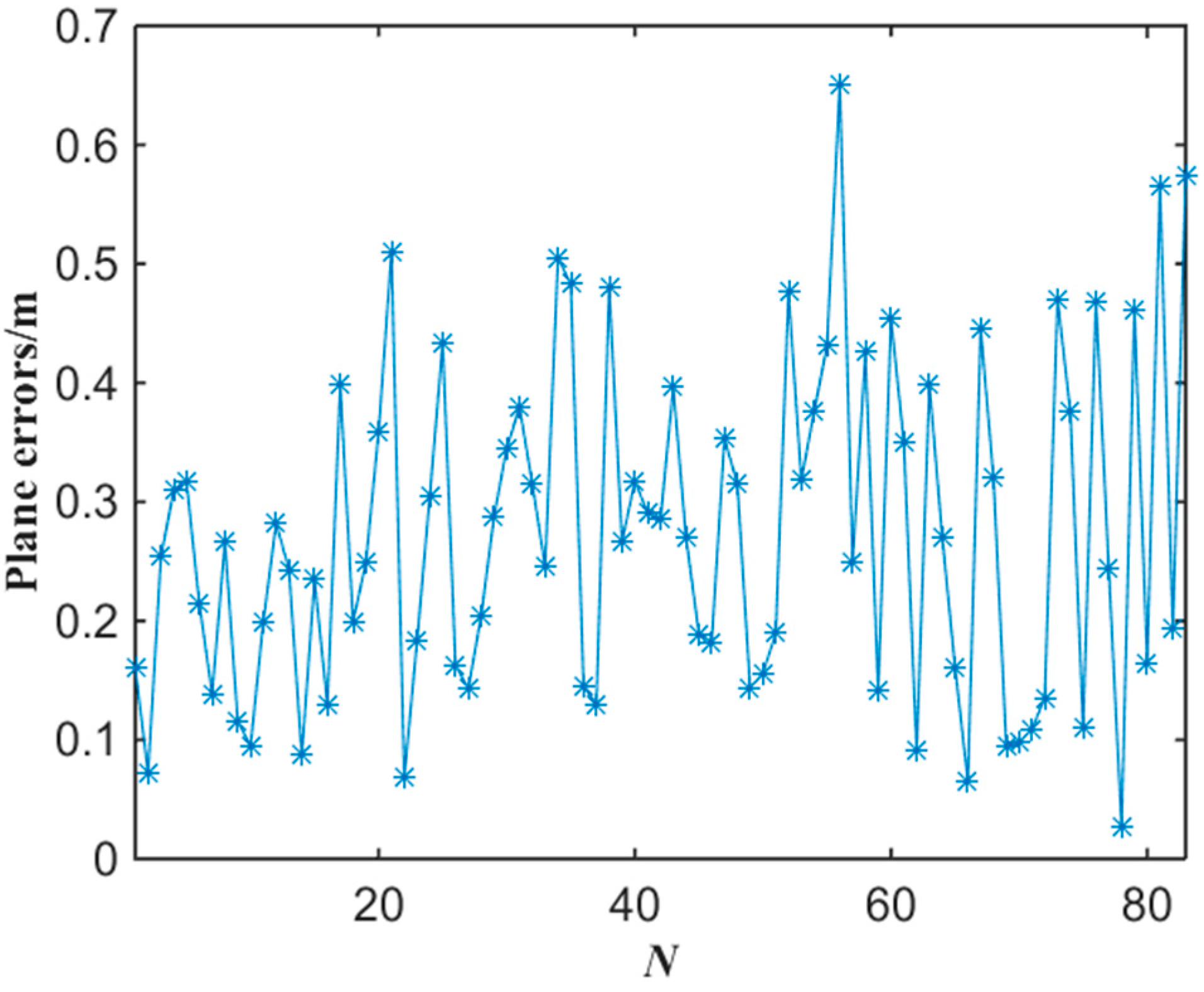
Figure 14 shows the experimental results of the plane localization of tester’s lamp with the proposed algorithm where the tester stood at each gauge point passed. Note that the intersection of grids in
Figure 14 is the gauge point with 1 m spacing. We can note that most of the location points estimated have errors in the same direction compared with the gauge points in
Figure 14. This is mainly because that the tester’s lamp was always toward the opposite direction of tunnel entrance while walking in the test. According to the experimental data of
Figure 14, the error of plane localization for up-right posture of the tester can be obtained by applying Equation (9) as shown in
Figure 15. When the number of gauge points is 83, the average error of the plane localization for up-right posture of the tester is 27.4 cm by applying Equation (10). Similarly, when the error of plane localization is less than 50 cm, there will be no obvious deviation for the estimation of plane localization or trajectory of miners along tunnels. The experimental results of
Figure 14 and
Figure 15 indicate that the plane coordinates of the tester on the ground of a tunnel can be precisely estimated with the proposed miner’s lamp video collaborative localization algorithm. It is worth mentioning that it can be ensured to recognize a miner’s lamp by adjusting the threshold effectively. However, since the illumination of miner’s lamp is generally intensive in different background illumination such as in
Figure 4 and
Figure 10, 60% maximum grey value of difference image was selected as the threshold, which provided a good performance of recognition and localization accuracy in both scenarios.
Figure 14.
Experimental data of plane localization with the miner’s lamp video collaborative localization.
Figure 14.
Experimental data of plane localization with the miner’s lamp video collaborative localization.
Figure 15.
The error of plane localization with the miner’s lamp video collaborative localization.
Figure 15.
The error of plane localization with the miner’s lamp video collaborative localization.
In order to evaluate the performance of the proposed algorithm under the condition that miner moves continuously, cameras
C1,
C2,
C3,
C4,
C5 and
C6 were also applied to detect the movement of the tester in the tunnel. The tester walked along a 90° broken line and a curved line in the tunnel at a normal pace, respectively.
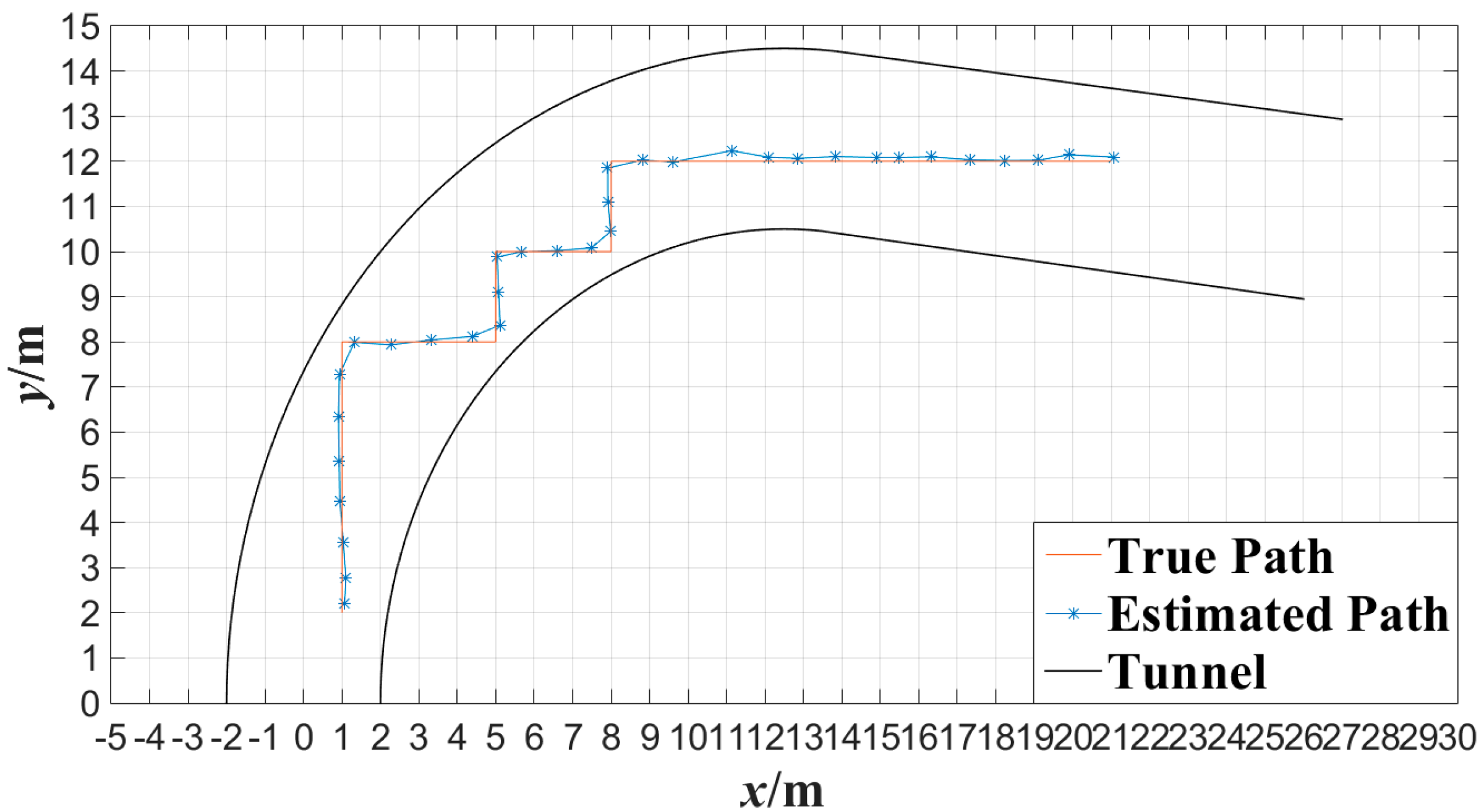
Figure 16 shows the tester’s actual motion trajectory along the 90° broken line as well as the estimated motion trajectory with the proposed algorithm at interval of 0.5 s.
Figure 16 shows the tester’s actual motion trajectory along the curved tunnel as well as the estimated motion trajectory with the proposed algorithm at interval of 0.5 s. In
Figure 16 and
Figure 17, the motion trajectory estimated is obtained by connecting two adjacent tester’s locations with line segments. From
Figure 16 and
Figure 17, it can be observed that the motion trajectory of a miner can be estimated accurately by locating the miner continuously with the proposed miner’s lamp video collaborative localization algorithm. By this way, a miner can be tracked along tunnels.
Figure 16.
Trajectory of broken line tracked with the miner’s lamp video collaborative localization.
Figure 16.
Trajectory of broken line tracked with the miner’s lamp video collaborative localization.
Figure 17.
Trajectory of curved line tracked with the miner’s lamp video collaborative localization.
Figure 17.
Trajectory of curved line tracked with the miner’s lamp video collaborative localization.