Normalized GNSS Interference Pattern Technique for Altimetry
Abstract
: It is well known that reflected signals from Global Navigation Satellite Systems (GNSS) can be used for altimetry applications, such as monitoring of water levels and determining snow height. Due to the interference of these reflected signals and the motion of satellites in space, the signal-to-noise ratio (SNR) measured at the receiver slowly oscillates. The oscillation rate is proportional to the change in the propagation path difference between the direct and reflected signals, which depends on the satellite elevation angle. Assuming a known receiver position, it is possible to compute the distance between the antenna and the surface of reflection from the measured oscillation rate. This technique is usually known as the interference pattern technique (IPT). In this paper, we propose to normalize the measurements in order to derive an alternative model of the SNR variations. From this model, we define a maximum likelihood estimate of the antenna height that reduces the estimation time to a fraction of one period of the SNR variation. We also derive the Cramér–Rao lower bound for the IPT and use it to assess the sensitivity of different parameters to the estimation of the antenna height. Finally, we propose an experimental framework, and we use it to assess our approach with real GPS L1 C/A signals.1. Introduction
Global Navigation Satellite Systems reflectometry (GNSS-R) is a well-established method for remotely sensing many relevant geophysical properties of the reflection surfaces. GNSS-R was first proposed within the frame of the PAssive Reflectometry Interferometric System (PARIS) project as a bistatic radar remote sensing technique for ocean altimetry using the L-band GPS signal [1]. Since then, GNSS-R has been demonstrated to be useful in other applications, such as monitoring water levels and snow height with a ground approach [2–4]. In this approach, the antenna, situated on a mast, receives a direct GNSS signal coming from the satellite and a nadir signal reflected by the observed surface. Assuming that the antenna position is known, we can compute the position of the surface of reflection. This approach provides precise localization and dating of the measures that allows for spatio-temporal comparison of water levels and snow cover, respectively [5–8]. These parameters are very important for flood monitoring and avalanche prevention, as well as for hydroelectric companies. Furthermore, the approach is noninvasive and can be easily implemented on a portable instrument and embedded in a vehicle with a mast [9].
GNSS-R altimetry can be carried out in two different ways, depending on the ranging principle: code altimetry and phase altimetry [10]. With code altimetry, only the GNSS code delay difference between the direct and reflected signals is used. With phase altimetry, the phase of the signal is also used for computing this delay difference [9]. The interference pattern technique (IPT) considers the behavior of the signal-to-noise ratio (SNR) of the received GNSS signal as a function of the satellite elevation [2,11]. The direct and reflected GNSS signals are combined at the antenna. Due to their different phase variations, the SNR oscillates at a rate proportional to the distance between the antenna and the surface of specular reflection. Unlike satellite or airborne reflection scenarios, ground GNSS receivers observe a coherent interference pattern if we consider a flat reflecting surface (compared to the carrier wavelength) on an area corresponding to the first Fresnel zone. A few previous works can be found analyzing the accuracy of these GNSS-R altimetry techniques [12–15]. Initial works proposed simple analytical models to describe the altimetry precision as a function of system/instrument parameters [12]. These methods rely on a considerable number of assumptions that might hold only for some specific scenarios and provide a pessimistic bound on the achievable precision. In [13], the authors proposed a Cramér–Rao lower bound (CRLB) closed expression for code altimetry. The CRLB is a statistical tool that provides a lower bound on the achievable estimation error for any unbiased estimator. A new derivation was proposed in [15] to compute the CRLB for code altimetry and a specific set of measurement data under multiple SNR scenarios.
Unfortunately, one of the main drawbacks of the IPT is that very long measurement times are usually needed. The observed SNR oscillates with the variation of the satellite elevation, but satellite elevation varies slowly, thus long measurement times are required to estimate the SNR frequency of oscillation. To reduce the estimation time to a fraction of one period of the SNR variations, we propose an alternative model for the measured SNR. This normalized model is based on the normalization of the measured signal amplitudes and is possible only after an initial calibration step. This calibration step consists of varying the antenna height of the receiver a value dh in order to obtain the minimum and maximum value of SNR for a given satellite elevation. Using the normalized model, we define a maximum likelihood estimate of the antenna height that allows for the reduction of the required estimation time to a fraction of one period of the SNR variation. We also derive the minimum antenna variation range dh as a function of the satellite elevation and deduce from this function the minimum observation time as a function of the satellite elevation rate. In addition, we derive the CRLB for the IPT and use it to assess the sensitivity of different parameters to the estimation of the antenna height. Finally, we propose a novel experimental framework, which we use to assess our approach with real signals.
This paper is organized as follows: Section 2 describes the interference pattern problem. The considered signal model is introduced as a function of the receiver height. The proposed estimator is presented in Section 3. Section 4 includes the derivation of the CRLB for the IPT and the proposed estimator performance assessment using synthetic signals. In Section 5, the proposed experimental framework is described, and the results obtained with real GPS L1 C/A signals within this framework are presented. Finally, Section 6 summarizes the paper, highlighting its main conclusions.
2. Interference Pattern Problem
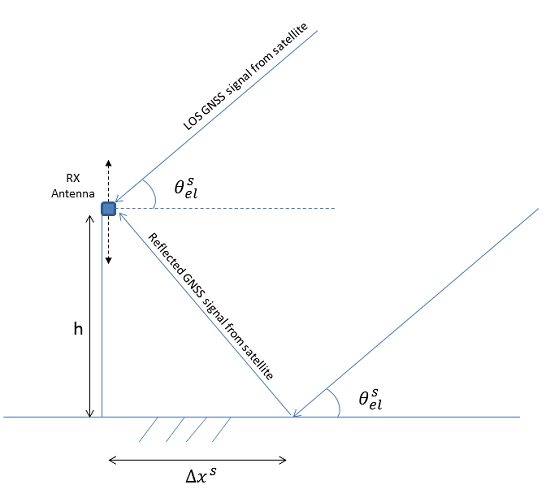
We show in Figure 1 the reflectometry principle for an antenna situated on a mast of height h. In our approach, we take into account the subset of satellites M that have a specular reflection on the surface to analyze. The antenna receives M scaled, time-delayed and Doppler-shifted signals with known signal structures. Each signal corresponds to the line-of-sight or direct signal (sDi) plus its corresponding specular reflection (sRi). The overall received signal can be modeled as:
In our current study, we will consider only the processing of the GPS L1 C/A signals. In this case, for an antenna mounted on a mast a few meters above the reflecting surface, the difference in GNSS signal path between the direct and the reflected signals will be small compared to the chip duration of the code. Thus, we can assume that Ri(t − τRi) ≈ Ri(t − τDi), where Ri(τ) is the autocorrelation of ci(t). According to the geometry depicted in Figure 1, it is easy to show that:
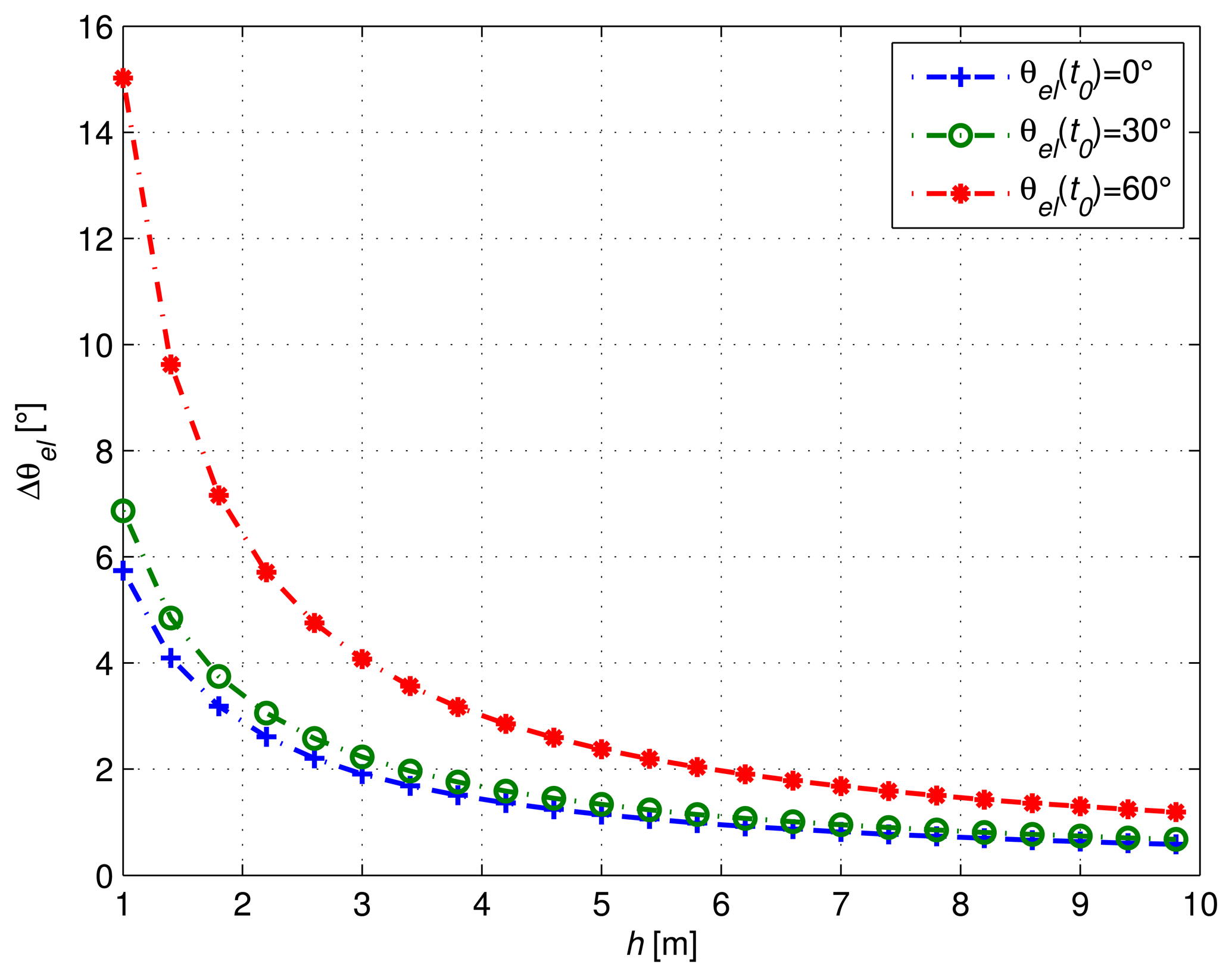
In order to get an accurate estimate of the frequency of cos(ϕR(t)) with classic approaches, one must observe at least one period of the signal. For a given initial elevation θel(t0), we define Δθel, the satellite elevation variation required to observe one period of the signal. Based on Equation (2) and using trigonometric identities, we can thus write:
Figure 2 shows the corresponding elevation variation required according to antenna height, for different θel(t0) values. In particular, we can see that for a height of 3 m, one period of the cosine can be observed for a satellite elevation variation of at least 2° when θel (t0) is close to 0°. If we consider, for example, a mean satellite elevation speed ωel = 10−3 °/s, we must thus wait at least 33 min to observe one period of the signal. In the next section, we propose a normalization procedure to decrease the required observation period.
3. Proposed Approach
3.1. Normalization of the GNSS Signal Amplitudes
As described in Equation (2), the phase ϕR(t) is a function of the satellite elevation and of the antenna height. Since the satellite elevation evolves slowly, we propose a calibration procedure that uses instead a variation of the antenna height. From Equation (6), the minimum and maximum values of AG(t) can be obtained when cos(ϕR(t)) is equal to −1 or one, respectively. They are defined by the following expressions:
From these two equations, we can deduce the sum of the square of the amplitudes and their product as:
Therefore, upon substituting Equations (11) and (10) into Equation (6), the single unknown parameter to estimate will be the phase delay ϕR(t), which is proportional to the height of the antenna and the sine of the known satellite elevation angle.
In order to always get the maximum and minimum value of AG, the variation of ϕR should be greater than or equal to 2π. According to Equation (2), the minimum variation of the antenna height dh should thus be equal to:
In Figure 3, we show the value of dhmin as a function of the satellite elevation. From this figure, we can see that a variation in the antenna height of 0.5 m is sufficient to observe a maximum and a minimum value for AG when the satellite elevation is higher than 12°.
3.2. Frequency Estimation
After down-conversion, the received signal is correlated with a local code replica. For the following derivation, we define the samples y[n] as the noisy post-correlation measurements obtained every t = nTint, where Tint is the coherent integration time. From Equation (6), we can define y[n] as:
Let us define:
Therefore, the factor β defines the frequency of cos(ϕR[n]), and its evolution is defined as a function of the sine of the elevation. The satellite elevation θel[n] is obtained from the current GPS ephemeris data and the estimated position of the GNSS receiver. In order to estimate β, after calibration, we can define the following model for AG[n]:
Finally ĥ a function of β̂ defined by
In the next section, we will derive the CRLB for Equation (14) in order to make a feasibility study and assess the expected performance of the proposed approach.
4. Performance Assessment
4.1. Cramér-Rao Lower Bound
We are interested in assessing the maximum theoretical accuracy that can be obtained when estimating the receiver height h. Unfortunately, Equation (14) is highly nonlinear, which makes it difficult to directly assess the impact of its different parameters over the estimation error. This nonlinearity is due mainly to the cosine function in the expression and is exacerbated by the presence of the root mean square. Instead, we propose to compute the CRLB for the signal model under consideration. The CRLB provides a lower bound on the variance of any unbiased estimator and, thus, will allow us to assess the performance of our estimator [17].
The signal model considered for AG [n] is provided in Equation (14). In order to provide more insightful results, we will express the reflected signal amplitude as AR = αAD, where α represents the attenuation coefficient due to reflection, assumed to be real and less than or equal to one. In addition, we define . Thus, we obtain:
The CRLB for h can be obtained by computing [I−1 (θ)]33, resulting in:
The purpose of the following discussion is to identify the effects of {h, α, λ, Δθel} parameters through simulation. In order to highlight the effect of a specific parameter, the CRLB is computed for different values of the parameter of interest, while the rest are kept fixed. We have set λ = λL1, corresponding to the GPS C/A L1 wavelength, a sampling period Ts = 1 sample/s and (water surface scenario for a typical smooth sea [18]) in all of the considered cases, unless otherwise specified.
4.2. Assessing the Initial Elevation on the CRLB
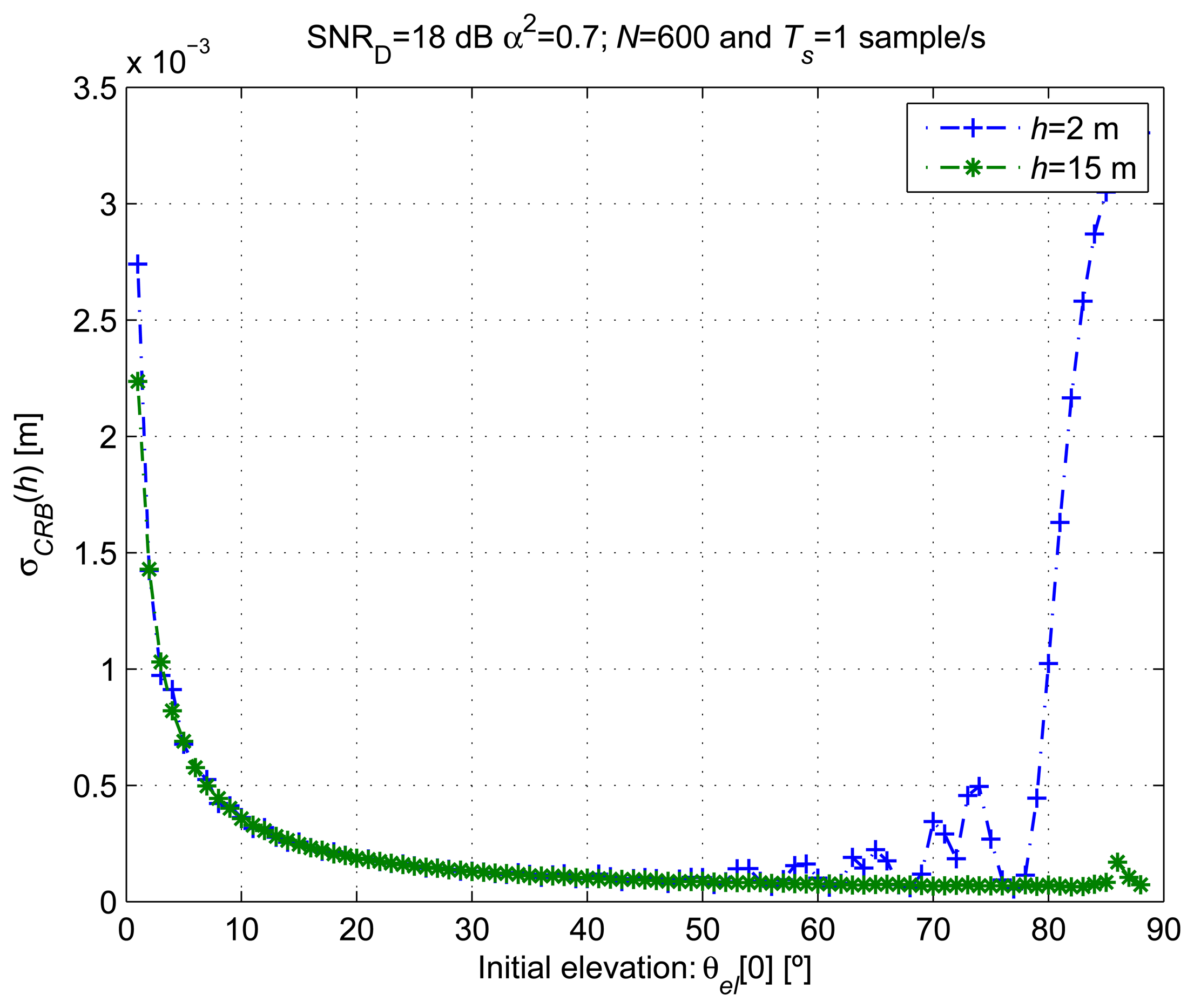
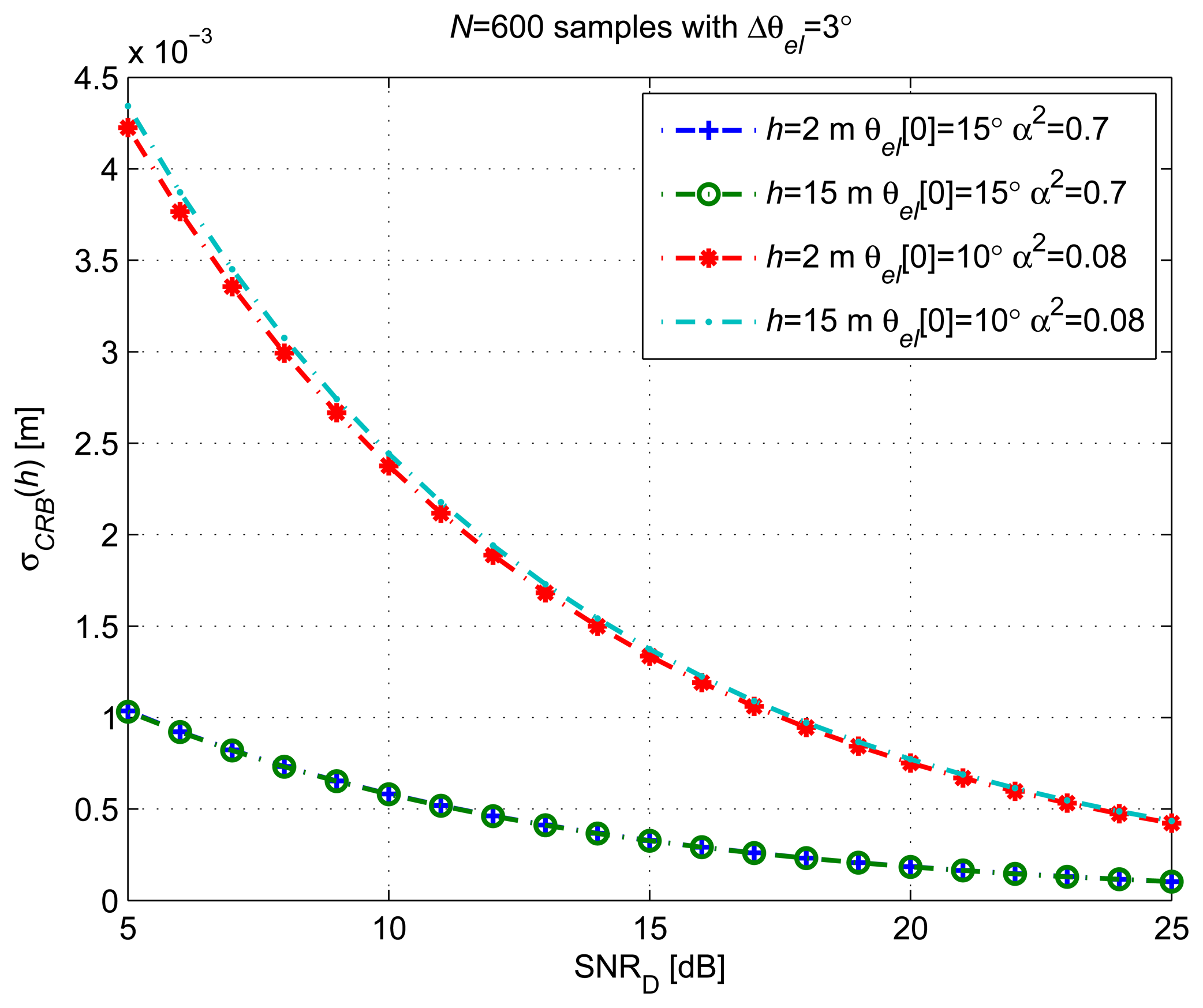
Figure 4 shows the for different satellite initial elevations (θel [0]) and antenna heights of h = 2 m and h = 15 m. Elevation variations of 3° were covered by N = 600 observations starting from the different θel [0] values. A reference SNRD = 18 dB was considered. The CRLB is computed from the probability density function (pdf) of the data observations. The estimation accuracy, lower-bounded by the CRLB, is related to the dependency of the data pdf on the unknown parameters (ξ). The CRLB is higher when the dependency between the observations and the parameter to estimate is weak.
Remarks:
When θel[0] is close to zero, the CRLB is several times higher than for higher θel[0] values and almost independent of h. In order to explain this behavior, we have shown in Figure 5Left the AG evolution for different h values over Δθel = 1° for θel [0] < 1°. The dependency between h and the observations becomes smaller when small θel[0] values are considered, even for the same number of samples.
When AG [n; ξ] (see Equation (19)) is at its maximum or minimum value, for a small period of observation, the signal tends to a constant equal to or , respectively. In this region, the signal evolution can be assumed to be monotone with almost null variation. The dependency between the observations and h decreases with the absolute value of the slope of AG [n; ξ] during the period of observation. In this case, the CRLB is as high as the slope of the signal is low.
We show in Figure 5Right that the frequency of the cosine evolution of AG [n;θ] decreases when θel tends to 90°. For h = 2 m and an observation interval of 600 s, we observe periodic CRLB increases with the satellite elevation when Equation (19) includes a minimum or a maximum. This situation corresponds to the peaks that appear in Figure 4 for h = 2 m and θel[0] > 50°. For h =15 m and an observation interval of 600 s, the minimum frequency of Equation (19) is too high to have a constant signal evolution in a period of observation. Thus, the CRLB for h =15 m does not present the peaks as when h = 2m.
From the observed behavior of the CRLB, we prefer using the proposed estimator with satellite elevations between 10° and 70° and antenna heights greater than 2 m to obtain better estimation accuracy. For low elevations, the CRLB is indeed high, independent of the antenna height. For elevations close to 90°, the CRLB increases for low antenna heights, because just a small portion of the signal AG [n; ξ] oscillation, considerably less than a period, is observed. As expected, this effect is exacerbated when the ωel is lower, and a shorter evolution of AG [n; ξ] is observed for the same measurement period.
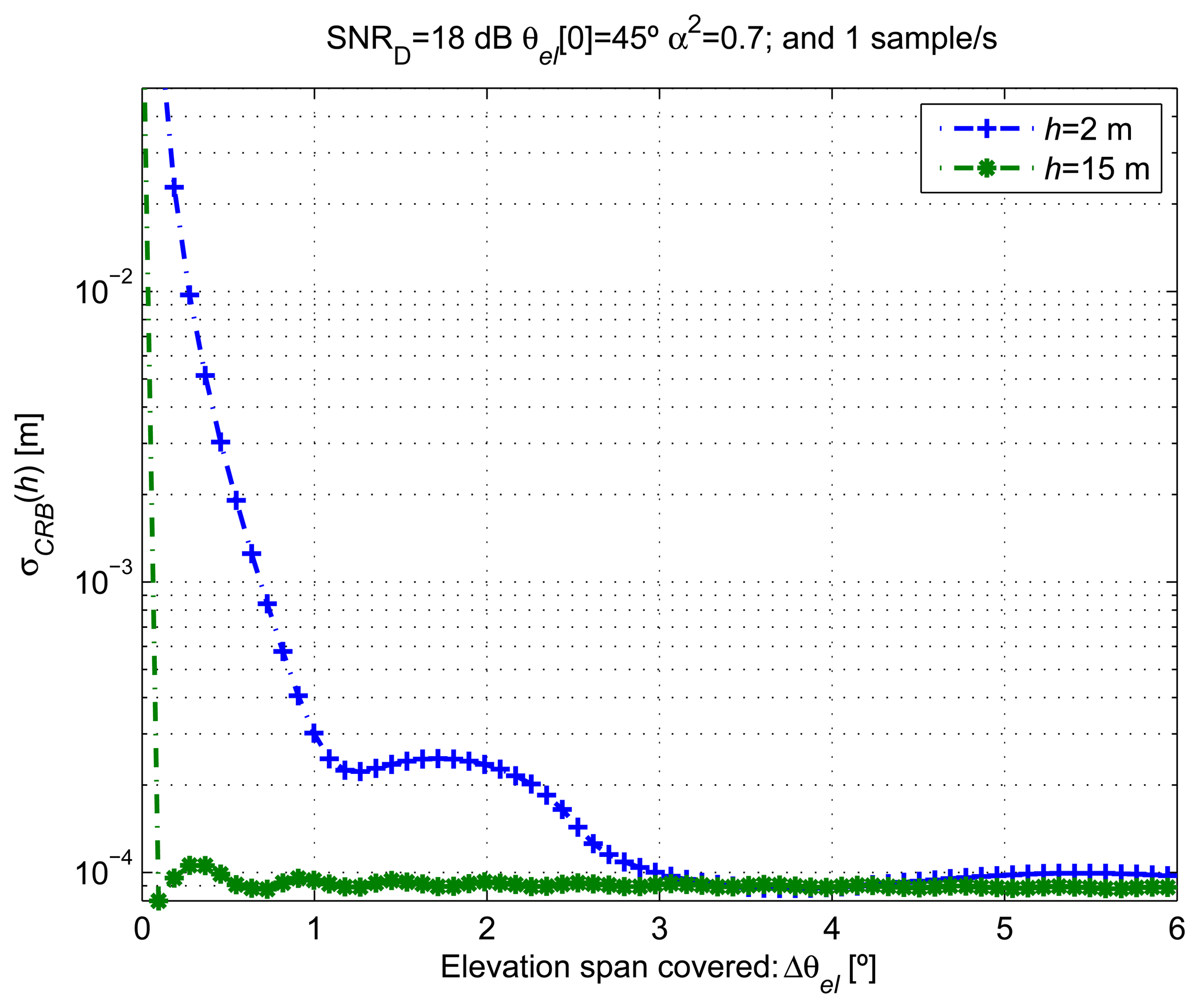
4.3. Assessing the Elevation Rate on the CRLB
Figure 6 shows the σCRB(h) computed for different elevation variations Δθ el from 0° to 6° with a fixed θel [0] = 45°. For receiver heights h = 2 m and h = 15 m, θel [0] = 45° was selected, since it approximately corresponds to a minimum of the AG [n; ξ] evolution, which corresponds to the worst scenario for the estimation of its frequency of oscillation. These Δθel values were generated by assuming constant ωel up to 10 × 10−3 °/s for a fixed measurement period of 600 s and a sampling rate of one sample/s. From the figure, we observe that by increasing Δθel, the variance decreases quickly at first, until an entire period of oscillation of the signal model is covered. This relation can be used to set the duration of the measurement time for our estimator, since we are interested in achieving the maximum possible accuracy with the minimum number of data observations. Unfortunately, the period of oscillation of our model depends on the true value of h and ωel. The measurement time required to achieve a certain target accuracy will depend on ωel, and in general, for faster ωel, shorter measurement periods will be required to achieve a similar estimation accuracy.
4.4. Assessing the Impact of Amplitude Ratio α on the CRLB
Figure 7 shows the αCRB(h) obtained for different receiver heights (h = 2 m and h = 15 m) and reflected/direct amplitude ratios (α) versus SNRD. The coefficient α can be interpreted as the square-root magnitude of the polarization-dependent reflection coefficient. For right-hand circular polarization (RHCP) of the incident signal and left-hand circular polarization (LHCP) of the reflected signal, α can be calculated as a function of θel and the dielectric constant of the scattering surface, assuming a smooth surface [18]. Two values for α have been selected. The first value, , corresponds to sea water, with a typical dielectric constant εW = 73.0 + i57.5 for λL1 = 0.19 m and an θel = 15° [18]. The second value, , corresponds to fresh snow at −2 °C, with εS = 1.45 + i2.76 × 10−4 for a θel ≃ 10° [19,20]. The Δθel considered covers a satellite elevation variation of 3° with an θel [0] = 15°, N = 600 samples and Ts = 1 sample/s.
The figure shows that the estimation error of h is inversely proportional to α. Some small differences are observed between different h values. These differences appear due to the differences on the oscillation period covered in each case by the interference pattern signal AG[n; ξ] used for computing the CRLB.
4.5. Estimator Performance Evaluation with Synthetic Data
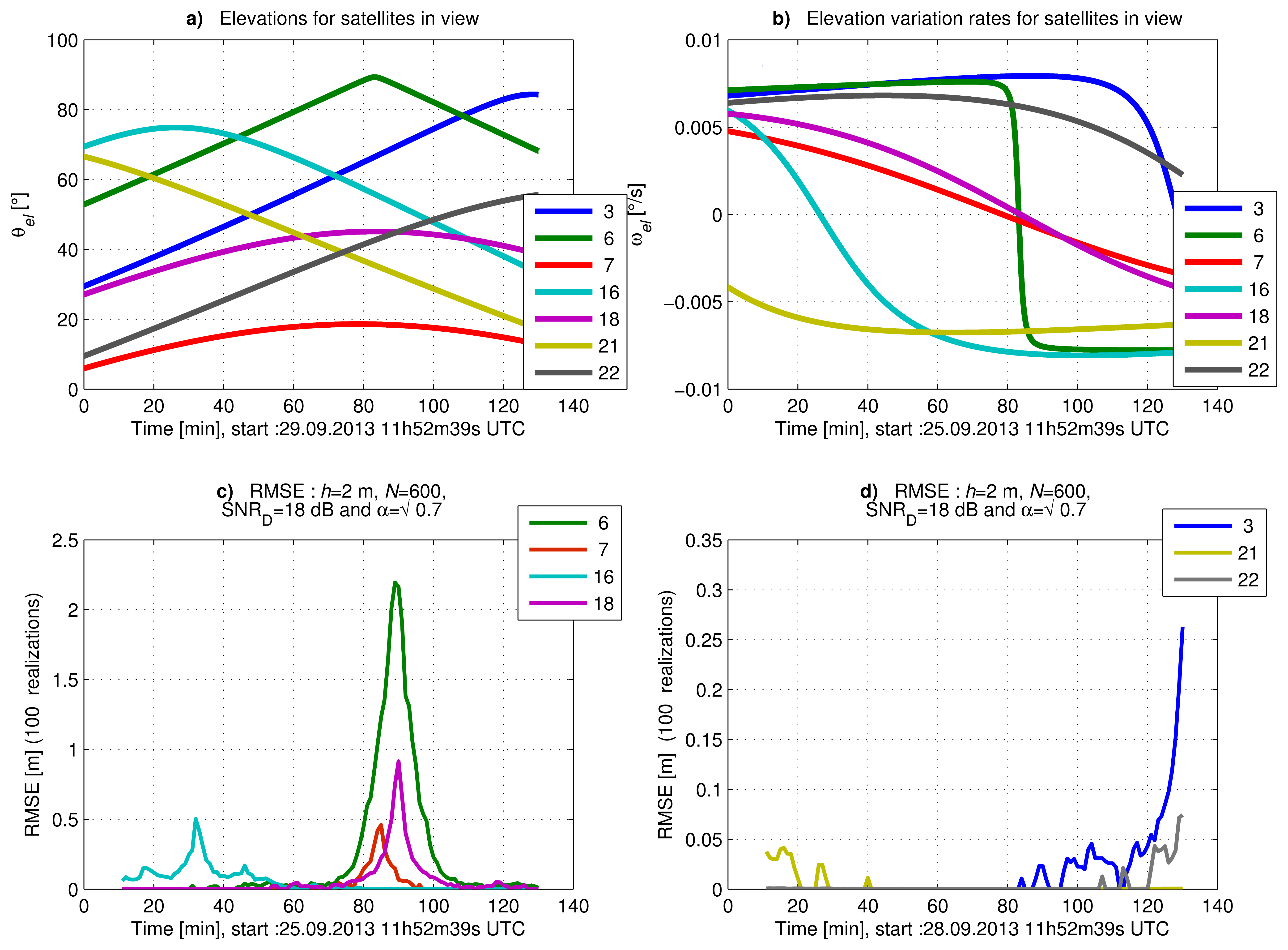
In order to complement the CRLB analysis, we want to assess the performance of the estimator proposed in Section 3 with synthetic data generated using real measurements of the satellites elevation (θel). These data were generated using the signal model defined in Equation (19) with a constant SNRD=18 dB for the direct signal and a sampling period of 1 s. The SNRD value selected is typically achieved at the post-correlation stage and matches the SNR corresponding to a carrier-to-receiver noise density C/N0 = 45 dB-Hz with a front-end bandwidth of 3 MHz, sampling at the Nyquist frequency, and a coherent integration time of 1 ms. The power ratio between the reflected and direct signals was set to . The satellite elevation measurements correspond to the satellites in view at Calais, France (50° 55′ 14.093″ N, 1° 56′ 59.44″ E), on 25 September 2013. The root-mean-square error (RMSE) was computed for 120 observation periods of 10 min, each period starting one minute later than the previous one, with N = 600 observations taken at one sample/s. We assume here that we are in a classic bistatic configuration depicted in Figure 1, where the receiver antenna is located at h = 2 m above the ground. The parameter ϕR is defined by Equation (2), and the height h is sought with a resolution step of 1 × 10−3 m in a bounded search space hspace = [0,5] m.
In Figure 8a,b, we show the satellites' elevations (θel) and their elevation rates (ωel), respectively, as a function of time. We present in Figure 8c,d the RMSE of ĥ for the proposed estimator as a function of time, computed using the Monte Carlo method with 100 realizations. Figure 8c shows the RMSE of the satellites reaching an elevation rate close to zero at some instant during the full observation interval. Figure 8d shows the RMSE of the satellites with a high elevation rate, except for the end of the observation interval.
We observe in Figure 8c that the RMSE increases when the satellite elevation rate decreases to less than 2 × 10−3 °/s. In the case of Satellite 6, the RMSE is higher, because the satellite elevation is close to 90°. We observe in Figure 8d that the RMSE of Satellites 3 and 22 increases for high elevations. This is due to a low elevation rate and, so, a low frequency of the SNR evolution. These results are in accordance with the CRLB study in Section 4.1.
Let us now compute the RMSE of ĥ for different SNR values and observation interval durations. As before, the SNR refers to the signal-to-noise ratio for the direct signal, and the power ratio between the direct and reflected signals is kept at . In Tables 1, 2 and 3, we report the RMSE obtained with 1000 realizations of the noisy AG signal, for observation intervals of 600 s, 300 s and 150 s, respectively. The duration of these observation intervals was selected considering that for a satellite elevation of 35° and an elevation rate ωel = 6.8 × 10−3 °/s (e.g., Satellite 3 at 12h02 UTC, in Figure 8), a complete period of signal is observed after 600 s, a half a period after 300 s and a quarter of a period after 150 s.
From the results in Tables 1, 2 and 3, we observe that the proposed estimator is consistent and that the RMSE increases when the SNR decreases, which was expected. In these tables, we have defined two different sets of satellites. The first set includes Satellites 3, 6, 21 and 22 (in bold in the Tables) with a high absolute elevation rate ωel ≥ 6 × 10−3 °/s. Satellites 3, 21 and 22 have low initial elevations between 20° and 35°, and Satellite 6 has a high elevation, superior to 70°. In the second set, we consider the Satellites 7, 16 and 18, with a low ωel. Satellite 7 has a low initial elevation of 18°; Satellite 18 has an initial elevation of 44°; and Satellite 16 has a high initial elevation of 75°.
For Satellites 3, 21 and 22, the RMSE values presented in Tables 1 and 2 approach the CRLB values computed in Section 4.1. In these cases, we reach centimeter accuracy due to the high elevation rate of these satellites. However, for a period of observation of 300 s and a C/N0 = 35 dB-Hz, we reach just decimeter accuracy, showing the limits of this technique. In Table 3, we see that centimeter accuracy is not reached for an observation interval of 150 s, even with C/N0 = 50 dB-Hz. For 150 s, the SNR evolution covers only a short part of the oscillation period during the interval of observation and can be considered monotonic. In this context, we observe in Table 3 that the RMSE strongly depends on the considered part of the SNR cosine evolution rather than on the satellite's ωel (e.g., Satellites 3, 6, 21 and 22).
For Satellite 6, the results shown in Tables 1 and 2 are less accurate despite the fact that its ωel is similar to those of Satellites 3, 21 and 22. This can be explained by the higher elevation of Satellite 6. This result is indeed in accordance with the CRLB study (Section 4.1), because in this case, the SNR evolves with a lower frequency, so we do not cover a full period of the SNR variation over the observation interval.
For Satellites 7, 16 and 18, the results shown in Tables 1, 2 and 3 are also in accordance with the expected accuracy from the CRLB study. In this case, we reach just meter accuracy, because we observe only a small fraction of the SNR variation period due to the the low θel of the satellites.
5. Experimental Framework
5.1. Experimental Results
In order to assess the proposed method, we constructed the following experimental setup to measure the height difference between two antennas, as depicted in Figure 9. The height difference is estimated with the interferometric approach described in Section 3. The advantage of the proposed assessment method is that we can have centimeter knowledge of the system geometry. Next, we derive the link between the height difference of the two antennas and the frequency of variation of the GNSS signal power.
For a height difference h between the two antennas, we have (see Appendix 2):
The phase delay between the direct signal received by the two antennas, , can be expressed as:
5.2. Assessment with Real Data
Figure 10 shows the experimental vehicle and the telescopic mast used. The figure also shows the system that gives us the ability to precisely change the height of the antenna installed on the top of the mast. The second direct antenna is situated on the roof of the car at a horizontal distance of Δx = 1.92 m. The height h between the two antennas is known, so we can derive the value of ϕ and define the complete geometry of the experimental system. We used the Novatel OEM4-G2 ProPak RT2W (GPS + WAAS/EGNOS) commercial receiver [21]. The two antennas were connected using a passive RF-combiner. The C/N0 measurements, as well as the satellite elevation values were provided by the receiver at a rate of 1 Hz.
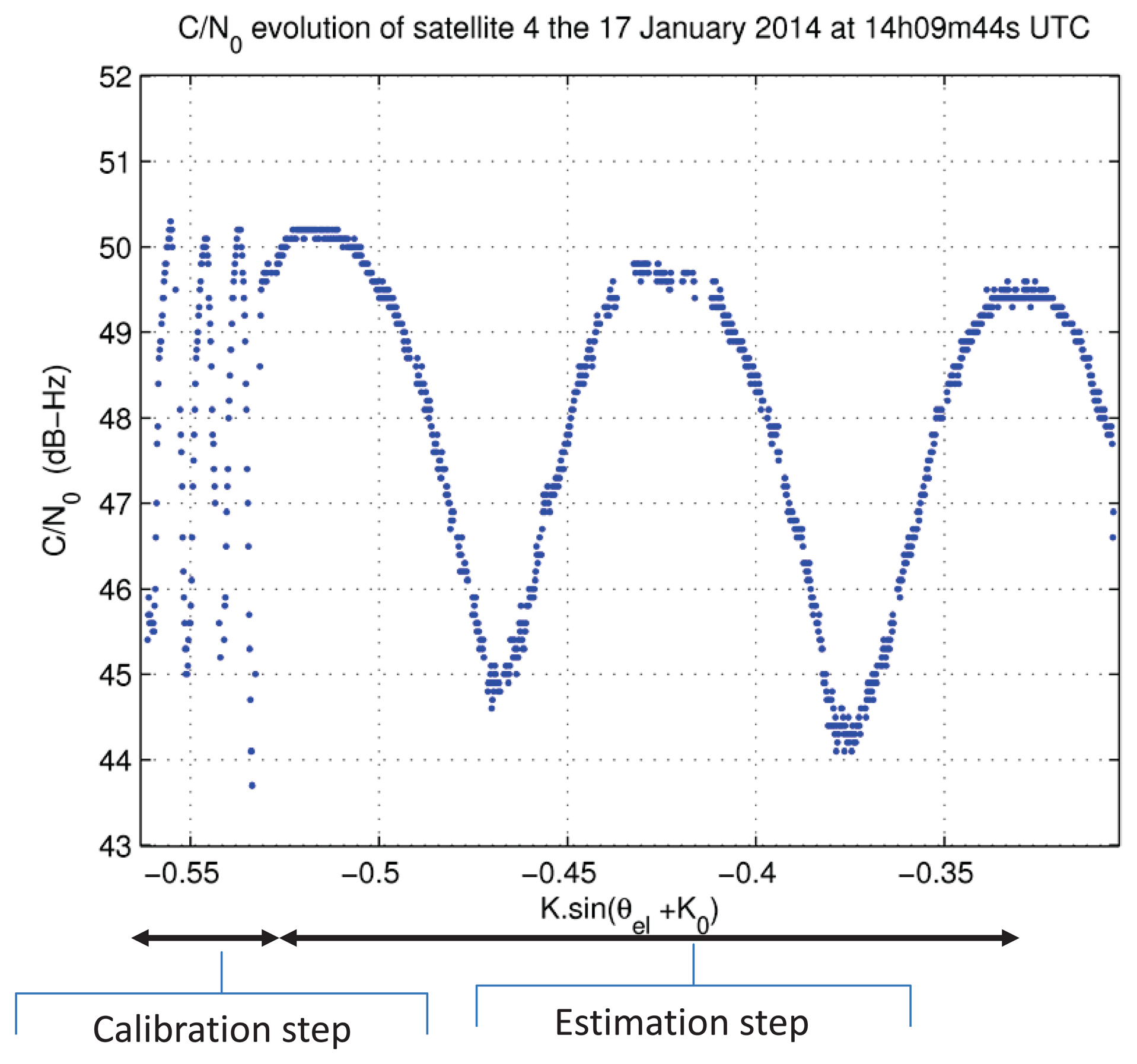
We show in Figure 11 an example of C/N0 evolution as a function of of K sin(θel + K0). In this figure, we differentiate two periods of time in the signal. These two periods correspond to two different processing steps: the calibration step and the estimation step.
We report in Tables 4 and 5 the estimated height (ĥ) obtained at Calais, France (50° 55′ 14.093″ N, 1° 56′ 59.44″ E), on 17 January 2014, with the proposed method. The reference height used was href = 2.13 m at 14h09 UTC and href = 8.24 m at 14h50 UTC. These heights were manually tape measured Figures 12 and 13 show the constellation of the visible satellites during the measurement periods and the direction of the experimental setup (working direction). We plotted in these figures the satellites' trajectories, with a star marking the end of each trajectory. In the experiments, ĥ was estimated with N = 600 observation samples and an search step resolution of 1 × 10−3 m in a bounded interval of ĥ = [href − 2, href + 2] m.
For href = 2 13 m the signals from Satellites 5 9 20 16 and 29 were not considered due to their low C/N0 and low elevation angles In these cases, the proposed estimator performed poorly, and the estimated height was far from href. The estimated height obtained for Satellites 4, 7, 10 and 23 showed a difference with the href between 2 cm and 9 cm. The mean estimated height is 2.15 m.
For href = 8.24 m, the signals from Satellites 16, 23, 26 and 29 were again not considered due to their low C/N0s. The results obtained with Satellites 2, 5, 8 and 9 are closer to href, with a difference between 1 cm and 5 cm. In this case, the mean estimated height is 8.25 m.
We can conclude that, after the calibration step, the proposed estimator can achieve centimeter accuracy under the experimental setup for a period of observation of 600 s.
6. Conclusions
In this article, we used an IPT to estimate the height between an antenna and a ground surface, where a GNSS signal has been reflected. We proposed to normalize the SNR measurements in order to construct a model of its evolution over time. The proposed estimator is based on two steps: A calibration step and an estimation step. The aim of the calibration step is to measure the maximum and minimum values of the SNR (or, equivalently, the C/N0) amplitude, in order to model the SNR variations for a bounded interval of possible surface heights.
The maximum likelihood estimate of the antenna height constructed with this nonlinear model was assessed in a study of the CRLB of the model. In this study, we showed that the accuracy of the estimation can be defined as a function of the satellite elevation, the elevation rate, the C/N0 and the power ratio between the direct and reflected signal.
In order to assess the method, we used synthetic data and verified that the proposed estimator is consistent with the number of observation samples and the C/N0 of the GNSS signal. We also showed that, using the proposed calibration step, we can expect centimeter accuracy with half a period of the SNR oscillation when we are in the best scenario. These conditions were identified using the CRLB.
Finally, we proposed an experimental framework that uses two direct signals received in different locations. The results using real data from field measurements showed that the proposed estimator can provide centimeter accuracy for a period of observation of 10 minutes within this framework.
Acknowledgments
This work has been partially supported by: the Swiss National Science Foundation (SNSF) under Grants No. 200020-134766/1 and 200020-153052/1; the Syndicat Mixte de la Côte d'Opale de la région Nord pas de Calais.
Author Contributions
The work presented in this paper was carried out in collaboration between all authors. Miguel Angel Ribot derived the CRLB for the IPT, carried out the simulations, and verified the experimental results against the theoretical derivation. Cyril Botteron and Serge Reboul contributed to CRLB-related analysis and discussions. Jean-Christophe Kucwaj, Georges Stienne, Jean-Bernard Choquel and Serge Reboul proposed the normalization concept, developed the experimental framework, and used it to perform the experimental campaign. All authors contributed to revisions of the manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix 1: FIM Computation
The Fisher information matrix (I (ξ)) for a deterministic parameter vector ξ is defined as [17]:
The observed samples are modeled as y [n; ξ] = AG [n; θ] + w [n], where AG [n; θ] is the signal component and w [n] is zero-mean AWGN with variance . In general, for a vector signal parameter estimated in the presence of AWGN, Equation (32) yields:
In Section 4.1, the signal model AG [n; ξ] considered is:
Every element of the FIM, [I(ξ)]ij, is computed using a combination of the following partial derivatives of AG[n; θ]:
In this way, the FIM is defined as a symmetric 3 × 3 matrix as follows:
Appendix 2: Experimental Framework Geometry Computation
Figure A1 shows the geometry of the experimental framework and defines two frames, (O,x,y,z) and (O,X,Y,Z), for the geometry computation. The plane (O,x,z) contains the car antenna A and the mast antenna B. The plane (O,X,Z) contains the mast antenna and the satellite in view.
The relation between both frames is:
The path difference a is defined with point H, which corresponds to the orthogonal projection of point A over BD, where BD is the line from the mast antenna to the satellite in view We thus have YH = 0, so yH = xH tan θel and .
, with XB = 0 and ZB = h, implies that ZH − h = XH tan θel and .
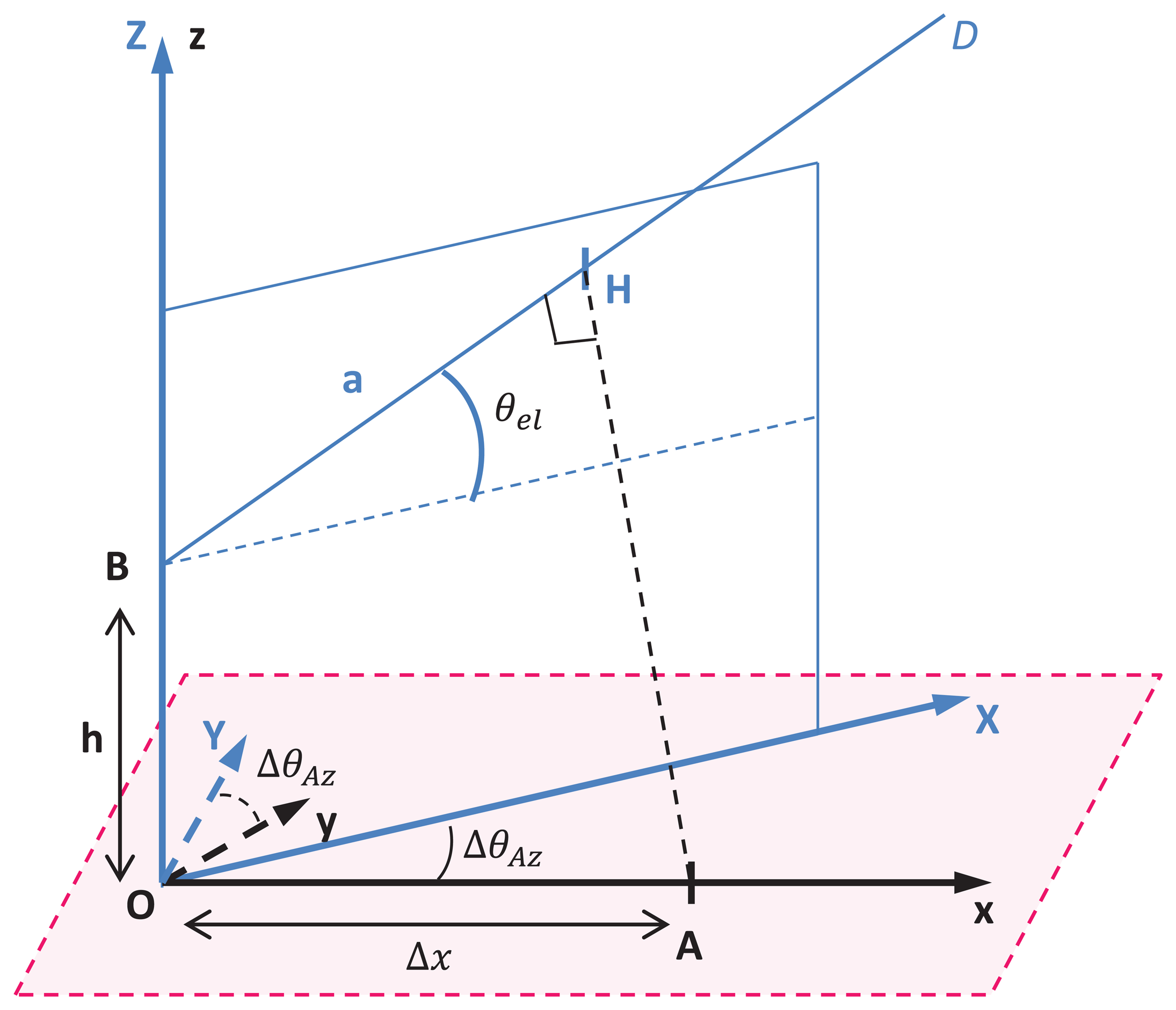
(AH) and (BH) being orthogonal, , so:
Finally,
And:
References
- Martin-Neira, M. A passive reflectometry and interferometry system (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Larson, K.M.; Small, E.E.; Gutmann, E.; Bilich, A.; Axelrad, P.; Braun, J. Using GPS multipath to measure soil moisture fluctuations: Initial results. GPS Solut. 2007, 12, 173–177. [Google Scholar]
- Rodriguez-Alvarez, N.; Aguasca, A.; Valencia, E.; Bosch-Lluis, X.; Camps, A.; Ramos-Perez, I.; Park, H.; Vall-llossera, M. Snow Thickness Monitoring Using GNSS Measurements. IEEE Geosci. Remote Sens. Lett. 2012, 9, 1109–1113. [Google Scholar]
- Jin, S.; Feng, G.; Gleason, S. Remote sensing using GNSS signals: Current status and future directions. Adv. Space Res. 2011, 47, 1645–1653. [Google Scholar]
- Botteron, C.; Dawes, N.; Leclère, J.; Skaloud, J.; Weijs, S.; Farine, P.A. Soil Moisture & Snow Properties Determination with GNSS in Alpine Environments: Challenges, Status, and Perspectives. Remote Sens. 2013, 5, 3516–3543. [Google Scholar]
- Cardellach, E.; Fabra, F.; Nogués-Correig, O.; Oliveras, S.; Ribó, S.; Rius, A. GNSS-R ground-based and airborne campaigns for ocean, land, ice, and snow techniques: Application to the GOLD-RTR data sets. Radio Sci. 2011, 46. n/a–n/a. [Google Scholar]
- Fabra, F.; Cardellach, E.; Nogues-Correig, O.; Oliveras, S.; Ribo, S.; Rius, A.; Belmonte-Rivas, M.; Semmling, M.; Macelloni, G.; Pettinato, S.; Zasso, R.; D'Addio, S. Monitoring sea-ice and dry snow with GNSS reflections. 3837–3840.
- Camps, A.; Bosch-Lluis, X.; Ramos-Perez, I.; Marchán-Hernández, J.F.; Rodríguez, N.; Valencia, E.; Tarongi, J.M.; Aguasca, A.; Acevo, R. New passive instruments developed for ocean monitoring at the Remote Sensing Lab - Universitat Politècnica de Catalunya. Sensors 2009, 9, 10171–10189. [Google Scholar]
- Stienne, G.; Reboul, S.; Choquel, J.B.; Benjelloun, M. GNSS code and phase processing techniques in a ground-based mobile altimetry system. 1–5.
- Ruffini, G. A brief introduction to remote sensing using GNSS reflections. IEEE Geosci. Remote Sens. Soc. Newslett. 2006, 15–22. [Google Scholar]
- Rodriguez-Alvarez, N.; Camps, A.; Vall-llossera, M.; Bosch-Lluis, X.; Monerris, A.; Ramos-Perez, I.; Valencia, E.; Marchan-Hernandez, J.F.; Martinez-Fernandez, J.; Baroncini-Turricchia, G.; Perez-Gutierrez, C.; Sanchez, N. Land Geophysical Parameters Retrieval Using the Interference Pattern GNSS-R Technique. IEEE Tran. Geosci. Remote Sens. 2011, 49, 71–84. [Google Scholar]
- Lowe, S.T.; LaBrecque, J.L.; Zuffada, C.; Romans, L.J.; Young, L.E.; Hajj, G.A. First spaceborne observation of an Earth-reflected GPS signal. Radio Sci. 2002, 37, 7:1–7:28. [Google Scholar]
- Germain, O.; Ruffini, G. A revisit to the GNSS-R code range precision.
- Camps, A.; Martin, F.; Park, H.; Valencia, E.; Rius, A.; D'Addio, S. Interferometric GNSS-R achievable altimetric performance and compression/denoising using the wavelet transform: An experimental study. 7512–7515.
- D'Addio, S.; Martin-Neira, M.; Martin, F.; Park, H.; Camps, A. GNSS-R altimeter performance: Analysis of Cramer-Rao lower bounds. 1–4.
- Pany, T. Navigation Signal Processing for GNSS Software Receivers. In GNSS Technology and Applications Series; Artech House: Norwood, MA, USA, 2010. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall PTR: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Zavorotny, V.; Voronovich, A. Scattering of GPS signals from the ocean with wind remote sensing application. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar]
- Jacobson, M. Dielectric-Covered Ground Reflectors in GPS Multipath Reception—Theory and Measurement. IEEE Geosci. Remote Sens. Lett. 2008, 5, 396–399. [Google Scholar]
- Larson, K.M.; Gutmann, E.D.; Zavorotny, V.U.; Braun, J.J.; Williams, M.W.; Nievinski, F.G. Can we measure snow depth with GPS receivers? Geophys. Res. Lett. 2009, 36, L17502. [Google Scholar]
- NovAtel Inc. NovAtel OEM4-G2 Receiver Product Brochure; NovAtel: Calgary, Canada. Available online: http://www.novatel.com./Documents/Papers/oem4g2.pdf (accessed on 4 June 2014).







| SNR | 18 dB | 13 dB | 8 dB |
|---|---|---|---|
| Satellite | |||
| Sat 3 at 11h57UTC | 0.001 | 0.001 | 0.027 |
| Sat 6 at 12h32 UTC | 0.005 | 0.016 | 0.090 |
| Sat 21 at 13h52 UTC | 0.001 | 0.001 | 0.014 |
| Sat 22 at 12h42 UTC | 0.001 | 0.001 | 0.045 |
| Sat 7 at 13h22 UTC | 0.072 | 0.131 | 0.432 |
| Sat 16 at 12h12 UTC | 0.107 | 0.143 | 0.596 |
| Sat 18 at 13h12 UTC | 0.098 | 0.1302 | 0.484 |
| SNR | 18 dB | 13 dB | 8 dB |
|---|---|---|---|
| Satellite | |||
| Sat 3 at 11h57 UTC | 0.005 | 0.027 | 0.152 |
| Sat 6 at 12h32 UTC | 0.059 | 0.080 | 0.286 |
| Sat 21 at 13h52 UTC | 0.001 | 0.018 | 0.224 |
| Sat 22 at 12h42 UTC | 0.001 | 0.011 | 0.152 |
| Sat 7 at 13h22 UTC | 0.183 | 0.245 | 0.849 |
| Sat 16 at 12h12 UTC | 0.232 | 0.313 | 1.162 |
| Sat 18 at 13h12 UTC | 0.457 | 0.625 | 1.558 |
| SNR | 18 dB | 13 dB | 8 dB |
|---|---|---|---|
| Satellite | |||
| Sat 3 at 11h57 UTC | 0.116 | 0.153 | 0.681 |
| Sat 6 at 12h32 UTC | 0.146 | 0.198 | 0.708 |
| Sat 21 at 13h52 UTC | 0.067 | 0.111 | 0.431 |
| Sat 22 at 12h42 UTC | 0.123 | 0.168 | 0.644 |
| Sat 7 at 13h22 UTC | 0.412 | 0.553 | 1.473 |
| Sat 16 at 12h12 UTC | 0.685 | 0.937 | 1.889 |
| Sat 18 at 13h12 UTC | 1.340 | 1.570 | 2.464 |
| Satellite PRN | Estimated height (ĥ) (m) | |K sin(θel + K0)| mean variation (s−1) | C/N0,min (dB-Hz) | C/N0,max (dB-Hz) | Comment |
|---|---|---|---|---|---|
| 2** | 2.86 | 7.0 × 10−5 | 43.8 | 50.5 | low variation of |K sin(θel + K0)| |
| 4 | 2.22 | 1.7 ×10−4 | 44.8 | 50.2 | |
| 7 | 2.16 | 1.5 × 10−4 | 45.6 | 49.8 | |
| 8* | 1.93 | 1.6 × 10−4 | 39.5 | 47 | low C/N0 |
| 10 | 2.10 | 1.0 × 10−4 | 47.5 | 51.4 | |
| 13** | 1.53 | 9.6 × 10−5 | 48.4 | 51.2 | |
| 16 | 2.11 | 1.4 × 10−4 | 35.5 | 45.3 | low C/N0 |
| 23 | 2.19 | 1.5 × 10−4 | 44.1 | 49.8 |
| Satellite PRN | Estimated height (ĥ) (m) | |K sin(θel + K0)| mean variation (s−1) | C/N0,min (dB-Hz) | C/N0,max (dB-Hz) | Comment |
|---|---|---|---|---|---|
| 2 | 8.29 | 7.2 × 10−5 | 44.5 | 50.2 | low variation of |K sin(θel + K0)| |
| 5 | 8.27 | 1 × 10−4 | 42.1 | 49.2 | |
| 7** | 8.79 | 5.9 × 10−5 | 47.6 | 50.9 | low variation of |K sin(θel + K0)| |
| 8 | 8.23 | 1.2 × 10−4 | 43.9 | 47.8 | |
| 9 | 8.19 | 1.3 × 10−4 | 44 | 49.1 | |
| 10** | 8.92 | 5.5 × 10−5 | 48.4 | 51.2 | low variation of |K sin(θel + K0)| |
| 13* | 8.01 | 8.9 × 10−5 | 45.6 | 50.8 | low variation of |K sin(θel + K0)| |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ribot, M.A.; Kucwaj, J.-C.; Botteron, C.; Reboul, S.; Stienne, G.; Leclère, J.; Choquel, J.-B.; Farine, P.-A.; Benjelloun, M. Normalized GNSS Interference Pattern Technique for Altimetry. Sensors 2014, 14, 10234-10257. https://doi.org/10.3390/s140610234
Ribot MA, Kucwaj J-C, Botteron C, Reboul S, Stienne G, Leclère J, Choquel J-B, Farine P-A, Benjelloun M. Normalized GNSS Interference Pattern Technique for Altimetry. Sensors. 2014; 14(6):10234-10257. https://doi.org/10.3390/s140610234
Chicago/Turabian StyleRibot, Miguel Angel, Jean-Christophe Kucwaj, Cyril Botteron, Serge Reboul, Georges Stienne, Jérôme Leclère, Jean-Bernard Choquel, Pierre-André Farine, and Mohammed Benjelloun. 2014. "Normalized GNSS Interference Pattern Technique for Altimetry" Sensors 14, no. 6: 10234-10257. https://doi.org/10.3390/s140610234
APA StyleRibot, M. A., Kucwaj, J.-C., Botteron, C., Reboul, S., Stienne, G., Leclère, J., Choquel, J.-B., Farine, P.-A., & Benjelloun, M. (2014). Normalized GNSS Interference Pattern Technique for Altimetry. Sensors, 14(6), 10234-10257. https://doi.org/10.3390/s140610234