A Novel Wireless and Temperature-Compensated SAW Vibration Sensor
Abstract
: A novel wireless and passive surface acoustic wave (SAW) based temperature-compensated vibration sensor utilizing a flexible Y-cut quartz cantilever beam with a relatively substantial proof mass and two one-port resonators is developed. One resonator acts as the sensing device adjacent to the clamped end for maximum strain sensitivity, and the other one is used as the reference located on clamped end for temperature compensation for vibration sensor through the differential approach. Vibration directed to the proof mass flex the cantilever, inducing relative changes in the acoustic propagation characteristics of the SAW travelling along the sensing device, and generated output signal varies in frequency as a function of vibration. A theoretical mode using the Rayleigh method was established to determine the optimal dimensions of the cantilever beam. Coupling of Modes (COM) model was used to extract the optimal design parameters of the SAW devices prior to fabrication. The performance of the developed SAW sensor attached to an antenna towards applied vibration was evaluated wirelessly by using the precise vibration table, programmable incubator chamber, and reader unit. High vibration sensitivity of ∼10.4 kHz/g, good temperature stability, and excellent linearity were observed in the wireless measurements.1. Introduction
In recent years, the surface acoustic wave (SAW) devices have gained increasing attraction for wireless sensing for temperature, pressure, chemical compositions, vapour, humidity, torque and others mechanical constraints [1–7]. Their most outstanding property is that they allow without a battery and wireless interrogation, as they are connected only by a radio frequency link to a transceiver or reader unit. Small size, light-weight, low cost, and maintenance-free are their other attractive features. All these SAW-based sensors work on the basis of measuring changes in the delay time or velocity of a surface wave due to the impact of a physical quantity being measured on the SAW propagation. For vibration sensing utilizing SAW technology, Filipiak et al. present some feasibility studies on such issue [8–10]. A prototype of SAW based vibration sensor with beam structure was developed for electronic warning system, and it was composed of a piezoelectric ST-cut quartz cantilever beam with a SAW delay line pattern fabricated on top of the beam surface and an aggregated mass attached on undamped end of the beam. The vibration directed the aggregated mass changes both the distance between the transducers and the stresses in the region where the surface wave propagates. The vibration is evaluated by measurements of changes in the delay time of SAW. A simple isotropic model with one degree of freedom was used to describe theoretically the sensor plate movement and identification of the vibrating sensor. Measurement range of 10 g, frequency range up to 20 Hz, and acceleration sensitivity of 8.5 kHz/g were obtained in the experimental results [8]. However, the present SAW vibration sensor still suffers from the poor temperature compensation, also, the active sensor structure makes the sensor is difficult for wireless vibration measurement in some extreme environments because of the power system. Additionally, the lack of the theoretical analysis on response mechanism inhibits the optimization of the sensor
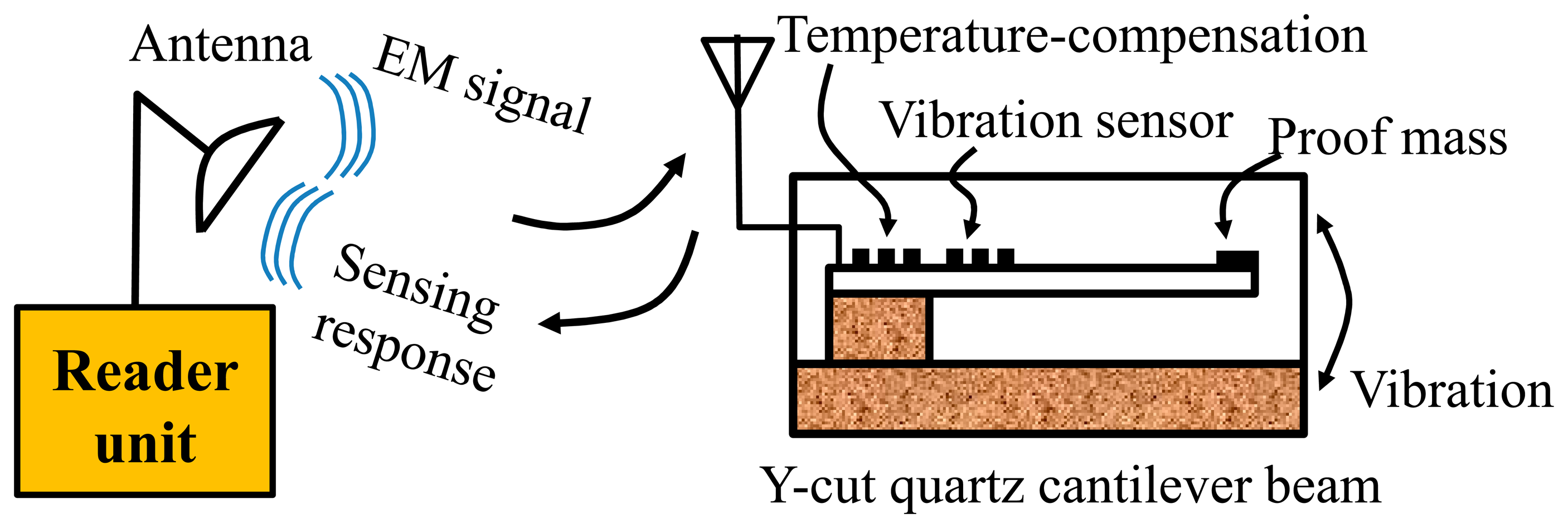
Operating the similar principle, a novel wireless and passive temperature-compensated vibration sensor based on SAW technology was present in this study for on-line vibration monitoring of larger mechanical equipment as reciprocating compressor. The schematic of the presented sensor is depicted in Figure 1, it is composed of a flexible piezoelectric Y-cut quartz cantilever beam with a relatively substantial proof mass at the undamped end, and two one-port SAW resonators deposited directly on surface of the beam by using the photolithographic technique. One resonator acts as the sensing device adjacent to the clamped end for maximum strain sensitivity, and the other one is used as the reference located on clamped end for temperature compensation through the differential approach [11]. Y-cut quartz is chosen as the piezoelectric material for the cantilever owing to its linear temperature characteristics and good strain sensitivity [12]. When the interdigital transducers (IDTs) of the resonators receive electromagnetic (EM) energy from reader unit through antennas, the SAW is generated and reflected by reflectors due to the piezoelectric effect. The reflected wave is reconverted into EM waves by the IDTs and transmitted to the reader unit. Vibration directed to the proof mass flex the cantilever, inducing relative changes in the acoustic propagation characteristics of the SAW travelling along the sensing device, and generated output signal varies in frequency as a function of vibration. The sensor signal is demodulated wirelessly by evaluating the differential frequency shifts of the reflected impulses utilizing the reader unit. This sensor presents many advantages over other currently available vibration sensors: (1) it provides high sensitivity through optimal design by using the established theory model on response mechanism; (2) the temperature dependence is compensated effectively by using the differential structure; (3) the sensor chip is absolutely passive and does not require a battery or any power supply to operate; and (4) it is light, small, and can withstand extremely harsh environmental conditions.
To determine the optimal dimensions of the cantilever beam, a theoretical modelization is proposed by analyzing the strain distribution along the piezoelectric cantilever beam [7,13], which allows to obtain analytical expressions of the acceleration sensitivity. Accordingly, the dimension of the cantilever beam is determined for best strain sensitivity. Also, coupling of modes (COM) model, an efficient technique for SAW device simulation [14–16], was used to find optimal design parameters of the SAW devices prior to fabrication. Using the precise vibration table, and programmable incubator chamber, the performance of the developed SAW based vibration sensor was evaluated in wireless measurement referring to the interrogation unit.
2. Theoretical Analysis
2.1. Vibration Response Mechanism
In this paper, we propose a theoretical approach for analyzing vibration response mechanism of SAW vibration sensor composed of a Y-cut quartz cantilever beam with a relatively substantial proof mass at the undamped end, and a SAW device deposited directly adjacent to the clamped end surface of the beam as shown in Figure 2. The length, width, and thickness of the cantilever beam are indicated as l, e, and h, respectively. Also, to simplify the numerical solution, the ST-X quartz beam is assumed as isotropic medium. The inertial force F (F = ma, m and a are the proof mass and applied acceleration respectively) from the vibration directed to the proof mass, and induces shifts in stress σAx and strain (longitudinal in x-direction and transverse in y-direction: εx and εy) along the beam, which are expressed as [16].
For the vibration sensing, the inertial force F directed to the piezoelectric cantilever, the induced bending changes the center distance of interdigital electrodes. Additionally, the shift in strain along the cantilever beam induces the change of the density and elastic modulus of the beam, and also the shifts of the SAW velocity and resonance frequency. The resonance frequency shift, Δf, depending on changes in strain induced by the vibration can be expressed as
2.2. Numerical Results and Discussion
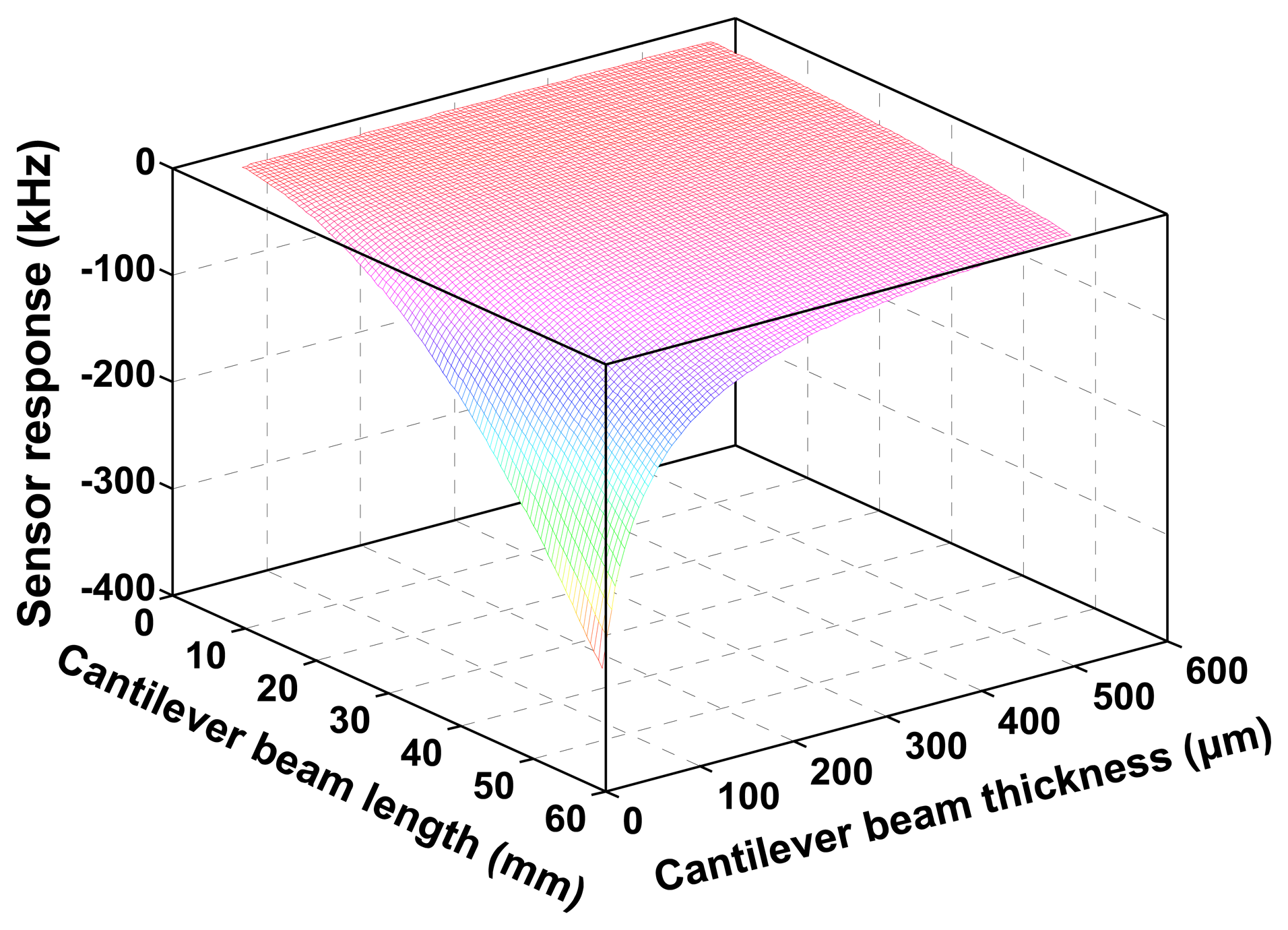
The relationship among the sensor response and the dimension of the cantilever beam was calculated as shown in Figure 3 using Equation (5) and simulation parameters listed in Table 1. From the picture, the sensor response relates to the geometric structure of cantilever beam and proof mass. Larger mass loading, longer and thinner beam will significantly contribute the sensitivity. However, to avoid the resonance phenomena between the dynamic load and the cantilever beam, higher resonance frequency of the beam itself is essential, and it is given by the Rayleigh method using determined Youngs modulus [8]. In this study, the beam resonance frequency is assumed to over 500 Hz, and hence, the length of Y-cut quartz beam with 0.2 mm should be less than 20 mm according to the analytical expressions of the beam resonance frequency mentioned in Ref. [9]. Notably, the width of the cantilever does not significantly contribute to the sensor response and resonance frequency as mentioned in Equation (5), so, the width of the beam is considered as a constant, and it is set to 1.5 mm in our study. Consequently, the geometric of the cantilever is determined as 1.5 mm × 20 mm × 0.2 mm, and the proof mass and the beam mass ratio is set to 5. Based on the determined design parameters, the frequency sensitivity to acceleration from the vibration can be illustrated as shown in Figure 7c, expected sensitivity is around 11 kHz/g.
3. Coupling of Modes (Com) Simulation on Saw Devices
It is well known that the (COM) model is an efficient technique for SAW device simulation [14,15], and it was used to determine the design parameters of the one-port SAW resonator prior to fabrication. The aim is to obtain low insertion loss and high quality value. For simulation on the one-port resonator configuration composed of one IDT and two adjacent shorted reflectors as shown in Figure 1a, the COM model was used to analyze the IDT and reflectors reflectively. By using the cascading mixed P-matrix of the IDT, reflectors, and cavity between the IDT and reflectors [13], the frequency response S11 and S12 are obtained as
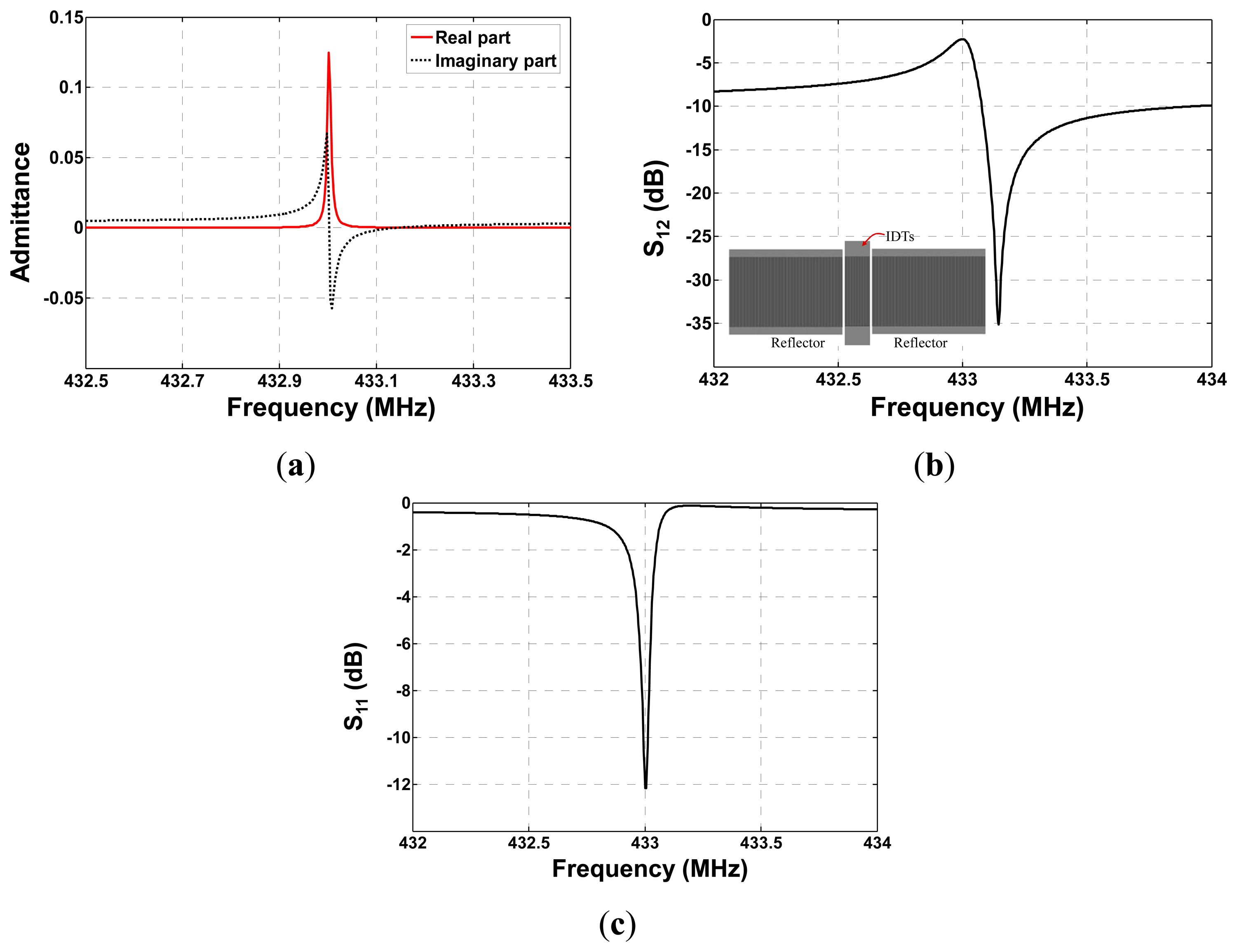
According to Equation (6), the admittance, frequency response S11 and S12 of the SAW resonator were simulated as shown in Figure 4. Y-cut quartz provides SAW velocity of 3159 m/s and electromechanical coupling constants of 0.12%. The operation frequency of the resonators is set to operate at 433 MHz. Number of IDT finger pairs and reflector electrodes with 1000 Å aluminum metallization of two resonators are set to 60 and 340, the finger widths are 1.823 μm, respectively. The cavity between the IDT and adjacent reflectors are both 0.625 λ (λ: wavelength at operation frequency). Larger Q-value over 14,000 and low insertion loss less than 3 dB were observed from the simulated results.
4. Technical Realization
Based on the extracted optimal design parameters for the SAW resonator and cantilver beam, the chip for vibration sensor was reproducibly fabricated on the Y-cut quartz substrate by standard photolithographic technique, on which 1000 Å aluminum IDTs and adjacent shorted grating reflectors were deposited. The operation frequencies of the resonators are designed to operate at 433 MHz and 434 MHz, respectively, which provides a differential frequency of 1 MHz for vibration sensing. Number of IDT finger pairs and reflector electrodes of two resonators are both set to 60 and 340, the finger widths are 1.823 μm and 1.819 μm, respectively. The cavities between the IDT and adjacent reflectors are both 0.625 λ (λ: wavelength at operation frequency), which provide lower insertion loss and higher unloaded quality (Q) value. The dimensions of the Y-cut quartz beam are set to 1.5 mm × 20 mm × 0.2 mm depending on the theoretical optimum. Then, the Y-cut quartz cantilever beam with two one-port SAW resonator patterns were clamped by using the fixed base made by Al. The proof mass with five times the mass of cantilever beam is affixed at the undamped end. Next, the fixed base was affixed firmly onto the metal package base. The developed packaged vibration sensor with a dipole antenna connected is depicted in Figure 5. The typical electrical resonance characteristics of the developed one-port SAW resonator are measured by using the Agilent E5071B Network analyzer, obtained unloaded Q-value is up to 12,000. The measured operation frequencies of two resonators are 433.02 MHz and 433.95 MHz, respectively. All measured S11 were well matched with predicted values from the COM simulation, as shown in Figure 6.
For wireless measurement, an interrogation unit (reader) utilizing the “frequency domain” method was employed (as shown in Figure 6), which interrogates a specific frequency with narrow-band pulse and then measures the returned signal power [17].
5. Experimental Results and Discussions
Then, the developed vibration sensor system is characterized wirelessly. The measurement setup consists of the developed SAW vibration sensor, reader unit, precision vibration table, incubator chamber, and commercial accelerometer for calibration as shown in Figure 6. The RF power from the reader unit is set to 20 dBm and the maximum readout distance of ∼1.5 m is observed. The precision vibration table provides acceleration range of 0∼10 g with varying vibration frequency and the applied vibration is monitored by using the commercial accelerometer. The SAW vibration sensor was bolted firmly to the vibration table. A self-made interface display program was use to real-time record and display the differential frequency signal.
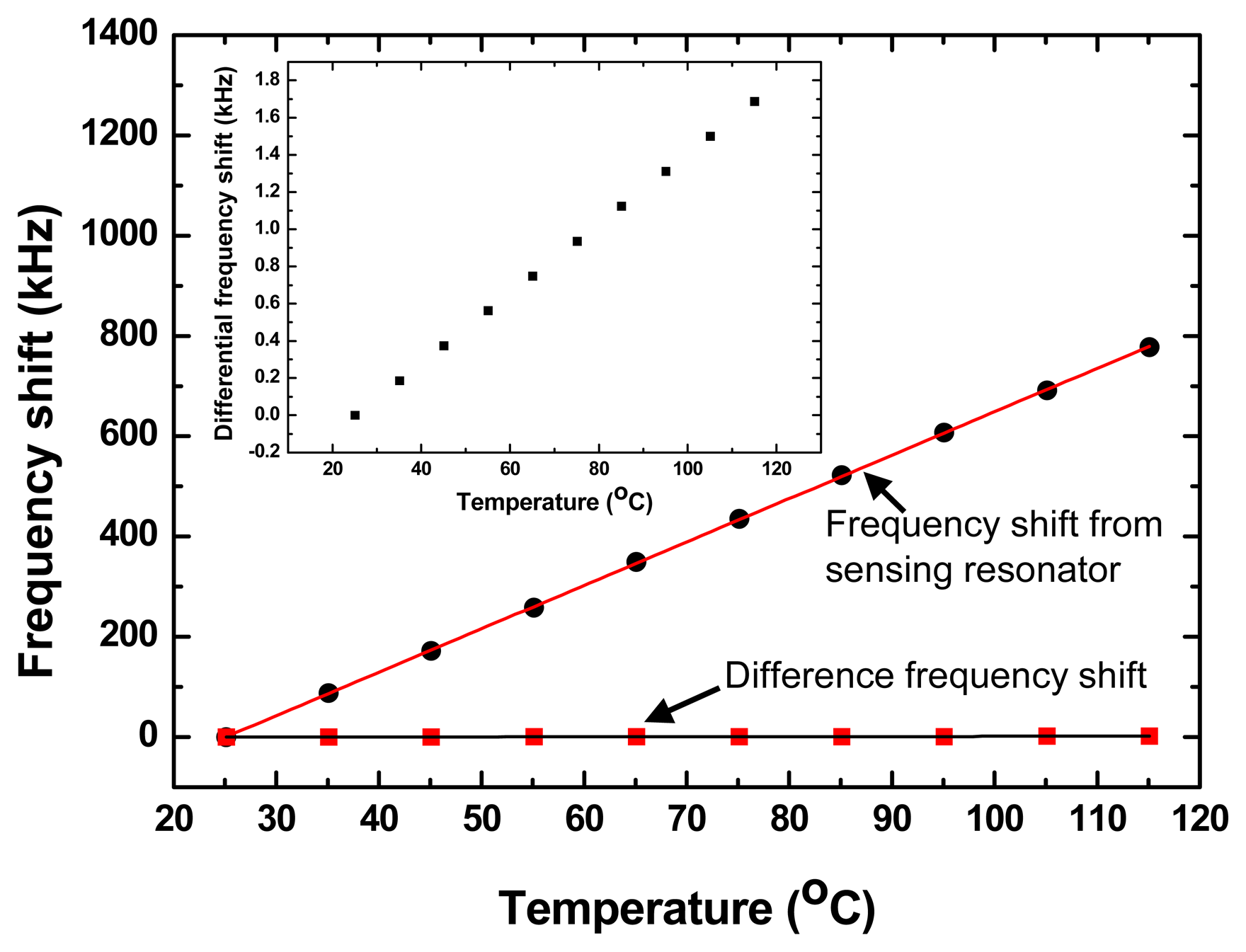
Figure 7a,b shows the continuous response and the spectrum of the stimulated sensor at a homogenous vibration with acceleration of 1.08 g and testing temperature of 25 °C. The frequency response t vibration was recorded every 18 ms, so that one point on the graph corresponds to an 18 ms interval. The spectrum in Figure 7b indicates the vibration frequency is ∼20 Hz, and it is obtained on FFT analysis of the continuous response in Figure 7a, and it consistent well with the settings of the vibration table. The magnitude of the recoding signals is proportional to the acceleration, as shown in Figure 7c. The measured results indicate that high sensitivity of ∼10.4 kHz/g and good linearity was obtained. Also, good agreement was observed among the measured sensitivity and calculated result. Additionally, the cross-temperature sensitivity of the vibration sensor was also characterized by using the incubator chamber, the difference frequency-dependence is only 18.6 Hz/°C in testing temperature range of 20∼120, far less than the cross-temperature sensitivity of the single sensing resonator (8.6 kHz/°C), as shown in Figure 8. It means good temperature compensation can be obtained in the vibration sensing by using the differential structure. From the results, we suggest that this prototype SAW vibration sensor is very promising for achieving wirelessly requestable and batteryless on-line vibration sensing application on the larger mechanical equipment.
6. Conclusions
A novel wireless and passive SAW based temperature-compensated vibration sensor incorporating a Y-cut quartz cantilever beam was successfully demonstrated. A theoretical analysis was performed to determine the optimal dimension of the cantilever beam. The SAW device used for the sensor was simulated by using the COM model prior to fabrication. The developed vibration sensor was wirelessly characterized by using the precision vibration table. High sensitivity of ∼10.4 kHz/g, excellent linearity, and good temperature compensation were obtained for vibration sensing.
Acknowledgments
The author gratefully acknowledges the support of the “The Hundred Talents Program” of Chinese Academy of Sciences, and National Natural Science Foundation of China: 11374254.
Author Contributions
All authors participated in the work presented here. Wang Wen defined the research topic and contribute the sensor chip design and simulation, Xue Xufeng, Huang Yangqing, and Liu XinluYong help to the sensor design and experiment. All authors read and approved the manuscript.
Conflicts of Interest
The authors hereby declare no conflict of interest.
References
- Springer, A.; Weigel, R.; Pohl, A.; Seifert, F. Wireless identification and sensing using surface acoustic wave devices. Mechatronics 1999, 9, 745–756. [Google Scholar]
- Reindl, L. Wireless Passive SAW Identification Marks and Sensors. Proceeding of Second International Symposium on Acoustic Wave Devices for Future Mobile Communication Systems, Chiba, Japan, 3–5 March 2004; pp. 1–15.
- Joo, B.-S.; Huh, J.; Lee, D. Fabrication of polymer SAW sensor array to calssfy chemical warfare agents. Sens. Actuators B Chem 2007, 121, 47–53. [Google Scholar]
- Wang, W.; Wang, W.; Liu, J.; Liu, M.; Yang, S. Wireless and passive gyroscope based on surface acoustic wave gyroscopic effect. Appl. Phys. Express 2011, 4. [Google Scholar] [CrossRef]
- Wang, W.; Oh, H.; Lee, K.; Yang, S. Enhanced Sensitivity of Wireless Chemical Sensor Based on Love Wave Mode. Jpn. J. Appl. Phys 2008. [Google Scholar]
- Huang, Y.; Chen, Y.; Wu, T. A passive wireless hydrogen surface acoustic wave sensor based on Pt-coated ZnO nanorods. Nanotechnology 2010, 21. [Google Scholar] [CrossRef]
- Lin, C.J.; Lin, C.R.; Yu, S.K.; Liu, G.X. Development of Wireless Torque Sensing Based on Surface Acoustic Wave Devices Using Embedded Microchip. Adv. Sci. Lett 2012, 8, 187–193. [Google Scholar]
- Filipiak, J.; Solarz, L.; Steczko, G. Surface Acoustic Wave (SAW) Vibration Sensors. Sensors 2011, 11, 11809–11832. [Google Scholar]
- Filipiak, J.; Kopycki, C. Surface acoustic waves for the detection of small vibrations. Sens. Actuators A Phys 1999, 76, 318–322. [Google Scholar]
- Filipiak, J.; Solarz, L.; Steczko, G. Determination of Parameters of Surface Acoustic Wave Vibration Sensors with the Help of Gravitational Field. Acta Phys. Pol. A 2013, 124, 410–412. [Google Scholar]
- Lin, C.M.; Yen, T.T.; Lai, Y.J.; Felmetsger, V.V.; Hopcroft, M.A.; Kuypers, J.H.; Pisano, A.P. Temperature-compensated aluminum nitride Lamb wave resonators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2010, 57, 524–532. [Google Scholar]
- Zhang, X.; Wang, F.; Li, L. Optimal selection of piezoelectric substrates and crystal cuts for SAW-based pressure and temperature sensors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 1207–1216. [Google Scholar]
- Wang, S.J.; Dong, Y.G.; Li, Y.; Feng, G.P. Research on resonant SAW accelerometer. Instrum. Tech. Sens 1998, 5, 4–6. [Google Scholar]
- Abbott, B.P.; Hartmann, C.S.; Nalocha, D.C. A Coupling of Modes Analysis of Chirped Transducers Containing Reflective Electrode Geometries. proceedings of IEEE Ultrasonic Symposium, Montreal, QC, Canada, 3–6 October 1989; pp. 129–134.
- Wu, T.-T.; Lin, C.-M. Analysis of SFIT SAW filters using coupling of modes model. J. Chin. Inst. Eng 2004, 27, 973–979. [Google Scholar]
- Hashimoto, K.Y. Surface Acoustic Wave Devices in Telecommunications: Modeling and Simulation; Springer: New York, NY, USA, 2000. [Google Scholar]
- Durdag, K. Wireless surface acoustic wave sensors. Sens. Transducers J 2009, 106, 1–5. [Google Scholar]




| r1 | r2 | E/N·m−2 | μ | ρ/kg·m−3 | f0/MHz | |
|---|---|---|---|---|---|---|
| Y-cut quartz | + 0.439 ± 0.030 | + 1.319 ± 0.064 | 7.83 × 1010 | 0.14 | 2631 | 434 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Xue, X.; Huang, Y.; Liu, X. A Novel Wireless and Temperature-Compensated SAW Vibration Sensor. Sensors 2014, 14, 20702-20712. https://doi.org/10.3390/s141120702
Wang W, Xue X, Huang Y, Liu X. A Novel Wireless and Temperature-Compensated SAW Vibration Sensor. Sensors. 2014; 14(11):20702-20712. https://doi.org/10.3390/s141120702
Chicago/Turabian StyleWang, Wen, Xufeng Xue, Yangqing Huang, and Xinlu Liu. 2014. "A Novel Wireless and Temperature-Compensated SAW Vibration Sensor" Sensors 14, no. 11: 20702-20712. https://doi.org/10.3390/s141120702
APA StyleWang, W., Xue, X., Huang, Y., & Liu, X. (2014). A Novel Wireless and Temperature-Compensated SAW Vibration Sensor. Sensors, 14(11), 20702-20712. https://doi.org/10.3390/s141120702





