Optimal Periodic Cooperative Spectrum Sensing Based on Weight Fusion in Cognitive Radio Networks
Abstract
: The performance of cooperative spectrum sensing in cognitive radio (CR) networks depends on the sensing mode, the sensing time and the number of cooperative users. In order to improve the sensing performance and reduce the interference to the primary user (PU), a periodic cooperative spectrum sensing model based on weight fusion is proposed in this paper. Moreover, the sensing period, the sensing time and the searching time are optimized, respectively. Firstly the sensing period is optimized to improve the spectrum utilization and reduce the interference, then the joint optimization algorithm of the local sensing time and the number of cooperative users, is proposed to obtain the optimal sensing time for improving the throughput of the cognitive radio user (CRU) during each period, and finally the water-filling principle is applied to optimize the searching time in order to make the CRU find an idle channel within the shortest time. The simulation results show that compared with the previous algorithms, the optimal sensing period can improve the spectrum utilization of the CRU and decrease the interference to the PU significantly, the optimal sensing time can make the CRU achieve the largest throughput, and the optimal searching time can make the CRU find an idle channel with the least time.1. Introduction
With the rapid increase of communication demands, the spectrum layout based on the static spectrum allocation methodology has caused a shortage of spectrum resources [1]. Measurements by the Federal Communications Commission (FCC) have shown that 70% of the allocated spectrum in the US. has not been well utilized [2]. In order to improve the utilization of the finite spectrum sources, a new intelligent communication system named cognitive radio (CR) is proposed. CR, which is based on software radio, can reuse the radio spectrum that has been allocated to a primary user (PU) but is temporally unused [3]. Therefore, CR technique can improve the spectrum utilization greatly through operating on the idle channel.
Energy sensing which is independent of the prior information about PU, is used by cognitive radio user (CRU) frequently because of its simple and practicable implementation [4]. However, the performance of energy sensing can be degraded in the fading or shadow environment [5]. It has been proven that cooperative spectrum sensing outperforms single-user detection, which combines the detection results of multiple users [6]. In cooperative spectrum sensing, every collaborative CRU senses spectrum independently by energy sensing, and then sends its sensing information to a fusion centre that makes a final decision on the presence of PU through combining all the received sensing information [7].
Light-weight cooperative spectrum sensing based on hard decisions was proposed by Mishra in order to improve the detection probability in the given false alarm probability scenario [8]. By its predominant soft decision nature, an optimal linear operation framework for cooperative spectrum sensing based on weight fusion was proposed by Zhi in order to improve the sensing performance [9]. However, the false alarm probability which is related to the spectrum utilization of CRU was not considered in [8,9].
For improving the detection efficiency, a periodic spectrum detection model was proposed by Wang [10], which might decrease interference to the PU. A sensing-throughput tradeoff model was proposed in [11], which maximized the throughput of CRU by selecting an optimal sensing time. However in this model, CRU had to vacate the occupied channel and search for another idle channel so that its transmission could be continued when the presence of the PU was detected. The first problem studied in [11] was to minimize the search time while guaranteeing enough detection probability for CRU to find at least one idle channel. Once the average searching time was confirmed, the sensing time was then optimized in order to make CRU achieve maximal throughput. In [12], the sensing period was optimized for improving the idle spectrum access of CRU, however, the interference to PU was not considered by the authors. The proposed models of [10–12] were all based on single-user detection, and the cooperative spectrum sensing models based on sensing-throughput tradeoff were proposed in [13–15], which could improve the throughput of CRU on the premise of guaranteeing detection performance. However, the cooperative overhead generated by the models of [13–15] decreases the transmission time with the increase of the number of cooperative users.
In this paper, a new cooperative spectrum sensing model based on soft decision is proposed. At the same time, the sensing period, the sensing time, and the searching time are well considered, which are all optimized in order to improve the performance of the CRU observably, including increasing the spectrum utilization, decreasing the interference, improving the throughput and reducing the searching time. The fusion center combines the sensing information from cooperative users with the selected optimal weight factors in order to decrease false alarm probability and improve spectrum utilization. Firstly the sensing period is optimized for improving spectrum access and reducing interference to PU, then both the local sensing time and the number of cooperative users are jointly optimized in order to make CR achieve the maximal throughput during each period, and finally the water-filling principle is adopted to obtain the minimal searching time. The simulation results show that the proposed optimization scheme improves the sensing performance and decreases the interference to PU significantly.
The rest of this paper is organized as follows: Energy sensing model, cooperative sensing model, and primary user occupation model are described in Section 2, respectively, then sensing period, sensing time, and searching time are analyzed and optimized in Section 3, respectively, and the performance of the proposed optimization scheme is evaluated by the simulations in Section 4. Finally, the conclusions are drawn in Section 5.
2. Cooperative Spectrum Sensing
Common notation as summarized in Table 1 is used throughout this paper.
2.1. Energy Sensing
Suppose that the centre frequency and bandwidth of the frequency band allocated to PU are fc and W, respectively, and the received signal is sampled at sampling frequency fs through the band-pass filter. The energy sensing model is shown in Figure 1, where the received signal R(t) is firstly passed through a band-pass filter with centre frequency fc and bandwidth W for getting the sampling signal in the frequency band of PU. The output of the filter y(t) is squared and integrated during the observed time T in order to obtain the energy of the received signal, then the energy statistic T(y) is obtained by normalizing the output of the integrator, and finally T(y) is compared with a threshold λ to decide whether PU is present or not.
The spectrum sensing problem can be seen as a binary hypothesis problem, which is given by:
If M ≥ 100, according to the Centre Limit Theorem (CRT), T(y) approximates to obey the Gaussian distribution, whose mean and variance under H0 are respectively given by:
By comparing T(y) with the threshold λ, the false alarm probability Pf is obtained by:
Hence, the miss detection probability is given by Pm = 1− Pd. On the other hand, by Equation (6), the threshold λ can also be related to the detection probability as follows:
By substituting Equation (7) into Equation (4), the false alarm probability is related to the detection probability as follows:
2.2. Cooperative Spectrum Sensing
Since if CRU is hidden by shadow or severe multipath fading, the sensing performance of single CRU is not accurate because of the received feeble power from PU, cooperative spectrum sensing is commonly used by CRU to solve hidden terminal problem [16].
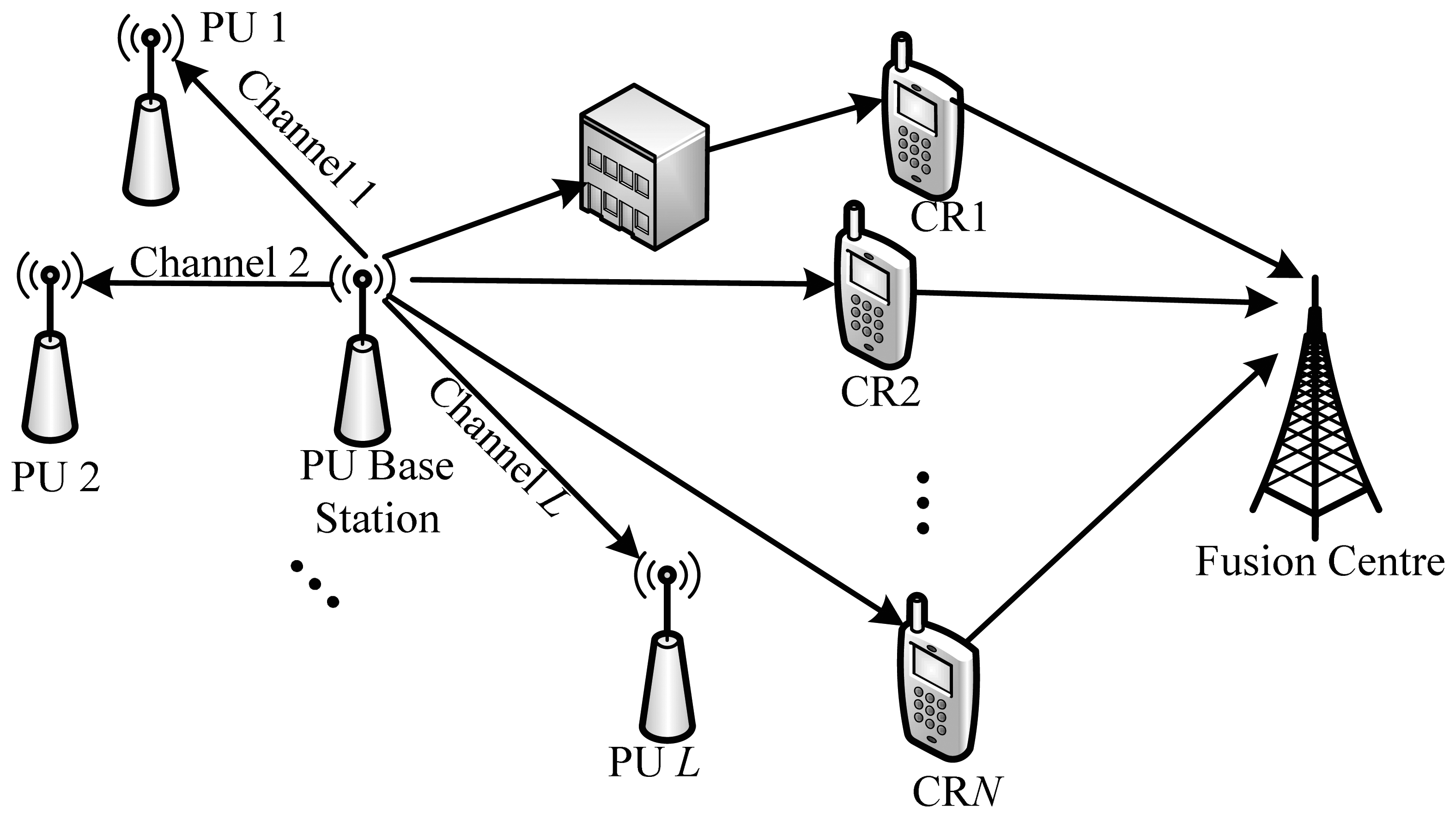
As shown in Figure 2, we consider a CR network where there are N CRUs that act as the sensor nodes to detect the presence of PU cooperatively and L channels that can be used by CRU if PU is idle. In this figure, CRU1 is a hidden terminal, and CRU2–CRUN are collaborative terminals. These CRUs send their local observed information to a fusion center that functions as a base station, and then the fusion center combines all the received information to obtain a final decision on the presence of PU. With the cooperative help of CRU2–CRUN, the sensing performance of CRU1 can be improved greatly. Since PU may appear in the channel at any time, CRU needs to detect PU periodically in order to find its presence in time [17].
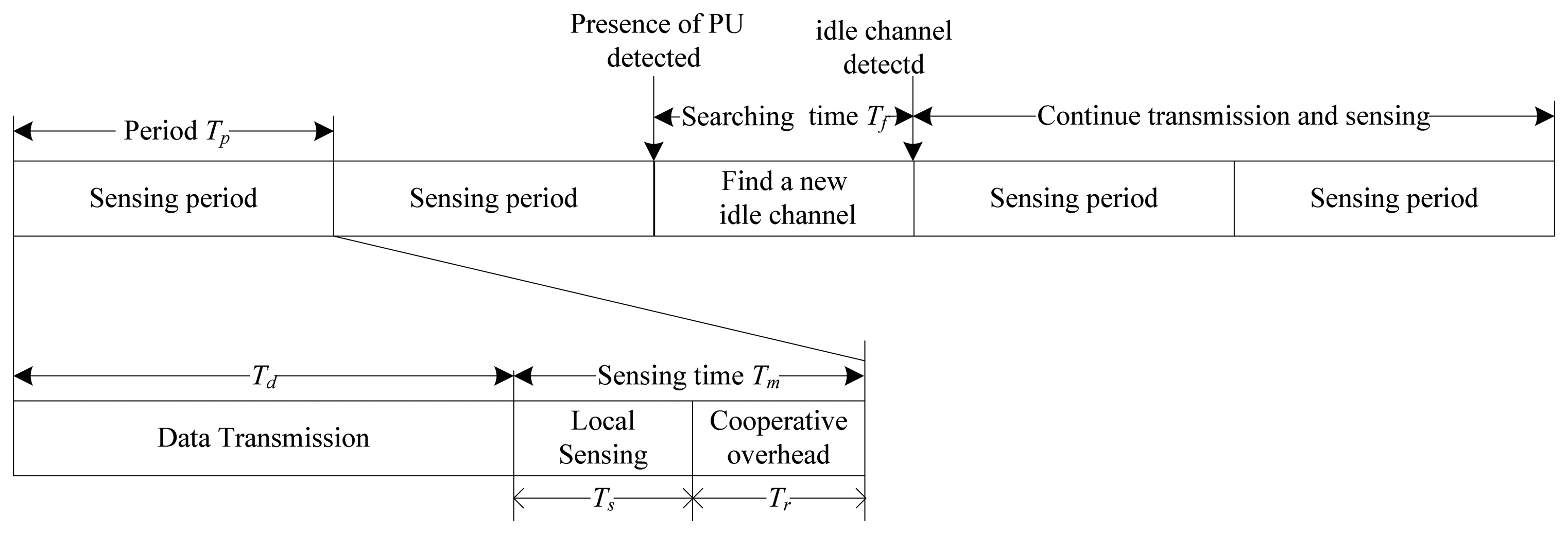
The periodic cooperative spectrum sensing model is shown in Figure 3. If an idle channel is detected currently, CRU can transmit and sense in this channel periodically. During each sensing period, after Td data transmission time, Tm sensing time is needed to detect the presence of PU in order to avoid causing interference to PU. If the absence of PU is detected, CRU will repeat the process described above within the sensing period Tp, however, if the presence of PU is detected during Tm, CRU should vacate this channel at once, and search for a new idle channel from the left L-1 channels during the searching time Tf. If another idle channel is found, CRU can switch to the channel and continue periodic transmission and sensing. Since CRUs detect PU by performing cooperative spectrum sensing, the cooperative overhead time Tr is used for exchanging the signaling information. The transmission time Td is given by:
Hence, a large Tr may decrease Td, which induces the debasement on the throughput of CRU.
2.3. Primary User Occupation Model
Supposing that each channel is independent, the busy/idle state of the channel can be modeled as the Markov random process with ON/OFF type [18]. Therefore to the channel j for j ∈ [1, L] the persistent time of ON/OFF state obeys the exponential distribution with mean uj/vj, which is given by:
3. Optimal Cooperative Spectrum Sensing
3.1. Optimal Sensing Period
With the increase of sensing period Tp, both the interference to PU and the loss of spectrum access may increase, while with the decrease of Tp, the sensing time may increase because of frequent detection, and therefore it is important to choose an appropriate Tp for CRU to achieve the maximal benefit. The sensing period of each channel is related with the activity of PU in this channel, and therefore the effect on Tp caused by PU should be firstly analyzed.
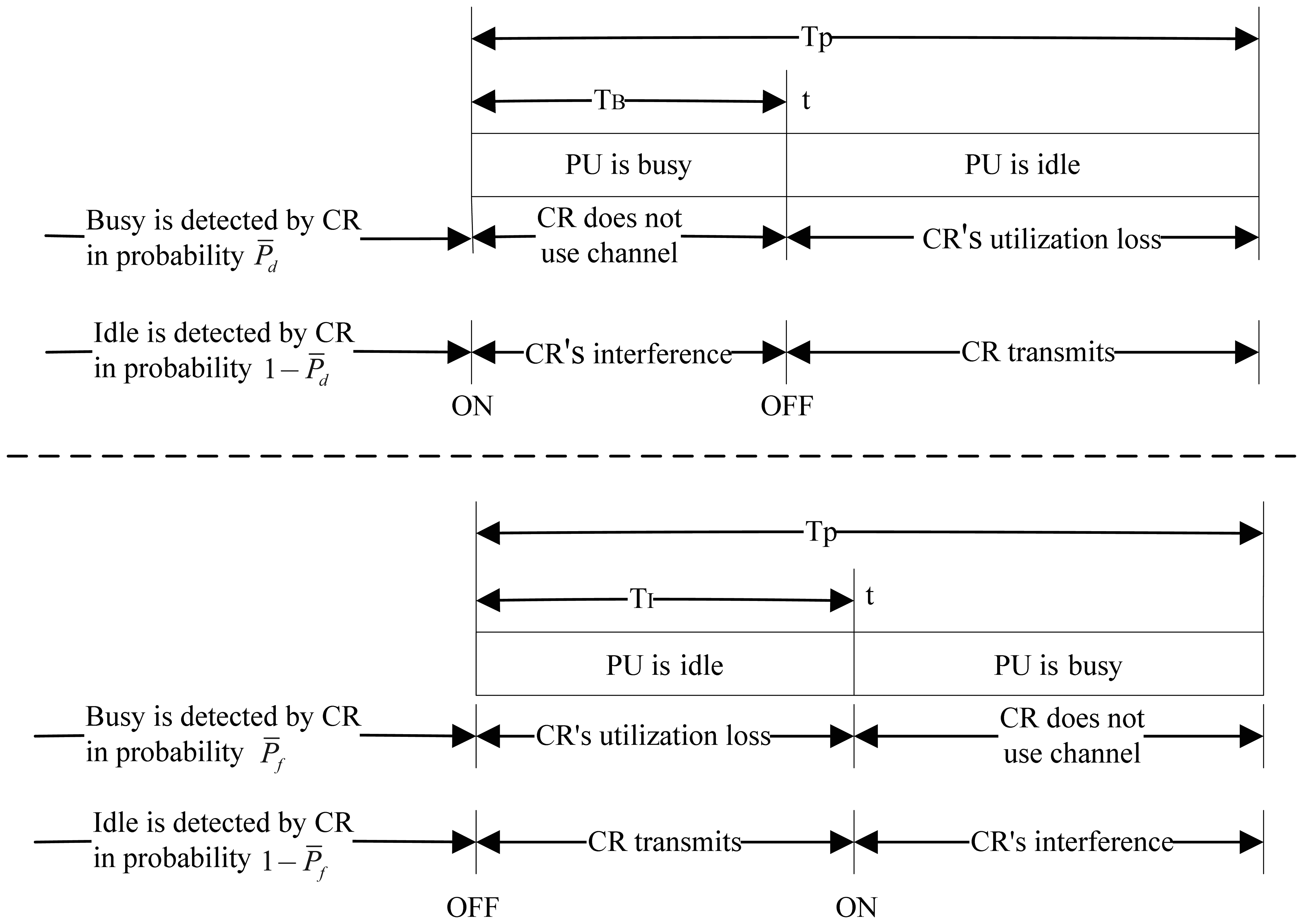
Suppose that and denote the average persistent busy time and idle time of channel j during Tp respectively, when the channel is ON at the initial time and OFF after t. If CRU detects the absence of PU falsely, it may use this channel and cause interference to PU during , while if CRU detects the presence of PU falsely, CRU may lose the opportunity to access the idle channel during . and are respectively given by:
Since the optimization of sensing period is the first step to optimize cooperative spectrum sensing, false alarm probability Qf and detection probability Qd cannot be obtained accurately. Hence, according to the characters of CR in IEEE 802.22, the constraints of Qf and Qd need to be set in order to guarantee spectrum utilization and avoid interfering PU.
CRU should have a lower false alarm probability in order to improve its spectrum utilization, and therefore Pf must be below a certain value, which may keep CRU owning sufficient spectrum resources for transmitting data. While CRU should have a high detection probability in order to avoid causing great interference to PU, and thus Pd must be above a certain value, which may make CRU give a more accurate detection on the presence of PU. Commonly, the constraints can be given by:
Figure 4 shows the interference to PU and the loss of spectrum access during one period. If PU is factually present at the initial time and the busyness of the channel was detected accurately during the previous period, CRU will avoid using this channel during this period and therefore have loss of spectrum access in probability P̅d. While if the idleness of the channel is detected falsely during the previous period, CRU will occupy this channel and cause interference to PU in probability 1−P̅d. Similarly, if PU is factually absent at the initial time, there will be loss of spectrum access in probability P̅d and interference to PU in probability 1−P̅f Hence, the average loss time of spectrum access and the average interference time are respectively given as follows:
CRU must sense PU during each period, and therefore when CRU is sensing a channel, it has to stop transmitting in this channel, and cause the loss of spectrum access that is called sensing overhead and denoted by TSloss. Supposing that Tm,max is the maximum of sensing time during each period, TSloss is given by:
In order to improve spectrum utilization and decrease interference to PU, loss time, interference time and sensing overhead are considered synthetically, and the minimal sensing loss can be achieved through optimizing the sensing period, whose optimization problem is defined as follows:
To describe the effect on the sensing performance of selecting Tp, two measurements that the probability of spectrum utilization ζuse and the probability of interference ζinf are defined as follows:
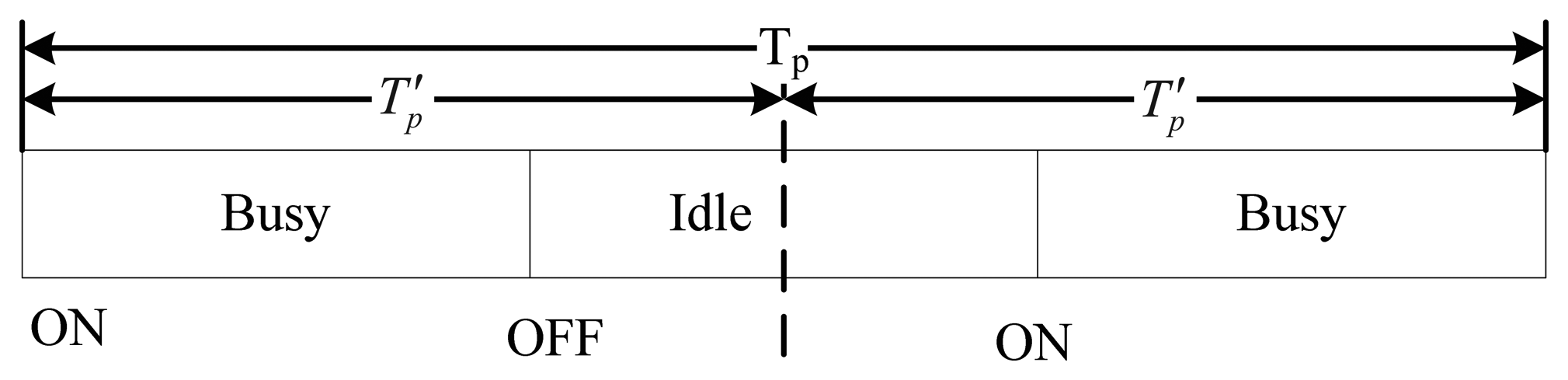
In the description above, we suppose that only one ON/OFF or OFF/ON state transition happens during one period, however, if larger sensing period Tp is chosen, there may be multiple state transitions during one period. In order to solve the problem, we need to divide Tp into multiple sub-periods. For example, as shown in Figure 5, PU undergoes both ON/OFF and OFF/ON state transitions during Tp, and after dividing Tp into two sub-periods , PU undergoes only one ON/OFF or OFF/ON state transition during . Hence, we can use the optimization of sensing period mentioned above to obtain the optimal . Choosing an appropriate sensing period is very important, if sensing period is too large or too small, spectrum sensing will not find the appearance of PU in time, and therefore CRU may cause great interference to PU.
3.2. Optimal Sensing Time
As shown in Figure 3, the sensing time Tm includes local sensing time Ts and cooperative overhead Tr. Each CRU senses PU for obtaining its local detection result by energy sensing independently during the local sensing time, and then these cooperative CRUs send their sensing information to the fusion centre one by one instead of synchronous transmission in order to avoid causing larger channel consumption and transmission collision to the CR network. Since the cooperative overhead time Tr is proportional to the number of the CRUs participating in cooperative spectrum sensing denoted by n for 1≤ n ≤ N, we have Tr=nξ where ξ denotes the time used for transmitting sensing information by each CRU. After the fusion centre receives the sensing information from all the collaborative CRUs, it may combine these information by the weight vector ω = [ω1, ω2,…,ωn] where ‖ω‖ = 1. Hence, the fusion statistic is given by:
By substituting Equation (27) into Equation (25), we have:
With the restriction condition ‖ω‖=1, the optimal weight factors is obtained as follows:
By comparing Equation (30) with Equation (8), it is seen evidently that with n ≥ 1, Qf,min < Pf which decreases with the increase of n. Suppose that C0 and C1 are the throughput of CRU operating in the idle channel and the busy channel respectively. For example, if there is only point-to-point transmission in the CR network, by assuming that the signals of PU and CRU are independent of each other, we can obtain C0 and C1 as follows:
There are following two scenarios where CRU can operate in the frequency band of PU [19].
- (1)
If PU is absent and CRU detects idleness of the channel exactly, the achievable throughput of CRU is (1 − Qf)C0Td / Tp;
- (2)
If PU is present but it is not detected by CRU, the achievable throughput of CRU is (1 − Qd)C1Td / Tp.
Hence, the average throughput of CRU related to Ts and n is given as follows:
Since the transmission time of CRU is Tp−Ts−Tr and the probability of interfering PU is Pon(1 − Qd), the average interfering time is given by:
Commonly, it is required that the average interfering time of CRU is less than a certain value, that is TI ≤ μ. The goal of optimizing sensing time is to identify the optimal local sensing time Ts and number of cooperative CRUs n during each sensing period, so that the achievable throughput of the CR network is maximal while PU is protected sufficiently. Mathematically, the optimization problem is proposed as follows:
According to Equation (22), with the given Ts and n, Qf may increase with the improvement of Qd, and according to Equation (32), both the increase of Qf and Qd may lead to the decrease of the average throughput R(Ts, n). Therefore in order to maximize R(Ts, n), Qd and Qf should both fall to their lower bounds, that is Qd = P̅d and Qf = Qf,min (as shown in Equation (30)). The optimal solution to Equation (34) is also achieved when the equality Qd = P̅d is satisfied, and supposing that P̅d ≈ 1, the optimization problem of Equation (34) is rewritten as follows:
Proposition 1: If n is given, there is an optimal Ts ∈ [0,Tp−nξ] that maximizes Φ(Ts,n).
Proof: see Appendix.
According to the first constraint of Equation (35), we have φ −nξ ≤ Ts ≤ Tm,max − nξ. By Proposition 1, if ▽Φ(Tm,max − nξ, n) > 0, the optimal , else if ▽Φ(φ− nξ, n) < 0, the optimal , and otherwise is the maximal point of Φ(Ts,n). With any given n, the iterative method to find an optimal is defined by the Algorithm 1.
| Algorithm 1. With any given n, find an optimal that makes Φ(Ts,n)achieve maximum |
| Given n and ε (error precision ), initialize τmin = φ − nξ and τmax = Tm,max −nξ. |
| If sign(▽Φ(τmin,n))==sign(▽Φ(Tp,n)), let ; |
| else if sign(▽Φ(τmax,n))== sign(▽Φ(0, n)), let ; else go to step 3. |
| Let τ= (τmin +τmax)/2. |
| If sign(▽Φ(τ,n))==sign(▽Φ(τmin,n)), let τmin=τ, and otherwise let τmax =τ. |
| Repeat step 3∼4 until | τmax− τmin| ≤ ε. |
| Let . |
The second sub-optimization problem is that with a given Ts, how to find an optimal n that maximizes Φ(Ts, n). Since n is an integer, it is not computationally expensive to search through n from 1 to N. The joint optimization algorithm of Ts and n is shown in Algorithm 2.
| Algorithm 2. Joint optimization algorithm of Ts and n. |
| Array the N CRUs as 1,2,…,N in descending order of their SNRs. |
| Initialize that equals to any value within (0, Tm,max], n(0)=1 and j = 0. |
| Given , enumerate n from 1 to N and calculate corresponding with the first n CRUs. |
| Find n* that maximizes for n=1,2,…,N, and let n(j+1) =n*. |
| Given n(j+1), calculate the optimal by Algorithm 1 and let . |
| Let j = j+1. |
| Repeat step 3∼6 until && n(j)== n(j−1). |
| Let and n*= n(j). |
The optimal sensing time can be given as follows:
3.3. Optimal Searching Time
After several transmission periods, CRU may detect the appearance of the PU, and therefore CRU has to stop transmission and search for a new idle channel. Once CRU finds the idle channel, it will stop searching to continue transmission in the new channel. As shown in Figure 6, CRU firstly finds an idle channel a through spectrum sensing, and then performs transmitting and sensing in channel a periodically. If CRU detects the appearance of PU during the sensing time in period l, in order to avoid interfering PU, CRU has to search for another idle channel. CRU will detect the spare channels one by one until a new idle channel b is found, and then continue transmitting and sensing in channel b periodically. Therefore the optimization of searching time is related with the sensing time and idle probability of single channel.
The current research on searching time such as [11] focuses on the selection of searching type, however, the research assumes that the sensing time of single channel is same, which is based on single-user detection. In [11], the author minimized the average searching time through optimizing the same sensing time of single channel, and this optimization problem is defined as follows:
Since the idle state of each channel is distinct, the selection of sensing time for single channel should also be different, and it is necessary to use a weight factor to allocate the sensing time for each channel. In this paper, the average searching time can achieve minimum through optimizing the weighed sensing time of single channel including local sensing time and cooperative overhead. Here continuous searching type that the channels are detected by CRU in turn is adopted, that is, if the busyness of the current searching channel is detected, CRU will select the next channel to continue detecting. Through multiplying the local sensing time by a weight factor decided by the idle state of single channel, the searching time of channel j is obtained as follows:
Since CRU can quickly find an idle channel with lower busy probability, the average searching time may degrade with the decrease of . According to Equations (30) and (39), the minimal used for minimizing the average searching time Tf is given if both of and reach their lower bounds. We have known that and , and it is obtained that:
According to Equations (30), (38), (39) and (40), are related with the parameters wj, and n′, and therefore the searching time is obtained as follows:
The weight vector w is related with the idle probability Pjoff for j = 1,2,…,L and w is commonly selected as follows:
In the Algorithm 3, the channel with idle probability lower than water-filling threshold ϑ, which is frequently use by PU, will not be detected by CRU in order to save searching time. By the algorithm, the channel with higher idle probability may have a larger weight factor, while the channel with lower idle probability may have a smaller weight factor, and therefore the searching time can be allocated to each channel reasonably. Once w is obtained, the optimal and n′ can be similarly determined by Algorithm 1 and Algorithm 2.
| Algorithm 3. Selection of w based on water-filling principle. |
|
4. Simulation
Suppose that the sampling frequency fs = 1 kHz, the upper limit of false alarm probability P̅f=0.4, the lower limit of detection probability P̅d=0.9, the number of CRUs N = 10, the number of available channels L = 10, the average received SNR γ̅ = −10∼0dB, the transition rates u, v =0∼0.1, the maximal sensing time Tm,max = 1 s, the maximal interfering time μ = 0.4 s, the time of transmitting sensing information ξ=0.05 s, and the tolerant accuracy ε = 10−5.
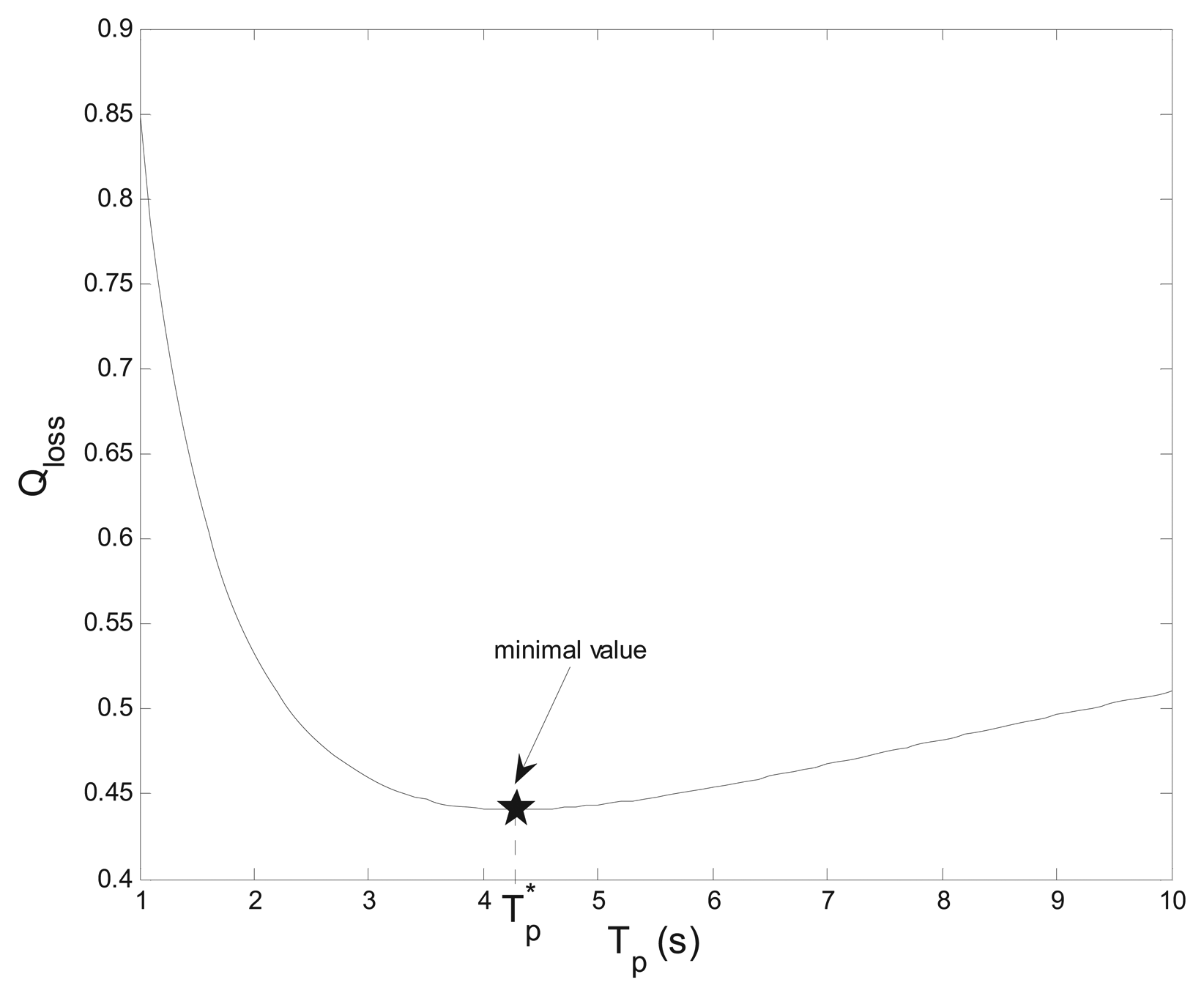
Figure 7 shows the total sensing loss probability Qloss vs. sensing period Tp with η1= η2 =1. There is an optimal Tp* = 4.3 s that minimizes Qloss. When Tm,max ≤ Tp ≤ Tp*, the higher sensing frequency leads to the increase of sensing time that may reduce the opportunity of spectrum access, and therefore Qloss increases. When Tp >Tp*, although the sensing frequency decreases, CRU can't detect the absence or presence of PU in time during larger Tp, and therefore the increase of the loss of spectrum access and the interference to PU also leads to the increase of Qloss.
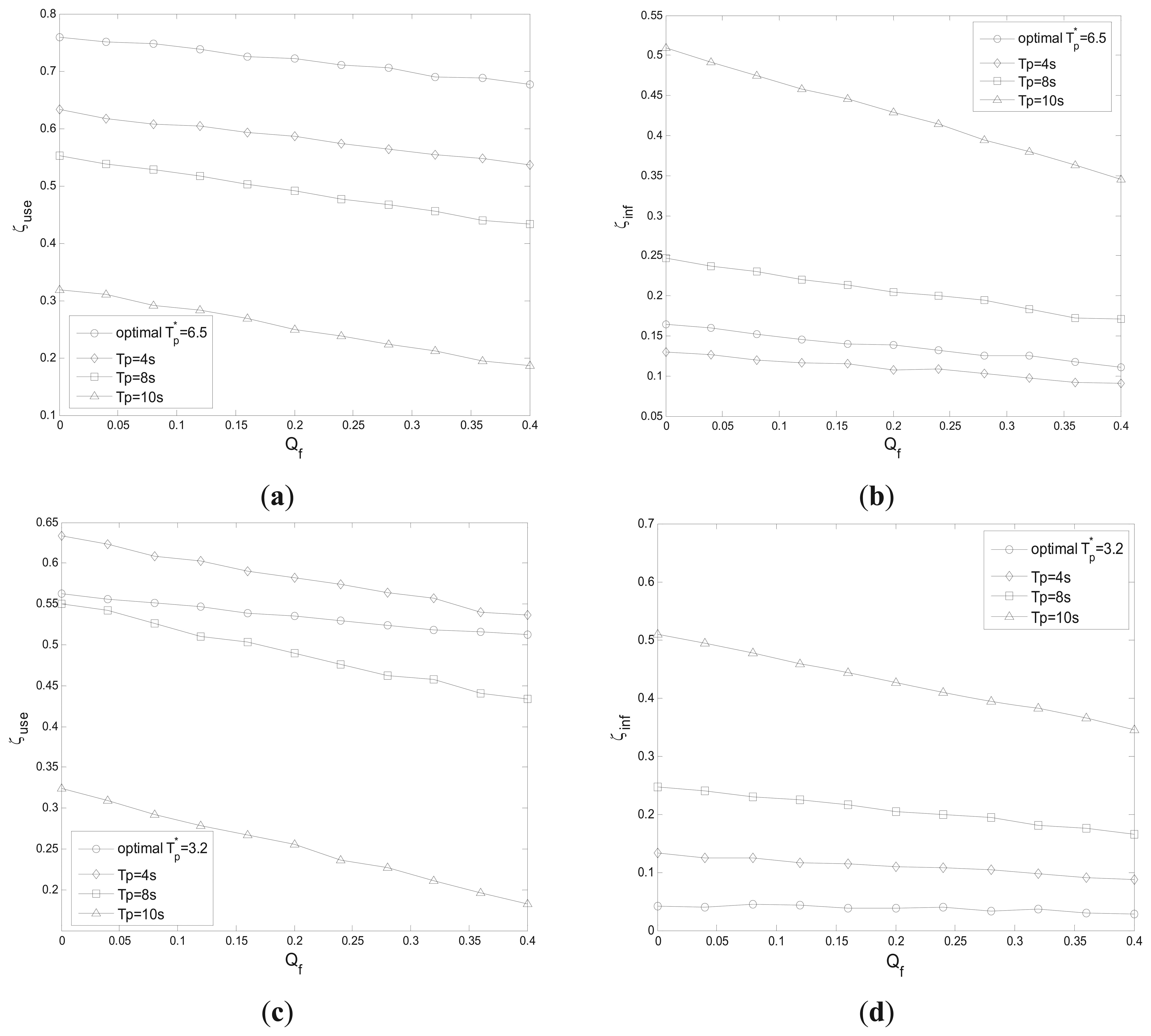
Figure 8 shows the probability of spectrum utilization ζuse and the probability of interference to PU ζinf vs. cooperative false alarm probability Qf with different η1 and η2. The performance of the optimal Tp is compared with that of the other Tp in these sub-figures. Figure 8(a,b) reflect spectrum utilization and interference with η1=1 and η2=0.1, respectively. The optimal Tp* = 6.5 s is obtained by solving the optimization problem (17). We can see that the spectrum utilization of the optimal Tp* = 6.5 s outperforms those of Tp = 4 s, 8 s and 10 s, while the interference of Tp* = 6.5 s is a little larger than that of Tp = 4 s. That is because if η1≫ η2, the loss of spectrum access is reduced greatly. The spectrum utilization and interference with η1=0.1and η2=1 are shown in Figure 8(c,d), respectively, and the interference of the optimal Tp* = 3.2 s is much lower than those of Tp = 4 s, 8 s and 10 s, while the spectrum utilization of Tp* = 3.2 s is only a little less than that of Tp = 4 s. That is because if η1≪ η2, the interference to PU is decreased greatly.
Figure 9 reflects the average throughput R vs. the sensing time Ts with n = 1, 5, 10. The convex curves in this figure prove the correctness of the theory proposed in Section 3.2, where exist the maximal values. With the initial increase of Ts, the average throughput improves because of the decrease of the false alarm probability, however, if Ts is larger, the average throughput decreases instead because of the decrease of transmission time. We can also see that the maximal throughput of n = 10 is lower than that of n = 5 because of the increase of cooperative overhead.
Figure 10 shows the average throughput R vs. the average received SNR γ̅ in the three schemes: the proposed joint optimization scheme, the cooperative spectrum sensing with all CRUs, and the single-user detection. We can see that R improves with the increase of γ̅, and the proposed optimization scheme outperforms the other two schemes. We also see that if γ̅ is lower, the performances of the proposed scheme and the cooperative spectrum sensing with all CRUs are more approximate. That is because cooperative spectrum sensing needs more collaborative users to decrease the false alarm probability, and therefore the optimal number of CRUs approaches to N. However, if γ̅ is larger, the performance of the single-user detection improves much, because the larger number of the collaborative CRUs may increase the cooperative overhead instead of the slight improvement on the detection performance. Hence, the proposed joint optimization scheme is predominant through finding an appropriate number of CRUs.
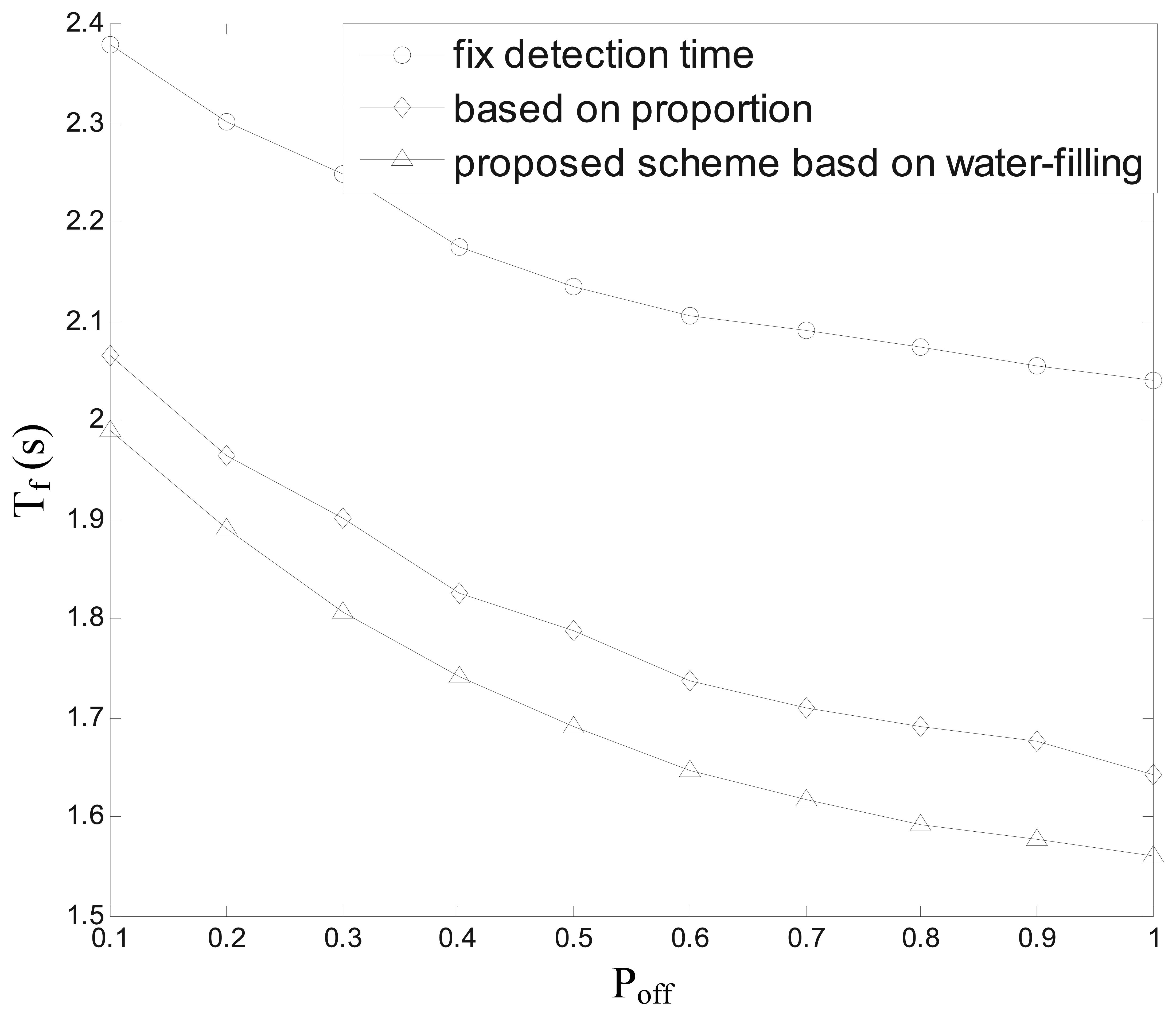
Figure 11 indicates the average searching time Tf vs. the average idle probability of the channels Poff in the three schemes: the searching with the fixed sensing time as Equation (37), the searching with the proportional sensing time as Equation (43) and the proposed scheme based on water-filling principle. In this figure, we can see that the searching time of the proposed scheme decreases observably compared with the other two schemes, because the proposed scheme need not detect the channels with lower Poff in order to save time.
Figure 12 compares the minimal single-channel searching time Tu of the three schemes vs. the number of cooperative CRUs, and the searching performance of the proposed scheme is always predominant. With the increase of n, Tu firstly decreases and then increases, because if n is larger, although the sensing performance improves, the increased cooperative overhead may prolong the searching time.
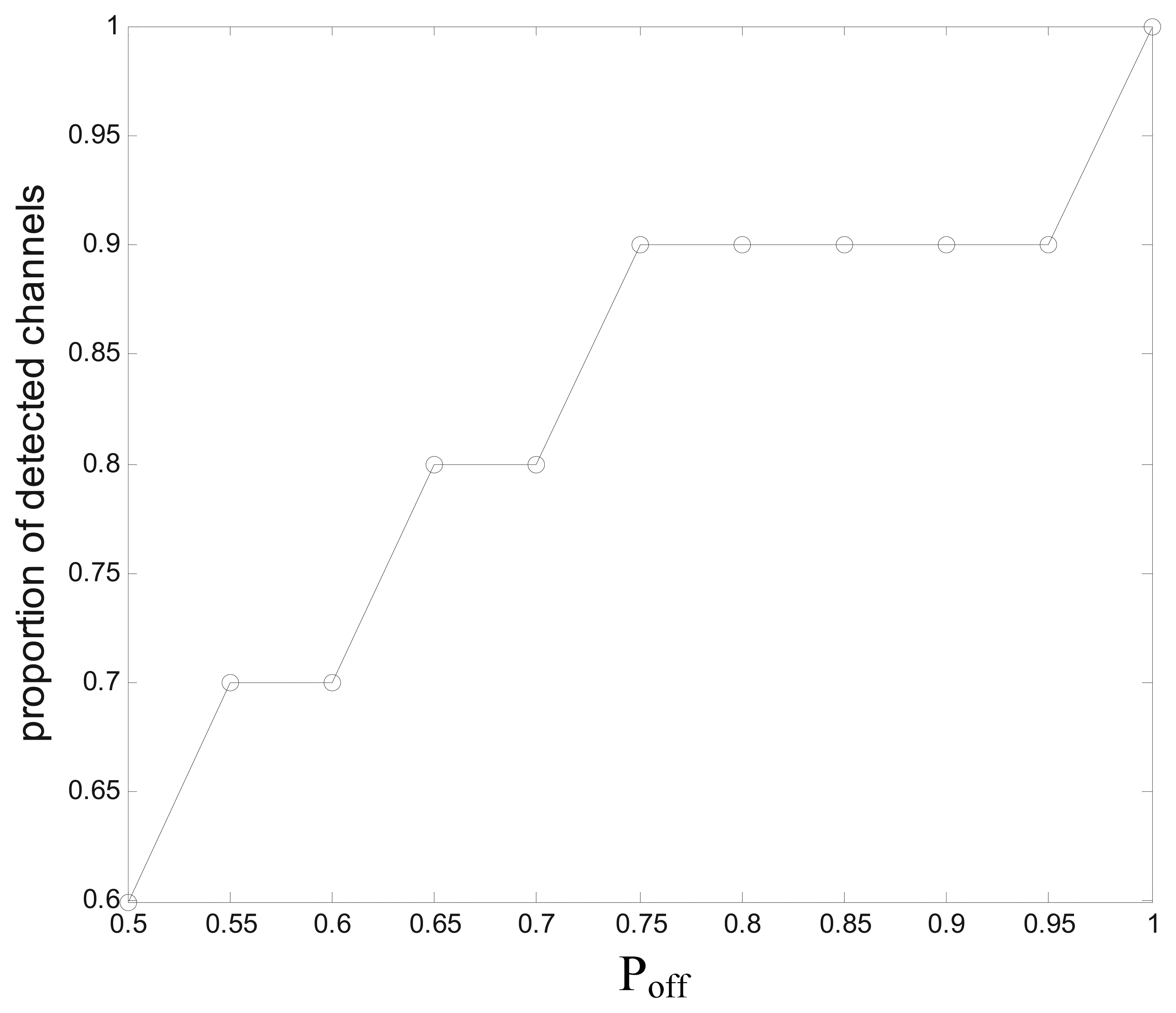
Figure 13 shows the proportion of the detected channels to all the L channels in the proposed scheme vs. the average channel idle probability Poff. With the decrease of Poff, the proportion also declines, and if Poff =0.5, only 60% of channels need to be detected. That is because the number of the channels with lower Poff increases with the decrease of Poff, and the channels with lower Poff should be excluded from the detected channels in order to save the searching time.
5. Conclusions
In cognitive radio networks, the interests of PU and CRU are contradictory. In this paper, we consider a cooperative spectrum sensing model where CRU senses the spectrum based on weight fusion periodically in order to avoid interfering PU. The sensing period is firstly optimized for improving the spectrum access and reducing the interference, then the joint optimization algorithm of the sensing time and the number of cooperative CRUs is proposed for making CRU achieve the maximal throughput during each period, and finally the water-filling principle is applied for decreasing the searching time of idle channels. The simulation results show that the significant improvement on the sensing performance and the throughput of CRU has been achieved by the proposed optimization scheme.
Acknowledgments
This work was supported by the National Natural Science Foundations of China (Grant No. 61201143 and 61102069), the Fundamental Research Fund for the Central Universities (Grant No. HIT. NSRIF. 2010091), the National Science Foundation for Post-doctoral Scientists of China (Grant No. 2012M510956), and the Post-doctoral Fund of Heilongjiang Province (Grant No. LBHZ11128). This work was also supported by the Communication Research Center of Harbin Institute of Technology and the College of Astronautics of Nanjing University of Aeronautics and Astronautics.
Appendix: Proof of Proposition 1
It can be verified from Equation (35) that the derivative ▽ Φ(Ts,n) is given by:
Equation (45) means that Φ(Ts,n) is a increasing function if Ts approaches to zero and a decreasing function if Ts approaches to Tp − nξ. Hence, there is a maximal point of Ts within the interval [0, Tp−nξ].
References
- Krenik, W.; Batra, A. Cognitive Radio techniques for wide area networks. Proceedings of 42nd Design Automation Conference (DAC 2005), San Diego, CA, USA, 13–17 June 2005; pp. 409–412.
- Mitola, J.; Maguire, G.Q. Cognitive radio: Making software radios more personal. IEEE Pers. Commun. 1999, 4, 13–18. [Google Scholar]
- Haykin, S. Cognitive radio: Brain-empowered wireless communications. IEEE J. Sel. Areas Commun. 2005, 2, 201–220. [Google Scholar]
- Shen, J.Y.; Liu, S.Y. Soft Versus Hard Cooperative Energy Detection under Low SNR. Proceedings of the 2008 Third International Conference on Communications and Networking in China, Hangzhou, China, 25–27 August 2008; pp. 128–131.
- Digham, F.F.; Alouini, M.S. On the energy detection of unknown signals over fading channels. IEEE Trans. Commun. 2007, 1, 21–24. [Google Scholar]
- Liu, Y.X.; Zeng, C.Y. Energy Detection Threshold Optimization for Cooperative Spectrum Sensing. Proceedings of 2nd IEEE International Conference on Advanced Computer Control, Shenyang, China, 27–29 March 2010; pp. 566–570.
- Ma, J.; Zhao, G.; Li, Y. Soft combination and detection for cooperative spectrum sensing in cognitive radio networks. IEEE Trans. Wirel. Commun. 2008, 11, 4502–4507. [Google Scholar]
- Mishra, S.M.; Sahai, A.; Brodersen, R.W. Cooperative Sensing Among Cognitive Radios. Proceedings of the 2006 IEEE International Conference on Communications, Istanbul, Turkey, 11–15 June 2006; pp. 1658–1663.
- Zhi, Q.; Cui, S.G.; Sayed, A.H. Optimal linear cooperation for spectrum sensing in cognitive radio networks. IEEE J. Sel. Top. Signal Process. 2008, 1, 28–40. [Google Scholar]
- Wang, P.; Xiao, L.M. Optimization of Detection Time for Channel Efficiency in Cognitive Radio Systems. Proceedings of the 8th IEEE Wireless Communications and Networking Conference, Kowloon, Hong Kong, China, 11–15 March 2007; pp. 111–115.
- Ghasemi, A.; Sousa, E.S. Optimization of Spectrum Sensing for Opportunistic Spectrum Access in Cognitive Radio Networks. Proceedings of the 4th Annual IEEE Consumer Communications and Networking Conference, Las Vegas, NV, USA, 11–13 January 2007; pp. 1022–1026.
- Kim, H.; Shin, K.G. Efficient discovery of spectrum opportunities with MAC-layer sensing in cognitive radio networks. IEEE Trans. Mob. Comput. 2008, 5, 533–545. [Google Scholar]
- Liang, Y.C.; Zeng, Y.H. Sensing-throughput tradeoff for cognitive radio networks. IEEE Trans. Wirel. Commun. 2008, 4, 1326–1336. [Google Scholar]
- Peh, E.C.Y.; Liang, Y.C.; Guan, Y.L. Optimization of cooperative sensing in cognitive radio networks: a sensing-throughput tradeoff view. IEEE Trans. Veh. Technol. 2009, 9, 5294–5299. [Google Scholar]
- Guo, C.; Peng, T.; Wang, W.B. Optimization of cooperative spectrum sensing mechanisms in cognitive radio networks. J. Electron. Inform. Technol. 2009, 7, 1525–1530. [Google Scholar]
- Bin, L.; Rondeau, T.W.; Bostian, C.W. Cognitive radio realities. Wirel. Commun. Mob. Comput. 2007, 9, 1037–1048. [Google Scholar]
- Liu, X.; Tan, X.Z. Optimization algorithm of periodical cooperative spectrum sensing in cognitive radio. Int. J. Commun. Syst. 2012, 5, 1–16. [Google Scholar]
- Weng, N.; Li, I.H.; Vespa, L. Information quality model and optimization for 802.15.4-based wireless sensor networks. J. Netw. Comput. Appl. 2011, 6, 1773–1783. [Google Scholar]
- Stewart, G.W. A generalization of Saad's theorem on Rayleigh-Ritz approximations. Linear Algebra Appl. 2011, 327, 115–119. [Google Scholar]





| Symbol | Denotation | Symbol | Denotation |
|---|---|---|---|
| R(t) | received signal | fc | sampling frequency |
| W | bandwidth of the frequency band | T | observed time |
| y(t) | sampled received signal | s(t) | PU's signal with variance |
| u(t) | Gaussian noise with variance | T(y) | statistic of energy sensing |
| λ | sensing threshold | Pf | false alarm probability |
| Pd | detection probability | γ | received signal noise |
| Pm | miss detection probability | Tp | sensing period |
| Tm | sensing time | Td | data transmission time |
| Tf | Searching time | N | number of the CRUs |
| L | number of available channels | uj | transition rates from busy to idle |
| vj | transition rates from idle to busy | busy probability of each channel | |
| idle probability of each channel | average persistent busy time | ||
| average persistent idle time | P̅f | upper limit of false alarm probability | |
| P̅d | lower limit of detection probability | Tloss | average loss time of spectrum access |
| Qf | cooperative false alarm probability | Qd | cooperative detection probability |
| Tinf | average interference time | TSloss | sensing overhead |
| Qloss | total sensing loss probability | Tm,max | maximum of sensing time |
| η1,η2 | weight factors configured by CR | ζuse | probability of spectrum utilization |
| ζinf | the probability of interference | w | weight vector |
| Tr | cooperative overhead time | ξ | time for sending sensing information |
| Ts | local detection time | TI | the average interfering time |
| Z | fusion statistic | gi | channel gain of CRi |
| C0,C1 | transmission rates of CR | R | the average throughput of CR |
| Tu | sensing time of single channel | busy probability of channel j |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, X.; Jia, M.; Gu, X.; Tan, X. Optimal Periodic Cooperative Spectrum Sensing Based on Weight Fusion in Cognitive Radio Networks. Sensors 2013, 13, 5251-5272. https://doi.org/10.3390/s130405251
Liu X, Jia M, Gu X, Tan X. Optimal Periodic Cooperative Spectrum Sensing Based on Weight Fusion in Cognitive Radio Networks. Sensors. 2013; 13(4):5251-5272. https://doi.org/10.3390/s130405251
Chicago/Turabian StyleLiu, Xin, Min Jia, Xuemai Gu, and Xuezhi Tan. 2013. "Optimal Periodic Cooperative Spectrum Sensing Based on Weight Fusion in Cognitive Radio Networks" Sensors 13, no. 4: 5251-5272. https://doi.org/10.3390/s130405251
APA StyleLiu, X., Jia, M., Gu, X., & Tan, X. (2013). Optimal Periodic Cooperative Spectrum Sensing Based on Weight Fusion in Cognitive Radio Networks. Sensors, 13(4), 5251-5272. https://doi.org/10.3390/s130405251




