Enhancement of Optical Adaptive Sensing by Using a Dual-Stage Seesaw-Swivel Actuator with a Tunable Vibration Absorber
Abstract
: Technological obstacles to the use of rotary-type swing arm actuators to actuate optical pickup modules in small-form-factor (SFF) disk drives stem from a hinge’s skewed actuation, subsequently inducing off-axis aberrations and deteriorating optical quality. This work describes a dual-stage seesaw-swivel actuator for optical pickup actuation. A triple-layered bimorph bender made of piezoelectric materials (PZTs) is connected to the suspension of the pickup head, while the tunable vibration absorber (TVA) unit is mounted on the seesaw swing arm to offer a balanced force to reduce vibrations in a focusing direction. Both PZT and TVA are designed to satisfy stable focusing operation operational requirements and compensate for the tilt angle or deformation of a disc. Finally, simulation results verify the performance of the dual-stage seesaw-swivel actuator, along with experimental procedures and parametric design optimization confirming the effectiveness of the proposed system.1. Introduction
Swing arm actuators have been applied to small form factor (SFF) optical pickup heads or near field hybrid recording systems. Trends in optical disk drives include developing small-form-factor (SFF) for holographic optics and extending the applications of near-field optics. In such a high speed positioning servo system, the head/disk spacing variation must be maintained as small as possible during disk operations. While attempting to reduce the size of optical heads, several works have scaled down all components of a conventional unit [1,2] and simplified the optical configuration, and micro optical elements, such as lenses and prisms. Other approaches integrate an optical module with a seesaw swivel actuator [3,4].
Two possible actuated mechanisms are available for active and passive head-positioning control. For active actuation, Yeack-Scranton devised a secondary stage PZT bender with an active slider for contact recording [5]. Following the PZT actuator and its applications, Tagawa proposed a self-loading slider featuring a twin structure piezo-actuator to maintain constant flying height spacing [6]. Kajitani developed an active slider associated with multilayered piezo-actuators to compensate for flying height variation [7]. In contrast with the above track-seek operations, Jun and Takashi investigated the feasibility of using a circular arc slider driven by a piezoelectric actuator to reduce the tilt motions of the lens in pitching/rolling directions [8]. Liu investigated the feasibility of a dynamic motion approach for a piezotube actuator subjected to disk deformation [9]. Moreover, in study involving a multilayered structure, Woosung used a flexure hinge mechanism to extend the allowable stroke to tracking and focusing motions [10]. Additionally, passive mass absorber utilizes an inertial mass and tuned support to mitigate mechanical vibration. Chung introduced a two-dimensional vibration model of a feeding deck system to reduce in-plane vibration [11]. According to their functional and structural identification, Heo characterized the dynamic behavior of a passive damper consisting of a rubber bobbin and plate ring [12]. Moreover, Chung established a design procedure to combine passive and active devices with an enlarged bandwidth control. That adaptive dynamic absorber is embedded with a voice coil motor (VCM) device [13]. However, to make use of the hollow space within the VCM, Jiang investigated the feasibility of a tuned dual mass damping device [14]. In particular, Kuwajima developed a novel shockproof structure by using a balanced type suspension, as well as investigated its performance on external shock resistance during read/write operations [15].
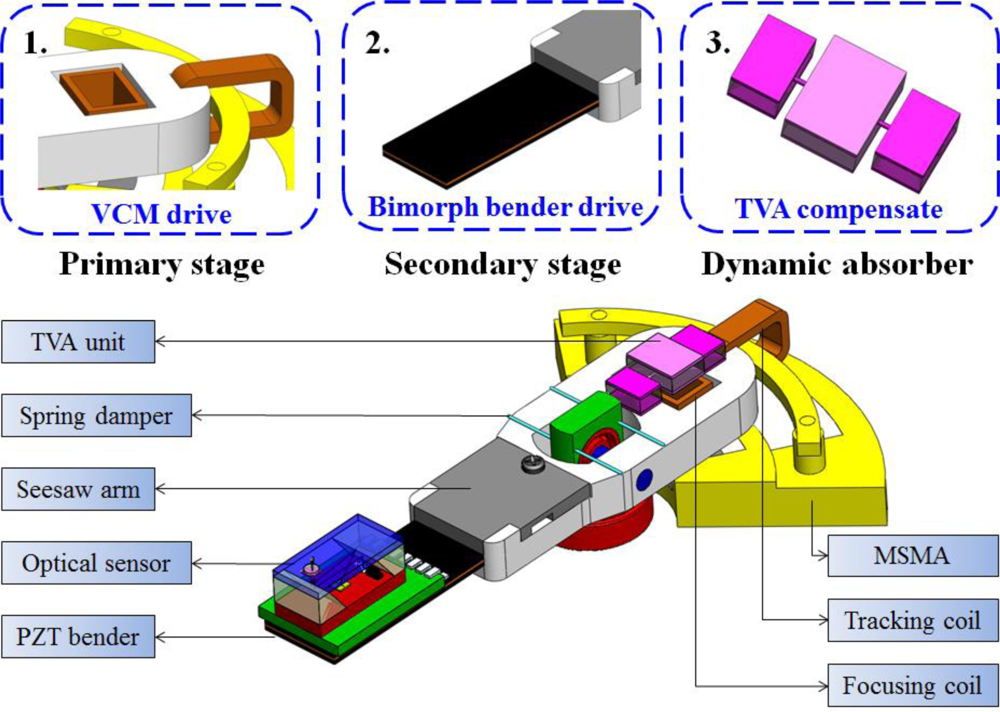
This work describes a novel a dual-stage seesaw-swivel actuator based on optical sensing by using a PZT bimorph component to compensate for the tilt angle variation in focusing stroke. A piezoelectric actuated suspension for a secondary-stage actuator is also developed to implement fine head positioning to assist the primary VCM actuator and maintain a constant flying height during the focusing operation, as shown in Figure 1. The secondary micro actuator functions mainly for fine and fast compensation, while a conventional VCM performs coarse positioning. A dynamic model for a bimorph structure is also developed to optimize and verify the natural frequency of actuating behavior. Additionally, a two dimensional vibration model of the optical sensing device with the absorber is established to ensure system stability and robustness. Based on multi-body dynamic analysis, a balanced mass associated with two cantilever springs provides a rotational reaction to the moving part under seesaw actuation. Moreover, this work investigates the feasibility of implementing a passive tunable vibration absorber (TVA) for spacing variation and head positioning control endowed with a bimorph micro actuator. Finally performance of biaxial motion is evaluated based on numerical simulations of optimization and experimental results.
2. Mechanical Design and Theoretical Analysis
The optical axis shift during the primary VCM actuation is compensated for by using the active bimorph micro actuator. A TVA can passively absorb the residual tilt variations while actively generating a reacting force for the moment conservation. The proposed mechanism is a seesaw type swivel actuator using piezoelectric active control collaboratively with passive TVA design. The following sections describe the proposed mechanism.
2.1. Angular Deviation Compensation
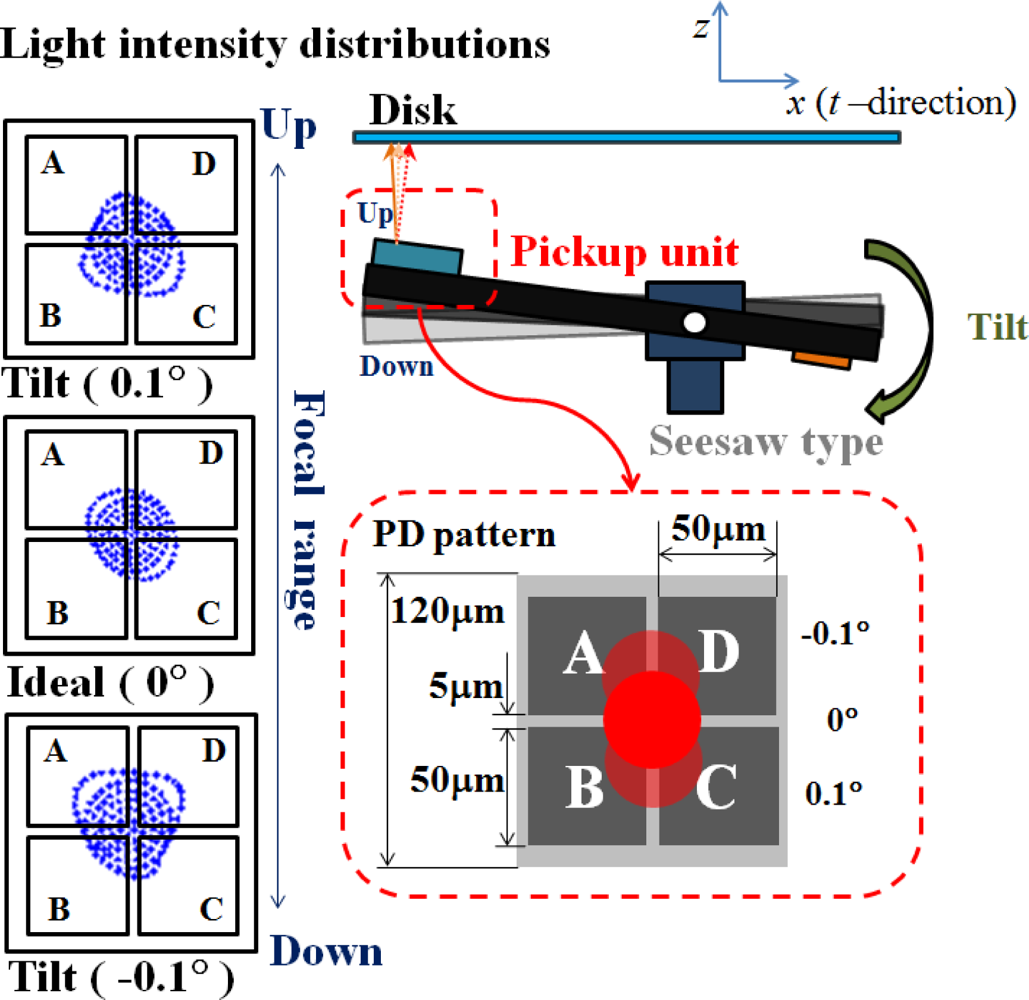
In actuated slider suspension, the tilt motion of the optical actuator causes the variation of focal spot position on the photo-detector, as shown in Figure 2. The middle figure of light intensity distribution is a well-symmetric focal spot on the PD center without tilting angle. If the focusing motion is achieved by z seesaw-type arm which generates a ±0.1° nutating angle, the returning beam would not be orthogonal to the optical sensor. The reflected focal spot on the PD will shift away from the center and the light distributions will approach one side of the photo-diode. Hence, given the increasing accuracy of head positioning, a drive capable of tilt control is necessary to reduce the tilt margin as the optical aberration is correspondingly increased. A compensation scheme is also developed for optical axis in-line calibration, and evaluated by driving a simply bimorph PZT bender.
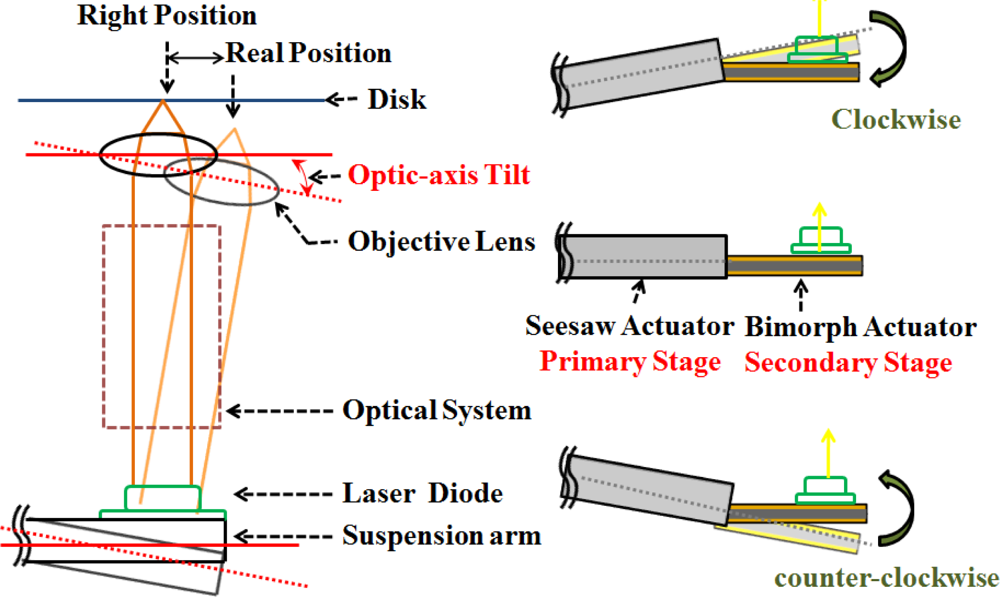
2.2. Dual-Stage Leveraged Mechanism
A common method of piezoelectric actuated suspension is driven along the opposite data (track) tangential direction in an allowable stroke. The proposed seesaw swivel-drive actuator uses a dual-stage leverage mechanism (Figure 3), through use of a coarse movement via VCM control and a secondary fine positioning via PZT. As PZT compensates the tilt angle of seesaw arm in the opposite way—the laser beam will be kept in orthogonal to the disk (Figure 3, left). Hence, PZT tilt control fixes the tangential displacement of focusing, and calibrates the asymmetry of the S-curve. Complete two-axis scanning is then performed by independently controlling the dual stage actuators.
2.3. Cantilever TVA Structure
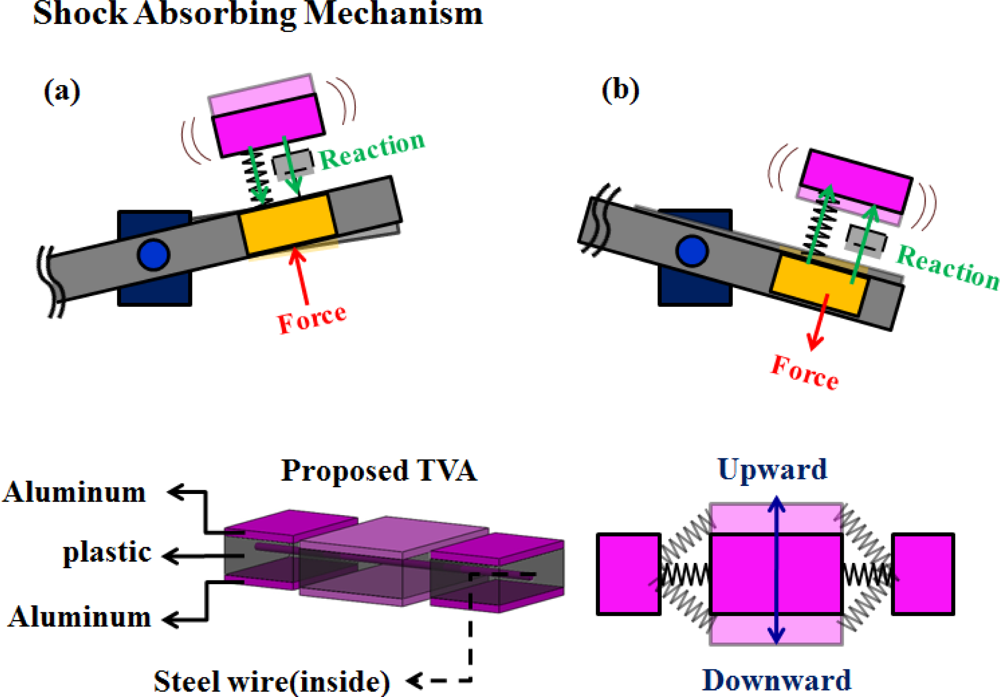
The primary structure with arbitrary distributions of mass, stiffness and damping is subjected to vibration suppression by an absorber subsystem. Sensing variation capabilities in the optic-axis direction are investigated to ensure the suppression of robust vibration. Consisting of two flexible cantilever beams extended from a balanced mass, a cantilever TVA subsystem is illustrated from the perspective of both improving bandwidth and increasing shock protection.
The vibration suppression of structures is based on independent design of dynamic absorbers, while taking into account the selected tuning mass of the subsystem structure. Effective structural stiffness is thus adjusted by adjusting the beam dimensions after a preliminary primitive design. Figure 4 illustrates the structural configuration of this work, which consists of a three-block structure called “soundmetal” that is pinned by a flexible wire.
3. Numerical Analysis
DeVoe and Pisano [16] developed a model for piezoelectric multi-morph cantilevers extended from Timoshenko’s approach to investigate the deflection of micro-actuators. To derive a simple working equation, Weinberg [17] obtained a simple closed-form solution for the bending of piezoelectric multi-morphs by using the Euler-Bernoulli beam theory and integrated equilibrium equations. This theory assumes that cross sections remain plane and normal to the deformed beam axis. Such assumptions are appropriate given the slender geometry of typical multi-morphs. Krommer developed the constitutive equations of a multi-morph by assuming two-dimensional kinematics of the structure [18]. Ha and Kim attempted to optimize bimorphs in order to maximize the tip stroke or vertical displacement by using the thickness ratio between the substrate (or shim layer) and PZT layers [19]. Pursuing a high bandwidth and a sufficient optical performance of the combined piezo-VCM actuator and design parameters of the PZT bender (i.e., length, width and thickness) are of priority concern. Generally, the rotary angle and deflection of the PZT bender is proportion to the square and cube of the length of the PZT bender (by basic beam theory). Other parameters affect the bandwidth (fundamental frequency).
3.1. Rotary Angle of PZT Bender
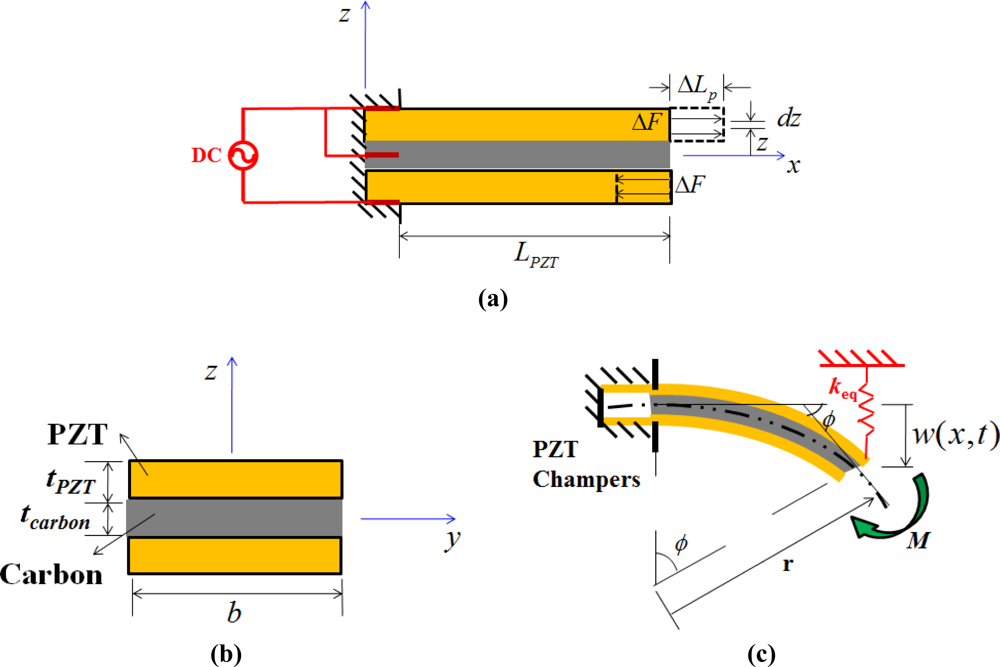
Figure 5 displays a “sandwich”-like PZT that consists of a carbon fiber chip with two d31-type PZT ceramics. This figure also considers a small piece element in the upper PZT material, in which the corresponding extension can be evaluated as follows:
The elongation force ΔF and momentum ΔM generated by the small element in the Figure 4(a) are:
Therefore, integrating Equation (2), the sum of bending moment in Figure 4 generated by the bimorph piezoelectric material is as follows:
Figure 5(a) shows a composed triple-layer beam that consists of both carbon fiber and piezoelectric material. The flexural rigidity of a multilayered beam is:
Additionally, the rotary angle of PZT is:
3.2. Natural Frequency of PZT Bender
The motion of a cantilever beam can be represented as [16]:
By using the separation of variables method, the general solution can be expressed as
Replacing Equation (8) with Equation (9) yields
The general solution of the mode shapes in x-direction can be expressed as
The boundary condition of Equation (10) is:
By substituting Equation (12) into Equation (11), the particular solution is
The natural frequency is solved from the following equation:
For n = 1, the fundamental frequency of the bimorph PZT is:
3.3. Optimization
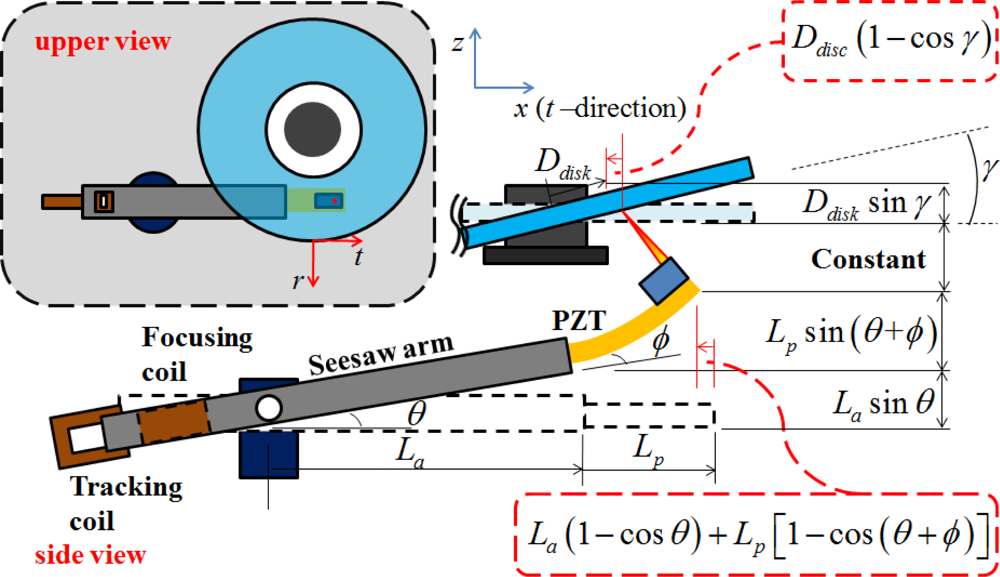
From the previous derivations of the equations, two objective functions of the optimization are selected: lateral displacement error E(tPZT, LPZT) and fundamental frequency ω(tPZT, LPZT). Figure 6 shows the relationship between PZT arm actuator and disk, while Table 1 lists its symbols.
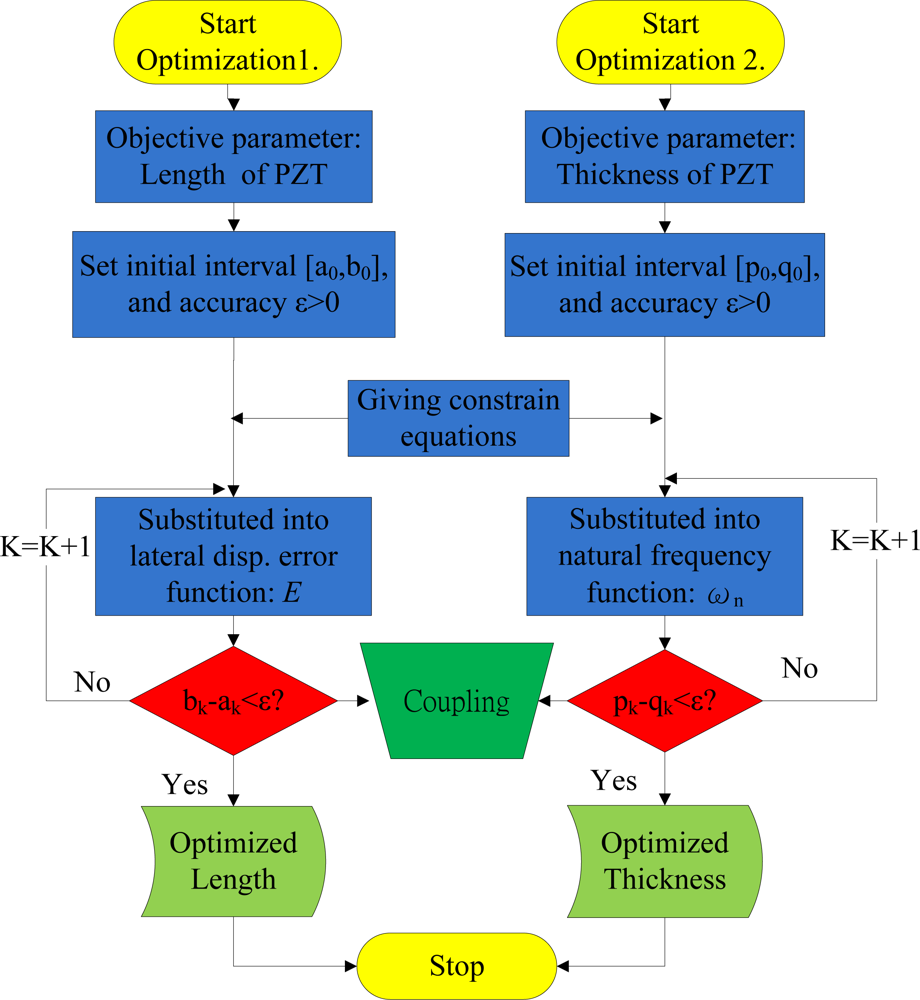
Figure 7 illustrates the optimization procedure, indicating that the PZT bender is optimized. Of the two coupling optimization processes, optimization 1 determines objective functions and sets the initial search interval and accuracy. Meanwhile, optimization 2 copes with constraint conditions for the process. The optimization of length LPZT and thickness tPZT, which minimize objective functions to PZT, are 14.13 mm and 0.11 mm after 64 and 59 iterations, respectively.
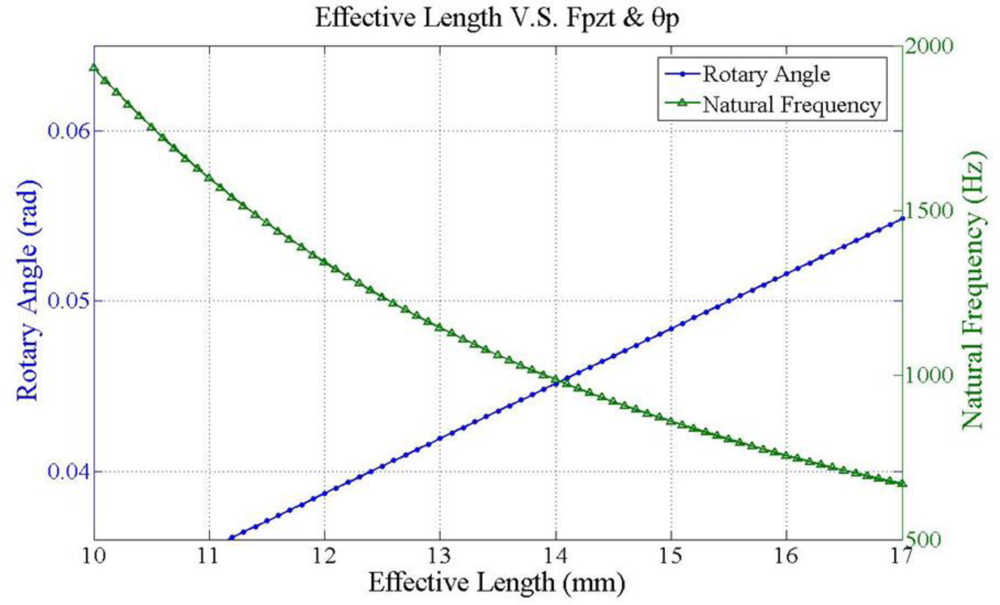
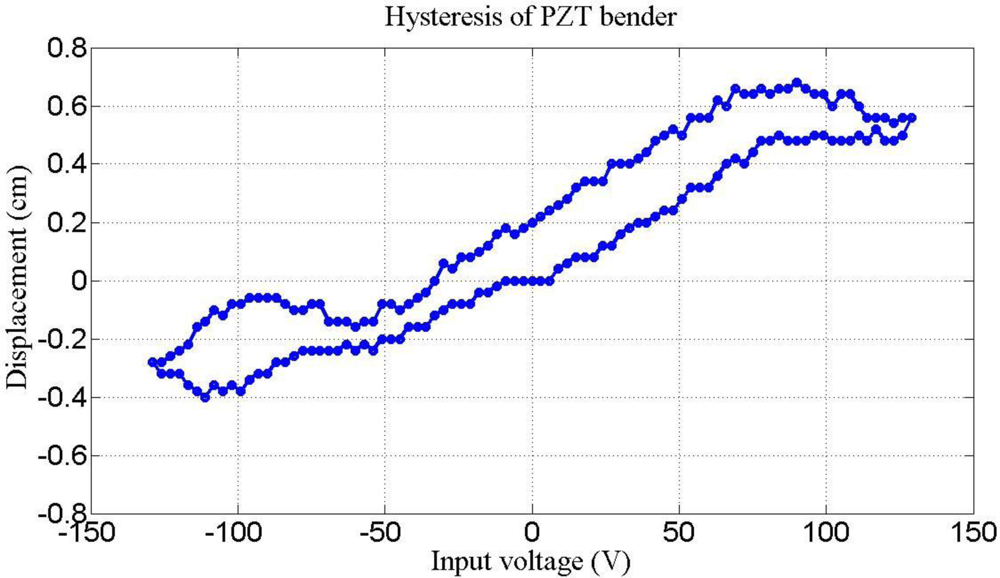
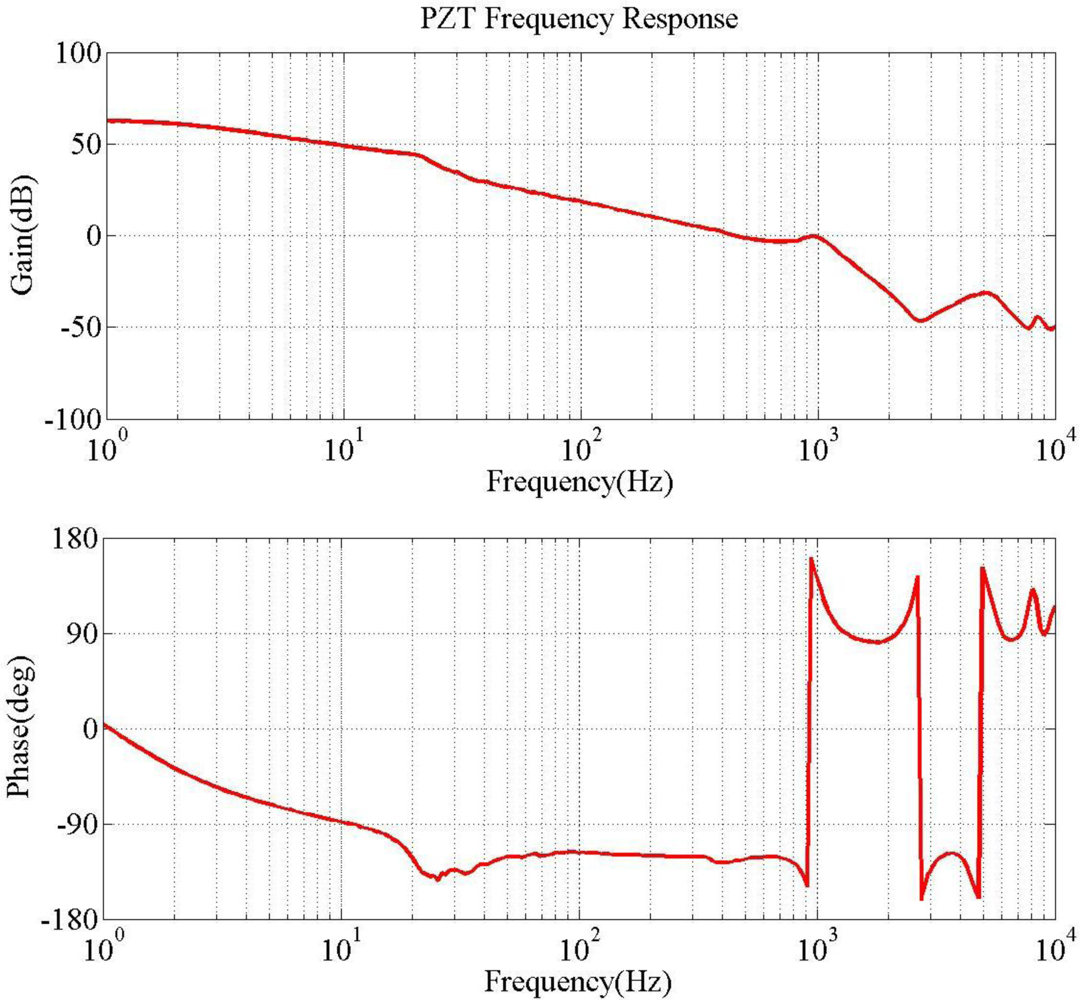
Figure 8 plots two parameters, rotary angle ϕ [Equation (7)] and fundamental frequency ω1 [Equation (15)] as a function of effective length. The crossover point is selected to verify the optimization results. Figure 9 illustrates the hysteresis curve of PZT displacement with maximum point is 4 mm when input a sine wave signal is swept from −125 to 125 V. Finally, the experimental results in Figure 10 demonstrate two modes frequency at 985 Hz and 5.8 kHz. Table 2 summarizes the modal analysis results between the numerical optimization and experiments, in which the errors vary by about 1.86% and 3.14%, respectively.
3.4. Absorber Mass Tuning
Several attempts have been made to seek optimum absorber parameters when the main system has significant damping. Den Hartog first tackled the optimum solution of a tuned mass damper that is connected to a primary system with the intention of reducing its dynamic response [20]. An optimal broadband attenuation was then achieved by a dynamic absorber design proposed by Ormondroyd and Den Hartog [21]. Based on their fixed-point theory, Brock found the optimum tuning parameter and defined the optimality for the optimum absorber damping [22]. By adopting a frequency locus approach, Thompson found the optimal damper parameters that minimize the structural response [23].
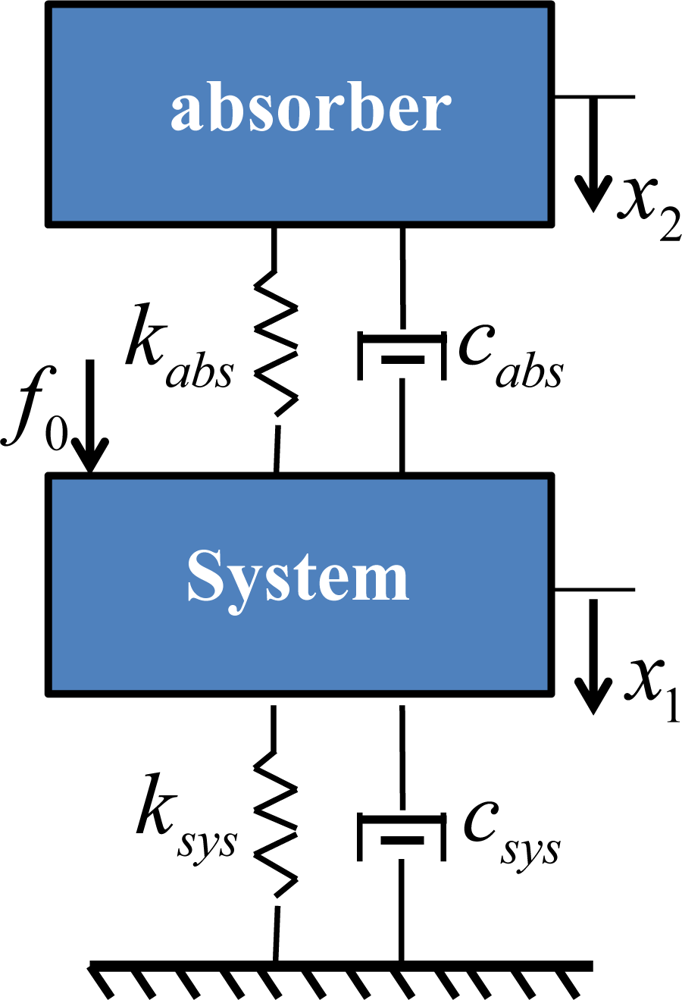
The equation of the damped model in Figure 11 can be expressed as
The amplitudes of the system displacement, X1, are expressed as:
Taking the absolute of X1:
Substituting the natural frequency, and , into the Equation (19), the normalized transfer function of an actuator is
According to Den Hartog’s theorem [17], the ratio of natural frequency between absorber and system is:
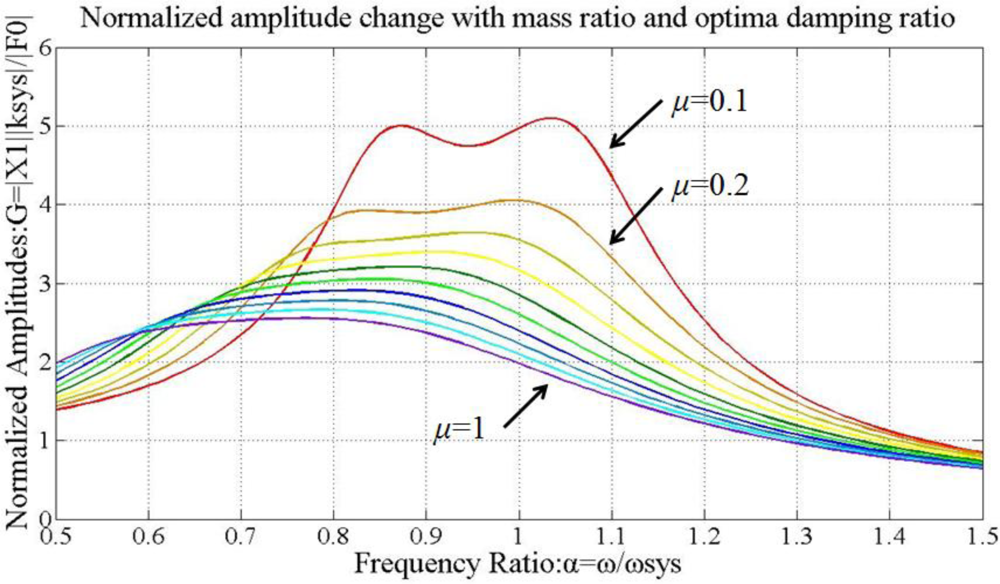
Figure 12(a) displays the relationship between μ and G. Hence, the peak is reduced with enlarged μ. According to Figure 12(b), the resonance peak frequency increases when ζabs decreases from 1 down to 0.1. The optimal damping ratio of the absorber, , is estimated as:
Figure 13 shows the normalized amplitude G as a function of μ. By assigning the optimal damping ratio ζabs and mass ratio μ, the vibration magnitudes are decreased effectively. (Therefore, the actual values of mass and stiffness of TVA are determined by selecting μ = 0.8 and = 0.408.
4. Experiments
4.1. Evaluation of Dynamic Performance
Figure 14 shows a prototype of proposed dual-stage PZT-VCM actuator assembly with small passive TVA actuation. The dynamic response of the dual-stage actuator and the PZT bender is obtained experimentally by LDV and a frequency response analyzer, as shown in Figure 15.
Figure 16 shows the effectiveness of TVA vibration suppression. The performance and robustness of the absorber are further enhanced by using optimal processes for dual stage actuation. According to simulation and experimental results, the passive TVA reduces the system vibration by 80% with respect to the peak amplitudes.
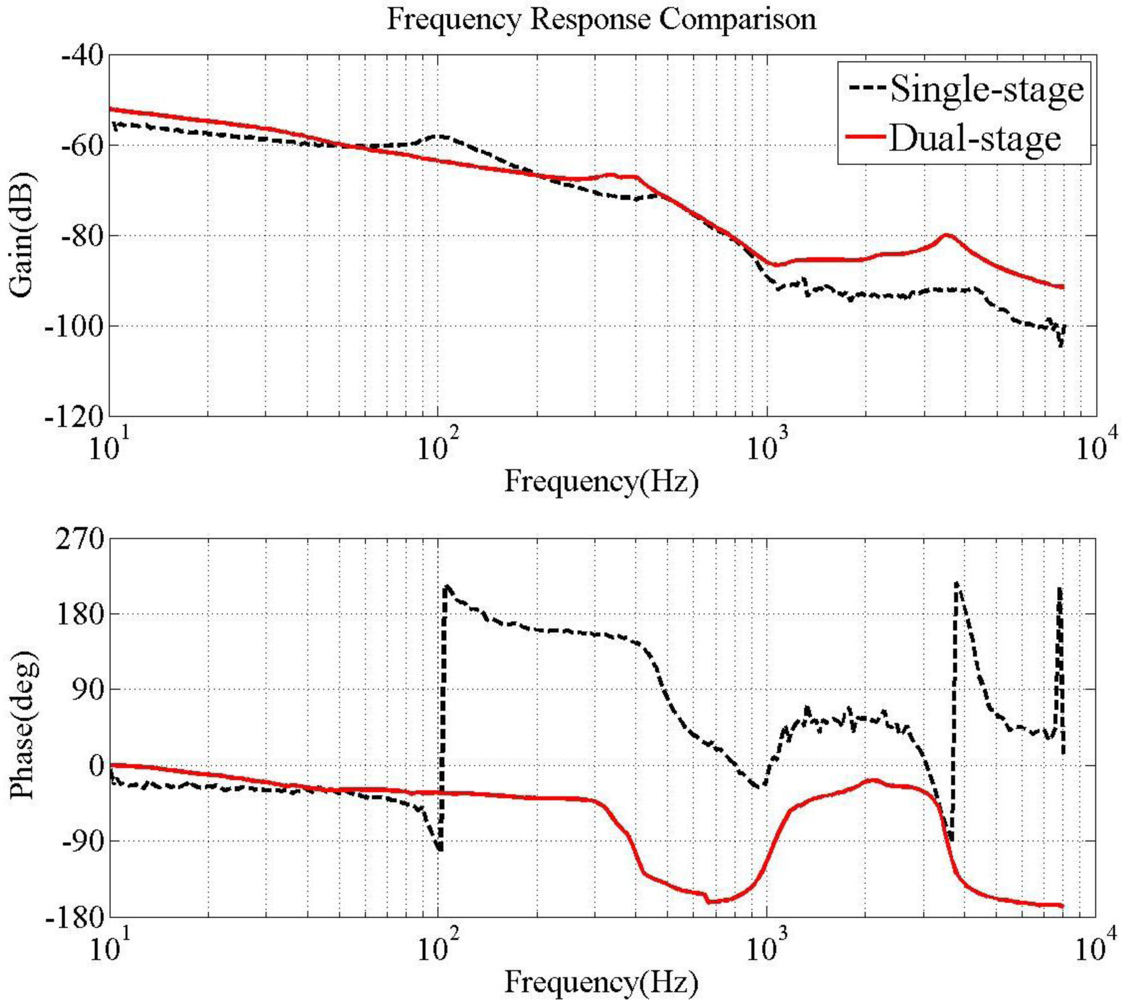
Design of the PZT loop compensator in the dual-stage actuator expands the bandwidth of the overall system. The primary VCM continuously provides coarse positioning, while the secondary actuator gives fine positioning, vibration and disturbances rejection. Figure 17 illustrates the open loop frequency response of the VCM and PZT dual-stage actuator, compared with the original single-stage VCM actuator.
The open loop bandwidth of the dual-stage system is approximately 3.8 kHz, with a phase margin of 30 degrees and a gain margin of 5 dB. This represents a significant enhancement over the single-stage VCM system, which has a 0.46 kHz bandwidth for the same stability margins. The PZT actuator can reject high frequency disturbances. Notably, the resonant peak of the PZT actuator at 0.9 kHz is lower than the open loop bandwidth and does not pose stability problems.
4.2. Tilt Angle Compensation
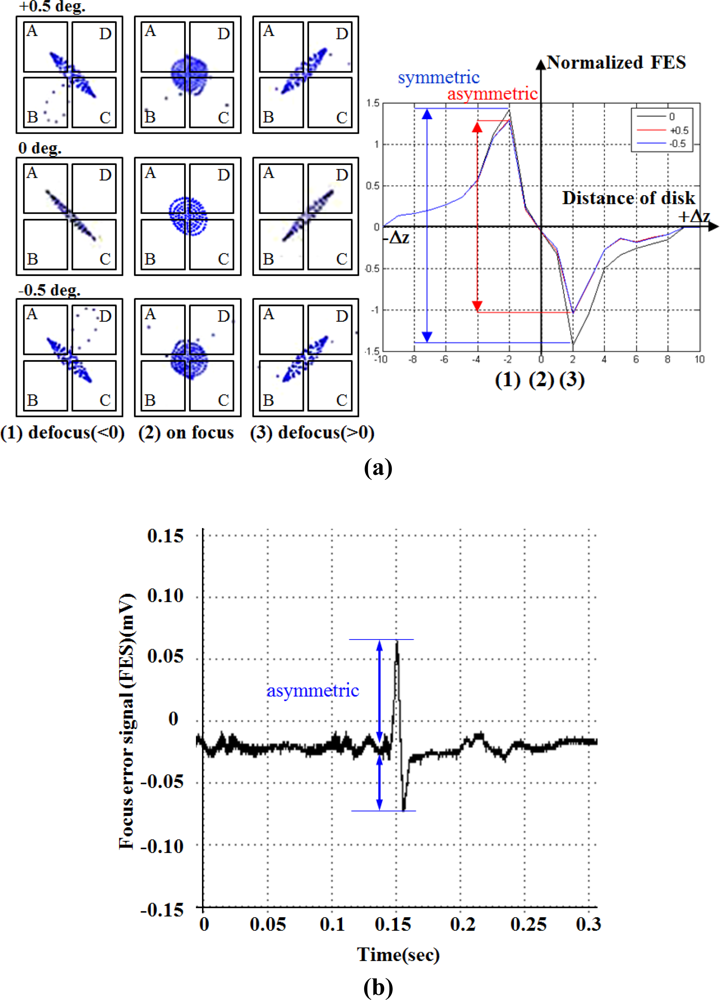
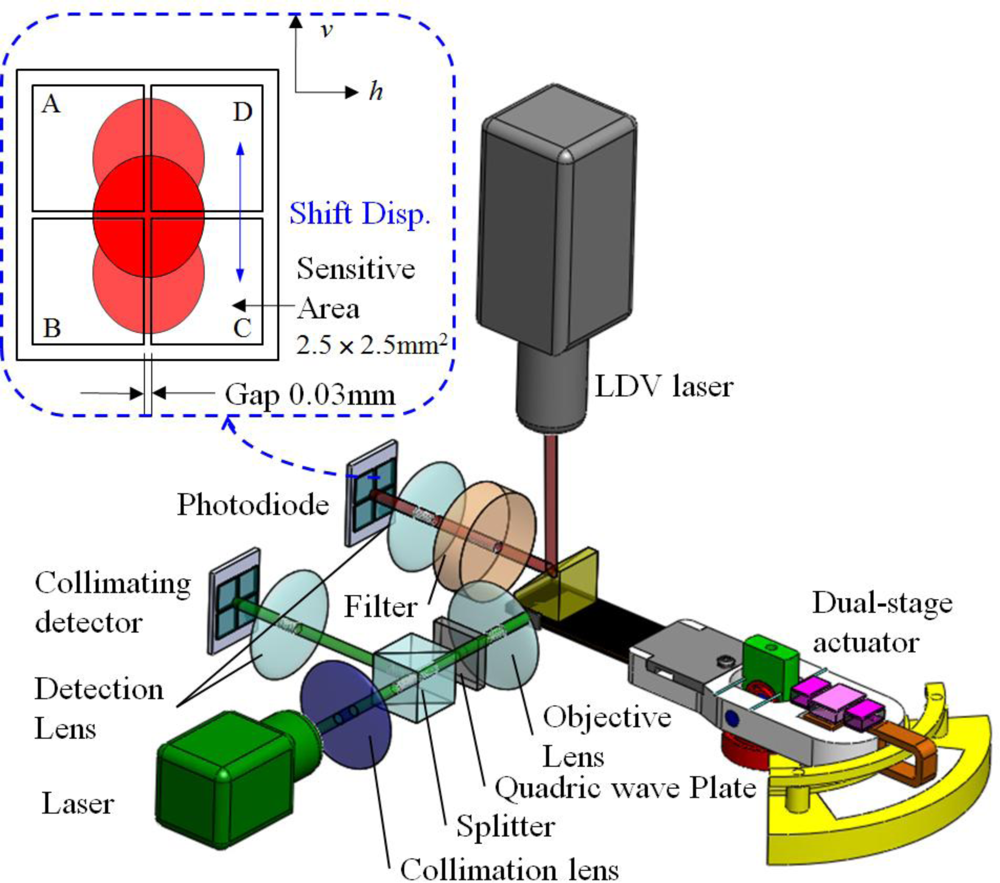
Figure 18(a) illustrates the simulated focusing error signal (S-curve) generated by the actuator tilting from −0.5○ to 0.5○, whereas the measured asymmetric S-curve is shown in Figure 18(b) for comparison. The astigmatic returning laser spot deteriorates considerably due to the tilt actuation, causing the asymmetric peak shapes of the S-curve. This unbalanced S-curve signal reduces the accuracy of optical sensing. The optical compensation for dual stage actuator is evaluated by designing the schematic layout of the reflection geometry for tilt measurement [24–26], as shown in Figure 19. The rotary angle measurement is performed by mounting a target 45° micro-prism on the precision VCM-Driven micro-positioning stage. The 635 nm wavelength laser, which is used to adjust tracking angle of dual-stage actuator, produces horizontal beam (green line) and passes through the collimating lens, the polarized beam splitter (PBS), the quarter-wave plate (QWP) to form circular polarization beam and focusing on the side of actuator by objective lens. The returning beam is reflected by the PBS and projected on the collimating detector. Furthermore, the LDV laser beam (red line, vertical) is focusing on the photo-diode to measure the dynamic tilt error motions of focus operation by varying the driving frequency in the range of 5–200 Hz. The distance of the seesaw actuator over the focus actuation stroke is 400 μm or less.
The proposed astigmatic detection method combined with differential phase detection (DPD) is verified through simulation and experimental results. By using the quadrant photo detector array, the astigmatic signal is generated (based on the phase difference between the sum of the diagonal elements, as shown in Equation (22).
Focus error signal (FES), f:
The DPD signal is defined versus the misalignment of the photo-detector in the plane (v, h) by using the following calculation [27,28].
DPD signal, dh:
DPD signal, dv:
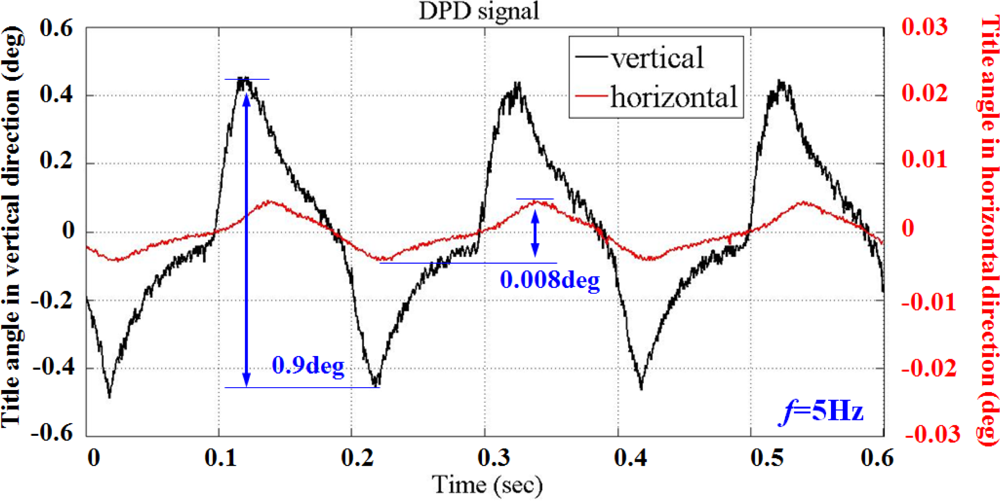
Feasibility of the proposed secondary stage PZT-actuator to compensate for the tilt actuation induced by the primary VCM actuator is demonstrated by conducting an experiment in which the dual stage actuator is kept in the in-focus condition. Figure 20 summarizes the experimental results by moving the prism with reflection geometry. The vertical (black) and horizontal (red) tilt angle are obtained based on differential phase variation with 5 Hz sine-wave excitation. Although the vertical angular displacement involves roll as well as pitch rotation, the phase variation from roll vibration is sufficiently small to be negligible compared with the actuator nutation.
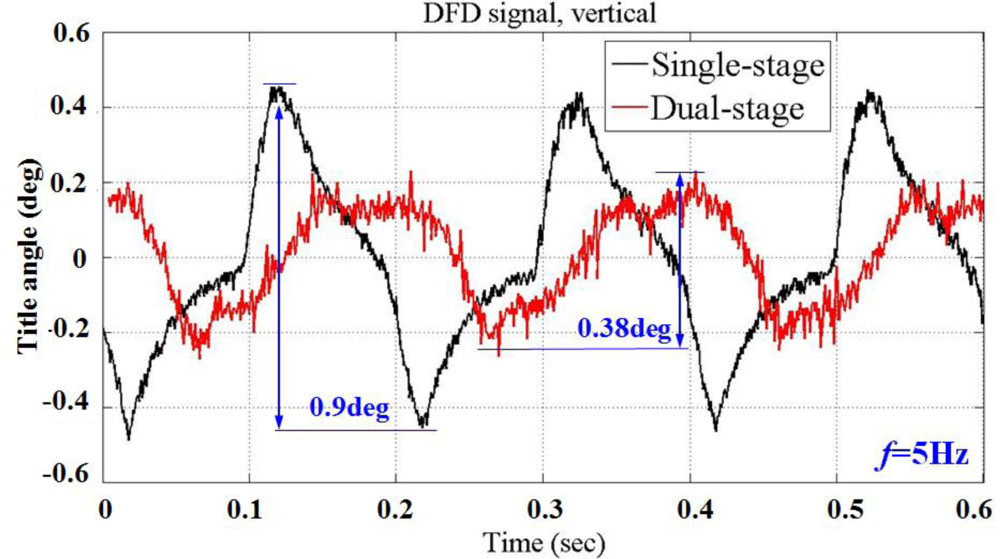
Both results closely correspond to the numerical calculations. The measurement accuracy of the photo-detector is validated. Figure 21 shows the tilt motions for both single and dual stage control. A sinusoidal signal with a frequency of 5 Hz and voltage amplitude of 6 V is applied to the seesaw actuator. As mentioned earlier, the angular displacement is within the restricted range ±0.19° (peak to peak) for the dual stage actuation than ±0.45° (peak to peak) for single-stage control. The tilt signal variance from a single-stage drive is reduced by 60% with the implementation of this dual stage compensation. Measurement results demonstrate a high stability for the application of adjusting the inclination angle of the optical axis with precision positioning, capable of satisfying the requirement for small tilt angle compensation of a dual stage actuator.
5. Conclusions
This work presents a miniaturized seesaw swivel actuator and suspension assembly with a piezoelectric-based micro-actuator and TVA absorber. Among the unique features of the proposed dual stage actuator include a rotary actuator for track-following and a combined piezo-VCM actuated suspension nutation for laser focusing. By using the optimization procedure, the original design is improved in terms of bandwidth and stability. The dynamic response of the dual-stage actuator is also shown, in which the PZT actuator rejects a higher frequency disturbance. The difference between the experimental frequency response of PZT bender and the numerical results is within 5.6%. Lower than the open loop bandwidth, the resonant peak of the PZT-actuator at 0.9 kHz does not pose stability problems. Simulation and experimental results indicate that the passive TVA reduces the system vibration by 80% with respect to the peak amplitudes. This work also investigates the relationship between the tilt sensor sensitivity and working distance of the dual stage actuator based on laser auto-collimation. The tilt variance of optical axis is reduced by 60% from a single-stage drive with the implementation of PZT compensation. Performance optimization of the combined piezo-VCM actuator is also evaluated to demonstrate the effectiveness of the proposed optical sensing applications.
Nomenclature
| LPZT | Effective length of PZT (mm) |
| Larm | Effective Length of arm (mm) |
| Ddisc | Distance from disk center(mm) |
| ϕ | Rotary angle of PZT bender (rad) |
| θ | Rotary angle of arm (rad) |
| γ | Rotary angle of disk (rad) |
| b | Width of PZT bender (mm) |
| tPZT | Thickness of PZT (mm) |
| tcarbon | Thickness of carbon (mm) |
| ρPZT | Density of PZT (kg/m3) |
| ρcarbon | Density of carbon (kg/m3) |
| ρabs | Density of TVA (kg/m3) |
| EPZT | Young’s modulus of PZT (GPa) |
| Ecarbon | Young’s modulus of carbon (GPa) |
| IPZT | Moment of inertia, PZT (m4) |
| Icarbon | Moment of inertia, carbon (m4) |
| d31 | Charging constant of PZT (C/N) |
| VPZT | PZT input Voltage (V) |
| A | The frequency ratio between system and input |
| B | The frequency ratio between system and TVA |
| M | Mass ratio between system and TVA |
| msys | Mass of dual-stage system (kg) |
| mabs | Mass of TVA (kg) |
| CPZT | Damping constant of PZT |
| Csys | Damping constant of arm |
| Cabs | Damping constant of TVA |
| ksys | Stiffness of system (N/m) |
| kPZT | Stiffness of PZT (N-m/rad) |
| keq | Equivalent stiffness of PZT (N/m) |
| kabs | Stiffness of TVA (N/m) |
| ζsys | Damping ratio of dual-stage system |
| ζabs | Damping ratio of TVA |
Acknowledgments
This work was supported by TDPA project 98-EC-17-A-07-S1-011, MOEA, and NSC project NSC 96-2221-E-009-149, Taiwan. The authors would like to thank the anonymous reviewers for useful comments and suggestions.
References
- Shih, HF; Chang, CL; Lee, KJ; Chang, CS. Design of optical head with holographic optical element for small form factor drive systems. IEEE Trans. Mag 2006, 41, 1058–1060. [Google Scholar]
- Shih, HF; Lee, YC; Chiu, Y; Chao, DWC; Lin, GD; Lu, CS; Chiou, JC. Micro Objective Lens with NA 0.65 for The Blue-light Small-form-factor Optical Pickup Head. Optics Express 2008, 16, 13150–13157. [Google Scholar]
- Chou, PC; Lin, YC; Cheng, S. Optimization of Seesaw Swing Arm Actuator Design for Small Form Factor Optical Disk Drive. Jpn. J. Appl. Phys 2010, 49, 052502. [Google Scholar]
- Chou, PC; Lin, YC; Cheng, C. A Novel Seesaw Swivel Actuator Design and Fabrication. IEEE Trans. Mag 2010, 46, 2603–2610. [Google Scholar]
- Yeak-Scranton, CE. Novel Piezoelectric Transducers to Monitor Head-disk Integrations. IEEE Trans. Mag 1986, 22, 1011–1016. [Google Scholar]
- Tagawa, N. State of The Art for Nanospacing Flying Head Slider Mechanisms in Magnetic Recording Disk Storage. Wear 1993, 168, 43–47. [Google Scholar]
- Kajitani, H; Hashimoto, M; Tagawa, N. Dynamic Loading Criteria for 3-1/2 Inch Inline HDD Using Multilayer Piezoelectric Load/Unload Mechanism. IEEE Trans. Mag 1991, 27, 5079–5081. [Google Scholar]
- Tominaga, J; Watabe, T; Yoshimoto, S. A Circular Arc Slider with a High Flying Height Supported by Parallel Flat Springs for Optical Disc Devices. Microsyst. Technol 2007, 13, 1131–1139. [Google Scholar]
- Chang, CS; Liu, TS; Tang, YC. A Tracking Motion Approach For a Piezotube Actuator in a Disk Drive subject to Disk Deformation and Disturbance. Smart Mater. Struct 2007, 16, 1542–1548. [Google Scholar]
- Yang, W; Lee, SY; You, BJ. A Piezoelectric Actuator with A Motion-Decoupling Amplifier for Optical Disk Drives. Smart Mater. Struct 2010, 19, 065027. [Google Scholar]
- Chung, J. Vibration Absorber for Reduction of the In-Plane Vibration in an Optical Disk Drive. IEEE Trans. Consum. Electron 2004, 50, 552–557. [Google Scholar]
- Heo, JW; Chung, J. Vibration and Noise Reduction of an Optical Disk Drive by Using a Vibration Absorber. IEEE Trans. Consum. Electron 2002, 48, 874–878. [Google Scholar]
- Chang, CS; Liu, TS. Design of Adaptive Dynamic Absorber to Reduce Optical Disk Drive Vibration at Multiple Rotating Speeds. Jpn. J. Appl. Phys 2006, 45, 1120–1123. [Google Scholar]
- Jiang, L; Miles, RN. A Passive Damper for the Vibration Modes of the Head Actuator in Hard Disk Drives. J. Sound Vibra 1999, 220, 683–694. [Google Scholar]
- Kuwajima, H; Kita, H; Hashi, H; Miyamoto, M; Ueno, Y; Inagaki, T; Matsuoka, K. Development of Balanced-type High Shock Suspension for 0.85-in Hard Disk Drive. IEEE Trans. Mag 2006, 42, 255–260. [Google Scholar]
- DeVoe, DL; Pisano, AP. Modeling and Optimal Design of Piezoelectric Cantilever Microactuators. IEEE J. Microelectromech. Syst 1997, 6, 266–270. [Google Scholar]
- Weinberg, MS. Working Equations for Piezoelectric Actuators and Sensors. IEEE J. Microelectromech. Syst 1999, 8, 529–533. [Google Scholar]
- Krommer, M. On the Correction of the Bernoulli–Euler Beam Theory for Smart Piezoelectric Beams. Smart Mater. Struct 2001, 10, 668–680. [Google Scholar]
- Ha, SK; Kim, YH. Analysis of a Piezoelectric Multimorph in Extensional and Flexural Motions. J. Sound Vibra 2002, 253, 1001–1014. [Google Scholar]
- Den Hartog, JP. Mechanical Vibrations; McGraw-Hill, Inc.: New York, NY, USA, 1956. [Google Scholar]
- Ormondroyd, J; Den Hartog, JP. Theory of The Dynamic Vibration Absorber Transactions of the Am. Soc. Mech. Eng. 1928, 50, 9–22. [Google Scholar]
- Brock, JE. A Note on the Damped Vibration Absorber. J Appl Mech 1946, 68, A-284. [Google Scholar]
- Thompson, AG. Optimizing the Untuned Viscous Dynamic Vibration Absorber with Primary System Damping. J. Sound Vibra 1980, 73, 469–412. [Google Scholar]
- Kim, SH; Kim, JH; Lee, YH; Yang, H; Park, JY; Park, KS; Park, YP. Tilt Error Measurement and Compensation Method for the Holographic Data Storage System Using Disturbance Observer. IEEE Trans. Mag 2009, 45, 2248–2251. [Google Scholar]
- Doh, TY; Ma, BI; Choi, BH; Park, IS; Chung, CS; Lee, YH; Kim, SJ; Shin, DH. Radial Tilt Detection Using one Beam and its Compensation in A High-density Read Only Memory. Jpn. J. Appl. Phys 2001, 40, 1680–1683. [Google Scholar]
- Lin, D; Yue, Z; Song, N; Meng, Y; Yin, C. A Double Common-path Heterodyne Interferometer for The Measurement of Flying Height Modulation. Meas. Sci. Technol 2008, 19, 055303. [Google Scholar]
- Shinoda, M; Nakai, K; Mori, K. Dependence of Differential Phase Detection Signals on Astigmatism in A Focused Spot. Jpn. J. Appl. Phys 2004, 43, 4870–4875. [Google Scholar]
- Saito, Y; Arai, Y; Gao, W. Investigation of An Optical Sensor for Small Tilt Angle Detection of A Precision Linear Stage. Meas. Sci. Technol 2010, 21, 054006. [Google Scholar]




| Optimization 1 | Optimization 2 | |
|---|---|---|
| Objective function | ||
| Optimization parameter | LPZT | tPZT |
| upper/lower bound | 10 ≤Larm ≤17 | 10 ≤LPZT ≤17 |
| 10 ≤LPZT ≤17 | 0.1 ≤tPZT ≤1.0 | |
| Constrain | Larm + LPZT = 27(mm) θ + ϕ – γ =0(rad) | 2tPZT + tcarbon ≤3(mm) |
| Algorithm | Medium-scale: SQP, Quasi-Newton, line-search | |
| Iterations | 64 | 59 |
| Optimization value | 0.271 | 985 Hz |
| FuncCount | 485 | 603 |
| Stepsize | 0.3014 | 0.31 |
| Firstorderopt | 80.1485 | 79.3485 |
| Constrviolation | 15.0831 | 21.2495 |
| result | 14.13 | 0.11 |
| Resonant Frequency(<10 kHz) | Numerical calculation | Experimental result | Error |
|---|---|---|---|
| 1st mode | 967 | 985 | 1.86% |
| 2nd mode | 6,065 | 5,874 | 3.14% |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chou, P.-C.; Lin, Y.-C.; Cheng, S. Enhancement of Optical Adaptive Sensing by Using a Dual-Stage Seesaw-Swivel Actuator with a Tunable Vibration Absorber. Sensors 2011, 11, 4808-4829. https://doi.org/10.3390/s110504808
Chou P-C, Lin Y-C, Cheng S. Enhancement of Optical Adaptive Sensing by Using a Dual-Stage Seesaw-Swivel Actuator with a Tunable Vibration Absorber. Sensors. 2011; 11(5):4808-4829. https://doi.org/10.3390/s110504808
Chicago/Turabian StyleChou, Po-Chien, Yu-Cheng Lin, and Stone Cheng. 2011. "Enhancement of Optical Adaptive Sensing by Using a Dual-Stage Seesaw-Swivel Actuator with a Tunable Vibration Absorber" Sensors 11, no. 5: 4808-4829. https://doi.org/10.3390/s110504808
APA StyleChou, P.-C., Lin, Y.-C., & Cheng, S. (2011). Enhancement of Optical Adaptive Sensing by Using a Dual-Stage Seesaw-Swivel Actuator with a Tunable Vibration Absorber. Sensors, 11(5), 4808-4829. https://doi.org/10.3390/s110504808




