High Accuracy Acoustic Relative Humidity Measurement inDuct Flow with Air
Abstract
:1. Introduction
2. Theory
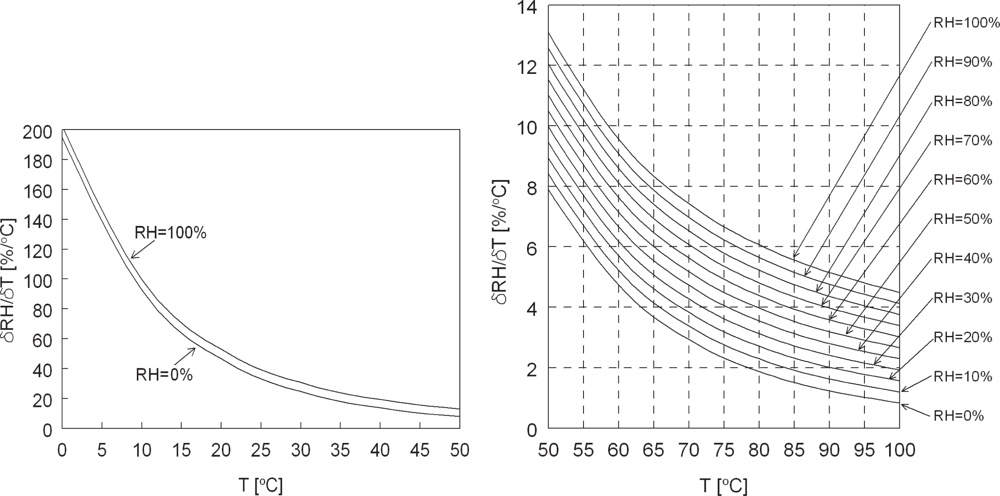
2.1. Sensitivity and Accuracy
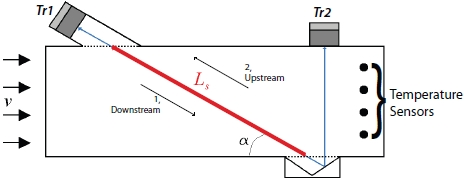
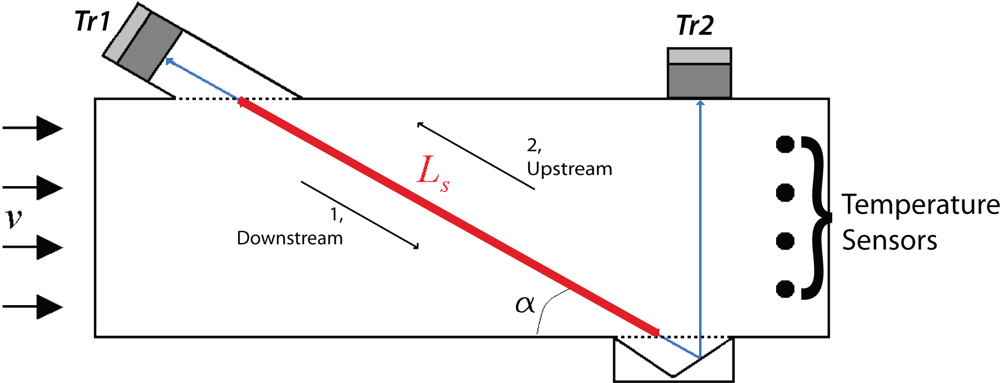
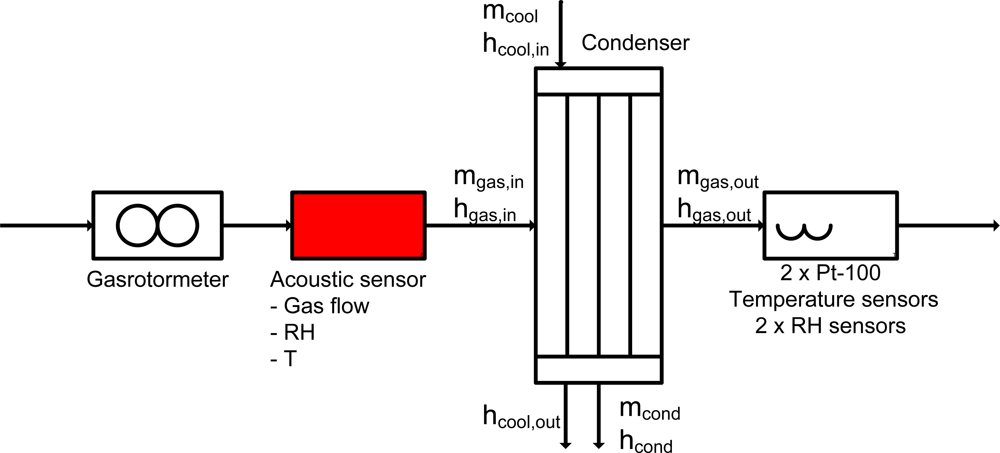
3. Construction
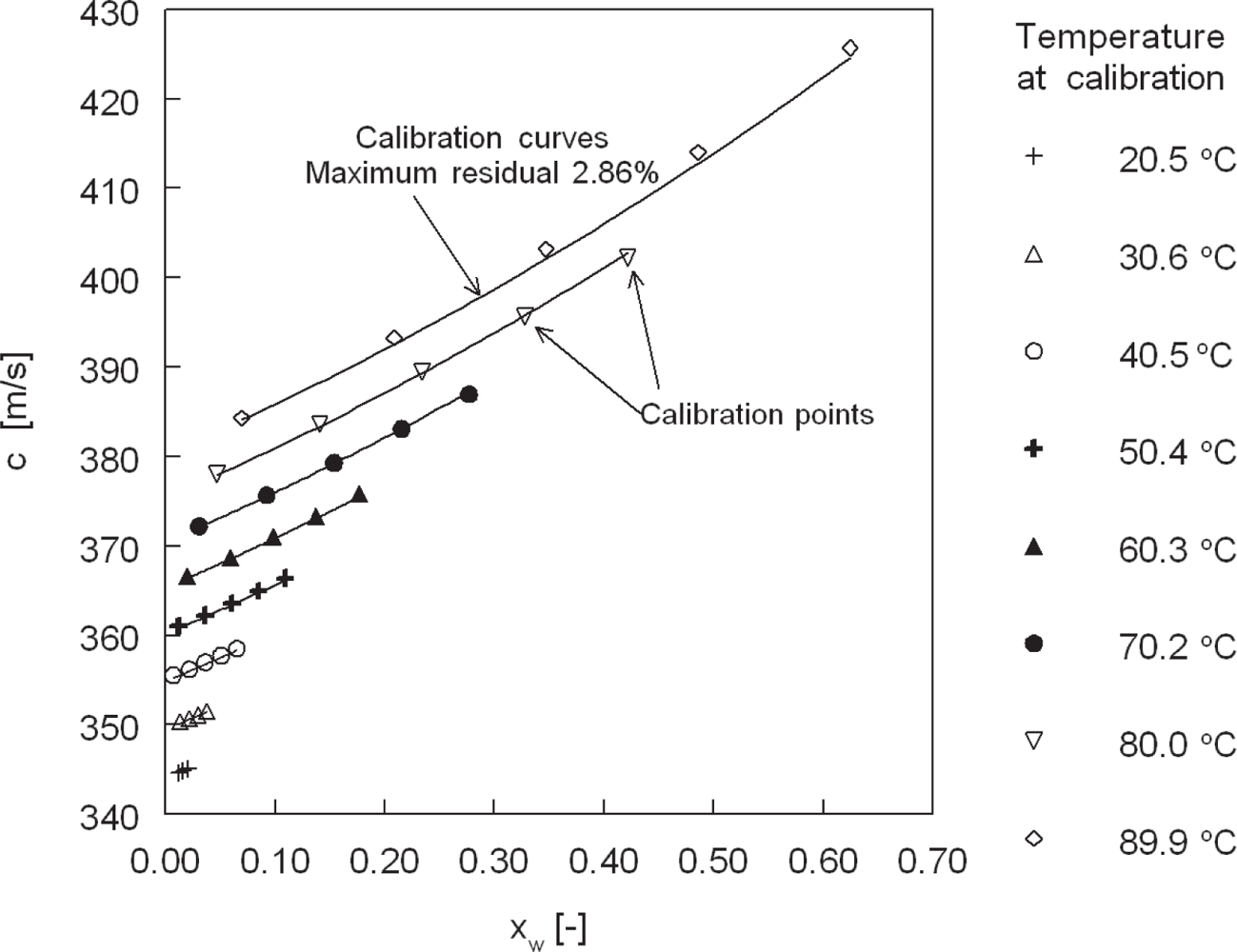
4. Calibration
5. Dynamic Response
- Use smaller temperature sensors, with smaller time constants.
- Damp the thermal fluctuations by installation of a large thermal mass at the duct inlet. This overcomes erroneous measurement of relative humidity due to temperature fluctuations, but cancels out the advantage of the fast response of the acoustics.
- Install temperature sensors with different time constants and use the derivative of the fastest temperature sensor to correct the slowest temperature sensor.
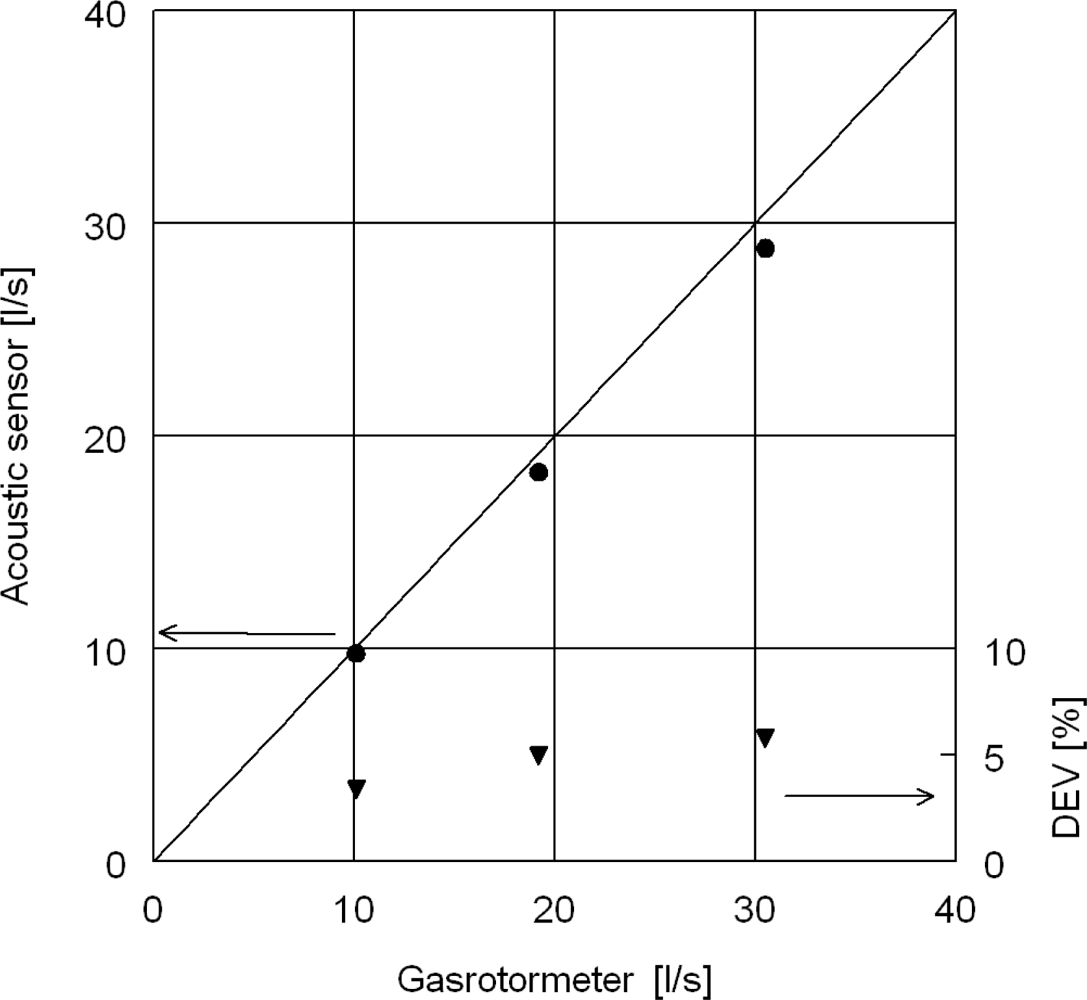
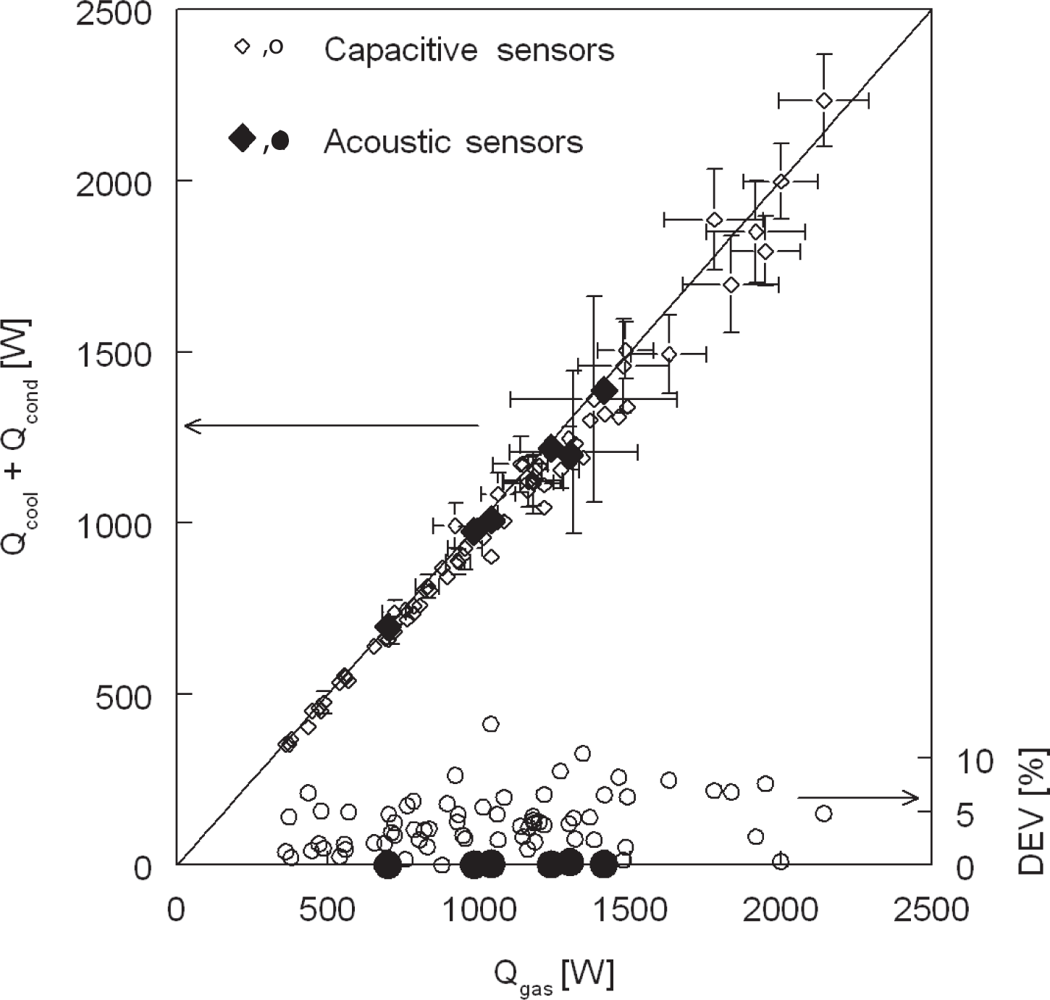
6. Results and Discussion
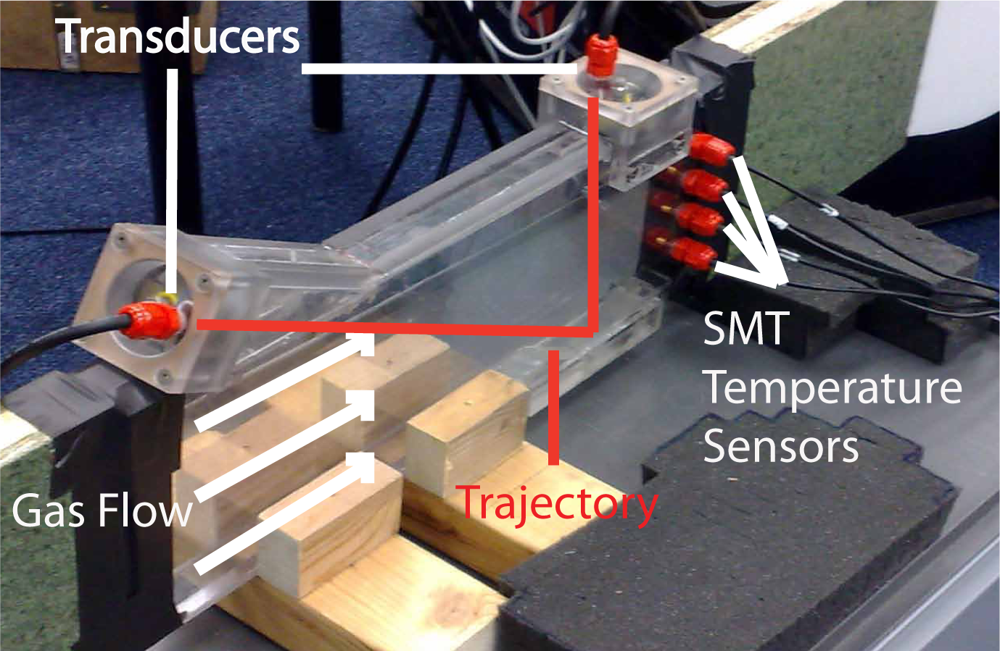
6.1. Preliminary Test in a Heat Exchanger Test Rig
7. Conclusions
Nomenclature
| B | Second virial coefficient | [m3mol−1] |
| L | Length | [m] |
| M | Molar mass | [kg · mol−1] |
| Q | Heat flow rate | [W] |
| R | Universal gas constant | [J · mol−1K−1] |
| RH | Relative Humidity | [%] |
| T | Temperature | [°C] |
| ai | Calibration coefficients | [−] |
| c | Speed of sound at measurement frequency | [m · s−1] |
| c0 | Speed of sound (zero frequency) | [m · s−1] |
| h | Enthalpy | [J · kg−1K−1] |
| ṁ | Mass flow rate | [kg · s−1] |
| p | Pressure | [Pa] |
| psv | Saturation pressure | [Pa] |
| t | Time | [s] |
| v | Velocity | [m · s−1] |
| xc | Mole fraction CO2 | [mole/mole mixture] |
| xw | Mole fraction water | [mole/mole mixture] |
| α | Angle | [°] |
| γ | Specific heat ratio, | [−] |
| σ | Standard deviation | [%] |
| χ | Error in relative humidity due to temperature error | [% ·° C−1] |
Acknowledgments
References
- Wernecke, R. Industrielle Feuchtemessung, Grundlagen, Messmethoden, Technische Anwendungen (in German); Wiley-VCH Verlag GmbH KGaA: Weinheim, Germany, 2003. [Google Scholar]
- Cramer, O. The variation of the specific heat ratio and the speed of sound in air with temperature, pressure, humidity, and CO2 concentration. J. Acoust. Soc. Am 1993, 93, 2510–2516. [Google Scholar]
- Wu, TT; Chen, Y; Chou, TH. A high sensitivity nanomaterial based SAW humidity sensor. J. Phys. D: Appl. Phys 2008, 41, 085101. [Google Scholar]
- Grimes, CA; Mungle, CS; Zeng, K; Jain, MK; Dreschel, WR; Paulose, M; Ong, KG. Wireless magnetoelastic resonance sensors: A critical review. Sensors 2002, 2, 294–313. [Google Scholar]
- Zipser, L; Franke, H; Bretschneider, WD. Acoustic sensors for analyzing binary gas mixtures. IEEE Sensor. J 2006, 6, 536–541. [Google Scholar]
- Tsai, WY; Chen, HC; Liao, TL. An ultrasonic air temperature measurement system with self-correction function for humidity. Meas. Sci. Technol 2005, 16, 548–55. [Google Scholar]
- Greenspan, M. Comments on “Speed of sound in standard air” [J. Acoust. Soc. Am. 79, 1359–1366 (1986)]. J. Acoust. Soc. Am 1987, 82, 370–372. [Google Scholar]
- NIST Standard Reference Database 69, June 2005 Release, NIST Chemistry WebBook. Available online: http://webbook.nist.gov/chemistry/ (accessed on 20 July 2010).
- Ganzevles, FLA; van der Geld, CWM. Heat and mass transfer from internal flows to hemispheres and flat parts in between. Int. J. Heat Mass Transfer 1998, 41, 3705–3718. [Google Scholar]
- Schaik, WV. Calibration Report; SMT90; Eindhoven: The Netherlands, 2009. [Google Scholar]
- Schaik, WV. Calibration Report; V90; Eindhoven: The Netherlands, 2009. [Google Scholar]
- Wendoloski, JC. On the theory of acoustic flow measurement. J. Acoust. Soc. Am 2001, 110, 724–737. [Google Scholar]
- Willatzen, M; Kmath, H. Nonlinearities in ultrasonic flow measurement. Flow Meas. Instrum 2008, 19, 79–84. [Google Scholar]
- Köchner, H; Melling, A; Baumgärtner, M. Optical flow field investigations for design improvements of an ultrasonic gas meter. Flow Meas. Instrum 1996, 7, 133–140. [Google Scholar]

| Constituent | Molar mass Mi [10−3kg · mol−1] | Mole fraction xi | Contribution xi Mi [10−3kg · mol−1] |
|---|---|---|---|
| N2 | 28.0134 | 0.78084 | 21.8739833 |
| O2 | 31.9988 | 0.209476 | 6.7029806 |
| Ar | 39.948 | 0.00934 | 0.3731143 |
| CO2 | 44.010 | 0.000314 | 0.0138191 |
| Ne | 20.183 | 18.18 · 10−6 | 0.0003669 |
| He | 4.0026 | 5.24 · 10−6 | 0.0000210 |
| CH4 | 16.04303 | 2.0 · 10−6 | 0.0000321 |
| Kr | 83.8 | 1.14 · 10−6 | 0.0000955 |
| H2 | 2.01594 | 0.5 · 10−6 | 0.0000010 |
| N2O | 44.0128 | 0.27 · 10−6 | 0.0000119 |
| CO | 28.01 | 0.19 · 10−6 | 0.0000053 |
| Xe | 131.3 | 0.087 · 10−6 | 0.0000114 |
| H2O | 18.01534 | 0.0 | 0.0 |
| Coefficient | Calibrated value |
|---|---|
| a0 | 332.2424 |
| a1 | 0.576691 |
| a2 | −0.000472 |
| a3 | 47.597133 |
| a4 | 0.1158039 |
| a5 | −0.000691 |
| a6 | −1.82 · 10−7 |
| a7 | 3.73 · 10−8 |
| a8 | 2.93 · 10−10 |
| a9 | −85.20931 |
| a10 | −0.228525 |
| a11 | 5.91 · 10−5 |
| a12 | 29.33397 |
| a13 | −2.15 · 10−13 |
| a14 | 29.179762 |
| a15 | 0.00483 |
| Lt | 0.5026 |
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Schaik, W.v.; Grooten, M.; Wernaart, T.; Geld, C.v.d. High Accuracy Acoustic Relative Humidity Measurement inDuct Flow with Air. Sensors 2010, 10, 7421-7433. https://doi.org/10.3390/s100807421
Schaik Wv, Grooten M, Wernaart T, Geld Cvd. High Accuracy Acoustic Relative Humidity Measurement inDuct Flow with Air. Sensors. 2010; 10(8):7421-7433. https://doi.org/10.3390/s100807421
Chicago/Turabian StyleSchaik, Wilhelm van, Mart Grooten, Twan Wernaart, and Cees van der Geld. 2010. "High Accuracy Acoustic Relative Humidity Measurement inDuct Flow with Air" Sensors 10, no. 8: 7421-7433. https://doi.org/10.3390/s100807421
APA StyleSchaik, W. v., Grooten, M., Wernaart, T., & Geld, C. v. d. (2010). High Accuracy Acoustic Relative Humidity Measurement inDuct Flow with Air. Sensors, 10(8), 7421-7433. https://doi.org/10.3390/s100807421