1. Introduction
A common problem in the field of autonomous robots is how to obtain the position and orientation of the robots within the environment with sufficient accuracy. Several methods have been developed to carry out this task. The localization methods can be classified into two groups: those that require sensors onboard the robots [
1] and those that incorporate sensors within the work environment [
2].
Although the use of sensors within the environment requires the installation of an infrastructure of sensors and processing nodes, it presents several advantages, it allows reducing the complexity of the electronic onboard the robots and facilitates simultaneous navigation of multiple mobile robots within the same environment without increasing the complexity of the infrastructure. Moreover, the information obtained from the robots movement is more complete, thereby it is possible to obtain information about the position of all of the robots, facilitating cooperation between them. This alternative includes “intelligent environments” [
3,
4] characterized by the use of an array of sensors located in fixed positions and distributed strategically to cover the entire field of movement of the robots. The information provided by the sensors should allow the localization of the robots and other mobile objects accurately.
The sensor system in this work is based on an array of calibrated and synchronized cameras. There are several methods to locate mobile robots using an external camera array. The most significant approaches can be divided into two groups. The first group includes those works that make use of strong prior knowledge by using artificial landmarks attached to the robots [
5,
6]. The second group includes the works that use the natural appearance of the robots and the camera geometry to obtain the positions [
2]. Intelligent spaces have a wide range of applications, especially in indoor environments such as homes, offices, hospital or industrial environments, where sensors and processing nodes are easy to install.
The proposal presented in this paper is included in the second group. It uses a set of calibrated cameras, placed in fixed positions within the environment to obtain the position of the robots and their orientation. This proposal does not rely on previous knowledge or invasive landmarks. Robots segmentation and position are obtained through the minimization of an objective function. There are many works that use an objective function [
7,
8]. However, the works in [
7,
8] present several disadvantages such as high computational cost or dependence on the initial values of the variables. Moreover, these methods are not robust because they use information from a single camera.
It is noteworthy that, although the proposal in this work has been evaluated in a small space (ISPACE-UAH), it can be easily extended to a larger number of rooms, corridors, etc. It allows covering a wider area, by adding more cameras to the environment and properly dimensioning the image processing hardware.
2. Multi-Camera Sensor System
The sensor system used in this work is based on a set of calibrated and synchronized cameras placed in fixed positions within the environment (Intelligent Space of University of Alcalá, ISPACE-UAH). These cameras are distributed strategically to cover the entire field of movement of the robots. As has been explained in the introduction, the use of sensors within the environment presents several advantages, it allows reducing the complexity of the electronic onboard the robots and facilitates simultaneous navigation of multiple mobile robots within the same environment without increasing the complexity of the infrastructure. Moreover, the information obtained from the movement of the robots is more complete, thereby it is possible to obtain information about the position of all of the robots, facilitating the cooperation between them.
2.1. Hardware Architecture
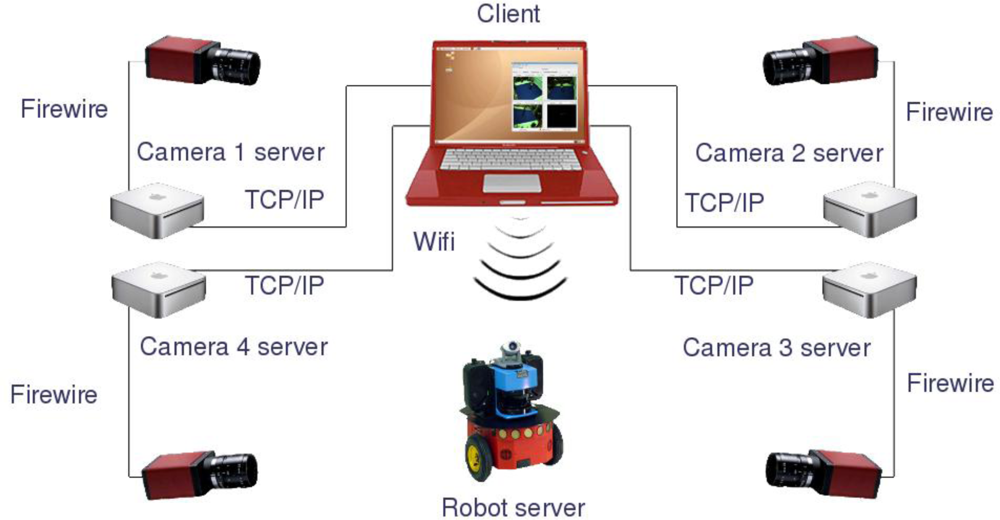
The hardware deployed in the ISPACE-UAH consists basically of a set of cameras with external trigger synchronization, a set of acquisition and processing nodes, mobile robots and a Local Area Network (LAN) infrastructure, that includes a wireless channel that the robots use to provide information from their internal sensors and to receive motion commands. All the cameras are built with a CCD sensor with a resolution of 640 × 480 and a size of 1/2” (8mm diagonal). The optical system is chosen with a focal length of 6.5 mm which gives about 45° of Field of View (FOV). Each camera is connected to a processing node through a Firewire (IEEE1394) local bus, which allows 25 fps RGB image acquisition speed and control of several camera parameters such as the exposure, gain or trigger mode.
The processing nodes are general purpose multi-core PC platforms with Firewire ports and Gigabit Ethernet hardware which allows them to connect to the LAN network. Each node has the capability of controlling and processing the information from one or several cameras. In the present paper each node is connected to a single camera.
The robotic platforms used in all experiments are provided by “Active Media Robotics”. More specifically, the model used is the P3-DX, which is a differential wheeled robot of dimensions 44.5 × 40 × 24.5 cm, equipped with low level controllers for each wheel, odometry systems and an embedded PC platform with IEEE 802.11 wireless network hardware.
2.2. Software Architecture
The software architecture chosen is a client-server system using common TCP/IP connections, where some servers (i.e., processing nodes and robots internal PCs) receive commands and requests from a client (i.e., computer or data storage device for batch tests).
Each processing node acts as a server that preprocesses the images and sends the results to the client platform. The preprocessing task of the servers consists of operations that can be clearly developed separately for each camera, such as image segmentation, image warping for computing occupancy grids, compression or filtering. The internal PC in each robot acts as a server which allows receiving control commands from a client and sending back the odometry readings obtained from its internal sensors. On the other hand, the client is in charge of performing data fusion using all information provided by the servers in order to achieve a certain task. In the case of the application proposed in this paper, the client receives robots odometry information, 3D occupancy grid representation of the scene and the client itself assures synchronization of the odometry values with the camera acquisition. In
Figure 1, a general diagram of the proposed hardware/software architecture is shown.
2.3. Reference Systems in the Intelligent Space
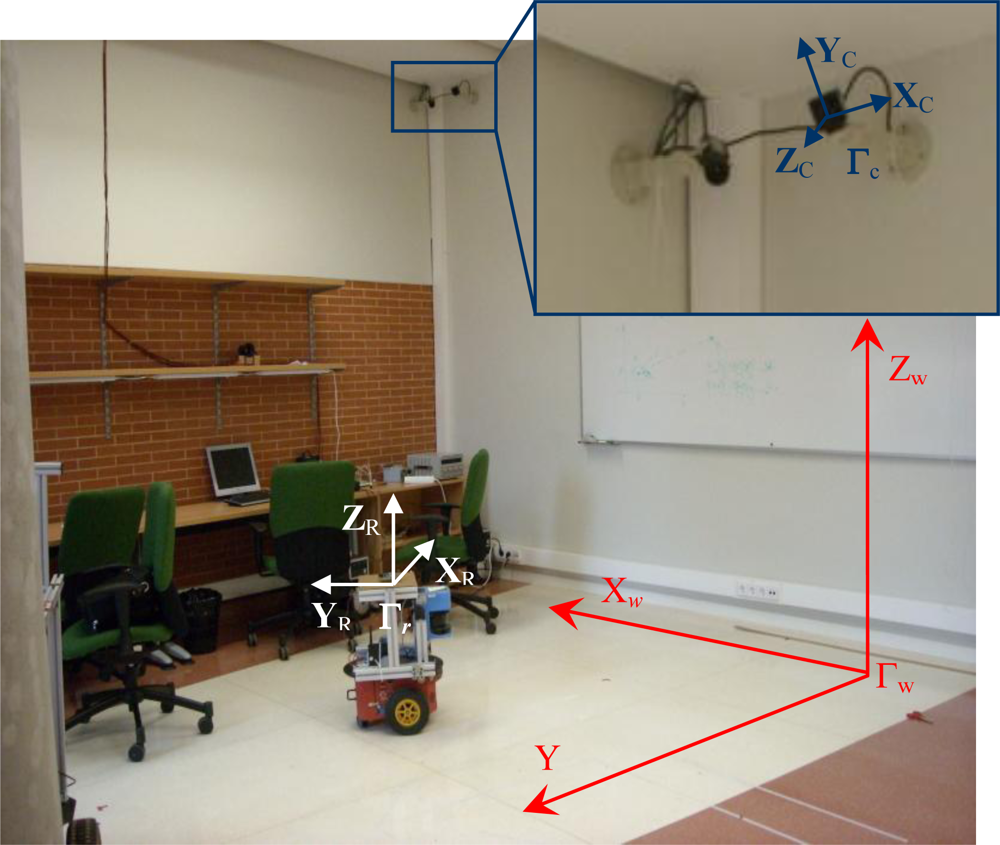
Before presenting the proposed algorithm for motion segmentation and 3D positioning of multiple mobile robots using an array of cameras, it is important to define the different coordinate systems used in this work. In the intelligent space, the 3D coordinates of a point
P = (
X,
Y,
Z)
T can be expressed in different coordinate systems. There is a global reference system named “world coordinate system” and represented by Γ
w. There is also a local reference system associated with each camera (Γ
ci,
i = 1,…,
nc) whose origin is located in the center of projection. These coordinate systems are represented in
Figure 2, where world coordinate system (Γ
w) has been represented in red color and the coordinate systems associated to the cameras (Γ
ci) have been represented in blue color.
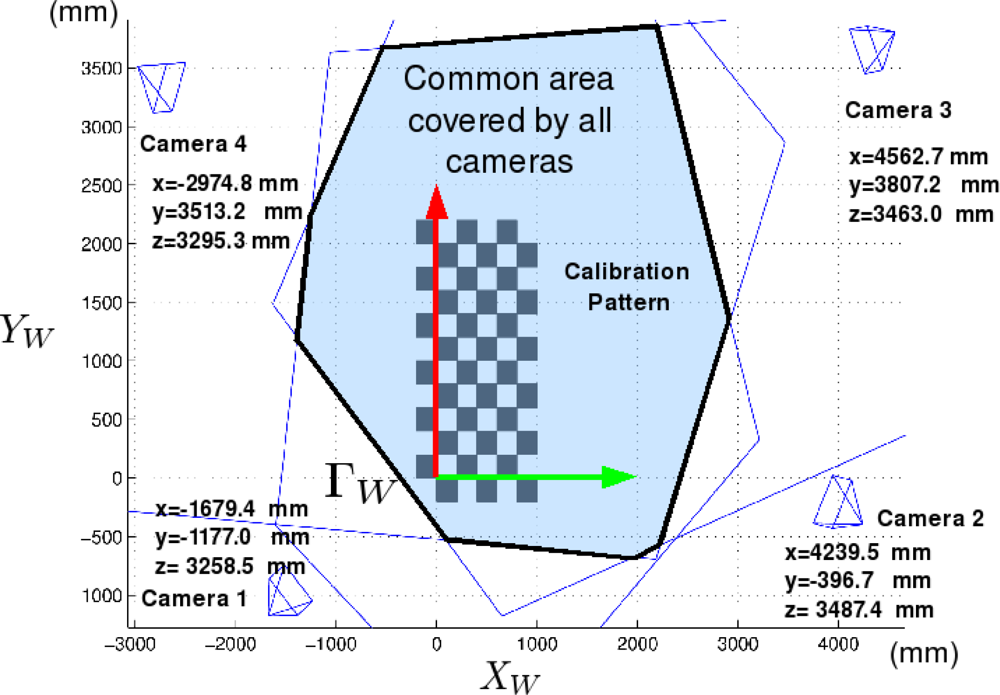
The cameras used in this work are placed in fixed positions within the environment (ISPACE-UAH). These cameras are distributed strategically to cover the entire field of movement of the robots.
Figure 3 shows the spatial distribution, and the area covered by the cameras used in this work.
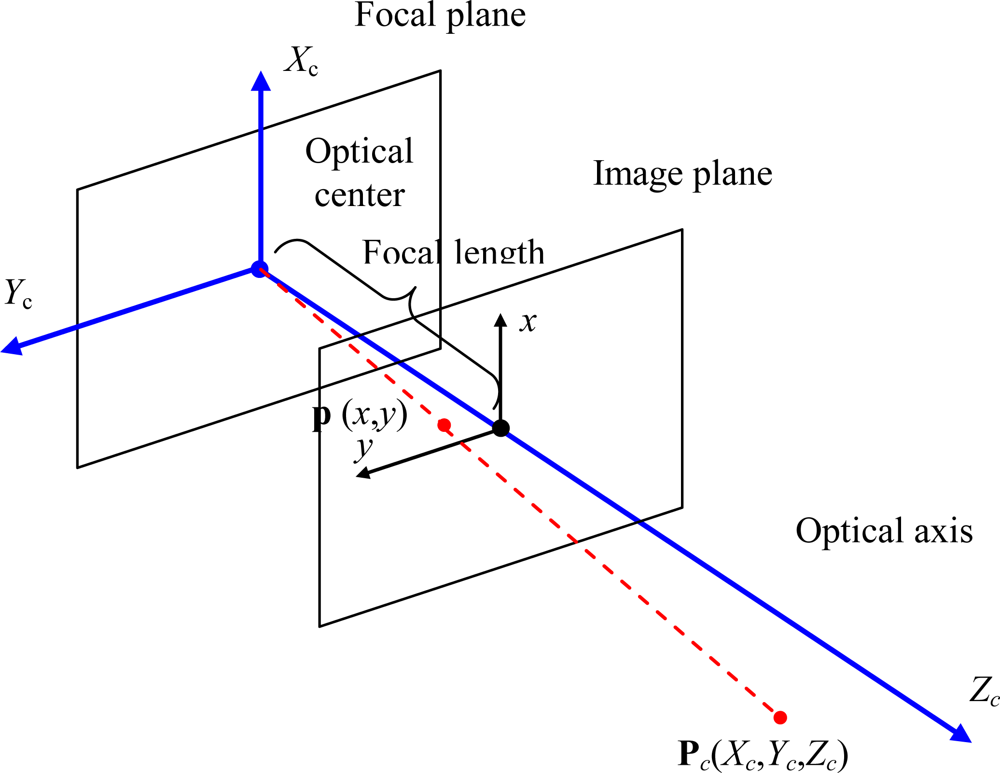
Cameras are modeled as pinhole cameras. This is a simple model that describes the mathematical relationship between the coordinates of a 3D point in the camera coordinate system (Γ
c) and its projection onto the image plane in an ideal camera without lenses through the expressions in
Equation (1) where
fx, fy are the camera focal lengths along
x and
y axis:
If the origin of the image coordinate system is not in the center of the image plane, the displacement (
s1,
s2) from the origin to the center of the image plane is included in the projection equations, obtaining the perspective projection
Equation (2):
These equations can be expressed using homogeneous coordinates, as shown in
Equation (3):
The geometry related to the mapping of a pinhole camera is illustrated in the
Figure 4.
4. Experimental Results
In order to validate the proposed system, several experiments have been carried out in the ISPACE-UAH. In these experiments we have used two five-hundred image sequences. These sequences have been acquired using three of the four cameras in the ISPACE-UAH.
Figure 7 shows one scene belonging to each sequence. As can be noticed in
Figure 7, sequence 1 contains one robot whereas sequence 2 contains two mobile robots. The proposed algorithm for motion segmentation and 3D localization using a multi-camera sensor system has been used to obtain motion segmentation and 3D position for each couple of images in each sequence. All the experiments shown in this work have been carried out on Intel® core 2, 6600 with 2.4 GHz using Matlab.
To start with the results, the boundaries of the motion segmentation in one image belonging to the sequence 1 [
Figure 7(a)] and the sequence 2 [
Figure 7(b)], respectively, are shown in
Figure 8 and
Figure 9 respectively.
Figure 8 shows the boundaries of the segmentation obtained for one image belonging to the sequence 1 [
Figure 7(a)] that contains only one robot. In this figure we can observe that the result of the motion segmentation is similar regardless of the number of cameras considered. In all the images, the segmentation boundary is close to the real contour of the mobile robot in the image plane.
However, the boundaries obtained for an image belonging to the sequence 2 [
Figure 7(b)] are notably different for 1, 2 or 3 cameras, as can be noticed in
Figure 9. If the segmentation is carried out from the images acquired using one [
Figure 9(a)] or two [
Figure 9(b)] cameras, the person in the background of the scene is considered as a mobile robot but, if the images from three cameras are used, this person is not detected.
The computational time depends on both, the number of cameras and the number of robots detected in the scene. If the number of detected robots remains constant (as in sequence 1, where only one robot is detected for 1, 2 or 3 cameras) the processing time increases with the number of cameras. It can be observed in
Table 1, where the average value of the computation time of each couple of images in the image sequences 1 and 2 is shown. In
Table 1 we can observe that, for the images belonging to the sequence 1 (with only 1 robot) computation time increases with the number of cameras.
On the other hand, the number of objects detected as mobile robots has a bigger impact in the computation time than the number of cameras, as can be noticed in
Table 1. The sequence 1, used to obtain the results in
Table 1, contains only one robot whereas the sequence 2 includes two robots. Comparing the results obtained for the sequence 1 and the sequence 2, it can be noticed that, regardless of the number of cameras, the processing time obtained for the sequence 2 (with two robots) is higher than the processing time obtained for the sequence 1 (including only one robot). Moreover, in case of the sequence 2, the computation time using two cameras is bigger than using three cameras. The reason is that the number of objects that have been segmented with 2 cameras is bigger.
With regard to 3D positioning,
Figure 10 shows the projection, onto the image plane, of the 3D trajectory of the mobile robot estimated by the algorithm (using 1, 2 and 3 cameras) and measured by the odometry sensors on board the robots. The represented trajectory has been calculated using 250 images belonging to each sequence.
The trajectories shown in
Figure 10 are obtained by projecting the estimated trajectory in Γ
w, obtained using the proposed algorithm, onto the image plane of the camera 1.
These trajectories obtained using 250 images belonging to each sequence can also be represented in the world coordinate system. The coordinates of the centroid of the points belonging to each robot are projected onto the plane (
Xw,
Yw) in Γ
w to obtain the 3D position. The result of this projection for a 250 images belonging to each sequence is shown in
Figure 11. In this figure, we have represented the estimated trajectory obtained using 2 and 3 cameras.
As can be observed in
Figure 10 and
Figure 11, the estimated trajectories are closer to the measurements of the odometry sensors as the number of cameras increases. This fact can also be observed in the positioning error calculated as the difference between the estimated and the measured positions along
Xw and
Yw axis, using
Equation (28):
The positioning error, calculated for 500 images belonging to each sequence, has been represented in
Figure 12. It is worth highlighting that the wheels of the robot in sequence 1 tend to skid on the floor. This is the reason why, in some positions, the difference between the estimated position and the measured one is high.
As can be observed in
Figure 12, using the multi-camera sensor system with 2 or 3 cameras the positioning error is lower than 300 millimeters. It can also be observed in
Table 2, where the average value of the positioning error for 500 images represented in
Figure 12 is shown. Moreover, the positioning error reduces as the number of cameras increases. This reduction is more important in the sequence 2. It is because sequence 2 is more complex than sequence 1 and the addition of more cameras allows removing the points that do not belong to mobile robots and dealing with robot occlusions.
Finally, it is noteworthy that although we have obtained better results using the images acquired by three cameras, two cameras are enough to obtain suitable 3D positions. For this reason, we can conclude that the proposal in this paper can work properly even if one of the three cameras looses track of one robot. Even in the worst case, if all the cameras lose some of the robots, they can still be controlled by the intelligent space. In this case, the positions of the unseen robots are estimated through the measurements of the odometry sensors they have onboard.
5. Conclusions
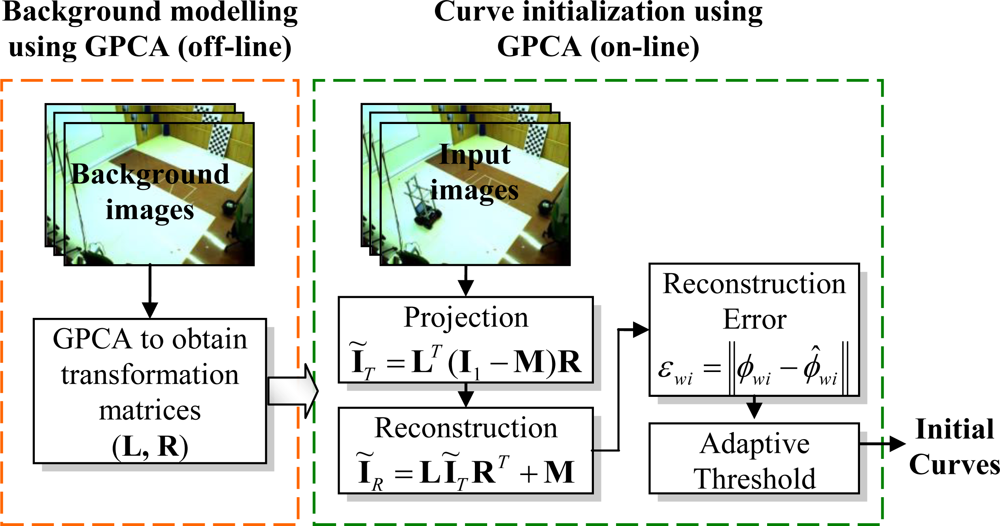
A method for obtaining the motion segmentation and 3D localization of multiple mobile robots in an intelligent space using a multi-camera sensor system has been presented. The set of calibrated and synchronized cameras are placed in fixed positions within the environment (in our case, the ISPACE-UAH). Motion segmentation and 3D position of the mobile robots are obtained through the minimization of an objective function that incorporates information from the multi-camera sensor. The proposed objective function has a high dependence on the initial values of the curves and depth. In this sense, the use of GPCA allows obtaining a set of curves that are close to the real contours of the mobile robots. Moreover, Visual Hull 3D allows us to relate the information from all the cameras, providing an effective method for depth initialization. The proposed initialization method guarantees that the minimization algorithm converges after a few iterations. The reduction in the number of iterations also decreases the processing time against other similar works.
Several experimental tests have been carried out in the ISPACE-UAH and the obtained results validate the proposal presented in this paper. It has been demonstrated that the use of a multi-camera sensor increases significantly the accuracy of the 3D localization of the mobile robots against the use of a single camera. It has also been proved that, the positioning error decreases as the number of cameras increases. In any case, using a multi-camera sensor, the positioning error is lower than 300 millimeters. With regard to the processing time, it depends on both, the number of cameras and the number of robots detected in the scene, having the second factor a bigger impact. In fact, the processing time can be reduced if the number of cameras is increased, because the noise measurements (that do not belong to mobile robots) are reduced when the number of cameras is increased.
Regarding to the future work, the most immediate task is the implementation of the whole system in real time. Currently the system is working in a small space (ISPACE-UAH). It will be extended, in order to cover a wider area, by adding more cameras to the environment and properly re-dimensioning the image processing hardware. This line of future work has a special interest towards its installation in buildings with multiple rooms.