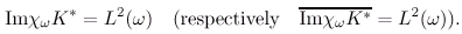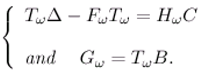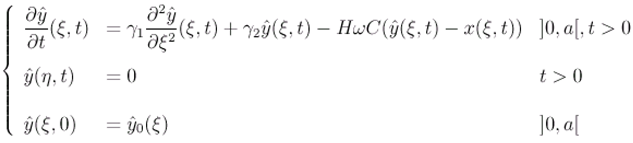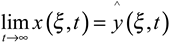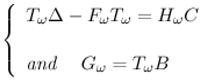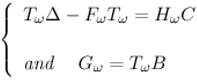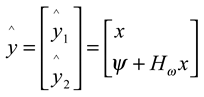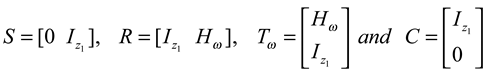Sensors and Asymptotic w-observer for Distributed Diffusion Systems
Abstract
:Introduction
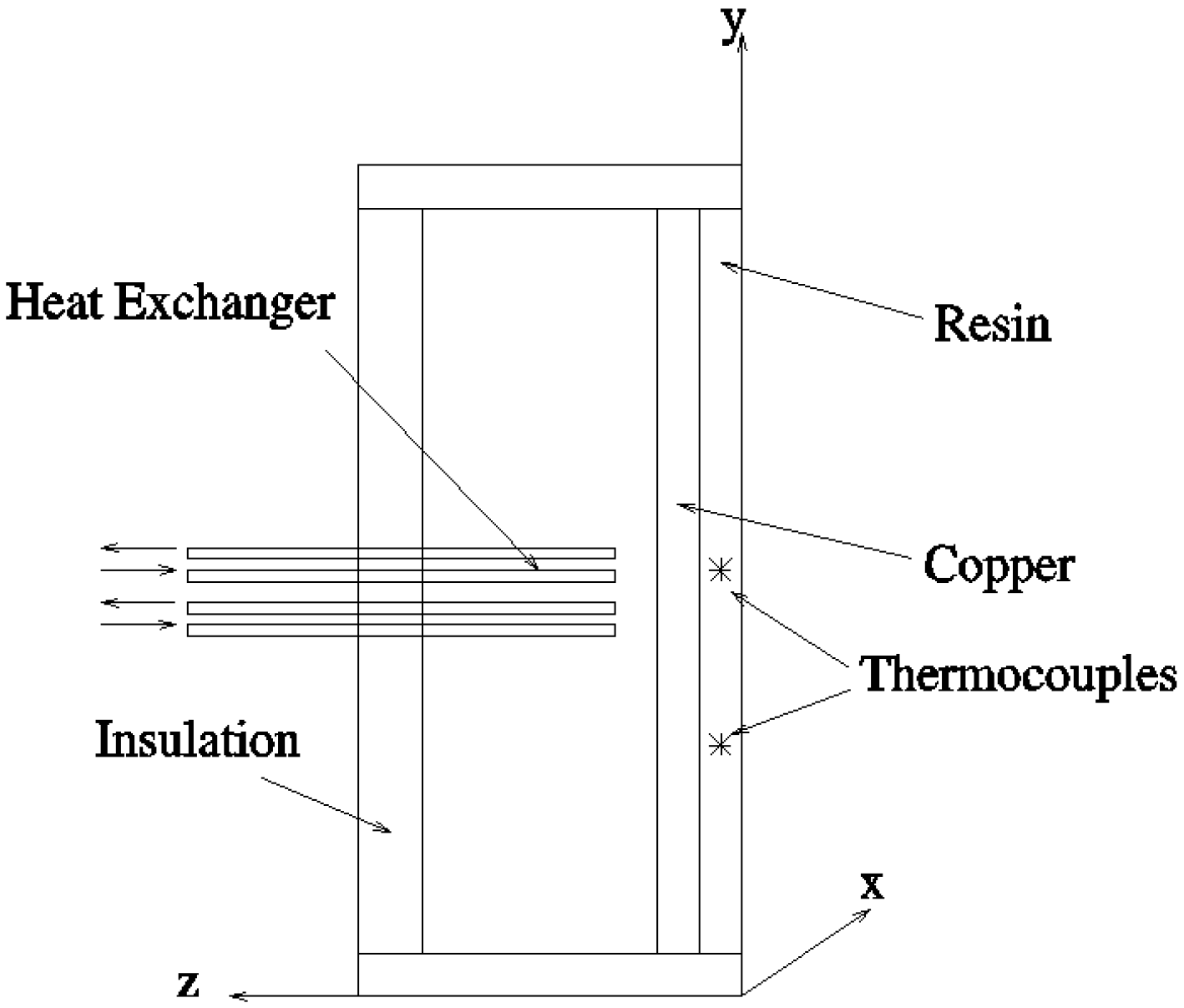
2. Asymptotic ω-observer
2.1 Description systems and preliminaries
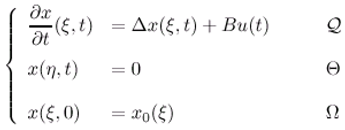
- The operators Δ is self-adjoint with compact resolvent.
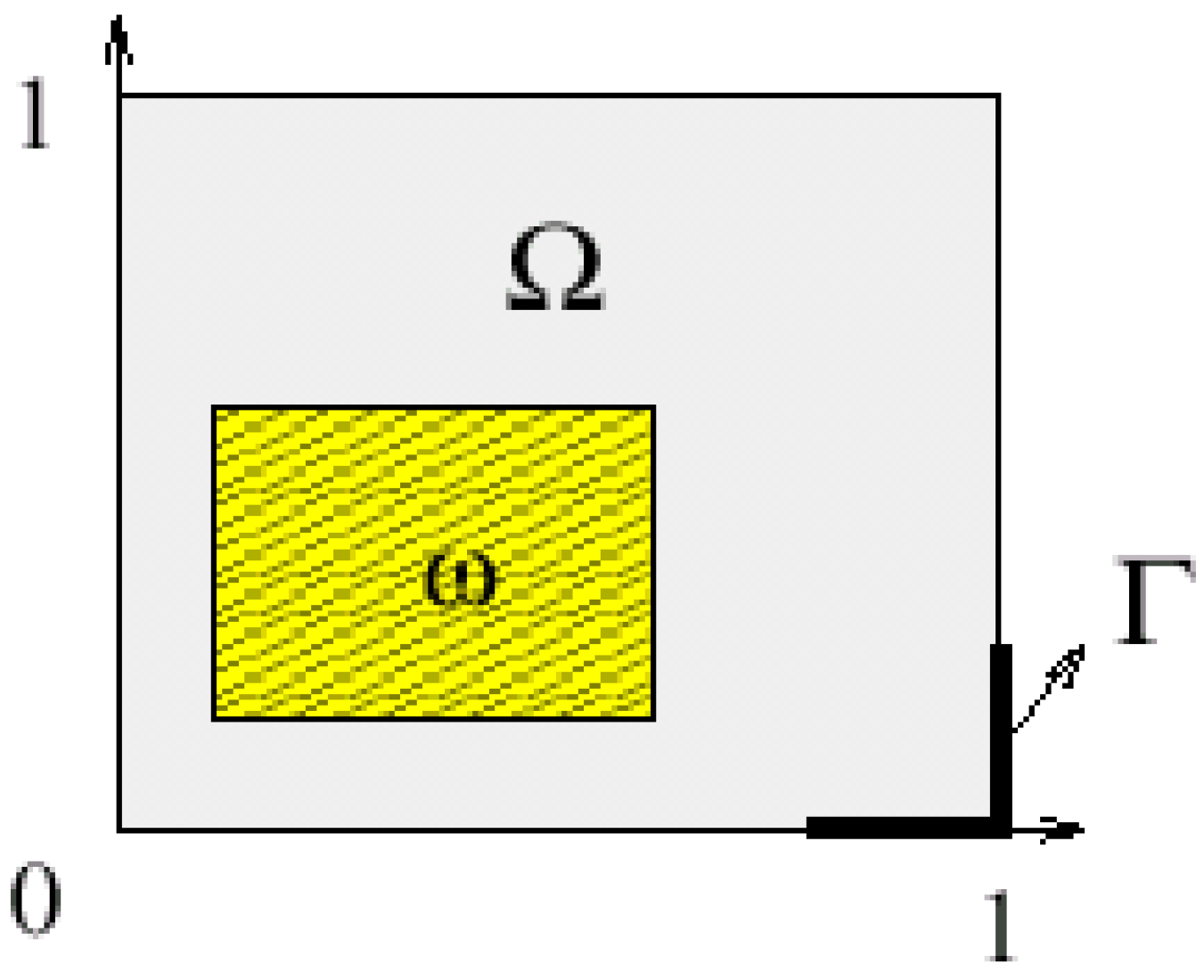
- Ω is an open regular bounded set of (n =1, 2, 3) with smooth boundary ∂Ω.
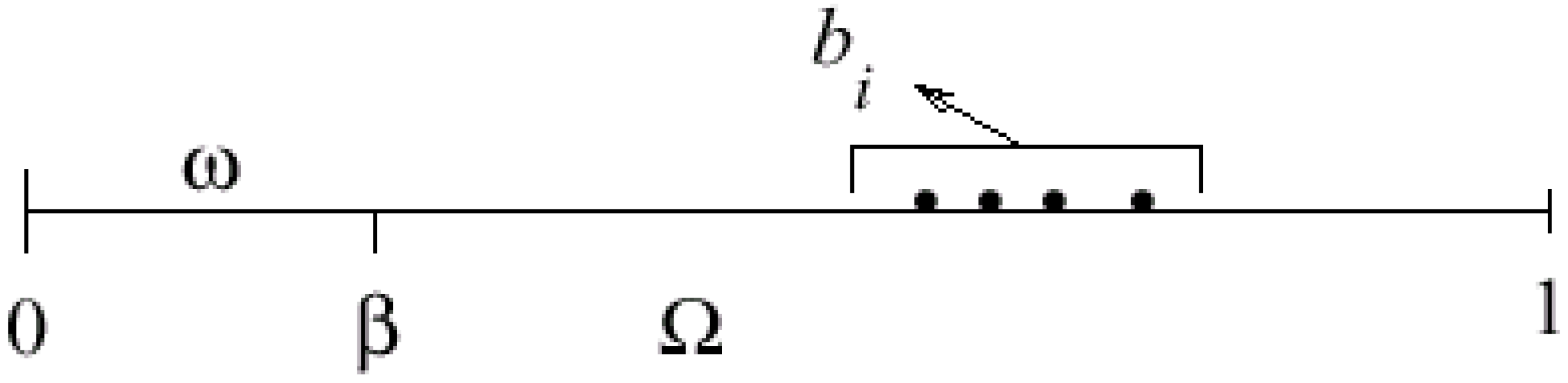
- ω is a nonempty given subregion of Ω.
- X, U, are separable Hilbert spaces where X is the state space, U the control space and the observation space and with X = L2 (Ω), U = L2 (0, ∞; ) and = L2 (0, ∞ ; ).
- The operators B : U → X and C : X → are bounded linear and depend on the structure of actuators and sensors [7]. Under the above assumption, the system (2.1) has a unique solution given by
- ■
- A sensor may be defined by any couple (D, g) where :
- D denotes a closed subset of , which is spatial support of sensors,
- g ∈ L 2 (D) defines the spatial distribution of measurements on D.
- The function χω is defined by
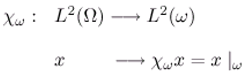
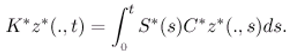
- ■
- The autonomous system associated to (2.1)-(2.2) is exactly (respectively weakly) ω-observable if :
- ■
- The suit of sensors (Di,gi)1 ≤ i ≤ q is ω-strategic if the system (2.1)-(2.2) is weakly ω-observable [12]. The concept of ω-strategic has been extended to the regional boundary case as in [13-15].
2.2 ω-observer
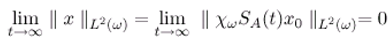
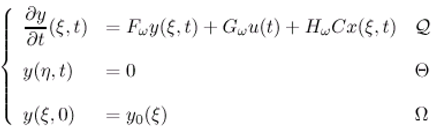
- [y(ξ,t)−χωTx(ξ,t)] = 0, ξ ∈ ω
- χωTx maps D(Δ) into D(Fω) where x(ξ, t) and y(ξ, t) are the solutions of (2.1) and (2.11).
- There exists R ∈ ( ,L2 (ω)) and S∈ (L2 (ω)) such that RC + SχωT = Iω
- χωTΔ - FωχωT = HωC and Gω = χωTB.
- The system (2.11) determines ω-estimator for χωTx(ξ, t).
- ■
- The system (2.11) is said to be an identity ω-observer for the system (2.1)-(2.2) if χωT=Iω and X=Y.
- ■
- The system (2.11) is said to be a reduced-order ω-observer for the system (2.1)-(2.2) if X= ⊕Y.
3. Sensors and ω-observer reconstruction
3.1 General case
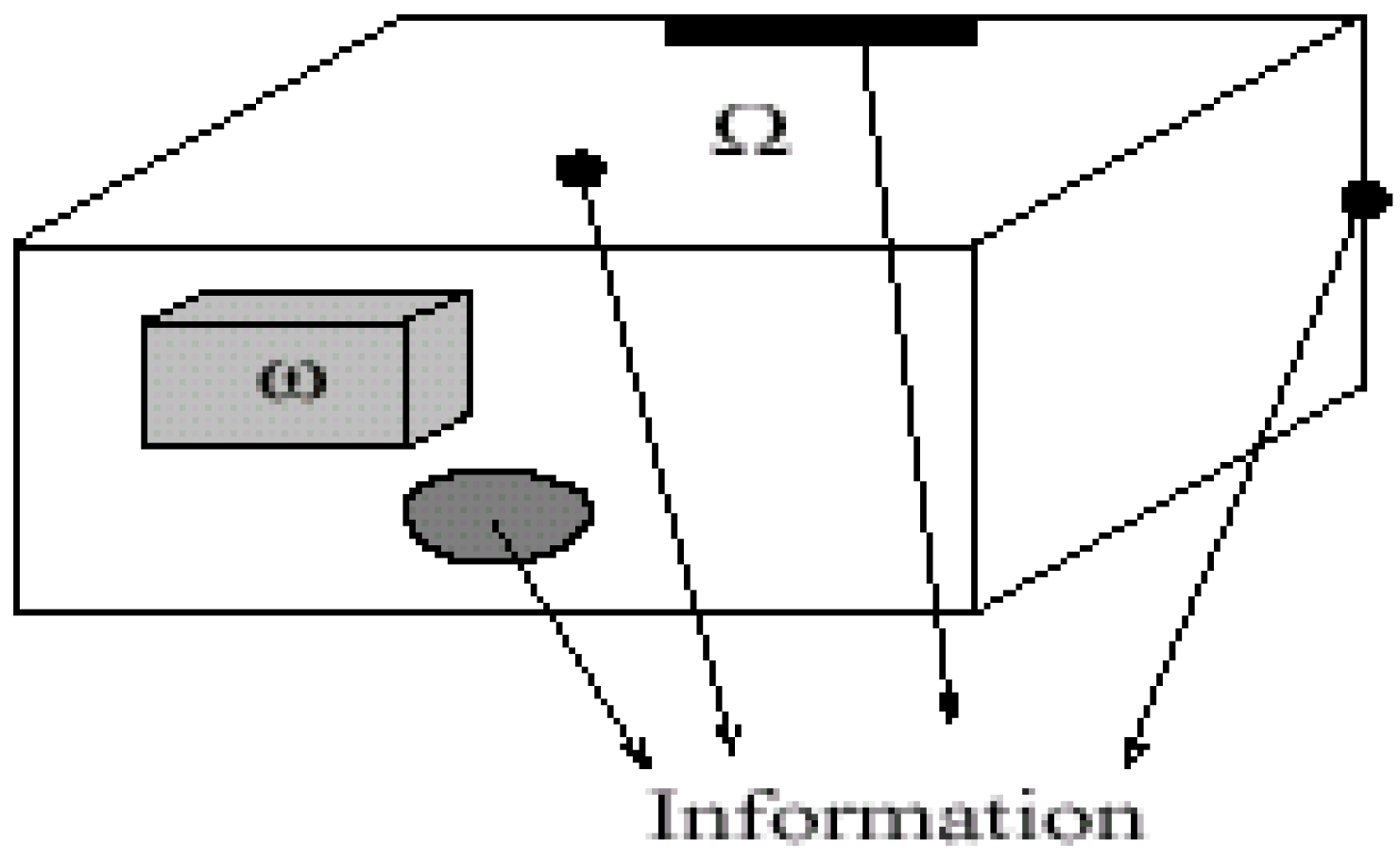
3.1.1 Case of pointwise sensors
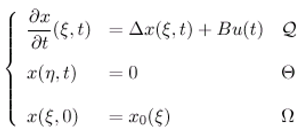

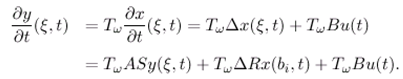
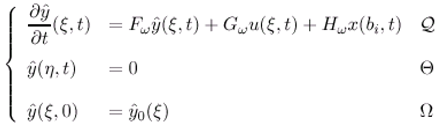
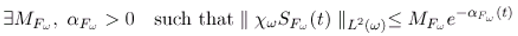
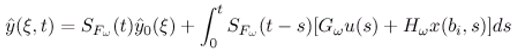

- There exist R ∈ (, L2(ω)) and S ∈ (L2(ω)) such that
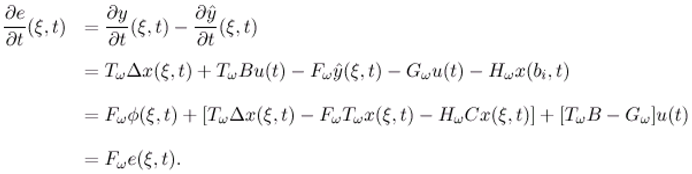
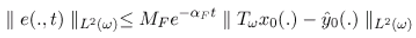
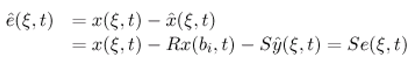
- This conditions (3.6) and (3.7) in theorem 3.1 guarantee that the dynamical system (3.5) is ω-observer for the system (3.1)-(3.1).
- A system which is an observer is ω-observer.
- If a system is ω-observer, then it is ω1-observer in every subset ω1 of ω, but the coverse is not true. This may be proven in the following example:
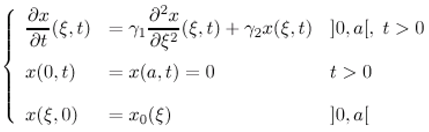
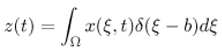
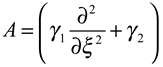 generates a strongly continuous semi-group (SA(t))t≥0 on the Hilbert space L2(Ω). Consider the dynamical system
generates a strongly continuous semi-group (SA(t))t≥0 on the Hilbert space L2(Ω). Consider the dynamical system
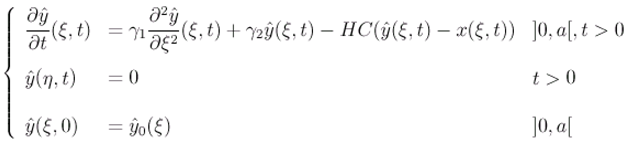
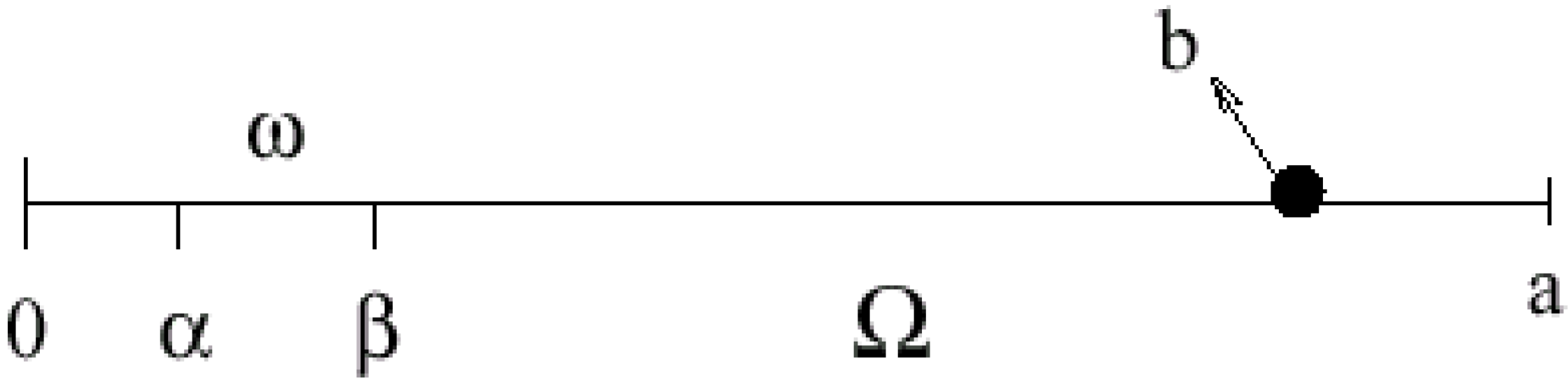
3.1.2 Case of zone sensors
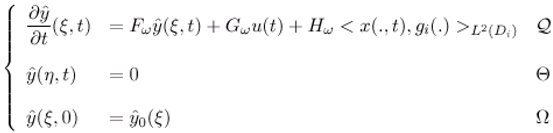
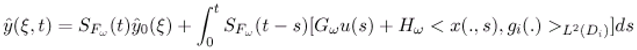
- The operator Fω generates a strongly continuous semi-group which is stable on the space L2(ω).
- There exist ∈ (, L2 (ω)) and S ∈ (L2(ω)) such thatRC + STω = I
3.1.3 Case of boundary sensors
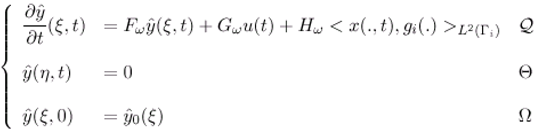
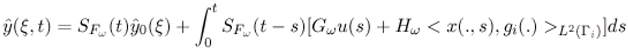
- The operator Fω generates a strongly continuous semi-group which is stable on the space L2 (ω).
- There exist ∈ (, L2 (ω)) and S ∈ (L2(ω)) such thatRC + STω = I
3.2 Identity ω-observer
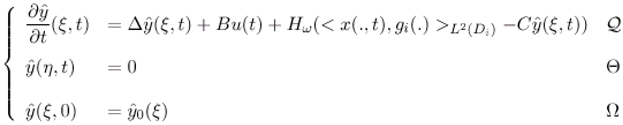
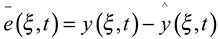 . Then by deriving (ξ,t), we get
. Then by deriving (ξ,t), we get
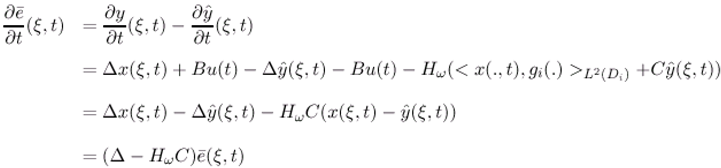
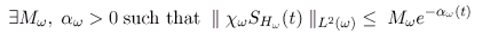
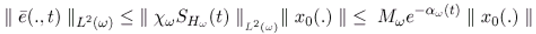
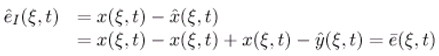
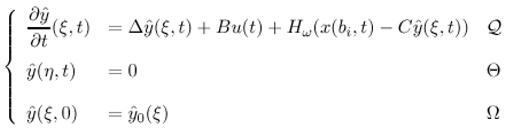
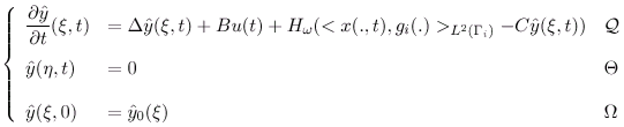
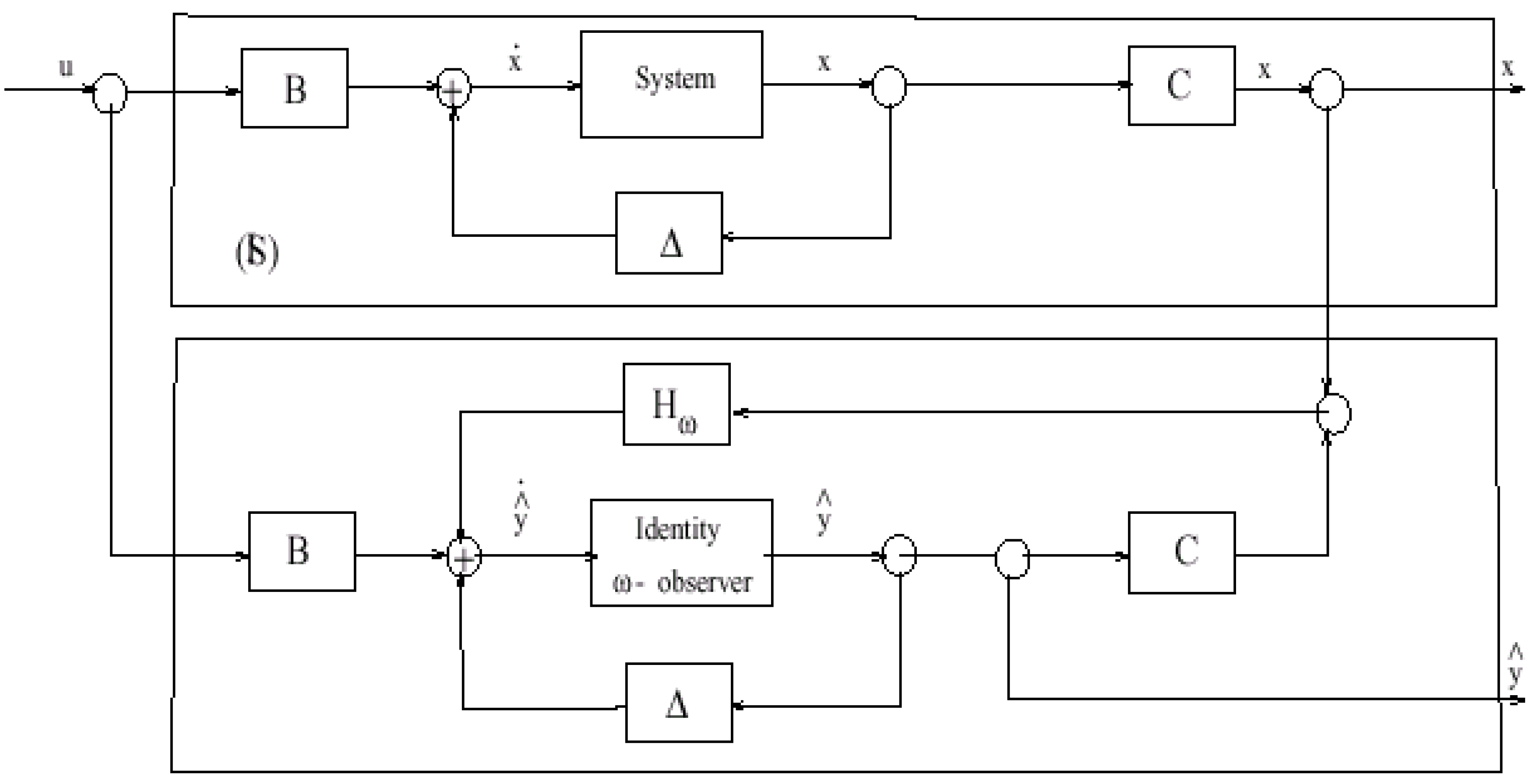
3.3 Application to an identity ω-observer in diffusion system
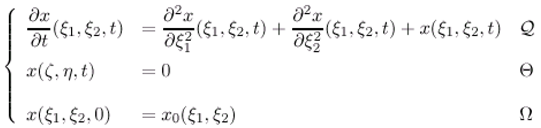
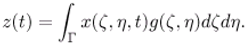
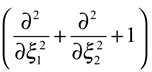 are given by
are given by
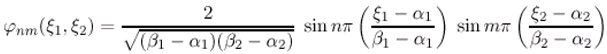
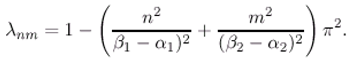


3.4 Reduced-order ω-observer
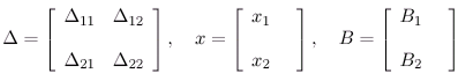
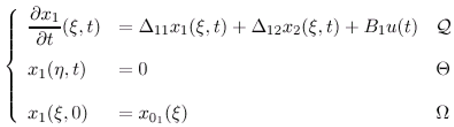
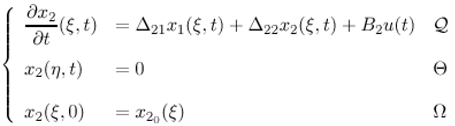
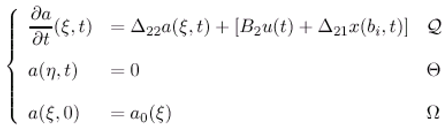
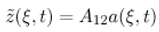
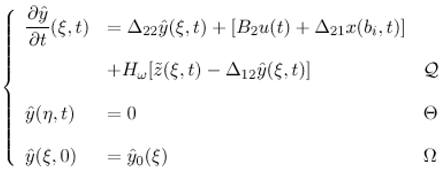
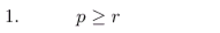
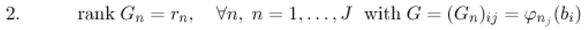
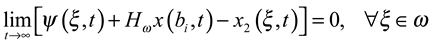
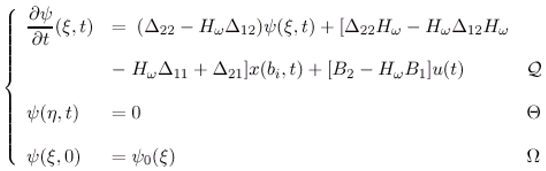
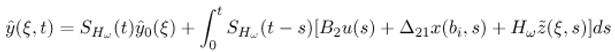
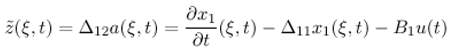
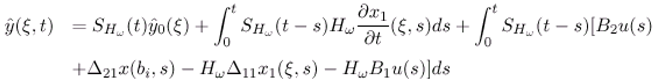
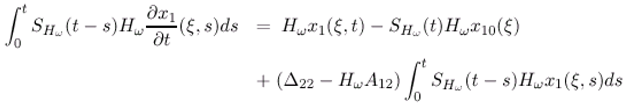
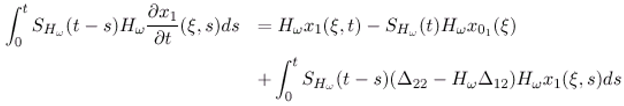
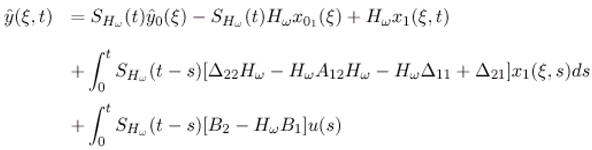
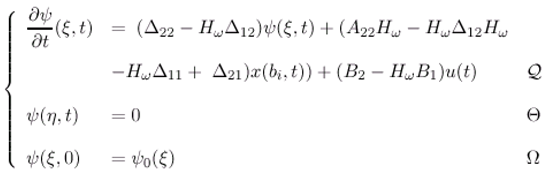
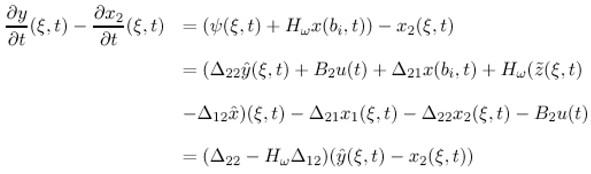
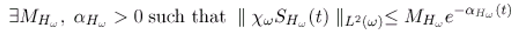
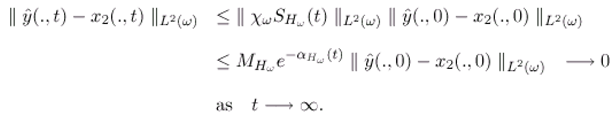
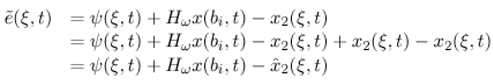
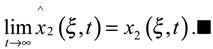
- The state vector (ξ,t) can be represented by
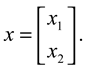
- 2.
- The component (ξ,t) is an asymptotically estimator of x2(ξ,t).
- 3.
- The system (3.26) is a reduced-order ω-observer for the system (3.24)-(3.25) (Fig. 6).
- 4.
- If we consider X1 = L2 (0, ∞; ) and X2 = Y where Y is the state space for the ω-observer. So, from the theorem 3.8, the reduced-order ω-observer can reconstruct the unknown state components (xp+1,xp+2, ...), thus the condition (3.7) of the theorem 3.1 is satisfied, if we define the following operators as below.and we obtain the relation RC + STω = Iz1.
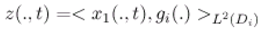
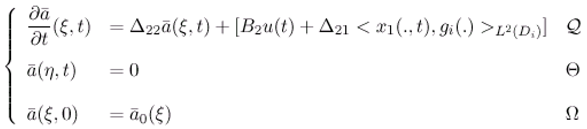
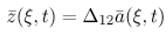

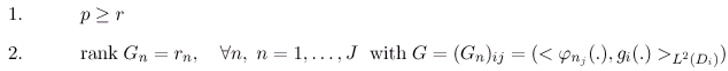
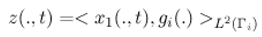
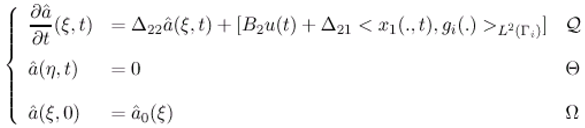
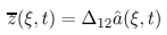

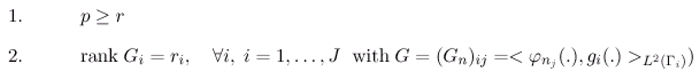
3.5 Application to a reduced-order ω-observer in diffusion systems
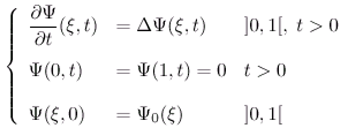
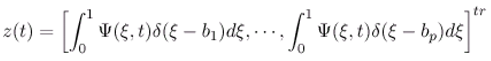
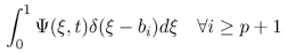
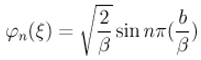
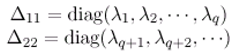
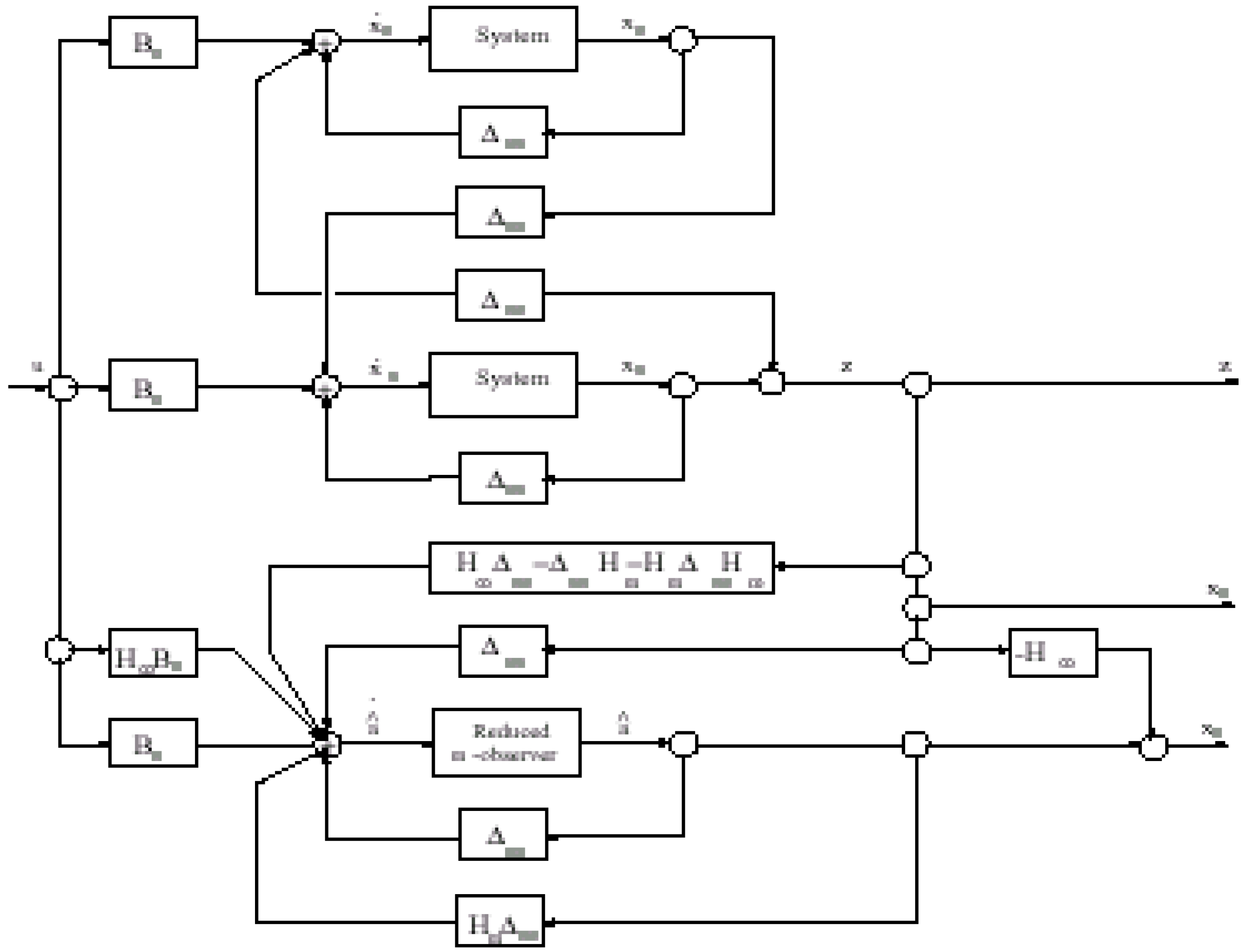
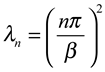 with λ1 > λ2 > ... λJ > 0 > λJ+1 > ... . The theorem 3.8 allow to estimate the unknown components Ψ asymptotically where =Ψp+1, Ψp+2,.... . . If the sensors areω-strategic for the unstable par of the subsystem with Δ11. That means, the following the relation holds:
with λ1 > λ2 > ... λJ > 0 > λJ+1 > ... . The theorem 3.8 allow to estimate the unknown components Ψ asymptotically where =Ψp+1, Ψp+2,.... . . If the sensors areω-strategic for the unstable par of the subsystem with Δ11. That means, the following the relation holds:
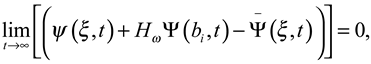 ∀ξ ∈ω with
∀ξ ∈ω with
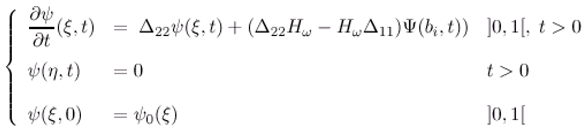
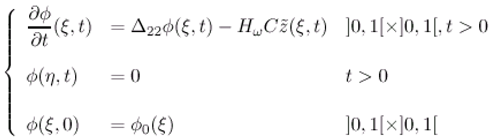
4. Conclusion
References
- Gressang, R.; Lamont, G. B. Observers for systems characterized by semi-groups. IEEE on Automatic and Control 1975, 20, 523–528. [Google Scholar] [CrossRef]
- Kitamura, S.; Sakairi, S.; Nishimura, M. Observer for distributed-parameter diffusion systems. Electrical engineering in Japan 1972, 92, 142–149. [Google Scholar] [CrossRef]
- Hautus, M. L. Strong detectability and observers. Linear Algebra and its Applications 1983, 5, 353–368. [Google Scholar] [CrossRef]
- El Jai, A.; Berrahmoune, L. Localisation d’actionneurs-zones pour la controlabilite de systemes paraboliques. C. R. Acad. Sc. 1983, 297, 647–650. [Google Scholar]
- El Jai, A.; Berrahmoune, L. Localisation d’actionneurs ponctuels pour la controlabilite de systemes paraboliques. C. R. Acad. Sc. 1984, 298, 47–50. [Google Scholar]
- El Jai, A.; Berrahmoune, L. Localisation d’actionneurs-frontiere pour la controlabilite de systemes paraboliques. C. R. Acad. Sc. 1984, 298, 177–180. [Google Scholar]
- El Jai, A.; Pritchard, A. J. Sensors and controls in the analysis of distributed systems; Ellis Horwood series in Mathematics and its Applications; Wiley: New York, 1988. [Google Scholar]
- El Jai, A.; Zerrik, E.; Simon, M. C.; Amouroux, M. Regional observability of a thermal process. IEEE Trans. on Automatic Control 1995, 40, 518–521. [Google Scholar] [CrossRef]
- El Jai, A.; Guisset, E.; Trombe, A.; Suleiman, A. Application of boundary obser-vation to a thermal system. In Conf. of MTNS 2000, Perpignan, France, June 19-23.
- Al-Saphory, R.; El Jai, A. Asymptotic regional state reconstruction. Int. J. of Systems Science 2000. submitted. [Google Scholar]
- Al-Saphory, R.; El Jai, A. Sensors structures and regional detectability of parabolic distributed systems. Sensors and Actuators 2001, 29, 163–171. [Google Scholar] [CrossRef]
- El Jai, A.; Simon, M. C.; Zerrik, E. Regional observability and sensor structures. Sensors and Actuators 1993, 39, 95–102. [Google Scholar] [CrossRef]
- Al-Saphory, R.; El Jai, A. Sensors characterizations for regional boundary detectability of distributed parameter systems. Sensors and Actuators 2001, 94, 1–10. [Google Scholar] [CrossRef]
- Sample Availability: Available from the author.
© 2001 by MDPI (http://www.mdpi.net). Reproduction is permitted for noncommercial purposes.
Share and Cite
Al-Saphory, R.; Jai, A.E. Sensors and Asymptotic w-observer for Distributed Diffusion Systems. Sensors 2001, 1, 161-182. https://doi.org/10.3390/s10500161
Al-Saphory R, Jai AE. Sensors and Asymptotic w-observer for Distributed Diffusion Systems. Sensors. 2001; 1(5):161-182. https://doi.org/10.3390/s10500161
Chicago/Turabian StyleAl-Saphory, R., and A. El Jai. 2001. "Sensors and Asymptotic w-observer for Distributed Diffusion Systems" Sensors 1, no. 5: 161-182. https://doi.org/10.3390/s10500161
APA StyleAl-Saphory, R., & Jai, A. E. (2001). Sensors and Asymptotic w-observer for Distributed Diffusion Systems. Sensors, 1(5), 161-182. https://doi.org/10.3390/s10500161