On the Spatial Distribution of Eagle Carcasses Around Wind Turbines: Implications for Collision Mortality Estimation
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Areas
2.2. Comparison of Fatality Search and Estimation Methods
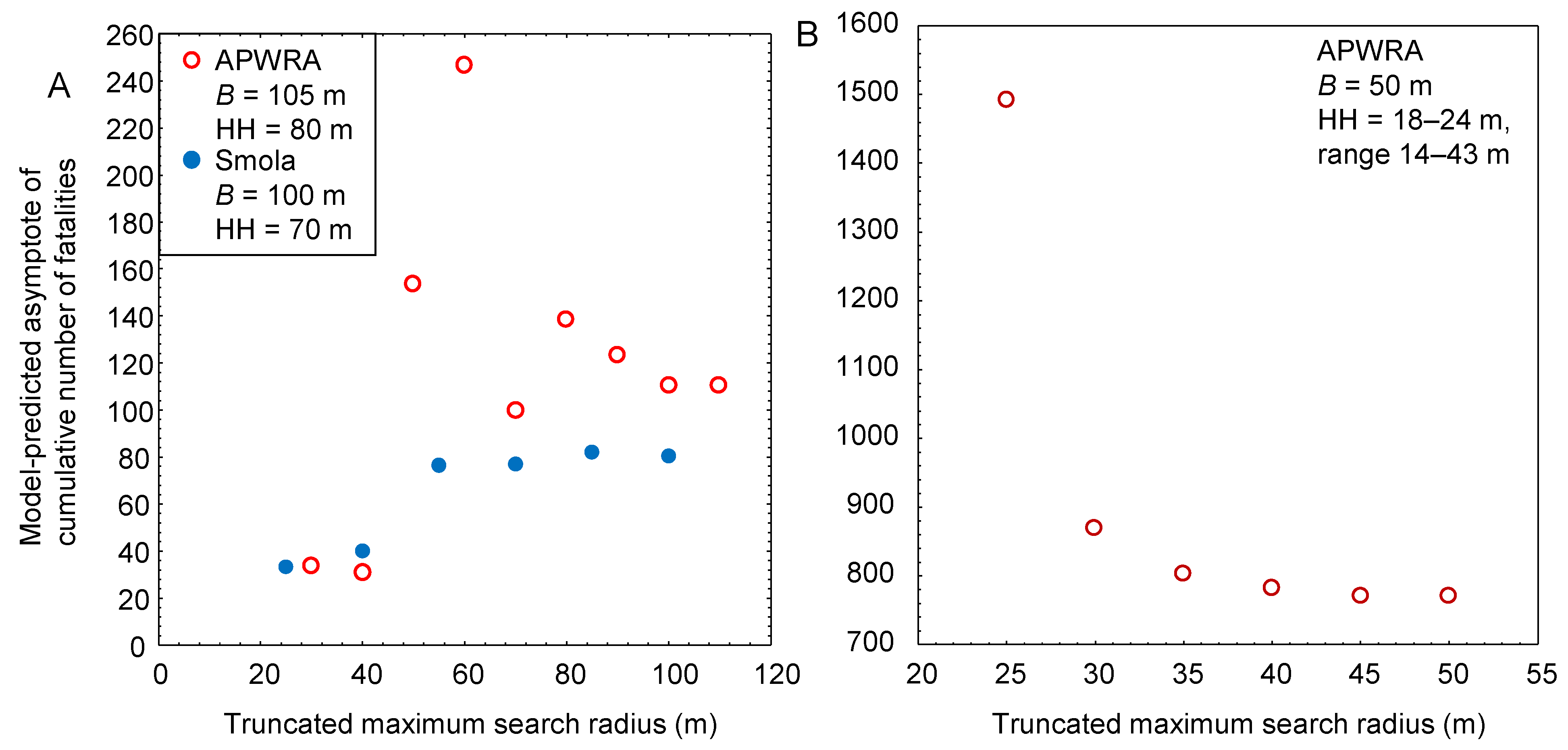
2.3. Changes in Model Predictions with Changes in B
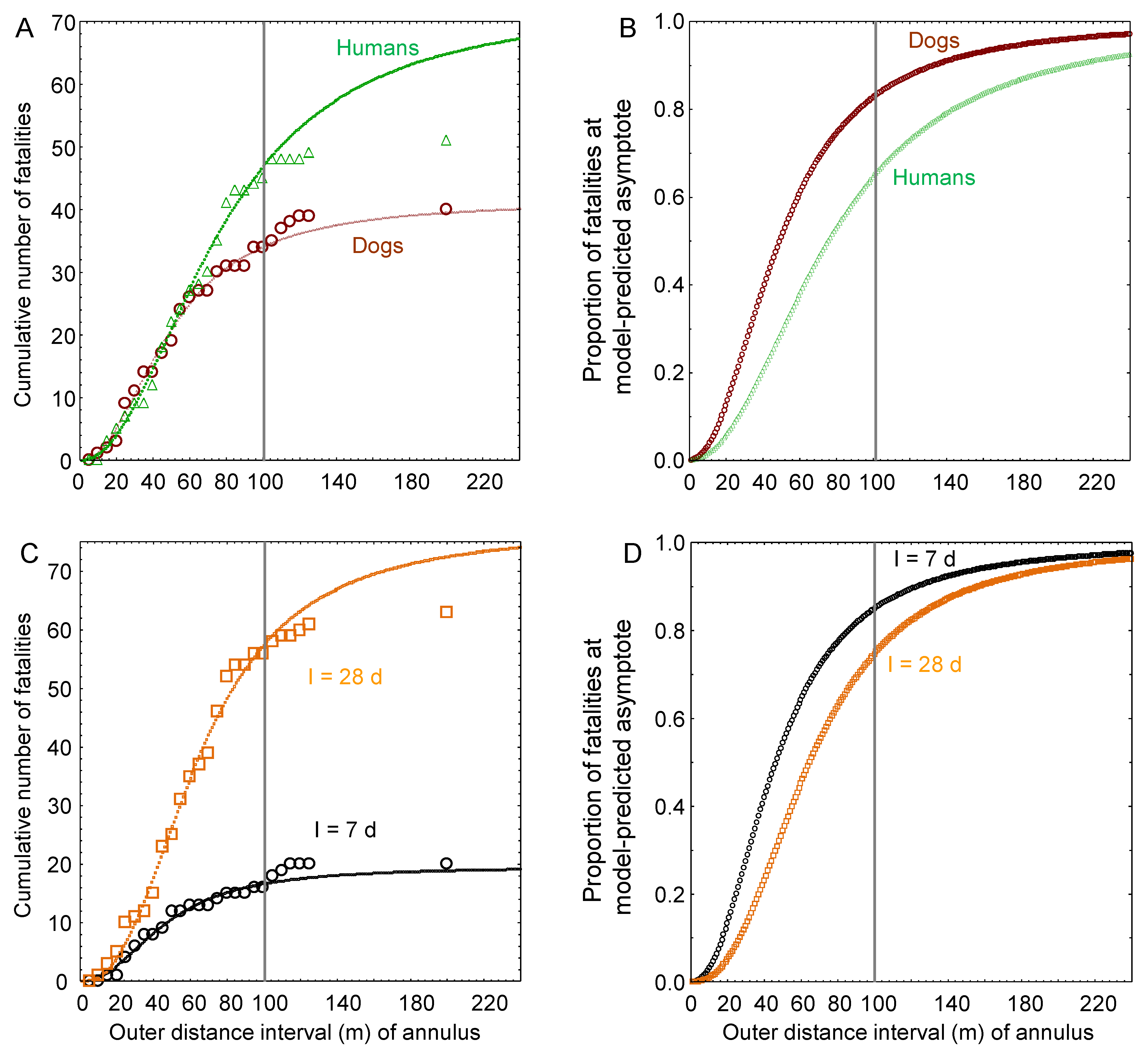
3. Results
Prediction Accuracy and Robustness to Misassignment of a Carcass Location
4. Discussion
4.1. Statistical Error Versus Measurement Error in the Field
4.2. Management Implications
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hull, C.L.; Muir, S. Search areas for monitoring bird and bat carcasses at wind farms using a Monte-Carlo model. Aust. J. Environ. Manag. 2010, 17, 77–87. [Google Scholar] [CrossRef]
- California Energy Commission and California Department of Fish and Game (CEC&CDFG). California Guidelines for Reducing Impacts to Birds and Bats from Wind Energy Development; Draft Staff Report CEC-700-2007-008-SD; California Energy Commission and California Department of Fish and Game (CEC & CDFG): Sacramento, CA, USA, 2007.
- Ontario Ministry of Natural Resources. Birds and Bird Habitats: Guidelines for Wind Power Projects; Ontario Ministry of Natural Resources: Peterborough, ON, Canada, 2011.
- U.S. Fish and Wildlife Service. U.S. Fish and Wildlife Service Land-Based Wind Energy Guidelines; OMB Control No, 1018-0148; U.S. Fish and Wildlife Service: Arlington, VA, USA, 2012.
- Smallwood, K.S. Comparing bird and bat fatality-rate estimates among North American wind-energy projects. Wildl. Soc. Bull. 2013, 37, 19–33. [Google Scholar] [CrossRef]
- Smallwood, K.S. Estimating wind turbine-caused bird mortality. J. Wildl. Manag. 2007, 71, 2781–2791. [Google Scholar] [CrossRef]
- Fiedler, J.K.; Henry, T.H.; Tankersley, R.D.; Nicholson, C.P. Results of Bat and Bird Mortality Monitoring at the Expanded Buffalo Mountain Windfarm, 2005; Tennessee Valley Authority: Knoxville, TN, USA, 2007.
- Huso, M.; Dalthorp, D. Accounting for unsearched areas in estimating wind turbine-caused fatality. J. Wildl. Manag. 2014, 78, 347–358. [Google Scholar] [CrossRef]
- Dalthorp, D.; Madsen, L.; Huso, M.; Rabie, P.; Wolpert, R.; Studyvin, J.; Simonis, J.; Mintz, J. GenEst Statistical Models—A Generalized Estimator of Mortality. In Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2018; Volume 7, Chapter A2; 13p. [Google Scholar] [CrossRef]
- Huso, M.; Dalthorp, D.; Mintz, J.; Nygard, T.; May, R. Modeling the spatial distribution of carcasses of eagles killed by wind turbines. J. Raptor Res. 2023, 57, 456–467. [Google Scholar] [CrossRef]
- Smallwood, K.S.; Bell, D.A.; Walther, E.L.; Leyvas, E.; Standish, S.; Mount, J.; Karas, B. Estimating wind turbine fatalities using integrated detection trials. J. Wildl. Manag. 2018, 82, 1169–1184. [Google Scholar] [CrossRef]
- Smallwood, K.S.; Bell, D.A.; Standish, S. Dogs detect larger wind energy impacts on bats and birds. J. Wildl. Manag. 2020, 84, 852–864. [Google Scholar] [CrossRef]
- Arnett, E. A Preliminary Evaluation on the use of dogs to recover bat fatalities at wind energy facilities. Wildl. Soc. Bull. 2006, 34, 1440–1445. [Google Scholar] [CrossRef]
- Mathews, F.; Swindells, M.; Goodhead, R.; August, T.A.; Hardman, P.; Linton, D.M.; Hosken, D.J. Effectiveness of search dogs compared with human observers in locating bat carcasses at wind-turbine sites: A blinded randomized trial. Wildl. Soc. Bull. 2013, 37, 34–40. [Google Scholar] [CrossRef]
- Reyes, G.A.; Rodriguez, M.J.; Lindke, K.T.; Ayres, K.L.; Halterman, M.D.; Boroski, B.R.; Johnston, D.S. Searcher efficiency and survey coverage affect precision of fatality estimates. J. Wildl. Manag. 2016, 80, 1488–1496. [Google Scholar] [CrossRef]
- H.T. Harvey and Associates. Golden Hills Wind Energy Center Post-Construction Fatality Monitoring Report: Final 3-Year Report; H.T. Harvey and Associates: Los Gatos, CA, USA, 2020. [Google Scholar]
- Great Basin Bird Observatory; H. T. Harvey and Associates. Golden Hills North Wind Energy Center Postconstruction Fatality Monitoring Final 3-Year Report; H.T. Harvey and Associates: Los Gatos, CA, USA, 2022. [Google Scholar]
- H.T. Harvey and Associates. Golden Hills Wind Energy Center Golden Eagle Adaptive Management Monitoring Project: Final 3-Year Report; H.T. Harvey and Associates: Los Gatos, CA, USA, 2023. [Google Scholar]
- WEST, Inc. Post-Construction Fatality Monitoring at the Summit Wind Repower Project Alameda County, California, September 2, 2022 to September 1, 2023; WEST, Inc.: Calgary, AB, Canada, 2023. [Google Scholar]
- Insignia Environmental. Final Report for the Buena Vista Avian and Bat Monitoring Project February 2008 to January 2011; Insignia Environmental: Palo Alto, CA, USA, 2012. [Google Scholar]
- Brown, K.; Smallwood, K.S.; Szewczak, J.; Karas, B. Final 2012–2015 Report Avian and Bat Monitoring Project Vasco Winds, LLC.; NextEra Energy Resources: Livermore, CA, USA, 2016. [Google Scholar]
- Loss, S.R.; Will, T.; Marra, P.P. Estimates of bird collision mortality at wind facilities in the contiguous United States. Biol. Conserv. 2013, 168, 201–209. [Google Scholar] [CrossRef]
- ICF International. Final Report Altamont Pass Wind Resource Area Bird Fatality Study, Monitoring Years 2005–2013; ICF International: Reston, VA, USA, 2016. [Google Scholar]
- Gauthreaux, S.A. Suggested practices for monitoring bird populations, movements and mortality in wind resource areas. In Proceedings of the National Avian-Wind Power Planning Meeting II, Palm Springs, CA, USA, 20–22 September 1995; Prepared for the Avian Subcommittee of the National Wind Coordination Committee. RESOLVE Inc.: Washington, DC, USA; LGL Ltd.: King City, ON, Canada; 152p. [Google Scholar]
- Smallwood, K.S.; Bell, D.A.; Snyder, S.A.; DiDonato, J.E. Novel scavenger removal trials increase estimates of wind turbine-caused avian fatality rates. J. Wildl. Manag. 2010, 74, 1089–1097. [Google Scholar] [CrossRef]
- Bell, D.A.; Snyder, S.A.; DiDonato, J.E.; Smallwood, K.S. Conspecific carcass removal from a wind project study plot by a great horned owl (Bubo virginanus). J. Raptor Res. 2023, 57, 489–492. [Google Scholar] [CrossRef]
- Dahl, E.L.; Bevanger, K.; Nygärd, T.; Røskaft, E.; Stokke, B.G. Reduced breeding success in White-tailed Eagles at Smøla windfarm, western Norway, is caused by mortality and displacement. Biol. Conserv. 2012, 145, 79–85. [Google Scholar] [CrossRef]
- Hunt, G.W.; Wiens, J.D.; Law, P.R.; Fuller, M.R.; Hunt, T.L.; Driscoll, D.E.; Jackman, R.E. Quantifying the demographic cost of human-related mortality to a raptor population. PLoS ONE 2017, 12, e0172232. [Google Scholar] [CrossRef]
- Gedir, J.V.; Gould, M.J.; Millsap, B.A.; Howell, P.E.; Zimmerman, G.S.; Bjerre, E.; White, H.M. Estimated golden eagle mortality from wind turbines in the western United States. Biol. Conserv. 2025, 302, 110961. [Google Scholar] [CrossRef]
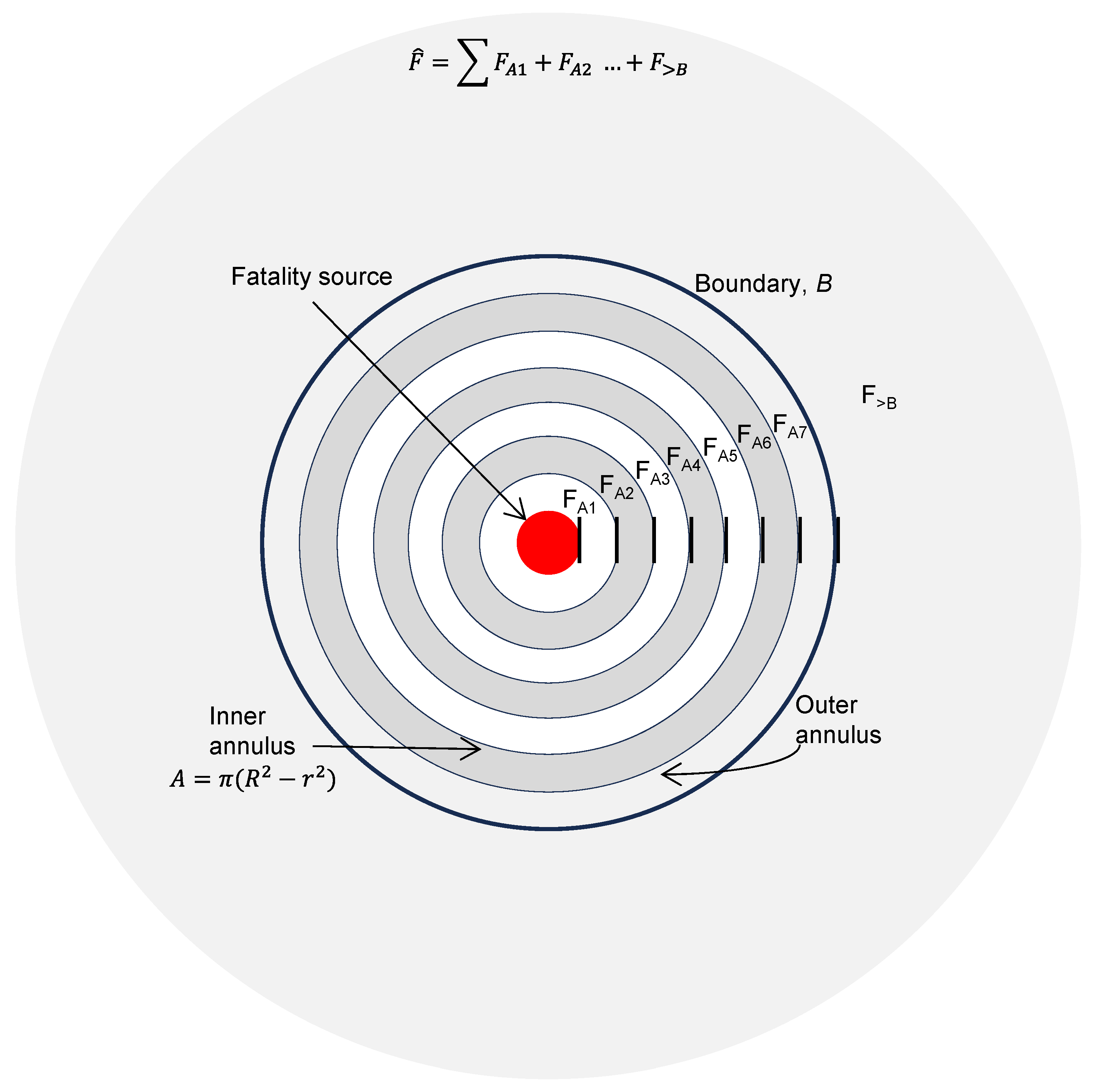
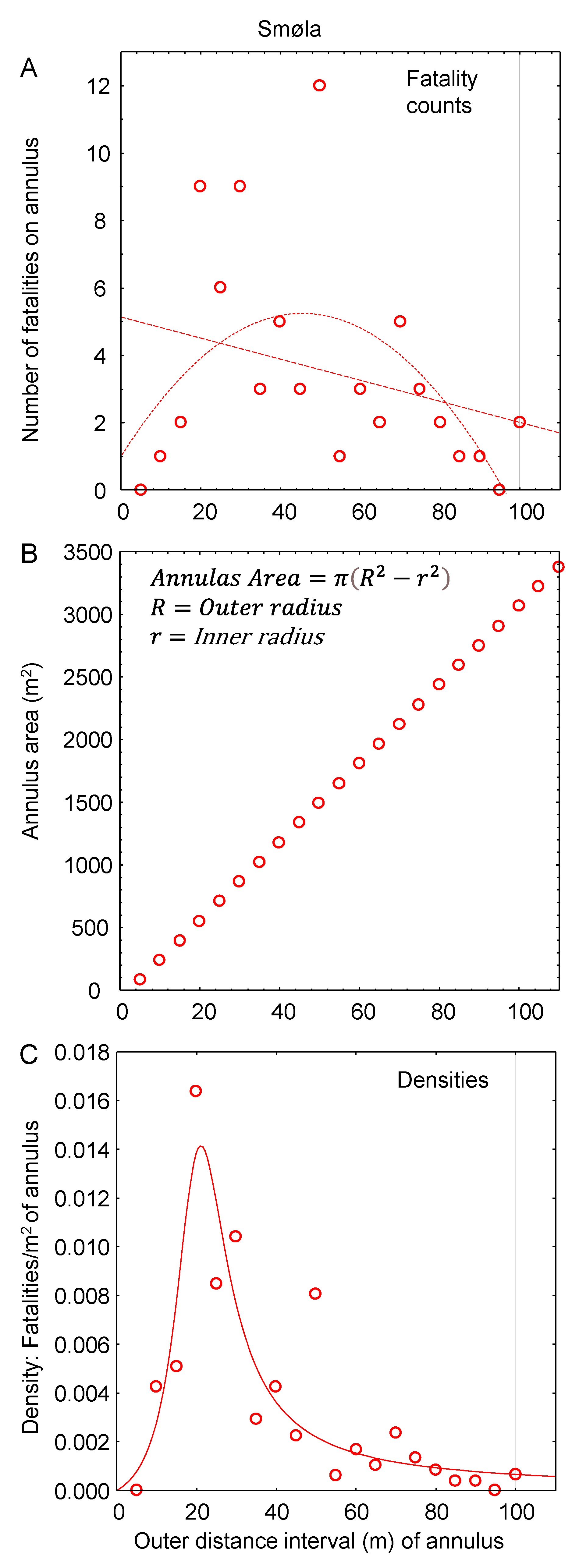
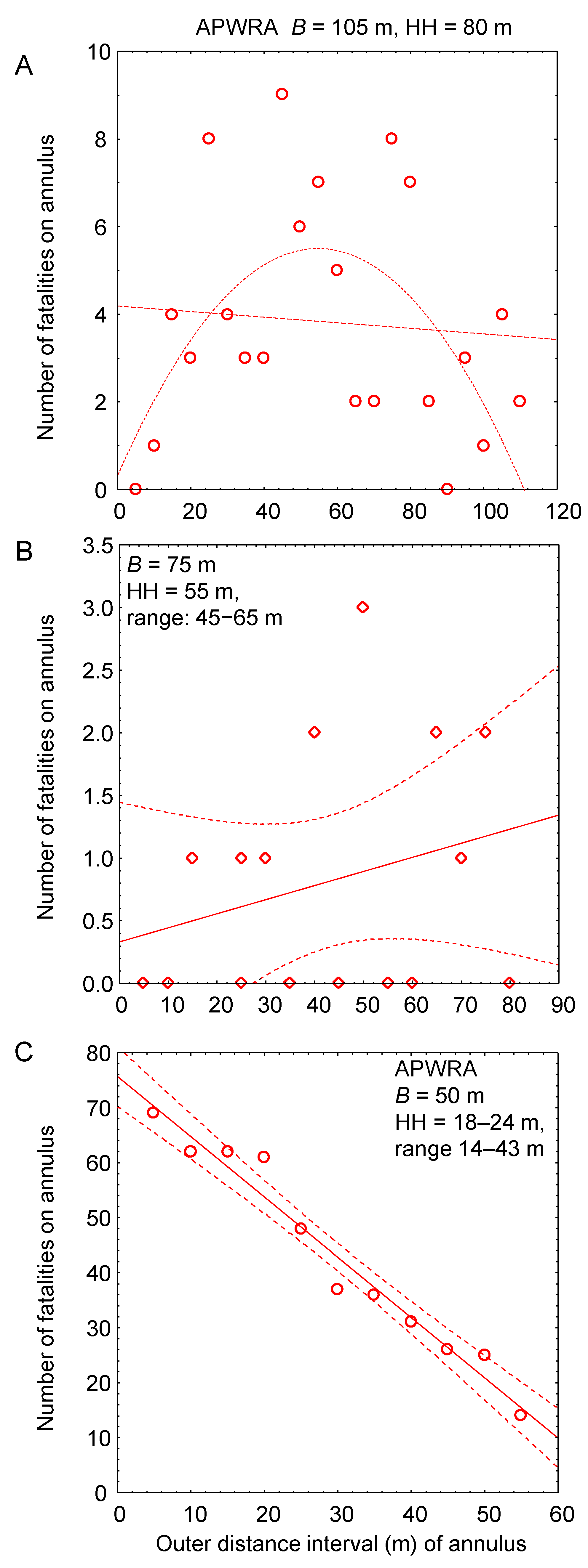
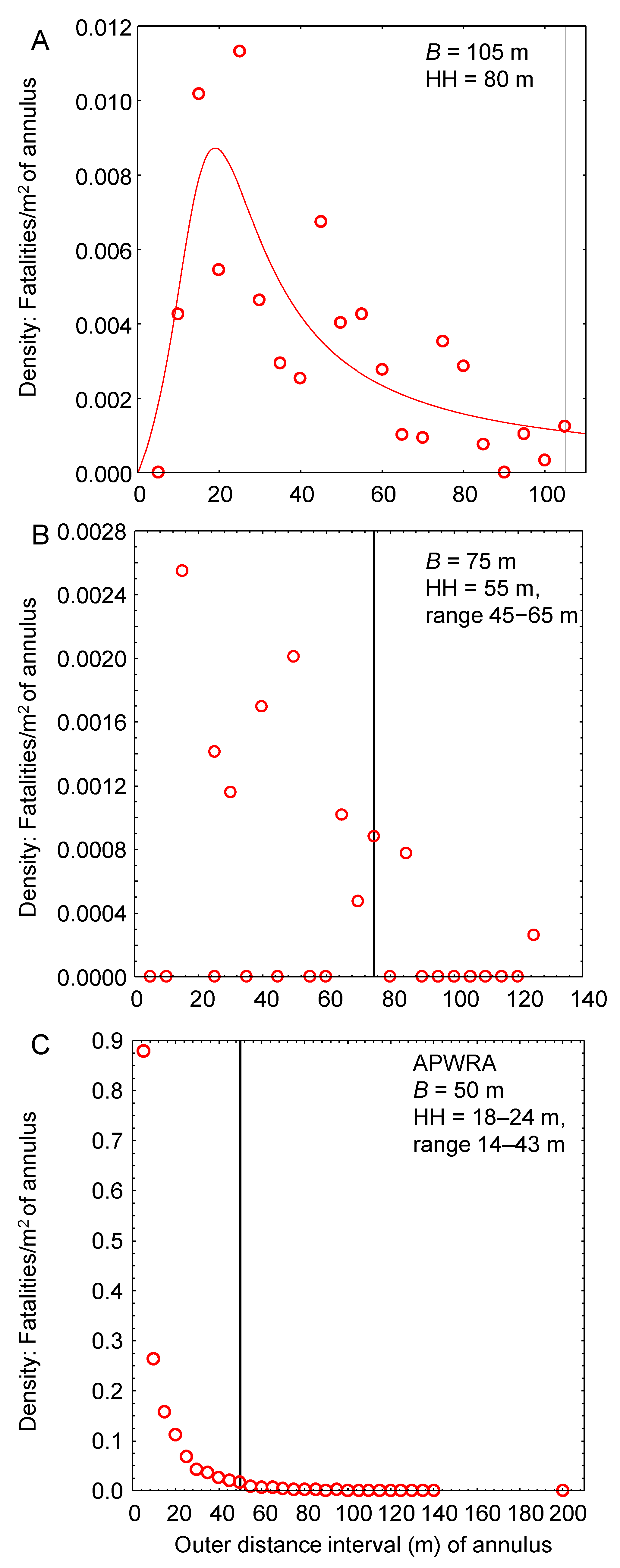





| Site | Project Name | B a | Model | MW | No. of Turbines | Hub Height (m) | Blade Length (m) | Period of Fatality Finds | Years of Scientific Searches |
|---|---|---|---|---|---|---|---|---|---|
| Smøla | Smøla Vindpark | 100 | Bonus | 2 | 20 | 70 | 39 | 2005–2020 | ≥5 b |
| Smøla | Smøla Vindpark | 100 | Siemens | 2.3 | 48 | 70 | 41 | 2005–2020 | ≥5 |
| APWRA | Vasco Winds | 105 | Siemens | 2.3 | 34 | 80 | 46.5 | 2012–2023 | 4 |
| APWRA | Golden Hills | 105 | GE | 1.79 | 48 | 80 | 50 | 2015–2023 | 6 |
| APWRA | Golden Hills North | 105 | GE | 2.3 | 20 | 80 | 55 | 2017–2021 | 3 |
| APWRA | Summit Winds | 122 | GE | 2.7 | 23 | 90 | 58 | 2021–2023 | 2 |
| APWRA | Buena Vista | 75 | Mitsubishi | 1 | 38 | 45–60 | 30.7 | 2008–2023 | 4 |
| APWRA | Diablo Winds | 75 | Vestas | 0.66 | 31 | 50–55 | 23.5 | 2005–2019 | 6 |
| APWRA | Tres Vaqueros | 60 | Howden | 0.33 | 85 | 25.2 | 15.7 | 2005–2008 | 3 |
| APWRA | Kenetech | 60 | KVS-33 | 0.4 | 41 | 24.6 | 16.6 | 2002–2011 | 11.5 |
| APWRA | Older projects | 50 | Varied c | 0.04–0.25 d | 4400 d | 14–43 d | 6.67–12.6 d | 1991–2014 | 13.5 |
| Site | B (m) | Searcher | Number of Dead or Injured Eagles a Found Relative to B | Missing Distance Data | Number Found Injured and Alive Relative to B | Total Fatalities Predicted by Spatial Pattern of Those Found | B Predicted to Include 99% of Predicted Total Fatalities | ||
|---|---|---|---|---|---|---|---|---|---|
| Within | Beyond | Within | Beyond | ||||||
| Smøla | 100 | Dogs | 70 b | 2 | 35 | 4 | 1 | 80 | >250 m |
| APWRA | 105 | Dogs | 34 | 5 | 0 | 0 | 0 | 41 | >250 m |
| APWRA | 105 | Humans | 48 | 3 | 3 | 1 | 2 | 73 | >250 m |
| APWRA | 105 | Dogs, humans | 82 | 8 | 3 | 1 | 2 | 109 | >250 m |
| APWRA | 75 | Humans | 13 | 3 | 2 | 2 | 9 | 37 | >250 m |
| APWRA | 60 | Humans | 5 | 2 | 6 | 1 | 0 | -- | -- |
| APWRA | 50 | Humans | 451 | 81 | 91 | 11 | 3 | 770 | >250 m |
| APWRA | 122 | Dogs, humans | 3 | 1 | 0 | 0 | 0 | -- | -- |
| Site | B (m) | B− (m) | Searcher | Search Interval (Days) | r2 | Loss | Best-Fit Model Coefficient | ||
|---|---|---|---|---|---|---|---|---|---|
| a | b | c | |||||||
| Smøla | 100 | Dogs | 14 | 0.995 | 59.6 | 79.886562 | 91.900454 | −2.363510 | |
| Smøla | 100 | Dogs | 14 | 0.990 | 147.7 | 77.416820 | 124.663951 | −2.44090 | |
| APWRA | 105 | Both | 7/28 | 0.997 | 70.2 | 108.951112 | 91.163916 | −2.212563 | |
| APWRA | 105 | Both | 7/28 | 0.996 | 69.34 | 108.452852 | 112.099593 | −2.253900 | |
| APWRA | 105 | Dogs | 7/28 | 0.992 | 23.6 | 41.354492 | 148.352762 | −2.226929 | |
| APWRA | 105 | Humans | 7/28 | 0.991 | 47.3 | 72.814355 | 178.752156 | −2.181351 | |
| APWRA | 75 | Humans | 14 | 0.980 | 5.1 | 37.050833 | 414.919661 | −1.207624 | |
| APWRA | 50 | Humans | 39 | 1.000 | 60.6 | 770.198214 | 0.097667 | −1.200675 | |
| Smøla | 100 | 85 | Dogs | 14 | 0.994 | 57.2 | 82.095280 | 75.939015 | −2.303190 |
| Smøla | 100 | 70 | Dogs | 14 | 0.991 | 53.9 | 77.025654 | 106.924085 | −2.414876 |
| Smøla | 100 | 55 | Dogs | 14 | 0.986 | 50.6 | 75.735805 | 120.658744 | −2.453624 |
| Smøla | 100 | 40 | Dogs | 14 | 0.996 | 6.3 | 40.359918 | 10,950.091478 | −3.999281 |
| Smøla | 100 | 25 | Dogs | 14 | 0.997 | 3.1 | 33.116229 | 12,169.987229 | −4.074688 |
| APWRA | 105 | 110 | Both | 7/28 | 0.996 | 70.5 | 110.155132 | 67.617923 | −2.146074 |
| APWRA | 105 | 100 | Both | 7/28 | 0.996 | 70.5 | 110.612820 | 66.242457 | −2.139995 |
| APWRA | 105 | 90 | Both | 7/28 | 0.995 | 62.1 | 123.124510 | 44.368496 | −2.018889 |
| APWRA | 105 | 80 | Both | 7/28 | 0.994 | 54.6 | 138.201567 | 32.812300 | −1.925618 |
| APWRA | 105 | 70 | Both | 7/28 | 0.993 | 41.0 | 99.518551 | 73.102395 | −2.180825 |
| APWRA | 105 | 60 | Both | 7/28 | 0.993 | 25.4 | 246.382918 | 23.377978 | −1.800482 |
| APWRA | 105 | 50 | Both | 7/28 | 0.987 | 23.9 | 153.373220 | 29.813167 | −1.889620 |
| APWRA | 105 | 40 | Both | 7/28 | 0.996 | 3.6 | 30.876527 | 3206.361800 | −3.559384 |
| APWRA | 105 | 30 | Both | 7/28 | 0.999 | 3.2 | 33.644829 | 2284.736900 | −3.420503 |
| APWRA | 50 | 45 | Humans | 39 | 0.999 | 60.5 | 769.513530 | 0.097643 | −1.200765 |
| APWRA | 50 | 40 | Humans | 39 | 0.999 | 69.0 | 782.344163 | 0.096261 | −1.192976 |
| APWRA | 50 | 35 | Humans | 39 | 0.998 | 57.9 | 803.370234 | 0.094283 | −1.181454 |
| APWRA | 50 | 30 | Humans | 39 | 0.999 | 53.2 | 870.062424 | 0.089872 | −1.153420 |
| APWRA | 50 | 25 | Humans | 39 | 0.999 | 19.4 | 1492.141011 | 0.076352 | −1.046971 |
| APWRA | 105 | Both | 7 | 0.980 | 15.5 | 19.600750 | 274.133735 | −2.240290 | |
| APWRA | 105 | Both | 28 | 0.992 | 71.1 | 76.879764 | 422.339737 | −2.489426 | |
| Method of Prediction | Fatalities Within B | (≥250 m from Turbine) | ||
|---|---|---|---|---|
| Smøla | APWRA | Smøla | APWRA | |
| Found by searching and used for prediction | 70.0 | 82.0 | ||
| Carcass density model | 66.7 | 82.3 | 118.5 | 177.0 |
| Cumulative count model | 70.2 | 81.6 | 80.0 | 109.0 |
| After 1 carcass reallocated to outer search annulus: | ||||
| Carcass density model | 62.0 | 83.0 | 106.8 | 179.6 |
| Cumulative count model | 68.9 | 81.5 | 77.4 | 108.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smallwood, K.S.; Bell, D.A. On the Spatial Distribution of Eagle Carcasses Around Wind Turbines: Implications for Collision Mortality Estimation. Diversity 2025, 17, 686. https://doi.org/10.3390/d17100686
Smallwood KS, Bell DA. On the Spatial Distribution of Eagle Carcasses Around Wind Turbines: Implications for Collision Mortality Estimation. Diversity. 2025; 17(10):686. https://doi.org/10.3390/d17100686
Chicago/Turabian StyleSmallwood, K. Shawn, and Douglas A. Bell. 2025. "On the Spatial Distribution of Eagle Carcasses Around Wind Turbines: Implications for Collision Mortality Estimation" Diversity 17, no. 10: 686. https://doi.org/10.3390/d17100686
APA StyleSmallwood, K. S., & Bell, D. A. (2025). On the Spatial Distribution of Eagle Carcasses Around Wind Turbines: Implications for Collision Mortality Estimation. Diversity, 17(10), 686. https://doi.org/10.3390/d17100686






