Analysis of Inbreeding Effects on Survival at Birth of Pannon White Rabbits Using the Inbreeding-Purging Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Population and Data Information
2.2. Inbreeding-Purging Analysis
- The value of the purging coefficient (d) was estimated using a heuristic approach suggested by García-Dorado et al. [30] covering the interval 0–0.5.
- For each d value assumed, this approach computes the gi value of each individual, where gi was calculated by the ip_g() function of the purgeR R package.
- In our case, the fitness trait (W) is the survival. Probit regression (glm function, stats package of R) was used to find suitable initial values for the non-linear regression model.
- The non-linear regression method was used to find the more accurate values of the coefficients of the model (nls function, stats package of R).
- The corrected Akaike information criterion AICc value was calculated by the AICcmodavg package.
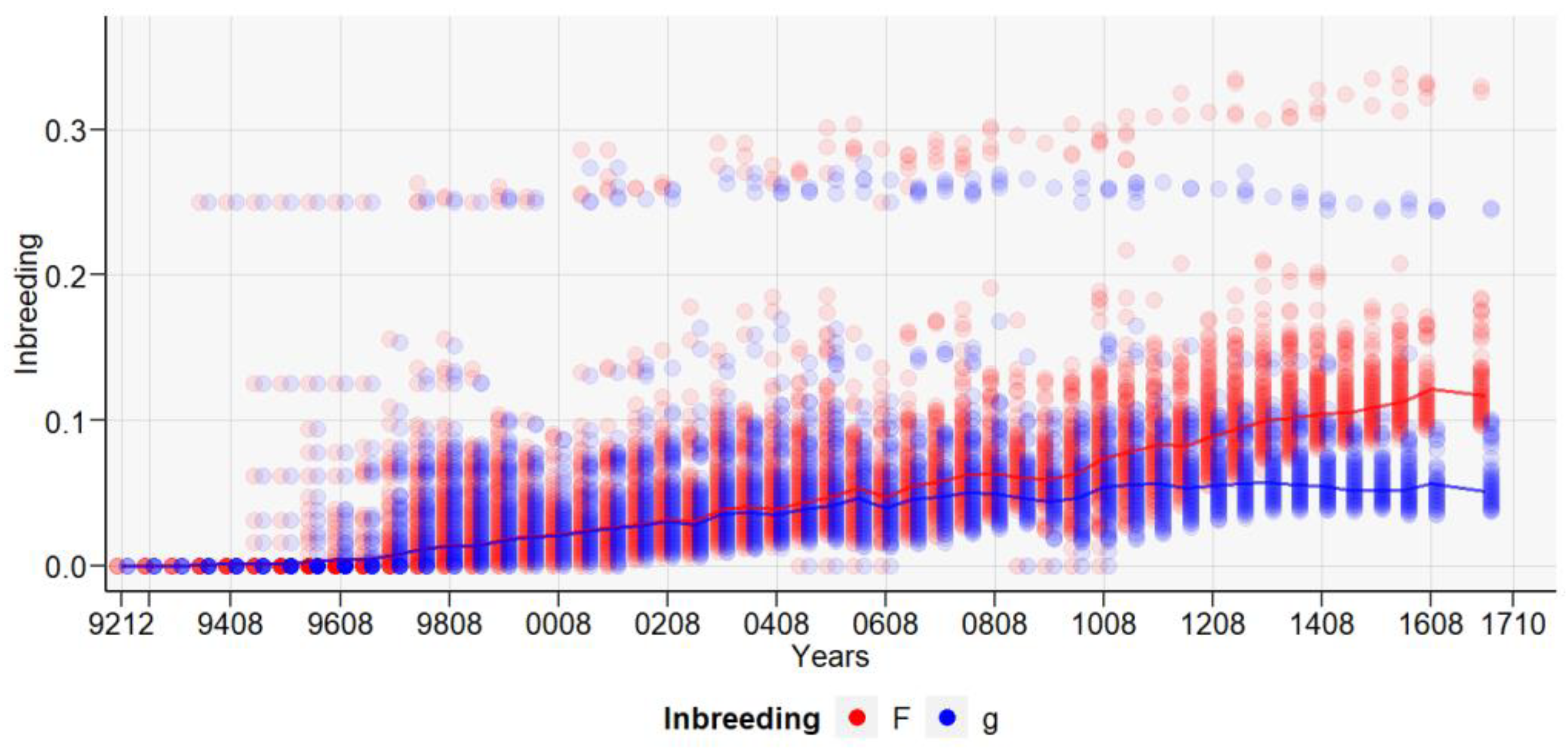
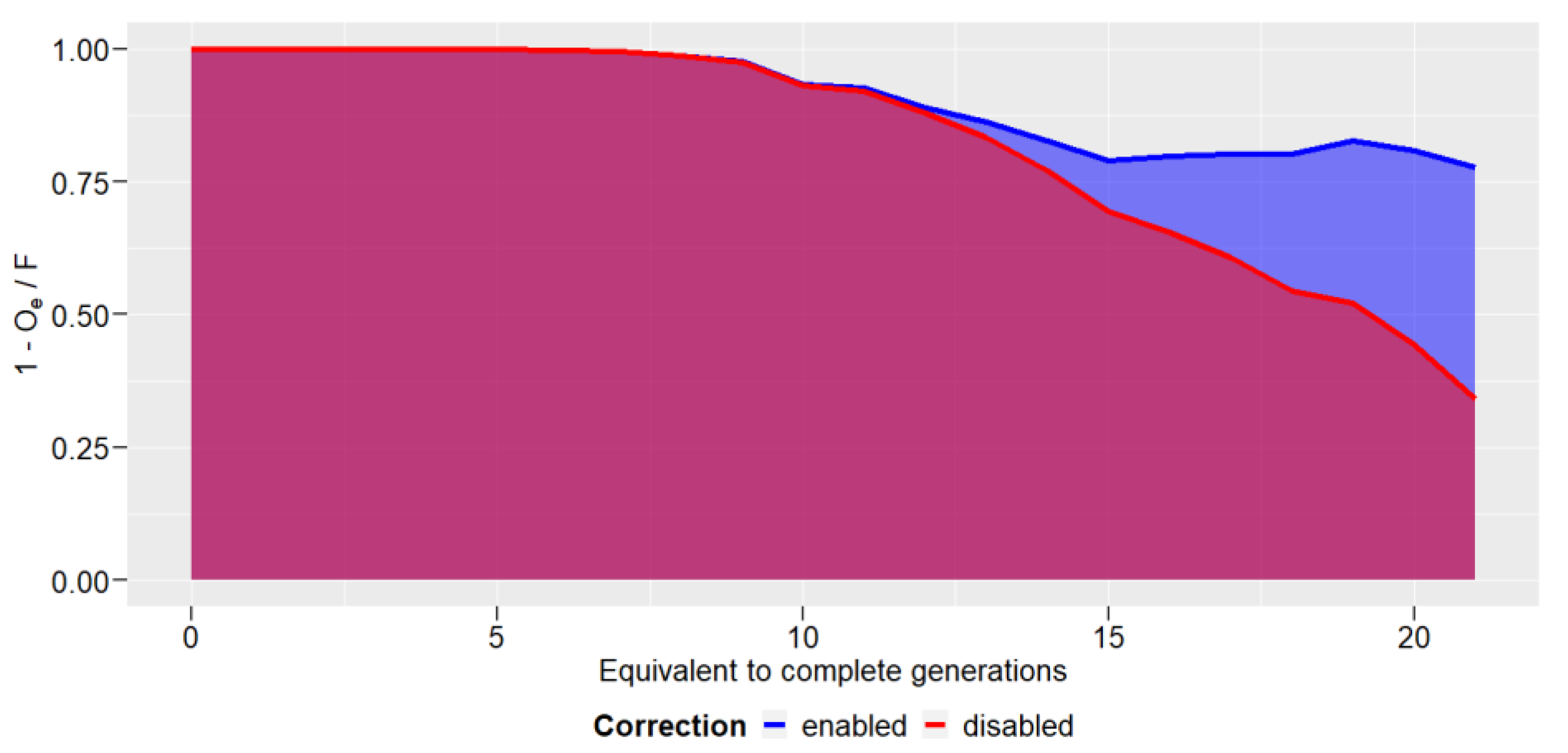
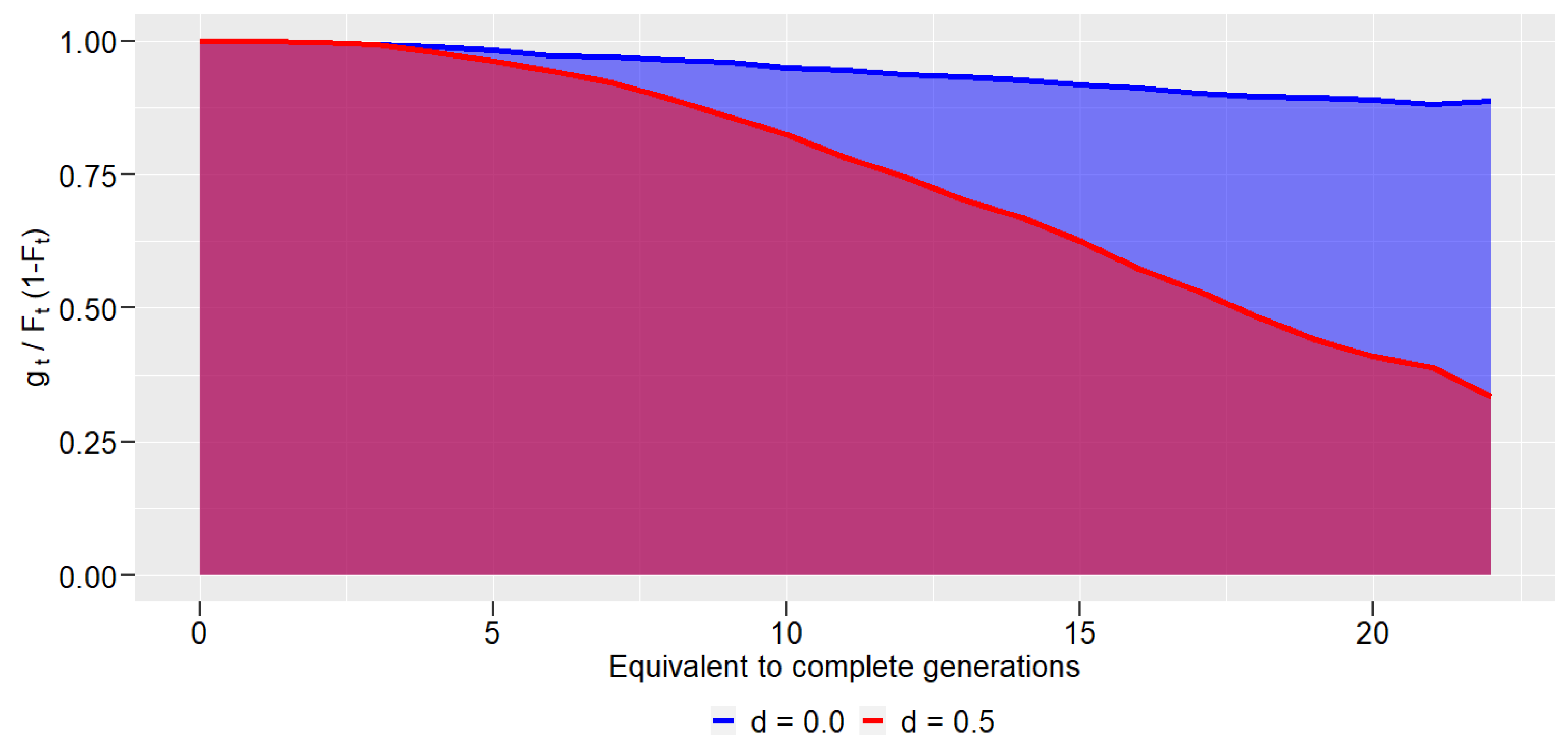
3. Results
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Perdomo-González, D.I.; Sánchez-Guerrero, M.J.; Molina, A.; Valera, M. Genetic structure analysis of the pura raza español horse population through partial inbreeding coefficient estimation. Animals 2020, 10, 1360. [Google Scholar] [CrossRef] [PubMed]
- Poyato-Bonilla, J.; Perdomo-González, D.I.; Sánchez-Guerrero, M.J.; Varona, L.; Molina, A.; Casellas, J.; Valera, M. Genetic inbreeding depression load for morphological traits and defects in the Pura Raza Española horse. Genet. Sel. Evol. 2020, 52, 62. [Google Scholar] [CrossRef] [PubMed]
- Casellas, J.; Ibáñez-Escriche, N.; Varona, L.; Rosas, J.P.; Noguera, J.I. Inbreeding depression load for litter size in Entrepelado and Retinto Iberian pig varieties. J. Anim. Sci. 2019, 97, 1979–1986. [Google Scholar] [CrossRef]
- Varona, L.; Altarriba, J.; Moreno, C.; Martínez-Castillero, M.; Casellas, J. A multivariate analysis with direct additive and inbreeding depression load effects. Genet. Sel. Evol. 2019, 51, 78. [Google Scholar] [CrossRef]
- Darwin, C. The Variation of Animals and Plants under Domestication, 2nd ed.; D. Appleton and Company: New York, NY, USA, 1883; pp. 1–473. [Google Scholar] [CrossRef]
- Darwin, C. The Effects of Cross and Self-Fertilization in the Vegetable Kingdom; D. Appleton and company: New York, NY, USA, 1892; pp. 1–482. [Google Scholar] [CrossRef]
- Ralls, K.; Ballou, J.D.; Templeton, A. Estimates of lethal equivalents and the cost of inbreeding in mammals. Conserv. Biol. 1988, 2, 185–193. [Google Scholar] [CrossRef]
- Crnokrak, P.; Roff, D.A. Inbreeding depression in the wild. Heredity 1999, 83, 260–270. [Google Scholar] [CrossRef] [PubMed]
- O’Grady, J.J.; Brook, B.W.; Reed, D.H.; Ballou, J.D.; Tonkyn, D.W.; Frankham, R. Realistic levels of inbreeding depression strongly affect extinction risk in wild populations. Biol. Conserv. 2006, 133, 42–51. [Google Scholar] [CrossRef]
- Kardos, M.; Taylor, H.R.; Ellegren, H.; Luikart, G.; Allendorf, F.W. Genomics advances the study of inbreeding depression in the wild. Evol. Appl. 2016, 9, 1205–1218. [Google Scholar] [CrossRef]
- Leroy, G. Inbreeding depression in livestock species: Review and meta-analysis. Anim. Genet. 2014, 45, 618–628. [Google Scholar] [CrossRef]
- Curik, I.; Ferencakovic, M.; Sölkner, J. Genomic dissection of inbreeding depression: A gate to new opportunities. Rev. Bras. Zootecn. 2017, 46, 773–782. [Google Scholar] [CrossRef]
- Doekes, H.P.; Bijma, P.; Windig, J.J. How depressing is inbreeding? A meta-analysis of 30 years of research on the effects of inbreeding in livestock. Genes 2021, 12, 926. [Google Scholar] [CrossRef] [PubMed]
- Boakes, E.H.; Wang, J.; Amos, W. An investigation of inbreeding depression and purging in captive breeding populations. Heredity 2007, 98, 172–182. [Google Scholar] [CrossRef] [PubMed]
- Kalinowski, S.T.; Hedrick, P.W.; Miller, P.S. Inbreeding depression in the Speke’s gazelle captive breeding program. Conserv. Biol. 2000, 14, 1375–1384. [Google Scholar] [CrossRef]
- Templeton, A.R.; Read, B. The elimination of inbreeding depression in a captive herd of Speke’s Gazelle. In Genetics and Conservation; Schonewald-Cox, C.M., MacBryde, S.M., Thomas, B.I., Eds.; Benjamin/Cummings: Menlo Park, CA, USA, 1983; pp. 241–261. [Google Scholar]
- Templeton, A.R.; Read, B. Factors eliminating inbreeding depression in a captive herd of Speke’s gazelle (Gazella spekei). Zoo Biol. 1984, 3, 177–199. [Google Scholar] [CrossRef]
- Leberg, P.L.; Firmin, B.D. Role of inbreeding depression and purging in captive breeding and restoration programmes. Mol. Ecol. 2008, 17, 334–343. [Google Scholar] [CrossRef]
- Pérez-Pereira, N.; Caballero, A.; García-Dorado, A. Reviewing the consequences of genetic purging on the success of rescue programs. Conserv. Genet. 2022, 23, 1–17. [Google Scholar] [CrossRef]
- Ballou, J.D. Ancestral inbreeding only minimally affects inbreeding depression in mammalian populations. J. Hered. 1997, 88, 169–178. [Google Scholar] [CrossRef]
- Keller, L.F.; Waller, D.M. Inbreeding effects in wild populations. Trends Ecol. Evol. 2002, 17, 230–241. [Google Scholar] [CrossRef]
- Bersabé, D.; García-Dorado, A. On the genetic parameter determining the efficiency of purging: An estimate for Drosophila egg-to-pupae viability. J. Evol. Biol. 2013, 26, 375–385. [Google Scholar] [CrossRef]
- López-Cortegano, E.; Vilas, A.; Caballero, A.; García-Dorado, A. Estimation of genetic purging under competitive conditions. Evolution 2016, 70, 1856–1870. [Google Scholar] [CrossRef]
- Curik, I.; Kover, G.; Farkas, J.; Szendrő, Z.; Romvari, R.; Sölkner, J.; Nagy, I. Inbreeding depression for kit survival at birth in a rabbit population under long-term selection. Genet. Sel. Evol. 2020, 52, 39. [Google Scholar] [CrossRef] [PubMed]
- Hinrichs, D.; Bennewitz, J.; Wellmann, R.; Thaller, G. Estimation of ancestral inbreeding effects on stillbirth, calving ease and birthweight in German Holstein dairy cattle. J. Anim. Breed. Genet. 2015, 132, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Mc Parland, S.; Kearny, F.; Berry, D. Purging of inbreeding depression with the Irish Holstein-Friesian population. Genet. Sel. Evol. 2009, 41, 16. [Google Scholar] [CrossRef] [PubMed]
- García-Dorado, A. Understanding and predicting the fitness decline of shrunk populations: Inbreeding, purging, mutation, and standard selection. Genetics 2012, 190, 1461–1476. [Google Scholar] [CrossRef]
- López-Cortegano, E.; Bersabé, D.; Wang, J.; García-Dorado, A. Detection of genetic purging and predictive value of purging pa- rameters estimated in pedigreed populations. Heredity 2018, 121, 38–51. [Google Scholar] [CrossRef]
- Blasco, A.; Nagy, I.; Hernández, P. Genetics of growth, carcass and meat quality in rabbits. Meat Sci. 2018, 145, 178–185. [Google Scholar] [CrossRef]
- García-Dorado, A.; Wang, J.; López-Cortegano, E. Predictive model and software for inbreeding-purging analysis of pedigreed populations. G3-Genes Genom. Genet. 2016, 6, 3593–3601. [Google Scholar] [CrossRef][Green Version]
- López-Cortegano, E.; Bersabé, D.; Wang, J.; García-Dorado, A. PURGd a Softvare to Detect Purging and to Estimate Inbreeding Genetic Parameters in Pedigreed Populations Version 2.3.2 User’s Guide Update in October 2022. Available online: https://www.ucm.es/gfm/mecanismos-geneticos. (accessed on 30 September 2022).
- López-Cortegano, E. PurgeR: Inbreeding and purging in pedigreed populations. Bioinformatics 2022, 38, 564–565. [Google Scholar] [CrossRef]
- Nagy, I.; Curik, I.; Radnai, I.; Cervantes, I.; Gyovai, P.; Baumung, R.; Farkas, J.; Szendrő, Z. Genetic diversity and population structure of the synthetic Pannon White rabbit revealed by pedigree analysis. J. Anim. Sci. 2010, 88, 1267–1275. [Google Scholar] [CrossRef]
- Moreno, E.; Pérez-González, J.; Carranza, J.; Moya-Laraño, J. Better fitness in captive Cuvier’s gazelle despite inbreeding increase: Evidence of purging? PLoS ONE 2015, 10, e0145111. [Google Scholar] [CrossRef]
- Ceballos, F.C.; Álvarez, G. Royal dynasties as human inbreeding laboratories: The Habsburgs. Heredity 2013, 111, 114–121. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Cortegano, E.; Moreno, E.; García-Dorado, A. Genetic purging in captive endangered ungulates with extremely low effective population sizes. Heredity 2021, 127, 433–442. [Google Scholar] [CrossRef] [PubMed]
- Gulisija, D.; Crow, J.F. Inferring purging from pedigree data. Evolution 2007, 61, 1043–1051. [Google Scholar] [CrossRef] [PubMed]
- Bundgaard, J.; Loeschke, V.; Schou, M.F.; Bijlsma, K.R. Detecting purging of inbreeding depression by a slow rate of inbreeding for various straits: The impact of environmental and experimental conditions. Heredity 2021, 127, 10–20. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Pereira, N.; López-Cortegano, E.; García-Dorado, A.; Caballero, A. Prediction of fitness under different breeding designs in conservation programs. Anim. Conserv. 2022. Early View. [Google Scholar] [CrossRef]

| d (P) | δ (Se) | δM (Se) | S2 (Se) | P2 (Se) | P3 (Se) | P4 (Se) | W0 (Se) | W’0 (Se) | AICc |
|---|---|---|---|---|---|---|---|---|---|
| Analyzed pedigree for the period between 1992 and 1997 | |||||||||
| 0.500 (0.294) | 0.466 (0.125) | NA | NA | NA | NA | NA | 0.945 (0.001) | 0.945 (0.000) | −4535.21 |
| 0.500 (0.294) | 0.466 (0.125) | 0.002 (0.169) | NA | NA | NA | NA | 0.945 (0.001) | 0.945 (0.000) | −4533.21 |
| 0.5000 (0.294) | 0.445 (0.125) | 0.003 (0.169) | 0.013 (0.003) | NA | NA | NA | 0.949 (0.001) | 0.945 (2.76 × 10−5) | −4553.38 |
| 0.5000 (0.289) | 0.442 (0.125) | −0.054 (0.169) | 0.012 (0.003) | −0.015 (0.004) | −0.024 (0.003) | −0.033 (0.004) | 0.931 (0.003) | 0.946 (6.03 × 10−5) | −4630.67 |
| 0.5000 (0.290) | 0.442 (0.125) | NA | 0.012 (0.003) | −0.015 (0.004) | −0.024 (0.003) | −0.032 (0.004) | 0.931 (0.003) | 0.946 (6.03 × 10−5) | −4632.57 |
| Analyzed pedigree for the period between 1992 and 2017 | |||||||||
| 0.2404 (0.158) | −0.093 (0.016) | NA | NA | NA | NA | NA | 0.946 (0.001) | 0.946 (0.000) | −38,718.32 |
| 0.1019 0.289 | −0.101 (0.023) | 0.027 (0.024) | NA | NA | NA | NA | 0.946 (0.001) | 0.946 (0.000) | −38,717.25 |
| 0.0000 | −0.098 (0.023) | 0.028 (0.023) | 0.015 (0.001) | NA | NA | NA | 0.950 (0.001) | 0.946 (2.92 × 10−5) | −38,866.47 |
| 0.0000 | −0.085 (0.023) | 0.018 (0.024) | 0.015 (0.001) | −0.018 (0.002) | −0.017 (0.001) | −0.014 (0.001) | 0.937 (0.001) | 0.946 (4.33 × 10−5) | −39,012.55 |
| 0.0000 | −0.071 (0.013) | NA | 0.015 (0.001) | −0.018 (0.002) | −0.017 (0.001) | −0.014 (0.002) | 0.937 (0.001) | 0.946 (4.34 × 10−5) | −39,013.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kövér, G.; Curik, I.; Vostry, L.; Farkas, J.; Mezőszentgyörgyi, D.; Nagy, I. Analysis of Inbreeding Effects on Survival at Birth of Pannon White Rabbits Using the Inbreeding-Purging Model. Diversity 2023, 15, 71. https://doi.org/10.3390/d15010071
Kövér G, Curik I, Vostry L, Farkas J, Mezőszentgyörgyi D, Nagy I. Analysis of Inbreeding Effects on Survival at Birth of Pannon White Rabbits Using the Inbreeding-Purging Model. Diversity. 2023; 15(1):71. https://doi.org/10.3390/d15010071
Chicago/Turabian StyleKövér, György, Ino Curik, Lubos Vostry, János Farkas, Dávid Mezőszentgyörgyi, and István Nagy. 2023. "Analysis of Inbreeding Effects on Survival at Birth of Pannon White Rabbits Using the Inbreeding-Purging Model" Diversity 15, no. 1: 71. https://doi.org/10.3390/d15010071
APA StyleKövér, G., Curik, I., Vostry, L., Farkas, J., Mezőszentgyörgyi, D., & Nagy, I. (2023). Analysis of Inbreeding Effects on Survival at Birth of Pannon White Rabbits Using the Inbreeding-Purging Model. Diversity, 15(1), 71. https://doi.org/10.3390/d15010071









