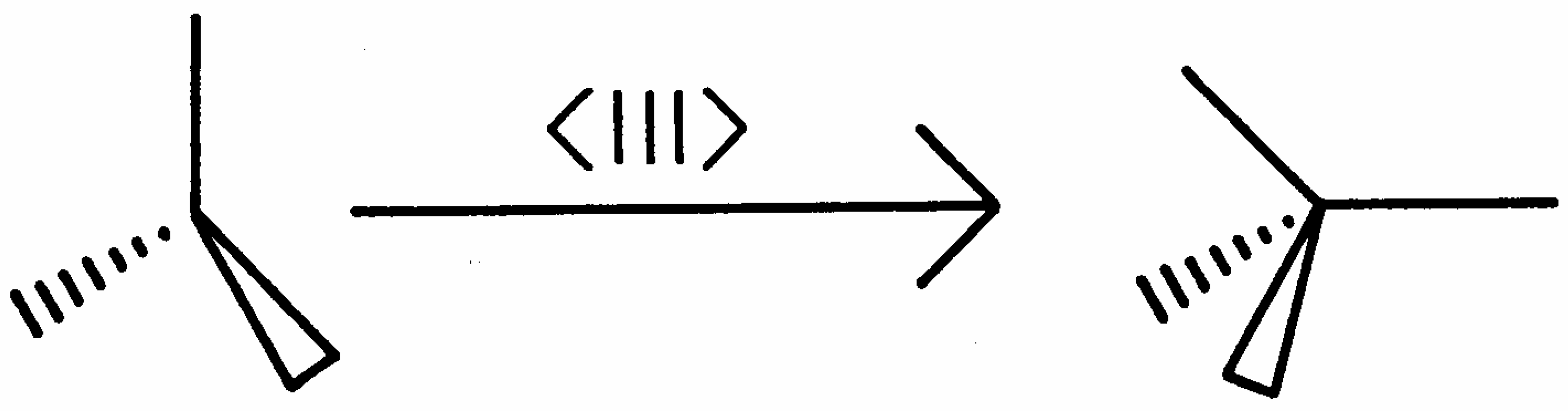Introduction
Waser and McClanahan solved the structure of a novel sodium platinate lattice, NaPt
3O
4, in 1954 [
1]. This structure was synthesized as a jet black powder by the reaction of dry sodium chloroplatinate with dry sodium carbonate in a platinum crucible heated to a temperature at which the powdered material became molten, as is shown in Equation 1 below:
Upon cooling the molten mixture, the resulting black powder of the product sodium platinate was purified and conductivity and powder diffraction studies were carried out [
1]. Conductivity measurements showed that the product phase NaPt
3O
4 was a good sodium ion conductor (specific resistance at room temperature measured as ≈ 10
4 ohm-cm) because of the loose association of the Na
+ ions in the lattice coordinated to the oxygen atoms at a relatively large distance of 2.46 Å. According to the investigators, the sodium ions could be reversibly removed from the Pt
3O
4 host lattice to some extent, but the sodium ions could not be completely removed. The Pt
3O
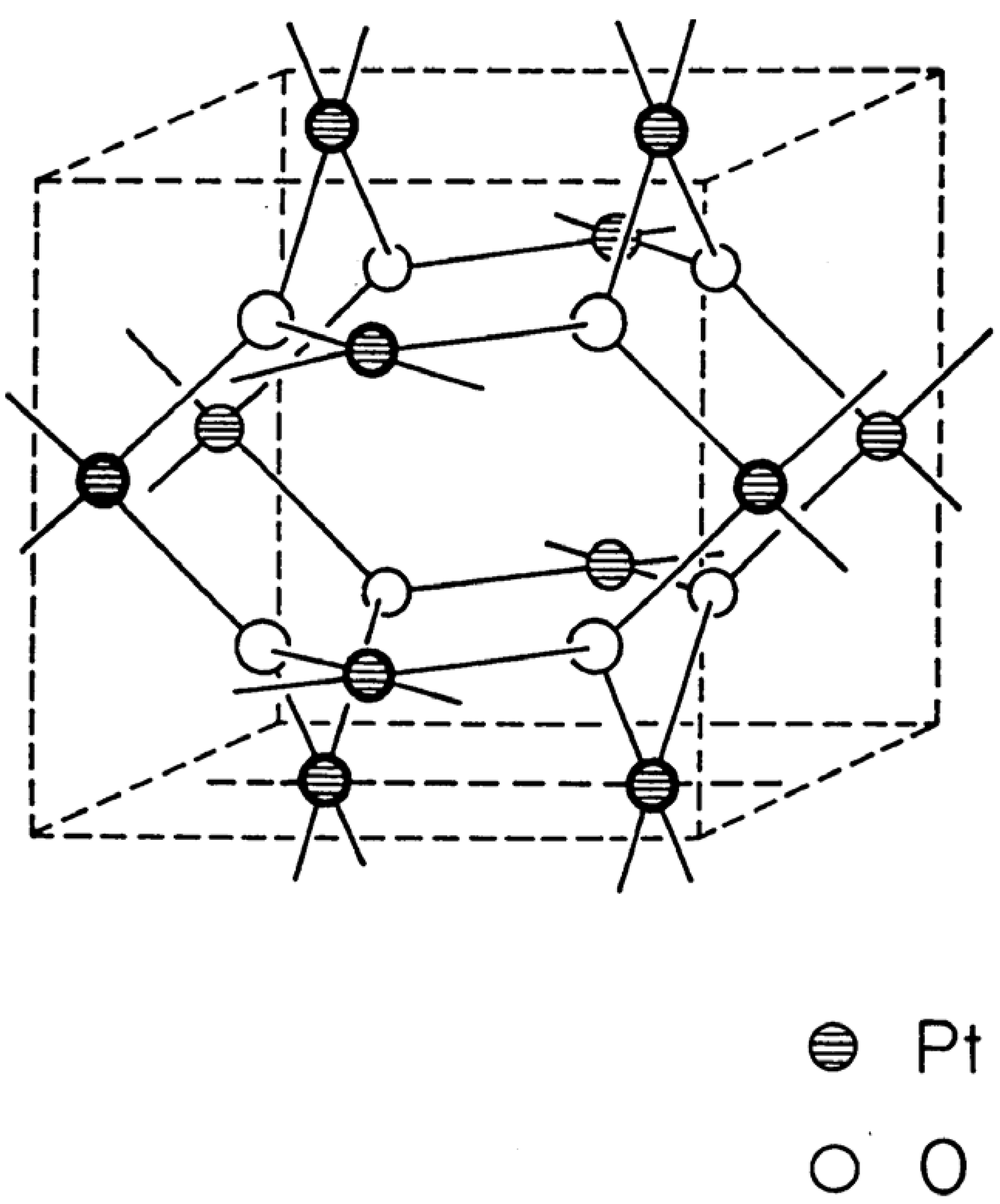
4 host lattice, herein called waserite in honor of its discoverer, is shown in
Figure 1.
This cubic structure-type represents a unique 3-,4-connected net which, to some degree, complements the hexagonal phenacite structure-type discovered in 1930 by Bragg and Zachariasen [
2]. Both networks consist of 3- and 4-connected vertices that alternate in 3 dimensions, giving rise to a connectivity index (weighted average atomic valency), p, of about 3.4285 [
3]. Interestingly, this index represents a continued fraction, and evidently the presence of high symmetry in these lattices does not preclude a connectivity index which is irrational [
4]. Pt
3O
4 lies in space group Pm3n, number 223, with 6 Pt's in the Wyckoff positions 6(c) ±(1/4, 0, 1/2) and 8 O's in the Wyckoff positions 8(e) ±(1/4, 1/4, 1/4) [
5]. In contrast, the phenacite structure-type, in a binary stoichiometry of A
3B
4, lies in space group P6
3/m, number 176, with three sets of atomic positions: N(1) 2(c) ±(1/3, 2/3, 1/4), N(2) 6(h) (±(u, v, 1/4); ±(-v, u-v, 1/4); ±(v-u, -u, 1/4)) and Si 6(h) (±(u, v, 1/4); ±(-v, u-v, 1/4); ±(v-u, -u, 1/4)) [
6].
Figure 1.
Waserite structure-type.
Figure 1.
Waserite structure-type.
The present communication describes a novel structure-type derived from waserite by replacing the trigonal planar, 3-connected vertices in Pt
3O
4 with tetrahedral, 4-connected vertices. In its most obvious form such a structure would possess 8 tetrahedral O vertices; in the Wyckoff positions 8(i) ±(x, x, x) of a Pm3 space group, number 200. Upon transforming waserite into the new structure-type by replacing the trigonal planar vertices with tetrahedral vertices, an 8-connected cube centered vertex is introduced into the unit cell, while the six 4-connected square planar vertices are retained, albeit slightly distorted, from waserite's structure. This novel structure-type is shown in
Figure 2 [
7].
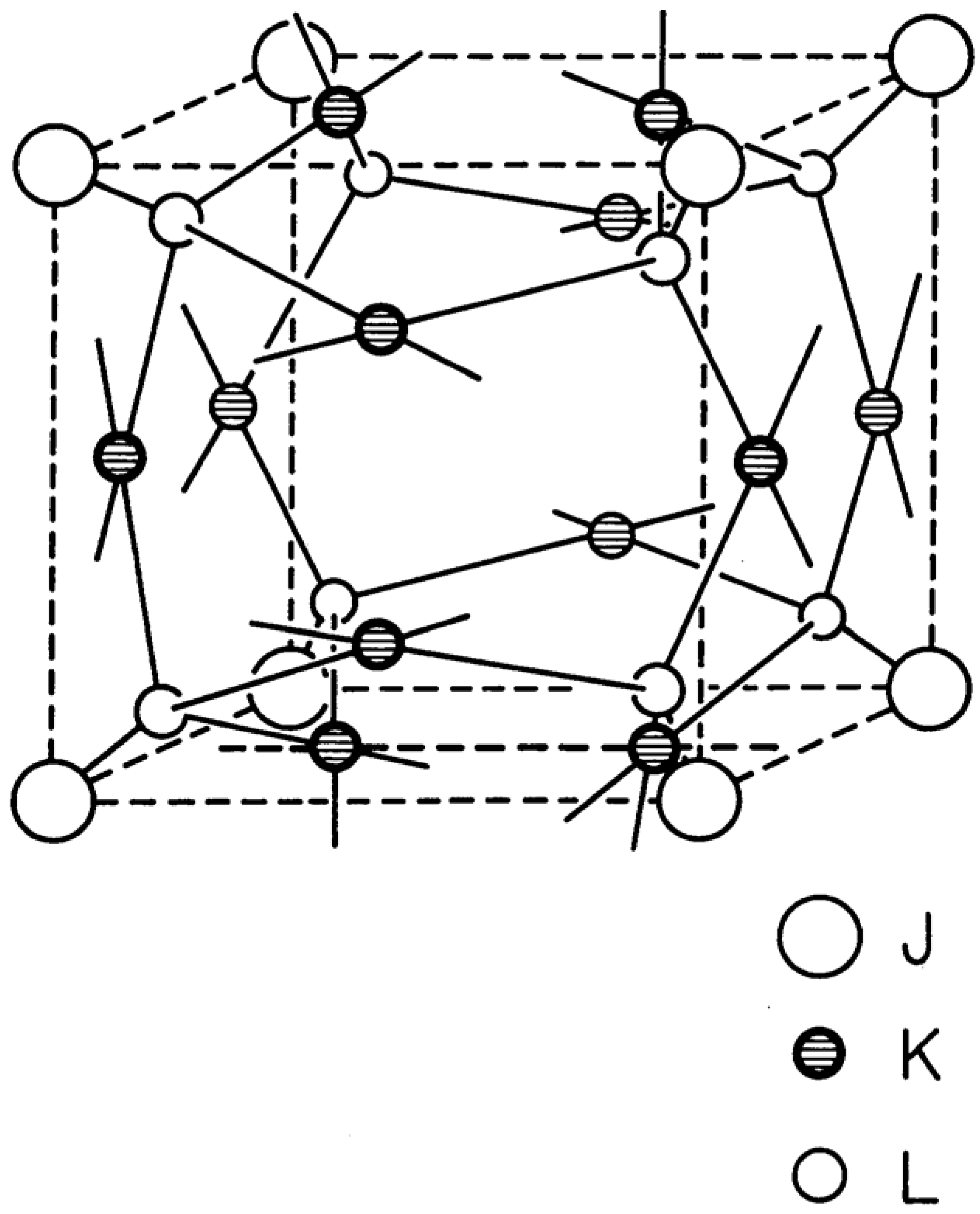
The new structure-type, hereafter called jubilite because of its discovery at the beginning of the new millenium, is cubic and lies in space group Pm3, number 200, with 1 atom in the Wyckoff position 1(a) (0, 0, 0), 6 atoms in the Wyckoff positions 6(f) ±(x, 0, 1/2) and 8 atoms in the Wyckoff positions 8(i) ±(x, x, x). It therefore has 15 atoms in the cubic unit cell, with a generic composition JK
6L
8. J is an 8-connected cube centered vertex, the 6 K correspond to the slightly distorted square planar vertices in
Figure 2, and the 8 L correspond to the slightly distorted tetrahedral vertices in
Figure 2.
Figure 2.
Jubilite structure-type.
Figure 2.
Jubilite structure-type.
The 4-connected vertices, both the square planar and the tetrahedral atoms, are forced to be distorted from their ideal bond angles of 90° (square planar) and 109.47° (tetrahedral) by the geometry of the lattice. In contrast, in waserite the 3-connected trigonal planar vertices and 4-connected square planar vertices are both completely undistorted from their ideal angles of 120° (trigonal planar) and 90° (square planar), respectively.
Transformations and Topology of the Jubilite Lattice
As has been previously discussed, the topological characteristics of crystalline materials may be described with reference to the two secondary topological parameters called the polygonality, n, and the connectivity, p, of the unit of pattern [
8]. The polygonality refers to a weighted average of all the shortest circuits about all of the atoms (vertices) in the unit cell of the structure; the connectivity is the weighted average valence over the atoms (vertices) in the unit cell. These parameters, n and p, are rigorously determined in all crystalline matter where links (bonds) between atoms are unambiguous. For some structure-types, it may be useful to view the lattice as consisting of interpenetrating component lattices with their respective polygonalities and connectivities.
As topological parameters, the polygonality and connectivity originate from the Euler relation for the sphere [
9] which rigorously describes the relation between the vertices, V, edges, E, and faces, F, of convex polyhedra; as shown in Equation 2.
This relation holds for any division of the sphere into vertices, edges and faces. By recognizing the identities, nF = 2E and pV = 2E, one may relate the secondary topological indexes, n and p, to the primary topological indexes, V, E and F, as is shown in Equation 3 [
10].
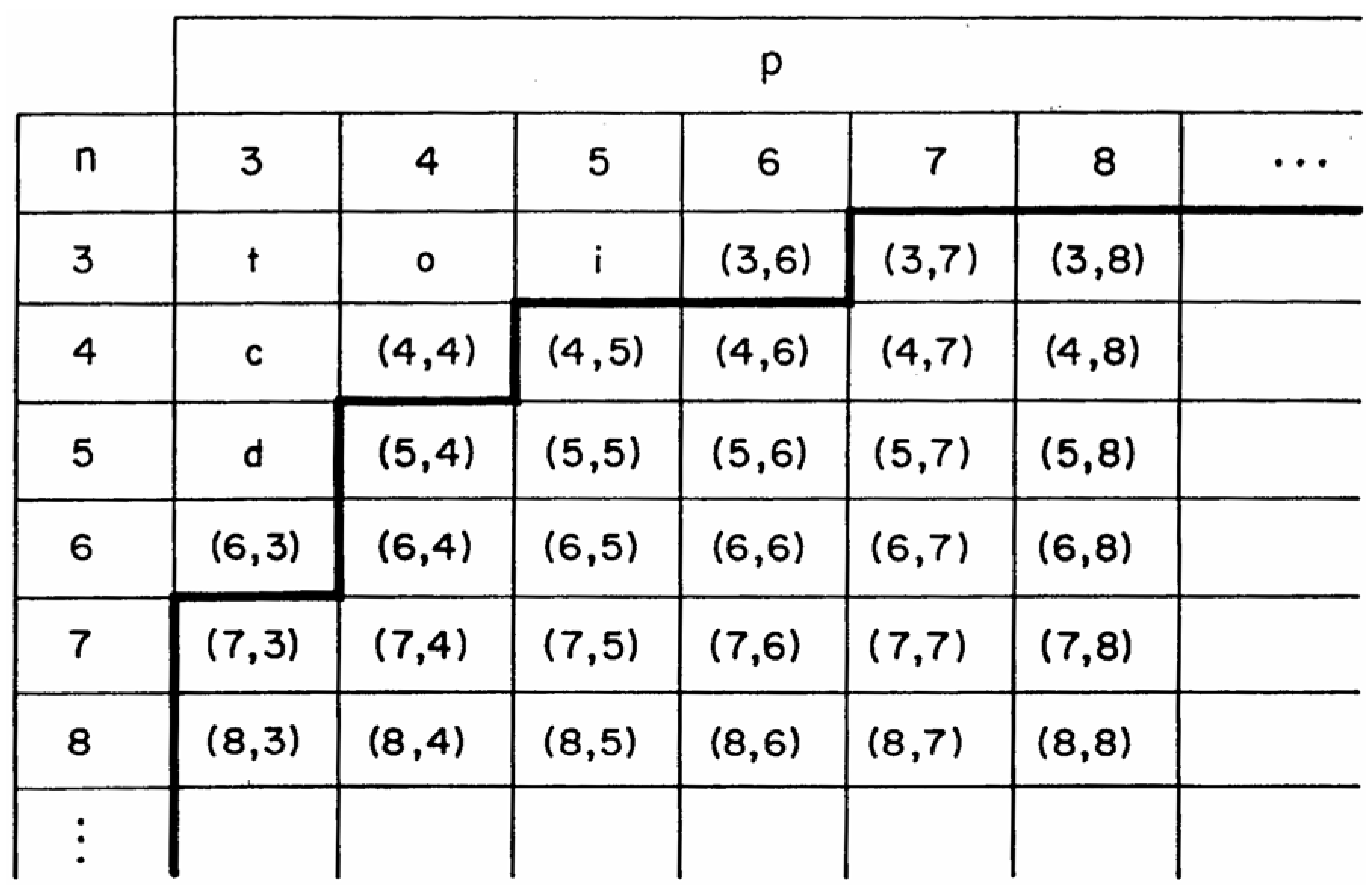
Equation 3 is rigorous for the polyhedra and polygons, but it does not hold for 2-dimensional and 3-dimensional extended structures. Evidently, the Euler relation needs to be modified in order to describe the structure of crystalline materials in a topological sense. At any event, the values of n and p can be rigorously calculated for any arbitrary unit cell and these indexes can be used to characterize the material topologically, as, for example, in the topology map shown in
Figure 3 below [
11]. The ordered pair of numbers (n, p) is called the Schläfli symbol of the unit of pattern. One can apply these ideas to topologically characterize the waserite, jubilite and fluorite lattices, which are related to each other through a continuous crystallographic structural transformation.
Figure 3.
Topology map of regular structures.
Figure 3.
Topology map of regular structures.
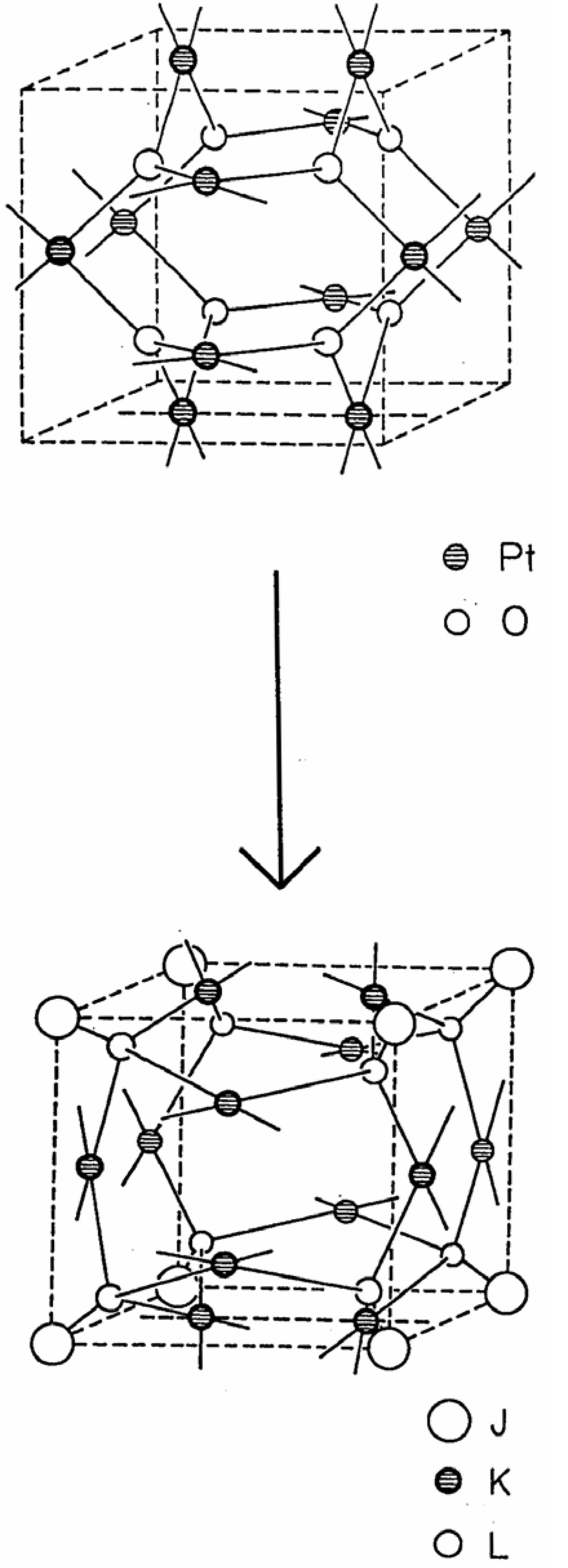
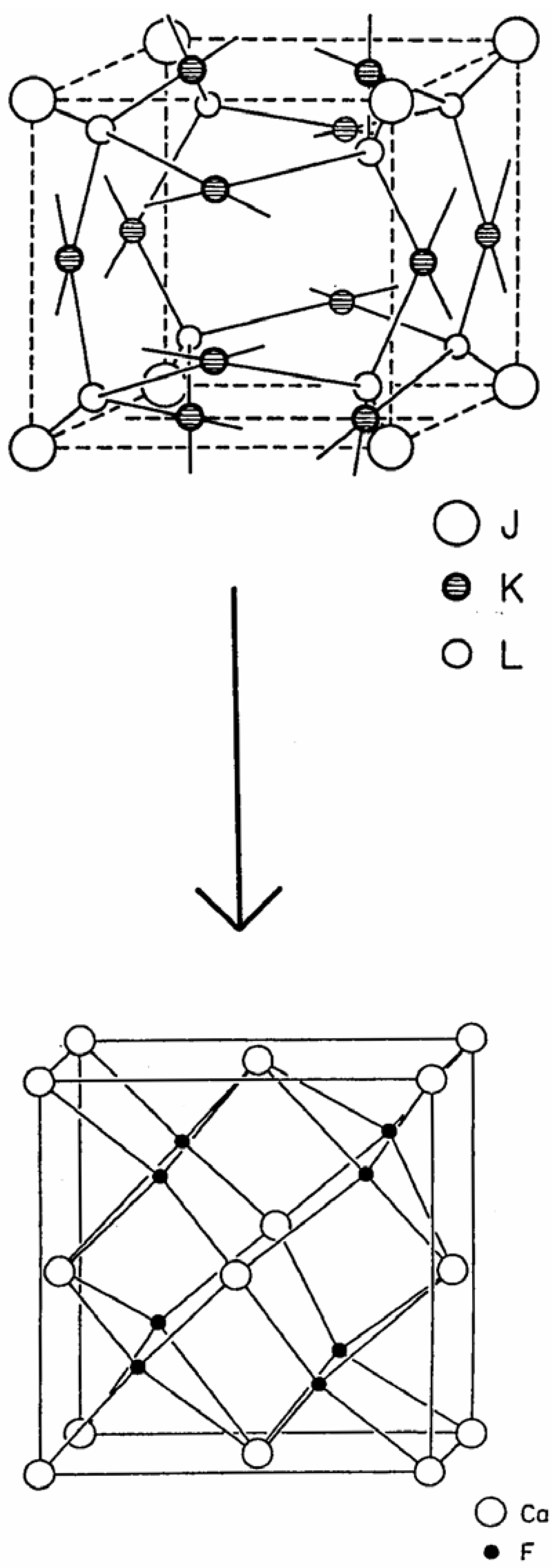
Beginning with the waserite lattice, shown on the top side in
Figure 4, one can envision a structural transformation in which the eight trigonal planar vertices, in Wyckoff positions 8(e) ±(1/4, 1/4, 1/4) of Pm3n, are deformed continuously by drawing these atoms towards their respective, adjacent cube vertices along the <111> axes, and preserving 3-fold symmetry along the continuous deformation pathway, to generate eight tetrahedral vertices, in Wyckoff positions 8(i) ±(x, x, x) of Pm3 of the jubilite lattice, shown on the bottom side of
Figure 4. During this continuous, cubic symmetry preserving structural transformation, the six 4-connected square planar vertices, originally in the Wyckoff positions 6(c) ±(1/4, 0, 1/2) of Pm3n of the waserite lattice, are held fixed relative to the deformation of the eight 3-connected trigonal planar vertices (in 8(e) ±(1/4, 1/4, 1/4) of Pm3n), and are transformed, through the change in space group symmetry, to occupy the Wyckoff positions 6(f) ±(x, 0, 1/2) in Pm3 of the product jubilite lattice.
Figure 4.
Continuous structural transformation of waserite to jubilate.
Figure 4.
Continuous structural transformation of waserite to jubilate.
The structural transformation is termed continuous because the deformation of the eight 3-connected trigonal planar vertices along <111>, to form eight 4-connected tetrahedral vertices, which is shown schematically in
Figure 5, can occur virtually infinitesimally inside the unit cell.
Figure 5.
Cubic symmetry preserving distortion of trigonal planar vertex into tetrahedral vertex.
Figure 5.
Cubic symmetry preserving distortion of trigonal planar vertex into tetrahedral vertex.
During this structural transformation, the topology of the original waserite unit cell, given by the Schläfli symbol (8, 3.4285), with the Wells point symbol (84)3(83)4, is discontinuously transformed into a topology represented by the Schläfli symbol (53/4, 4.2667) of the jubilite unit cell, with a Wells point symbol given by (4166484)(4282)6(4383)8. In the topological change accompanying the structural transformation, the polygonality is compressed from a value of n = 8 in waserite to n = 53/4 in the latter jubilite structure-type. In contrast, the change from trigonal planar connectivity to tetrahedral connectivity results in the connectivity index increasing from 3.4285 to 4.2667. The space group symmetry is concomitantly lowered from Pm3n, number 223, in waserite to Pm3, number 200, in the jubilite lattice.
In a subsequent continuous structural transformation, the jubilite lattice, shown on the top in
Figure 6, is continuously transformed into the fluorite lattice, shown on the bottom of
Figure 6, by coalescing the six 4-connected square planar vertices in 6(f) ±(x, 0, 1/2) of Pm3 jubilite into three 8-connected cube centered vertices (the fourth 8-connected cube centered vertex located at (0, 0, 0) is retained undeformed from the parent jubilite lattice) in Wyckoff positions 4(a) (0, 0, 0) of Fm3m, number 225, fluorite [
12]. In such a structural transformation, each of three pairs of adjacent 4-connected square planar vertices in {100} of jubilite is condensed into each of three corresponding single 8-connected cube centered vertices in {100} of fluorite. It is interesting to note that once again, as in the original waserite lattice, in the fluorite lattice there is no angle strain as the resulting eight 4-connected tetrahedral vertices in 8(c) ±(1/4, 1/4, 1/4) all have the ideal tetrahedral angle of 109.47° and all four 8-connected cube centered vertices, in 4(a) (0, 0, 0) of Fm3m of fluorite, have the ideal cubical angle of 70.53°.
During the continuous structural transformation from jubilite to fluorite, the topology once again changes discontinuously as the polygonality is reduced from jubilite (5
3/4, 4.2667) to fluorite (4, 5
1/3), represented by the Wells point symbol (4
24)(4
6)
2, and the connectivity is once again increased in the structural transformation; this time from 4.2667 to 5.3333. The symmetry of the lattice is curiously decreased from waserite in Pm3n, number 223, to jubilite in Pm3, number 200, and then increased from jubilite to fluorite in Fm3m, number 225. Finally, the l index [
9]; which is a measure of the form of a structural pattern in terms of the ratio, shown in Equation 4, of the average polygonality in the unit cell, n, to the average connectivity in the unit cell, p;
decreases monotonically in the sequence from waserite, where l is 2.3333, to jubilite, where l is 1.3476, to fluorite, where l is 0.7500. This change in l to some extent reflects a transition from a relatively open structure (waserite) into more highly connected structures which are topologically more closed (jubilite and fluorite).
Figure 6.
Continuous structural transformation of jubilite into fluorite.
Figure 6.
Continuous structural transformation of jubilite into fluorite.
It is quite interesting in this connection to compare the ratios of the form indexes for the members in this series of 3 patterns related through a continuous crystallographic structural transformation. The ratios l
waserite/l
jubilite and l
jubilite/l
fluorite can be formed and their values compared, as shown in Equation 5:
Evidently, the transformation of the topological form of the structure in changing from waserite to jubilite and then from jubilite to fluorite, manifests as nearly the same number. The similarity of the form change reveals the transformations are in some sense proportional, in other words the ratio of polygonality change to connectivity change is proportional in the 2 related continuous structural transformations.
Presence of Strain in Jubilite
In the structural transformations represented in
Figure 4 and
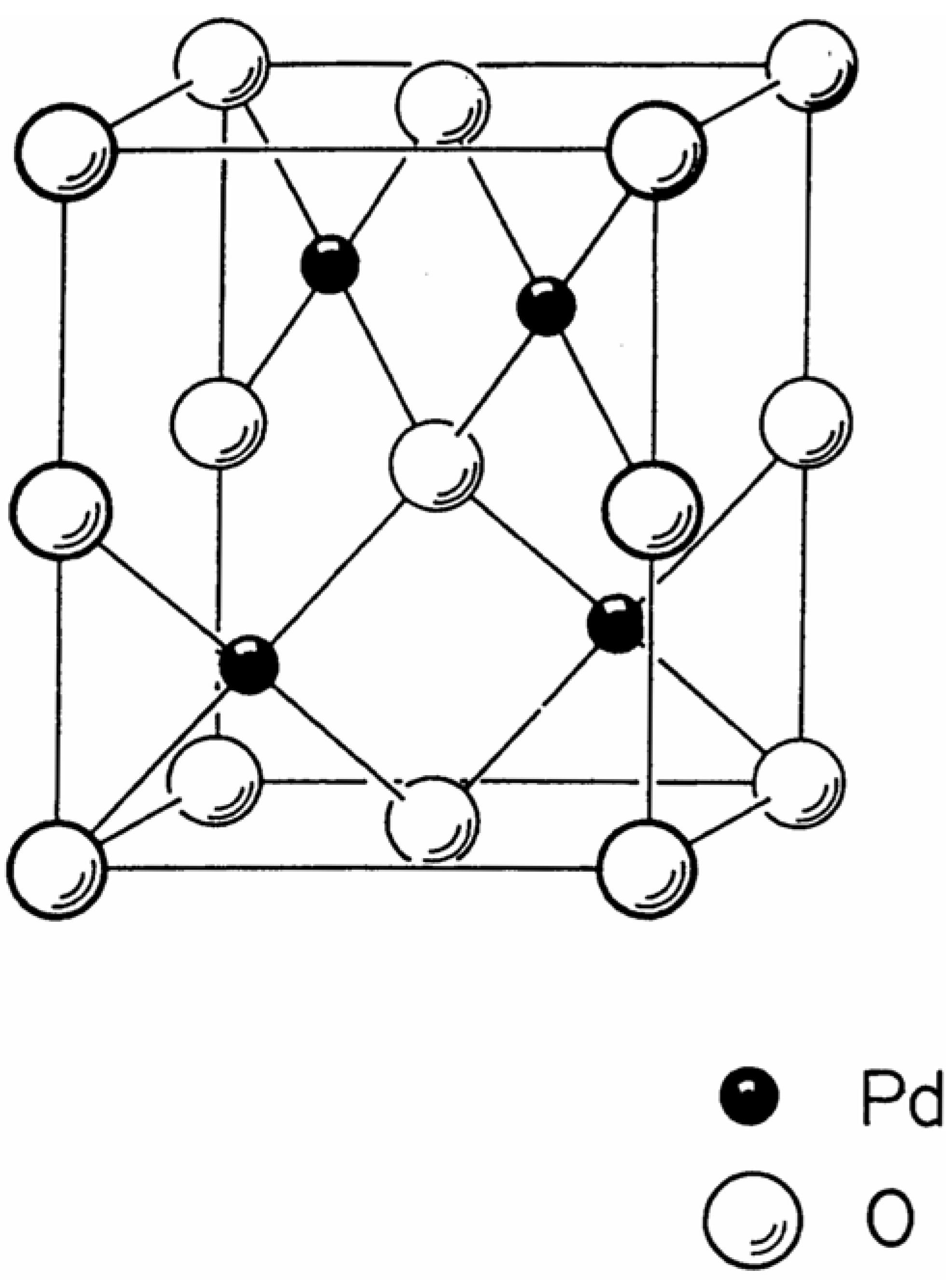
Figure 6, one sees the generation of a strained intermediate lattice, jubilite, occurring between the continuous structural transformation from one unstrained structure-type, waserite, into another unstrained structure-type, fluorite. The question naturally arises as to the occurrence of structure-types with strain in them. One prominent example of a strained lattice is the cooperite structure-type shown in
Figure 7 [
13].
Figure 7.
Cooperite structure-type.
Figure 7.
Cooperite structure-type.
This structure-type is observed as the sulfide mineral PtS, and the oxide PdO. The lattice lies in space group P4
2/mmc, number 131. The structure, which contains one 4-connected tetrahedral vertex, the S or O atom, and one 4-connected square planar vertex, the Pt or Pd atom, is forced by its geometry to have strain. The bond angles observed in the lattice are distorted from the ideal tetrahedral angle of 109.47°, and the ideal square planar angle of 90° [
11].
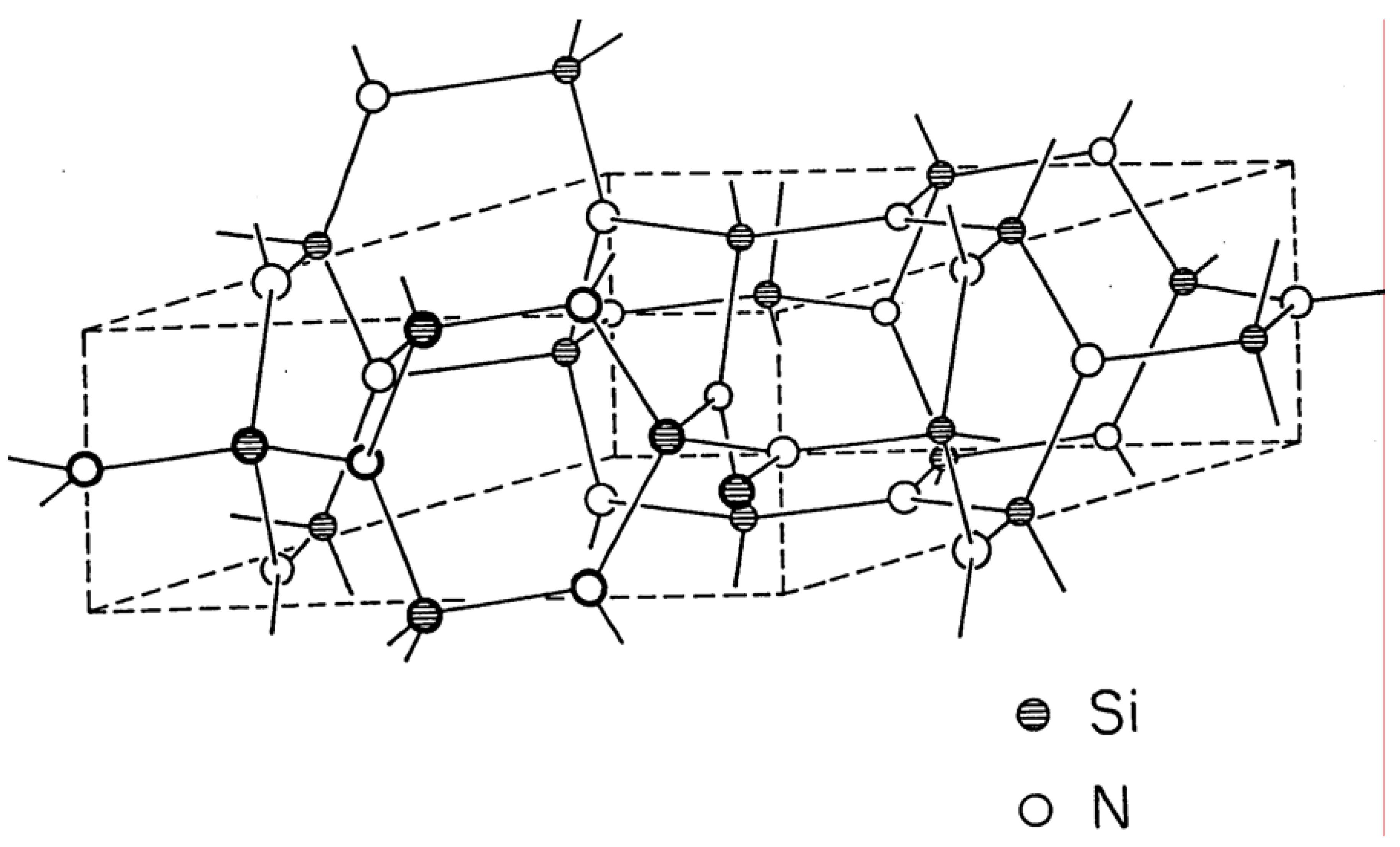
Yet another prominent example of a strained lattice is the phenacite structure-type [
2], which is the structure of Si
3N
4 and Ge
3N
4 and several other oxides and fluorides [
14]. Its structure is shown in
Figure 8, for a binary stoichiometry it has the space group symmetry P6
3/m, number 176, as discussed above. The lattice contains three 4-connected tetrahedral vertices and four 3-connected trigonal planar vertices in the unit of pattern. Once again, the geometry of the lattice forces the trigonal planar and tetrahedral vertices to be distorted from their ideal bond angle values of 120° and 109.47°, respectively.
Figure 8.
Phenacite structure-type.
Figure 8.
Phenacite structure-type.
It is interesting to speculate whether in analogy to the waserite-jubilite-fluorite triad, there may exist strain-free end-member structures that are related to the strained lattices of cooperite and phenacite through continuous structural transformations.
Finally, some important groundbreaking theoretical [
15] and synthetic [
16] work has been carried out on the jubilite structure-type very recently in 2004. The work of Balakrishnarajan et al. includes theoretical analysis of the bonding in a potential transition metal realization of the jubilite structure-type that suggests that quadruply bonded transition metal dumbbell pairs may be stabilized in the cube faces of the structure (atom “K” in
Figure 2) when atom “J” is an alkaline earth metal and atom “L” is a chalcogenide, in
Figure 2. In other work by Pley et al., a Pt-containing cluster anion has been synthesized that exhibits the core jubilite structure.