Kinetics and Mechanism of Acetoxymercuration and Acid-Catalysed Hydration of α-Alkylstyrenes
Abstract
:Introduction
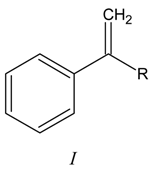
Results and Discussion
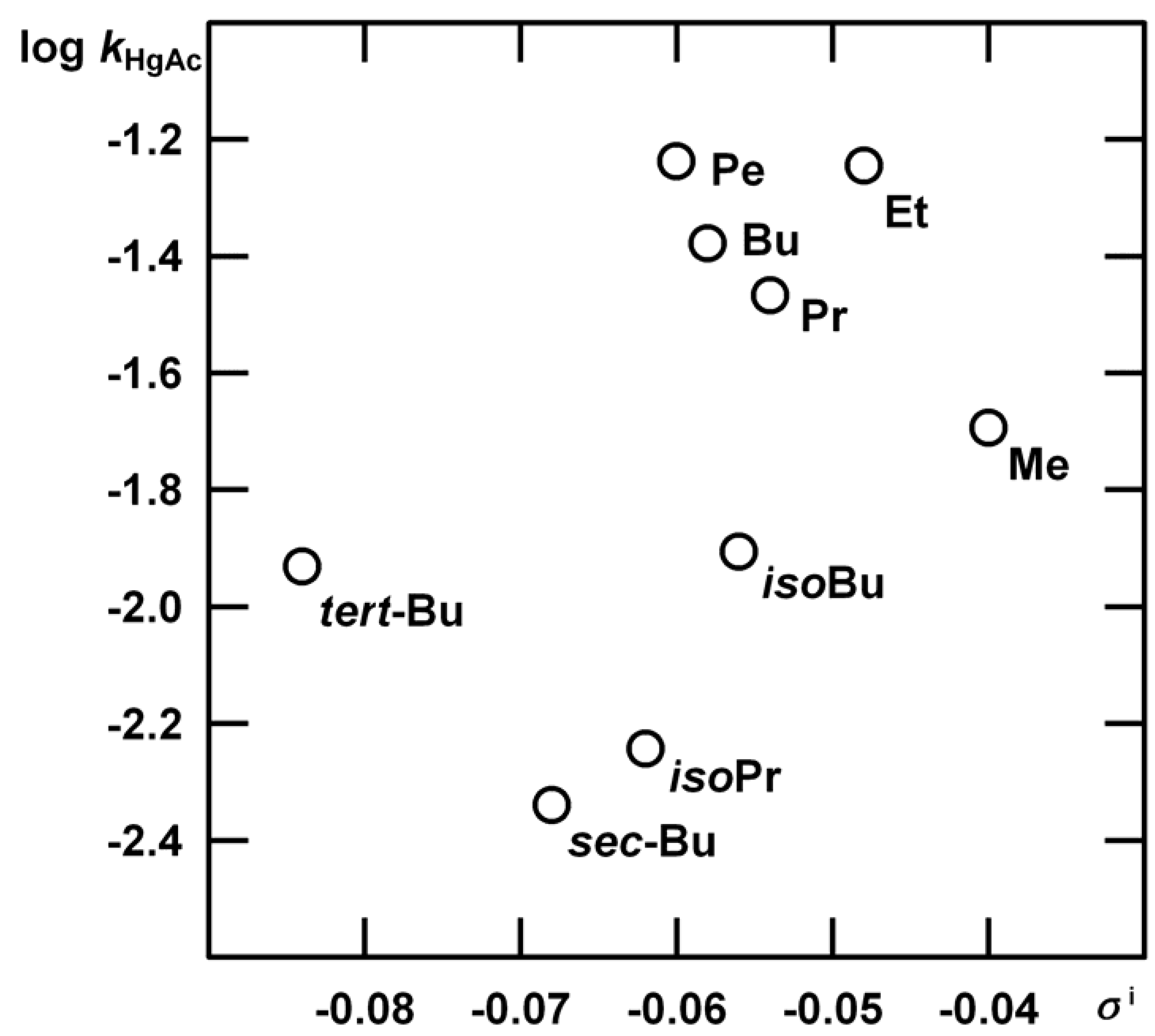
Acetoxymercuration
| c | Me | Et | Pr | Bu | Pe | isoBu | isoPr | sec-Bu | tert-Bu |
| 262 | 270 | 268 | 269 | 268 | 270 | 268 | 262 | 260 | |
| 5.00 10-3 | 9.90 10-5 | 3.12 10-4 | 1.88 10-4 | 2.19 10-4 | 2.66 10-4 | 6.90 10-5 | 2.47 10-5 | 2.24 10-5 | 6.07 10-5 |
| 6.67 10-3 | 1.44 10-4 | 4.01 10-4 | 2.40 10-4 | 2.86 10-4 | 3.33 10-4 | 8.83 10-5 | 3.20 10-5 | 2.86 10-5 | 9.00 10-5 |
| 7.67 10-3 | 1.51 10-4 | 4.83 10-4 | 2.84 10-4 | 3.29 10-4 | 3.73 10-4 | 9.80 10-5 | 3.77 10-5 | 2.66 10-5 | 1.08 10-4 |
| 8.33 10-3 | 1.72 10-4 | 5.24 10-4 | 2.96 10-4 | 3.52 10-4 | 4.08 10-4 | 1.06 10-4 | 4.00 10-5 | 3.60 10-5 | 1.04 10-4 |
| 9.00 10-3 | 1.88 10-4 | 5.62 10-4 | 3.18 10-4 | 3.84 10-4 | 4.44 10-4 | 1.19 10-4 | 4.30 10-5 | 3.88 10-5 | 1.10 10-4 |
| 1.00 10-2 | 2.02 10-4 | 5.75 10-4 | 3.39 10-4 | 4.15 10-4 | 4.87 10-4 | 1.27 10-4 | 5.43 10-5 | 3.65 10-5 | 1.21 10-4 |
| 1.17 10-2 | 2.26 10-4 | 6.73 10-4 | 3.88 10-4 | 4.84 10-4 | 5.73 10-4 | 1.46 10-4 | 6.30 10-5 | 4.25 10-5 | 1.35 10-4 |
| 1.33 10-2 | 2.63 10-4 | 7.22 10-4 | 4.42 10-4 | 5.46 10-4 | 6.67 10-4 | 1.60 10-4 | 6.80 10-5 | 4.79 10-5 | 1.55 10-4 |
| 1.43 10-2 | 2.77 10-4 | 7.49 10-4 | 4.58 10-4 | 5.71 10-4 | 8.25 10-4 | 1.71 10-4 | 7.50 10-5 | 5.18 10-5 | 1.78 10-4 |
| 1.50 10-2 | 2.87 10-4 | 7.96 10-4 | 4.88 10-4 | 5.84 10-4 | 8.35 10-4 | 1.75 10-4 | 8.37 10-5 | 5.76 10-5 | 1.69 10-4 |
| 1.60 10-2 | 2.96 10-4 | 8.55 10-4 | 5.16 10-4 | 6.38 10-4 | 8.93 10-4 | 1.87 10-4 | 8.90 10-5 | 6.07 10-5 | 1.67 10-4 |
| 1.67 10-2 | 3.13 10-4 | 8.86 10-4 | 5.23 10-4 | 6.44 10-4 | 9.04 10-4 | 1.91 10-4 | 9.63 10-5 | 6.62 10-5 | 1.73 10-4 |
| 1.80 10-2 | 3.32 10-4 | 9.08 10-4 | 5.57 10-4 | 6.92 10-4 | 1.08 10-3 | 2.04 10-4 | 1.06 10-4 | 8.16 10-5 | 1.90 10-4 |
| 2.00 10-2 | 3.73 10-4 | 9.93 10-4 | 6.03 10-4 | 7.46 10-4 | 1.20 10-3 | 2.18 10-4 | 1.04 10-4 | 1.26 10-4 | 1.97 10-4 |

n = 9, s = 0.058, R = 0.995.
Acid-Catalysed Hydration of α‑Alkylstyrenes
| c | Me | Et | Pr | Bu | Pe | isoBu | isoPr | sec-Bu | tert-Bu |
| 250 | 242 | 242 | 246 | 250 | 240 | 238 | 240 | 226 | |
| 1.00 | 2.64 10-4 | 2.44 10-4 | 5.39 10-5 | 1.13 10-4 | 1.46 10-4 | 1.15 10-4 | |||
| 1.50 | 6.16 10-4 | 5.59 10-4 | 4.93 10-4 | 1.21 10-4 | 2.68 10-4 | 3.90 10-4 | 2.50 10-4 | ||
| 2.00 | 1.34 10-3 | 1.19 10-3 | 9.26 10-4 | 2.50 10-4 | 5.62 10-4 | 7.26 10-4 | 4.96 10-4 | ||
| 2.50 | 2.61 10-3 | 2.24 10-3 | 1.83 10-3 | 5.59 10-4 | 1.10 10-3 | 1.40 10-3 | 1.03 10-3 | ||
| 3.01 | 6.59 10-3 | 4.95 10-3 | 3.82 10-3 | 1.41 10-3 | 2.94 10-3 | 3.26 10-3 | 2.65 10-3 | ||
| 3.08 | 1.57 10-3 | ||||||||
| 3.39 | 1.36 10-3 | ||||||||
| 3.50 | 1.11 10-2 | 9.84 10-3 | 6.85 10-3 | 4.60 10-3 | 6.64 10-3 | 4.27 10-3 | |||
| 3.56 | 1.21 10-2 | 9.92 10-3 | 9.18 10-3 | 4.62 10-3 | 6.55 10-3 | 6.72 10-3 | |||
| 3.89 | 2.63 10-3 | ||||||||
| 4.09 | 2.62 10-2 | 1.83 10-2 | 1.68 10-2 | 6.19 10-3 | 1.06 10-2 | 1.39 10-2 | 8.49 10-3 | 6.28 10-5 | |
| 4.44 | 3.04 10-2 | 3.08 10-2 | |||||||
| 4.51 | 4.21 10-2 | 3.62 10-2 | 2.79 10-2 | 9.68 10-3 | 1.89 10-2 | 2.03 10-2 | 1.92 10-2 | 1.08 10-4 | |
| 4.82 | 4.24 10-2 | 4.16 10-2 | 2.93 10-2 | ||||||
| 5.00 | 9.78 10-2 | 6.88 10-2 | 4.36 10-2 | 1.13 10-2 | 3.42 10-2 | 5.55 10-2 | 3.39 10-2 | 2.28 10-4 | |
| 5.10 | 8.38 10-3 | ||||||||
| 5.56 | 7.89 10-3 | ||||||||
| 5.97 | 1.72 10-2 | ||||||||
| 6.89 | 5.12 10-3 | ||||||||
| 7.33 | 2.02 10-2 |
| c | Et | Pr | Bu | Pe | isoBu |
| 2.00 | 1.16 10-4 | 1.87 10-4 | |||
| 2.06 | 1.35 10-3 | ||||
| 3.01 | 6.24 10-4 | ||||
| 3.50 | 9.08 10-4 | 1.06 10-3 | |||
| 4.09 | 2.31 10-3 | 3.59 10-3 | 2.30 10-3 | 1.57 10-2 | |
| 4.51 | 3.33 10-3 | 4.86 10-3 | 5.89 10-3 | 2.09 10-2 | |
| 5.00 | 1.24 10-2 | 1.28 10-2 | 2.50 10-2 | 3.74 10-2 | |
| 5.56 | 3.34 10-2 | ||||
| 5.97 | 5.48 10-2 | ||||
| 6.50 | 9.66 10-2 |

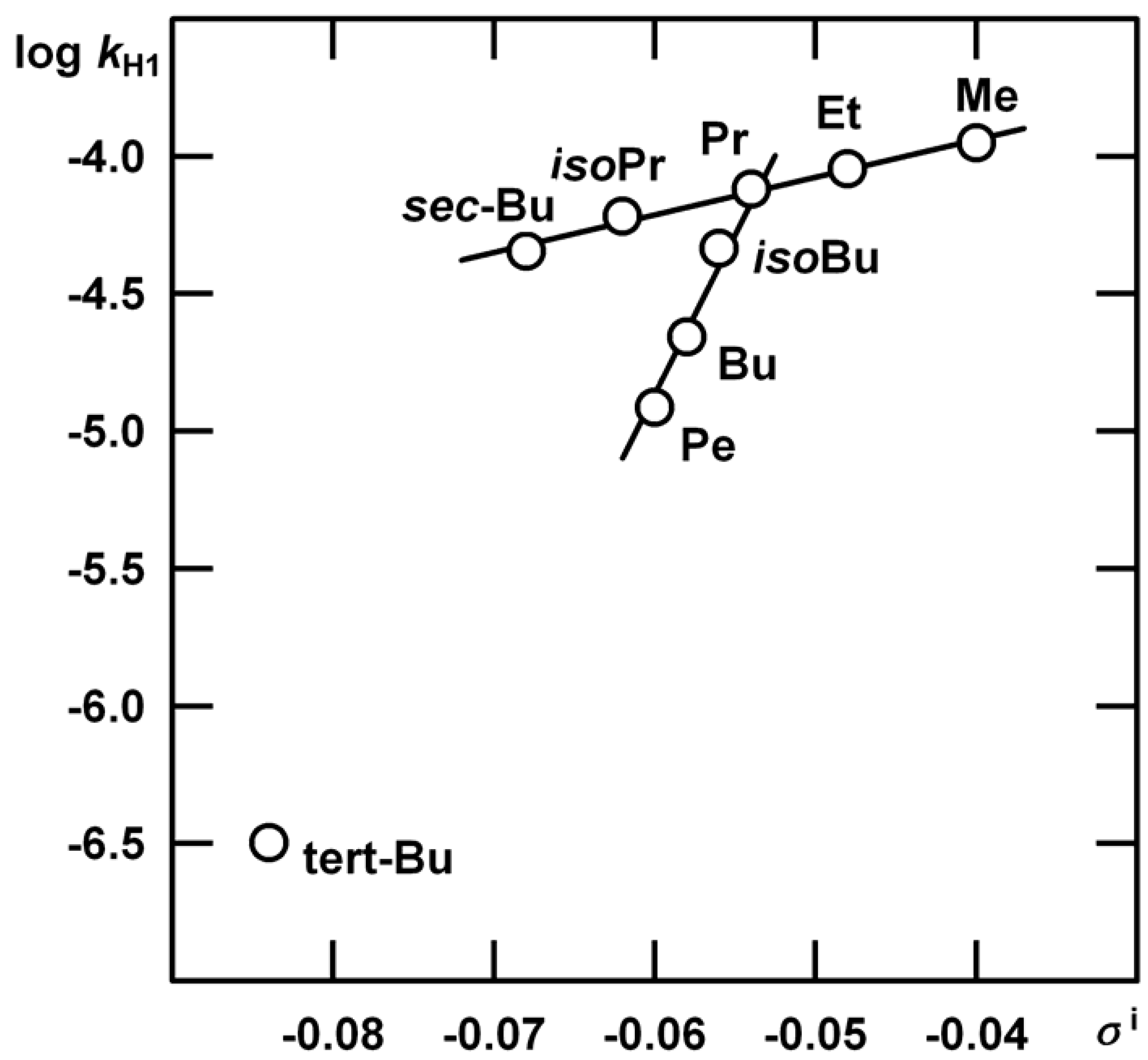
n = 5, s = 0.0204, R = 0.9933.

| R | kHgAc | kH1 | m‡m* | kH2 |
| Me | (1.35±0.03) 10-2 | (1.12±0.06) 10-4 | 1.35±0.01 | Indiscernible |
| Et | (3.80±0.07) 10-2 | (9.00±0.47) 10-5 | 1.13±0.14 | (2.08±0.55) 10-5 |
| Pr | (2.27±0.05) 10-2 | (7.60±0.33) 10-5 | 1.32±0.13 | (2.83±0.43) 10-5 |
| Bu | (2.79±0.05) 10-2 | (2.20±0.21) 10-5 | 1.02±0.27 | (3.66±0.22) 10-5 |
| Pe | (3.86±0.07) 10-2 | (1.22±0.08) 10-5 | 0.73±0.35 | (1.17±0.16) 10-4 |
| iso-Bu | (8.30±0.03) 10-3 | (6.04±0.06) 10-5 | 1.25±0.11 | (1.21±0.12) 10-4 |
| iso-Pr | (3.81±0.03) 10-3 | (4.62±0.58) 10-5 | 1.27±0.14 | very slow |
| sec-Bu | (3.05±0.03) 10-3 | (4.51±0.17) 10-5 | 1.31±0.19 | very slow |
| tert-Bu | (7.83±0.03) 10-3 | (2.29±0.07) 10-8 | 3.28±0.97 | Insensitive |
Experimental
Syntheses of Compounds Studied
| R | b.p.[°C]/press[torr], exp. | b.p.[°C]/press[torr], lit. | nD (20 °C), exp. | nD (20 °C), lit. | Yield, % |
| Me | 59-61/20 | 52-60/15 [47] | 1.525 | 1.536 [53] | 78 |
| Et | 76-79/20 | 73-74/15 [48] | 1.525 | 1.527 [54] | 60 |
| Pr | 78-82/10 | 77-78/10 [49] | 1.514 | 1.521 [55] | 68 |
| Bu | 80-85/05 | 89-90/10 [50] | 1.523 | 1.523 [56] | 83 |
| Pe | 65-70/ 1 | 93-95/10 [51] | 1.511 | 1.510 [57] | 90 |
| iso-Pr | 72-78/10 | 71-72/10 [49] | 1.514 | 1.518 [57] | 51 |
| iso-Bu | 74-79/ 5 | 83-84/10 [49] | 1.511 | 1.510 [58] | 48 |
| sec-Bu | 74-80/ 5 | - | 1.510 | - | 42 |
| tert-Bu | 84-90/10 | 73/10 [52] | 1.502 | 1.499 [59] | 14 |
Kinetic Measurements
Mathematical-Statistical Treatment of Results
Acknowledgements
References
- Bassetti, M.; Floris, B.; Illuminati, G. J. Organometallic Chem. 1980, 202, 351–362. [CrossRef]
- Lewis, A.; Azoro, J. J. Org. Chem. 1981, 46, 1764–1769. [CrossRef]
- Lewis, A. J. Org. Chem. 1984, 49, 4682–4687. [CrossRef]
- Brown, H. C.; Kurek, J. T.; Rei, M; Thompson, K. L. J. Org. Chem. 1984, 49, 2551–2557. [CrossRef]
- Lewis, A. J. Org. Chem. 1987, 52, 3099–3101. [CrossRef]
- Hendricks, I. S.; Lewis, A. J. Org. Chem. 1999, 64, 7342–7346. [CrossRef]
- Inaki, Y.; Nozakura, S.; Murahashi, S. Bull. Chem. Soc. Jpn. 1969, 42, 2605–2610. [CrossRef]
- Freeman, F. Chem. Rev. 1975, 75, 439–483.
- Ambidge, I. C.; Dwight, S. K.; Rynard, C. M.; Tidwell, T. T. Can. J. Chem. 1977, 55, 3086–3095. [CrossRef]
- Fukuzumi, S.; Kochi, J. K. J. Am. Chem. Soc. 1981, 103, 2783–2791. [CrossRef]
- Bassetti, M.; Floris, B. J. Chem. Soc., Perkin Trans. 2 1988, 227–233.
- Nelson, D. J.; Cooper, P. J.; Soundararajan, R. J. Am. Chem. Soc. 1989, 111, 1414–1418. [CrossRef]
- Vardhan, H. B.; Bach, R. D. J. Org. Chem. 1992, 57, 4948–4954. [CrossRef]
- Karmashov, V. R.; Sokolova, T. N.; Timofeev, I.V.; Skorobozamova, E. V.; Zefirov, N. S. Izv. Akad. Nauk., Ser. Khim. 1994, 819–826.
- Karmashov, V. R.; Sokolova, T. N.; Radbil, A. B.; Skorobozamova, E. V. Izv. Akad. Nauk., Ser. Khim. 1995, 344–351.
- Mayo, P.; Orlova, G.; Goddard, J. D.; Tam, W. J. Org. Chem. 2001, 66, 5182–5191. [CrossRef]
- Dewar, M. J. S.; Merz, K. M. Organometallics 1985, 4, 1967–1972.
- Mahapatra, B. P.; Aditya, S.; Prasad, B. J. Indian Chem. Soc. 1953, 30, 509–513.
- Cooney, R. P. J.; Hall, J. R. J. Inorg. Nucl. Chem. 1972, 34, 1519–1527. [CrossRef]
- Tackett, J. E. Appl. Spectroscopy 1989, 43, 483–489. [CrossRef]
- Quiles, F.; Burneau, A.; Gross, N. Appl. Spectroscopy 1999, 53, 1061–1070. [CrossRef]
- Rochester, C. H. Acidity functions; Academic Press: London, 1970; pp. 157–161. [Google Scholar]
- Ellis, G. W. L.; Johnson, C. D. J. Chem. Soc., Perkin. Trans. 2 1982, 1025–1027.
- Allen, A. D.; Rosenbaum, M.; Seto, N. O. L.; Tidwell, T. T. J. Org. Chem. 1982, 47, 4234–4239. [CrossRef]
- Schubert, W. M.; Keeffe, J. R. J. Am. Chem. Soc. 1972, 94, 559–566. [CrossRef]
- Schubert, W. M.; Jensen, J. L. J. Am. Chem. Soc. 1972, 94, 566–572. [CrossRef]
- Cox, R. A. Can. J. Chem. 1999, 77, 709–718.
- Deno, N. C.; Kish, F. A.; Peterson, H. J. J. Am. Chem. Soc. 1965, 87, 2157–2161.
- Durand, J. P.; Davidson, M.; Hellin, M.; Coussemant, F. Bull. Soc. Chim. Fr. 1966, 43–51.
- Simandoux, J. C.; Torck, B.; Hellin, M.; Coussemant, F. Bull. Soc. Chim. Fr. 1972, 4402–4409.
- Koshy, K. M.; Roy, D.; Tidwell, T. T. J. Am. Chem. Soc. 1979, 101, 357–363. [CrossRef]
- Mishima, M.; Yamataka, H. Bull. Chem. Soc. Jpn. 1998, 71, 2427–2432. [CrossRef]
- Doering, W. E.; Benkhoff, J.; Carleton, P. S.; Pagnotta, M. J. Am. Chem. Soc. 1997, 119, 10947–10955. [CrossRef]
- Cram, D. J.; Sahyun, M. R. V. J. Am. Chem. Soc. 1963, 85, 1257–1263. [CrossRef]
- Schwartz, R. S.; Yokokawa, H.; Graham, E. W. J. Am. Chem. Soc. 1972, 94, 1247–1249. [CrossRef]
- Opeida, I. O.; Suprun, W. Y. J. Chem. Soc., Perkin Trans. 2 2000, 1273–1279.
- Opeida, I. A.; Suprun, V. Ya.; Dmitruk, A. F. Teor. Eksperim. Khim. 1998, 34, 36–42.
- Anderson, J. E. Tetrahedron 1987, 43, 3041–3046.
- Tidwell, T. T. Angew. Chem. Int. Ed. 1984, 23, 20–32. [CrossRef]
- Lee, I.; Chung, D. S.; Jung, H. J. Tetrahedron 1994, 50, 7981–7986.
- Tsuno, Y.; Fujio, M. Chem. Soc. Rev. 1996, 129–139.
- Tsuno, Y.; Fujio, M. Advances in Physical Organic Chemistry 1999, 32, 267–385.
- Richard, J. P.; Rothenberg, M. E.; Jencks, W. P. J. Am. Chem. Soc. 1984, 106, 1361–1372. [CrossRef]
- Ta‑Shma, R.; Jencks, W. P. J. Am. Chem. Soc. 1986, 108, 8040–8050. [CrossRef]
- Mishima, M.; Nakata, K.; Nomura, H.; Fujio, M.; Tsuno, Y. Chem. Lett. 1992, 2435–2438.
- Yasufuku, K.; Nozakura, S.; Murahashi, S. Bull. Soc. Chem. Japan 1967, 40, 2146–2149. [CrossRef]
- Ager, D. J. J. Chem. Soc., Perkin Trans. 1 1986, 183–194. [CrossRef]
- Normant, J. F.; Cahiez, G.; Bourgain, M.; Chuit, C.; Villieras, J. Bull. Soc. Chim. Fr. 1974, 1656–1660.
- Barluenga, J.; Yus, M.; Concellon, J. M.; Bernad, P. J. Org. Chem. 1983, 48, 3116–3118. [CrossRef]
- Butler, G. B.; Brooks, T. W. J. Org. Chem. 1963, 28, 2699–2701. [CrossRef]
- Fiandanese, V.; Marchese, G.; Naso, F.; Ronzini, L. Synthesis 1987, 11, 1034–1036.
- Vejdělek, Z. J.; Trčka, V.; Vaňeček, M.; Kakáč, B.; Holubek, J. Collect. Czech. Chem. Commun. 1970, 35, 2810–2830. [CrossRef]
- Levina, R. JA.; Gembiikij, P. A.; Efremov, E. S.; Treshova, E. G. Zh. Obshch. Khim. 1963, 33, 2825–2828.
- Cadogan, J. I.G.; Sadler, I. H. J. Chem. Soc. B 1966, 1191–1205. [CrossRef]
- Westmijze, H.; Meijer, J.; Bos, H. J. T.; Vermeer, P. Recl. Trav. Chim. Pays-Bas 1976, 95, 299–303. [CrossRef]
- Gilman, H.; Meals, R. N. J. Org. Chem. 1943, 8, 126–139. [CrossRef]
- Adam, W.; Baeza, J.; Liu, J. C. J. Amer. Chem. Soc. 1972, 94, 2000–2006. [CrossRef]
- Hughes, G. M. K. J. Chem. Soc. 1958, 3703–3706.
- Suprun, W. Y; Blau, K.; Reinker, K. J. Prakt. Chem. 1995, 337, 496–503. [CrossRef]
- Kosmikov, R. R.; Molchanov, A. P. Zh. Org. Khim. 1978, 14, 355–360.
- Pytela, O.; Štumrová, S.; Ludwig, M.; Večeřa, M. Collect. Czech. Chem. Commun. 1986, 51, 564–572. [CrossRef]
- Pytela, O. Collect. Czech. Chem. Commun. 1997, 62, 645–655. [CrossRef]
- Pytela, O. Collect. Czech. Chem. Commun. 1995, 60, 1502–1528. [CrossRef]
- Pytela, O. Collect. Czech. Chem. Commun. 1996, 61, 704–712. [CrossRef]
- Charton, M. Steric Effect in Drug Design; Springer-Verlag: Berlin, 1983; pp. 57–91. [Google Scholar]
- Sample availability: Available from the corresponding author.
© 2005 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Svoboda, J.; Pelcová, M.; Nevěčná, T.; Pytela, O. Kinetics and Mechanism of Acetoxymercuration and Acid-Catalysed Hydration of α-Alkylstyrenes. Int. J. Mol. Sci. 2005, 6, 30-44. https://doi.org/10.3390/i6010030
Svoboda J, Pelcová M, Nevěčná T, Pytela O. Kinetics and Mechanism of Acetoxymercuration and Acid-Catalysed Hydration of α-Alkylstyrenes. International Journal of Molecular Sciences. 2005; 6(1):30-44. https://doi.org/10.3390/i6010030
Chicago/Turabian StyleSvoboda, Jan, Monika Pelcová, Taťjana Nevěčná, and Oldřich Pytela. 2005. "Kinetics and Mechanism of Acetoxymercuration and Acid-Catalysed Hydration of α-Alkylstyrenes" International Journal of Molecular Sciences 6, no. 1: 30-44. https://doi.org/10.3390/i6010030
APA StyleSvoboda, J., Pelcová, M., Nevěčná, T., & Pytela, O. (2005). Kinetics and Mechanism of Acetoxymercuration and Acid-Catalysed Hydration of α-Alkylstyrenes. International Journal of Molecular Sciences, 6(1), 30-44. https://doi.org/10.3390/i6010030




