Electronic Density Approaches to the Energetics of Noncovalent Interactions
Abstract
:Introduction
- 1)
- the electrostatic interaction between the unperturbed Mi;
- 2)
- their mutual polarization of each other’s charge distributions;
- 3)
- dispersion effects, involving intermolecular electronic correlation; and
- 4)
Evaluation of Ees and Epol from electronic densities
Methodology
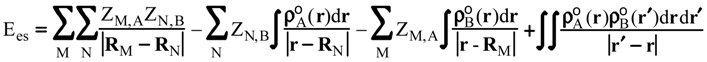
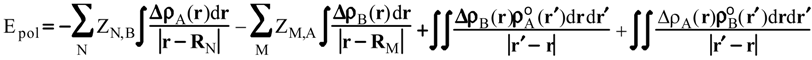
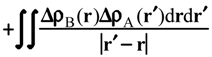
Applications
| Dimer | Computational | ρmin, au | ||||
| level | ||||||
| 1.0 x 10−3 | 1.0 x 10−4 | 1.0 x 10−5 | 1.0 x 10−6 | 1.0 x 10−7 | ||
| Face-to-face | HF/aug-cc-pVDZ | −6.69 | −10.06 | −11.79 | −12.07 | −12.07 |
| HF/aug-cc-pVTZ | −6.56 | −10.30 | −12.24 | −12.42 | −12.42 | |
| HF/aug-cc-pVQZ | −6.34 | −10.08 | −12.10 | −12.26 | −12.26 | |
| Face-to-back | HF/aug-cc-pVDZ | −4.46 | −4.28 | −4.95 | −5.16 | −5.16 |
| HF/aug-cc-pVTZ | −4.19 | −5.69 | −5.01 | −5.11 | −5.11 | |
| HF/aug-cc-pVQZ | −3.98 | −4.02 | −5.01 | −5.10 | −5.10 | |
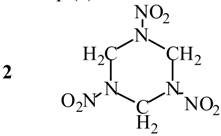
Evaluation of Eint from electronic densities
Methodology
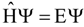
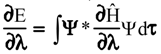
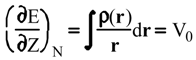
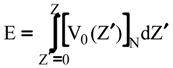
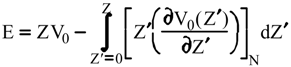
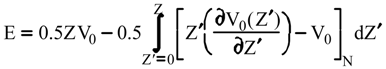
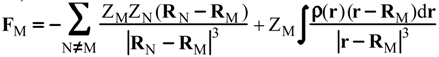
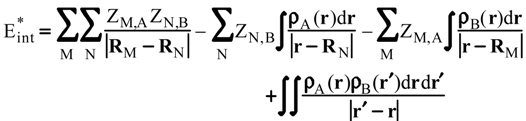
Applications
Discussion and summary
Acknowledgement
References
- Szalewicz, K.; Cole, S. J.; Kolos, W.; Bartlett, R. J. A Theoretical Study of Water Dimer Interaction. J. Chem. Phys. 1988, 89, 3662–3673. [Google Scholar] [CrossRef]
- Davidson, E. R.; Chakravorty, S. J. A Possible Definition of Basis Set Superposition Error. Chem. Phys. Lett. 1994, 217, 48–54. [Google Scholar] [CrossRef]
- van Duijneveldt, F. B.; van Duijneveldt-van de Rijdt, J. G. C. M.; van Lenthe, J. H. State of Art in Counterpoise Theory. Chem. Rev. 1994, 94, 1873–1885. [Google Scholar] [CrossRef]
- Boys, S. F.; Bernardi, F. The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Chalasinski, G.; Szczesniak, M. M. State of the Art and Challenges of the ab Initio Theory of Intermolecular Interactions. Chem. Rev. 2000, 100, 4227–4252. [Google Scholar] [CrossRef] [PubMed]
- Rappe, A. K.; Bernstein, E. R. Ab Initio Calculation of Nonbonded Interactions: Are We There Yet? J. Phys. Chem. A 2000, 104, 6117–6128. [Google Scholar] [CrossRef]
- Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of Van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
- Engkvist, O.; Astrand, P.-O.; Karlstrom, G. Accurate Intermolecular Potentials Obtained from Molecular Wave Functions: Bridging the Gap between Quantum Chemistry and Molecular Simulations. Chem. Rev. 2000, 100, 4087–4108. [Google Scholar] [CrossRef] [PubMed]
- Langlet, J.; Caillet, J.; Berges, J.; Reinhardt, P. Comparison of Two Ways to Decompose Intermolecular Interactions for Hydrogen-Bonded Dimer Systems. J. Chem. Phys. 2003, 118, 6157–6166. [Google Scholar] [CrossRef]
- Nobeli, I.; Price, S. L. A Non-Empirical Intermolecular Potential for Oxalic Acid Crystal Structures. J. Phys. Chem. A 1999, 103, 6448–6457. [Google Scholar] [CrossRef]
- Politzer, P.; Boyd, S. Molecular Dynamics Simulations of Energetic Solids. Struct. Chem. 2002, 13, 105–113. [Google Scholar] [CrossRef]
- Gavezzotti, A. Calculation of Intermolecular Interaction Energies by Direct Numerical Integration over Electron Densities. 2. An Improved Polarization Model and the Evaluation of Dispersion and Repulsion Energies. J. Phys. Chem. B 2003, 107, 2344–2353. [Google Scholar] [CrossRef]
- Seminario, J. M.; Concha, M. C.; Politzer, P. A Density-Functional/Molecular Dynamics Study of the Structure of Liquid Nitromethane. J. Chem. Phys. 1995, 102, 8281–8282. [Google Scholar] [CrossRef]
- Chipot, C.; Dehez, F.; Angyan, J.; Millot, C.; Orozco, M.; Luque, F. J. Alternative Approaches for the Calculation of Induction Energies: Characterization, Effectiveness, and Pitfalls. J. Phys. Chem. A 2001, 105, 11505–11514. [Google Scholar] [CrossRef]
- Ma, Y.; Politzer, P. Calculation of Electrostatic and Polarization Energies from Electron Densities. J. Chem. Phys. 2004, 120, 3152–3157. [Google Scholar] [CrossRef]
- Gavezzotti, A. Calculation of Intermolecular Interaction Energies by Direct Numerical Integration over Electron Densities. I. Electrostatic and Polarization Energies in Molecular Crystals. J. Phys. Chem. B 2002, 106, 4145–4154. [Google Scholar] [CrossRef]
- Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Zakrezewski, V. G.; Montgomery, J. A.; Stratmann, R. E.; Burant, J. C.; Dappich, S.; Millam, J. M.; Daniels, A. D.; Kudin, K. N.; Strain, M. C.; Farkas, O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennucci, B.; Pomelli, C.; Adamo, C.; Clifford, S.; Ochterski, J.; Petersson, G.; Aayala, P. Y.; Cui, Q.; Morokuma, K.; Malick, D. K.; Rubuck, A. D.; Raghavachari, K.; Foresman, J. B.; Cioslowski, J.; Ortiz, J. V.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Gomperts, R.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Gonzalez, C.; Challacombe, M.; Gill, P. M. W.; Johnson, B. G.; Chen, W.; Wong, M. W.; Andres, J. L.; Head-Gordon, M.; Replogle, E. S.; Pople, J. A. Gaussian 98, Revision A.7; Gaussian, Inc.: Pittsburgh, PA, 1998. [Google Scholar]
- Morokuma, K. Molecular Orbital Studies of Hydrogen Bonds. III. C=O---H4O Hydrogen Bond in H2CO---H2O and H2CO---2H2O. J. Chem. Phys. 1971, 55, 1236–1244. [Google Scholar] [CrossRef]
- Morokuma, K.; Kitaura, K. Chemical Applications of Atomic and Molecular Electrostatic Potentials; Politzer, P., Truhlar, D. G., Eds.; Plenum: New York, 1981; Chapter 10; pp. 215–242. [Google Scholar]
- Stevens, W. J.; Fink, W. H. Frozen Fragment Reduced Variational Space Analysis of Hydrogen Bonding Interactions. Application to Water Dimer. Chem. Phys. Lett. 1987, 139, 15–22. [Google Scholar] [CrossRef]
- Leininger, M. L.; Nielsen, I. M. B.; Colvin, M. E.; Janssen, C. L. Accurate Structures and Binding Energies for Stacked Uracil Dimers. J. Phys. Chem. A 2002, 106, 3850–3854. [Google Scholar] [CrossRef]
- Politzer, P.; Ma, Y. Noncovalent Intermolecular Energetics: RDX Crystal. submitted to. Int. J. Quantum Chem.
- Sorescu, D. C.; Rice, B. M.; Thompson, D. L. Energetic Materials. Part I. Decomposition, Crystal and Molecular Properties; Politzer, P., Murray, J. S., Eds.; Elsevier: Amsterdam, 2003; pp. 125–184. [Google Scholar]
- Hellmann, H. Einfuhrung in die Quantenchemie; Franz Deuticke: Leipzig, 1937. [Google Scholar]
- Feynman, R. P. Forces in Molecules. Phys. Rev. 1939, 56, 340–343. [Google Scholar] [CrossRef]
- Berlin, T. Binding Regions in Diatomic Molecules. J. Chem. Phys. 1951, 19, 208–213. [Google Scholar] [CrossRef]
- Foldy, L. L. A Note on Atomic Binding Energies. Phys. Rev. 1951, 83, 397–399. [Google Scholar] [CrossRef]
- Gaspar, R. Many-Electron Problems. I. Energy Relations in the Theory of Neutral Atoms. Int. J. Quantum Chem. 1967, I, 139–145. [Google Scholar] [CrossRef]
- Politzer, P.; Parr, R. G. Some New Energy Formulas for Atoms and Molecules. J. Chem. Phys. 1974, 61, 4258–4262. [Google Scholar] [CrossRef]
- Politzer, P. Fundamental World of Quantum Chemistry. A Tribute to the Memory of Per-Olov Lowdin; Vol. I, Brandas, E. J., Kryachko, E. S., Eds.; Kluwer: Dordrecht, 2003; pp. 631–638. [Google Scholar]
- Wilson, E. B., Jr. Four-Dimensional Electron Density. J. Chem. Phys. 1962, 36, 2232–2233. [Google Scholar] [CrossRef]
- Hurley, A. C. The Electrostatic Calculation of Molecular Energies. I - III. Proc. Roy. Soc. (London) 1954, A226, 170-178, 179-192, 193-205. [Google Scholar] [CrossRef]
- Bader, R. F. W. The Use of the Hellmann-Feynman Theorem to Calculate Molecular Energies. Can. J. Chem. 1960, 38, 2117–2127. [Google Scholar] [CrossRef]
- Bader, R. F. W. The Force Concept in Chemistry; Deb, B. M., Ed.; Van Nostrand Reinhold: New York, 1981; Chapter 2; pp. 39–136. [Google Scholar]
- Ma, Y.; Politzer, P. Determination of Noncovalent Interaction Energies from Electronic Densities. J. Chem. Phys. 2004, 120, 8955–8959. [Google Scholar]
- Xantheas, S. S. On the Importance of the Fragment Relaxation Energy Terms in the Estimation of the Basis Set Superposition Error Correction to the Intermolecular Interaction Energy. J. Chem. Phys. 1996, 104, 8821–8824. [Google Scholar] [CrossRef]
- Peterson, K. A.; Dunning, T. H., Jr. Benchmark Calculations with Correlated Molecular Wave Functions. VII. Binding Energy and Structure of the HF Dimer. J. Chem. Phys. 1995, 102, 2032–2041. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Uchimaru, T.; Matsumura, K.; Mikami, M.; Tanabe, K. Effects of Basis Set and Electron Correlation on the Calculated Interaction Energies of Hydrogen Bonding Complexes: MP2/cc-pV5Z Calculations of H2O--MeOH, H2O--Me2O, H2O--H2CO, MeOH--MeOH, and HCOOH--HCOOH Complexes. J. Chem. Phys. 1999, 110, 11906–11910. [Google Scholar] [CrossRef]
- Bukowski, R.; Szalewicz, K.; Chabalowski, C. F. Ab Initio Interaction Potentials for Simulations of Dimethylnitramine Solutions in Supercritical Carbon Dioxide with Cosolvents. J. Phys. Chem. A 1999, 103, 7322–7340. [Google Scholar] [CrossRef]
© 2004 by MDPI (http://www.mdpi.org).
Share and Cite
Ma, Y.; Politzer, P. Electronic Density Approaches to the Energetics of Noncovalent Interactions. Int. J. Mol. Sci. 2004, 5, 130-140. https://doi.org/10.3390/i5040130
Ma Y, Politzer P. Electronic Density Approaches to the Energetics of Noncovalent Interactions. International Journal of Molecular Sciences. 2004; 5(4):130-140. https://doi.org/10.3390/i5040130
Chicago/Turabian StyleMa, Yuguang, and Peter Politzer. 2004. "Electronic Density Approaches to the Energetics of Noncovalent Interactions" International Journal of Molecular Sciences 5, no. 4: 130-140. https://doi.org/10.3390/i5040130
APA StyleMa, Y., & Politzer, P. (2004). Electronic Density Approaches to the Energetics of Noncovalent Interactions. International Journal of Molecular Sciences, 5(4), 130-140. https://doi.org/10.3390/i5040130




