Scalar Relativistic Study of the Structure of Rhodium Acetate
Abstract
:Introduction
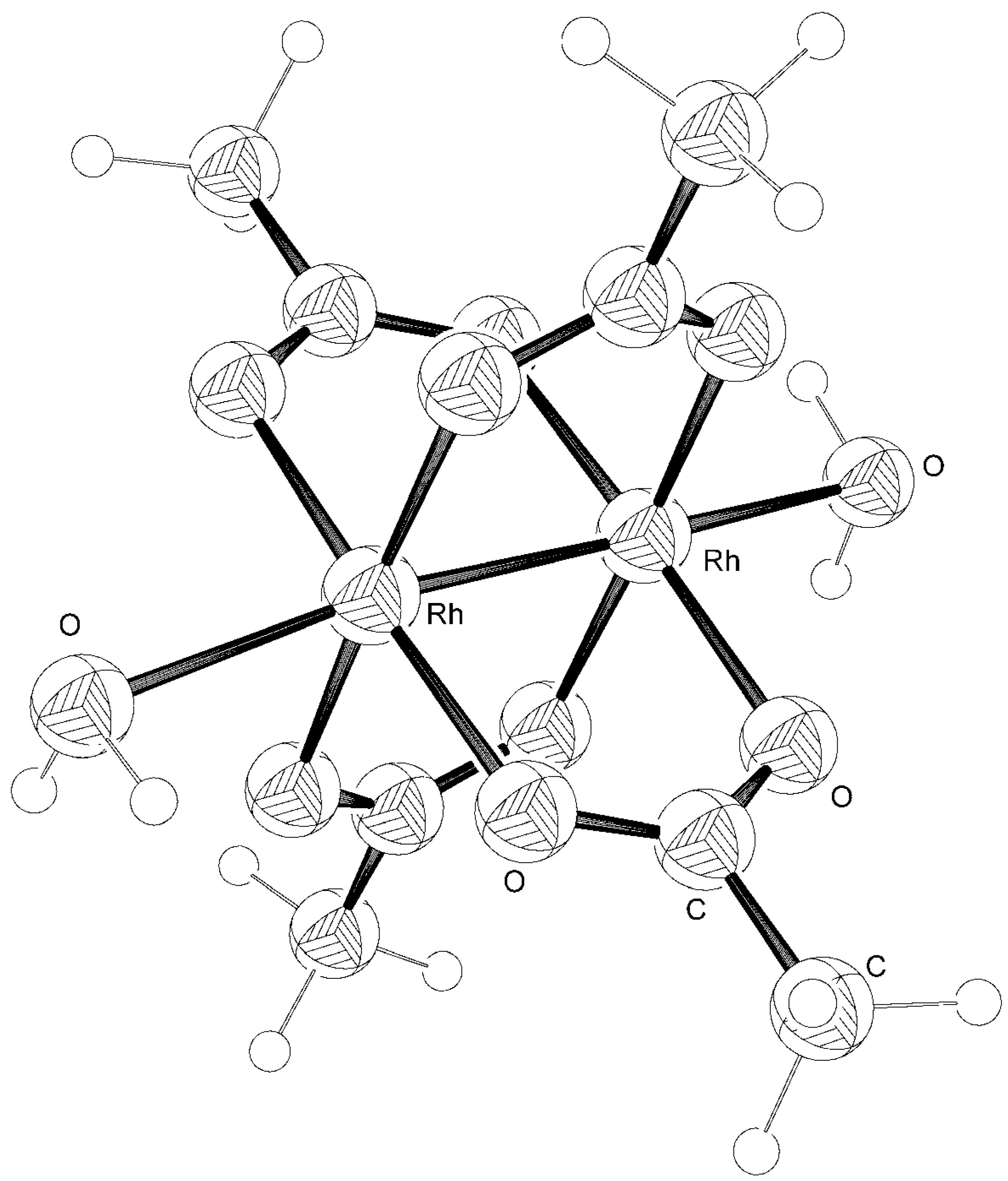
Computations
Results and Discussion
| Functional | PBE | PW91-PW91 | BOP | BLYP |
| Relativistic Bond Length | 2.411 | 2.409 | 2.439 | 2.438 |
| Non-Relativistic Bond Length | 2.421 | 2.42 | 2.451 | 2.449 |
| Functional | PBE | rPBE | revPBE | PW91-PW91* | BLYP | BP |
| ZORA Relativistic Bond Length | 2.402 | 2.411 | 2.407 | 2.401 | 2.430 | 2.405 |
| Non-Relativistic Bond Length | 2.416 | 2.428 | 2.425 | 2.416 | 2.446 | 2.420 |
| Functional | BP | BLYP | B88-PW91 | PW91-PW91 |
| Effective Core Potential | ||||
| Stevens-Krauss, Relativistic | 2.423 | 2.443 | 2.423 | 2.420 |
| Christiansen-Ermler, Relativistic | 2.393 | 2.413 | 2.393 | 2.392 |
| Hay-Wadt, Relativistic | 2.420 | 2.440 | 2.420 | 2.419 |
| Stuttgart, Relativistic | 2.415 | 2.436 | 2.415 | 2.415 |
| DGAUSS, Non-Relativistic | 2.471 | 2.488 | 2.466 | 2.466 |
| All Electron, Non-Relativistic (no ECP) | 2.418 | 2.439 | 2.417 | 2.416* |
Conclusions
Acknowledgment
References
- Doyle, M. P.; McKervey, M. A.; Ye, T. Modern Catalytic Methods for Organic Synthesis with Diazo Compounds from Cyclopropanes to Ylides; John Wiley & Sons: New York, 1998. [Google Scholar]
- Cotton, F. A.; DeBoer, B. G.; Laprade, M. D.; Pipal, J. R.; Ucko, D. A. Acta Crystallogr. 1971, B27, 1664.
- Norman, J. G., Jr.; Kolari, H. J. J. Am. Chem. Soc. 1978, 100, 791. Nakatsuji, H.; Onishi, Y.; Ushio, J.; Yonezawa, T. Inorg. Chem. 1983, 22, 1623–1630. Mougenot, P.; Demuynck, J.; Benard, M. Chem. Phys. Lett. 1987, 136, 279–282. Nakatsuji, H.; Ushio, J.; Kanda, K.; Onishi, Y.; Kawamura, T.; Yonezawa, T. Chem. Phys. Lett. 1981, 79, 299–304. Rodriguez-Garcia, C.; Gonzalez-Blanco, O.; Oliva, A.; Ortuno, R. M.; Branchadell, V. Eur. J. Inog. Chem. 2000, 5, 1073–1078. Doyle, M. P.; Winchester, W. R.; Hoorn, J. A. A.; Lynch, V.; Simonsen, S. H.; Ghosh, R. J. Am. Chem. Soc. 1993, 125, 9968–9978. Padwa, A.; Snyder, J. P.; Curtis, E. A.; Sheehan, S. M.; Worsencroft, K. J.; Kappe, C.O. J. Am. Chem. Soc. 2000, 122, 8155–8167. Morehead, A. T., Jr. Mechanistic Investigation of the Dirhodium(II) Catalyzed Decomposition of Diazocarbonyl Compounds. Ph. D. dissertation, Duke University, Durham, NC, 1996. [Google Scholar]
- Cotton, F. A.; Feng, X. J. Am. Chem. Soc. 1998, 120, 3387–3397.
- Pyykko, P. Chem. Rev. 1988, 88, 563–594. Balasubramanian, K. Relativistic Effects in Chemistry, Part A Theory and Techniques; John Wiley and Sons: New York, 1997. [Google Scholar]
- Desclaux, J. P. Atom. Data Nucl. Data 1973, 12, 311. [CrossRef]
- Diefenbach, A.; Bickelhaupt, F. M. J. Chem. Phys. 2001, 115, 4030.
- Faegri, K., Jr.; Saue, T. J. Chem. Phys. 2001, 115, 2456–2464.
- Baerends, E. J.; Autschbach, J.A.; Bérces, A.; Bo, C.; Boerrigter, P. M.; Cavallo, L.; Chong, D.P.; Deng, L.; Dickson, R. M.; Ellis, D. E.; Fan, L.; Fischer, T. H.; Fonseca Guerra, C.; van Gisbergen, S. J. A.; Groeneveld, J. A.; Gritsenko, O. V.; Grüning, M.; Harris, F. E.; van den Hoek, P.; Jacobsen, H.; van Kessel, G.; Kootstra, F.; van Lenthe, E.; Osinga, V. P.; Patchkovskii, S.; Philipsen, P. H. T.; Post, D.; Pye, C. C.; Ravenek, W.; Ros, P.; Schipper, P. R. T.; Schreckenbach, G.; Snijders, J. G.; Sola, M.; Swart, M.; Swerhone, D.; te Velde, G.; Vernooijs, P.; Versluis, L.; Visser, O.; van Wezenbeek, E.; Wiesenekker, G.; Wolff, S. K.; Woo, T. K.; Ziegler, T. ADF2002.03; SCM. Theoretical Chemistry, Vrije Universiteit: Amsterdam, The Netherlands. http://www.scm.com. te Velde, G.; Bickelhaupt, F.M.; van Gisbergen, S.J.A.; Fonseca Guerra, C.; Baerends, E.J.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] Fonseca Guerra, C.; Snijders, J. G.; te Velde, G.; Baerends, E. J. Theor. Chem. Acc. 1998, 99, 391.
- Delley, B. Int. J. Quantum. Chem. 1998, 69, 423–433.
- van Lenthe, E.; Baerends, E. J.; Snijders, J. G. J. Chem. Phys. 1993, 99, 4597. van Lenthe, E.; Baerends, E. J.; Snijders, J. G. J. Chem. Phys. 1994, 101, 9783. van Lenthe, E.; Ehlers, A. E.; Baerends, E. J. J. Chem. Phys. 1999, 110, 8943. van Lenthe, E.; Snijders, J. G.; Baerends, E. J. J. Chem. Phys. 1996, 105, 6505. van Lenthe, E.; van Leeuwen, R.; Baerends, E. J.; Snijders, J. G. Int. J. Quantum Chem. 1996, 57, 281.
- Stevens, W. J.; Krauss, M.; Basch, H.; Jasien, P. G. Can. J. Chem. 1992, 70, 612–629.
- LaJohn, L. A.; Christiansen, P. A.; Ross, R. B.; Atashroo, T.; Ermler, W. C. J. Chem. Phys. 1987, 87, 2812–2824.
- Wadt, W. R.; Hay, P. J. J. Chem. Phys. 1985, 82, 284–298. Hay, P. J.; Wadt, W. R. J. Chem. Phys. 1985, 82, 299–310.
- Kuchle, W.; Dolg, M.; Stoll, H.; Preuss, H. Mol. Phys. 1991, 74, 1245–1263.
- Chen, H.; Krasowski, M.; Fitzgerald, G. J. Chem. Phys. 1998, 11, 8710–8717.
- Tsuneda, T.; Hirao, K. Chem. Phys. Lett. 1997, 268, 510–520.
- Perdew, J. P.; Burke, K.; Ernzerhof, M. Phys. Rev. Lett. 1996, 77, 3865–3868. [CrossRef]
- Hammer, B.; Hansen, L. B.; Norskov, J. K. Phys. Rev. 1999, B59, 7413.
- Zhang, Y.; Yang, W. Phys. Rev. Lett. 1998, 80, 890.
- Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Zakrzewski, V. G.; Montgomery, J. A., Jr.; Stratmann, R. E.; Burant, J. C.; Dapprich, S.; Millam, J. M.; Daniels, A. D.; Kudin, K. N.; Strain, M. C.; Farkas, O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennucci, B.; Pomelli, C.; Adamo, C.; Clifford, S.; Ochterski, J.; Petersson, G. A.; Ayala, P. Y.; Cui, Q.; Morokuma, K.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Cioslowski, J.; Ortiz, J. V.; Baboul, A. G.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Gomperts, R.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Andres, J. L.; Gonzalez, C.; Head-Gordon, M.; Replogle, E. S.; Pople, J. A. Gaussian 98; Revision A.11.3; Gaussian, Inc.: Pittsburgh, PA, 2002. [Google Scholar]
- Cotton, F. A.; Felthouse, T. R. Inorg. Chem. 1982, 21, 2667–2675.
© 2004 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Williams, S.D.; Edwards, E.E. Scalar Relativistic Study of the Structure of Rhodium Acetate. Int. J. Mol. Sci. 2004, 5, 67-74. https://doi.org/10.3390/i5020067
Williams SD, Edwards EE. Scalar Relativistic Study of the Structure of Rhodium Acetate. International Journal of Molecular Sciences. 2004; 5(2):67-74. https://doi.org/10.3390/i5020067
Chicago/Turabian StyleWilliams, Stephen D., and Emily E. Edwards. 2004. "Scalar Relativistic Study of the Structure of Rhodium Acetate" International Journal of Molecular Sciences 5, no. 2: 67-74. https://doi.org/10.3390/i5020067
APA StyleWilliams, S. D., & Edwards, E. E. (2004). Scalar Relativistic Study of the Structure of Rhodium Acetate. International Journal of Molecular Sciences, 5(2), 67-74. https://doi.org/10.3390/i5020067




