Introduction
The quantum mechanical behavior of hydrogen and hydrogen-like (hydrogenic) atoms is well understood and is standard regimen in introductory quantum mechanics texts [
1,
2,
3]. Since the early part of the last century the behavior of
confined atoms has been of interest. Early analytical results for hydrogen confined within a non-interacting impenetrable spherical cavity [
4,
5] (with infinite potential outside the sphere so the wave function vanishes on its surface) showed that as the size of the confining sphere lessens the energy levels raise, and there ultimately comes a point where the electron becomes delocalized, behaving somewhat like a particle in a sphere [
5]. Although of general theoretical interest, such calculations had little practical importance until the relatively recent discovery of Fullerenes [
6] and other structures capable of quantum confinement of atoms, that is, localizing atoms such that their electronic states are considerably altered.
Obviously a non-interacting spherical cage does not provide an acceptable model for a Fullerene, and a full density functional theory treatment with the intent of obtaining an effective valence electron interaction potential is exceedingly difficult. So, in many cases, a “jellium-shell” model is employed in order to simulate the attraction of an electron with the cage, which involves a spherical step function potential well. Such models have been utilized to calculate the photoabsorption spectrum of C
60 as well as that for endohedral Xe and Ba [
7]. In addition, the jellium-shell model has been used to reproduce certain aspects of the photoionization cross section of C
60 [
8] and it has been successfully applied to other endohedral Fullerene systems [
9,
10,
11].
With the recent surge in knowledge about novel nanoscale devices there is currently intense scientific interest in a variety of confining systems to which both relativistic and non-relativistic quantum mechanical formalisms may be applied with varying degrees of success [
12] as well as in molecular species confined within Fullerenes [
13]. However, some relevant recent works on confined hydrogen - the most simple system to study theoretically - nicely compliment the earliest papers [
4,
5]. For example, variational perturbation theory is used to study the positional behavior of confined H [
14] and a numerical solution to Schrödinger’s Equation is employed to examine the behavior of confined H which is isotropically compressed [
15]. In the interest of better understanding the behavior of species encapsulated within Fullerenes, a jellium shell model has been used in a recent study of the behavior of H confined at the center of a deformable cage [
16], showing outstanding agreement with experiment and other theoretical results.
Interestingly, results of various investigations suggest that the encapsulated species might reside off-center [
13], especially in the case where the confining cage is attractive, but not repulsive. Since the studies of confined and encapsulated hydrogen are of great interest, it is beneficial to generalize the existing model to any encapsulated system with the effective atomic/ionic nucleus placed at some arbitrary position within the encapsulating shell. The purpose of the work presented here is to calculate the spectral behavior of on-center as well as off-center hydrogenic species (with one valence electron) in a spherical jellium-shell. Particular emphasis is placed on H@C
60 and Mg
+@C
60 in order to not only provide comparisons and contrasts with existing work on the relatively well-explored encapsulated hydrogen system, but to also utilize the computational method for the relatively new terrain of encapsulated magnesium, as recent experimental optical and mass spectroscopic studies of magnesium-Fullerene systems show a small fraction of endohedral complex formation [
17].
Discussion and Conclusions
Before discussing important aspects of the results of this work it is worthwhile to mention how the electronic states for the various species are labeled. In the case of H, the calculated states correspond exactly to the physical atomic states. In the case of Mg
+, however, the physical ground state configuration begins at 3s, while the calculated ground state for its pseudo-hydrogenic model begins at 1s. This occurs because the model involving the pseudopotential ignores detailed electronic structure of the core and effectively washes out some of the radial wavefunction nodes. Therefore the node counter for the pseudo-hydrogenic model is reset at
n=1 for the ground state. The result is a re-labeling of the pseudo-hydrogenic s and p states, as summarized in
Table II. The remainder of the discussion refers to the
calculated Mg
+ states with their
physical labels clarifying, for example, why the
calculated 3s state has no nodes while the
physical 3s state has
n-
l-1=2 nodes; it is really a pseudo-hydrogenic 1s state.
Table II.
Mg+ electronic states and their corresponding pseudo-hydrogenic states.
Table II.
Mg+ electronic states and their corresponding pseudo-hydrogenic states.
Mg+
State | Pseudo-Hydrogenic
State |
|---|
| 3s | 1s |
| 3p | 2p |
| 3d | 3d |
| 4s | 2s |
| 4p | 3p |
| 4d | 4d |
| 4f | 4f |
| 5s | 3s |
| 5p | 4p |
| 5d | 5d |
| 5f | 5f |
| 5g | 5g |
| 6s | 4s |
| 6p | 5p |
| 6d | 6d |
| 6f | 6f |
| 6g | 6g |
| 6h | 6h |
| 7s | 5s |
| 7p | 6p |
| 7d | 7d |
| 7f | 7f |
| 7g | 7g |
| 7h | 7h |
| 8s | 6s |
| 8p | 7p |
| 9s | 7s |
For validation of the computational method presented and valence electron interaction potentials used, species not confined within a Fullerene cage (free species) are first considered. Such simulations entail placement of the atom or ion at the center of the hard spherical shell without the jellium potential present. The radius of the shell is chosen to be
R=50Å and there are
N=3000 radial divisions. The spectra and energy levels of unconfined Mg
+ and H are well known; accepted values as well as our calculated values for several energy levels for both species are shown in
Table III.
Table III.
Accepted and our calculated values for selected energy levels of H [
21] and Mg
+ [
22]. Due to the computational algorithm the series calculated for the
n≥7 states are incomplete. All values are in eV and are calculated so the free electron has energy
E=0. States do not correspond across rows.
Table III.
Accepted and our calculated values for selected energy levels of H [21] and Mg+ [22]. Due to the computational algorithm the series calculated for the n≥7 states are incomplete. All values are in eV and are calculated so the free electron has energy E=0. States do not correspond across rows.
| H State | H
Accepted | H
calculated in
this work | Mg+ State | Mg+
Accepted | Mg+ calculated in
this work |
|---|
| 1s | -13.6057 | -13.6039 | 3s | -15.03527 | -15.03539 |
| | | | 3p | -10.612838 | -10.61292 |
| 2s | -3.40125 | -3.40131 | 3d | -6.171505 | -6.17166 |
| 2p | -3.40125 | -3.40146 | | | |
| | | | 4s | -6.380556 | -6.38061 |
| 3s | -1.51174 | -1.51172 | 4p | -5.039722 | -5.03976 |
| 3p | -1.51174 | -1.51176 | 4d | -3.46617 | -3.46626 |
| 3d | -1.51174 | -1.51175 | 4f | -3.40572 | -3.40562 |
| | | | | | |
| 4s | -0.85035 | -0.85035 | 5s | -3.53071 | -3.53074 |
| 4p | -0.85035 | -0.85037 | 5p | -2.95238 | -2.9524 |
| 4d | -0.85035 | -0.85036 | 5d | -2.21282 | -2.21288 |
| 4f | -0.85035 | -0.85036 | 5f | -2.17949 | -2.17938 |
| | | | 5g | -2.17753 | -2.17742 |
| 5s | -0.54423 | -0.54422 | | | |
| 5p | -0.54423 | -0.54423 | 6s | -2.2405 | -2.24052 |
| 5d | -0.54423 | -0.54423 | 6p | -1.93977 | -1.93978 |
| 5f | -0.54423 | -0.54423 | 6d | -1.53337 | -1.5334 |
| 5g | -0.54423 | -0.54423 | 6f | -1.51339 | -1.51328 |
| | | | 6g | -1.51218 | -1.51207 |
| 6s | -0.37794 | -0.37653 | 6h | -1.51182 | -1.51183 |
| 6p | -0.37794 | -0.37675 | | | |
| 6d | -0.37794 | -0.3771 | 7s | -1.54773 | -1.54774 |
| 6f | -0.37794 | -0.37747 | 7p | -1.37177 | -1.37178 |
| 6g | -0.37794 | -0.37776 | 7d | -1.12459 | -1.12462 |
| 6h | -0.37794 | -0.37799 | 7f | -1.11178 | -1.11167 |
| | | | 7g | -1.11100 | -1.11089 |
| 7s | -0.27766 | -0.25009 | 7h | -1.11072 | -1.11073 |
| 7p | -0.27766 | -0.2525 | | | |
| 7d | -0.27766 | -0.2569 | 8s | -1.13314 | -1.13303 |
| 7f | -0.27766 | -0.26252 | 8p | -1.0213 | -1.0213 |
| 7g | -0.27766 | -0.26835 | | | |
| 7h | -0.27766 | -0.27774 | 9s | -0.86519 | -0.86519 |
The values obtained from the simulation generally have excellent agreement with the accepted ones [
21], and the patterns of variation from experimental results can give considerable insight into the workings and limitations of our model. The degeneracy in hydrogen is split by the large spherical hard shell because various angular momentum states with differing symmetry are affected uniquely by the boundary conditions imposed on the hard spherical shell. Such results agree well with the much more pronounced selective alterations of various wave functions under the influence of the deformable, prolate-ellipsoidal confining cage of Connerade and co-workers [
16]. Likewise, those states corresponding to higher electronic probability densities at larger distances from the origin are affected more profoundly by a spherical cutoff. Magnesium energy levels are naturally non-degenerate in
but its calculated spectrum has a higher percent error than does hydrogen because the magnesium has a broader wave function that doesn’t go to zero so fast as hydrogen’s does at the shell boundary. Such considerations also explain why higher energy levels have larger percent errors than the smaller ones for a given species. Overall, inspection of the data in
Table III suggests that the calculation method and model used are reasonable, and that the hard spherical shell does not adversely affect the results in a considerable way. Moreover, the valence electron pseudo-potential used for the magnesium ion gives excellent agreement with experiment and therefore seems to be very reasonable over a wide range of energy levels.
The next set of calculations involves modeling endohedral species, so the jellium potential is introduced.
Table IV shows our calculated encapsulated hydrogen and magnesium energy levels, along with those for encapsulated hydrogen obtained from an analytical treatment of a jellium-shell model by Connerade [
16].
Table IV.
Our calculated values for selected energy levels in H and Mg
+ in the jellium-shell cage, along with those for H calculated by Connerade
et al. [
16]. All energies are in eV and calculated so that the free electron has energy
E=0. States do not correspond across rows.
Table IV.
Our calculated values for selected energy levels in H and Mg+ in the jellium-shell cage, along with those for H calculated by Connerade et al. [16]. All energies are in eV and calculated so that the free electron has energy E=0. States do not correspond across rows.
| H State | Calculated
(Endohedral H)
Connerade et al. [16] | Calculated
(Endohedral H)
this work | Mg+ State | Calculated
(Endohedral Mg+)
this work |
|---|
| 1s | -13.616 | -13.6143 | 3s | -15.2064 |
| | | | 3p | -11.5874 |
| 2s | -6.78244 | -6.78127 | 3d | -9.10792 |
| 2p | -6.28502 | -6.28401 | | |
| | | | 4s | -10.2391 |
| 3s | -1.57282 | -1.57318 | 4p | -7.94433 |
| 3p | -1.6803 | -1.68037 | 4d | -6.87706 |
| 3d | -4.73846 | -4.73729 | 4f | -3.51847 |
| | | | | |
| 4s | -0.88192 | -0.88206 | 5s | -3.7327 |
| 4p | -1.04016 | -1.04026 | 5p | -3.29791 |
| 4d | -1.05907 | -1.05912 | 5d | -4.39126 |
| 4f | -2.83312 | -2.83367 | 5f | -2.48727 |
| | | | 5g | -2.41528 |
| 5s | -0.56613 | -0.56621 | | |
| 5p | -0.65131 | -0.65141 | 6s | -2.34147 |
| 5d | -0.62804 | -0.62793 | 6p | -2.06313 |
| 5f | -0.76556 | -0.76555 | 6d | -1.85264 |
| 5g | -0.72233 | -0.7233 | 6f | -1.9166 |
| | | | 6g | -1.63594 |
| 6s | | -0.39234 | 6h | -1.67474 |
| 6p | | -0.43927 | | |
| 6d | | -0.42076 | 7s | -1.61911 |
| 6f | | -0.48961 | 7p | -1.43158 |
| 6g | | -0.50989 | 7d | -1.38456 |
| 6h | | -0.37796 | 7f | -1.32519 |
| | | | 7g | -1.74139 |
| 7s | | -0.26773 | 7h | -1.21262 |
| 7p | | -0.3069 | | |
| 7d | | -0.29267 | 8s | -1.161911 |
| 7f | | -0.34121 | 8p | -1.0555 |
| 7g | | -0.35716 | | |
| 7h | | -0.2734 | 9s | -0.90325 |
In addition,
Figure 1 and
Figure 2 show comparisons of the energy levels with and without encapsulation for hydrogen and magnesium, respectively, and
Figure 3 and
Figure 4 show selected radial wave functions
for the same systems.
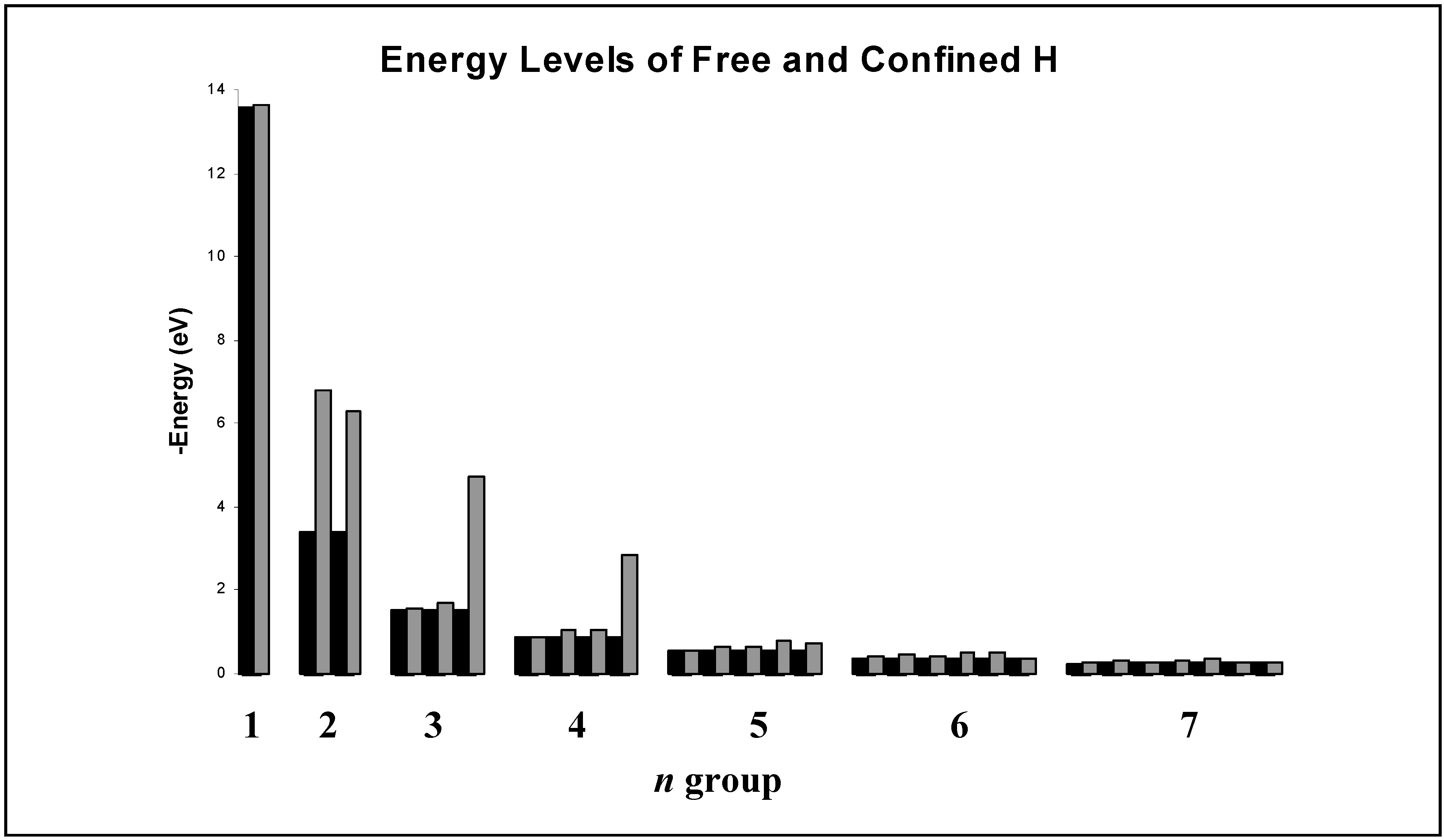
Figure 1.
Comparison of free and encapsulated (“confined”) hydrogen energy levels in eV for n=1-7 as calculated in our work. Results are grouped by principal quantum number n and are arranged within each group by increasing angular momentum quantum number . Free hydrogen energies are in black and those for encapsulated hydrogen are in gray.
Figure 1.
Comparison of free and encapsulated (“confined”) hydrogen energy levels in eV for n=1-7 as calculated in our work. Results are grouped by principal quantum number n and are arranged within each group by increasing angular momentum quantum number . Free hydrogen energies are in black and those for encapsulated hydrogen are in gray.
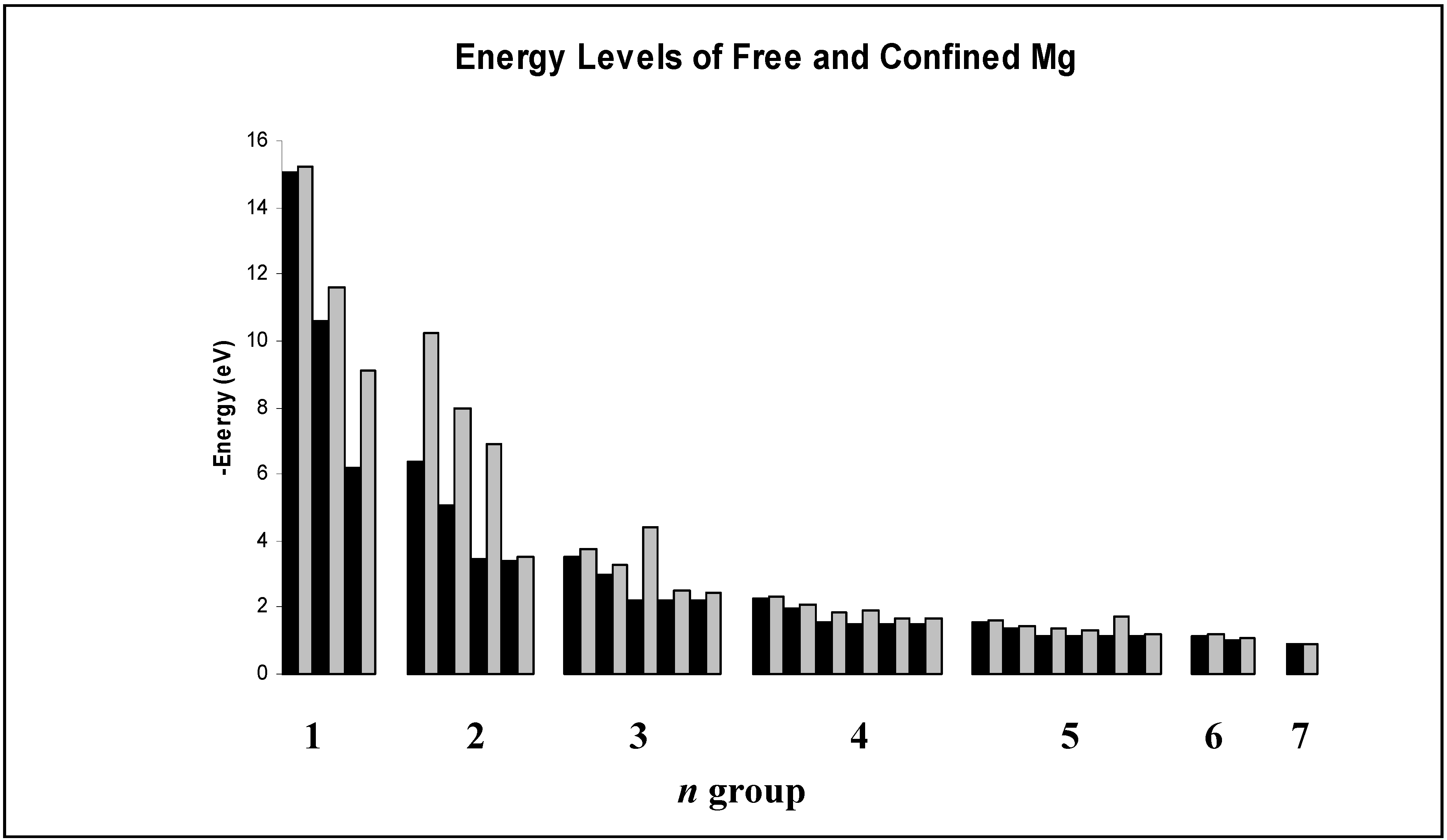
Figure 2.
Comparison of energy levels in eV for free and encapsulated magnesium as calculated in our work. Format is the same as in
Figure 1.
Figure 2.
Comparison of energy levels in eV for free and encapsulated magnesium as calculated in our work. Format is the same as in
Figure 1.
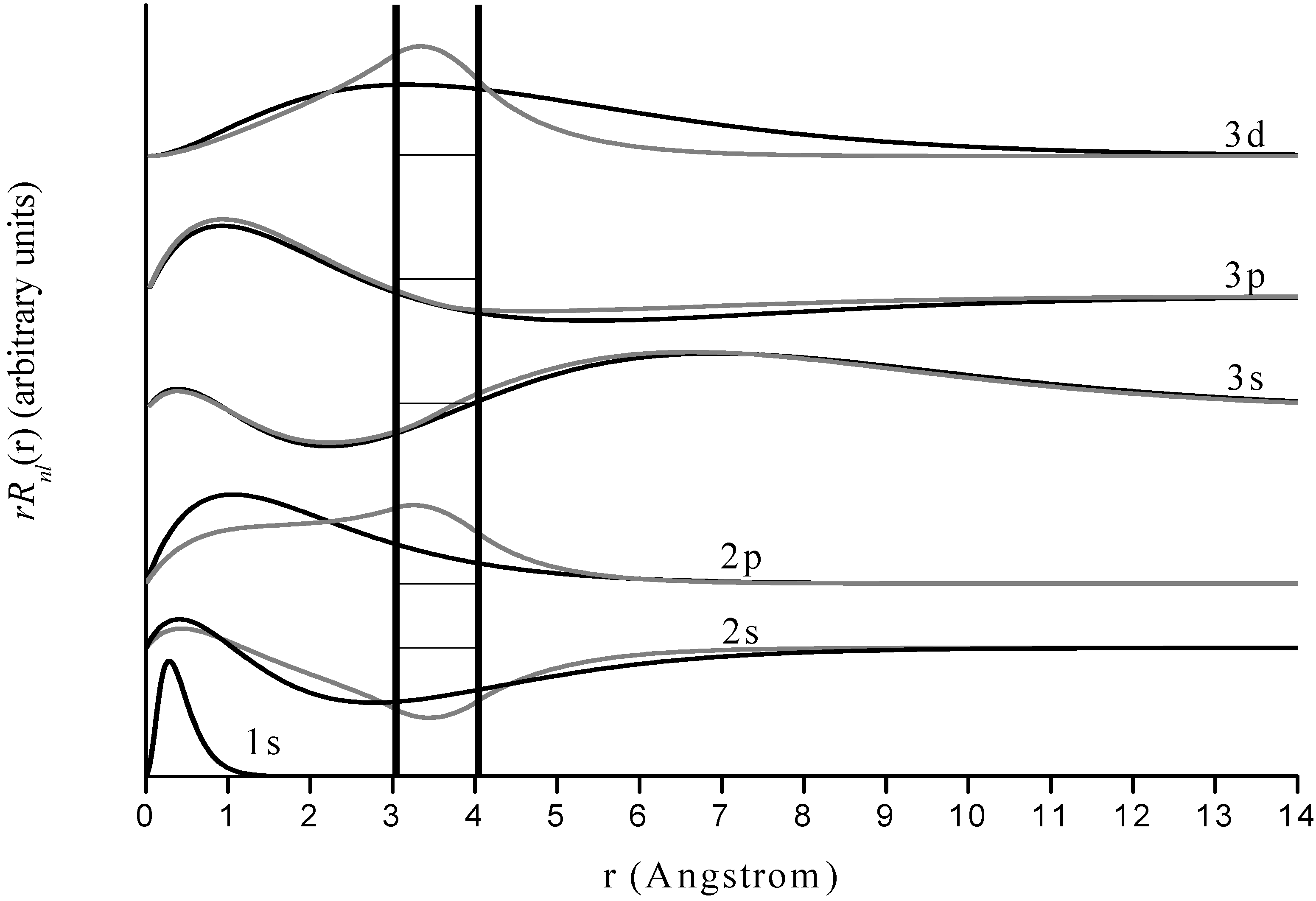
Figure 3.
Radial wave functions of free and encapsulated hydrogen for n=1-3. Results for the former are in black and for the latter in gray. The horizontal axis is distance from the nucleus in Angstroms and the vertical axes are arbitrary but identical for both encapsulated and free species for a given quantum state. The boundaries of the jellium-shell are represented by vertical black lines. Various pairs of states are normalized and offset by different vertical amounts for visual clarity, and dashed horizontal lines within the jellium boundary indicate the respective wave function zeroes.
Figure 3.
Radial wave functions of free and encapsulated hydrogen for n=1-3. Results for the former are in black and for the latter in gray. The horizontal axis is distance from the nucleus in Angstroms and the vertical axes are arbitrary but identical for both encapsulated and free species for a given quantum state. The boundaries of the jellium-shell are represented by vertical black lines. Various pairs of states are normalized and offset by different vertical amounts for visual clarity, and dashed horizontal lines within the jellium boundary indicate the respective wave function zeroes.
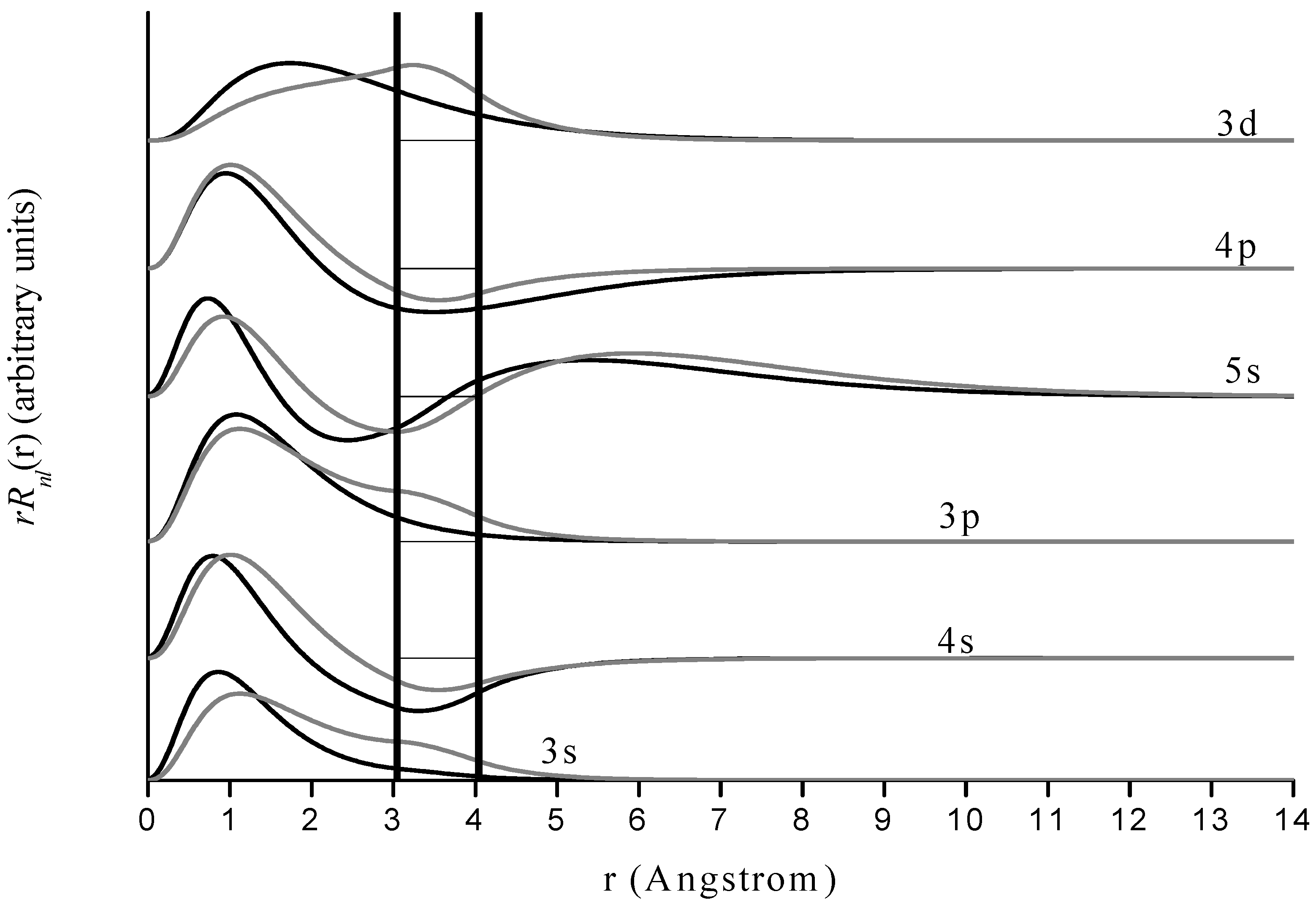
Figure 4.
Radial wave functions
of free and encapsulated magnesium for states corresponding to those for hydrogen in
Figure 3. Format is the same as in
Figure 3 but vertical scales do not correspond.
Figure 4.
Radial wave functions
of free and encapsulated magnesium for states corresponding to those for hydrogen in
Figure 3. Format is the same as in
Figure 3 but vertical scales do not correspond.
Our results for encapsulated H agree well with Connerade’s, suggesting that the jellium-shell model utilized in this study yields reasonable results in the context of other similar models. Most of the hydrogen energy levels are altered only slightly by encapsulation, with the exception of some of those corresponding to higher n and highest angular momentum () states within a given n level. Inspection of the wave functions shows that the energy levels are altered considerably in two types of situations. The first case includes those states where the electron probability density for the free species is near a maximum inside the jellium-shell. Examples are the 2s and 3d states. Such a consideration makes obvious sense because the jellium-shell is affecting the electron in a region of space where it would tend to spend most of its time. The second case is when the free species electron probability density is not near a maximum inside the cage but the shell induces a global maximum electron probability density inside it. Examples include the 2p state, and the corresponding physical interpretation is that the attractive cage is causing the electron to spend most of its time where the confining potential can affect it. The 1s state practically vanishes throughout the cage radius, so the corresponding wave function and energy level are virtually unaffected by confinement. The same is true for other states having a zero within or near the cage.
The behavior of magnesium is quite similar to that of hydrogen, with an interesting difference. Since the 3s wave function of magnesium vanishes much more slowly with increasing r than does the corresponding (1s) state for hydrogen, it does not vanish within the cage so encapsulation does have an effect on that state for magnesium. However there is neither a probability density maximum near the cage nor does the cage induce a global maximum in probability density within it. Hence, even though the cage deforms the wave function and induces a larger probability density within the cage than is present in the free species, the 1s energy level is still almost unaffected by its presence. Other examples are the 3p and 5s states. We emphasize that for Mg+ one must be very careful with interpretation of the results because of the re-labeling of the s and p states discussed earlier. We suspect that the results for encapsulation have physical significance due to the close agreement of the free Mg+ calculations and the accepted energy levels. However, it could be that the presence of more nodes in the physical s and p states than in the corresponding pseudo-hydrogenic states may have some effect on spectral changes in the encapsulated species, especially when there are nodes or anti-nodes of the wave function within the jellium shell.
The calculations for the off-center hydrogen take considerable computational time and memory and are thus limited in scope. Investigations of off-center hydrogen reveal that the lowest energy for the system occurs when the hydrogen atom sits slightly off-center at around a=0.1 Å (2.8% of the cage radius) and has a value of around –14.01 eV. In addition there seems to be some undulation present in the ground state energy as the nuclear offset varies, which is not well understood. Preliminary off-center calculations suggest that p states have no off-center minima. Off-center calculations are not presented for magnesium because, due to the broadness of its wave functions, radial and colatitudinal partitioning yielding sufficient accuracy in calculation was not possible.