Vertical Ionization Energies of α-L-Amino Acids as a Function of Their Conformation: an Ab Initio Study
Abstract
:Introduction
Computational tools and conformation choice
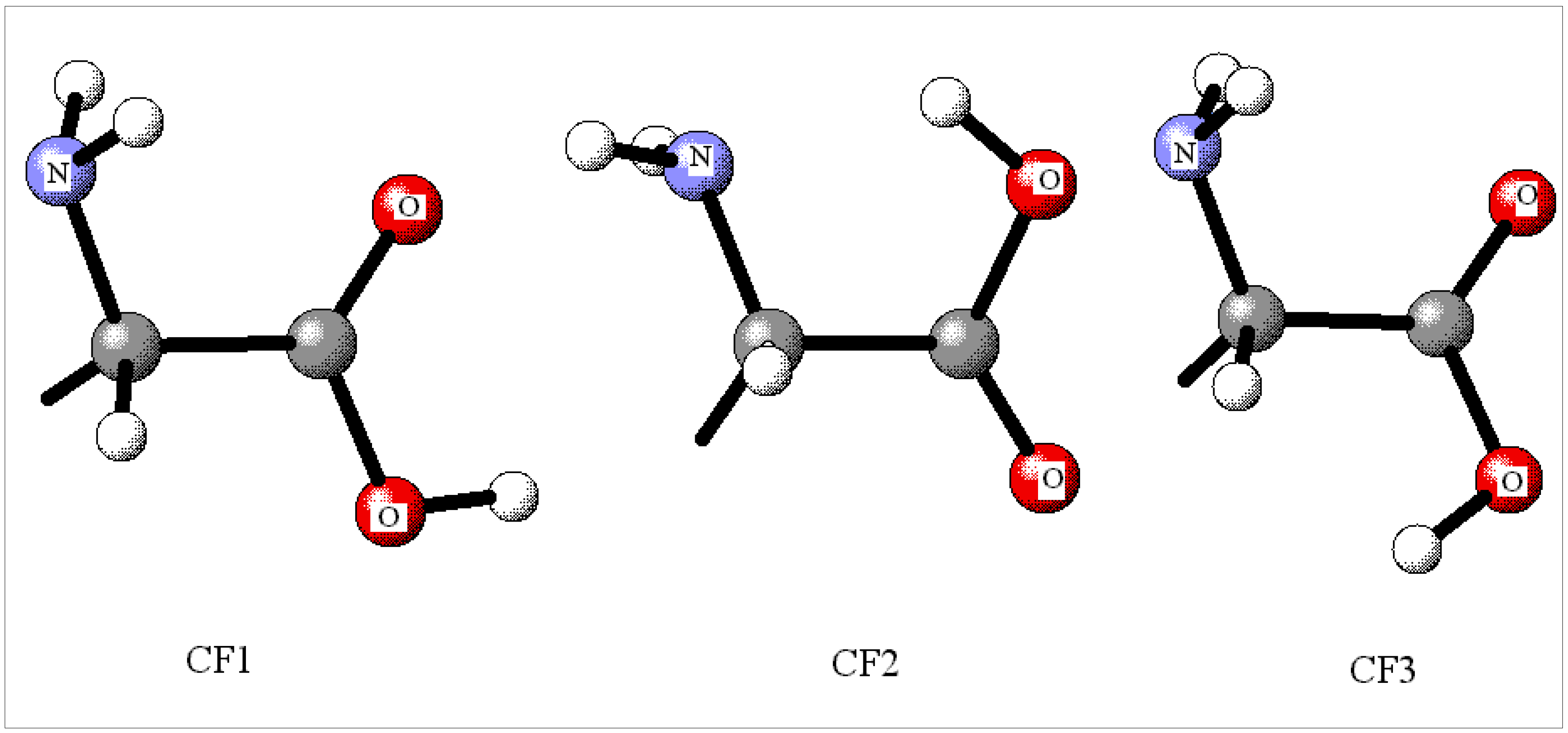
Influence of the electronic correlation description level
| Amino acid | conformation | B3LYP//B3LYP | QCISD//QCISD [CCSD//QCISD, CCSD(T)//QCISD] | MP2//MP2 |
|---|---|---|---|---|
| Ala | CF1 | 1.64 | 0.0 | 0.0 |
| CF2 | 0.0 | 4.27 | 2.52 | |
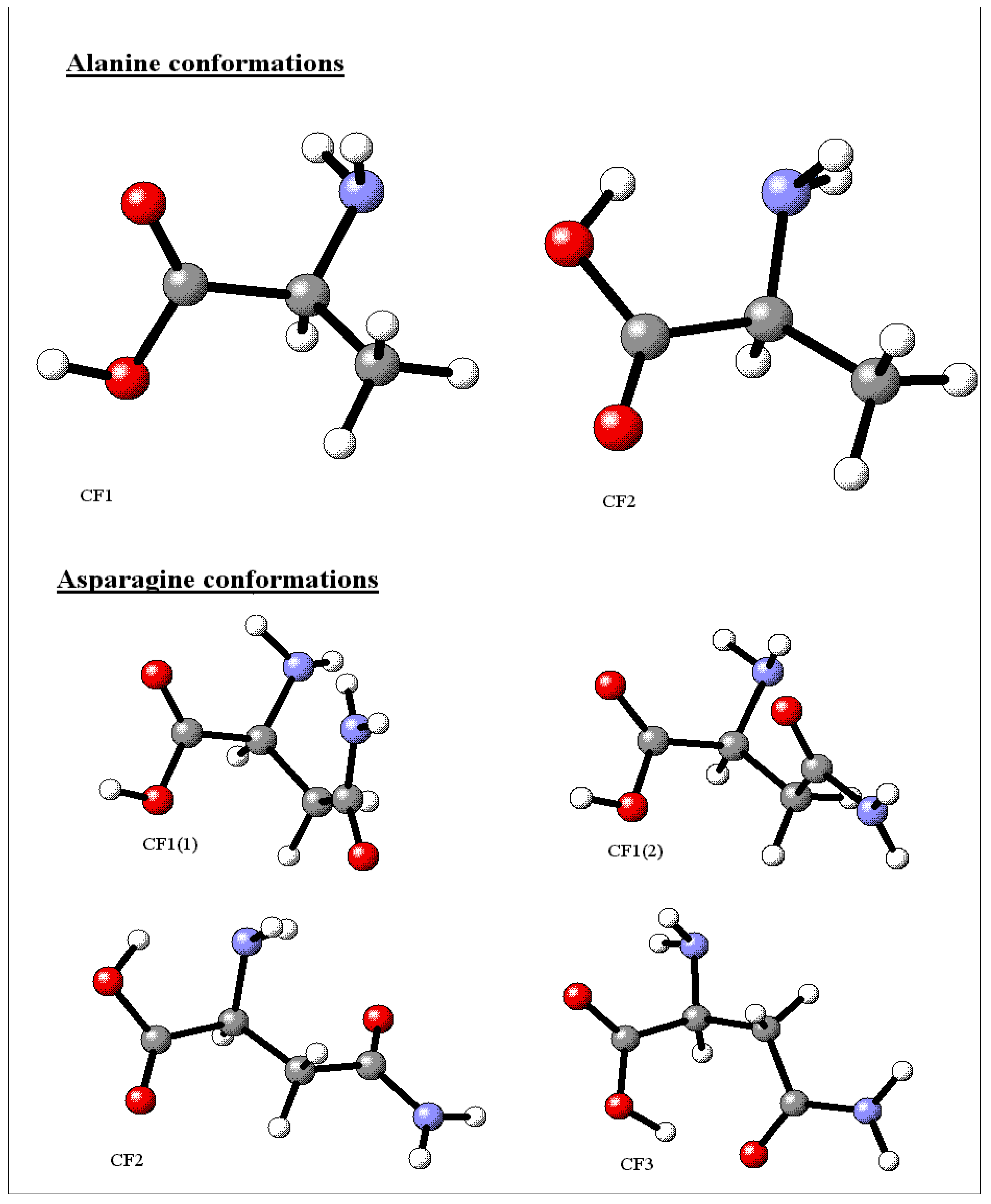
| Asn | CF1(1) | 8.19 | 2.62 [2.67, 1.81] | 0.32 |
| CF1(2) | 9.07 | 0.0 [0.0, 0.13] | 0.0 | |
| CF2 | 0.0 | 0.83 [0.85, 0.0] | 0.04 | |
| CF3 | 0.44 | 3.37 [3.52, 2.24] | 2.64 | |
| Lys | CF1 | 15.91 | ND | 15.01 |
| CF2(1) | 3.80 | ND | 8.14 | |
| CF2(2) | 11.49 | ND | 16.44 | |
| CF3 | 0.0 | ND | 0.0 | |
| Trp | CF1 | 9.99 | ND | 4.84 |
| CF2(1) | 0.0 | ND | 0.0 | |
| CF2(2) | 7.20 | ND | 12.09 | |
| Tyr | CF1 | 6.54 | ND | 0.06 |
| CF2(1) | 0.0 | ND | 0.0 | |
| CF2(2) | 3.41 | ND | 6.93 | |
| Arg | CF1(1) | 15.65 | ND | 12.83 |
| CF1(2) | 24.08 | ND | 25.08 | |
| CF1(3) | 15.32 | ND | 17.92 | |
| CF2 | 0.0 | ND | 0.0 | |
| CF3 | 0.41 | ND | 3.24 |
Choice of the virtual orbital space in the OVGF calculation
| conformation | # of IE | OVGF | Koopmans | MP2 | QCISD | ||
|---|---|---|---|---|---|---|---|
| RG1 | RG2 | FC | |||||
| Gly-CF1 | IE1 | 9.82 | 9.55 | 9.73 | 11.17 | ||
| IE2 | 11.16 | 10.87 | 11.09 | 12.61 | |||
| IE3 | 11.93 | 12.03 | 12.12 | 13.17 | |||
| Gly-CF2 | IE1 | 9.98 | 9.72 | 9.95 | 11.41 | ||
| IE2 | 11.11 | 11.20 | 11.32 | 12.39 | |||
| IE3 | 11.29 | 11.03 | 11.20 | 12.71 | |||
| Ala-CF1 | IE1 | 9.67 | 9.45 | 9.56 | 11.07 | 9.75 | 9.46 |
| IE2 | 10.91 | 10.79 | 10.85 | 12.39 | 10.82 | 10.43 | |
| IE3 | 11.80 | 11.92 | 11.97 | 13.08 | 12.26 | 11.69 | |
| Ala-CF2 | IE1 | 9.85 | 9.69 | 9.79 | 11.31 | 10.20 | 9.67 |
| IE2 | 11.07 | 11.18 | 11.23 | 12.39 | 11.68 | 11.02 | |
| IE3 | 11.04 | 10.88 | 10.96 | 12.47 | 10.67 | 10.90 | |
| Asn-CF1(1) | IE1 | 9.31 | 10.69 | 9.99 | |||
| Asn-CF1(2) | IE1 | 9.36 | 10.87 | 9.49 | |||
| Asn-CF2 | IE1 | 9.80 | 11.34 | 9.64 | |||
| Asn-CF3 | IE1 | 9.54 | 11.12 | 9.81 | |||
| Tyr-CF2(1) | IE1 | 7.94 | 8.51 | 8.76 | |||
| Trp-CF2(1) | IE1 | 7.22 | 7.69 | 7.88 | |||
| phenol | IE1 | 7.92 | 7.88 | 8.12 | 8.40 | 8.81 | 8.13 |
| IE2 | 8.70 | 8.67 | 8.90 | 9.17 | 9.35 | 8.95 | |
| IE3 | 11.44 | 11.37 | 11.44 | 12.96 | 11.61 | 11.83 | |
| formamide | IE1 | 10.14 | 10.09 | 10.26 | 11.25 | 10.87 | 10.12 |
| IE2 | 10.36 | 10.17 | 10.37 | 11.65 | 10.20 | 9.82 | |
Labeling and description of some MOs involved in the ionization
The carboxylic head
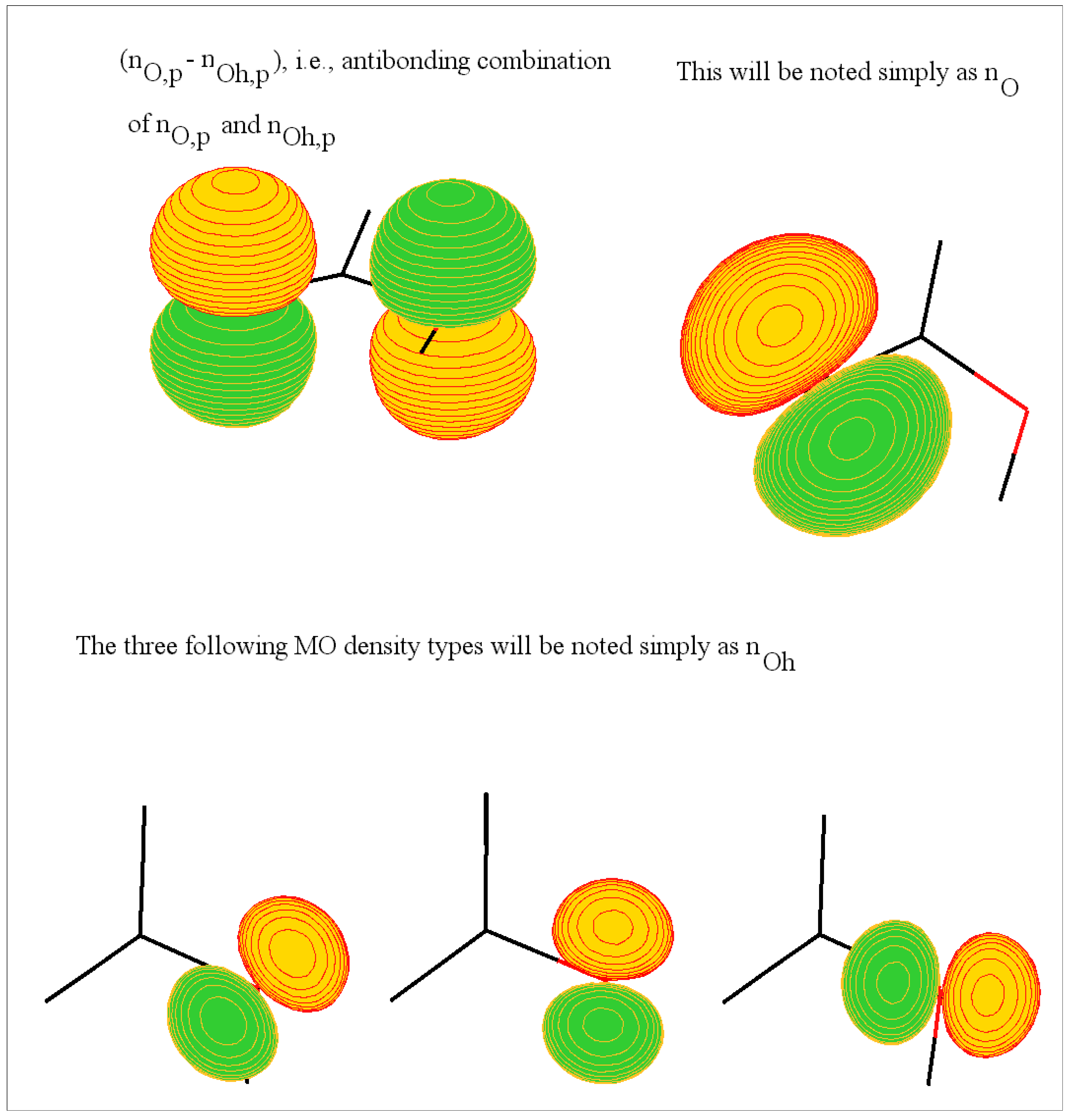
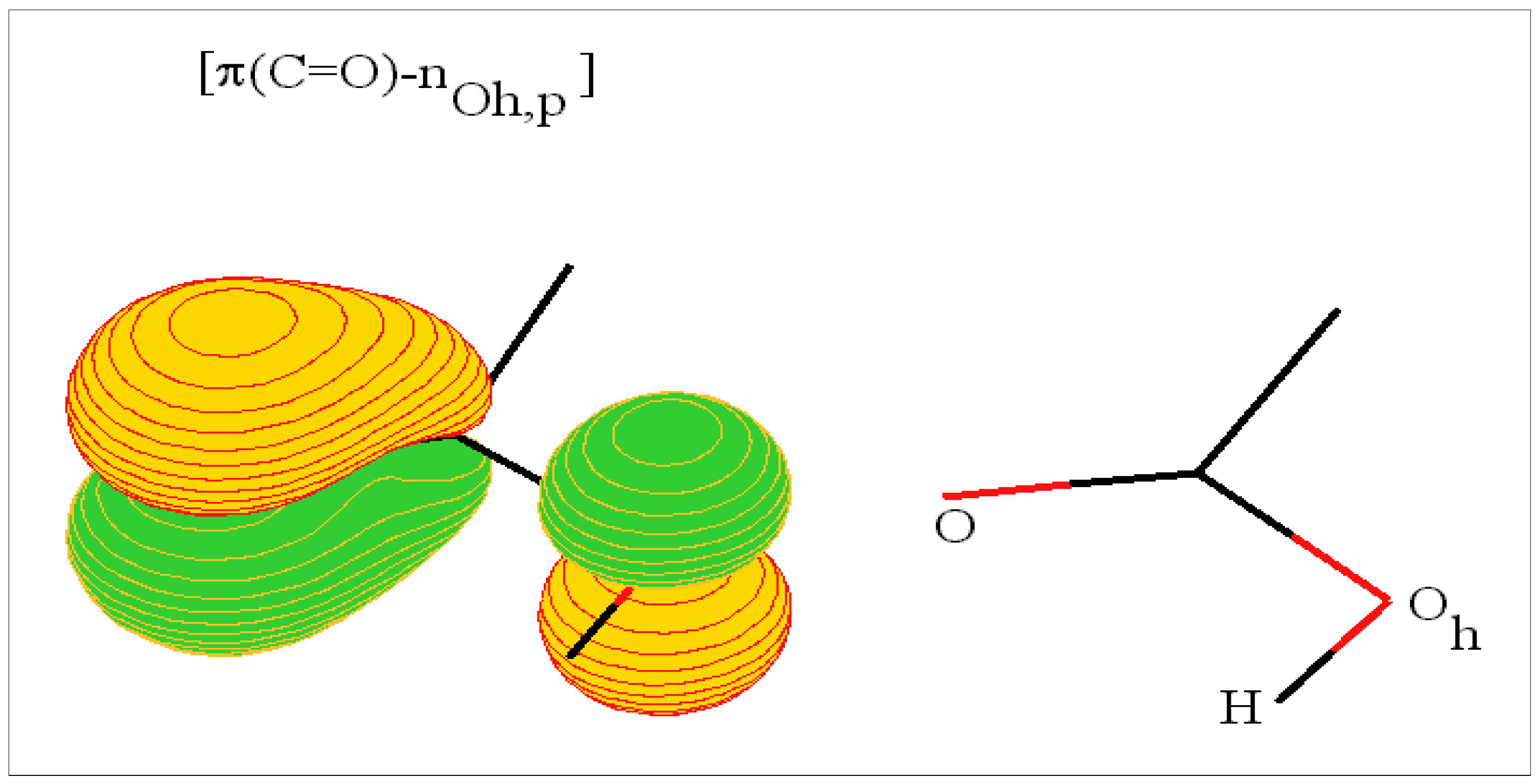
The amide or peptide link
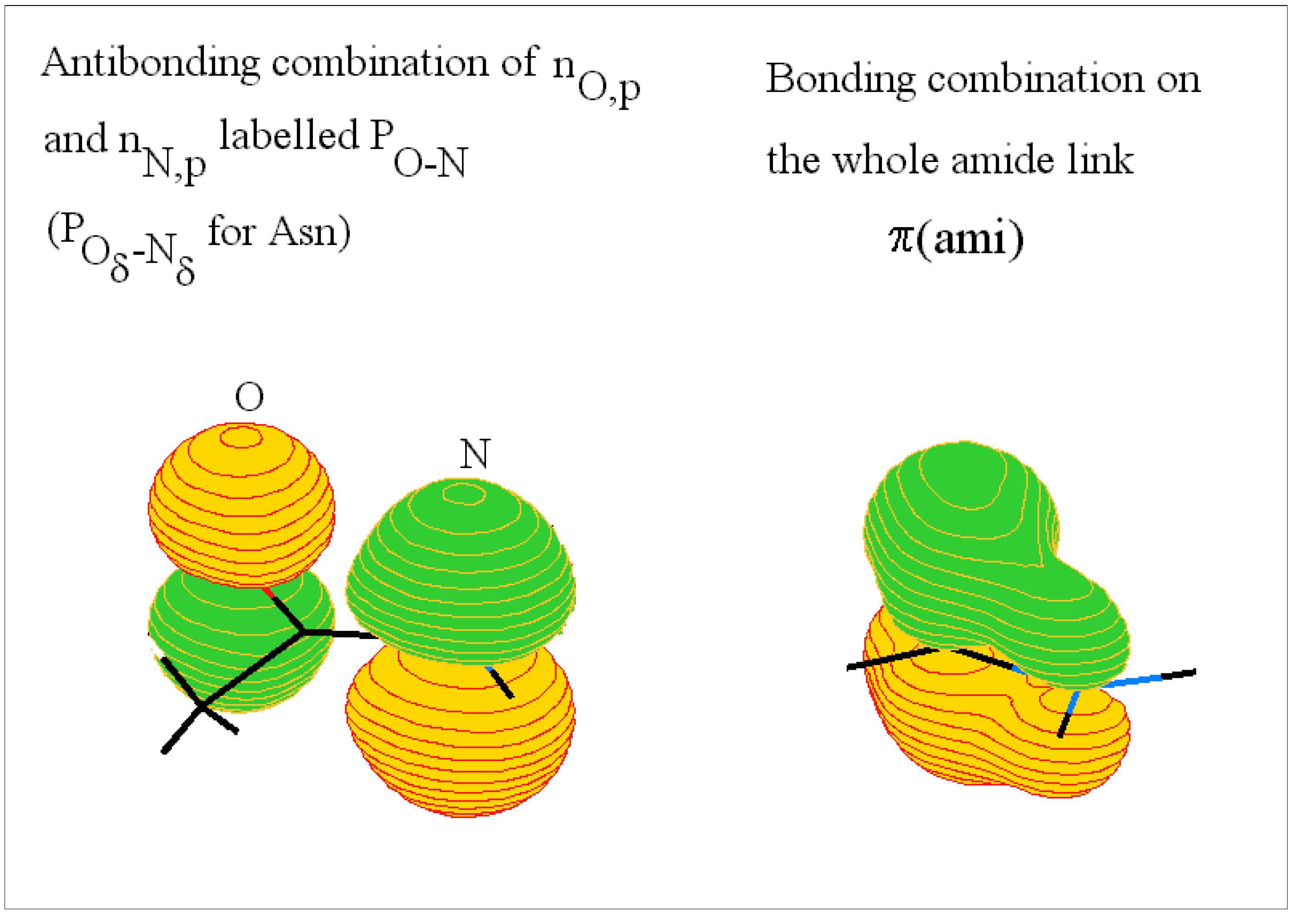
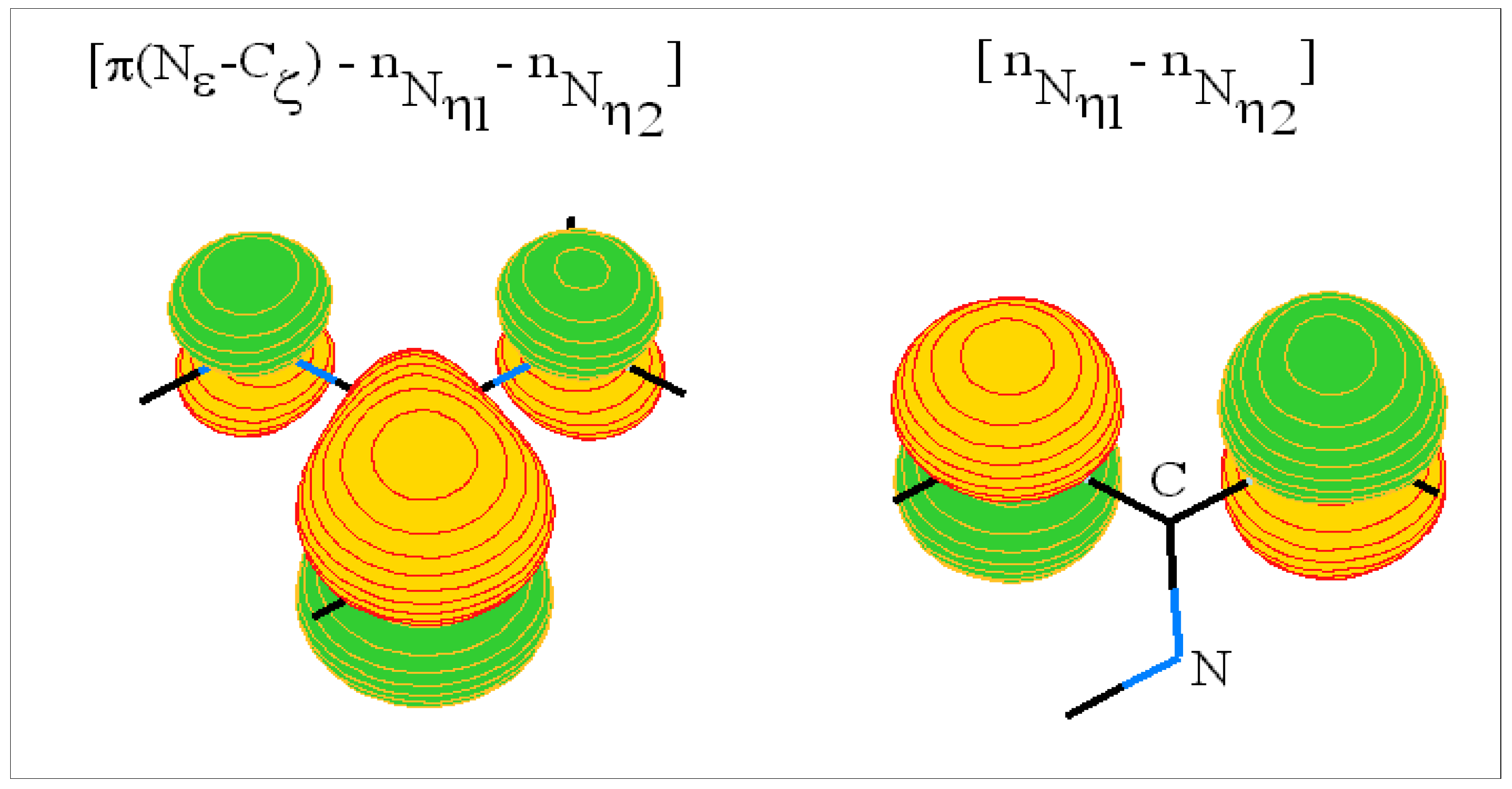
The arginine side chain
Results and Discussion
Relative stability of the neutral conformers
| Conformations | ||||
|---|---|---|---|---|
| Gly [48,58,59,60,61,62,63,64,65] | CF1 | CF2 | ||
| 0.0 {0.0} [63,65] | 2.93 {4.44} [63], {0.46} [65] | |||
| Ala[27,60,61,66,67] | CF1 | CF2 | ||
| 1.64 {0.0}[27] | 0.0 {1.99}[27] | |||
| Val [68,69,70] | CF1 | CF2 | ||
| 2.36 {1.79}[70] | 0.0 {0.0}[70] | |||
| Leu | CF1 | CF2 | ||
| 1.01 | 0.0 | |||
| Ile | CF1(1) | CF1(2) | CF2(1) | CF2(2) |
| 2.36 | 4.58 | 0.0 | 1.90 | |
| Asn | CF1(1) | CF1(2) | CF2 | CF3 |
| 8.19 | 9.07 | 0.0 | 0.44 | |
| Asp | CF1 | CF2 | CF3 | |
| 2.19 | 0.0 | 8.28 | ||
| Ser [66,71] | CF1 | CF2(1) | CF2(2) | |
| 3.72 {0.0}[66] | 0.0 {5.86}[66] | 1.00 {0.42}[66] | ||
| Thr [69] | CF1(1) | CF1(2) | CF2(1) | CF2(2) |
| 3.34 | 7.10 | 0.0 | 1.17 | |
| 5.84 | 8.69 | 0.0 | 4.37 | |
| S-Thr | CF1(1) | CF1(2) | CF2(1) | CF2(2) |
| Cys [66,72] | CF1 | CF2 | ||
| 6.45 {1.26}[66] | 0.0 {0.0}[66] | |||
| Met | CF1 | CF2(1) | CF2(2) | |
| 4.09 | 0.0 | 3.46 | ||
| Lys | CF1 | CF2(1) | CF2(2) | CF3 |
| 15.91 | 3.80 | 11.49 | 0.0 | |
| Arg [76] | CF1 | CF2 | CF3 | |
| 15.65 | 0.0 | 0.41 | ||
| His "Nδ1" | CF1 | CF2 | ||
| 2.66 | 0.0 | |||
| His "Nε2" | CF2(1) | CF2(2) | CF3 | |
| 0.0 | 6.31 | 6.09 | ||
| Phe [74] | CF1 | CF2(1) | CF2(2) | |
| 6.87 {3.03} | 0.0 {0.0} | 3.54 {4.82} | ||
| Tyr | CF1 | CF2(1) | CF2(2) | |
| 6.54 | 0.0 | 3.41 | ||
| Trp [75] | CF1 | CF2(1) | CF2(2) | |
| 9.99 {5.97} | 0.0 {0.0} | 7.20 {8.94} | ||
| Pro [57,73] | CF1 | CF2 | ||
| 7.36 {6.96}[73] | 0.0 {0.0}[73] | |||
Variation of the IE as a function of the conformations
| MO # | description | IE | description | IE | description | IE | description | IE |
|---|---|---|---|---|---|---|---|---|
| Glycine | ||||||||
| CF1 | CF2 | |||||||
| 20 | nN,σ(Cα-C), nO,σ(C-Oh) | 9.82 | nO, nN, nOh, σ(Cα-C) | 9.98 | ||||
| 19 | nO, nN, nOh, σ(Cα-C) | 11.16 | [π(C=O)-nOh,p] | 11.11 | ||||
| 18 | [π(C=O)-nOh,p] | 11.93 | nN, nO, nOh. | 11.29 | ||||
| 17 | σ(Cα-Hα), σ(N-H), nOh. | 13.16 | nOh, nO, σ(Cα-C), σ(Cα-Hα) | 13.40 | ||||
| Alanine | ||||||||
| CF1 | CF2 | |||||||
| 24 | nN,σ(Cα-C), σ(Cα-N),nO. | 9.67 | nO, nN, σ(Cα-C), σ(Cα-Cβ), σ(C-Oh), nOh. | 9.85 | ||||
| 23 | nO, nN, σ(Cα-C), nOh. | 10.91 | [π(C=O)-nOh,p], σ(Cα-Cβ), nN. | 11.07 | ||||
| Alanine (Cont.) | ||||||||
| 22 | [π(C=O)-nOh,p], σ(Cα-Cβ) | 11.80 | nN,n(O,p), σ(Cα-Cβ), σ(Cα-N), nOh. | 11.04 | ||||
| 21 | σ(Cα-Cβ), σ(Cα-Hα), σ(Cβ-Hβ), σ(N-H) | 12.50 | σ(Cα-Cβ), σ(Cα-Hα), σ(Cβ-Hβ), σ(Cα-N), nOh, nO. | 12.96 | ||||
| Valine | ||||||||
| CF1 | CF2 | |||||||
| 32 | nN,σ(Cα-C), σ(Cα-Cβ), nO. | 9.50 | nN, nO, σ(Cα-C), σ(Cα- Cβ), nOh. | 9.69 | ||||
| 31 | nO, nN, nOh, σ’s(sdc). | 10.80 | nO, nN, nOh, σ’s(sdc). | 10.83 | ||||
| 30 | σ’s(sdc), nO, nOh. | 11.39 | [π(C=O)-nOh,p], nN. | 10.99 | ||||
| 29 | σ’s(sdc). | 11.67 | σ’s(sdc). | 12.01 | ||||
| 28 | [π(C=O)-nOh,p], σ’s(sdc). | 12.03 | σ’s(sdc). | 12.06 | ||||
| 27 | [π(C=O)-nOh,p], σ’s(sdc). | 12.01 | σ’s(sdc), nOh. | 12.39 | ||||
| Leucine | ||||||||
| CF1 | CF2 | |||||||
| 36 | nN,σ(Cα-C), σ(Cα-Cβ), σ(Cβ-Cγ), nO. | 9.51 | nN, nO, σ(Cα-C), σ(Cα-Cβ), nOh. | 9.70 | ||||
| 35 | nN, nO, nOh, σ’s(sdc). | 10.77 | [π(C=O)-nOh,p], σ(Cα-Cβ). | 10.97 | ||||
| 34 | σ’s(sdc). | 11.27 | nN, nO, nOh, σ’s(sdc). | 10.95 | ||||
| 33 | σ’s(sdc). | 11.44 | σ’s(sdc). | 11.73 | ||||
| 32 | nO, nOh, σ’s(sdc). | 11.58 | σ’s(sdc). | 11.79 | ||||
| 31 | [π(C=O)-nOh,p], σ(Cβ-Cγ), σ(Cγ-Cδ1). | 11.90 | σ’s(sdc). | 11.86 | ||||
| Isoleucine | ||||||||
| CF1(1) | CF1(2) | CF2(1) | CF2(2) | |||||
| 36 | nN,σ(Cα-C), σ(Cα-Cβ), σ(Cβ-Cγ2), nO | 9.45 | nN,σ(Cα-C), σ(Cα-Cβ), σ(Cβ-Cγ1), nO | 9.39 | nN, nO, σ(Cα-C), σ(Cα-Cβ), σ(Cβ-Cγ2), nOh | 9.65 | nN, nO, σ(Cα-C), σ(Cα-Cβ), nOh | 9.59 |
| 35 | nO, σ’s(sdc), nN, nOh. | 10.79 | nO, nN, σ’s(sdc), nOh. | 10.85 | nO, nN, σ’s(sdc), nOh. | 10.76 | [π(C=O)-nOh,p], nN, σ(Cα-Cβ), σ(Cβ-Cγ1), σ(Cα-Hα) | 10.82 |
| 34 | nO, nN, σ’s(sdc) | 11.10 | σ’s(sdc) | 11.23 | [π(C=O)-nOh,p], nN. | 10.96 | nN, nO, nOh, σ(Cα-C), σ(Cα-Cβ) | 10.94 |
| 33 | σ’s(sdc), nO, nOh. | 11.39 | σ’s(sdc), nO. | 11.48 | σ’s(sdc), nO, nN, nOh. | 11.58 | σ’s(sdc), nO, nOh. | 11.53 |
| 32 | σ’s(sdc), nO, nOh. | 11.63 | nO, σ’s(sdc), nOh. | 11.37 | σ’s(sdc) | 11.80 | σ’s(sdc), nO. | 11.81 |
| 31 | [π(C=O)-nOh,p], σ(Cβ-Cγ2), σ(Cγ1-Cδ) | 11.90 | [π(C=O)-nOh,p], σ(Cβ-Cγ1), σ(Cγ1-Cδ) | 11.98 | σ’s(sdc), nOh. | 12.11 | σ’s(sdc), nN, nOh. | 12.01 |
| Asparagine | ||||||||
| CF1(1) | CF1(2) | CF2 | CF3 | |||||
| 35 | POδ-Nδ. | 9.31 | nN, σ(Cα-C) | 9.36 | nN, σ(Cα-C), σ(Cα-Cβ), nO, nOδ, n(Nδ,p), nOh, σ(Cβ-Cγ) | 9.80 | nN, σ(Cα-C),σ(Cα-Cβ), nO, nOh. | 9.54 |
| 34 | nOδ, σ(Cβ-Cγ), σ(Cα-Cβ), σ(Cγ-Nδ) | 9.42 | POδ-Nδ. | 10.04 | POδ-Nδ. | 10.31 | nO, nN, n(Nδ,p), nOδ. | 10.32 |
| 33 | nN, σ(Cα-Cβ), σ(Cα-Hα) | 10.11 | nOδ, σ(Cβ-Cγ), σ(Cγ-Nδ) | 10.10 | nOδ, nO, σ(Cβ-Cγ) | 10.40 | POδ-Nδ, [π(C=O)-nOh,p] | 10.68 |
| 32 | nO, σ(Cα-Cβ), σ(Cα-C), nOh. | 10.99 | nO, nN, σ(Cα-C), nOh. | 10.64 | nN, nO, σ(Cα-Cβ), σ(Cα-C), σ(Cβ-Cγ), nOh. | 10.78 | [π(C=O)-nOh,p], POδ-Nδ. | 10.96 |
| Asparagine (Cont.) | ||||||||
| 31 | [π(C=O)-nOh,p] | 12.04 | [π(C=O)-nOh,p] | 11.56 | [π(C=O)-nOh,p] | 11.14 | nOδ, σ(Cβ-Cγ), nOh, σ(Cβ-Hβ), σ(Cγ-Nδ) | 10.88 |
| 30 | π(ami) σ(Cβ-Hβ) | 12.59 | σ(Cα-Cβ), σ(Cα-Hα), σ(N-H) | 12.53 | π(ami) σ(Cβ-Hβ), σ(Cα-Cβ), σ(Cα-Hα), σ(Cα-N) | 12.73 | σ(Cα-Cβ), σ(Cα-Hα), σ(Cβ-Hβ), σ(N-H), nOh,nO,nOδ. | 12.52 |
| 29 | σ’s(sdc). | 12.99 | π(ami) σ(Cβ-Hβ), σ(Cα-N) | 12.75 | nO, nOh, σ(Cα-C), σ(Cα-Cβ) | 13.07 | σ’s(sdc). | 13.26 |
| Aspartic acid | ||||||||
| CF1 | CF2 | CF3 | ||||||
| 35 | nOδ, σ(Cβ-Cγ), nOhδ, σ(Cα-C) | 10.08 | nN, σ(Cα-C), nO, nOh, σ(Cα-Cβ) | 9.99 | nN, σ(Cα-C), nO, nOh, σ(Cα-Cβ) | 9.78 | ||
| 34 | [π(Cγ=Oδ)-nOhδ,p], nN. | 10.89 | nN, nO, σ(Cα-Cβ), nOh, nOδ, σ(Cβ-Cγ) | 10.95 | nN, nO, nOh, σ(Cα-C) | 10.84 | ||
| 33 | nN, σ(Cα-C), nOδ, nOhδ. | 10.96 | [π(C=O)-nOh,p], nN. | 11.17 | [π(C=O)-nOh,p] | 11.41 | ||
| 32 | nO, σ(Cα-C), nN, nOh. | 12.15 | nOδ, nN, σ(Cβ-Cγ), nOhδ. | 11.61 | nOδ, nOhδ, σ(Cβ-Cγ), nOh. | 12.02 | ||
| 31 | [π(C=O)-nOh,p], σ(Cα-Cβ) | 12.73 | [π(Cγ=Oδ)-nOhδ,p] | 12.44 | [π(Cγ=Oδ)-nOhδ,p] | 12.86 | ||
| Serine | ||||||||
| CF1 | CF2(1) | CF2(2) | ||||||
| 27 | nOγ,p, nN, σ(Cβ-Hβ). | 10.69 | nOγ,p, nO, σ(Cα-C), σ(Cα-Cβ). | 10.64 | nO, nN, σ(Cα-C), σ(Cα-Cβ), nOγ, nOh. | 10.82 | ||
| Serine (Cont.) | ||||||||
| 26 | nO, nN, nOγ, nOh, σ(Cα-C). | 11.11 | [π(C=O)-nOh,p]. | 11.57 | [π(C=O)-nOh,p]. | 11.38 | ||
| 25 | [π(C=O)-nOh,p], σ(Cα-Cβ), nOγ. | 11.86 | nN, nOγ,p, nO, nOh. | 11.70 | nN, nOγ,p, nOh. | 11.67 | ||
| 24 | [π(C=O)-nOh,p], σ(Cα-Cβ), nOγ, σ(Cβ-Hβ). | 12.40 | nOγ, σ(Cα-Cβ), nO, nN, nOh. | 12.77 | nOγ, σ(Cβ-Hβ). | 12.46 | ||
| Threonine (R-Cβ) | ||||||||
| CF1(1) | CF1(2) | CF2(1) | CF2(2) | |||||
| 32 | nN, nOγ,p, σ(Cα-C), σ(Cα-Cβ). | 9.80 | nN, σ(Cα-C), nO. | 9.35 | nN, nO, σ(Cα-C), σ(Cα-Cβ), nOγ,p, nOh. | 9.81 | nN, nOγ,p, nO, σ(Cα-C), σ(Cα-Cβ), nOh. | 9.75 |
| 31 | nN, nOγ,p, σ(Cα-C), σ(Cβ-Cγ). | 10.53 | nOγ,p, σ(Cα-Cβ). | 10.42 | nO, nN, nOγ,p, σ(Cα-C), σ(Cα-Cβ). | 10.72 | nOγ,p, nO, σ’s(sdc). | 10.45 |
| 30 | nO, nN, nOγ, nOh, σ(Cβ-Cγ), σ(Cα-C), σ(Cα-Cβ). | 11.07 | nO, nN, nOγ, σ’s(sdc). | 11.33 | [π(C=O)-nOh,p]. | 11.32 | [π(C=O)-nOh,p]. | 11.46 |
| 29 | nO, σ’s(sdc), nOγ, nOh. | 11.56 | nO, nOh, σ’s(sdc), nOγ, nN. | 11.94 | nN, nOγ,p, nOh. | 11.56 | nN, nOγ,p, nO, nOh, σ(Cα-Cβ), σ(Cβ-Cγ). | 11.60 |
| 28 | [π(C=O)-nOh,p], σ’s(sdc), nOγ. | 12.16 | [π(C=O)-nOh,p], nOγ. | 12.20 | σ’s(sdc), nOγ,p. | 12.08 | σ’s(sdc), nN, nOγ,p, nO, nOh. | 12.37 |
| S-Threonine (S-Cβ) | ||||||||
| CF1(1) | CF1(2) | CF2(1) | CF2(2) | |||||
| 32 | nN, σ(Cα-C), σ(Cα-Cβ), σ(Cβ-Cγ), nOγ,p. | 9.80 | nN, σ(Cα-C), nO. | 9.37 | nN, nOγ,p, nO, σ(Cα-C), σ(Cα-Cβ), nOh. | 9.77 | nN, nO, σ(Cα-C), σ(Cα-Cβ), σ(Cβ-Cγ), nOγ,p, nOh. | 9.83 |
| S-Threonine (S-Cβ) (Cont,) | ||||||||
| 31 | nN, nOγ,p, σ(Cβ-Cγ). | 10.55 | nOγ,p, σ(Cα-Cβ), σ(Cβ-Cγ). | 10.45 | nOγ,p, nO, σ(Cα-C), σ(Cα-Cβ), σ(Cβ-Cγ). | 10.48 | nO, nOγ,p, nN, σ(Cβ-Cγ), σ(Cα-C), σ(Cα-Cβ). | 10.57 |
| 30 | nO, nN, nOγ, σ(Cα-C), σ(Cα-Cβ). | 10.98 | nO, nN, nOγ, σ’s(sdc). | 11.16 | [π(C=O)-nOh,p]. | 11.48 | [π(C=O)-nOh,p]. | 11.36 |
| 29 | nO, σ’s(sdc), nOγ, nOh. | 11.60 | nO, nOh, σ(Cα-Cβ). | 12.00 | nN, nOγ,p, nO, nOh. | 11.61 | nN, nOγ,p, nOh. | 11.52 |
| 28 | [π(C=O)-nOh,p]. | 12.13 | [π(C=O)-nOh,p], nOγ, σ(Cα-Cβ), nN. | 12.09 | σ(Cα-Cβ), σ(Cβ-Cγ), nOγ,p, nO, nN, nOh. | 12.48 | σ’s(sdc), nO. | 11.96 |
| Cysteine | ||||||||
| CF1 | CF2 | |||||||
| 32 | nSγ, σ(Cα-Cβ) | 8.66 | nSγ, σ(Cα-Cβ) | 9.21 | ||||
| 31 | nN, σ(Cα-C), σ(Cα-Cβ) | 10.00 | nN, nO, σ(Cα-C), σ(Cα-Cβ) | 10.08 | ||||
| 30 | nSγ, σ(Sγ-Cβ), nO, nN, σ(Cα-Cβ), σ(Cα-C) | 10.95 | nSγ, σ(Sγ-Cβ), σ(Cα-Cβ), nN, nO, nOh. | 11.30 | ||||
| 29 | nO, nSγ, nOh, σ(Cα-Cβ) | 11.73 | [π(C=O)-nOh,p] | 11.29 | ||||
| 28 | [π(C=O)-nOh,p] | 12.16 | nN, nSγ, nO, nOh, σ(Sγ-Cβ) | 11.54 | ||||
| Methionine | ||||||||
| CF1 | CF2(1) | CF2(2) | ||||||
| 40 | nSδ,p. | 8.09 | nSδ,p. | 8.60 | nSδ,p. | 8.58 | ||
| 39 | nN, σ(Cα-C), σ(Cα-Cβ). | 9.63 | nO, nN, nOh, σ(Cα-C), σ(Cα-Cβ), nSδ. | 9.72 | nO, nN, nOh, σ(Cα-C), σ(Cα-Cβ). | 9.77 | ||
| 38 | nSδ, σ(Cγ-Sδ), σ(Sδ-Cε). | 10.61 | nSδ, nO, nOh, σ(Cα-C). | 10.81 | nSδ, σ(Cγ-Sδ), σ(Sδ-Cε). | 10.89 | ||
| Methionine (Cont.) | ||||||||
| 37 | nO, nN, nOh, σ(Cα-C), σ(Cβ-Cγ). | 10.91 | [π(C=O)-nOh,p] | 11.09 | [π(C=O)-nOh,p] | 11.08 | ||
| 36 | σ’s(sdc), nO. | 11.80 | nN, nSδ, nO, nOh, σ(Cα-Cβ), σ(Cγ-Sδ). | 11.29 | nN, nO, σ(Cα-Cβ), nOh. | 11.02 | ||
| 35 | [π(C=O)-nOh,p], σ(Cα-Cβ). | 11.72 | σ’s(sdc), nO. | 12.05 | σ’s(sdc), nO. | 12.18 | ||
| Lysine | ||||||||
| CF1 | CF2(1) | CF2(2) | CF3 | |||||
| 40 | nNζ, σ(Cδ-Cε) | 8.98 | nO, nN, σ(Cα-C), σ(Cα-Cβ), nOh, nNζ. | 9.09 | nNζ, σ(Cδ-Cε) | 8.67 | nN, nO, σ(Cα-C), σ(Cα-Cβ), nOh. | 9.07 |
| 39 | nN, σ(Cα-C), σ(Cα-Cβ), σ(Cβ-Cγ), nO, σ(Cγ-Cδ) | 9.59 | nNζ, σ(Cδ-Cε), σ(Cε-Hε), nO. | 10.00 | nN, nO, σ(Cα-C), σ(Cα-Cβ), nOh. | 9.92 | nNζ, nO, nN, nOh, σ(Cε-Hε) | 10.11 |
| 38 | nO, nN, σ’s(sdc) | 10.83 | [π(C=O)-nOh,p] | 10.52 | nN, nO, σ’s(sdc) | 10.86 | nN, nO, nNζ, σ(Cε-Hε) | 10.45 |
| 37 | σ’s(sdc), nN, nO. | 11.09 | nN, nO, nOh, σ(Cα-C) | 10.62 | [π(C=O)-nOh,p] | 11.25 | [π(C=O)-nOh,p] | 10.67 |
| 36 | σ’s(sdc), nO. | 11.42 | σ’s(sdc) | 11.74 | σ’s(sdc), nOh, nO. | 11.64 | σ’s(sdc) | 11.45 |
| 35 | nO,σ’s(sdc), nOh. | 11.68 | σ’s(sdc), nO. | 11.83 | σ’s(sdc), nN, nOh, nO. | 11.72 | σ’s(sdc) | 11.92 |
| 34 | [π(C=O)-nOh,p], σ’s(sdc) | 11.89 | σ’s(sdc), nNζ. | 11.92 | σ’s(sdc), nNζ. | 12.17 | σ’s(sdc), nNζ. | 11.97 |
| Arginine | ||||||||
| CF1 | CF2 | CF3 | ||||||
| 47 | [π(Nε=Cζ)- nNη1- nNη2], σ(Cγ-Cδ) | 8.46 | [π(Nε=Cζ)- nNη1- nNη2], σ(Cγ-Cδ) | 8.67 | [π(Nε=Cζ)- nNη1- nNη2], σ(Cγ-Cδ) | 8.95 | ||
| 46 | nN, σ(Cα-C), σ(Cα-Hα) | 8.61 | nN, nO, σ(Cα-C), σ(Cα-Cβ), nOh, nNε. | 9.11 | nN, nO, σ(Cα-C), σ(Cα-Cβ), nOh. | 8.92 | ||
| Arginine (Cont.) | ||||||||
| 45 | nNε, σ(Cδ-Nε), σ(Cδ-Hδ) | 9.36 | nNε, σ(Cδ-Nε), σ(Cδ-Hδ) | 9.71 | nNε, nO, nN, nOh, σ(Cδ-Nε), σ(Cδ-Hδ) | 9.77 | ||
| 44 | [nNη1- nNη2] | 10.25 | [π(C=O)-nOh,p], nN, σ(Cα-Cβ) | 10.47 | nNε, nO, nN, nOh, σ(Cδ-Nε), σ(Cδ-Hδ) | 10.22 | ||
| 43 | nO, σ(Cα-C), σ(Cα-Cβ), nOh. | 10.44 | nN, nO, nOh. | 10.46 | [π(C=O)-nOh,p], nNε. | 10.42 | ||
| 42 | σ(Cα-Cβ), σ(Cβ-Cγ), [π(C=O)-nOh,p], nN. | 11.24 | [nNη1- nNη2] | 10.48 | [nNη1- nNη2] | 10.66 | ||
| Histidine “Nδ1” | ||||||||
| CF1 | CF2 | |||||||
| 41 | π1 | 7.76 | π1 | 7.85 | ||||
| 40 | π2 | 9.37 | π2 | 9.40 | ||||
| 39 | nNε2, σ’s(cycle). | 9.69 | nNε2, σ’s(cycle), nO. | 9.68 | ||||
| 38 | nN, σ(Cα-C), σ(Cα-Cβ), nO. | 10.28 | nN, nO, σ(Cα-C), σ(Cα-Cβ), nNε2, nOh. | 10.59 | ||||
| 37 | nN, nO, nOh, σ(Cα-C). | 11.33 | nN, nO, σ(Cα-C), σ(Cα-Cβ), nOh. | 11.32 | ||||
| 36 | [π(C=O)-nOh,p], σ(Cα-Cβ). | 12.08 | [π(C=O)-nOh,p] | 11.62 | ||||
| Histidine “Nε2” | ||||||||
| CF2(1) | CF2(2) | CF3 | ||||||
| 41 | π1 | 8.34 | π1 | 8.43 | π1 | 8.76 | ||
| 40 | nN,nO, σ(Cα-C), σ(Cα-Cβ), nOh, [nNδ1,p- nNε2,p]. | 9.41 | nN,nO, σ(Cα-C), σ(Cα-Cβ), [nNδ1,p- nNε2,p], nOh. | 9.56 | nN, σ(Cα-C), nO, nOh, σ(Cα-Cβ). | 9.14 | ||
| Histidine “Nε2” (Cont.) | ||||||||
| 39 | π2, nN, nO. | 9.93 | π2, nN, nO. | 9.98 | nO, nN, [nNδ1,p- nNε2,p], nOh. | 9.97 | ||
| 38 | nNδ1, nN,nO, σ’s(cycle) ,nOh. | 10.23 | nO, nN, σ(Cα-C), σ(Cα-Cβ), nNδ1, nOh. | 10.21 | π2 | 10.38 | ||
| 37 | [π(C=O)-nOh,p] | 10.67 | [π(C=O)-nOh,p] | 10.83 | [π(C=O)-nOh,p] | 10.51 | ||
| 36 | nNδ1, nN,nO, σ’s(cycle), nOh. | 10.82 | nNδ1, nN, σ’s(cycle). | 10.85 | nNδ1, σ’s(cycle), nOh, nN. | 11.04 | ||
| Phenylalanine | ||||||||
| CF1 | CF2(1) | CF2(2) | ||||||
| 44 | π1 | 8.40 | π1 | 8.57 | π1 | 8.65 | ||
| 43 | π2 | 8.61 | π2 | 8.76 | π2 | 8.91 | ||
| 42 | nN, σ(Cα-C), nO. | 9.54 | nO,nN, σ(Cα-C), σ(Cα-Cβ), nOh, σ(C-Oh). | 9.72 | nO,nN, σ(Cα-C), σ(Cα-Cβ), nOh, σ(C-Oh). | 9.87 | ||
| 41 | nO, nN, σ(Cα-C), nOh. | 10.74 | [π(C=O)-nOh,p], nN, σ(Cα-Cβ). | 10.84 | nN,nO, σ(Cα-Cβ), nOh, σ(Cα-C). | 10.87 | ||
| 40 | σ’s(sdc), π(C=O) | 11.44 | nN,nO, nOh, σ(Cα-Cβ). | 10.91 | [π(C=O)-nOh,p], nN. | 11.04 | ||
| 39 | σ’s(cycle), σ(Cβ-Cγ), [π(C=O)-nOh,p] | 11.63 | σ(Cβ-Cγ), σ’s(cycle). | 11.74 | σ(Cβ-Cγ), σ’s(cycle). | 11.86 | ||
| 38 | σ’s(cycle), [π(C=O)-nOh,p] | 11.83 | σ’s(cycle). | 11.85 | σ’s(cycle), σ(Cβ-Cγ). | 12.00 | ||
| 37 | π3 | 11.81 | π3 | 11.99 | π3 | 12.10 | ||
| Tyrosine | ||||||||
| CF1 | CF2(1) | CF2(2) | ||||||
| 48 | π1 | 7.77 | π1 | 7.94 | π1 | 8.00 | ||
| 47 | π2 | 8.72 | π2 | 8.84 | π2 | 8.98 | ||
| 46 | nN, σ(Cα-C). | 9.51 | nO,nN, nOh, σ(Cα-C), σ(Cα-Cβ). | 9.67 | nN,nO, nOh, σ(Cα-C), σ(Cα-Cβ). | 9.78 | ||
| Tyrosine (Cont.) | ||||||||
| 45 | nN,nO, nOh. | 10.71 | [π(C=O)-nOh,p], nN, σ(Cα-Cβ). | 10.82 | nN,nO, nOh, σ(Cα-Cβ). | 10.83 | ||
| 44 | π3 | 11.23 | nN,nO, nOh, σ(Cα-Cβ). | 10.87 | [π(C=O)-nOh,p], nN. | 10.98 | ||
| 43 | [π(C=O)-nOh,p]. | 11.62 | π3 | 11.45 | π3 | 11.55 | ||
| Tryptophan | ||||||||
| CF1 | CF2(1) | CF2(2) | ||||||
| 54 | π1 | 7.07 | π1 | 7.22 | π1 | 7.34 | ||
| 53 | π2 | 7.53 | π2 | 7.78 | π2 | 7.78 | ||
| 52 | π3 | 9.18 | π3 | 9.42 | π3 | 9.35 | ||
| 51 | nN, σ(Cα-C). | 9.41 | nN,nO, σ(Cα-C), σ(Cα-Cβ), nOh. | 9.63 | nN,nO, σ(Cα-C), σ(Cα-Cβ), nOh. | 9.80 | ||
| 50 | nO, σ(Cα-C), nN, nOh. | 10.65 | nN,nO, σ(Cα-C), σ(Cα-Cβ), nOh. | 10.74 | nN,nO, σ(Cα-C), σ(Cα-Cβ), nOh. | 10.74 | ||
| 49 | π4 | 10.96 | [π(C=O)-nOh,p], nN. | 10.84 | [π(C=O)-nOh,p], nN. | 10.86 | ||
| 48 | σ’s(sdc) | 11.26 | π4 | 11.20 | π4 | 11.22 | ||
| 47 | [π(C=O)-nOh,p]. | 11.61 | σ’s(sdc) | 11.47 | σ’s(sdc) | 11.52 | ||
| Proline | ||||||||
| CF1 | CF2 | |||||||
| 31 | nN, σ(Cγ-Cδ), σ’s(C-H). | 8.75 | nN, nO, σ(Cα-C), nOh. | 9.36 | ||||
| 30 | nO, σ(Cα-C), σ(Cα-Cβ), nOh. | 10.76 | nO, nN, σ(Cα-C), nOh. | 10.57 | ||||
| 29 | σ’s(sdc), [π(C=O)-nOh,p]. | 11.70 | [π(C=O)-nOh,p]. | 10.88 | ||||
| 28 | σ’s(sdc), nO, nOh. | 12.00 | σ’s(sdc), nO. | 12.30 | ||||
| Amino acid-conformation | Ionized MO description | Nuclei (ASD) |
|---|---|---|
| Gly-CF1 | nN, σ(Cα-C), nO, σ(C-Oh) | N(1.08), Cα(-0.11) |
| nO, nN, nOh, σ(Cα-C) | O=C(1.01,-0.18) | |
| Gly-CF2 | nO, nN, nOh, σ(Cα-C) | O=C(1.02,-0.17) |
| [π(C=O)-nOh,p] | O=C-Oh(0.83,-0.57,0.73). | |
| nN, nO, nOh. | N(1.05) | |
| Ala-CF1//QCISD | nN, σ(Cα-C), σ(Cα-N), nO. | N(.68), O(0.22) |
| nO, nN, σ(Cα-C), nOh. | O=C(0.83,-0.11) | |
| [π(C=O)-nOh,p], σ(Cα-Cβ) | O=C-Oh(0.67,-0.17,0.50) | |
| Ala-CF2//QCISD | nO, nN, σ(Cα-C), σ(Cα-Cβ), σ(C-Oh), nOh. | O(0.76), N(0.13) |
| [π(C=O)-nOh,p], σ(Cα-Cβ), nN. | O=C-Oh(0.66,-0.20,0.55) | |
| nN,n(O,p), σ(Cα-Cβ), σ(Cα-N), nOh. | N(0.55),O(0.31), Oh (0.10). | |
| Ile-CF1(1) | nN, σ(Cα-C), σ(Cα-Cβ), σ(Cβ-Cγ2), nO | N(1.07), Cα(-0.11). |
| nO, σ’s(sdc), nN, nOh. | O=C(0.51,-0.25), Hα(0.1), Cβ(0.21), Cγ1(0.24) | |
| nO, nN, σ’s(sdc) | O=C(0.58,-0.35), N(0.18), Cα(0.18), Cβ(0.16), Cγ1(0.11) | |
| σ’s(sdc), nO, nOh. | Cβ(0.27), Hβ(0.35), Cγ2(0.11), Hγ2,1(0.11) | |
| σ’s(sdc), nO, nOh. | O=C(0.28,-0.10), Cγ1(0.25), Hγ1,1(0.17), Cδ(0.20), Hδ,1(0.11) | |
| [π(C=O)-nOh,p], σ(Cβ-Cγ2), σ(Cγ1-Cδ) | O=C-Oh(0.86,-0.45,0.58). | |
| Ile-CF2(1) | nN, nO, σ(Cα-C), σ(Cα-Cβ), σ(Cβ-Cγ2), nOh | N(0.64), O=C(0.43,-0.11) |
| nO, nN, σ’s(sdc), nOh. | N(0.44), O=C(0.69,-0.32) | |
| [π(C=O)-nOh,p], nN. | O=C-Oh(0.84,-0.56,0.72) | |
| σ’s(sdc), nO, nN, nOh. | Cβ(0.38), Cγ1(0.39) | |
| σ’s(sdc) | Cγ1(0.20), Hγ1,1(0.22), Hγ1,2(0.21), O(0.17) | |
| Cys-CF1 | nSγ, σ(Cα-Cβ) | Sγ(1.10) |
| nN, σ(Cα-C), σ(Cα-Cβ) | N(1.08), Cα(-0.11) | |
| nSγ, σ(Sγ-Cβ), nO, nN, σ(Cα-Cβ), σ(Cα-C) | Sγ(0.62), Cβ(0.25) | |
| nO, nSγ, nOh, σ(Cα-Cβ) | O=C(1.00,-0.18) | |
| Cys-CF2 | nSγ, σ(Cα-Cβ) | Sγ(1.10) |
| nN, nO, σ(Cα-C), σ(Cα-Cβ) | O=C(1.01,-0.17) | |
| nSγ, σ(Sγ-Cβ), σ(Cα-Cβ), nN, nO, nOh. | Sγ(0.65), Cβ(0.26) | |
| [π(C=O)-nOh,p] | O=C-Oh(0.83,-0.58,0.74) | |
| nN, nSγ, nO, nOh, σ(Sγ-Cβ) | N(0.33), Sγ(0.32), O=C(0.31,-0.15) | |
| Lys-CF2(1) | nO, nN, σ(Cα-C), σ(Cα-Cβ), nOh, nNζ. | N(0.65), O=C(0.45,-0.10) |
| nNζ, σ(Cδ-Cε), σ(Cε-Hε), nO. | Nζ(1.04) | |
| [π(C=O)-nOh,p] | O=C-Oh(0.84,-0.57,0.72) | |
| nN, nO, nOh, σ(Cα-C) | N(0.62), O=C(0.51,-0.16) | |
| Lys-CF3 | nN, nO, σ(Cα-C), σ(Cα-Cβ), nOh. | N(1.06), Cα(-0.11) |
| nNζ, nO, nN, nOh, σ(Cε-Hε) | Nζ(0.67), O=C(0.47,-0.16), Oh(0.11) | |
| nN, nO, nNζ, σ(Cε-Hε) | Nζ(0.46), N(0.31), O=C(0.36,-0.14) | |
| [π(C=O)-nOh,p] | O=C-Oh(0.81,-0.59,0.78) | |
| His"Nδ1"-CF1 | π1 | Cγ(0.54), Cδ2(0.54), Cε1(0.55), Nε2(-0.35), Nδ1(-0.20) |
| π2 | Nε2(0.83), Nδ1(0.79), Cε1(-0.66) | |
| nNε2, σ's(cycle). | Nε2(1.15), Cγ(0.14),Cε1(-0.24), Cδ2(-0.12) | |
| nN, σ(Cα-C), σ(Cα-Cβ), nO. | N(1.0), Cα(-0.11), Cγ(-0.21), Cδ2(0.26), Cε1(0.23), Nε2(-0.18) | |
| His"Nδ1"-CF2 | π1 | Cγ(0.56), Cδ2(0.53), Cε1(0.54), Nε2(-0.34), Nδ1(-0.20) |
| π2 | Nε2(0.83), Nδ1(0.79), Cε1(-0.67) | |
| nNε2, σ's(cycle), nO. | Nε2(1.14), Cγ(0.13), Cε1(-0.23), Cδ2(-0.12) | |
| His"Nε2"-CF2(1) | π1 | Cγ(0.47), Cδ2(0.62), Cε1(0.49), Nε2(-0.18), Nδ1(-0.31) |
| nN, nO, σ(Cα-C), σ(Cα-Cβ), nOh, [nNδ1,p- nNε2,p]. | N(0.58), O=C(0.44,-0.11) | |
| π2, nN, nO. | Nε2(0.72), Nδ1(0.65), Cε1(-0.66), Cγ(0.79), Cδ2(-0.48) | |
| nNδ1, nN, nO, σ's(cycle), nOh. | N(0.38), O=C(0.48,-0.23), Nδ1(0.34), Cε1(-0.14) | |
| [π(C=O)-nOh,p] | O=C-Oh(0.84,-0.56,0.71) | |
| nNδ1, nN, nO, σ's(cycle), nOh. | Nδ1(0.58), N(0.47), Cε1(-0.19) | |
| His"Nε2"-CF3 | π1 | Cγ(0.43), Cδ2(0.64), Cε1(0.46), Nε2(-0.18), Nδ1(-0.29) |
| nN, σ(Cα-C), nO, nOh, σ(Cα-Cβ). | N(1.06), Cα(-0.11) | |
| nO, nN, [nNδ1,p- nNε2,p], nOh. | O(1.02), C(-0.16), Cα(-0.10) | |
| π2 | Nε2(0.78), Nδ1(0.88), Cε1(-0.69), Cγ(-0.25), Cδ2(0.30) | |
| [π(C=O)-nOh,p] | O=C-Oh(0.81,-0.60,0.78) | |
| nNδ1, σ's(cycle), nOh, nN. | Nδ1(1.06), Cδ2(0.20), Cγ(-0.17), Cε1(-0.18), Oh(0.11) | |
| Arg-CF2 | [π(Nε=Cζ)- nNη1- nNη2], σ(Cγ-Cδ) | Nε=Cζ(0.88,-0.13), Nη1(0.16), Nη2(0.11), Cδ(-0.11). |
| nN, nO, σ(Cα-C), σ(Cα-Cβ), nOh, nNε. | N(0.62), O=C(0.46,-0.11) | |
| nNε, σ(Cδ-Nε), σ(Cδ-Hδ) | Nε(1.04), Cζ(-0.11) | |
| [π(C=O)-nOh,p], nN, σ(Cα-Cβ) | O=C-Oh(0.84,-0.58,0.73) | |
| nN, nO, nOh. | N(0.58), O=C(0.48,-0.14) | |
| [nNη1- nNη2] | Nη2(0.76), Nη1(0.64), Nε=Cζ(-0.55,0.24) | |
| Arg-CF3 | [π(Nε=Cζ)- nNη1- nNη2], σ(Cγ-Cδ) | Nε=Cζ(0.90,-0.20), Nη1(0.21), Cδ(-0.11). |
| nN, nO, σ(Cα-C), σ(Cα-Cβ), nOh. | Nε(1.06), Cζ(-0.11) | |
| nNε, nO, nN, nOh, σ(Cδ-Nε), σ(Cδ-Hδ) | Nε=Cζ(0.66,-0.11), O=C-Oh(0.51,-0.18,0.14), HOh(-0.10) | |
| nNε, nO, nN, nOh, σ(Cδ-Nε), σ(Cδ-Hδ) | Nε(0.46), O=C(0.40,-0.17), N(0.32) | |
| [π(C=O)-nOh,p], nNε. | O=C-Oh(0.80,-0.61,0.80) | |
| [nNη1- nNη2] | Nη2(0.82), Nη1(0.60), Nε=Cζ(-0.52,0.19) | |
| Phe-CF1 | π1 | Cγ(0.50), Cδ1(0.24), Cδ2(0.40), Cζ(0.75), Cε1(-0.34), Cε2(-0.49) |
| π2 | Cγ(-0.44), Cδ1(0.51), Cδ2(0.49), Cζ(-0.38), Cε1(0.45), Cε2(0.46) | |
| nN, σ(Cα-C), nO. | N(1.08), Cα(-0.11) | |
| nO, nN, σ(Cα-C), nOh. | O(1.00), C(-0.18) | |
| σ’s(sdc), π(C=O) | O=C(0.51,-0.34), Cβ(0.25), Cγ(0.22), Cα(0.15), Hα(0.12) | |
| σ's(cycle), σ(Cβ-Cγ), [π(C=O)-nOh,p] | O=C-Oh(0.33,-0.26,0.28), Cβ(0.19), Cγ(0.15), Cδ2(0.11) | |
| σ's(cycle), [π(C=O)-nOh,p] | O=C(0.37,-0.19), Cγ(0.20), Cδ2(0.14) | |
| π3 | Cγ(0.13), Cδ1(0.09), Cδ2(0.09), Cζ(0.13), Cε1(0.24), Cε2(0.24) | |
| Phe-CF2(1) | π1 | Cγ(0.46), Cδ1(0.51), Cδ2(-0.34), Cζ(0.52), Cε1(-0.47), Cε2(0.37) |
| π2 | Cγ(-0.42), Cδ1(0.55), Cδ2(0.41), Cζ(-0.39), Cε1(0.42), Cε2(0.49) | |
| nO, nN, σ(Cα-C), σ(Cα-Cβ), nOh, σ(C-Oh). | O(1.0), C(-0.11) | |
| [π(C=O)-nOh,p], nN, σ(Cα-Cβ). | O=C-Oh(0.84,-0.56,0.71) | |
| nN, nO, nOh, σ(Cα-Cβ). | O=C(0.64,-0.16), Cγ(0.17), Cδ1(0.27), Cδ2(-0.10), Cζ(0.25), Cε1(-0.26), Cε2(0.11) | |
| σ(Cβ-Cγ), σ's(cycle). | Cβ(0.33), Cγ(0.22), Cδ1(0.14), Cδ2(0.15), Cζ(0.10), O(0.11) | |
| σ's(cycle). | Cγ(0.31), Cδ1(0.24), Hδ1(0.12) | |
| π3 | Cγ(0.15), Cδ1(0.11), Cδ2(0.16), Cζ(0.14), Cε1(0.18), Cε2(0.20) | |
| Phe-CF2(2) | π1 | Cγ(0.49), Cδ1(0.30), Cδ2(0.39), Cζ(0.76), Cε1(-0.40), Cε2(-0.48) |
| π2 | Cγ(-0.45), Cδ1(0.47), Cδ2(0.55), Cζ(-0.37), Cε1(0.47), Cε2(0.41) | |
| nO, nN, σ(Cα-C), σ(Cα-Cβ), nOh, σ(C-Oh). | O(1.01), C(-0.18) | |
| Th(SCF)=10–5. | nN, nO, σ(Cα-Cβ), nOh, σ(Cα-C). | O=C(0.58,-0.31), N(0.50), Cδ2(0.12) |
| [π(C=O)-nOh,p], nN. | Variational collapse | |
| Th(SCF)=10–5. | σ(Cβ-Cγ), σ's(cycle). | Cβ(0.32), Cγ(0.22), Cδ1(0.25) |
| σ's(cycle). | Cγ(0.15), Cζ(0.15), Cδ2(0.12), Cε1(0.12) | |
| π3 | Cγ(0.14), Cδ1(0.13), Cδ2(0.15), Cζ(0.15), Cε1(0.18), Cε2(0.17) |
Thermodynamical relative stability
| Amino acid | conformation | ΔE | ΔE+δZPE | ΔG(298) |
|---|---|---|---|---|
| Asn(QCISD) | CF1(1) | 2.62 | 4.58 | 6.86 |
| CF1(2) | 0.0 | 0.0 | 0.0 | |
| CF2 | 0.83 | 2.67 | 4.07 | |
| CF3 | 3.37 | 4.96 | 7.27 | |
| Arg(MP2) | CF2 | 0.0 | 0.0 | 0.0 |
| CF3 | 3.24 | 0.76 | 0.38 | |
| Lys(MP2) | CF2(1) | 8.14 | 8.13 | 5.94 |
| CF3 | 0.0 | 0.0 | 0.0 | |
| Tyr(MP2) | CF1 | 0.06 | 0.0 | 0.0 |
| CF2(1) | 0.0 | 1.90 | 4.31 |
Conclusions
Acknowledgments
References
- Bolton, J.R.; Mataga, N.; McLendon, G. Electron Transfer in Inorganic,Organic and Biological Systems; Adv. Chemistry Series 228; ACS: Washington, DC, 1991. [Google Scholar]
- Fox, M.A.; Chanon, M. Photoinduced Electron Transfer; Elsevier: Amsterdam, 1988; Parts A-D. [Google Scholar]
- Kavernos, G.J. Fundamentals of Photoinduced Electron Transfer; VCH Publishers Inc.: New York, 1993. [Google Scholar]
- Michel-Beyerle, M.E. Reaction Centers of Photosynthetic Bacteria; Springer Series in Biophysics 6; Springer-Verlag: Berlin, 1990. [Google Scholar]
- Regan, J.J.; Risser, S.M.; Beratan, D.N.; Onuchic, J.N. Protein electron transport: single versus multiple pathways. J. Phys. Chem. 1993, 97, 13083–13088. [Google Scholar] [CrossRef]
- Regan, J.J.; Onuchic, J.N. Electron-transfer tubes. Adv. Chem.Phys. 1999, 107, 497–553. [Google Scholar]
- Onuchic, J.N.; Beratan, D.N. A predictive theoretical model for electron tunneling pathways in proteins. J. Chem. Phys. 1990, 92, 722–733. [Google Scholar] [CrossRef]
- Antonello, S.; Formaggio, F.; Moretto, A.; Toniolo, C.; Maran, F. Anomalous Distance Dependence of Electron Transfer across Peptide Bridges. J. Am. Chem. Soc. 2003, 125, 2874–2875. [Google Scholar] [CrossRef] [PubMed]
- Remacle, F.; Levine, R.D. Superexchange, Localized, and Domain-Localized Charge States for Intramolecular Electron Transfer in Large Molecules and in Arrays of Quantum Dots. J. Phys. Chem. B 2001, 105, 2153–2162. [Google Scholar] [CrossRef]
- Pispisa, B.; Stella, L.; Venanzi, M.; Palleschi, A.; Viappiani, C.; Polese, A.; Formaggio, F.; Toniolo, C. Quenching mechanisms in bichromophoric, 310-helical Aib-based peptides, modulated by chain-length-dependent topologies. Macromolecules 2000, 33, 906–915. [Google Scholar] [CrossRef]
- Lang, K.; Kuki, A. Long-range electron transfer in rigid 310-helical oligopeptides containing redox cyclic α-amino acids. Photochem. Photobiol. 1999, 70, 579–584. [Google Scholar] [PubMed]
- Burdi, D.; Aveline, B.M.; Wood, P.D.; Stubbe, J.; Redmond, R.W. Generation of a Tryptophan Radical in High Quantum Yield from a Novel Amino Acid Analog Using Near-UV/Visible Light. J. Am. Chem. Soc. 1997, 119, 6457–6460. [Google Scholar] [CrossRef]
- Del Re, G.; Peluso, A.; Minichino, C. Hydrogen bridges and electron transfer in biomolecules. Study of a possible mechanism on a model charge-recombination system. Can. J. Chem. 1985, 63, 1850–1856. [Google Scholar] [CrossRef]
- Weinkauf, R.; Schanen, P.; Yang, D.; Soukara, S.; Schlag, E.W. Elementary Processes in Peptides: Electron Mobility and Dissociation in Peptide Cations in the Gas Phase. J. Phys. Chem. 1995, 99, 11255–11265. [Google Scholar] [CrossRef]
- Weinkauf, R.; Schanen, P.; Metsala, A.; Schlag, E.W.; Bürgle, M.; Kessler, H. Highly Efficient Charge Transfer in Peptide Cations in the Gas Phase: Threshold Effects and Mechanism. J. Phys. Chem. 1996, 100, 18567–18585. [Google Scholar] [CrossRef]
- Weinkauf, R.; Schlag, E.W.; Martinez, T.J.; Levine, R.J. Nonstationary Electronic States and Site-Selective Reactivity. J. Phys. Chem. A 1997, 101, 7702–7710. [Google Scholar] [CrossRef]
- Remacle, F.; Levine, R.D.; Schlag, E.W.; Weinkauf, R. Electronic Control of Site Selective Reactivity: A Model Combining Charge Migration and Dissociation. J. Phys. Chem. A 1999, 103, 10149–10158. [Google Scholar] [CrossRef]
- Weinkauf, R.; Lehrer, F.; Schlag, E.W.; Metsala, A. Investigation of charge localization and charge delocalization in model molecules by multiphoton ionization photoelectron spectroscopy and DFT calculations. Faraday Discuss. 2000, 115, 363–381. [Google Scholar] [CrossRef] [PubMed]
- Cui, W.; Hu, Y.; Lifshitz, C. Time resolved photodissociation of small peptide ions combining laser desorption with ion trap/reflectron TOF mass spectrometry. Eur. Phys. J. D 2002, 20, 565–571. [Google Scholar] [CrossRef]
- Baranov, L.Y.; Schlag, E.W. New Mechanism for Facile Charge Transport in Polypeptides. Z. Naturforsch. 1999, 54a, 387–396. [Google Scholar]
- On the website http://webbook.nist.gov, the adiabatic and some vertical ionization potentials from references 22-26 are given for the following amino acids: Gly, Ala, Val, Leu, Ile, Thr, Met, Lys, Trp, Pro.
- Slifkin, M.A.; Allison, A.C. Measurement of ionization potentials from contact charge transer spectra. Nature 1967, 215, 949. [Google Scholar] [CrossRef]
- Akopyan, M.E.; Loginov, Y.V. Mass-spectrometric study of the photoionization of free α-aminoacids. High Energy Chem. 1967, 1, 83. [Google Scholar]
- Debies, T.P.; Rabalais, J.W. Electronic structure of amino acids and ureas. J. Electron Spectrosc. Relat. Phenom. 1974, 3, 315. [Google Scholar] [CrossRef]
- Klasinc, K. Application of photoelectron spectroscopy to biologically active molecules and their constituent parts. J. Electron Spectrosc. Relat. Phenom. 1976, 8, 161. [Google Scholar] [CrossRef]
- Cannington, P.H.; Ham, N.S. He(I) and He(II) photoelectron spectra of glycine and related molecules. J. Electron Spectrosc. Relat. Phenom. 1983, 32, 139. [Google Scholar] [CrossRef]
- Powis, I.; Rennie, E.E.; Hergenhahn, U.; Kugeler, O.; Bussy-Socrate, R. Investigation of the Gas-Phase Amino Acid Alanine by Synchrotron Radiation Photoelectron Spectroscopy. J. Phys. Chem. A 2003, 107, 25–34. [Google Scholar] [CrossRef]
- Cederbaum, L.S. Direct calculation of ionization potentials of closed-shell atoms and molecules. Theor. Chim. Acta 1973, 31, 239–260. [Google Scholar] [CrossRef]
- Cederbaum, L.S.; Domcke, W.; Von Niessen, W. Theoretical photoelectron spectrum of cyanogen by a Green-function method. Chem. Phys. 1975, 10, 459–470. [Google Scholar] [CrossRef]
- Von Niessen, W.; Cederbaum, L.S.; Schirmer, J.; Diercksen, G.H.F.; Kraemer, W.P. Ionization energies of some molecules found in interstellar clouds calculated by a Green’s function method. J. Electron Spectrosc. Relat. Phenom. 1982, 28, 45–78. [Google Scholar] [CrossRef]
- Von Niessen, W.; Schirmer, J.; Cederbaum, L.S. Computational methods for the one-particle Green’s function. Comput. Phys. Rep. 1984, 1, 57–125. [Google Scholar] [CrossRef]
- Zakrzewski, V.G.; Ortiz, J.V. Vertical ionization energies of cubane. Chem. Phys. Lett. 1994, 230, 313–316. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Zakrzewski, V.G.; Montgomery, J.A., Jr.; Stratmann, R.E.; Burant, J.C.; Dapprich, S.; Millam, J.M.; Daniels, A.D.; Kudin, K.N.; Strain, M.C.; Farkas, O.; Tomasi, J.; Barone, V.; Cossi, M.; Cammi, R.; Mennucci, B.; Pomelli, C.; Adamo, C.; Clifford, S.; Ochterski, J.; Petersson, G.A.; Ayala, P.Y.; Cui, Q.; Morokuma, K.; Malick, D.K.; Rabuck, A.D.; Raghavachari, K.; Foresman, J.B.; Cioslowski, J.; Ortiz, J.V.; Baboul, A.G.; Stefanov, B.B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Gomperts, R.; Martin, R.L.; Fox, D.J.; Keith, T.; Al-Laham, M.A.; Peng, C.Y.; Nanayakkara, A.; Gonzalez, C.; Challacombe, M.; Gill, P.M.W.; Johnson, B.; Chen, W.; Wong, M.W.; Andres, J.L.; Gonzalez, C.; Head-Gordon, M.; Replogle, E.S.; Pople, J.A. Gaussian 98, Revision A.7; Gaussian, Inc.: Pittsburgh PA, 1998. [Google Scholar]
- Parr, R.G.; Yang, W. Density functional theory of atoms and molecules; Oxford University Press: New York, 1989. [Google Scholar]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self-consistent molecular orbital methods. XII. Further extensions of Gaussian-type basis sets for use in molecular orbital studies of organic molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-Consistent Molecular Orbital Methods 25: Supplementary Functions for Gaussian Basis Sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on the approximation treatment for many-electron systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Head-Gordon, M.; Pople, J.A; Frisch, M.J. MP2 energy evaluation by direct methods. Chem. Phys. Lett. 1988, 153, 503–506. [Google Scholar] [CrossRef]
- Pople, J.A.; Head-Gordon, M.; Raghavachari, K. Quadratic configuration interaction. A general technique for determining electron correlation energies. J. Chem. Phys. 1987, 87, 5968–5975. [Google Scholar] [CrossRef]
- Scuseria, G.E.; Schaefer, H.F., III. Is coupled cluster singles and doubles (CCSD) more computationally intensive than quadratic configuration interaction (QCISD)? J. Chem. Phys. 1989, 90, 3700–3703. [Google Scholar] [CrossRef]
- Koopmans, T. The distribution of wave function and characteristic value among the individual electrons of an atom. Physica 1933, 1, 104–113. [Google Scholar] [CrossRef]
- Hehre, W.J.; Radom, L.; von Ragué-Schleyer, P.; Pople, J.A. Ab initio molecular orbital theory; Wiley Interscience: New York, 1986. [Google Scholar]
- Deleuze, M.S.; Delhalle, J. Outer-Valence Green’s Function Study of Cycloalkane and Cycloalkyl-Alkane Compounds. J. Phys. Chem. A 2001, 105, 6695–6702. [Google Scholar] [CrossRef]
- Deleuze, M.S. Valence one-electron and shake-up ionization bands of polycyclic aromatic hydrocarbons. II. Azulene, phenanthrene, pyrene, chrysene, triphenylene, and perylene. J. Chem. Phys. 2002, 116, 7012–7026. [Google Scholar] [CrossRef]
- Deleuze, M.S.; Claes, L.; Kryachko, E.S.; François, J-P. Benchmark theoretical study of the ionization threshold of benzene and oligocenes. J. Chem. Phys. 2003, 119, 3106–3119. [Google Scholar] [CrossRef]
- Dykstra, C.E.; Chiles, R.A.; Garrett, M.D. Recent computational developments with the self-consistent electron pairs method and application to the stability of glycine conformers. J. Comput. Chem. 1981, 2, 266–272. [Google Scholar] [CrossRef]
- Yu, C-H.; Norman, M.A.; Schäfer, L.; Ramek, M.; Peeters, A.; van Alsenoy, C. Ab initio conformational analysis of N-formyl L-alanine amide including electron correlation. J. Mol. Struct. 2001, 567-568, 361–374. [Google Scholar]
- Jensen, K.P.; Ryde, U. Theoretical Predictions of the Co-C Bond Strength in the Cobalamins. J. Phys. Chem. A 2003, 107, 7539–7545. [Google Scholar] [CrossRef]
- Siegbahn, P.E.M. Quantum chemical studies of redox-active enzymes. Faraday Discuss. 2003, 124, 289–296. [Google Scholar] [CrossRef] [PubMed]
- Sustmann, R.; Sicking, W.; Huisgen, R. Thioformaldehyde S-methylide thioacetone S-methylide: An Ab initio MO study of structure and cycloaddition reactivity. Chem. Eur. J. 2003, 9, 2245–2255. [Google Scholar] [CrossRef] [PubMed]
- Guirgis, G.A.; Zheng, C.; Shen, S.; Durig, J.R. Spectra and structure of silicon containing compounds. XXXVII. Comparison of experimentally determined enthalpy differences of the conformers of CH2:CHSiClnY3-n (Y=H or CH3, n=1 or 2) with theoretical values. J. Mol. Struct. 2003, 651-653, 759–770. [Google Scholar] [CrossRef]
- Hermann, A.; Mora Valdez, M.I.; Cutin, E.H.; Della Vedova, C.O.; Oberhammer, H. Structures and Conformations of ((Trifluoroacetyl)imido)(trifluoromethyl)sulfur Fluoride, CF3C(O)N:S(F)CF3. J. Phys. Chem. A 2003, 107, 7874–7878. [Google Scholar] [CrossRef]
- Swart, M.; Snijders, J.G. Accuracy of geometries: influence of basis set, exchange-correlation potential, inclusion of core electrons, and relativistic corrections. Theor. Chem. Acc. 2003, 110, 34–41. [Google Scholar] [CrossRef]
- Pecul, M.; Helgaker, T. The spin-spin coupling constants in ethane, methanol and methylamine: A comparison of DFT, MCSCF and CCSD results. Int. J. Mol. Sci. 2003, 4, 143–157. [Google Scholar] [CrossRef]
- Stepanian, S.G.; Reva, I.D.; Radchenko, E.D.; Adamowicz, L. Conformers of Nonionized Proline. Matrix-Isolation Infrared and Post-Hartree-Fock ab Initio Study. J. Phys. Chem. A 2001, 105, 10664–10672. [Google Scholar] [CrossRef]
- Vishveshwara, S.; Pople, J.A. Molecular orbital theory of the electronic structures of organic compounds. 32. Conformations of glycine and related systems. J. Am. Chem. Soc. 1977, 99, 2422–2426. [Google Scholar] [CrossRef]
- Sellers, H.L.; Schäfer, L. Investigations concerning the apparent contradiction between the microwave structure and the ab initio calculations of glycine. J. Am. Chem. Soc. 1978, 100, 7728–7729. [Google Scholar] [CrossRef]
- Wright, L.R.; Borkman, R.R. Ab initio self-consistent field calculations on some small amino acids. J. Am. Chem. Soc. 1980, 102, 6207–6210. [Google Scholar] [CrossRef]
- Siam, K.; Klimkowski, V.J.; Ewbank, J.D.; Van Alsenoy, C.; Schäfer, L. Ab initio studies of structural features not easily amenable to experiment. Part 39. Conformational analysis of glycine and alanine. J. Mol. Struct. Theochem 1984, 110, 171–182. [Google Scholar] [CrossRef]
- Császár, A.G. Conformers of Gaseous Glycine. J. Am. Chem. Soc. 1992, 114, 9568–9575. [Google Scholar] [CrossRef]
- Hu, C-H.; Shen, M.; Schaefer, H.F., III. Glycine Conformational Analysis. J. Am. Chem. Soc. 1993, 115, 2923–2929. [Google Scholar] [CrossRef]
- Godfrey, P.D.; Brown, R.D.; Rodgers, F.M. The missing conformers of glycine and alanine: relaxation in seeded supersonic jets. J. Mol. Struct. Theochem 1996, 376, 65–81. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Scheiner, A.C.; Andzelm, J.W.; Sirois, S.; Salahub, D.R.; Hagler, A.T. A Density Functional Study of the Glycine Molecule: Comparison with Post-Hartree-Fock Calculations and Experiment. J. Comp. Chem. 1997, 18, 1609–1631. [Google Scholar] [CrossRef]
- Gronert, S.; O’Hair, R.A.J. Ab initio studies of amino acid conformations. 1. The conformers of alanine, serine, and cysteine. J. Am. Chem. Soc. 1995, 117, 2071–2081. [Google Scholar] [CrossRef]
- Cao, M.; Newton, S.Q.; Pranata, J.; Schäfer, L. Ab initio conformational analysis of alanine. J. Mol. Struct. Theochem 1995, 332, 251–267. [Google Scholar] [CrossRef]
- Shirzian, S.; Gronert, S. The gas-phase conformations of valine: an ab initio study. J. Mol. Struct. Theochem 1997, 397, 107–112. [Google Scholar] [CrossRef]
- Schäfer, L.; Klup-Newton, S.Q.; Siam, K.; Klimkowski, V.J.; Van Alsenoy, C. Ab initio studies of structural features not easily amenable to experiment. Part 71. Conformational analysis and structure of valine and threonine. J. Mol. Struct. Theochem 1990, 209, 373–385. [Google Scholar] [CrossRef]
- Stepanian, S.G.; Reva, I.D.; Radchenko, E.D.; Adamowicz, L. Combined Matrix-Isolation Infrared and Theoretical DFT and ab Initio Study of the Nonionized Valine Conformers. J. Phys. Chem. A 1999, 103, 4404–4412. [Google Scholar] [CrossRef]
- Van Alsenoy, C.; Klup, S.; Siam, K.; Klimkowski, V.J.; Ewbank, J.D.; Schäfer, L. Ab initio studies of structural features not easily amenable to experiment. Part 63. Conformational analysis and structure of serine. J. Mol. Struct. Theochem 1988, 181, 169–178. [Google Scholar] [CrossRef]
- Schäfer, L.; Siam, K.; Klimkowski, V.J.; Ewbank, J.D.; Van Alsenoy, C. Ab initio studies of structural features not easily amenable to experiment. Part 69. Conformational analysis and structure of cysteine. J. Mol. Struct. Theochem 1990, 204, 361–372. [Google Scholar] [CrossRef]
- Czinki, E.; Császár, A.G. Conformers of Gaseous Proline. Chem.-Eur. J. 2003, 9, 1008–1019. [Google Scholar] [CrossRef] [PubMed]
- Snoek, L.C.; Robertson, E.G.; Kroemer, R.T.; Simons, J.P. Conformational landscapes in amino acids: infrared and ultraviolet ion-dip spectroscopy of phenylalanine in the gas phase. Chem. Phys. Lett. 2000, 321, 49–56. [Google Scholar] [CrossRef]
- Snoek, L.C.; Kroemer, R.T.; Hockridge, M.R.; Simons, J.P. Conformational landscapes of armoatic amino acids in the gas phase: Infrared and ultraviolet ion dip spectroscopy of tryptophan. Phys. Chem. Chem. Phys. 2001, 3, 1819–1826. [Google Scholar] [CrossRef]
- Skurski, P.; Gutowski, M.; Barrios, R.; Simons, J. Non-ionic and zwitterionic forms of neutral arginine – an ab initio study. Chem. Phys. Lett. 2001, 337, 143–150. [Google Scholar] [CrossRef]
- Mc Quarrie, D.A. Statistical Thermodynamics; Harper and Row: New York, 1973. [Google Scholar]
© 2004 by MDPI (http://www.mdpi.org).
Share and Cite
Dehareng, D.; Dive, G. Vertical Ionization Energies of α-L-Amino Acids as a Function of Their Conformation: an Ab Initio Study. Int. J. Mol. Sci. 2004, 5, 301-332. https://doi.org/10.3390/i5110301
Dehareng D, Dive G. Vertical Ionization Energies of α-L-Amino Acids as a Function of Their Conformation: an Ab Initio Study. International Journal of Molecular Sciences. 2004; 5(11):301-332. https://doi.org/10.3390/i5110301
Chicago/Turabian StyleDehareng, Dominique, and Georges Dive. 2004. "Vertical Ionization Energies of α-L-Amino Acids as a Function of Their Conformation: an Ab Initio Study" International Journal of Molecular Sciences 5, no. 11: 301-332. https://doi.org/10.3390/i5110301
APA StyleDehareng, D., & Dive, G. (2004). Vertical Ionization Energies of α-L-Amino Acids as a Function of Their Conformation: an Ab Initio Study. International Journal of Molecular Sciences, 5(11), 301-332. https://doi.org/10.3390/i5110301




