Nucleic Acid Quadratic Indices of the “Macromolecular Graph’s Nucleotides Adjacency Matrix”. Modeling of Footprints after the Interaction of Paromomycin with the HIV-1 Ψ-RNA Packaging Region
Abstract
:Introduction
Materials and methods
Computational Methods
| Purine and pyrimidine bases (RNA/ADN) | f1 | f2 | Є260/1000 | ΔE1 | ΔE2 |
|---|---|---|---|---|---|
| Adenine (A) | 0.28 | 0.54 | 15.4 | 4.75 | 5.99 |
| Guanine (G) | 0.20 | 0.27 | 11.7 | 4.49 | 5.03 |
| Uracil (U) | 0.18 | 0.3 | 9.9 | 4.81 | 6.11 |
| Thymine (T) | 0.18 | 0.37 | 9.2 | 4.67 | 5.94 |
| Cytosine (C) | 0.13 | 0.72 | 7.5 | 4.61 | 6.26 |
= 0 otherwise
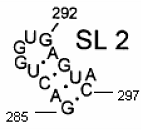 Secondary structure of an RNA fragment of the SL 2 motif (see Figure 1) | 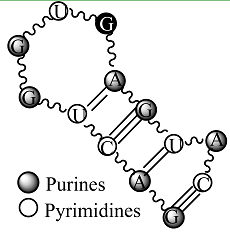 Macromolecular graph’s: an undirected graph with multiple edges Gm Macromolecular graph’s: an undirected graph with multiple edges Gm | Xm = [G A C U G G U G A G U A C]; Xm ∈ℜ13 In the definition of
Xm, as macromolecular vector, the symbol of the bases is used to indicate the corresponding AND-RNA bases property, for instance, f1. That is: if we write A it means f1(A), adenine first oscillator strength values or some bases property, which characterizes each nucleotide in the nucleic acid molecule. So, if we use the canonical bases of ℜ13, the coordinates of any macromolecular vector Xm coincide with the components of that macromolecular vector. [Xm]t = [0.20 0.28 0.13 0.18 0.20 0.20 0.18 0.20 0.28 0.20 0.18 0.28 0.13] [Xm]t: Transposed of [Xm] and it means the vector of the coordinates of Xm in Canonical base of ℜ13 (a row matrix) [Xm]: vector of the coordinates of Xm in Canonical base of ℜ13 (a columns matrix) 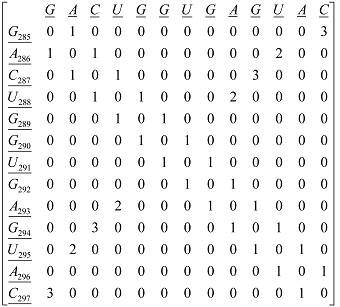 M1(Gm): Macromolecular graph’s nucleotide Adjacency Matrix | |||
| = [mX]tM0(Gm) [mX] = 0.5662 | |||||
| = [mX]tM1(Gm) [mX] = 1.7124 | |||||
| = [mX]tM2(Gm) [mX] = 6.7533 | |||||
| = [mX]tM3(Gm) [mX] = 25.3806 | |||||
| = [mX]tM4(Gm) [mX] = 105.5649 | |||||
| Nucleotide (N) | q0L(Xm, N) | q1L(Xm, N) | q2L(Xm, N) | q3L(Xm, N) | q4L(Xm, N) |
| G285 | 0.04 | 0.134 | 0.666 | 2.154 | 9.654 |
| A286 | 0.0784 | 0.1932 | 1.0668 | 3.5112 | 17.2256 |
| C287 | 0.0169 | 0.1378 | 0.5369 | 2.8223 | 10.1634 |
| U288 | 0.0324 | 0.1602 | 0.5328 | 2.0844 | 8.9226 |
| G289 | 0.04 | 0.076 | 0.254 | 0.748 | 2.738 |
| G290 | 0.04 | 0.076 | 0.156 | 0.422 | 1.136 |
| U291 | 0.0324 | 0.072 | 0.1512 | 0.3492 | 1.0872 |
| G292 | 0.04 | 0.092 | 0.232 | 0.786 | 2.8 |
| A293 | 0.0784 | 0.2128 | 0.8652 | 3.3768 | 12.6308 |
| G294 | 0.04 | 0.17 | 0.996 | 3.604 | 18.342 |
| U295 | 0.0324 | 0.1872 | 0.4572 | 2.6136 | 8.6328 |
| A296 | 0.0784 | 0.0868 | 0.5376 | 1.3608 | 7.4004 |
| C297 | 0.0169 | 0.1144 | 0.3016 | 1.5483 | 4.8321 |
| ARN fragment | 0.5662 | 1.7124 | 6.7533 | 25.3806 | 105.5649 |
= 1/2 kaij if vi or vj are contained within FR
= 0 otherwise
Footprinting Data
TOMOCOMD-CANAR Software
Statistical Analysis
Results and Discussion
Development of the Discrimination Function: Local (Nucleotide) quadratic indices and the probability of footprinting after RNA-Paromomycin interaction.
N = 101 λ = 0.43 D2 = 6.0 F(3.97) = 43.342 ρ = 10.1 p < 0.000
Local (Nucleotide) quadratic indices and modeling of Paromomycin’s affinity constant with HIV-1 Ψ-RNA
| Nucleotide | ΔP%a | P%-cvb | Nucleotide | ΔP%a | P%-cvb | Nucleotide | ΔP%a | P%-cvb |
|---|---|---|---|---|---|---|---|---|
| Training Set (Nucleotide non-‘footprinted’) | ||||||||
| RNA-A235 | 98.44 | 99.22 | RNA-A301 | 98.40 | 99.15 | RNA-A332 | 99.61 | 99.80 |
| RNA-G241 | 90.65 | 94.94 | RNA-A302 | 99.41 | 99.70 | RNA-G333 | 86.70 | 92.78 |
| RNA-C243 | -97.92* | 99.49* | RNA-U303 | 86.59 | 92.63 | RNA-A334 | 99.62 | 98.81 |
| RNA-U244 | -92.03* | 97.05* | RNA-U304 | 89.23 | 94.06 | RNA-G335 | 87.77 | 93.36 |
| RNA-G251 | -96.81* | 99.17* | RNA-A306 | 96.57 | 99.14 | RNA-G338 | 58.59 | 78.02 |
| RNA-G257 | 93.56 | 96.51 | RNA-G317 | 84.47 | 91.60 | RNA-G339 | -93.85* | 98.55* |
| RNA-G259 | 95.11 | 97.35 | RNA-G320 | 62.44 | 80.17 | RNA-G340 | 58.67 | 78.19 |
| RNA-G261 | 96.06 | 97.87 | RNA-A326 | 92.93 | 96.13 | RNA-G344 | 73.39 | 85.85 |
| RNA-C267 | -99.24* | 99.86* | RNA-A327 | 99.35 | 99.67 | RNA-A356 | 99.60 | 99.80 |
| RNA-A268 | -46.31* | 79.05* | RNA-G328 | 91.63 | 95.46 | RNA-A359 | 99.46 | 99.73 |
| RNA-A269 | 96.94 | 98.35 | RNA-G329 | 89.54 | 99.33 | |||
| RNA-A276 | -96.63* | 99.49* | RNA-A330 | 99.57 | 97.77 | |||
| Training Set (Nucleotides ‘footprinted’) | ||||||||
| RNA-G214 | -98.79 | 99.37 | RNA-G265 | -44.42 | 71.41 | RNA-G321 | -92.24 | 95.90 |
| RNA-C218 | -97.21 | 98.53 | RNA-G266 | -92.87 | 96.14 | RNA-C322 | -98.44 | 99.18 |
| RNA-C219 | -98.90 | 99.42 | RNA-A271 | -84.60 | 90.81 | RNA-U323 | -96.61 | 98.22 |
| RNA-A220 | -84.39 | 90.90 | RNA-G272 | -98.83 | 95.00 | RNA-A324 | -93.41 | 96.24 |
| RNA-G221 | -99.85 | 99.93 | RNA-C274 | -96.61 | 98.20 | RNA-G325 | -99.62 | 99.81 |
| RNA-A222 | -84.19 | 90.35 | RNA-G275 | -98.20 | 99.04 | RNA-G342 | -93.34 | 96.53 |
| RNA-A225 | -42.56 | 56.29 | RNA-G277 | -98.51 | 99.21 | RNA-C343 | -98.23 | 99.06 |
| RNA-C227 | 22.41* | 66.90 | RNA-G282 | -92.64 | 96.01 | RNA-C349 | -98.05 | 98.97 |
| RNA-C229 | -98.28 | 99.09 | RNA-G283 | -96.27 | 97.85 | RNA-C352 | -97.26 | 98.50 |
| RNA-U230 | -94.75 | 97.26 | RNA-C284 | -98.33 | 99.10 | RNA-G361 | -93.71 | 96.70 |
| RNA-C231 | -97.00 | 98.41 | RNA-G285 | -95.59 | 97.58 | RNA-C362 | -99.20 | 99.58 |
| RNA-U232 | -38.37 | 68.06 | RNA-C287 | -99.42 | 99.70 | RNA-A368 | -95.09 | 97.19 |
| RNA-C233 | -95.44 | 97.56 | RNA-U288 | -88.23 | 93.75 | RNA-A370 | -81.08 | 88.79 |
| RNA-C236 | -97.60 | 98.73 | RNA-A293 | -79.98 | 88.22 | RNA-U372 | -5.37 | 51.07* |
| RNA-G237 | -94.75 | 97.14 | RNA-G294 | -99.35 | 99.66 | RNA-U377 | -93.70 | 96.61 |
| RNA-G246 | -90.80 | 95.03 | RNA-U295 | -96.61 | 98.21 | RNA-C378 | -98.51 | 99.21 |
| RNA-C248 | -97.08 | 98.45 | RNA-C297 | -98.11 | 98.99 | RNA-U381 | -92.45 | 96.07 |
| RNA-U249 | -94.54 | 97.11 | RNA-G298 | -85.42 | 89.43 | RNA-G382 | -98.74 | 99.34 |
| RNA-C252 | -97.80 | 98.83 | RNA-C299 | -96.23 | 97.91 | RNA-G383 | -97.99 | 98.93 |
| RNA-U253 | -53.65 | 76.07 | RNA-C307 | -98.35 | 99.12 | RNA-C387 | -97.18 | 98.49 |
| RNA-C258 | 67.07* | 88.75* | RNA-U308 | -98.12 | 99.00 | RNA-C388 | -84.47 | 91.70 |
| RNA-C262 | 59.31* | 85.25 | RNA-A309 | -85.79 | 91.59 | |||
| RNA-C264 | -98.03 | 98.94 | RNA-G310 | -99.10 | 99.53 | |||
| nucleotide | ΔP%a | nucleotide | ΔP%a | nucleotide | ΔP%a |
|---|---|---|---|---|---|
| Test Set (Nucleotides non-‘footprinted’) | |||||
| RNA-A239 | 98.33 | RNA-A286 | -80.84* | RNA-A336 | 99.68 |
| RNA-A242 | 97.15 | RNA-C300 | -95.83* | RNA-G346 | 90.17 |
| RNA-C245 | 98.23 | RNA-G318 | 90.46 | RNA-A360 | 94.68 |
| RNA-G254 | 62.44 | RNA-G331 | 87.67 | ||
| Test Set (Nucleotides ‘footprinted’) | |||||
| RNA-G213 | -85.46 | RNA-U250 | -97.07 | RNA-G348 | -97.29 |
| RNA-G226 | -21.29 | RNA-G273 | 35.31* | RNA-G369 | -99.76 |
| RNA-U228 | -87.28 | RNA-C311 | -97.87 | RNA-U373 | -92.40 |
| RNA-C238 | -98.32 | RNA-U341 | 47.94* | ||
N = 23 R = 0.96 R2 = 0.92 s = 0.07 q2 = 0.85 scv = 0.09 F(4.18) = 54.910 p<0.0000
+0.083(±0.035) 4O(Θ8)
N = 24 R = 0.91 R2 = 0.83 s = 0.115 q2 = 0.825 F(3.20) = 31.48 p<0.0000
| NUC | Obsa | Predb | P-cvc | Predd | P-cvf | NUC | Obsa | Predb | P-cvc | Predd | P-cvf |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A235 | 1.204 | 1.132 | 1.111 | 1.166 | 0.359 | G335 | 0.845 | 0.852 | 0.853 | 0.862 | 0.845 |
| A239 | 1.204 | 1.173 | 1.164 | 1.166 | 0.359 | G338 | 0.778 | 0.736 | 0.732 | 0.672 | 0.778 |
| G251 | 0.447 | 0.350 | 0.304 | 0.518 | 0.032 | G339 | 0.778 | 0.647 | 0.566 | 0.545 | 0.778 |
| G254 | 0.447 | 0.552 | 0.578 | 0.518 | 0.032 | G340 | 0.778 | 0.734 | 0.730 | 0.672 | 0.778 |
| C267 | 0.903 | 0.893 | 0.879 | 0.856 | 0.058 | G344 | 0.845 | 0.814 | 0.811 | 0.735 | 0.845 |
| A268 | 0.903 | 1.003 | 1.049 | 0.856 | 0.125 | G346 | 0.845 | 0.855 | 0.856 | 0.862 | 0.845 |
| A269 | 0.903 | 0.984 | 1.026 | 0.987 | 0.125 | G363 | 0.415 | 0.488 | 0.522 | 0.399 | 0.415 |
| A286 | 0.778 | 0.704 | 0.667 | 1.024 | -0.067 | G364 | 0.415 | 0.477 | 0.495 | 0.399 | 0.415 |
| G328 | 0.845 | 0.851 | 0.852 | 0.862 | 0.430 | G365 | 0.415 | 0.542 | 0.564 | 0.399 | 0.415 |
| G329 | 0.845 | 0.852 | 0.853 | 0.862 | 0.430 | G366 | 0.415 | 0.394 | 0.386 | 0.594 | 0.415 |
| G331 | 0.845 | 0.852 | 0.853 | 0.862 | 0.430 | G367 | 0.415 | 0.378 | 0.369 | 0.594 | 0.415 |
| G333 | 0.845 | 0.852 | 0.853 | 0.862 | 0.845 |
| f2q3L(xm) | ΔE1q0L(xm) | ΔE1q10L(xm) | ∈250q3L(xm) | |
|---|---|---|---|---|
| f2q3L(xm) | 1 | -0.55 | -0.68 | -0.41 |
| ΔE1q0L(xm) | 1 | 0.37 | 0.17 | |
| ΔE1q10L(xm) | 1 | -0.31 | ||
| ∈250q3L(xm) | 1 |
Concluding Remarks
Acknowledgements
References
- Hua, S.; Sun, Z. Support Vector Machine Approach for Protein Subcelular Localization Prediction. Bioinformatics. 2001, 17, 721–728. [Google Scholar]
- Benson, D. A.; Karsch-Mizrachi, I.; Lipman, D. J.; Ostell, J.; Rapp, B. A.; Wheeler, D. L. Gen bank. Nucleic Acid Res. 2000, 28, 15–18. [Google Scholar]
- Yuan, Z. Prediction of Proteins Subcellular Location Using Markov Chain Models. FEBS Lett. 1999, 451, 23–26. [Google Scholar]
- Tullius, T. D. Physical Studies of Protein-DNA Complexes by Footprinting. Ann. Rev. Biophys. Bio. 1989, 18, 213–237. [Google Scholar]
- Brenowitz, M.; Senear, D. F.; Shea, M. A.; Ackers, G. K. Quantitative Dnase Footprint Titration: a Method for Studying Protein-DNA Interactions. Methods Enzymol. 1986, 130, 132–181. [Google Scholar]
- Henn, A.; Halfon, J.; Kela, I.; Orion, I.; Sagi, I. Nucleic Acid Fragmentation on the Millisecond Timesacale Using a Conventional x-Ray Rotating Anode Source: Application to Protein-DNA Footprinting. Nucleic Acid Res. 2001, 29, e122. [Google Scholar]
- Galas, D. J.; Schmithz, A. Dnase Footprinting: a Simple Method for the Detection of Protein-DNA Binding Specificity. Nucleic Acids Res. 1978, 5, 3157–3170. [Google Scholar]
- Ozoline, O. N.; Fujita, N.; Ishihama, A. Mode of DNA-protein Interaction between the C-terminal Domain of Escherichia Coli RNA Polymerase α Subunit and T7D Promoter UP Element. Nucleic Acids Res. 2001, 29, 4909–4919. [Google Scholar]
- McPike, P. M.; Goodisman, J.; Dabrowiak, C. J. Footprinting and Circular Dichroims Studies on Paromomycin Binding to the Packaging Region of the Human Immunodeficiency Virus Type-1. Bioorg. Med. Chem. 2002, 10, 3663–3672. [Google Scholar]
- Sullivan, J. M.; Goodisman, J.; Dabrowiak, C. J. Absorption Studies on Aminoglycosides Binding to the Packaging Region of the Human Immunodeficiency Virus Type-1. Bioorg. Med. Chem. Lett. 2002, 12, 615–618. [Google Scholar]
- Gale, E. F.; Gundliff, E.; Reynolds, P. E.; Richmon, M. H.; Waring, M. J. The Molecular Basis of Antibiotic Action; John Wiley & Sons: London, 1981. [Google Scholar]
- Lynch, S. R.; Recht, M. I.; Puglisi, J. D. Biochemical and Nuclear Magnetic Resonance Studies of Aminoglycoside-RNA Complexes. Meth. Enzymol. 2000, 317, 240–261. [Google Scholar]
- Weiss, R.; Teich, N.; Varmus, H.; Coffin, J., (Eds). RNA Tumor Viruses; Cold Spring Harbor Laboratory: Cold Spring Harbor (N.Y.), 1984. [Google Scholar]
- Wilson, W. D.; Li, K. Targeting RNA with Small Molecules. Curr. Med. Chem. 2000, 7, 73–98. [Google Scholar]
- Marrero-Ponce, Y. Total and Local Quadratic Indices of the “Molecular Pseudograph`s Atom Adjacency Matrix”: Applications to the Prediction of Physical Properties of Organic Compounds. Molecules 2003, 8, 687–726, http://www.mdpi.org. [Google Scholar]
- Marrero-Ponce, Y. Linear Indices of the “Molecular Pseudograph’s Atom Adjacency Matrix”: Definition, Significance-Interpretation and Application to QSAR Analysis of Flavone Derivatives as HIV-1 Integrase Inhibitors. J. Chem. Inf. Comput. Sci. In Press. [CrossRef]
- Marrero-Ponce, Y.; Cabrera, M. A.; Romero, V.; Ofori, E.; Montero, L. A. Total and Local Quadratic Indices of the “Molecular Pseudograph’s Atom Adjacency Matrix”. Application to Prediction of Caco-2 Permeability of Drugs. Int. J. Mol. Sci. 2003, 4, 512–536, www.mdpi.org/ijms/. [Google Scholar]
- Marrero, Y.; Cabrera, M. A.; Romero, V.; González, D. H.; Torrens, F. A New Topological Descriptors Based Model for Predicting Intestinal Epithelial Transport of Drugs in Caco-2 Cell Culture. J. Pharm. Pharm. Sci. 2004, 7, 186–199. [Google Scholar]
- Marrero, Y.; González, H.; Romero, V.; Torrens, F.; Castro, E. A. 3D-Chiral Quadratic Indices of the “Molecular Pseudograph’s Atom Adjacency Matrix” and Their Application to Central Chirality Codification: Classification of ACE Inhibitors and Prediction of σ-Receptor Antagonist Activities. Bioorg. Med. Chem. 2004, 12, 5331–5342. [Google Scholar]
- Stryer, L. Biochemistry; W. H. Freeman and Company: New York, 1995. [Google Scholar]
- Mathews, C. K.; van Holde, K. E.; Ahern, K. G. Biochemistry; Addison Wesley Longman: San Francisco, 2000. [Google Scholar]
- Lehninger, A. L.; Nelson, D. L.; Cox, M. M. Principles of Biochemistry; Worth Publishers: New York, 1993. [Google Scholar]
- Alberts, B.; Bray, D.; Lewis, J.; Raff, M.; Roberts, K.; Watson, J. D. Molecular Biology of the Cell; Garland: New York and London, 1994. [Google Scholar]
- Pogliani, L. From Molecular Connectivity Indices to Semiempirical Connectivity Terms: Recent Trends in Graph Theoretical Descriptors. Chem. Rev. 2000, 100, 3827–3858. [Google Scholar]
- Randić, M. Generalized Molecular Descriptors. J. Math. Chem. 1991, 7, 155–168. [Google Scholar]
- Marrero-Ponce, Y.; Romero-Zaldivar, V. TOMO-COMD software; Central University of Las Villas. TOMOCOMD, (TOpological MOlecular COMputer Design) for Windows, version 1.0 is a preliminary experimental version; in future a professional version will be available on request from Y. Marrero: yovanimp@qf.uclv.edu.cu; ymarrero77@yahoo.es; 2002. [Google Scholar]
- STATISTICA version. 5.5; Statsoft, Inc., 1999.
- McFarland, J. W.; Gans, D. J. Linear Discrminant Analysis and Cluster Significance Analysis. In Comprehesive Medicinal Chemistry; Hansch, C., Sammes, P. G., Taylor, J. B., Eds.; Pergamon Press: Oxford, 1990; vol. 4, pp. 667–689. [Google Scholar]
- Golbraikh, A.; Tropsha, A. Beware of q2! J. Mol. Graph. Modell. 2002, 20, 269–276. [Google Scholar]
- Wold, S.; Erikson, L. Statistical Validation of QSAR Results. Validation Tools. In Chemometric Methods in Molecular Design; van de Waterbeemd, H., Ed.; VCH Publishers: New York, 1995; pp. 309–318. [Google Scholar]
- García-Domenech, R.; de Julián-Ortíz, J. V. Antimicrobial Activity in a Heterogeneous Group of Compounds. J. Chem. Inf. Comput. Sci. 1998, 38, 445–449. [Google Scholar]
- González, H.; Ramos, R.; Molina, R. Markovian Negentropies in Bioinformatics. 1. A picture of Footprints after the Interaction of the HIV-1 ψ-RNA Packaging Region with Drugs. Bioinformatics 2003, 16, 2079–2087. [Google Scholar]
- Basak, S. C.; Balaban, A. T.; Grunwald, G. D.; Gute, B. D. Topological Indices: Their Nature and Mutual Relatedness. J. Chem. Inf. Comput. Sci. 2000, 40, 891–898. [Google Scholar]
- Cronin, M. T. D.; Schultz, T. W. Pitfalls in QSAR. J. Mol. Struct. (Theochem) 2003, 622, 39–51. [Google Scholar]
- Alzina, R. B. Introduccion Conceptual al Análisis Multivariable. Un Enfoque Informático con los paquetes SPSS-X, BMDP, LISREL Y SPAD; PPU SA: Barcelona, 1989; Chapter 8; Vol. 1, p. 202. [Google Scholar]
- Randić, M. Orthogonal Molecular Descriptors. New J. Chem. 1991, 15, 517–525. [Google Scholar]
- Randić, M. Fitting of Nonlinear Regression by Orthogonalized Power Series. J. Comput. Chem. 1993, 14, 363–370. [Google Scholar]
© 2004 by MDPI (http://www.mdpi.org).
Share and Cite
Ponce, Y.M.; Nodarse, D.; Díaz, H.G.; De Armas, R.R.; Zaldivar, V.R.; Torrens, F.; Castro, E.A. Nucleic Acid Quadratic Indices of the “Macromolecular Graph’s Nucleotides Adjacency Matrix”. Modeling of Footprints after the Interaction of Paromomycin with the HIV-1 Ψ-RNA Packaging Region. Int. J. Mol. Sci. 2004, 5, 276-293. https://doi.org/10.3390/i5110276
Ponce YM, Nodarse D, Díaz HG, De Armas RR, Zaldivar VR, Torrens F, Castro EA. Nucleic Acid Quadratic Indices of the “Macromolecular Graph’s Nucleotides Adjacency Matrix”. Modeling of Footprints after the Interaction of Paromomycin with the HIV-1 Ψ-RNA Packaging Region. International Journal of Molecular Sciences. 2004; 5(11):276-293. https://doi.org/10.3390/i5110276
Chicago/Turabian StylePonce, Yovani Marrero, Delvin Nodarse, Humberto González Díaz, Ronal Ramos De Armas, Vicente Romero Zaldivar, Francisco Torrens, and Eduardo A. Castro. 2004. "Nucleic Acid Quadratic Indices of the “Macromolecular Graph’s Nucleotides Adjacency Matrix”. Modeling of Footprints after the Interaction of Paromomycin with the HIV-1 Ψ-RNA Packaging Region" International Journal of Molecular Sciences 5, no. 11: 276-293. https://doi.org/10.3390/i5110276
APA StylePonce, Y. M., Nodarse, D., Díaz, H. G., De Armas, R. R., Zaldivar, V. R., Torrens, F., & Castro, E. A. (2004). Nucleic Acid Quadratic Indices of the “Macromolecular Graph’s Nucleotides Adjacency Matrix”. Modeling of Footprints after the Interaction of Paromomycin with the HIV-1 Ψ-RNA Packaging Region. International Journal of Molecular Sciences, 5(11), 276-293. https://doi.org/10.3390/i5110276




