A. Potential energy curves
The potential energy curves have been carried out using the MOLPRO suite of
ab initio programs [
14] at the state average CASSCF-MRCI level of theory. The active space includes the n=3 and n=4(sp) orbitals for the sulfur element, and the 1s orbital for hydrogen. A pseudopotential has been used to take account of the core electrons of the sulfur atom. Tests have been performed for the choice of this pseudopotential and the basis of atomic orbitals. The ECP10sdf 10 core-electron relativistic pseudopotential has been used for the sulfur atom [
15] with correlation-consistent aug-cc-pVQZ basis sets of Dunning for sulfur and hydrogen [
16]. Such a basis set shows a quite good agreement with experiment [
17] for the atomic energy levels with a discrepancy in the range 0.01-0.14 eV (
Table I).
Table I.
Comparison of atomic energy levels with experiment [
17] (in eV).
Table I.
Comparison of atomic energy levels with experiment [17] (in eV).
| | MRCI calculation | Experiment |
|---|
| S3+(3s23p)2P° | 35.11 | 34.98 |
| S2+(3s3p3)3S° + H+ | | 17.05 |
| S2+(3s3p3)3P° + H+ | 12.31 | 12.17 |
| S2+(3s3p3)3D° + H+ | 10.34 | 10.35 |
| S2+(3s23p2)3P + H+ | 0.0 | 0.0 |
The spin-orbit effects may be neglected in the energy range of interest so triplet and singlet manifolds can be considered separately. From the atomic energy level data, it appears clearly that the S
2+(3s
23p3d)
3P° electron capture level cannot account for the present charge transfer mechanism. Effectively, the asymptotic energy difference between the entry channel
1,3Π,
1,3Σ
+ {S
3+(3s
23p)
2P° + H(1s)
2S} and the capture levels correlated to the {S
2+(3s
23p3d)
3P° + H
+1S} configuration is shown in tables to be equal to 3.65 eV, quite different from the energy defect of 6.2 eV observed experimentally for peak A. From the asymptotical repulsion term, this energy difference would lead to a long range interaction with an avoided crossing around R=15 a.u. which could hardly explain an important population of the corresponding capture channel. It seems thus likely, as proposed by Wilson
et al. [
6], to consider the capture level S
2+(3s
23p3d)
3F°, accessible from the entry channel
1,3Π,
1,3Σ
+ {S
3+(3s
23p)
2P° + H(1s)
2S}. The collisional system appears thus relatively complex, and a great number of states have to be taken into account in both the triplet and singlet manifold including one-electron capture processes as well as reactions of capture and excitation of the 3s electron:
| S3+(3s23p)2P° + H(1s)2S | 3Π, 3Σ+ | 1Π, 1Σ+ | entry channel |
| S2+(3s3p3)1P° + H+1S | | 1Π, 1Σ+ | |
| S2+(3s3p3)3S° + H+1S | 3Σ- | | |
| S2+(3s23p3d)3F° + H+1S | 3Φ, 3Π, 3Δ, 3Σ+ | | |
| S2+(3s3p3)1D° + H+1S | | 1Π, 1Δ, 1Σ- | |
| S2+(3s3p3)3P° + H+1S | 3Π, 3Σ+ | | |
| S2+(3s3p3)3D° + H+1S | 3Π, 3Δ, 3Σ- | | |
| S2+(3s23p2)1S + H+1S | | 1Σ+ | |
| S2+(3s23p2)1D + H+1S | | 1Π, 1Δ, 1Σ+ | |
| S2+(3s23p2)3P + H+1S | 3Π, 3Σ- | | |
The potentials correlated to the S
3+(3s
23p)
2P° + H entry channel are displayed in
Figures 1a,b for singlet states, and in
Figure 2a,b for triplet ones. The Σ
- levels have not been taken into account.
Figures 1a,b.
Adiabatic potential energy curves of the
1Σ
+,
1Δ and
1Π states of the S
3+(3s
23p) + H collisional system.
![Ijms 05 00265 i001]() 1
1Σ
+ states;
![Ijms 05 00265 i002]() 1
1Δ states;
![Ijms 05 00265 i003]() 1
1Π states. 1,
1Σ
+,
1Δ and
1Π states corresponding to {S
2+(3s
23p
2)
1D + H
+1S}; 2,
1Σ
+ state corresponding to {S
2+(3s
23p
2)
1S + H
+1S}; 3,
1Δ and
1Π states corresponding to {S
2+(3s3p
3)
1D° + H
+1S}; 4,
1Σ
+ and
1Π states corresponding to {S
2+(3s3p
3)
1P° + H
+1S}; 5,
1Σ
+ and
1Π states corresponding to {S
3+(3s
23p)
2P° + H(1s)
2S}, entry channel.
Figures 1a,b.
Adiabatic potential energy curves of the
1Σ
+,
1Δ and
1Π states of the S
3+(3s
23p) + H collisional system.
![Ijms 05 00265 i001]() 1
1Σ
+ states;
![Ijms 05 00265 i002]() 1
1Δ states;
![Ijms 05 00265 i003]() 1
1Π states. 1,
1Σ
+,
1Δ and
1Π states corresponding to {S
2+(3s
23p
2)
1D + H
+1S}; 2,
1Σ
+ state corresponding to {S
2+(3s
23p
2)
1S + H
+1S}; 3,
1Δ and
1Π states corresponding to {S
2+(3s3p
3)
1D° + H
+1S}; 4,
1Σ
+ and
1Π states corresponding to {S
2+(3s3p
3)
1P° + H
+1S}; 5,
1Σ
+ and
1Π states corresponding to {S
3+(3s
23p)
2P° + H(1s)
2S}, entry channel.
For the singlet manifold, the potential energy curves show clearly a relatively long range crossing, around R=13 a.u., between both the 1Π and 1Σ+ entry channels and the corresponding capture levels of the {S2+(3s3p3)1P° + H+1S} configuration. This crossing is associated with an energy defect of about 4.0 eV and cannot be attributed to any experimental peak, in fact such a long range crossing might be considered as almost inactive in the charge transfer mechanism. However, an efficient avoided crossing may be considered near R=7 a.u. corresponding to the interaction with the 1Π {S2+(3s3p3)1D° + H+1S} level, it corresponds to an energy defect of 8.2 eV and may contribute to the experimental peak B.
According to the statistical weight, the triplet manifold accounts for ¾ of the population of the ground state entry channel, against ¼ for the singlet manifold, and appears thus to be preponderant in the charge transfer mechanism. The triplet potential energy curves show several avoided crossings which may play a quite important role. Two short range avoided crossings are observed with the
3Π,
3Σ
+ levels corresponding to the {S
2+(3s3p
3)
3P° + H
+1S} configuration, around R=6 a.u.; they are associated with an energy defect of 9.19 eV and may contribute to the experimental peak B. Another interaction appears with the
3Π {S
2+(3s3p
3)
3D° + H
+1S} level, around R=5 a.u., which may contribute to peak C, with an energy defect of 11.16 eV. But the most important feature appears for the state quoted 4 in
Fig. 2a,b which exhibits an avoided crossing around R=9.7 a.u., corresponding to an energy defect of 5.6 eV, with the entry channel in both
3Σ
+ and
3Π symmetries. This channel is associated simultaneously with state symmetry
3Σ
+,
3Δ,
3Π, and
3Φ and may thus be attributed without any ambiguity to the {S
2+(3s
23p3d)
3F° + H
+1S} configuration, confirming the experimental deduction of Wilson et al. [
6]. The energy defect appears however slightly lower than evidenced for the experimental peak A. From our
ab-initio MRCI calculations, the S
2+(
3F°) capture level appears at an energy of 15.8 eV above the S
2+(3s
23p
2)
3P ground state, a somewhat higher value than the 15.03 eV experimental value of Wilson et al. [
6] and the 15.8 eV value given by the NIST Database [
13], although the set of molecular calculations appears to be globally in good accordance with the tabulated energies as shown in
Table II.
Table II.
Comparison with experiment [
17] for asymptotic energy levels (in a.u.)
Table II.
Comparison with experiment [17] for asymptotic energy levels (in a.u.)
| | MRCI calculation | Experiment |
|---|
| S3+(3s23p)2P° + H(1s)2S | 0.0 | 0.0 |
| S2+(3s3p3)3S° + H+ | | -0.1572 |
| S2+(3s3p3)1P° + H+ | -0.1477 | -0.1628 |
| S2+(3s3p3d)3F° + H+ | -0.2063 | -0.2313a |
| S2+(3s3p3)1D° + H+ | -0.3019 | -0.3117 |
| S2+(3s3p3)3P° + H+ | -0.3379 | -0.3363 |
| S2+(3s3p3)3D° + H+ | -0.4105 | -0.4032 |
| S2+(3s23p2)1S + H+ | -0.6601 | -0.6625 |
| S2+(3s23p2)1D + H+ | -0.7371 | -0.7347 |
| S2+(3s23p2)3P + H+ | -0.7905 | -0.7837 |
Figures 2a,b.
Adiabatic potential energy curves of the
3Σ
+,
3Δ,
3Π and
3Φ states of the S
3+(3s
23p) + H collisional system.
![Ijms 05 00265 i001]() 3
3Σ
+ states;
![Ijms 05 00265 i002]() 3
3Δ states;
![Ijms 05 00265 i003]() 3
3Π states;
![Ijms 05 00265 i004]()
Φ state. 1,
3Π state corresponding to {S
2+(3s
23p
2)
3P + H
+1S}; 2,
3Δ and
3Π states corresponding to {S
2+(3s3p
3)
3D° + H
+1S}; 3,
3Σ
+ and
3Π states corresponding to {S
2+(3s3p
3)
3P° + H
+1S}; 4,
3Σ
+,
3Δ,
3Π and
3Φ states corresponding to {S
2+(3s
23p3d)
3F° + H
+1S}; 5,
3Σ
+ and
3Π states corresponding to {S
3+(3s
23p)
2P° + H(1s)
2S}, entry channel.
Figures 2a,b.
Adiabatic potential energy curves of the
3Σ
+,
3Δ,
3Π and
3Φ states of the S
3+(3s
23p) + H collisional system.
![Ijms 05 00265 i001]() 3
3Σ
+ states;
![Ijms 05 00265 i002]() 3
3Δ states;
![Ijms 05 00265 i003]() 3
3Π states;
![Ijms 05 00265 i004]()
Φ state. 1,
3Π state corresponding to {S
2+(3s
23p
2)
3P + H
+1S}; 2,
3Δ and
3Π states corresponding to {S
2+(3s3p
3)
3D° + H
+1S}; 3,
3Σ
+ and
3Π states corresponding to {S
2+(3s3p
3)
3P° + H
+1S}; 4,
3Σ
+,
3Δ,
3Π and
3Φ states corresponding to {S
2+(3s
23p3d)
3F° + H
+1S}; 5,
3Σ
+ and
3Π states corresponding to {S
3+(3s
23p)
2P° + H(1s)
2S}, entry channel.
B. Radial and rotational coupling matrix elements
The radial coupling matrix elements between all pairs of states of the same symmetry have been calculated by means of the finite difference technique:
with the parameter Δ=0.0012 a.u. as previously tested. The sulfur nucleus has been chosen as origin of electronic coordinates. The main matrix elements are displayed in
Figure 3 for the singlet manifold, and in
Figures 4a,b for the triplet manifold.
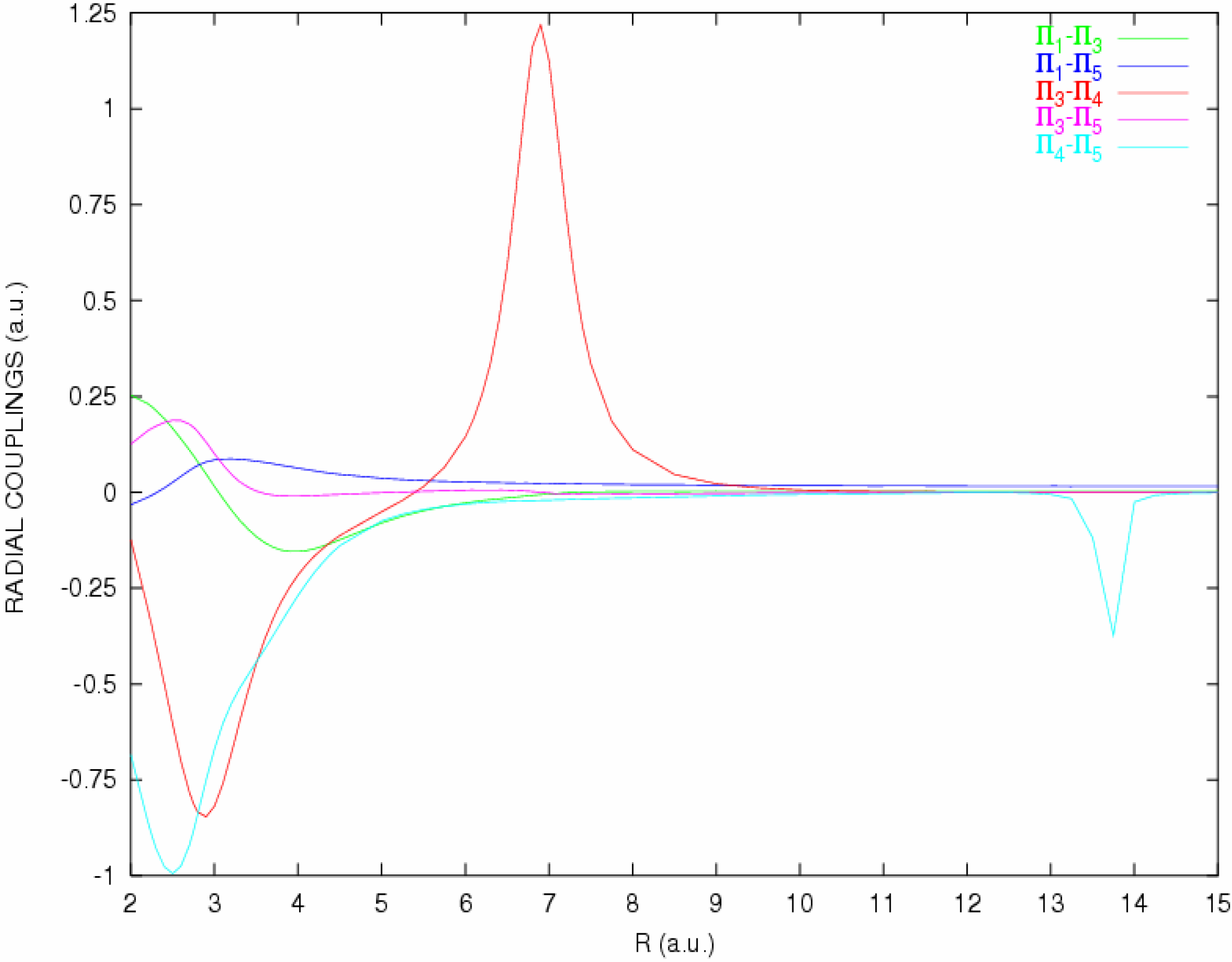
Figure 3.
Radial coupling matrix elements between
1Π states of the S
3+(3s
23p) + H collisional system (see labels in
Figures 1a,b).
Figure 3.
Radial coupling matrix elements between
1Π states of the S
3+(3s
23p) + H collisional system (see labels in
Figures 1a,b).
They present the same features as exhibited by the potential energy curves. For the singlet manifold, the couplings between the 1Σ+ and 1Δ states remain small for all distances, lower than 0.2 a.u., in relation with the smooth interactions observed between the corresponding potentials. The only sharp peak is observed between 1Π states, around R=7 a.u and about 1.25 a.u. high, in correspondence with the avoided crossing between the 1Π entry channel and the 1Π {S2+(3s3p3)1D° + H+1S} capture channel.
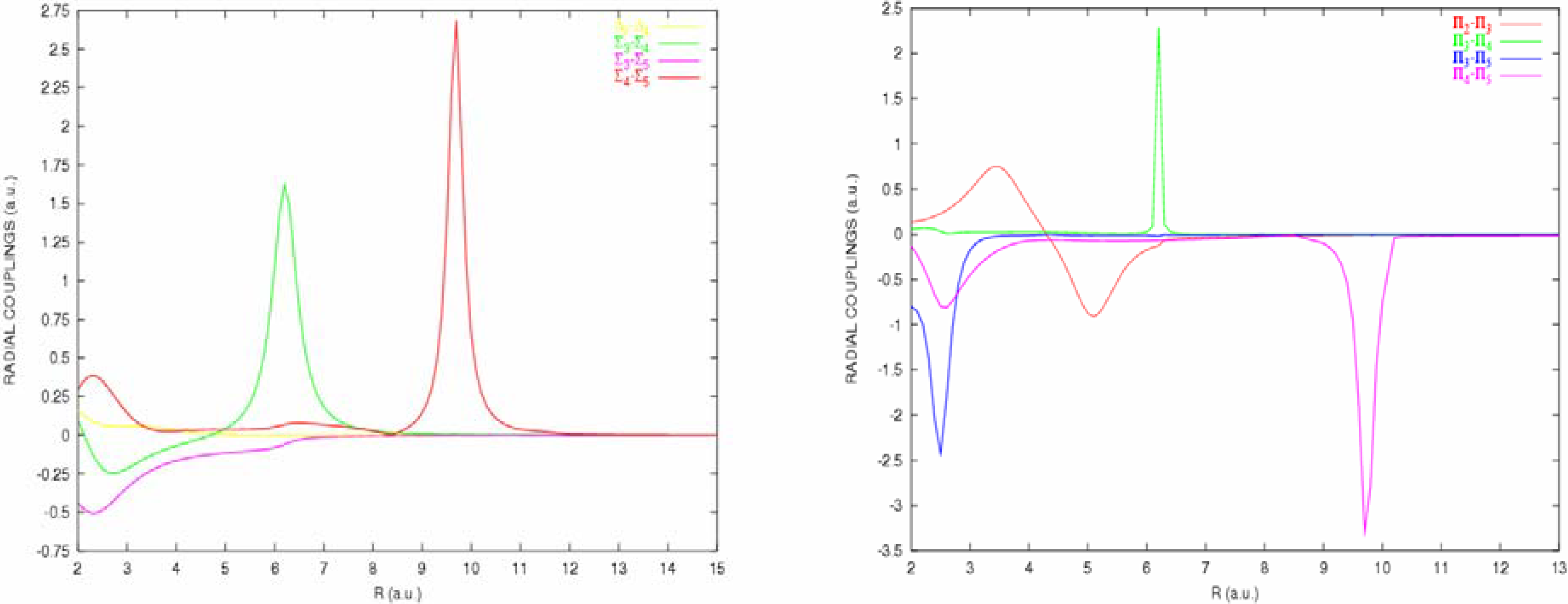
For the triplet manifold, 3Σ+ states show two peaks, one around R=6 a.u. corresponding to the avoided crossing between the entry channel and the 3Σ+{S2+(3s3p3)3P° + H+1S} capture level associated with the experimental peak B, and a sharper one, around R=9.7 a.u., in correspondence with the strong avoided crossing between the entry channel and the 3Σ+ {S2+(3s23p3d)3F° + H+1S} excited one-electron capture level. This radial coupling matrix element reaches 2.75 a.u. and is clearly the most important one for the charge transfer process, associated with the experimental peak A. Radial coupling between 3Δ states remain small for all internuclear distances. The 3Π levels show also such a sharp peak for the radial coupling corresponding to the avoided crossing with the 3Π {S2+(3s23p3d)3F° + H+1S} capture channel. It reaches even 3.5 a.u. and is markedly higher that the other radial coupling matrix elements. The coupling associated with the avoided crossing between the 3Π entry channel and the 3Π{S2+(3s3p3)3P° + H+1S} level presents a peak, 2.5 a.u. high, around R=6 a.u. and the interaction with the 3Π {S2+(3s3p3)3D° + H+1S} capture channel shows a smooth variation of the radial coupling matrix element with a hump around R=5 a.u..
Figures 4a,b.
Radial coupling matrix elements between
3Σ
+,
3Δ and
3Π states of the S
3+(3s
23p) + H collisional system (see labels in
Figures 2a,b).
Figures 4a,b.
Radial coupling matrix elements between
3Σ
+,
3Δ and
3Π states of the S
3+(3s
23p) + H collisional system (see labels in
Figures 2a,b).
The rotational matrix elements
between states of angular moment ΔΛ=±1 have been calculated directly from the quadrupole moment tensor. The coupling matrix elements for the triplet manifold are displayed in
Figure 5. Rotational couplings between Σ-Π and Π-Δ are zero at long range for states corresponding to different configurations, as shown for example for the coupling between
3Σ
+{S
3+(3s3p
3)
3P° + H
+1S} and
3Π{S
2+(3s3p
3)
3D° + H
+1S} levels. The couplings corresponding to the same configuration reach the asymptotical value 1.0 a.u., as shown for the
3Σ
+-
3Π couplings corresponding to the {S
3+(3s
23p)
2P° + H(1s)
2S} and the {S
2+(3s3p
3)
3P + H
+1S} configurations, as well as to the
3Π-
3Δ rotational couplings associated with the {S
2+(3s3p
3)
3D° + H
+1S} configuration. For the {S
2+(3s
23p3d)
3F° + H
+1S} capture channel, both
3Σ
+ and
3Δ states contribute to the rotational coupling with the
3Π level, giving a double value for the matrix element. In correspondence with the crossing between this S
2+(3s
23p3d)
3F° capture level and the entry channel, an abrupt decrease may be observed for this rotational coupling to reach the value around 1.0 a.u. corresponding to the 5
3Σ-5
3Π coupling of the entry channel, and inversely.
Figure 5.
Rotational coupling matrix elements between
3Σ
+-
3Π and
3Π-
3Δ states of the S
3+(3s
23p) + H collisional system (see labels in
Fig. 2a,b).
______ 4
3Σ + 4
3Δ/ 4
3Π;
![Ijms 05 00265 i003]()
5
3Σ / 5
3Π;
![Ijms 05 00265 i004]()
3
3Σ / 3
3Π;
![Ijms 05 00265 i005]()
2
3Δ / 2
3Π;
![Ijms 05 00265 i001]()
3
3Σ / 2
3Π
Figure 5.
Rotational coupling matrix elements between
3Σ
+-
3Π and
3Π-
3Δ states of the S
3+(3s
23p) + H collisional system (see labels in
Fig. 2a,b).
______ 4
3Σ + 4
3Δ/ 4
3Π;
![Ijms 05 00265 i003]()
5
3Σ / 5
3Π;
![Ijms 05 00265 i004]()
3
3Σ / 3
3Π;
![Ijms 05 00265 i005]()
2
3Δ / 2
3Π;
![Ijms 05 00265 i001]()
3
3Σ / 2
3Π
C. Collision dynamics
The collision dynamics has been performed in the 2-8 keV laboratory energy range by a semi-classical approach using the EIKONXS code based on an efficient propagation method [
18]. Radial and rotational couplings have been taken into account in the calculation allowing consideration of all the states coupled to the
1,3Σ
+ and
1,3Π entry channels. The translation effects may be taken into account in the frame of the common translation factor approximation developed by Errea
et al. [
19] which introduces a correction over the radial and rotational coupling matrix elements determined from the quadrupole moment tensor. The radial and rotational coupling matrix elements may indeed be transformed respectively into
and
where
εK and
εL are the electronic energies of states
ψK and
ψL, and
z2 and
zx are the components of the quadrupole moment tensor. The sulfur nucleus has been taken as origin of the electronic coordinates.
The cross sections corresponding to the different exit channels have been calculated with respect to the statistical weights ¼ and ¾ for respectively the singlet and triplet manifold, and taking account of the 1/3 and 2/3 statistical weight for respectively the Σ and Π entry channels. The results are presented in
Table III and
Figure 6 and appear to be in good agreement with the experimental data.
Table III.
Partial cross sections on the exit channels in the S3+(3s23p)2P° + H process (in 10-16 cm2).
Table III.
Partial cross sections on the exit channels in the S3+(3s23p)2P° + H process (in 10-16 cm2).
| Elab (keV) | 2.00 | 2.88 | 3.92 | 5.12 | 6.49 | 8.01 |
|---|
| S2+(3s3p3)1P° | 0.06 | 0.79 | 0.63 | 0.73 | 0.73 | 0.87 |
| S2+(3s23p3d)3F° | 17.63 | 16.29 | 14.57 | 13.54 | 13.08 | 11.85 |
| σA |
| S2+(3s3p3)1D° | 0.02 | 0.03 | 0.05 | 0.12 | 0.23 | 0.31 |
| σ1B |
| S2+(3s3p3)3P° | 9.49 | 11.90 | 12.19 | 10.54 | 9.52 | 8.37 |
| σ2B |
| S2+(3s3p3)3D° | 6.40 | 6.85 | 8.08 | 7.78 | 7.87 | 7.63 |
| σC |
| S2+(3s23p2)3P | 0.0001 | 0.0004 | 0.0006 | 0.0016 | 0.0018 | 0.0036 |
| σA/σB | 1.85 | 1.36 | 1.19 | 1.27 | 1.34 | 1.36 |
| σB/σC | 1.48 | 1.74 | 1.51 | 1.37 | 1.24 | 1.14 |
Effectively, the S2+(3s23p3d)3F° capture channel attributed to peak A is clearly the dominant charge transfer channel. With regard to the energy defect, two exit channels may contribute to the experimental peak B and σB=σ1B+σ2B with a dominant contribution σ2B of the S2+(3s3p3)3P° capture level, this leads to a ratio σA/σB for the partial cross sections between peak A and peak B mainly around 1.3 as observed on the experimental spectra.
Figure 6.
Calculated cross-sections on peak A, B, C (in 10
-16 cm
2) and comparison with experimental data [
6].
(experiment)/
(calculation), σ
A/σ
B;
(experiment)/
(calculation), σ
B /σ
C.
Figure 6.
Calculated cross-sections on peak A, B, C (in 10
-16 cm
2) and comparison with experimental data [
6].
(experiment)/
(calculation), σ
A/σ
B;
(experiment)/
(calculation), σ
B /σ
C.
Both peaks A and B are shown to decrease at higher energies. The partial cross section on peak C corresponding to the S2+(3s3p3)3D° exit channel is slightly underestimated and remains always lower than peak B, nevertheless it increases at higher energies and reaches the same order of magnitude as peak B as observed experimentally. The partial cross sections on the S2+(3s3p3)1P° channel increases also with energy but remains much lower. The cross sections towards the S2+(3s23p2)1S and S2+(3s23p2)1D exit channels are almost zero for all collision energies, and the cross sections on the S2+(3s23p2)3P capture channel remain negligible.
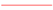 1Σ+ states;
1Σ+ states;  1Δ states;
1Δ states; 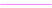 1Π states. 1, 1Σ+, 1Δ and 1Π states corresponding to {S2+(3s23p2)1D + H+1S}; 2, 1Σ+ state corresponding to {S2+(3s23p2)1S + H+1S}; 3, 1Δ and 1Π states corresponding to {S2+(3s3p3)1D° + H+1S}; 4, 1Σ+ and 1Π states corresponding to {S2+(3s3p3)1P° + H+1S}; 5, 1Σ+ and 1Π states corresponding to {S3+(3s23p)2P° + H(1s)2S}, entry channel.
1Π states. 1, 1Σ+, 1Δ and 1Π states corresponding to {S2+(3s23p2)1D + H+1S}; 2, 1Σ+ state corresponding to {S2+(3s23p2)1S + H+1S}; 3, 1Δ and 1Π states corresponding to {S2+(3s3p3)1D° + H+1S}; 4, 1Σ+ and 1Π states corresponding to {S2+(3s3p3)1P° + H+1S}; 5, 1Σ+ and 1Π states corresponding to {S3+(3s23p)2P° + H(1s)2S}, entry channel.
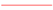 1Σ+ states;
1Σ+ states;  1Δ states;
1Δ states; 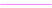 1Π states. 1, 1Σ+, 1Δ and 1Π states corresponding to {S2+(3s23p2)1D + H+1S}; 2, 1Σ+ state corresponding to {S2+(3s23p2)1S + H+1S}; 3, 1Δ and 1Π states corresponding to {S2+(3s3p3)1D° + H+1S}; 4, 1Σ+ and 1Π states corresponding to {S2+(3s3p3)1P° + H+1S}; 5, 1Σ+ and 1Π states corresponding to {S3+(3s23p)2P° + H(1s)2S}, entry channel.
1Π states. 1, 1Σ+, 1Δ and 1Π states corresponding to {S2+(3s23p2)1D + H+1S}; 2, 1Σ+ state corresponding to {S2+(3s23p2)1S + H+1S}; 3, 1Δ and 1Π states corresponding to {S2+(3s3p3)1D° + H+1S}; 4, 1Σ+ and 1Π states corresponding to {S2+(3s3p3)1P° + H+1S}; 5, 1Σ+ and 1Π states corresponding to {S3+(3s23p)2P° + H(1s)2S}, entry channel.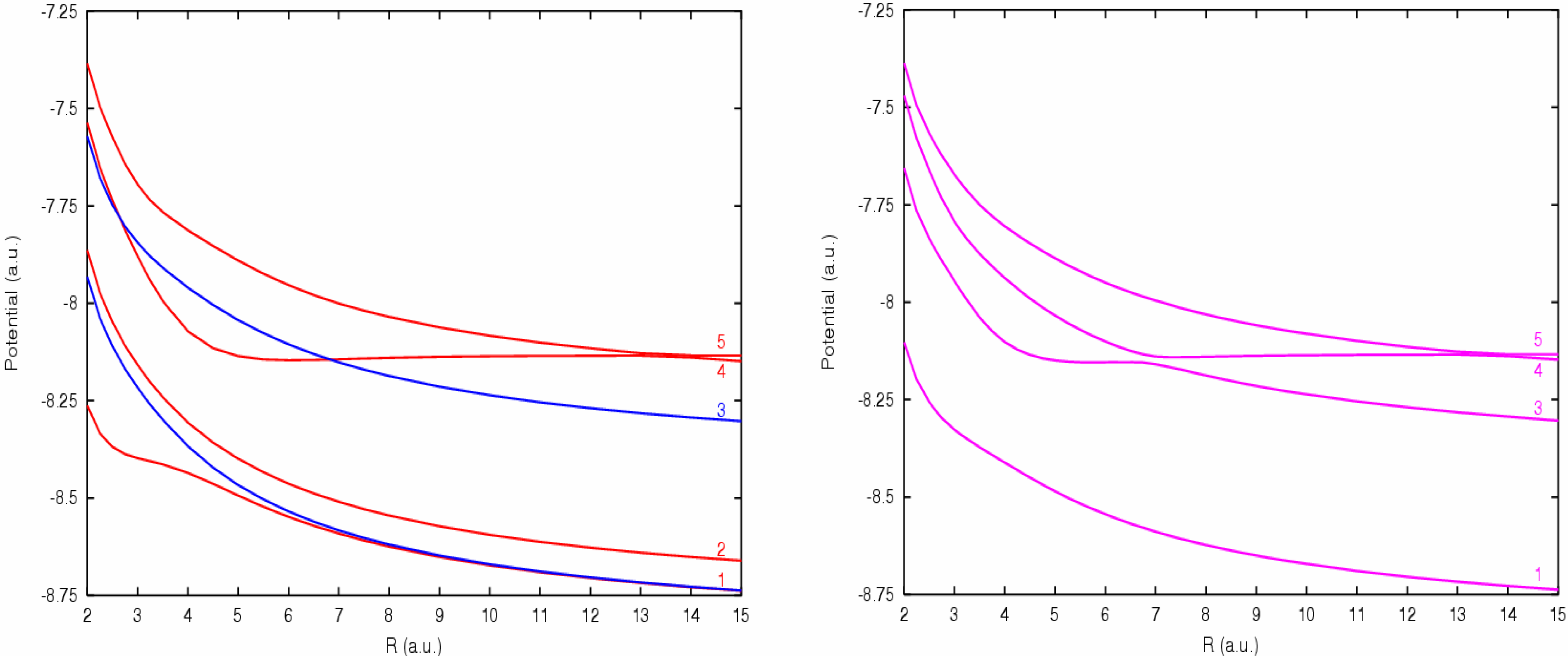
 3Σ+ states;
3Σ+ states;  3Δ states;
3Δ states;  3Π states;
3Π states;  Φ state. 1, 3Π state corresponding to {S2+(3s23p2)3P + H+1S}; 2, 3Δ and 3Π states corresponding to {S2+(3s3p3)3D° + H+1S}; 3, 3Σ+ and 3Π states corresponding to {S2+(3s3p3)3P° + H+1S}; 4, 3Σ+, 3Δ, 3Π and 3Φ states corresponding to {S2+(3s23p3d)3F° + H+1S}; 5, 3Σ+ and 3Π states corresponding to {S3+(3s23p)2P° + H(1s)2S}, entry channel.
Φ state. 1, 3Π state corresponding to {S2+(3s23p2)3P + H+1S}; 2, 3Δ and 3Π states corresponding to {S2+(3s3p3)3D° + H+1S}; 3, 3Σ+ and 3Π states corresponding to {S2+(3s3p3)3P° + H+1S}; 4, 3Σ+, 3Δ, 3Π and 3Φ states corresponding to {S2+(3s23p3d)3F° + H+1S}; 5, 3Σ+ and 3Π states corresponding to {S3+(3s23p)2P° + H(1s)2S}, entry channel.
 3Σ+ states;
3Σ+ states;  3Δ states;
3Δ states;  3Π states;
3Π states;  Φ state. 1, 3Π state corresponding to {S2+(3s23p2)3P + H+1S}; 2, 3Δ and 3Π states corresponding to {S2+(3s3p3)3D° + H+1S}; 3, 3Σ+ and 3Π states corresponding to {S2+(3s3p3)3P° + H+1S}; 4, 3Σ+, 3Δ, 3Π and 3Φ states corresponding to {S2+(3s23p3d)3F° + H+1S}; 5, 3Σ+ and 3Π states corresponding to {S3+(3s23p)2P° + H(1s)2S}, entry channel.
Φ state. 1, 3Π state corresponding to {S2+(3s23p2)3P + H+1S}; 2, 3Δ and 3Π states corresponding to {S2+(3s3p3)3D° + H+1S}; 3, 3Σ+ and 3Π states corresponding to {S2+(3s3p3)3P° + H+1S}; 4, 3Σ+, 3Δ, 3Π and 3Φ states corresponding to {S2+(3s23p3d)3F° + H+1S}; 5, 3Σ+ and 3Π states corresponding to {S3+(3s23p)2P° + H(1s)2S}, entry channel.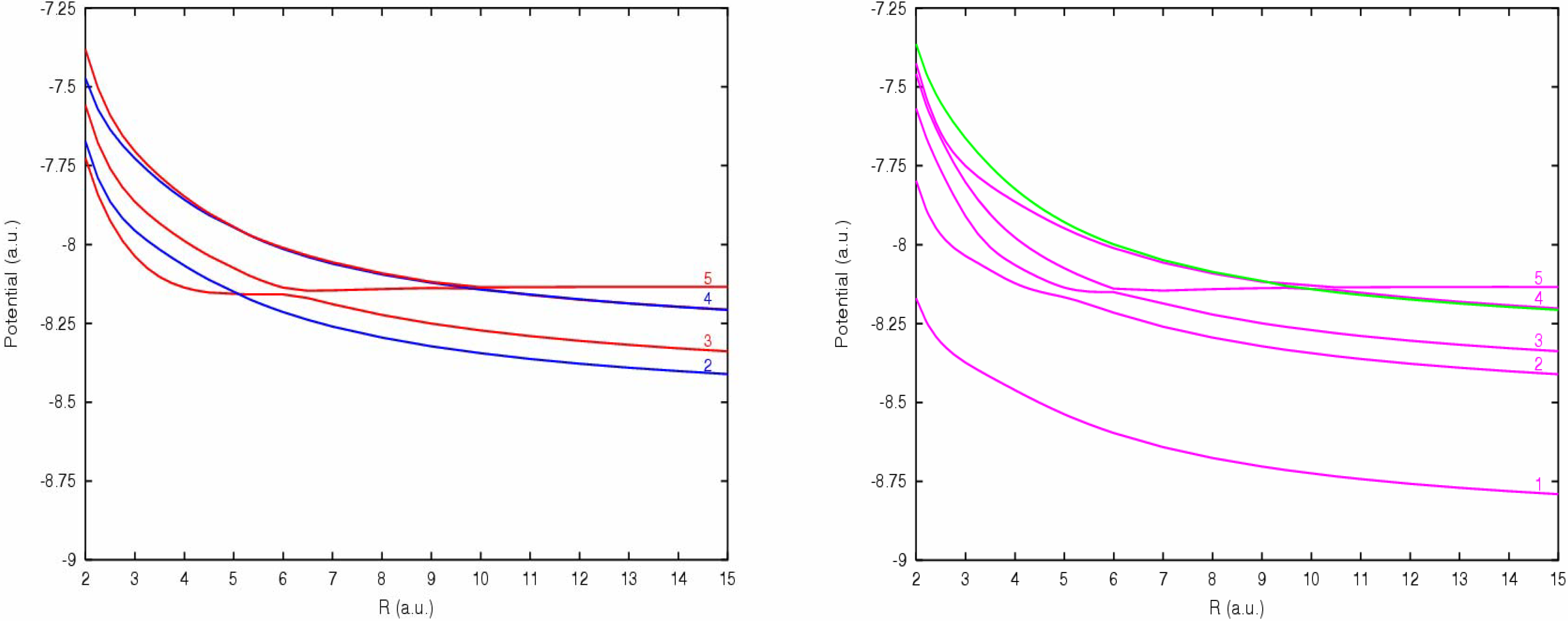
 53Σ / 53Π;
53Σ / 53Π;  33Σ / 33Π;
33Σ / 33Π;  23Δ / 23Π;
23Δ / 23Π;  33Σ / 23Π
33Σ / 23Π
 53Σ / 53Π;
53Σ / 53Π;  33Σ / 33Π;
33Σ / 33Π;  23Δ / 23Π;
23Δ / 23Π;  33Σ / 23Π
33Σ / 23Π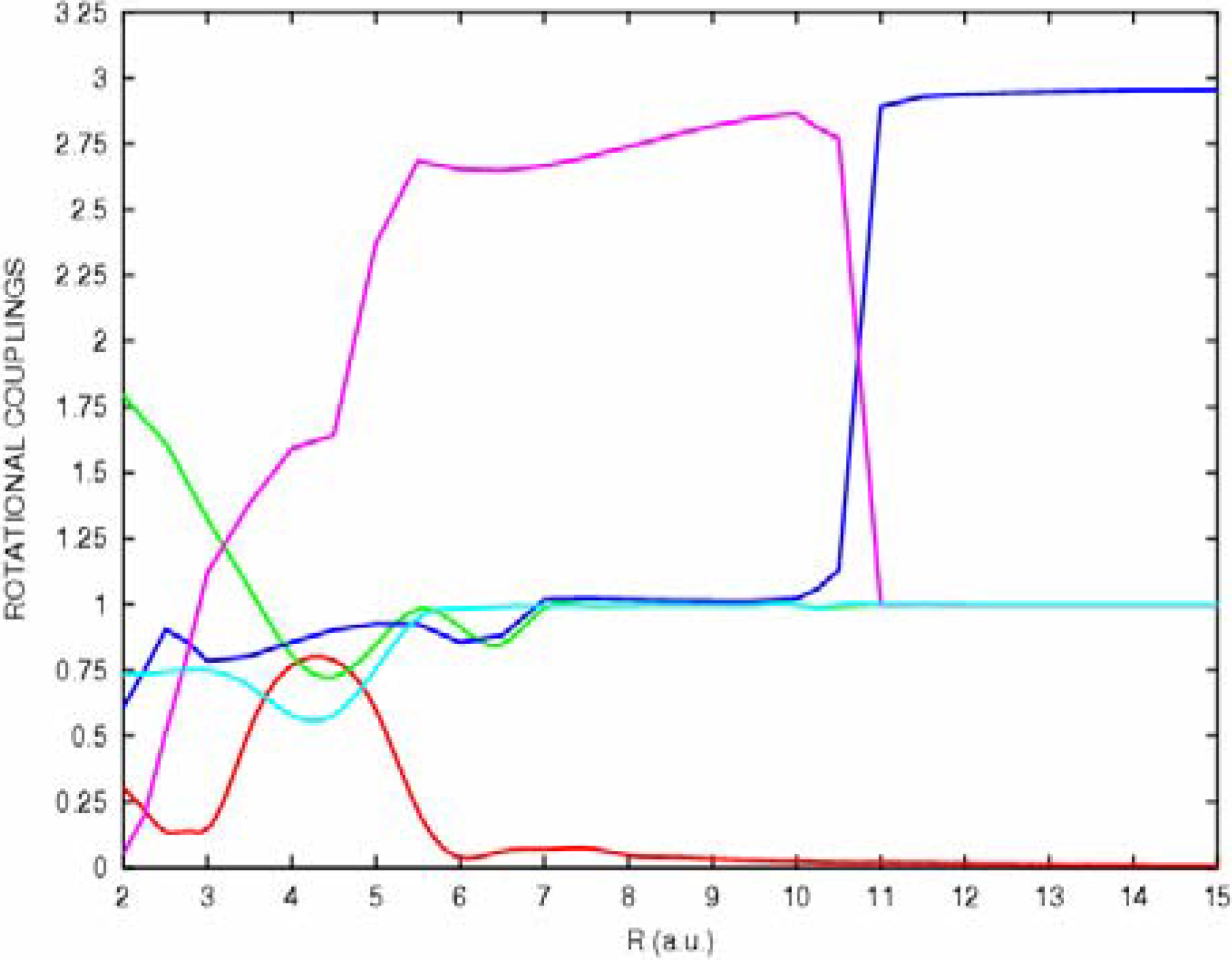

 2Π states;
2Π states;  2Σ states;
2Σ states;  Δ state in decreasing energy order : S3+(3s23p)2P + He(1s2)1S, entry channel; S2+(3s23p2)1S + He+(1s)2S; S2+(3s23p2)1D + He+(1s)2S; S2+(3s23p2)3P + He+(1s)2S.
Δ state in decreasing energy order : S3+(3s23p)2P + He(1s2)1S, entry channel; S2+(3s23p2)1S + He+(1s)2S; S2+(3s23p2)1D + He+(1s)2S; S2+(3s23p2)3P + He+(1s)2S.
 2Π states;
2Π states;  2Σ states;
2Σ states;  Δ state in decreasing energy order : S3+(3s23p)2P + He(1s2)1S, entry channel; S2+(3s23p2)1S + He+(1s)2S; S2+(3s23p2)1D + He+(1s)2S; S2+(3s23p2)3P + He+(1s)2S.
Δ state in decreasing energy order : S3+(3s23p)2P + He(1s2)1S, entry channel; S2+(3s23p2)1S + He+(1s)2S; S2+(3s23p2)1D + He+(1s)2S; S2+(3s23p2)3P + He+(1s)2S.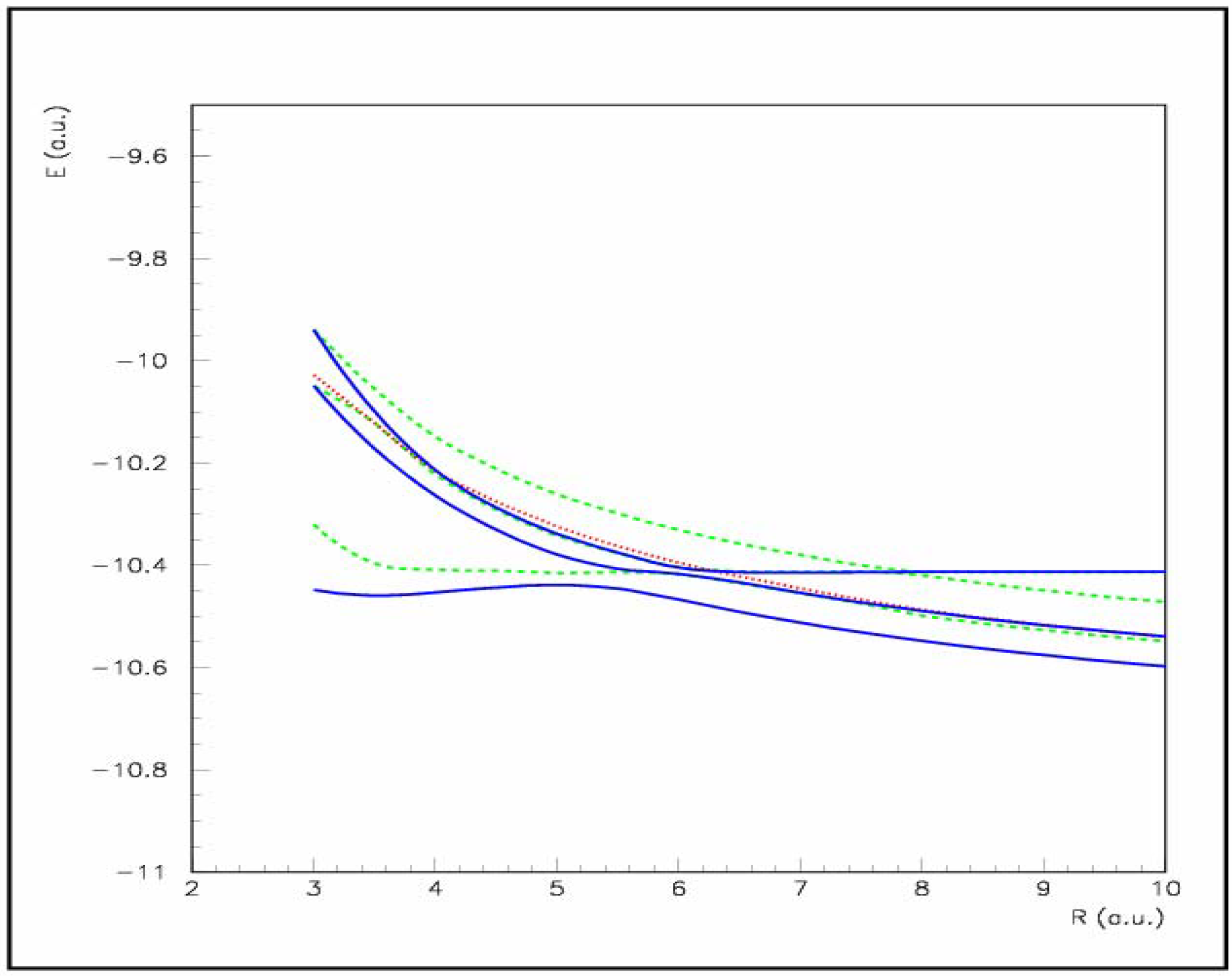
 peak A ;
peak A ;  peak B;
peak B;  peak C;(experiment [6]) /
peak C;(experiment [6]) /  (calculation), ratio σB/σA.
(calculation), ratio σB/σA.
 peak A ;
peak A ;  peak B;
peak B;  peak C;(experiment [6]) /
peak C;(experiment [6]) /  (calculation), ratio σB/σA.
(calculation), ratio σB/σA.




