Through-Space Spin-Spin Coupling In Acetylenic Systems. Ab Initio and DFT Calculations

Abstract

We have investigated, by means of ab initio and DFT calculations, the magnitude of through-space spin-spin couplings (J_CH and J_HH) in CH/π bonded van der Waals dimers involving acetylene, and in a structurally related covalent compound (4-ethynylphenanthrene). Within regions where the interaction is stabilizing J_HH couplings are very small (< 0.1 Hz) for all complexes. In the acetylene-methane complex J_CH is also very small, whereas in the acetylene-benzene complex and the acetylene dimer it shows a relatively large dependence on the tilt angle from the T-shaped arrangement, for which the smallest values are calculated, to a parallel slipped arrangement where J_CH is ca. 0.5 Hz. The relative magnitude of through-space couplings in 4-ethynylphenanthrene and a tilted acetylene-benzene dimer, featuring the same internuclear arrangement as in model dimers, are compared.

Introduction

Although spin-spin coupling is normally considered as a signature of covalent bonding, several cases have been known for a long time where non-negligible couplings are observed between nuclei (notably ¹⁹F) separated by many covalent bonds. Thus, through-space transmission of spin-spin coupling was postulated to explain the relatively large J_FF and J_CF coupling observed in some fluorinated compounds,[1,2] where the atoms involved in the coupling are separated by 5-7 bonds. Quantum chemical calculations [3,4,5] have confirmed such a hypothesis, revealing that it suffices to have an overlap of the electronic clouds to produce a spin-spin coupling between two nuclei, regardless of whether there is a covalent bond between the atoms. This recognition has spawned much research aimed at better characterizing this phenomenon.

Recently [6,7] we have investigated several model van der Waals system dimers showing the CH/  interaction, whereby a C-H bond is directed, more or less perpendicularly, towards a π system, typically an aromatic ring. The model systems were composed by a benzene or an ethylene molecule as the electron density donors in the CH/π interaction, while the CH bond acceptors were represented by methane, ethylene or benzene. For the smaller dimers we ran calculations at ab initio (RASSCF, Restricted Active Space SCF and SOPPA, Second Order Polarization Propagator Approach) and DFT (Density Functional Theory) levels of theory. The remaining larger systems were investigated only at the DFT level. Nuclear spin-spin J_CH and J_HH couplings were calculated between the hydrogen of the acceptor CH bond and the carbon or hydrogen atoms of the donor π system, which belong to two different molecules. The calculations consistently predicted a through-space J_CH coupling in the CH/π interacting dimers amounting to ca. 0.2-0.3 Hz, thus above the resolution of modern NMR spectroscopy, while the J_HH couplings were negligible.

These results prompted us to extend the study to compounds known to have stable, long-lived CH/π interactions, unlike the small model dimers, so that the NMR couplings may be detected within the lifetime of the compound. DFT calculations on some covalent compounds stabilized by the CH/π interaction gave results in agreement with those obtained for the model system dimers. They confirmed that, also in these cases, the CH coupling must occur through space.

We also studied the effect of substituents, both on the aromatic donor part as well as on the acceptor CH bond of the CH/π interacting system. We found that very small effects, if any, are present in such systems. This is mainly due to the fact that substituents mostly influence the π-electron system, while the FC contribution to the spin-spin coupling is mainly determined by electrons in σ-type orbitals.[8]

In this paper we extend our investigation to model van der Waals complexes involving triple bonds and to a stable, rigid covalent molecule (4-ethynylphenanthrene) where a C-H bond is forced to point towards the π system of the triple CC bond, so that through-space coupling may be detectable. As in our previous investigations, the spin-spin couplings are calculated between the hydrogen of the acceptor CH bond and the carbon and hydrogen atoms of the acetylenic moiety.

Results and Discussion

Van der Waals Complexes. We have investigated the van der Waals complexes model systems shown in Figure 1. The structure of each monomer was optimized, with the software package Gaussian 98[9] at the MP2/cc-pVTZ level of theory. For each complex we determined the interaction energy at the same level of theory, correcting for the basis set superposition error (BSSE) by means of the counterpoise method.[10] For the majority of the systems, the through-space J_CH and J_HH have been calculated using density functional theory as implemented in the software package deMon-NMR.[11,12,13,14,15,16] We used the local exchange-correlation functional of Vosko, Wilk and Nusair with the IGLO-III basis set (hereafter referred simply as DFT level) as in our previous works. For the acetylene dimer 3, a comparison is made with results obtained at the ab initio SOPPA level with the aug-cc-pVDZ-su1 basis set, extensively employed by Pecul and coworkers to this purpose,[17] which is an augmentation of the cc-pVDZ basis set with a diffuse function, plus a tight s function, with all s functions deconstructed. For the ab initio calculations we employed the software DALTON.[18] The dimer 3 has also been investigated as a function of the relative orientation of the monomers, as shown in 4, while in the other cases only the distance was varied.

Figure 1. The systems investigated, with numbering scheme.

Figure 1. The systems investigated, with numbering scheme.

We previously used this combined approach (ab initio for selected small molecules plus DFT for the larger systems) to study CH/π interacting van der Waals molecules and covalent compounds.[7] There we found a remarkable agreement between ab initio and DFT results, with nonsystematic differences.

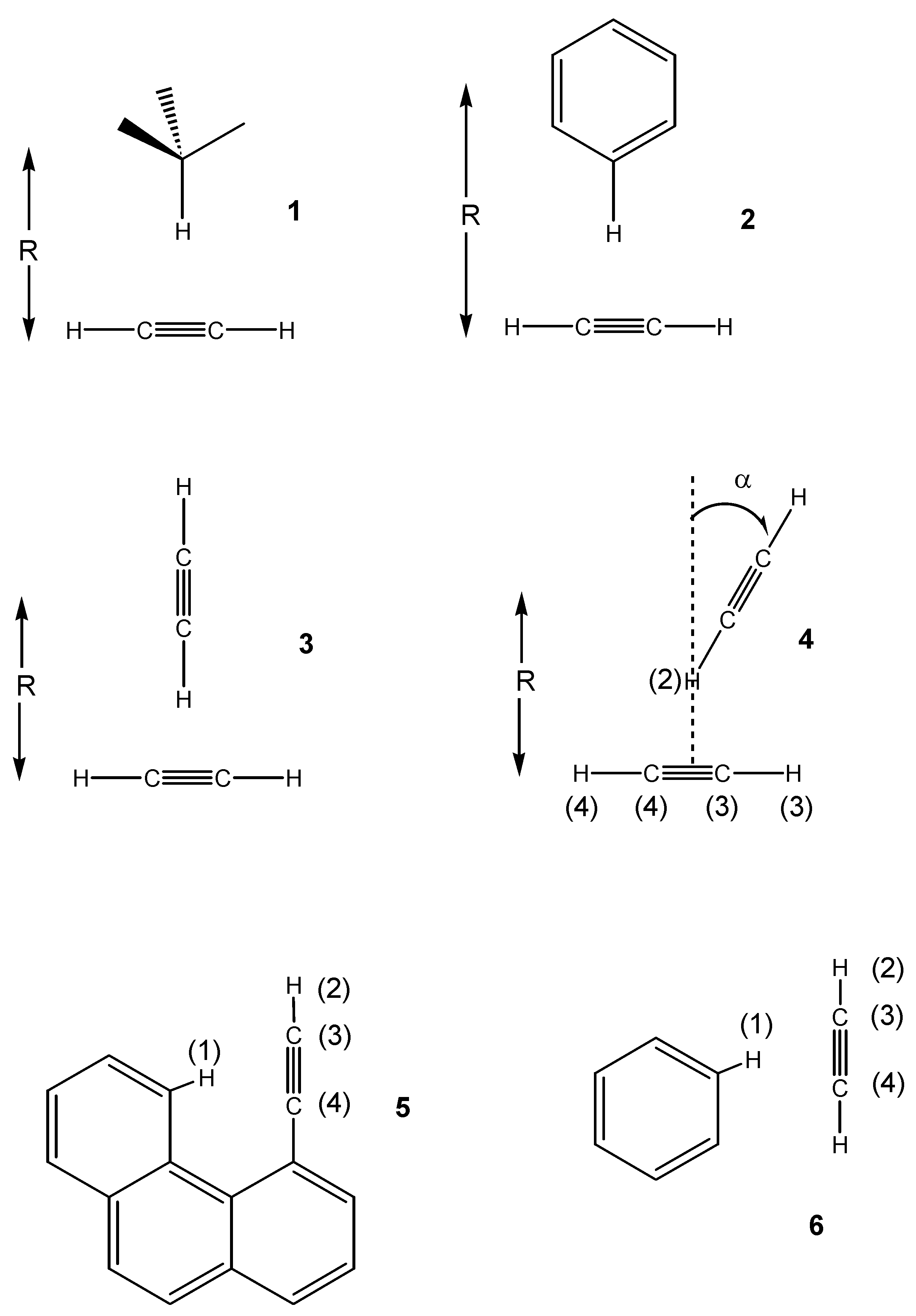
In Figure 2 we report the interaction energy (to identify the stabilizing region of the complex), and the calculated J_CH and J_HH couplings for the acetylene-methane van der Waals complex 1. The complex is stabilized by –0.38 Kcal/mol at the equilibrium distance of 4.2 Å. The through-space couplings are essentially zero in the region of interest. This is in contrast with the results obtained for previously investigated CH/π interacting systems, where a small but non-negligible coupling of about 0.2-0.3 Hz was calculated [7]. As we can see in the figure, here such values are reached only at very short distances, where the interaction is strongly repulsive. 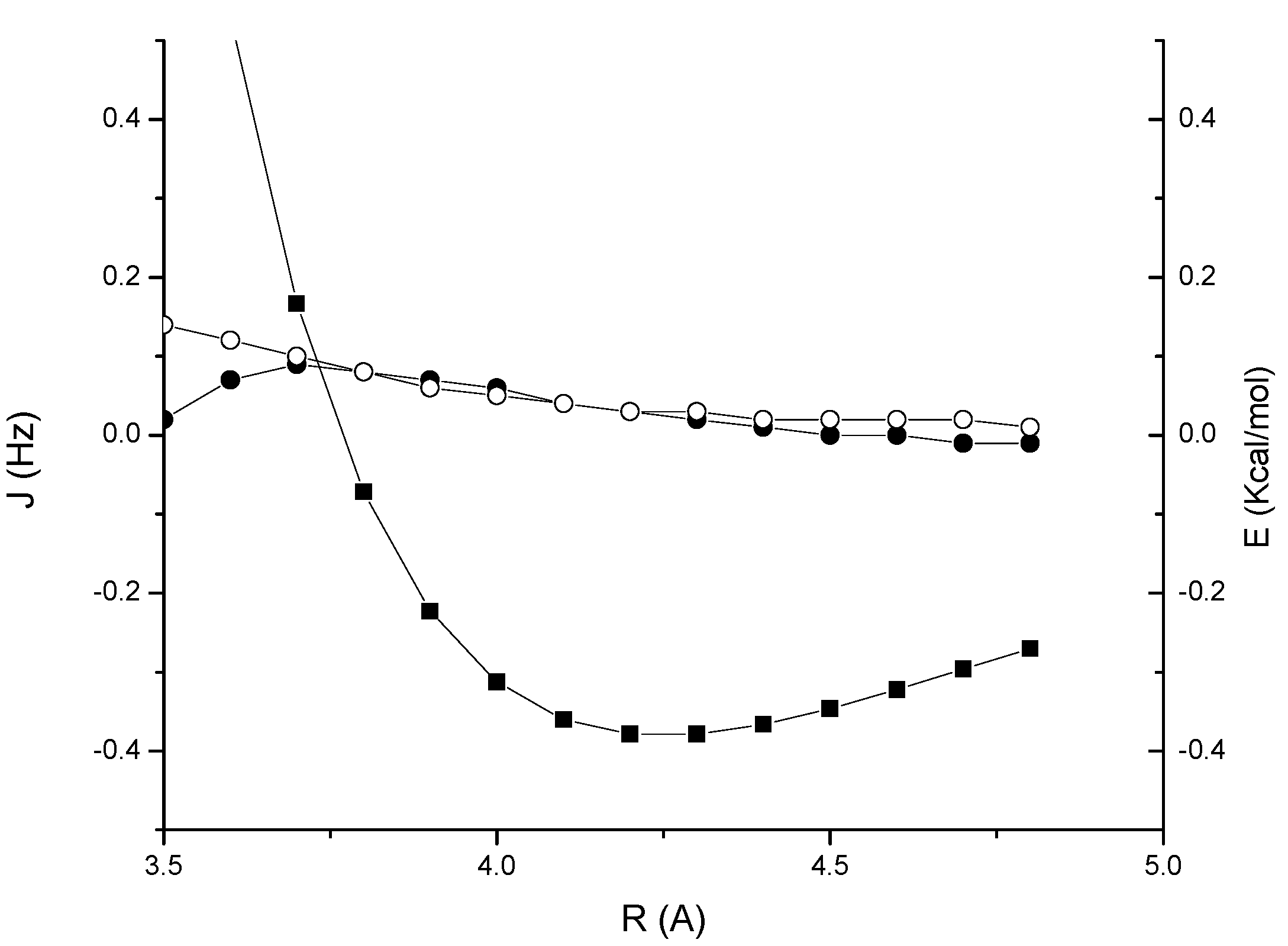A very similar qualitative behaviour is obtained for the acetylene-benzene van der Waals complex 2, as shown in Figure 3, which has an interaction energy of –0.96 Kcal/mol at the equilibrium separation of 5.4 Å. The reason of this result is understood if we consider the three main contributions to the spin-spin coupling, that is the Fermi-contact (FC) term and the diamagnetic and paramagnetic spin-orbit, (DSO and PSO) terms. While in the CH/π interacting systems investigated in Ref. [6,7] the sum of spin-orbit terms is positive in the stabilizing region, thus adding up to the FC contribution, in this case it has a negative sign, thereby largely cancelling the FC term.

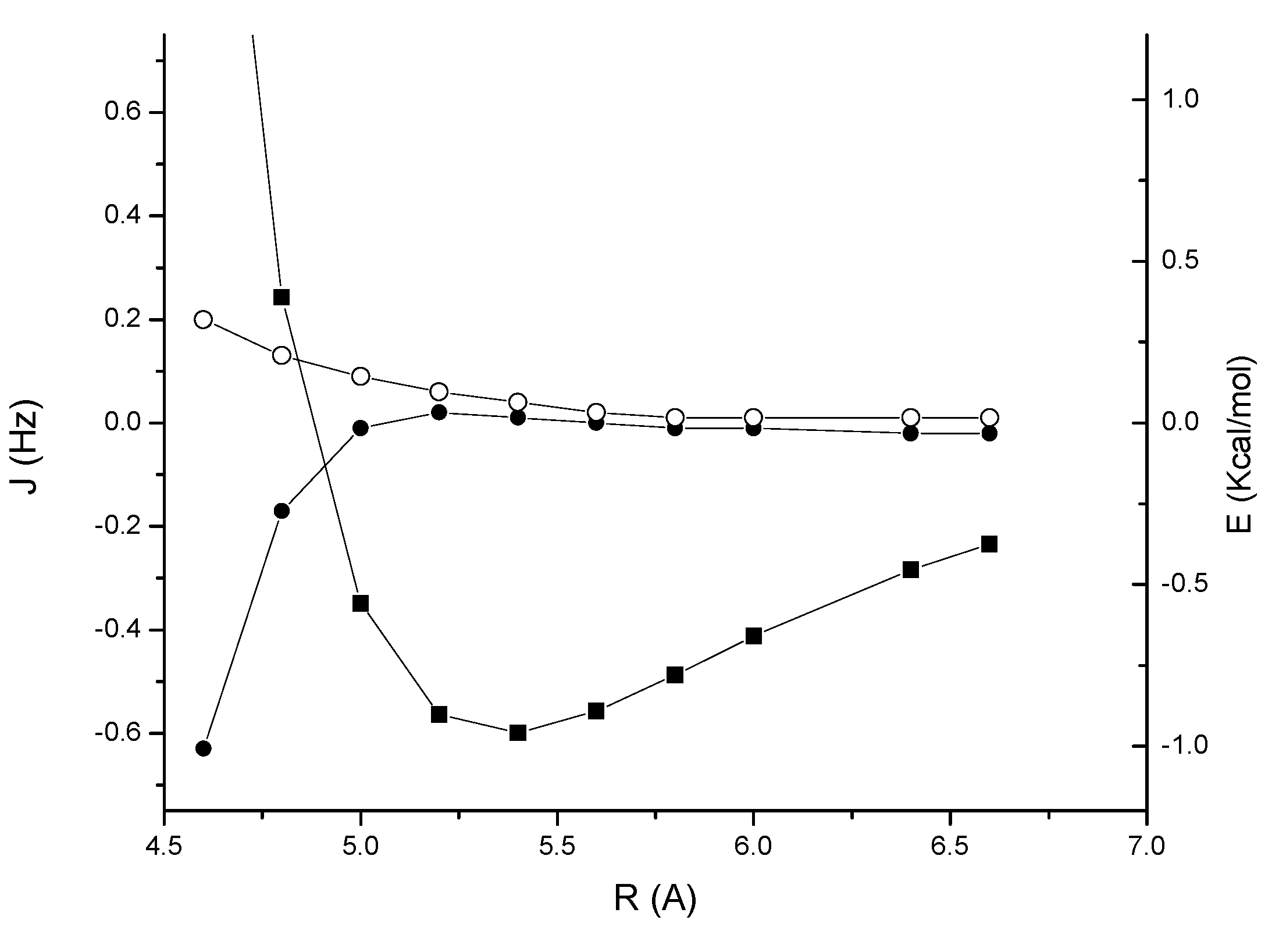
A more interesting behaviour is observed for the acetylene dimer 3 (Figure 4). The minimum of the interaction is at a distance of about 4.3 Å, with an interaction energy of –1.36 Kcal/mol. At this distance the J_HH coupling is negligible and the J_CH coupling is also relatively small, about –0.1 Hz. However, it increases rapidly in magnitude as the distance is decreased, and reaches a value of –0.4 Hz at the contact distance of about 4.0 Å. In the range 4.0–4.5 Å, J_CH is mainly determined by a non-complete cancellation of the DSO and PSO terms, while the FC term is small; for example at a distance of 4.1 Å, the FC, DSO and PSO terms to J_CH are –0.04, –0.60 and 0.41 respectively for a total coupling of –0.23 Hz). In contrast, the contributions to J_HH are 0.06, –0.46 and 0.44 Hz respectively, for a total coupling of only 0.04 Hz.

Figure 2. Acetylene-methane complex 1: MP2/cc-pVTZ interaction energy (BSSE corrected) (solid squares); through-space J_HH coupling (open circles); through-space J_CH coupling (solid circles).

Figure 2. Acetylene-methane complex 1: MP2/cc-pVTZ interaction energy (BSSE corrected) (solid squares); through-space J_HH coupling (open circles); through-space J_CH coupling (solid circles).

Figure 3. Acetylene-benzene complex 2: MP2/cc-pVTZ interaction energy (BSSE corrected) (solid squares); through-space J_HH coupling (open circles); through-space J_CH coupling (solid circles).

Figure 3. Acetylene-benzene complex 2: MP2/cc-pVTZ interaction energy (BSSE corrected) (solid squares); through-space J_HH coupling (open circles); through-space J_CH coupling (solid circles).

Figure 4. Acetylene dimer 3: MP2/cc-pVTZ interaction energy (BSSE corrected) (solid squares); through-space J_HH coupling (open circles); through-space J_CH coupling (solid circles).

Figure 4. Acetylene dimer 3: MP2/cc-pVTZ interaction energy (BSSE corrected) (solid squares); through-space J_HH coupling (open circles); through-space J_CH coupling (solid circles).

It is important to further investigate these results, at least for such a small dimer like 3, with high-level ab initio methods. We choose the SOPPA/aug-cc-pVDZ-su1 method as in our previous investigation.[7] We also deemed interesting to see the angular dependence of the couplings, as schematically shown by dimer 4. Thus, for a distance of 4.3 Å (about the minimum of the interaction energy), we have rotated one acetylene molecule, as shown in Figure 1, from a T-shaped configuration (α = 0°, like 3) to a parallel slipped one (α = 90°). The rotation was performed by keeping the closest hydrogen (H2) fixed. These results show a strong dependence of the couplings on the relative orientation. 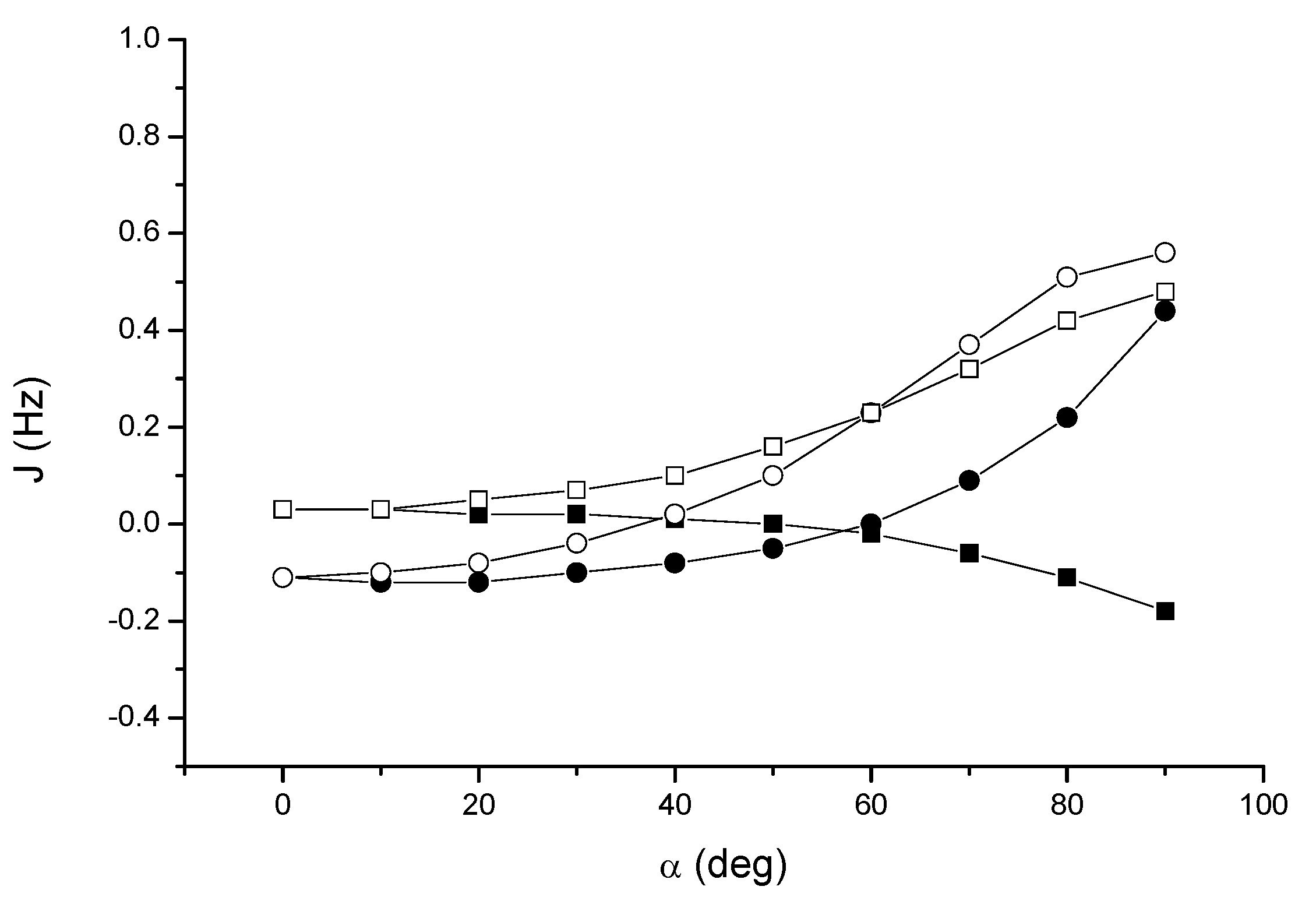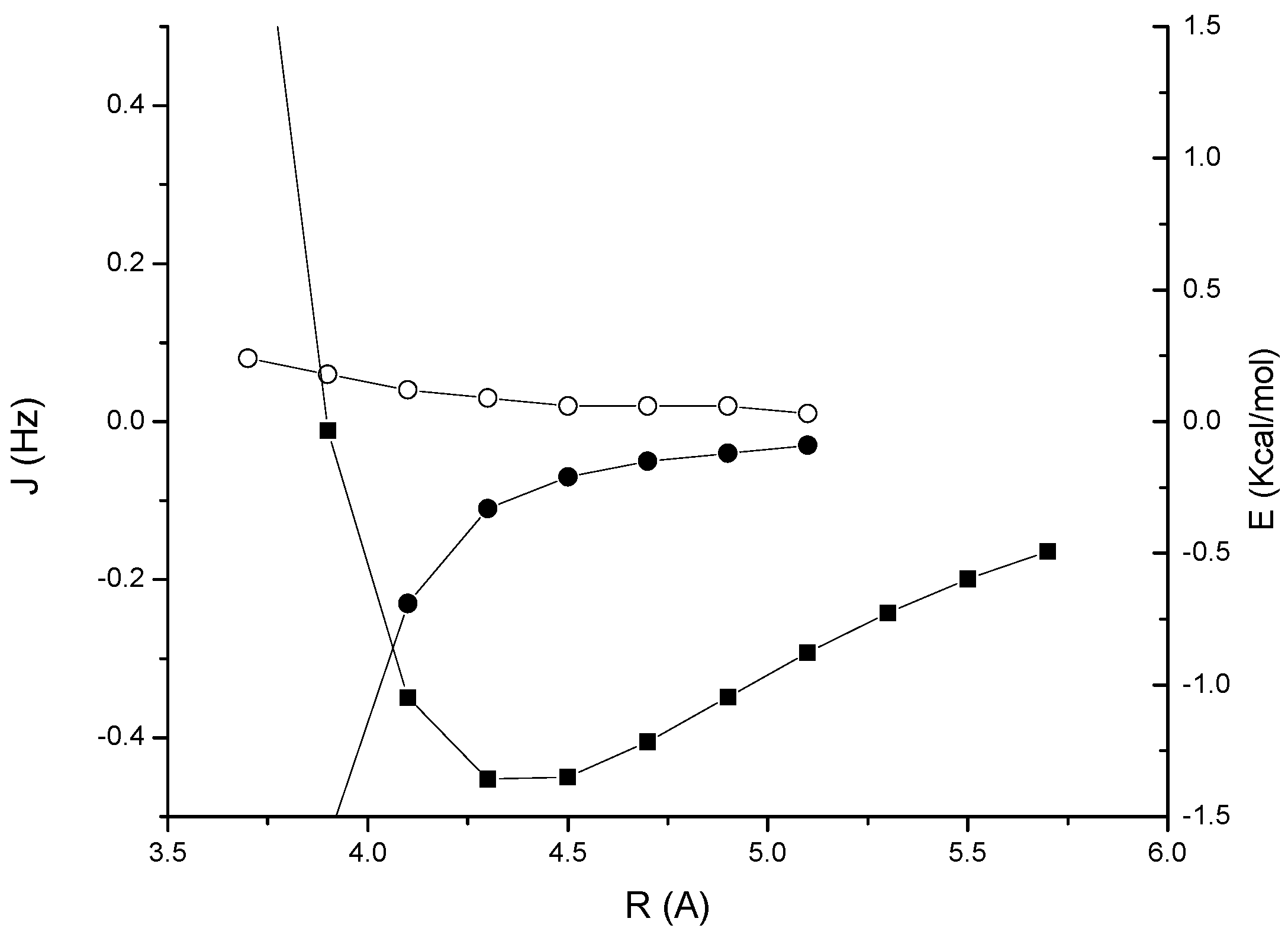In Figure 5 and Figure 6 we report the results at the DFT and SOPPA levels, respectively.

At the DFT level, J_H2H3 increases from about zero in the T-shaped arrangement up to 0.48 Hz for a slipped parallel configuration, while J_H2H4 takes negative values decreasing to –0.18 Hz. In contrast, both J_H2C3 and J_H2C4 increase from –0.11 Hz to 0.56 and 0.44 Hz respectively, albeit with a different angular dependence. These results clearly demonstrate that the perpendicular arrangment of two acetylene units is the least favorable in order to detect a through-space coupling (however, for α = 90° and a distance of 4.3 Å the interaction is slightly repulsive).

Figure 5. Acetylene dimer 4: angular dependence of the through-space coupling calculated at the DFT level. J_H2H3 (open squares); J_H2H4 (solid squares); J_H2C3 (open circles); J_H2C4 (solid circles) .

Figure 5. Acetylene dimer 4: angular dependence of the through-space coupling calculated at the DFT level. J_H2H3 (open squares); J_H2H4 (solid squares); J_H2C3 (open circles); J_H2C4 (solid circles) .

Figure 6. Acetylene dimer 4: angular dependence of the through-space coupling calculated at the ab initio SOPPA level. J_H2H3 (open squares); J_H2H4 (solid squares); J_H2C3 (open circles); J_H2C4 (solid circles).

Figure 6. Acetylene dimer 4: angular dependence of the through-space coupling calculated at the ab initio SOPPA level. J_H2H3 (open squares); J_H2H4 (solid squares); J_H2C3 (open circles); J_H2C4 (solid circles).

It is interesting to investigate which components (FC or spin-orbit) are responsible for this increase. In Table 1 we report the components for J_H2H3 and J_H2C3. The spin-orbit component only changes slightly as the dimer change conformation while the FC term increases substantially, even though the distance between H2 and H3 remains fixed.

Essentially the same behaviour, although less marked, is found for J_H2H4, with the spin-orbit contribution practically constant while the FC term decreases to –0.15 Hz in the parallel slipped conformation.

Concerning the coupling with the carbon nuclei, we note that the independence of spin-orbit terms on the relative orientation of the monomer is even more marked than for J_H2H3. The overall change is almost entirely due to an increase of the FC term. Essentially the same result, but slightly less pronounced, is found also for J_H2C4.

The results obtained at the SOPPA level are in semiquantitative agreement with those at the DFT level, see Table 2. As we can see from Figure 6, the dependence of the through-space couplings on the relative orientation of the monomers is essentially the same. We should take also into account that DALTON gives all four contributions (FC, PSO, DSO and spin-dipole, SD) to the coupling, while deMon does not calculate the SD term. This is, in general, not negligible but appears to be relatively small  in  these  cases.  In conclusion,  both  levels  of  theory  predict  a  non-negligible  through-space coupling for the acetylene dimer, which increases as the dimer goes from the T-shaped, perpendicular conformation to the parallel slipped one.

Table 1. Angular dependence of J_H2H3 and J_H2C3 in the acetylene dimer 4 calculated at the DFT level.

α (°)		JH2H3 (Hz)				JH2C3 (Hz)
	FC	DSO + PSO	TOT		FC	DSO + PSO	TOT
0	0.04	0.00	0.03		0.02	–0.14	–0.11
10	0.05	–0.01	0.03		0.04	–0.14	–0.10
20	0.06	–0.02	0.05		0.06	–0.14	–0.08
30	0.09	–0.02	0.07		0.10	–0.14	–0.04
40	0.13	–0.03	0.10		0.16	–0.14	0.02
50	0.20	–0.04	0.16		0.24	–0.14	0.10
60	0.28	–0.05	0.23		0.36	–0.14	0.23
70	0.38	–0.07	0.32		0.50	–0.13	0.37
80	0.50	–0.08	0.42		0.62	–0.12	0.51
90	0.59	–0.11	0.48		0.66	–0.10	0.56

Table 1. Angular dependence of J_H2H3 and J_H2C3 in the acetylene dimer 4 calculated at the DFT level.

α (°)		JH2H3 (Hz)				JH2C3 (Hz)
	FC	DSO + PSO	TOT		FC	DSO + PSO	TOT
0	0.04	0.00	0.03		0.02	–0.14	–0.11
10	0.05	–0.01	0.03		0.04	–0.14	–0.10
20	0.06	–0.02	0.05		0.06	–0.14	–0.08
30	0.09	–0.02	0.07		0.10	–0.14	–0.04
40	0.13	–0.03	0.10		0.16	–0.14	0.02
50	0.20	–0.04	0.16		0.24	–0.14	0.10
60	0.28	–0.05	0.23		0.36	–0.14	0.23
70	0.38	–0.07	0.32		0.50	–0.13	0.37
80	0.50	–0.08	0.42		0.62	–0.12	0.51
90	0.59	–0.11	0.48		0.66	–0.10	0.56

Table 2. Angular dependence of J_H2H3 and J_H2C3 in the acetylene dimer 4 calculated at the SOPPA level.

α(°)		JH2H3 (Hz)					JH2C3 (Hz)
	FC	DSO + PSO	SD	TOT		FC	DSO + PSO	SD	TOT
0.0	0.05	0.13	-0.01	0.17		-0.13	0.02	0.03	-0.08
30.0	0.13	0.09	-0.00	0.22		-0.07	0.01	0.02	-0.04
60.0	0.36	-0.01	0.03	0.38		0.14	0.00	0.01	0.15
90.0	0.91	-0.29	0.02	0.64		0.20	0.01	0.01	0.22

Table 2. Angular dependence of J_H2H3 and J_H2C3 in the acetylene dimer 4 calculated at the SOPPA level.

α(°)		JH2H3 (Hz)					JH2C3 (Hz)
	FC	DSO + PSO	SD	TOT		FC	DSO + PSO	SD	TOT
0.0	0.05	0.13	-0.01	0.17		-0.13	0.02	0.03	-0.08
30.0	0.13	0.09	-0.00	0.22		-0.07	0.01	0.02	-0.04
60.0	0.36	-0.01	0.03	0.38		0.14	0.00	0.01	0.15
90.0	0.91	-0.29	0.02	0.64		0.20	0.01	0.01	0.22

4-Ethynylphenanthrene. An interesting system for experimentally testing the theoretical predictions just seen for the model van der Waals complexes is 4-ethynylphenanthrene 5 (Figure 1). In this molecule, a CH aromatic bond is forced to lie close to the π system of the triple bond in the 4 position, and is a textbook example of the deshielding effect of the magnetic anisotropy of the π system in the triple bond,[19] since the chemical shift of that proton (H1) is 1.71 ppm downfield from the resonance of the protons in phenanthrene itself. The geometry of the molecule was optimized at the B3LYP/6-31G(d,p) level, and the resulting structure was subjected to vibrational analysis, thus confirming that the planar structure so obtained was a minimum on the PES. In the calculated structure, the H1 hydrogen is very close to the triple bond of the ethynyl residue: the distances from C4, C3 and H2 are 2.21, 2.52 and 3.14 Å, respectively. This renders 5 a suitable candidate for an experimental verification of through-space spin-spin coupling. Being a covalent molecule, however, the issue arises whether any such coupling would really occur through space or is rather a conventional example of through-bond coupling. In this latter case, we note that the number of connecting bonds is rather large, i.e. ⁵J_H1C4, ⁶J_H1C3 and ⁷J_H1H2. This large number of bonds renders through-bond coupling unlikely. To address this issue, we ran calculations also for the benzene-acetylene model 6, which was built with the interesting atoms arranged as in 5 (and adding hydrogens where necessary, whose C-H distance was set to the same values obtained for 5). Since in this system the coupled spins are not covalently bonded, any coupling necessarily takes place through space. The DFT results for 5 and 6 are reported in Table 3.

A comparison of the results for 5 and 6 shows, firstly, that J_H1C4 and J_H1C3 are larger in the non-covalent model 6 than in 4-ethynylphenanthrene, while J_H1H2 is essentially identical.

The general behavior is qualitatively similar: the H1-C4 coupling has a relatively large negative FC term and a negligible spin-orbit contribution, so that the total coupling is significant; in contrast, for the H1-C3 coupling the positive FC term is largely canceled by spin-orbit terms, so that the total coupling is much smaller. The delicate balance of these terms is responsible for the different sign of J_H1C3 in the two cases. Finally, the J_H1H2 coupling is small since both the FC and the spin-orbit terms are small in magnitude.

Table 3. DFT spin-spin couplings (Hz) for 4-ethynylphenanthrene 5 and the benzene-acetylene complex 6.

		5				6
	FC	DSO + PSO	TOT		FC	DSO + PSO	TOT
JH1C4	–0.36	0.01	–0.35		–0.65	0.03	–0.62
JH1C3	0.42	–0.50	–0.07		0.54	–0.42	0.12
JH1H2	–0.02	–0.09	–0.11		–0.02	–0.07	–0.09

Table 3. DFT spin-spin couplings (Hz) for 4-ethynylphenanthrene 5 and the benzene-acetylene complex 6.

		5				6
	FC	DSO + PSO	TOT		FC	DSO + PSO	TOT
JH1C4	–0.36	0.01	–0.35		–0.65	0.03	–0.62
JH1C3	0.42	–0.50	–0.07		0.54	–0.42	0.12
JH1H2	–0.02	–0.09	–0.11		–0.02	–0.07	–0.09

The magnitude of both CH couplings (between 0.1-0.6 Hz) is remarkable. Although the larger magnitude of J_H1C4 might be naively ascribed to the shorter H1-C4 distance, as seen above, Table 3 shows that the situation is more complex, since it is rather the relative sign of FC and spin-orbit terms that dictate the result. Finally, we remark that the similar values calculated for 5 and 6 imply that these couplings occur through space.

Conclusions

DFT and ab initio methods consistently predict small but non-negligible values of spin-spin coupling between ¹³C and ¹H in weakly bound van der Waals dimers involving acetylene, where the coupling must occur through space. Although such couplings tend to be smaller than for other similar cases involving other π systems (ethylene, benzene), a relatively large angular dependence brings through-spcae couplings into values (up to 0.5 Hz) amenable to experimental observation. The comparison with 4-ethynylphenanthrene allows to extend these predictions to a stable, covalent system free from the obvious complications related to weakly interacting molecules.