Experimental Determination of Pseudorotation Potentials for Disubstituted Cyclopentanes Based on Spin–Spin Coupling Constants
Abstract
:Introduction
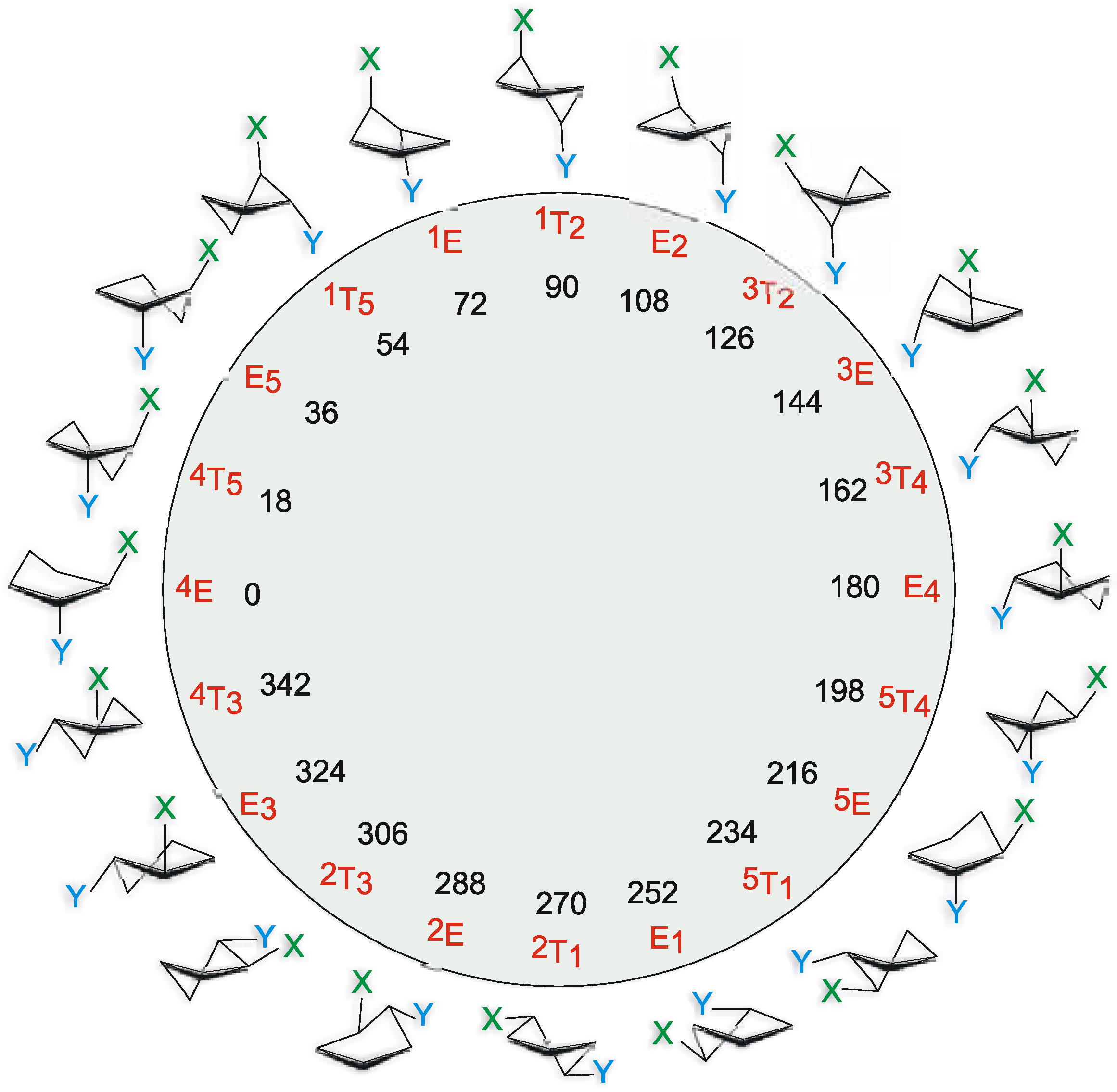
Experimental
Calculation and Results
Experimental SSCCs
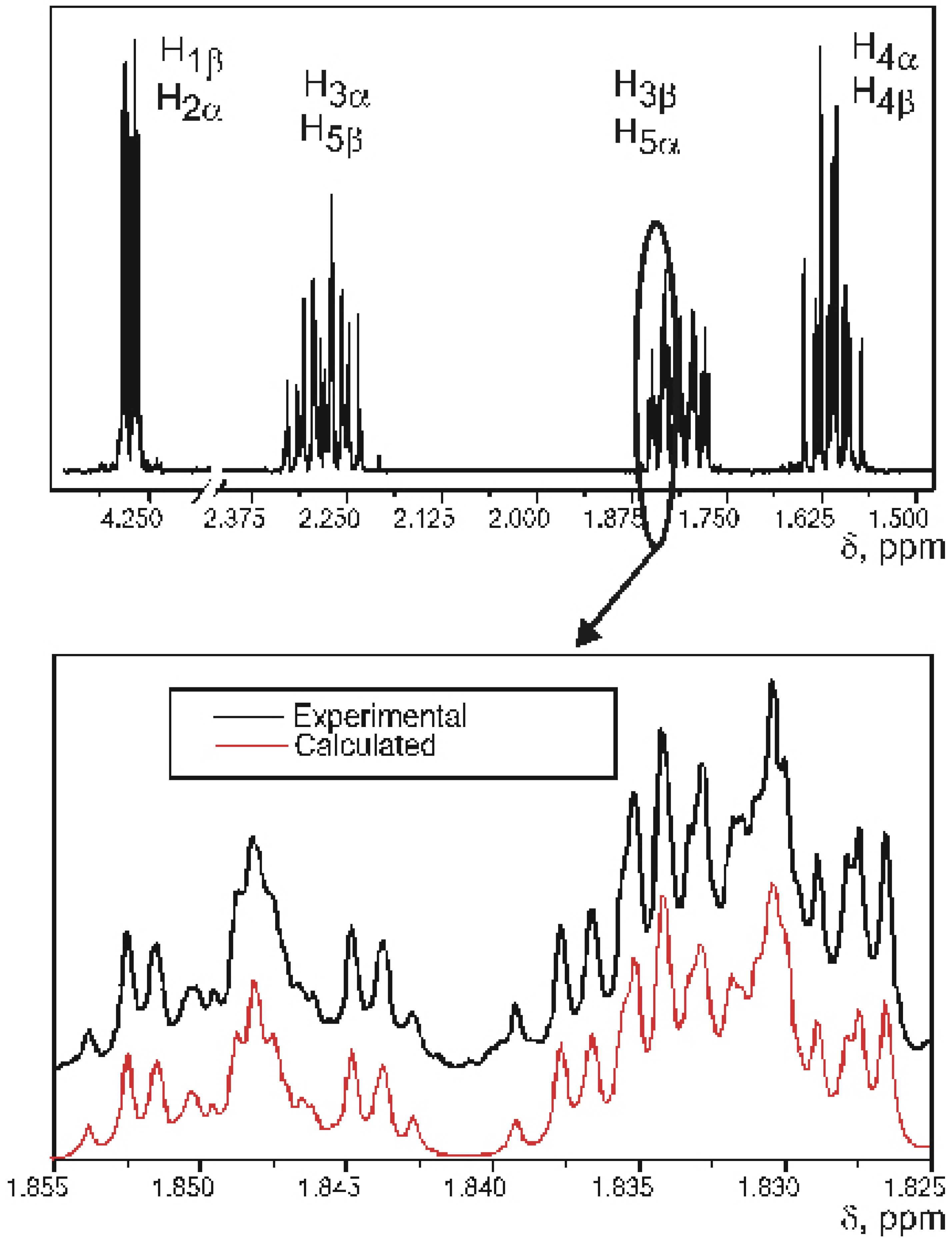
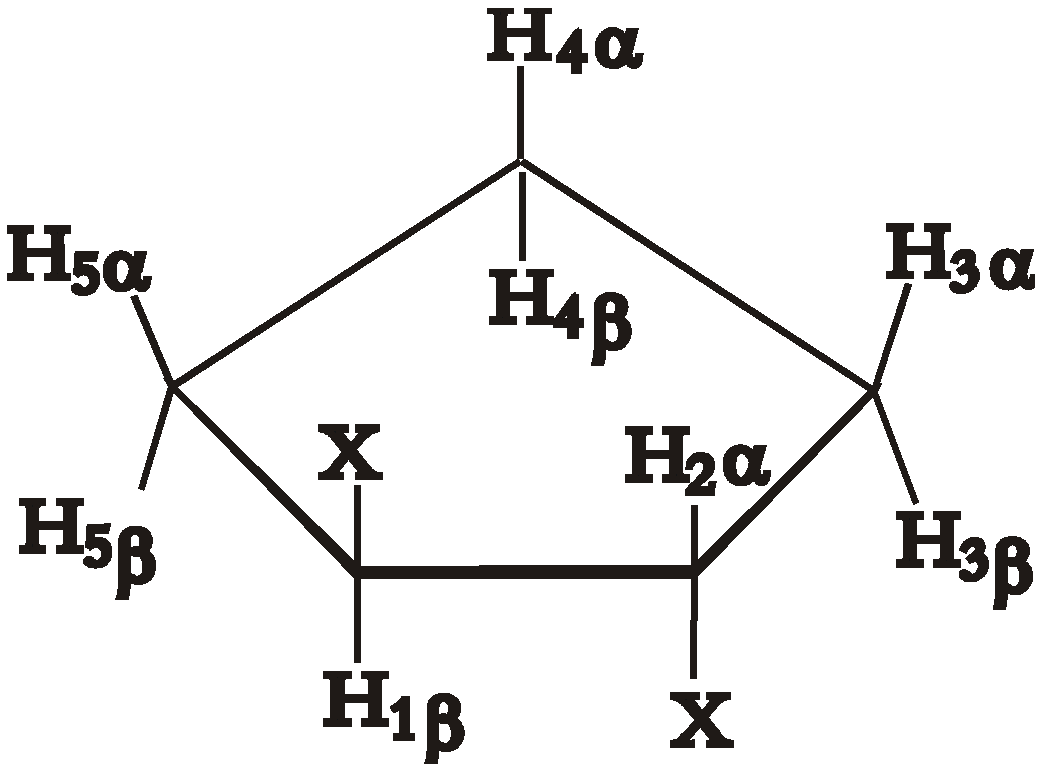
| J1β2α | J1β5β, J2α3α | J2α3β, J1β5α | J3α4α, J5β4β | J3α4β, J5β4α | J3β4α, J5α4β | J3β4β, J5α4α | |
|---|---|---|---|---|---|---|---|
| C6D6 | 2.860(6) | 6.610(6) | 3.280(6) | 9.830(7) | 7.080(8) | 4.210(7) | 9.090(5) |
| CCl4 | 2.510(5) | 5.980(6) | 2.080(5) | 10.030(7) | 7.470(8) | 4.040(8) | 8.880(7) |
| CD3CN | 3.340(7) | 6.310(6) | 3.910(8) | 9.810(6) | 6.540(6) | 5.030(9) | 9.140(9) |
| J1β2α | J1β5β, J2α3α | J2α3β, J1β5α | J3α4α, J5β4β | J3α4β, J5β4α | J3β4α, J5α4β | J3β4β, J5α4α | |
|---|---|---|---|---|---|---|---|
| C6D6 | 1.631(1) | 5.615(1) | 1.912(1) | 10.173(1) | 7.400(1) | 3.93(1) | 8.951(1) |
| CCl4 | 1.171(2) | 5.446(1) | 1.395(2) | 10.314(3) | 7.594(3) | 3.635(2) | 8.918(2) |
| CD3CN | 2.352(3) | 5.877(1) | 2.685(2) | 10.002(4) | 7.087(4) | 4.346(4) | 9.053(4) |
Theoretical SSCCs
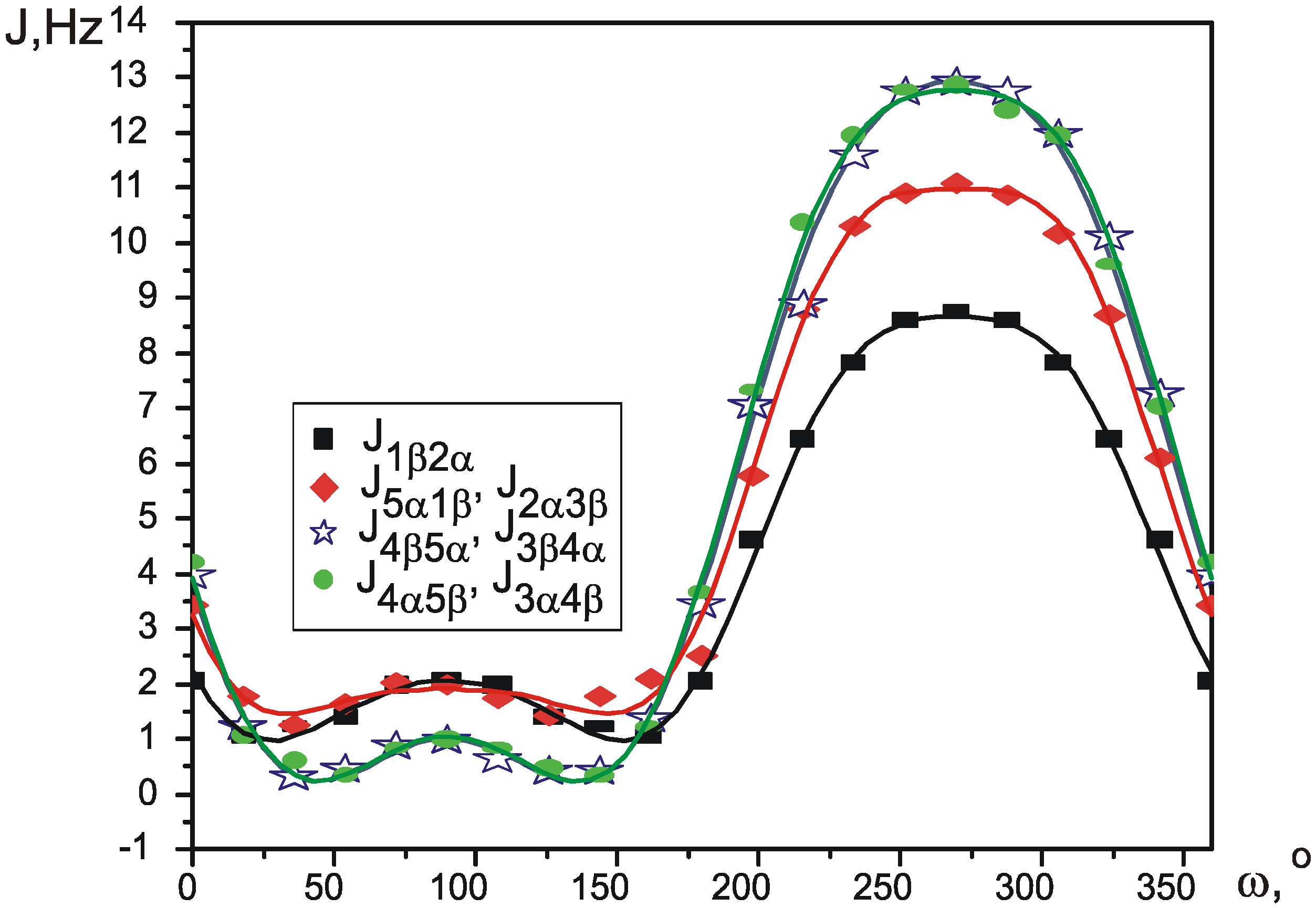
| J0 | J1 | J2 | J3 | J4 | s | χ2 | R | |
|---|---|---|---|---|---|---|---|---|
| J1β2α | 4.040 | -1.575 | -0.248 | -3.802 | -0.498 | 0 | 0.031 | 0.997 |
| J5α1β, J2α3β | 5.225 | -1.618 | -0.383 | -5.127 | -0.619 | +0.2π, -0.2π | 0.072 | 0.996 |
| J3α4β, J4α5β | 5.540 | -1.536 | -0.167 | -6.792 | -0.921 | +0.6π, -0.6π | 0.051 | 0.998 |
| J4β5α, J3β4α | 5.459 | -1.612 | -0.093 | -6.745 | -0.789 | +0.4π, -0.4π | 0.091 | 0.997 |
| J2α3α, J5β1β | 7.067 | 0.675 | -2.385 | -0.105 | 0.325 | 0.3π, 0.7π | 0.047 | 0.987 |
| J3α4α, J4β5β | 8.524 | 0.173 | -3.192 | -0.206 | 0.115 | 0.1π, 0.9π | 0.083 | 0.988 |
| J4α5α, J3β4β | 8.472 | 0.272 | -3.158 | -0.222 | 0.205 | 0.1π, -0.1π | 0.065 | 0.991 |
| J0 | J1 | J2 | J3 | J4 | S | χ2 | R | |
|---|---|---|---|---|---|---|---|---|
| J1β2α | 4.292 | -1.677 | -0.233 | -4.077 | -0.552 | 0 | 0.016 | 0.999 |
| J5α1β, J2α3β | 5.241 | -1.678 | -0.340 | -5.283 | -0.666 | +0.2π, -0.2π | 0.041 | 0.998 |
| J3α4β, J4α5β | 5.555 | -1.554 | -0.186 | -6.796 | -0.933 | +0.6π, -0.6π | 0.048 | 0.998 |
| J4β5α, J3β4α | 5.520 | -1.527 | -0.039 | -6.741 | -0.847 | +0.4π, -0.4π | 0.086 | 0.997 |
| J2α3α, J5β1β | 7.127 | 0.717 | -2.466 | -0.166 | 0.342 | 0.3π, 0.7π | 0.058 | 0.987 |
| J3α4α, J4β5β | 8.392 | 0.151 | -3.183 | -0.103 | 0.204 | 0.1π, 0.9π | 0.045 | 0.993 |
| J4α5α, J3β4β | 8.402 | 0.283 | -3.181 | -0.241 | 0.207 | 0.1π, -0.1π | 0.050 | 0.993 |
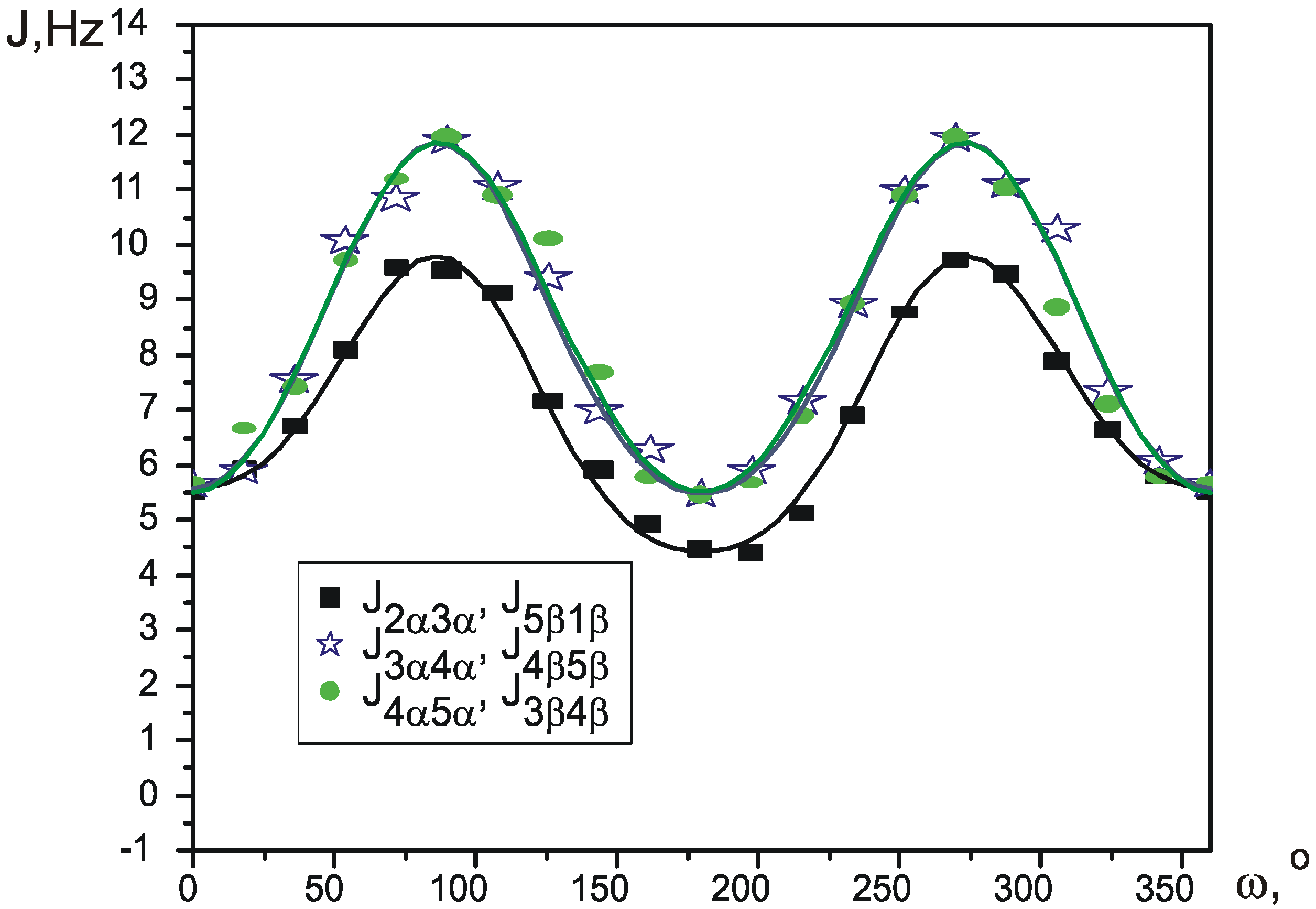
Pseudorotation potential.
| V1 | V2 | RMS, Hz | Vmax-Vmin | V(2T1)-V(1T2) | precision* | |||
|---|---|---|---|---|---|---|---|---|
| CD3CN | C6D6 | CCl4 | ||||||
| ab initio | 0.394 | -0.5678 | 0.58 | 0.56 | 0.97 | 1.563 | 0.788 | n/a |
| CD3CN | 0.3393 | -0.2942 | 0.45 | 0.976 | 0.679 | 0.01 | ||
| C6D6 | 0.6028 | -0.2341 | 0.41 | 1.264 | 1.206 | 0.03 | ||
| CCl4 | 1.4035 | 0.07861 | 0.59 | 2.807 | 2.807 | 0.7 | ||
| V1 | V2 | RMS, Hz | Vmax-Vmin | V(2T1)-V(1T2) | precision | |||
|---|---|---|---|---|---|---|---|---|
| CD3CN | C6D6 | CCl4 | ||||||
| ab initio | 1.403 | -0.721 | 0.96 | 0.83 | 0.86 | 3.191 | 2.806 | n/a |
| CD3CN | 0.8205 | -0.2174 | 0.53 | 1.642 | 1.641 | 0.06 | ||
| C6D6 | 2.4222 | 0.3886 | 0.61 | 4.844 | 4.844 | 2.0 | ||
| CCl4 | 4.9797 | 1.1819 | 0.72 | 9.959 | 9.959 | 5.8 | ||
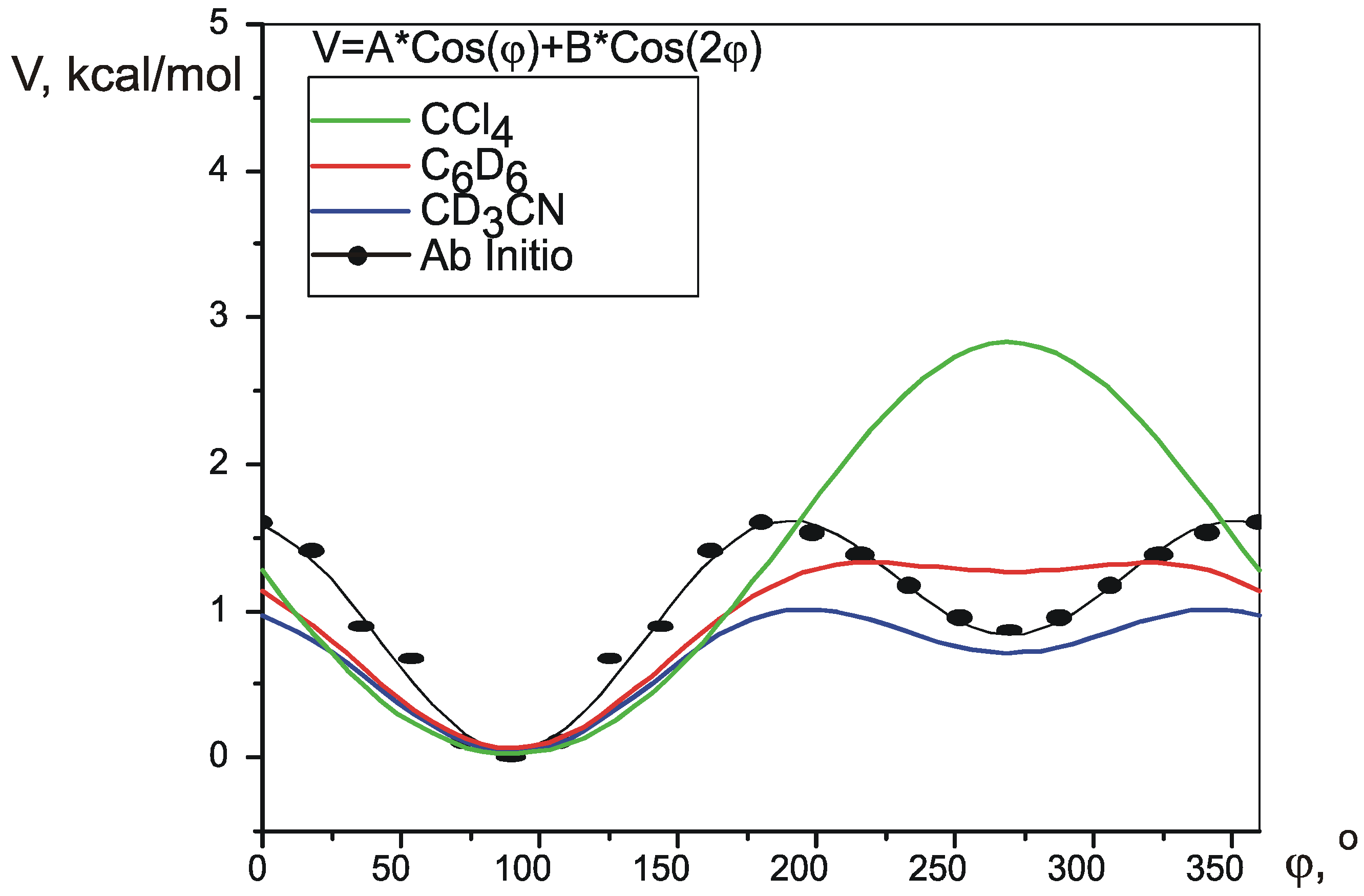
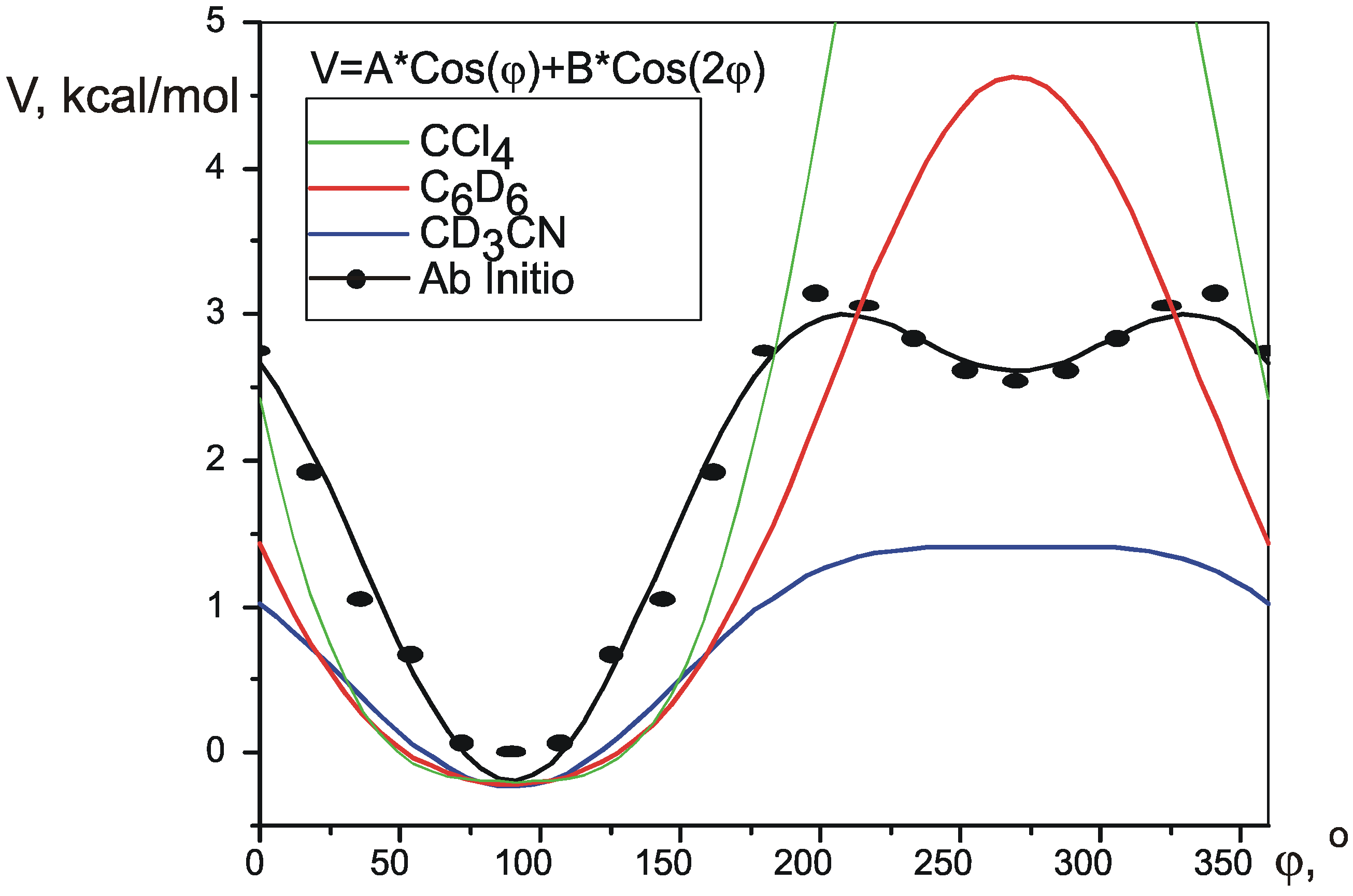
Acknowledgment
References and Notes
- Claridge, T. D. W. High-Resolution NMR Techniques in Organic Chemistry; Pergamon: Amstrdam, 1999. [Google Scholar]
- Altona, G.; Buys, H. R.; Havinga, E. Rec. Trav. Chim. 1966, 85, 983.
- Castellano, S. M.; Bothner-By, A. A. J. Chem. Phys. 1964, 41, 3963.
- Golotvin, S. S.; Chertkov, V. A. Russ. Chem. Bull. (Engl. Transl.) 1997, 46, 423.
- Diehl, P.; Sykora, S.; Vogt, J. J. Magn. Reson. 1975, 19, 67.
- Laatikainen, R. J. Magn. Reson. 1990, 92, 1.
- Pulkkinen, J.; Laatikainen, R.; Vepsalainen, J.; Ahlgren, M. Magn. Reson. Chem. 1999, 37, 119. [CrossRef]
- Heinzer, J. J. Magn. Reson. 1977, 26, 301.
- Stephenson, D. S.; Binsch, G. J. Magn. Reson. 1980, 37, 409.
- Zubkov, S.V; Golotvin, S.S.; Chertkov, V. A. Proceedings of the 15th European Experimental NMR Conference 2000, 42.
- Cremer, D.; Pople, J. A. J. Am. Chem. Soc. 1975, 97, 1354.
- Wu, A.; Cremer, D.; Auer, A. A.; Gauss, J. J. Phys. Chem. A 2002, 106, 657.
- Lipnick, R. L. J. Mol. Struct. 1974, 21, 423.
- Freedberg, D. I. J. Amer. Chem. Soc. 2002, 124, 2358. [CrossRef]
- Boeyens, J. C. A. J. Cryst. Mol. Struct. 1978, 8, 317.
- Gaussian 94, Revision E.1. Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Gill, P. M. W.; Johnson, B. G.; Robb, M. A.; Cheeseman, J. R.; Keith, T.; Petersson, G. A.; Montgomery, J. A.; Raghavachari, K.; Al-Laham, M. A.; Zakrzewski, V. G.; Ortiz, J. V.; Foresman, J. B.; Cioslowski, J.; Stefanov, B. B.; Nanayakkara, A.; Challacombe, M.; Peng, C. Y.; Ayala, P. Y.; Chen, W.; Wong, M. W.; Andres, J. L.; Replogle, E. S.; Gomperts, R.; Martin, R. L.; Fox, D. J.; Binkley, J. S.; Defrees, D. J.; Baker, J.; Stewart, J. P.; Head-Gordon, M.; Gonzalez, C.; Pople, J. A. (Eds.) Gaussian, Inc.: Pittsburgh PA, 1995.
- Foresman, J. B.; Frisch, Æ. Exploring Chemistry with Electronic Structure Methods; Gaussian Inc.: Pittsburgh, 1996. [Google Scholar]
- Haasnoot, C. A. G.; de Leeuw, F. A. A. M.; Altona, C. Tetrahedron Lett 1980, 36, 783.
© 2003 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Zubkov, S.V.; Chertkov, V.A. Experimental Determination of Pseudorotation Potentials for Disubstituted Cyclopentanes Based on Spin–Spin Coupling Constants. Int. J. Mol. Sci. 2003, 4, 107-118. https://doi.org/10.3390/i4030107
Zubkov SV, Chertkov VA. Experimental Determination of Pseudorotation Potentials for Disubstituted Cyclopentanes Based on Spin–Spin Coupling Constants. International Journal of Molecular Sciences. 2003; 4(3):107-118. https://doi.org/10.3390/i4030107
Chicago/Turabian StyleZubkov, Sergei V., and Vyacheslav A. Chertkov. 2003. "Experimental Determination of Pseudorotation Potentials for Disubstituted Cyclopentanes Based on Spin–Spin Coupling Constants" International Journal of Molecular Sciences 4, no. 3: 107-118. https://doi.org/10.3390/i4030107
APA StyleZubkov, S. V., & Chertkov, V. A. (2003). Experimental Determination of Pseudorotation Potentials for Disubstituted Cyclopentanes Based on Spin–Spin Coupling Constants. International Journal of Molecular Sciences, 4(3), 107-118. https://doi.org/10.3390/i4030107




