Potential Functions of Al2 by the Relativistic Fock-Space Coupled Cluster Method
Abstract
:1 Introduction
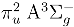 . The adiabatic energy separation Te of the two states has not been determined experimentally; theoretical predictions [2,3] are about 200 cm−1.
. The adiabatic energy separation Te of the two states has not been determined experimentally; theoretical predictions [2,3] are about 200 cm−1.2 Methodology
2.1 The relativistic Hamiltonian
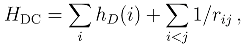

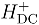 provides the framework for the calculations reported here.
provides the framework for the calculations reported here.2.2 The Fock space coupled cluster method
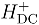 may be rewritten in second-quantized form [9,11] in terms of normal-ordered products of spinor creation and annihilation operators {r†s} and {r†s†ut},
may be rewritten in second-quantized form [9,11] in terms of normal-ordered products of spinor creation and annihilation operators {r†s} and {r†s†ut},
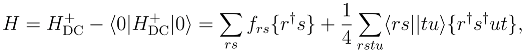
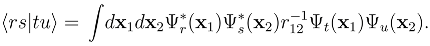


2.3 The intermediate Hamiltonian coupled cluster method
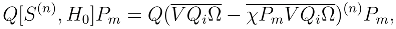
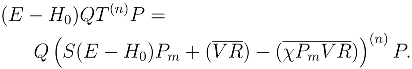
3 Calculations
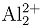 ion was used as reference, and the Al2 states were obtained by the Fock-space scheme
ion was used as reference, and the Al2 states were obtained by the Fock-space scheme

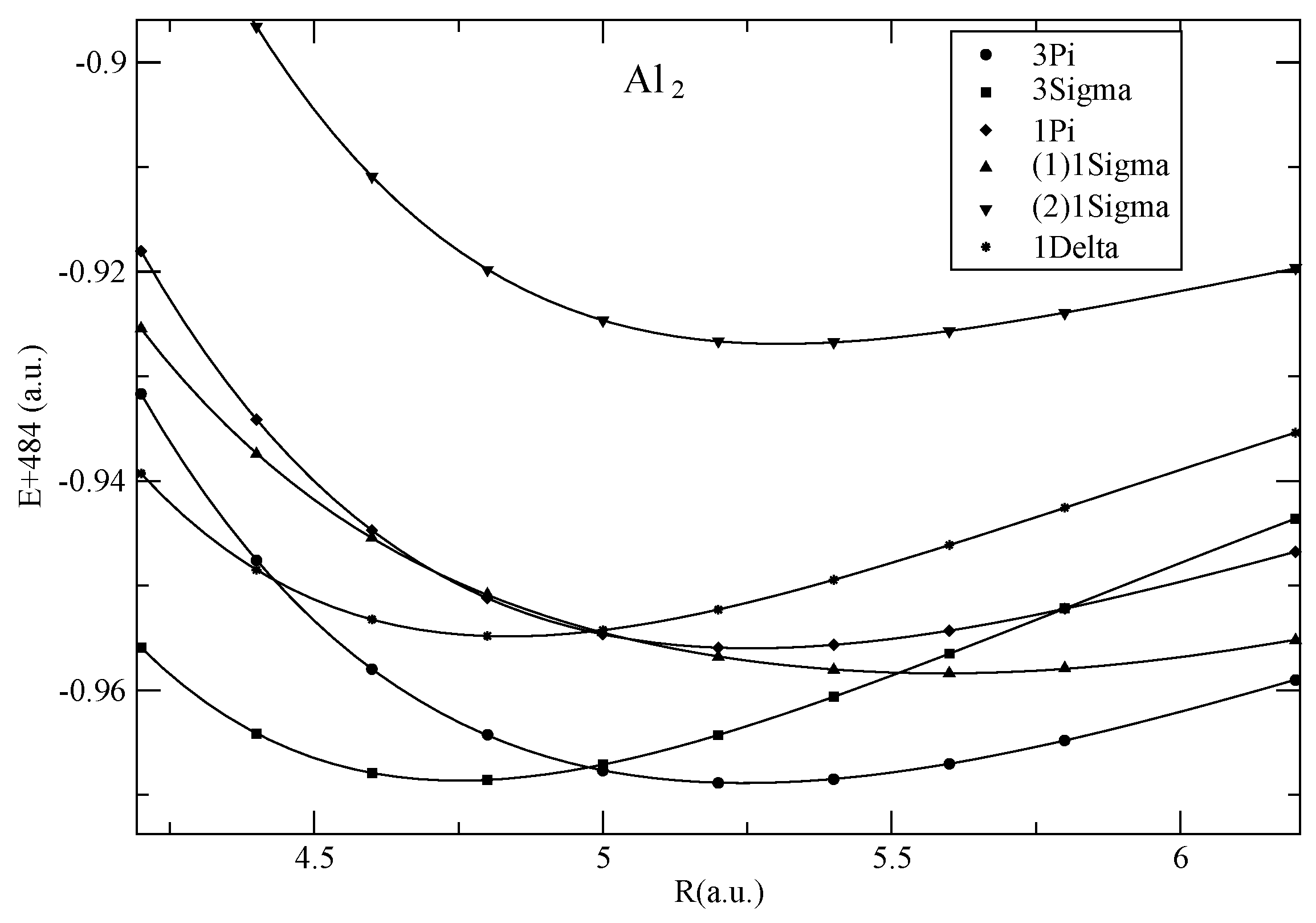
4 Results and Discussion
 spectroscopic constants show similar behavior, with the calculated Re 2.52 Å compared with the experimental [4] 2.47 Å, ωe = 335 cm−1 (expt. 350 cm−1), and ωexe = 2.0 cm−1 (expt. 2.0 cm−1). Values uncorrected for BSSE are again closer to experiment and to the Langhoff and Bauschlicher numbers.
spectroscopic constants show similar behavior, with the calculated Re 2.52 Å compared with the experimental [4] 2.47 Å, ωe = 335 cm−1 (expt. 350 cm−1), and ωexe = 2.0 cm−1 (expt. 2.0 cm−1). Values uncorrected for BSSE are again closer to experiment and to the Langhoff and Bauschlicher numbers.| R | 3Π0+u | 3Π0−u | 3Π1u | 3Π2u |  |
| 4.2 | -0.9316700 | -0.9316700 | -0.93149 | -0.93131 | -0.95592 |
| 4.8 | -0.9475860 | -0.9475860 | -0.94741 | -0.94724 | -0.96414 |
| 4.6 | -0.9579970 | -0.9579970 | -0.95783 | -0.95766 | -0.96791 |
| 4.8 | -0.9642450 | -0.9642450 | -0.96418 | -0.96401 | -0.96856 |
| 5.0 | -0.9676862 | -0.9676851 | -0.96753 | -0.96737 | -0.96711 |
| 5.2 | -0.9688693 | -0.9688680 | -0.96872 | -0.96856 | -0.96429 |
| 5.4 | -0.9684924 | -0.9684909 | -0.96835 | -0.96819 | -0.96064 |
| 5.6 | -0.9670160 | -0.9670150 | -0.96687 | -0.96672 | -0.95650 |
| 5.8 | -0.9647870 | -0.9647850 | -0.96464 | -0.96450 | -0.95219 |
| 6.2 | -0.9590180 | -0.9590150 | -0.95888 | -0.95873 | -0.94361 |
| 6.4 | -0.9558050 | -0.9558020 | -0.95566 | -0.95552 | -0.93956 |
| R | 1Πu |  |  | 1∆g |
| 4.2 | -0.91804 | -0.92544 | -0.87523 | -0.93929 |
| 4.4 | -0.93415 | -0.93743 | -0.89657 | -0.94851 |
| 4.6 | -0.94472 | -0.94544 | -0.91091 | -0.95324 |
| 4.8 | -0.95120 | -0.95084 | -0.91982 | -0.95482 |
| 5.0 | -0.95466 | -0.95449 | -0.92466 | -0.95426 |
| 5.2 | -0.95595 | -0.95683 | -0.92664 | -0.95230 |
| 5.4 | -0.95567 | -0.95805 | -0.92673 | -0.94946 |
| 5.6 | -0.95431 | -0.95838 | -0.92568 | -0.94612 |
| 5.8 | -0.95220 | -0.95790 | -0.92395 | -0.94256 |
| 6.2 | -0.94678 | -0.95523 | -0.91966 | -0.93539 |
| 6.4 | -0.94380 | -0.95328 | -0.91743 | -0.93199 |
| State | re (Å) | De (eV) | ωe | ωexe | Te(cm−1) |
| 3Π0−u | 2.78 | 1.21 | 265 | 0.91 | 0 |
| 3Π0+u | 2.78 | 1.22 | 265 | 0.90 | 0.3 |
| 3Π1u | 2.78 | 1.21 | 266 | 1.4 | 32.7 |
| 3Π2u | 2.78 | 1.22 | 266 | 1.4 | 66.3 |
 | 2.52 | 1.22 | 335 | 2.0 | 70.7 |
 | 2.95 | 0.94 | 200 | 1.6 | 2310 |
| 1Πu | 2.79 | 0.88 | 262 | 1.6 | 2830 |
| 1∆g | 2.57 | 0.85 | 310 | 2.1 | 3080 |
 | 2.81 | 0.10 | 264 | 2.9 | 9240 |
References
- Cai, M. F.; Carter, C. C.; Miller, T. A.; Bondybey, V. E. Chem. Phys. 1991, 155, 233–245.
- Sunil, K. K.; Jordan, K. D. J. Phys. Chem. 1988, 92, 2774–81.
- Langhoff, S. R.; Bauschlicher, C. W. J. Chem. Phys. 1990, 92, 1879–86.
- Fu, Z.; Lemire, G. W.; Bishea, G. A.; Morse, M. D. J. Chem. Phys. 1990, 93, 8420–41.
- Kaldor, U.; Eliav, E. Advan. Quantum Chem. 1998, 31, 313–336.
- See, e.g. Sucher, J. Relativistic, Quantum Electrodynamic, and Weak Interaction Effects in Atoms; Johnson, W., Mohr, P., Sucher, J., Eds.; American Institute of Physics: New York, 1989; p. 28. [Google Scholar]
- Brown, G.E.; Ravenhall, D.G. Proc. Roy. Soc. A 1951, 208, 552–559.
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of One- and Two-Electron Atoms; Springer-verlag: Berlin, 1957. [Google Scholar]
- Sucher, J. Phys. Rev. A 1980, 22, 348–362.Phys. Scr. 1987, 36, 271–281.
- Buchmüller, W.; Dietz, K. Z. Phys. C 1980, 5, 45–54.
- Ishikawa, Y.; Binning, R.C.; Sekino, H. Chem. Phys. Lett. 1989, 160, 206.Ishikawa, Y. Phys. Rev. A 1990, 42, 1142–50.Chem. Phys. Lett. 1990, 166, 321.Ishikawa, Y.; Quiney, H.M. Phys. Rev. A 1993, 47, 1732–39.Ishikawa, Y.; Koc, K. Phys. Rev. A 1994, 50, 4733–42.
- Lindgren, I.; Morrison, J. Atomic Many-Body Theory, 2nd ed; Springer Verlag: Berlin, 1986. [Google Scholar]
- Hughes, S.R.; Kaldor, U. Chem. Phys. Lett. 1992, 194, 99–104.Chem. Phys. Lett. 1993, 204, 339–343.Phys. Rev. A 1993, 47, 4705–12.J. Chem. Phys. 1993, 99, 6773–76.Intern. J. Quantum Chem. 1995, 55, 127–133.
- Mukherjee, D.; Pal, S. Advan. Quantum Chem. 1989, 20, 292–373.
- Kaldor, U. Theor. Chim. Acta 1991, 80, 427–439.
- Landau, A.; Eliav, E.; Kaldor, U. Chem. Phys. Lett. 1999, 313, 399–403.Landau, A.; Eliav, E.; Ishikawa, Y.; Kaldor, U. J. Chem. Phys. 2000, 113, 9905–10.Landau, A.; Eliav, E.; Kaldor, U. Advan. Quantum Chem. 2001, 39, 172–188.
- Malrieu, J.-P.; Durand, Ph.; Daudey, J.-P. J. Phys. A 1985, 18, 809–826.
- Aerts, P.J.C.; Visser, O.; Visscher, L.; Merenga, H.; de Jong, W.A.; Nieuwpoort, W.C. MOLFDIR Program Package; University of Groningen: The Netherlands.
- Woon, D. E.; Dunning, T. H. J. Chem. Phys. 1993, 98, 1358–71.
- Partridge, H.; Bauschlicher, C. W.; Visscher, L. Chem. Phys. Lett. 1995, 246, 33–39.
- Lide, D. R. (Ed.) Handbook of Chemistry and Physics, 81st edition; CRC Press: Boca Raton, 2000; pp. 1–13.
- Moore, C. E. Atomic Energy Levels; Natl. Bur. of Stand. (U.S.) Circ. No. 467. U.S. GPO; Washington, DC, 1948. [Google Scholar]
- Boys, S.F.; Bernardi, F. Mol. Phys. 1970, 19, 553–566.
© 2002 by MDPI, Basel, Switzerland. Reproduction for noncommercial purposes permitted.
Share and Cite
Landau, A.; Eliav, E.; Visscher, L.; Kaldor, U. Potential Functions of Al2 by the Relativistic Fock-Space Coupled Cluster Method. Int. J. Mol. Sci. 2002, 3, 498-507. https://doi.org/10.3390/i3050498
Landau A, Eliav E, Visscher L, Kaldor U. Potential Functions of Al2 by the Relativistic Fock-Space Coupled Cluster Method. International Journal of Molecular Sciences. 2002; 3(5):498-507. https://doi.org/10.3390/i3050498
Chicago/Turabian StyleLandau, Arie, Ephraim Eliav, Lucas Visscher, and Uzi Kaldor. 2002. "Potential Functions of Al2 by the Relativistic Fock-Space Coupled Cluster Method" International Journal of Molecular Sciences 3, no. 5: 498-507. https://doi.org/10.3390/i3050498
APA StyleLandau, A., Eliav, E., Visscher, L., & Kaldor, U. (2002). Potential Functions of Al2 by the Relativistic Fock-Space Coupled Cluster Method. International Journal of Molecular Sciences, 3(5), 498-507. https://doi.org/10.3390/i3050498




