Evaluating and Selecting Kinetic and Isotherm Models for Copper and Nickel Removal Using Cow Bone Char as an Adsorbent via Excel Solver Functions
Abstract
1. Introduction
2. Results and Discussions
2.1. Effect of Contact Time and Concentration of Cu(II) Ions and Ni(II) Ions Removal onto Cow Bone Char
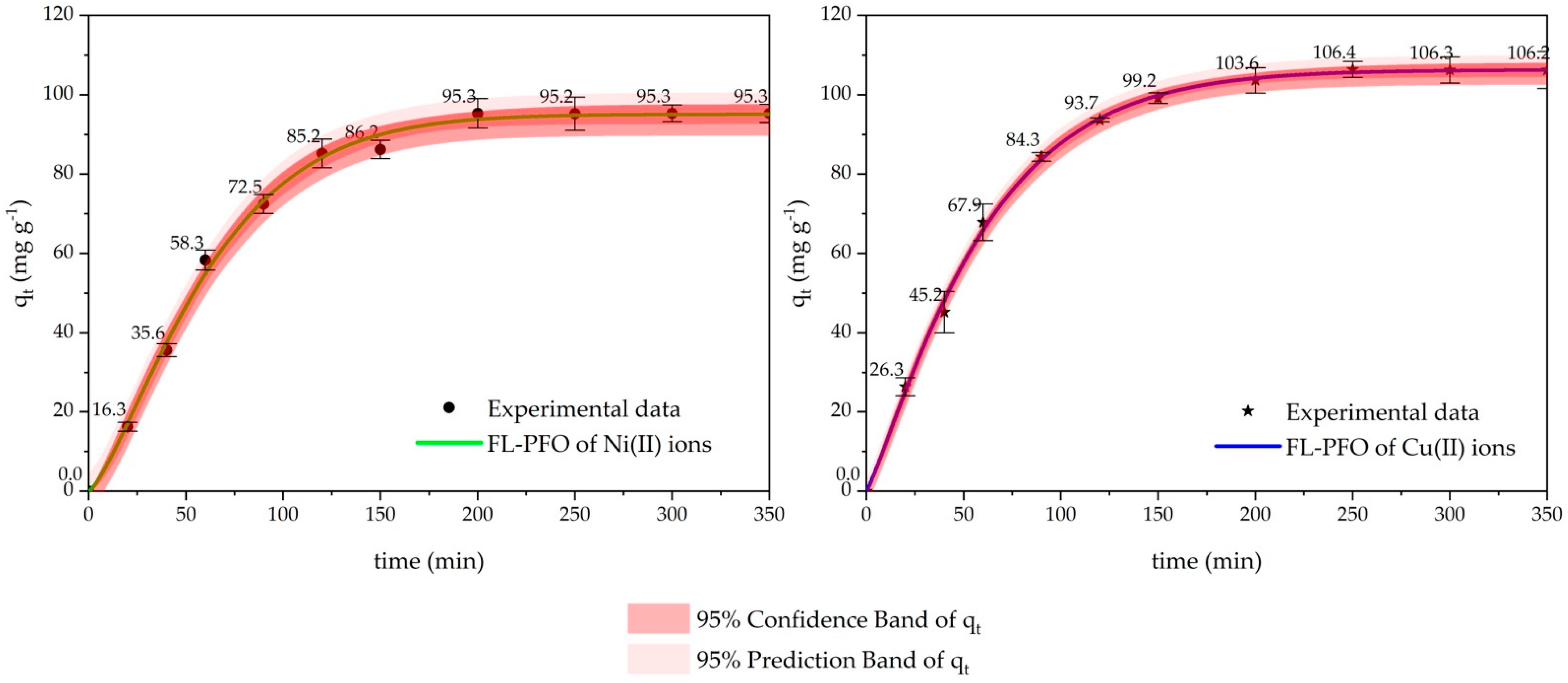
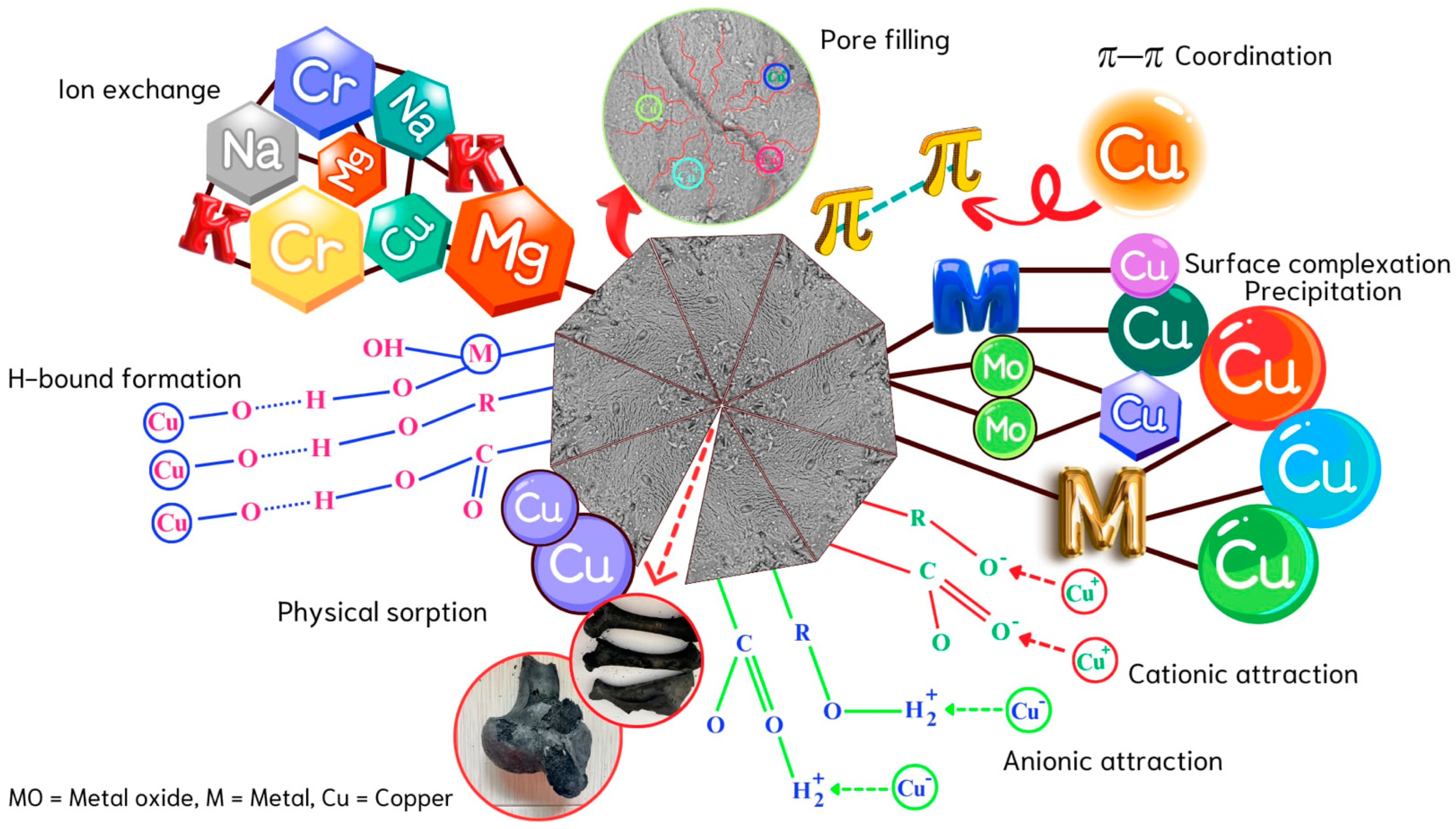
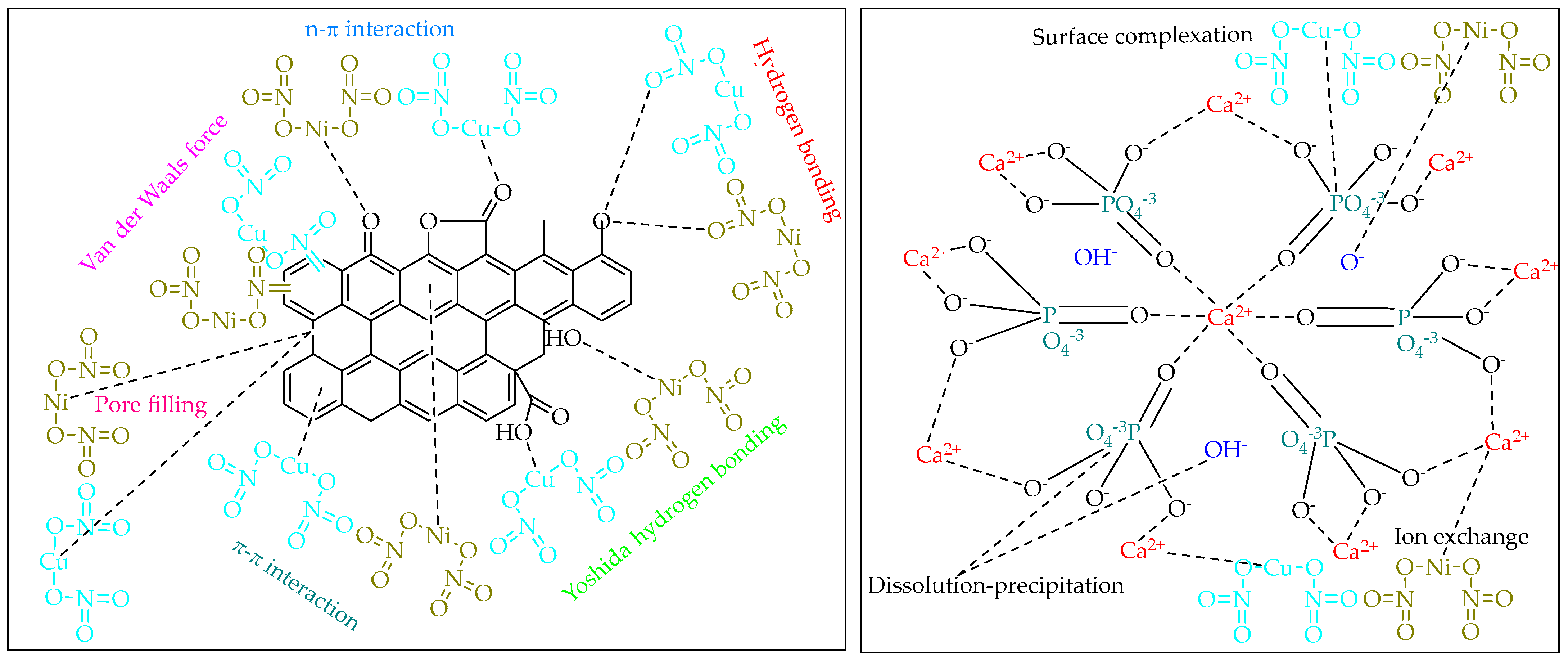
2.2. Kinetic Adsorption Studies
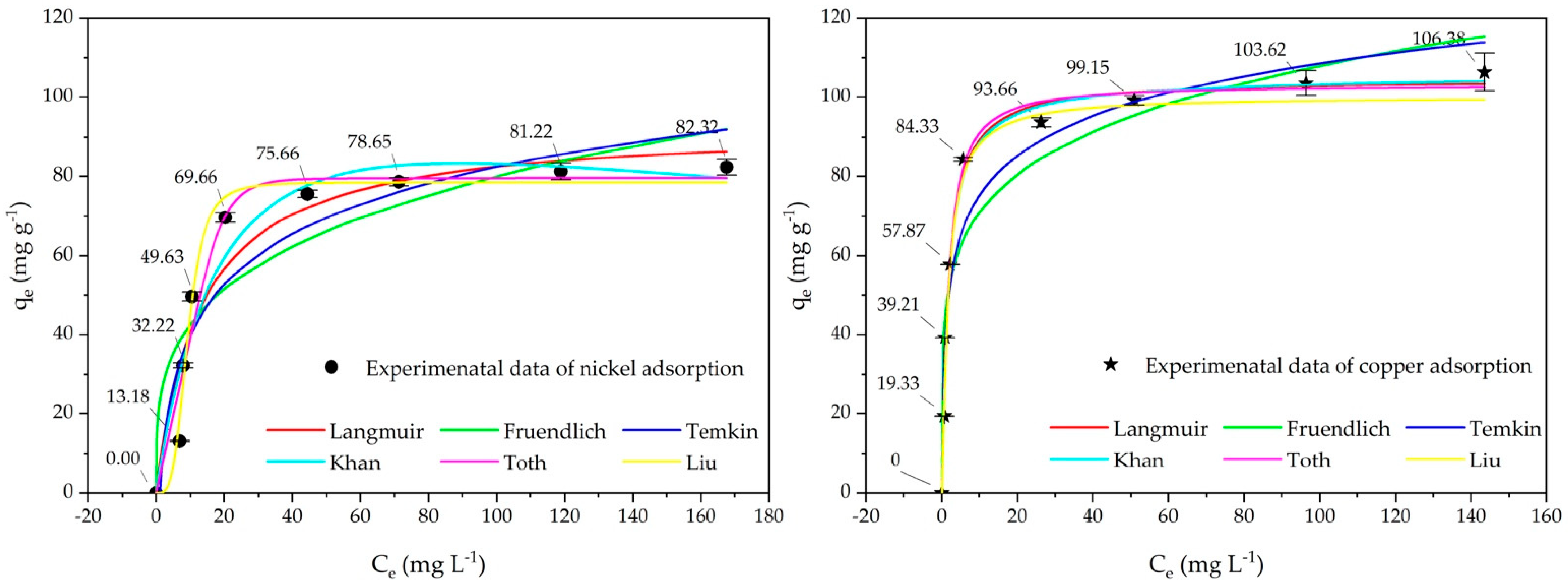
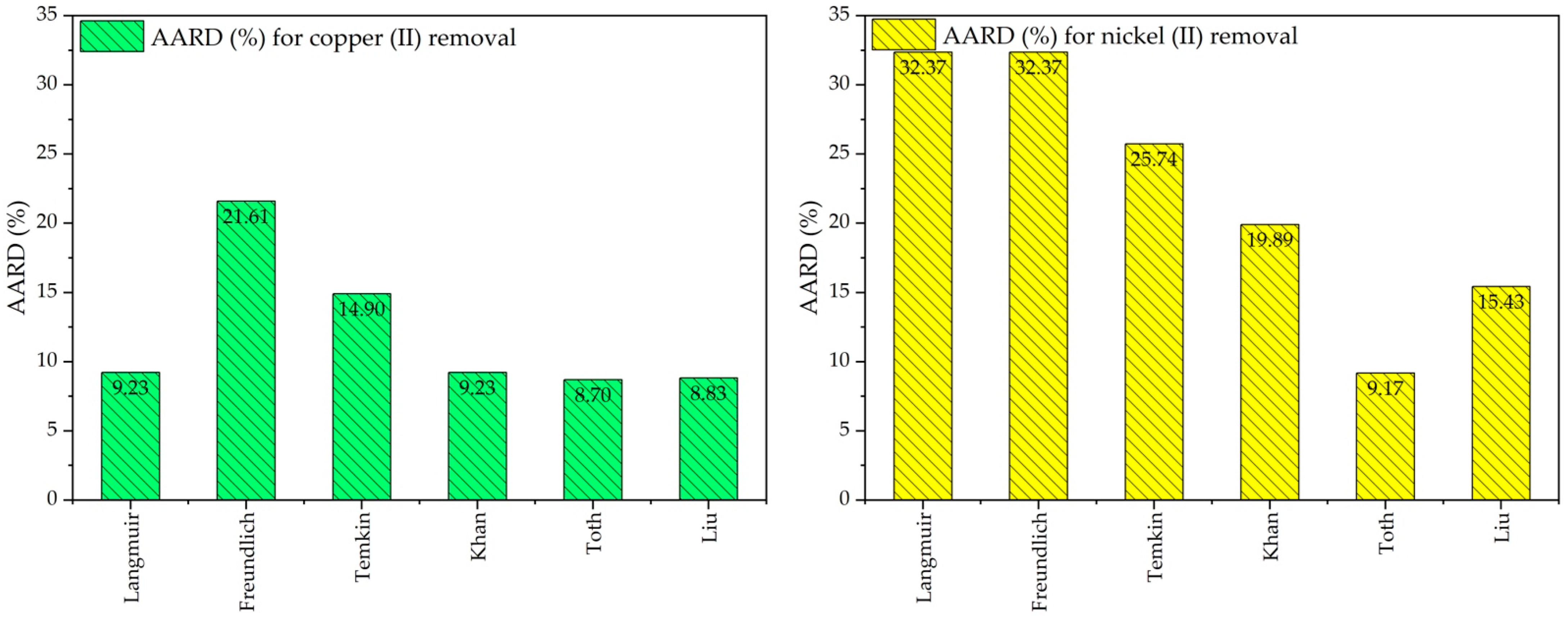
2.3. Adsorption Isotherm Studies
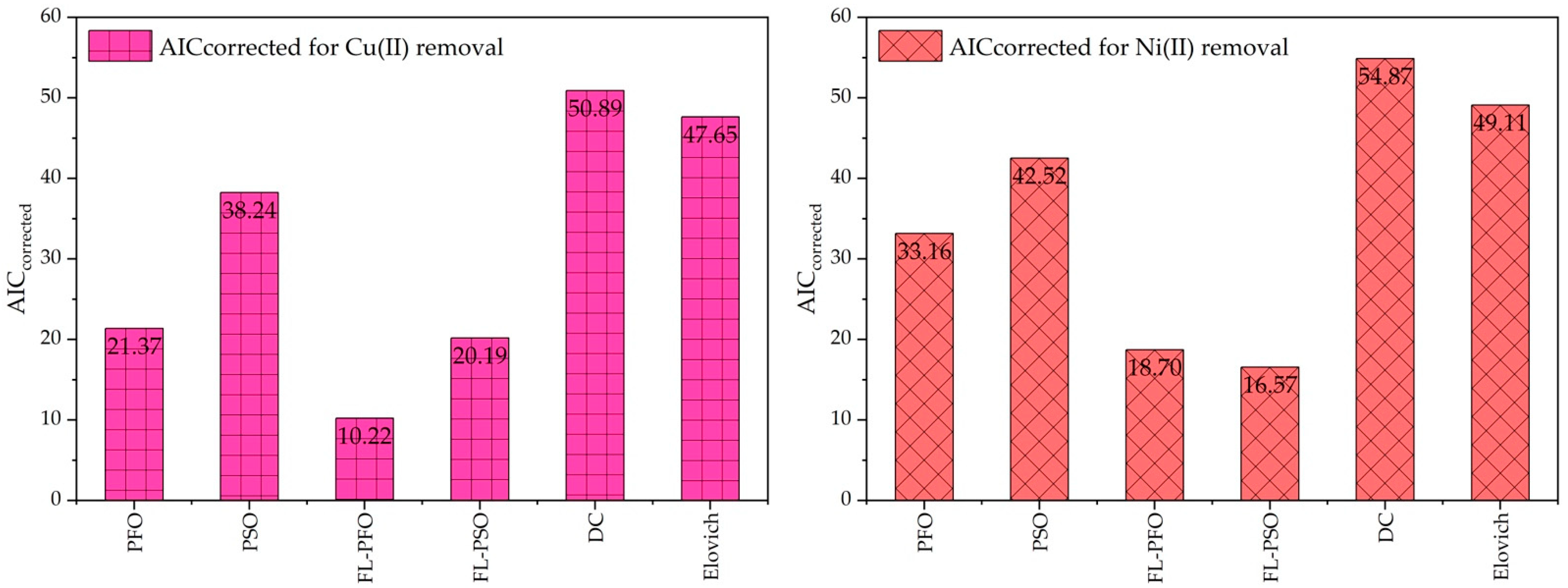
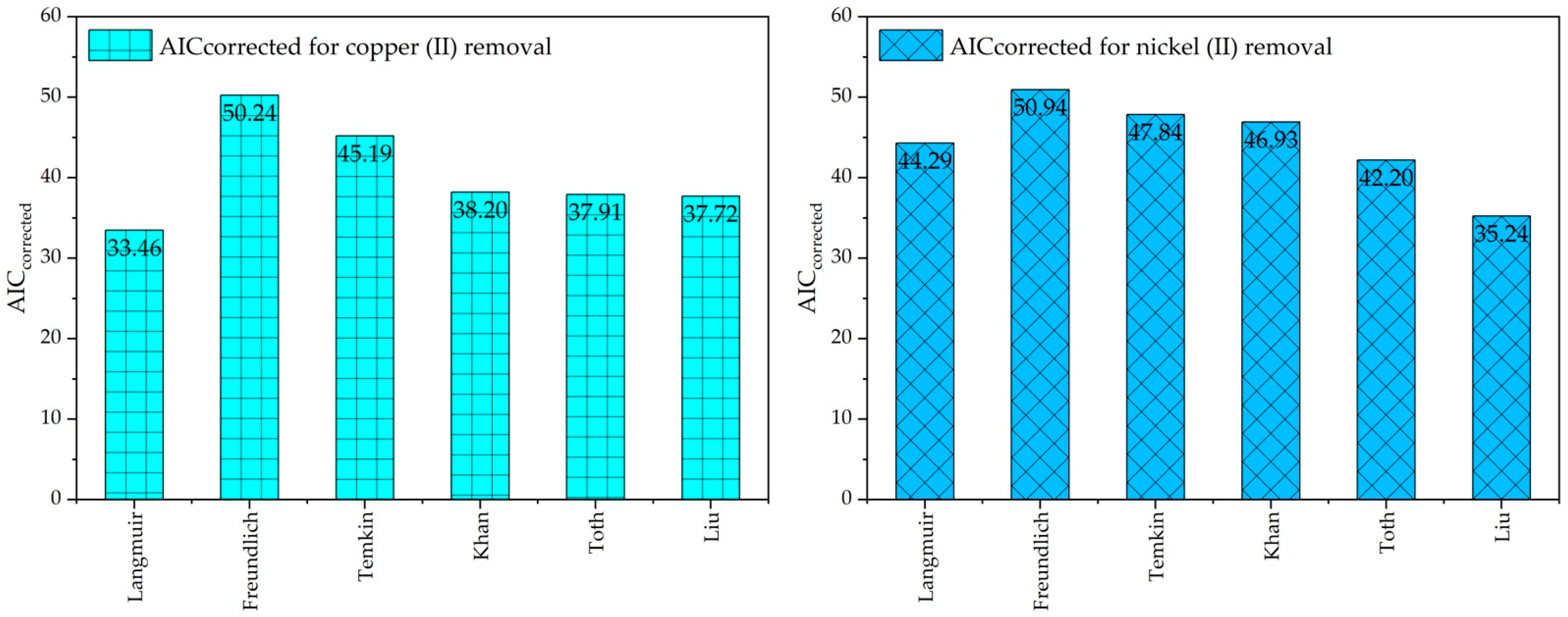
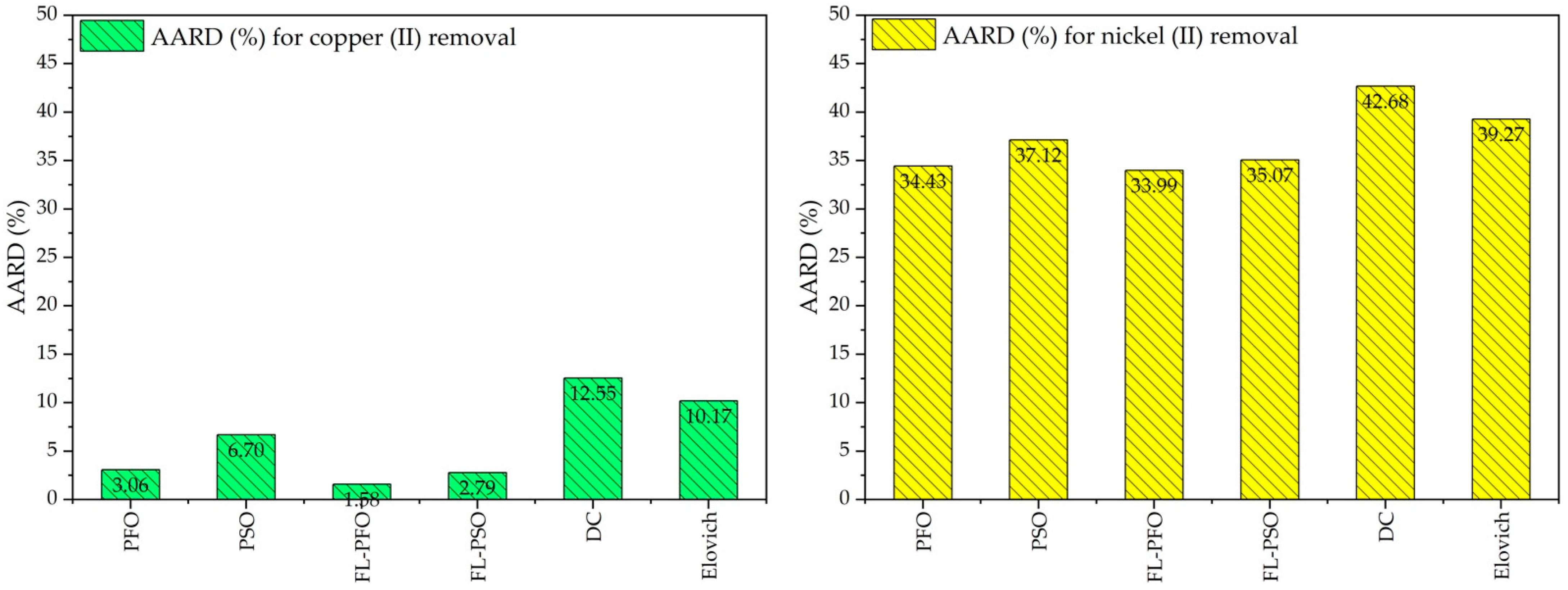
2.4. Statical Analysis and Akaike’s Information Criterion Its Appropriate Selection
2.5. Desorption and Reusability
3. Materials and Methods
3.1. Synthetic Copper and Nickel Acidic Solution Preparation
3.2. Kinetic Adsorption Studies
3.3. Adsorption Isotherm Studies
3.4. Experimental Kinetic and Isotherm Data Fitting in Microsoft Excel
3.5. Error Function and Calculation
3.6. Statical Analysis and Its Appropriate Selection
3.7. Desorption and Reusability
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Q.-G.; Liu, G.-H.; Qi, L.; Wang, H.-C.; Ye, Z.-F.; Zhao, Q.-L. Heavy metal-contained wastewater in China: Discharge, management and treatment. Sci. Total Environ. 2022, 808, 152091. [Google Scholar] [CrossRef] [PubMed]
- Munir, N.; Jahangeer, M.; Bouyahya, A.; El Omari, N.; Ghchime, R.; Balahbib, A.; Aboulaghras, S.; Mahmood, Z.; Akram, M.; Ali Shah, S.M. Heavy metal contamination of natural foods is a serious health issue: A review. Sustainability 2021, 14, 161. [Google Scholar] [CrossRef]
- Chai, W.S.; Cheun, J.Y.; Kumar, P.S.; Mubashir, M.; Majeed, Z.; Banat, F.; Ho, S.-H.; Show, P.L. A review on conventional and novel materials towards heavy metal adsorption in wastewater treatment application. J. Clean. Prod. 2021, 296, 126589. [Google Scholar] [CrossRef]
- Benalia, M.C.; Youcef, L.; Bouaziz, M.G.; Achour, S.; Menasra, H. Removal of heavy metals from industrial wastewater by chemical precipitation: Mechanisms and sludge characterization. Arab. J. Sci. Eng. 2022, 47, 5587–5599. [Google Scholar] [CrossRef]
- Suwannahong, K.; Wongcharee, S.; Kreetachat, T.; Imman, S.; Suriyachai, N.; Hongthong, S.; Rioyo, J.; Dechapanya, W.; Noiwimol, P. Comprehensive Cost–Benefit and Statistical Analysis of Isotherm and Kinetic Models for Heavy Metal Removal in Acidic Solutions Using Weakly Base Polymeric Chelating Resin as Adsorbent. Water 2024, 16, 2384. [Google Scholar] [CrossRef]
- Suwannahong, K.; Wongcharee, S.; Rioyo, J.; Sirilamduan, C.; Kreetachart, T. Insight into molecular weight cut off characteristics and reduction of melanoidin using microporous and mesoporous adsorbent. Eng. Appl. Sci. Res. 2022, 49, 47–57. [Google Scholar]
- Sreedevi, P.; Suresh, K.; Jiang, G. Bacterial bioremediation of heavy metals in wastewater: A review of processes and applications. J. Water Process Eng. 2022, 48, 102884. [Google Scholar] [CrossRef]
- Prajapati, A.K.; Mondal, M.K. Comprehensive kinetic and mass transfer modeling for methylene blue dye adsorption onto CuO nanoparticles loaded on nanoporous activated carbon prepared from waste coconut shell. J. Mol. Liq. 2020, 307, 112949. [Google Scholar] [CrossRef]
- Tomczyk, A.; Sokołowska, Z.; Boguta, P. Biochar physicochemical properties: Pyrolysis temperature and feedstock kind effects. Rev. Environ. Sci. Bio/Technol. 2020, 19, 191–215. [Google Scholar] [CrossRef]
- Saldaña, E.; Martins, M.M.; Behrens, J.H.; Valentin, D.; Selani, M.M.; Contreras-Castillo, C.J. Looking at non-sensory factors underlying consumers’ perception of smoked bacon. Meat Sci. 2020, 163, 108072. [Google Scholar] [CrossRef]
- Agbenorku, P.; Ansah, S.; Acheampong, A.; Sabbah, D.; Bankas, D.; Adu, E.; Plange-Rhule, G.; Adiyiah, Y.; Donkor, P. Komfo anokye teaching hospital multidisciplinary cleft clinic. J. Craniofacial Surg. 2011, 22, 532–536. [Google Scholar] [CrossRef] [PubMed]
- Tejada-Tovar, C.; Gonzalez-Delgado, A.D.; Villabona-Ortiz, A. Characterization of residual biomasses and its application for the removal of lead ions from aqueous solution. Appl. Sci. 2019, 9, 4486. [Google Scholar] [CrossRef]
- Fiyadh, S.S.; Alardhi, S.M.; Al Omar, M.; Aljumaily, M.M.; Al Saadi, M.A.; Fayaed, S.S.; Ahmed, S.N.; Salman, A.D.; Abdalsalm, A.H.; Jabbar, N.M. A comprehensive review on modelling the adsorption process for heavy metal removal from waste water using artificial neural network technique. Heliyon 2023, 9, e15455. [Google Scholar] [CrossRef] [PubMed]
- Marmiroli, B.; Messagie, M.; Dotelli, G.; Van Mierlo, J. Electricity generation in LCA of electric vehicles: A review. Appl. Sci. 2018, 8, 1384. [Google Scholar] [CrossRef]
- Yu, S.; Zhang, G.; Li, J.; Zhao, Z.; Kang, X. Effect of endogenous hydrolytic enzymes pretreatment on the anaerobic digestion of sludge. Bioresour. Technol. 2013, 146, 758–761. [Google Scholar] [CrossRef]
- Bartoli, M.; Giorcelli, M.; Jagdale, P.; Rovere, M.; Tagliaferro, A. A Review of Non-Soil Biochar Applications. Materials 2020, 13, 261. [Google Scholar] [CrossRef]
- Chao, H.-P.; Chang, C.-C.; Nieva, A. Biosorption of heavy metals on Citrus maxima peel, passion fruit shell, and sugarcane bagasse in a fixed-bed column. J. Ind. Eng. Chem. 2014, 20, 3408–3414. [Google Scholar] [CrossRef]
- Sousa, F.W.; Oliveira, A.G.; Ribeiro, J.P.; Rosa, M.F.; Keukeleire, D.; Nascimento, R.F. Green coconut shells applied as adsorbent for removal of toxic metal ions using fixed-bed column technology. J. Environ. Manag. 2010, 91, 1634–1640. [Google Scholar] [CrossRef]
- Demirbas, A. Heavy metal adsorption onto agro-based waste materials: A review. J. Hazard. Mater. 2008, 157, 220–229. [Google Scholar] [CrossRef]
- Hart, A.; Ebiundu, K.; Peretomode, E.; Onyeaka, H.; Nwabor, O.F.; Obileke, K. Value-added materials recovered from waste bone biomass: Technologies and applications. RSC Adv. 2022, 12, 22302–22330. [Google Scholar] [CrossRef]
- Tansomros, P.; Aungthitipan, P.; Janthakot, A.; Chanthakhot, A.; Maskhunthod, P.; Wongcharee, S.; Hongthong, S.; Sangsida, W.; Suwannahong, K.; Kreetachat, T. Slow Pyrolysis of Waste Cow Bone for Biochar Production and Its Application in Copper Removal From Acidic Solutions. Int. J. Chem. Eng. 2024, 2024, 5571034. [Google Scholar] [CrossRef]
- Tejada-Tovar, C.; Villabona-Ortíz, A.; González-Delgado, Á.D. High-efficiency removal of lead and nickel using four inert dry biomasses: Insights into the adsorption mechanisms. Materials 2023, 16, 4884. [Google Scholar] [CrossRef]
- Cavanaugh, J.E.; Neath, A.A. The Akaike information criterion: Background, derivation, properties, application, interpretation, and refinements. Wiley Interdiscip. Rev. Comput. Stat. 2019, 11, e1460. [Google Scholar] [CrossRef]
- Neath, A.A.; Cavanaugh, J.E. The Bayesian information criterion: Background, derivation, and applications. Wiley Interdiscip. Rev. Comput. Stat. 2012, 4, 199–203. [Google Scholar] [CrossRef]
- Fenga, C.; Gangemi, S.; Di Salvatore, V.; Falzone, L.; Libra, M. Immunological effects of occupational exposure to lead. Mol. Med. Rep. 2017, 15, 3355–3360. [Google Scholar] [CrossRef]
- Wang, Y.; Li, H.; Lin, S. Advances in the Study of Heavy Metal Adsorption from Water and Soil by Modified Biochar. Water 2022, 14, 3894. [Google Scholar] [CrossRef]
- Shan, R.; Shi, Y.; Gu, J.; Wang, Y.; Yuan, H. Single and competitive adsorption affinity of heavy metals toward peanut shell-derived biochar and its mechanisms in aqueous systems. Chin. J. Chem. Eng. 2020, 28, 1375–1383. [Google Scholar] [CrossRef]
- Yuan, S.; Tan, Z. Effect and mechanism of changes in physical structure and chemical composition of new biochar on Cu(II) adsorption in an aqueous solution. Soil Ecol. Lett. 2022, 4, 237–253. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, D.; Feng, S.; Chen, Y.; Xie, R. Ammonium thiocyanate functionalized graphene oxide-supported nanoscale zero-valent iron for adsorption and reduction of Cr (VI). J. Colloid Interface Sci. 2020, 580, 345–353. [Google Scholar] [CrossRef]
- Kumar, K.V. Linear and non-linear regression analysis for the sorption kinetics of methylene blue onto activated carbon. J. Hazard. Mater. 2006, 137, 1538–1544. [Google Scholar] [CrossRef]
- Azizian, S.; Fallah, R.N. A new empirical rate equation for adsorption kinetics at solid/solution interface. Appl. Surf. Sci. 2010, 256, 5153–5156. [Google Scholar] [CrossRef]
- Sutherland, C.; Venkobachar, C. A diffusion-chemisorption kinetic model for simulating biosorption using forest macro-fungus, fomes fasciatus. Int. Res. J. Plant Sci. 2010, 1, 107–117. [Google Scholar]
- Azizian, S.; Bagheri, M. Enhanced adsorption of Cu 2+ from aqueous solution by Ag doped nano-structured ZnO. J. Mol. Liq. 2014, 196, 198–203. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 40, 1361–1403. [Google Scholar] [CrossRef]
- Giles, C.H. The History and Use of the Freundlich Adsorption Isotherm. J. Soc. Dye. Colour. 1973, 89, 287–291. [Google Scholar] [CrossRef]
- Temkin, M. Kinetics of ammonia synthesis on promoted iron catalysts. Acta physiochim. URSS 1940, 12, 327–356. [Google Scholar]
- Khan, A.; Ataullah, R.; Al-Haddad, A. Equilibrium adsorption studies of some aromatic pollutants from dilute aqueous solutions on activated carbon at different temperatures. J. Colloid Interface Sci. 1997, 194, 154–165. [Google Scholar] [CrossRef]
- Bergmann, C.P.; Machado, F.M. Carbon Nanomaterials as Adsorbents for Environmental and Biological Applications; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Tóth, J. A uniform interpretation of gas/solid adsorption. J. Colloid Interface Sci. 1981, 79, 85–95. [Google Scholar] [CrossRef]
- Wongphat, A.; Wongcharee, S.; Chaiduangsri, N.; Suwannahong, K.; Kreetachat, T.; Imman, S.; Suriyachai, N.; Hongthong, S.; Phadee, P.; Thanarat, P.; et al. Using Excel Solver’s Parameter Function in Predicting and Interpretation for Kinetic Adsorption Model via Batch Sorption: Selection and Statistical Analysis for Basic Dye Removal onto a Novel Magnetic Nanosorbent. ChemEngineering 2024, 8, 58. [Google Scholar] [CrossRef]
- Suwannahong, K.; Wongcharee, S.; Kreetachart, T.; Sirilamduan, C.; Rioyo, J.; Wongphat, A. Evaluation of the Microsoft Excel Solver Spreadsheet-Based Program for Nonlinear Expressions of Adsorption Isotherm Models onto Magnetic Nanosorbent. Appl. Sci. 2021, 11, 7432. [Google Scholar] [CrossRef]
- Rahman, M.M.; Pal, A.; Uddin, K.; Thu, K.; Saha, B.B. Statistical Analysis of Optimized Isotherm Model for Maxsorb III/Ethanol and Silica Gel/Water Pairs. 2018. Available online: https://catalog.lib.kyushu-u.ac.jp/opac_detail_md/?lang=0&amode=MD100000&bibid=2174852 (accessed on 29 April 2025).
- Jasper, E.E.; Ajibola, V.O.; Onwuka, J.C. Nonlinear regression analysis of the sorption of crystal violet and methylene blue from aqueous solutions onto an agro-waste derived activated carbon. Appl. Water Sci. 2020, 10, 132. [Google Scholar] [CrossRef]
- Kapoor, A.; Yang, R. Correlation of equilibrium adsorption data of condensible vapours on porous adsorbents. Gas Sep. Purif. 1989, 3, 187–192. [Google Scholar] [CrossRef]
- Azqhandi, M.H.A.; Foroughi, M.; Yazdankish, E. A highly effective, recyclable, and novel host-guest nanocomposite for Triclosan removal: A comprehensive modeling and optimization-based adsorption study. J. Colloid Interface Sci. 2019, 551, 195–207. [Google Scholar] [CrossRef] [PubMed]
- Bruce, P.; Bruce, A.; Gedeck, P. Practical Statistics for Data Scientists: 50+ Essential Concepts Using R and Python; O’Reilly Media: Sebastopol, CA, USA, 2020. [Google Scholar]
- Shah, K.J.; Gandhi, V. Advances in Wastewater Treatment II; Materials Research Forum LLC: Millersville, PA, USA, 2021. [Google Scholar]
- Foo, K.Y.; Hameed, B.H. Insights into the modeling of adsorption isotherm systems. Chem. Eng. J. 2010, 156, 2–10. [Google Scholar] [CrossRef]
- Chan, L.; Cheung, W.; Allen, S.; McKay, G. Error analysis of adsorption isotherm models for acid dyes onto bamboo derived activated carbon. Chin. J. Chem. Eng. 2012, 20, 535–542. [Google Scholar] [CrossRef]
- López-Luna, J.; Ramírez-Montes, L.E.; Martinez-Vargas, S.; Martínez, A.I.; Mijangos-Ricardez, O.F.; González-Chávez, M.d.C.A.; Carrillo-González, R.; Solís-Domínguez, F.A.; Cuevas-Díaz, M.d.C.; Vázquez-Hipólito, V. Linear and nonlinear kinetic and isotherm adsorption models for arsenic removal by manganese ferrite nanoparticles. SN Appl. Sci. 2019, 1, 950. [Google Scholar] [CrossRef]
- Bapat, S.; Jaspal, D.; Malviya, A. Efficacy of parthenium hysterophorus waste biomass compared with activated charcoal for the removal of CI Reactive Red 239 textile dye from wastewater. Color. Technol. 2021, 137, 234–250. [Google Scholar] [CrossRef]
- Deb, H.; Hasan, K.; Islam, M.Z.; Kai, L.; Yang, S.; Zhang, Y.; Yao, J. The Statistical Error Optimization of Dye Sorption Equilibria for the Precise Prediction of Adsorption Isotherms on Activated Graphene. Appl. Sci. 2023, 13, 8106. [Google Scholar] [CrossRef]

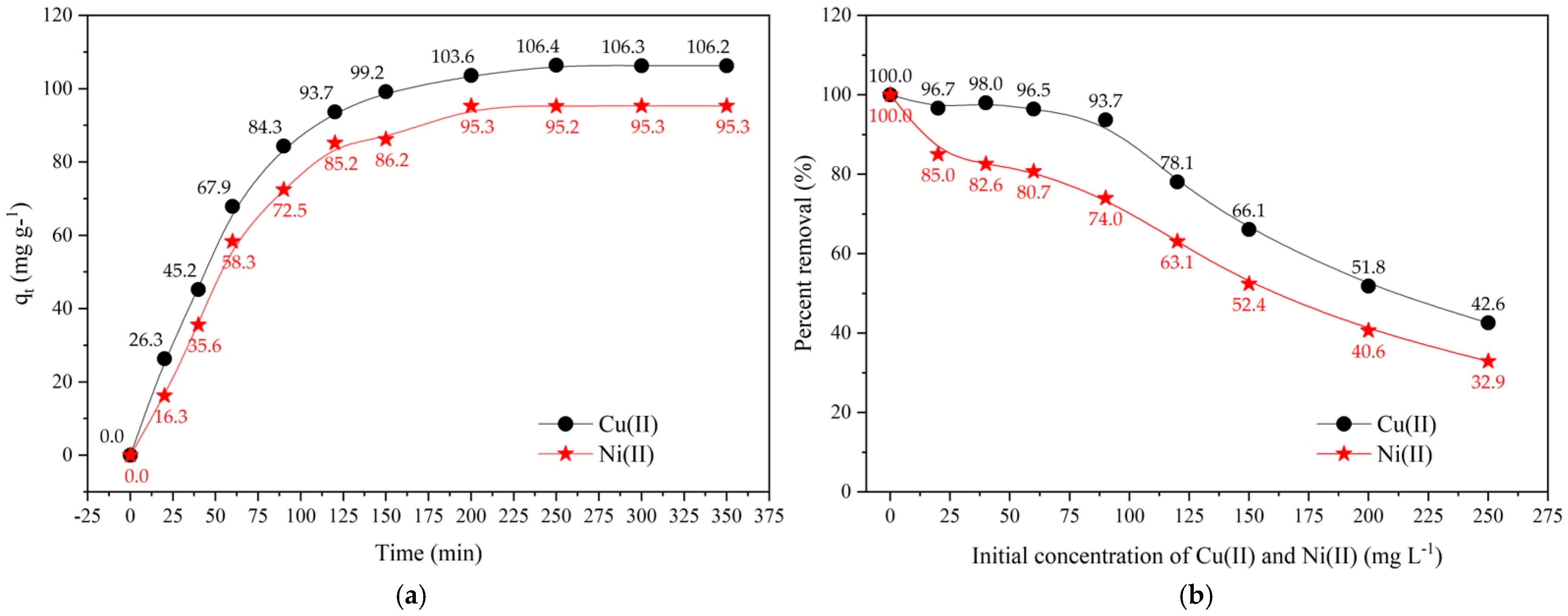

| Kinetic Adsorption Model of Factor and Error Function | Cu(II) Ions | Ni(II) Ions | Kinetic Adsorption Model of Factor and Error Function | Cu(II) Ions | Ni(II) Ions |
|---|---|---|---|---|---|
| Pseudo First Order (PFO) | Pseudo second order (PSO) | ||||
| qe (mg g−1) | 108.4 | 98.91 | qe (mg g−1) | 131.7 | 123.5 |
| k1 (min−1) | 0.016 | 0.014 | k2 (g mg−1 min−1) | 0.0001 | 0.0001 |
| RMSE | 2.435 | 4.161 | RMSE | 5.243 | 6.367 |
| Chi-square | 1.091 | 2.340 | Chi-square | 4.494 | 10.64 |
| NSD | 230.9 | 394.7 | NSD | 497.4 | 604.0 |
| ARE | −1.511 | −5.132 | ARE | −2.953 | −6.946 |
| SSE | 53.35 | 155.83 | SSE | 247.4 | 364.8 |
| EABS | 18.48 | 32.22 | EABS | 44.12 | 52.94 |
| HYBRID | −1.888 | −6.647 | HYBRID | −3.692 | −8.683 |
| MPSD | 10.68 | 37.60 | MPSD | 20.88 | 49.12 |
| R-square | 0.9961 | 0.9871 | R-square | 0.9819 | 0.9697 |
| Fractal-like pseudo first order (FL-PFO) | Fractal-like pseudo second order (FL-PSO) | ||||
| qe (mg g−1) | 106.3 | 95.1 | qe (mg g−1) | 112.3 | 99.4 |
| k1 (g mg−1 min−1) | 0.008 | 0.004 | k2 (g mg−1 min−1) | 0.000017 | 0.000005 |
| α | 1.162 | 1.334 | α | 1.629 | 1.910 |
| RMSE | 1.339 | 1.969 | RMSE | 2.107 | 1.958 |
| Chi-square | 0.327 | 0.566 | Chi-square | 0.973 | 0.738 |
| NSD | 127.0 | 186.8 | NSD | 199.9 | 185.7 |
| ARE | 0.103 | −0.669 | ARE | 0.672 | 0.841 |
| SSE | 16.14 | 34.89 | SSE | 39.96 | 34.49 |
| EABS | 9.40 | 14.21 | EABS | 15.51 | 17.19 |
| HYBRID | 0.128 | −0.836 | HYBRID | 0.840 | 1.051 |
| MPSD | 0.726 | 4.728 | MPSD | 4.752 | 5.946 |
| R-square | 0.9988 | 0.9971 | R-square | 0.9978 | 0.9971 |
| Diffusion-Chemisorption (DC) | Elovich | ||||
| qe (mg g−1) | 254.6 | 282.8 | αe (mg g−1 min−1) | 3.526 | 2.395 |
| kDC (mg g−1 min−n) | 11.40 | 8.98 | βe (g mg−1) | 0.031 | 0.031 |
| RMSE | 9.32 | 10.19 | RMSE | 8.040 | 8.591 |
| Chi-square | 16.73 | 30.91 | Chi-square | 10.10 | 17.50 |
| NSD | 883.9 | 966.8 | NSD | 762.8 | 815.0 |
| ARE | −6.11 | −11.98 | ARE | −3.873 | −8.008 |
| SSE | 781.3 | 934.7 | SSE | 581.8 | 664.3 |
| EABS | 77.19 | 82.82 | EABS | 68.73 | 73.19 |
| HYBRID | −7.64 | −14.98 | HYBRID | −4.84 | −10.01 |
| MPSD | 43.23 | 84.73 | MPSD | 27.39 | 56.63 |
| R-square | 0.9429 | 0.9225 | R-square | 0.9575 | 0.9449 |
| Adsorption Isotherm Model/Factor and Error Function | Cu(II) Ions | Ni(II) Ions | Adsorption Isotherm Model/Factor and Error Function | Cu(II) Ions | Ni(II) Ions |
|---|---|---|---|---|---|
| Langmuir | Freundlich | ||||
| qm (mg g−1) | 104.7 | 92.9 | kf (mg g−1)(L g−1)n | 46.48 | 22.72 |
| kl (L mg−1) | 0.573 | 0.078 | nf | 0.182 | 0.273 |
| RMSE | 0.243 | 0.695 | RMSE | 0.543 | 0.445 |
| Chi-square | 5.14 | 16.34 | Chi-square | 22.72 | 28.89 |
| NSD | 487.6 | 889.8 | NSD | 1238 | 1287 |
| ARE | −4.53 | −17.73 | ARE | −14.75 | −23.98 |
| SSE | 190.2 | 633.5 | SSE | 1227.5 | 1327.1 |
| EABS | 31.15 | 53.02 | EABS | 79.55 | 86.98 |
| HYBRID | 6.57 | 32.14 | HYBRID | 37.42 | 58.88 |
| MPSD | 0.288 | 2.186 | MPSD | 1.627 | 3.837 |
| R-square | 0.9848 | 0.9202 | R-square | 0.9430 | 0.9030 |
| Temkin | Khan | ||||
| bt (J mol−1) | 14.51 | 18.45 | kk (L mg−1) | 0.603 | 0.033 |
| kt (L mol−1) | 17.749 | 0.868 | ak | 0.992 | 1.342 |
| RMSE | 0.000059 | 0.000027 | qm (mg g−1) | 101.6 | 178.2 |
| Chi-square | 13.62 | 21.61 | RMSE | 0.268 | 0.664 |
| NSD | 936.0 | 1084.4 | Chi-square | 5.17 | 13.61 |
| ARE | −8.56 | −16.98 | NSD | 486.0 | 789.6 |
| SSE | 700.8 | 941.0 | ARE | −4.73 | −15.62 |
| EABS | 56.78 | 73.13 | SSE | 189.0 | 498.8 |
| HYBRID | 19.24 | 37.49 | EABS | 30.26 | 47.06 |
| MPSD | 0.797 | 2.345 | HYBRID | 6.73 | 25.85 |
| R-square | 0.9674 | 0.9312 | MPSD | 0.300 | 1.766 |
| R-square | 0.9912 | 0.9635 | |||
| Toth | Liu | ||||
| qm (mg g−1) | 103.2 | 78.5 | qm (mg g−1) | 103.2 | 80.2 |
| kth (L mg−1) | 0.502 | 0.109 | kg (L mg−1) | 0.601 | 0.869 |
| nth | 1.146 | 0.262 | ng | 0.894 | 0.739 |
| RMSE | 0.128 | 0.185 | RMSE | 0.087 | 0.080 |
| Chi-square | 4.986 | 3.510 | Chi-square | 4.915 | 5.492 |
| NSD | 478.3 | 383.8 | NSD | 473.3 | 412.4 |
| ARE | −3.614 | −4.540 | ARE | −3.289 | −5.116 |
| SSE | 183.0 | 117.9 | SSE | 179.2 | 136.0 |
| EABS | 31.17 | 26.69 | EABS | 31.13 | 23.94 |
| HYBRID | 5.798 | 4.293 | HYBRID | 5.521 | 6.558 |
| MPSD | 0.239 | 0.245 | MPSD | 0.222 | 0.400 |
| R-square | 0.9915 | 0.9913 | R-square | 0.9916 | 0.9901 |
| Model | Cu(II) Ions Kinetic Adsorption Model | Ni(II) Ions Kinetic Adsorption Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | K | SSE | AIC | AICcorrected | N | K | SSE | AIC | AICcorrected | |
| PFO | 11 | 2 | 53.345 | 21.367 | 22.867 | 11 | 2 | 155.825 | 33.159 | 34.659 |
| PSO | 11 | 2 | 247.357 | 38.242 | 39.742 | 11 | 2 | 364.843 | 42.517 | 44.017 |
| FL-PFO | 11 | 3 | 16.138 | 10.216 | 13.644 | 11 | 3 | 34.894 | 18.698 | 22.127 |
| FL-PSO | 11 | 3 | 39.965 | 20.191 | 23.619 | 11 | 2 | 34.495 | 16.572 | 18.072 |
| DC | 11 | 2 | 781.276 | 50.893 | 52.393 | 11 | 3 | 934.708 | 54.865 | 58.294 |
| Elovich | 11 | 2 | 581.819 | 47.651 | 49.151 | 11 | 2 | 664.297 | 49.109 | 50.609 |
| Model | Cu(II) Ions Adsorption Isotherm Model | Ni(II) Ions Adsorption Isotherm Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N | K | SSE | AIC | AICcorrected | N | K | SSE | AIC | AICcorrected | |
| Langmuir | 9 | 2 | 190.173 | 31.46 | 33.46 | 9 | 2 | 633.454 | 42.29 | 44.29 |
| Freundlich | 9 | 2 | 1227.548 | 48.24 | 50.24 | 9 | 2 | 1327.07 | 48.94 | 50.94 |
| Temkin | 9 | 2 | 7.01 × 102 | 43.19 | 45.19 | 9 | 2 | 9.41 × 102 | 45.84 | 47.84 |
| Khan | 9 | 3 | 188.961 | 33.40 | 38.20 | 9 | 3 | 498.793 | 42.13 | 46.93 |
| Toth | 9 | 3 | 182.989 | 33.11 | 37.91 | 9 | 3 | 294.658 | 37.40 | 42.20 |
| Liu | 9 | 3 | 179.176 | 32.92 | 37.72 | 9 | 3 | 136.037 | 30.44 | 35.24 |
| Named of the Model | Model Equation | Reference |
|---|---|---|
| Pseudo first order (PFO) | [30] | |
| pseudo second order (PSO) | [30] | |
| Fractal like-pseudo first order (FL-PFO) | [31] | |
| Fractal like-pseudo second order (FL-PSO) | [31] | |
| Diffusion-Chemisorption (DC) | [32] | |
| Elovich | [33] |
| Named of the Model | Model Equation | Reference |
|---|---|---|
| Langmuir | [34] | |
| Freundlich | [35] | |
| Temkin | [36] | |
| Khan | [37] | |
| Liu | [38] | |
| Toth | [39] |
| Row/ Column | A, Ce | B, qe, exp | C, qe, cal | D, Upper CI | E, Lower CI | F, Residual | G, Residaul2 | H, Langmuir Isotherm Model Factors | I, Error Function Statistical Results | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0.00 | 12.33 | −12.33 | 0.00 | 0.00 | kl | 0.573 | RMSE | 0.243 |
| 2 | 0.67 | 19.33 | 29.07 | 41.39 | 16.74 | −9.74 | 94.83 | qm | 104.736 | Chi-square | 5.148 |
| 3 | 0.79 | 39.21 | 32.65 | 44.98 | 20.33 | 6.56 | 43.02 | SSR | 190.173 | NSD | 487.561 |
| 4 | 2.13 | 57.87 | 57.58 | 69.91 | 45.26 | 0.29 | 0.08 | Mean of qe,exp | 67.061 | ARE | −4.529 |
| 5 | 5.67 | 84.33 | 80.10 | 92.42 | 67.77 | 4.23 | 17.91 | df | 7.000 | SSE | 190.173 |
| 6 | 26.34 | 93.66 | 98.23 | 110.56 | 85.91 | −4.57 | 20.91 | SE of qe,exp | 5.212 | EABS | 31.144 |
| 7 | 50.85 | 99.15 | 101.26 | 113.59 | 88.94 | −2.11 | 4.47 | Critical t | 2.364 | HYBRID | 6.569 |
| 8 | 96.38 | 103.62 | 102.88 | 115.2 | 90.55 | 0.74 | 0.55 | CI | 12.325 | MPSD | 0.287 |
| 9 | 143.62 | 106.38 | 103.48 | 115.81 | 91.16 | 2.90 | 8.41 | R-square | 0.9848 | ||
| Row/ Column | A, Time, t | B, qt, exp | C, qt, cal | D, Upper CI | E, Lower CI | F, Residual | G, Residaul2 | H, PFO Model Factors | I, Error Function Statistical Results | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0.00 | 0.00 | 0.89 | −0.89 | 0.00 | 0.00 | k1 | 0.016 | RMSE | 0.24 |
| 2 | 20 | 26.33 | 29.06 | 29.95 | 28.17 | 2.73 | 7.46 | qe | 108.411 | Chi-square | 1.091 |
| 3 | 40 | 45.21 | 50.33 | 51.22 | 49.45 | 5.12 | 26.24 | SSR | 190.17 | NSD | 230.965 |
| 4 | 60 | 67.87 | 65.90 | 66.79 | 65.01 | −1.97 | 3.87 | Mean of qt,exp | 76.277 | ARE | −1.511 |
| 5 | 90 | 84.33 | 81.79 | 82.68 | 80.91 | −2.54 | 6.44 | df | 9.00 | SSE | 53.345 |
| 6 | 120 | 93.66 | 91.74 | 92.63 | 90.86 | −1.92 | 3.68 | SE of qt,exp | 0.392 | EABS | 18.479 |
| 7 | 150 | 99.15 | 97.97 | 98.86 | 97.09 | −1.18 | 1.38 | Critical t | 2.262 | HYBRID | −1.888 |
| 8 | 200 | 103.62 | 103.63 | 104.51 | 102.74 | 0.01 | 0.00 | CI | 0.887 | MPSD | 10.682 |
| 9 | 250 | 106.38 | 106.22 | 107.11 | 105.33 | −0.16 | 0.03 | R-square | 0.9961 | ||
| 10 | 300 | 106.26 | 107.41 | 108.29 | 106.52 | 1.15 | 1.31 | ||||
| 11 | 350 | 106.24 | 107.95 | 108.84 | 107.06 | 1.71 | 2.93 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tansomros, P.; Aungthitipan, P.; Wongcharee, S.; Hongthong, S.; Kreetachat, T.; Suriyachai, N.; Dechapanya, W.; Papukdee, N.; Jareanpon, C. Evaluating and Selecting Kinetic and Isotherm Models for Copper and Nickel Removal Using Cow Bone Char as an Adsorbent via Excel Solver Functions. Int. J. Mol. Sci. 2025, 26, 4316. https://doi.org/10.3390/ijms26094316
Tansomros P, Aungthitipan P, Wongcharee S, Hongthong S, Kreetachat T, Suriyachai N, Dechapanya W, Papukdee N, Jareanpon C. Evaluating and Selecting Kinetic and Isotherm Models for Copper and Nickel Removal Using Cow Bone Char as an Adsorbent via Excel Solver Functions. International Journal of Molecular Sciences. 2025; 26(9):4316. https://doi.org/10.3390/ijms26094316
Chicago/Turabian StyleTansomros, Pornmongkol, Poramed Aungthitipan, Surachai Wongcharee, Sukanya Hongthong, Torpong Kreetachat, Nopparat Suriyachai, Wipada Dechapanya, Nipada Papukdee, and Chatklaw Jareanpon. 2025. "Evaluating and Selecting Kinetic and Isotherm Models for Copper and Nickel Removal Using Cow Bone Char as an Adsorbent via Excel Solver Functions" International Journal of Molecular Sciences 26, no. 9: 4316. https://doi.org/10.3390/ijms26094316
APA StyleTansomros, P., Aungthitipan, P., Wongcharee, S., Hongthong, S., Kreetachat, T., Suriyachai, N., Dechapanya, W., Papukdee, N., & Jareanpon, C. (2025). Evaluating and Selecting Kinetic and Isotherm Models for Copper and Nickel Removal Using Cow Bone Char as an Adsorbent via Excel Solver Functions. International Journal of Molecular Sciences, 26(9), 4316. https://doi.org/10.3390/ijms26094316






