Abstract
Simple and complex clustered DNA damage represent the critical initial damage caused by radiation. In this paper, a multinomial probability model of clustered damage is developed with probabilities dependent on the energy imparted to DNA and surrounding water molecules. The model consists of four probabilities: (A) direct damage of sugar-phosphate moieties leading to SSB, (B) OH− radical formation with subsequent SSB and BD formation, (C) direct damage to DNA bases, and (D) energy imparted to histone proteins and other molecules in a volume not leading to SSB or BD. These probabilities are augmented by introducing probabilities for the relative location of SSB using a ≤10 bp criteria for a double-strand break (DSB) and for the possible success of a radical attack that leads to SSB or BD. Model predictions for electrons, 4He, and 12C ions are compared to the experimental data and show good agreement. Thus, the developed model allows an accurate and rapid computational method to predict simple and complex clustered DNA damage as a function of radiation quality and to explore the resulting challenges to DNA repair.
1. Introduction
Ionizing radiation (IR) produces, through direct and indirect action, many types of DNA lesions, such as single-strand breaks (SSBs), double-strand breaks (DSBs), and a variety of base modifications (base damage (BD)). Clustered DNA damage sites are defined as two or more elemental lesions that are formed within one or two helical turns of DNA (~base pairs) by a single radiation track [1,2,3]. Complex clustered damage is defined by the occurrence of three or more SSBs or BDs within 10 bp. IR is an efficient inducer of both complex DSB and non-DSB end structures, including the presence of BD or SSBs near DSBs and complex SSBs. The co-location of BD near DSBs or SSBs may interfere with the repair pathway choice and efficient repair [4,5,6,7,8]. Therefore, complex clustered lesions are expected to play a major role in determining the repairability of DNA lesions [4,5,6,7,8], with a wide range of implications for describing radiation-induced cell death and mutations, including chromosomal aberrations, genomic instability, and aberrant signaling pathways. The understanding of complex clustered DNA damage thus plays an important role in mechanistic models of low-dose risk assessments and in radiation oncology.
Monte-Carlo (MC) track-structure simulations of DNA damage, including simple and complex breaks, have been developed using detailed volume or atomistic models of DNA and the hydration shell surrounding DNA, including models of the early chemistry leading to indirect DNA damage [9,10,11,12,13,14,15]. MC-based simulations have made comparisons of the total yields of SSBs and DSBs to experimental data for a variety of particle types as a function of linear energy transfer (LET) while providing predictions of complex clustered damage of a variety of SSB and DSB types with or without additional base damage. Predictions of the role of BD, such as abasic sites, have been more limited in MC simulations.
Experimental approaches to describe DNA damage include pulsed-field electrophoresis (PFGE) on DSB yields, including studies with restriction enzymes [5,6,16,17,18,19,20] to study the role of damaged bases and abasic sites near SSBs or DSBs and their possible role in inhibiting repair. The use of atomic force microscopy has recently provided data on a wider variety of clustered damage types [21]. Immunohistochemistry is used to observe DNA repair foci for proteins specific to non-homologous end-joining (NHEJ), homologous recombination (HR), and other signaling pathways [22,23,24,25,26]. The kinetics of the loss of foci with time after exposure, studied with different doses, radiation qualities, and time after irradiation, has been used as an indicator of complex damage. However, experimental methods to measure the wide spectrum of damage types predicted by computational models have not been developed.
In Charlton et al. [9], MC track-structure simulations using a cylindrical volume representing a segment of DNA with 54 base pairs were used to consider the types of complex breaks induced by electrons and high LET α-particles. The results suggested a model where the spectrum of energy imparted in the volume containing DNA folded with the probability of producing DNA damage was predictive of yields for a variety of combinations of simple and complex SSBs and DSBs. In this approach, the yield of a specific damage type, j, per Gy, is evaluated as:
where E0 is the incident energy, c is the conversion constant for evaluating the yields as per Gy per bp (or similarly for per Gy per Dalton or per Gy per cell), and dF/dε is the differential distribution of the energy imparted, ε per Gy. The function is the probability of producing a specific damage type j for energy imparted ε. Based on track-structure MC simulations, Charlton et al. [9] found these probabilities to be largely independent of radiation quality, and a strong correlation occurs between the energy imparted to a volume model of DNA containing 54 bp and the probability of simple and complex break types. Charlton et al. [9] considered only the direct effects for SSB and DSB formation for a 54 bp segment while ignoring the BD and indirect effects and found a negligible probability of no damage above ~100 eV.
In this paper, I develop a multinomial probability model that predicts the spectrum of DNA damage types, including the yield of simple and complex DNA breaks and BD that can be applied to all types of radiation, including photons, electrons, protons, helium ions, and heavy ions. The model is based on probabilities for SSBs, DSBs, BD, and their combinations using a multinomial probability formalism. Charlton et al. [9] found that a 54 bp segment was sufficient to describe DNA damage for high LET alpha particles. However, to describe 12C and other heavy ions, I use a larger segment. For comparisons to the experiment, I apply the frequency distribution of energy imparted for a 5 × 5 nm cylindrical volume representing a significant fraction of a nucleosome containing ~73 bp. The model provides predictions of SSBs and DSBs of increasing complexity along with the frequency of breaks with or without BD.
2. Multinomial Probability Model
A multinomial distribution is a generalization of a binomial distribution extended to the case of multiple event outcomes. In applying this model to predict clustered DNA lesions, I consider four types of events that result from energy imparted to the volume: (A) direct ionization of sugar-phosphate moieties, with probability PA leading to a SSB; (B) ionization of water leading to OH− radicals, with probability PB; (C) direct damage to DNA bases with probability PC; and (D) energy imparted to histone proteins and other co-located molecules in the volume not leading to SSBs or BDs, PD. DNA-protein crosslinks are not considered. Evaluating the distributions in a number of the A, B, C, and D probabilities to a high order allows for predictions of clustered damages of increasing complex clustered damage.
The threshold energy imparted for each type of damage (A, B, C, and D) varies to some extent with the threshold energy for OH− production of 13 eV, and several MC-based simulation results use 17.5 eV for SSBs [10,11,12]. Threshold energies for BD ionization are reported in a similar range [27]. In order to simplify the formalism, I assume the threshold is approximately the same for each type and use a normal distribution with a central estimate of th = 17.5 eV and a standard deviation of 5 eV in the calculations. The assumption of a single threshold for each type of event can be removed, as discussed below.
Above the energy threshold for a single event (denoted as first order), the following condition occurs for the summed probability of each outcome,
Because the energy thresholds for ionization across the molecules considered have similar values, the probabilities in Equation (2) are estimated simply by the fractional molecular weight of each component. As the energy imparted ε increases, the number of possible events increases. I introduce an index JTOT(ε) to evaluate the total number of events for a given energy imparted , which is found as
The number of each type of event that occurs is constrained by
The multinomial probability for various combinations of events is
The probabilities of Equation (5) are enumerated, and marginal distributions are formed to evaluate various types and combinations of DNA damage. Note that, based on calculations of frequency distributions for a 5 × 5 nm cylindrical volume considered [28,29,30], the order of importance is up to JTOT~6 for low LET radiation and much higher values (JTOT > 10) of importance for high LET radiation.
As JTOT increases, complex clustered damage occurs, including multiple SSBs, DSBs, and BD within 10 bp. An application of the model will show that a large fraction of SSBs and DSBs are formed in combination with the BD for JTOT > 2. The frequency of simple SSBs is denoted as nSSB(S), and complex SSBs are defined as the occurrence of two SSBs on the same strand within 10 bp, denoted as nSSB(+). If the two SSBs are on opposite strands within 10 bp, a simple DSB occurs, denoted as nDSB(S). If more than one isolated SSB occurs, its frequency is denoted as nSSB(Sm), where m is the number of ‘isolated’ simple SSBs. Similarly, complex DSBs, with the frequency denoted as nDSB(+), are the occurrence of a DSB with an additional SSB within 10 bp. More complex SSBs and DSBs containing >3 SSBs or >2 DSBs are grouped together and are denoted nDSB(++) and nSSB(++), respectively. In this report, BD is considered using the notation nBD(m). Analyses of the probabilities for SSB and DSB frequencies that consider the spatial distance to BD with a higher resolution than within the 73 bp segment will be considered in a future report.
Additional probabilities are needed to evaluate SSBs, DSBs, and BD and their combination probabilities. The first is to account for the spatial location of multiple SSBs in accordance with two or more within the bp ≤ 10 criteria for a DSB or a complex SSB. I assume this possibility is equally probable with an operation that adds a SSB on opposite and identical strands with the mathematical operators and with the magnitude . This leads to the following condition, with being the mathematical operator for the introduction of an additional SSB that is farther than 10 bp apart from the previous one. The overall magnitude of these operations obeys unit probability:
The values in Equation (6) are dependent on the number of SSBs induced because as the number increases, they are more likely to fall within a 10 bp separation. Estimates of the probability of not producing a cluster for the addition on each additional SSB are added, and q0 were made for 73 bp segments using Monte-Carlo sampling for J = 2, 3, 4, 5, 6, and 7 and were found to be 0.87, 0.74, 0.6, 0.475, 0.35, and 0.12, respectively. A similar consideration holds as JB is increased, allowing for increased radical production, such that additional SSBs are added into a lesion.
A second probability is needed to estimate if an SSB or a BD is formed by an OH− radical attack, with the probabilities denoted as r1 and r2, respectively. Schoel et al. [31] made an estimate of the interactions by OH− radicals being 80% with bases and 20% with sugar-phosphate moieties. This estimate is combined with an estimated 65% probability of conversion to SSBs in MC codes [10,11,12] after fitting the experimental data, which leads to an overall 13% probability for SSBs caused by OH− radicals. The same criteria are used here to estimate a probability for BD, which is 0.8 × 65% = 52%. This leads to the parameter estimate of r1~0.13 for conversion to a SSB and r2~0.52 for conversion to BD. Therefore r3 = 1 − r1 − r2 represents the probability that no SSB or BD were formed after OH− induction.
To evaluate the terms with multiplicative probabilities, such as PAPA, I treat the probabilities using a mathematical operator with a numerical value, denoted by lower-case pj multiplied by the operator that combines multiple damages in the volume, considering the ≤10 bp criteria to determine the type of damage that occurs. The operator describes the lesion’s location and its possible complexity as SSBs are added into a volume representing a small DNA segment. The A-operator is defined as:
where the operand appears in square brackets. In addition, to simplify notation, the magnitude of product terms to order JA is written as
In the following, the pj constant factors are not shown to simplify the formula, while their values for various permutations in Equation (5) are easily identified. The second-order term PAPA is found to contain three branching probabilities that are weighted with the identical multinomial probabilities defined in Equation (5):
The third-order term leads to five branches:
In Equation (9), nSSB(++) denotes the occurrence of three SSBs within 10 bp, located on a single strand. Equation (9) shows that the probability of the lesion DSB+ exceeds that of the SSB++ probability by 3-fold in their first occurrence of the third-order term, while DSB and SSB+ have equivalent weighing at both the second and third orders. Table 1 illustrates the action of the A-operator on various operands (several SSB and DSB types). A factor of 2 occurs in Equation (9) when the A-operator acts on prior lesions with two SSBs since the operator acts on both SSBs; note that a factor of 2 is also needed to obey the conservation rule of Equation (6).

Table 1.
Action of the A-operator on several SSB and DSB operands of increasing complexity.
The operator for the formation of SSBs and BD by OH− radical attack is defined as:
Then,
At the first order, the r3 probability does not produce any effect; however, in general, the r3 component of the B-operator on any operand [O] is simply r3O.
At the second order, the first term in Equation (10) introduces clustered SSBs, and six branching probabilities occur, as follows:
In Equation (12), the last branch involving B1 is applied with the multinomial coefficient of Equation (5) for the B2 probability.
2.1. Higher-Order Terms
The higher-order terms in AJ and BJ or their products will have many components. For higher-order terms in Bj, an accurate approximation is to keep only the terms up to r12 since for higher powers, p > 2, r1p << 1. For the case of a mixture of three and higher-order terms with the involvement of OH− radicals, this leads to the approximation:
Useful recursion relations for the B-operator acting on products of A-terms are found as:
And for B2 acting on A-terms:
In Equations (14) and (15) and several equations below, for compactness of notation, the terms are written with additions; however, each term in these equations represents a probability of a specific damage cluster event.
Higher-order terms in the C, D, or mixtures of C and D probabilities are evaluated as simple products. The terms with B or A probabilities with C and D to any order are evaluated as simple products; however, the A and B terms are more complex to evaluate. Mixtures with B probabilities then involve the use of the approximation of Equation (13) and recursion relations of Equations (14) and (15). For mixtures of heterogeneous terms, the order of the probabilities is invariant. The results for first- and second-order terms JTOT-JD are shown in Table 2, and in Table 3 for the third order in JTOT-JD. For JTOT-JD = 4, there are 15 terms amongst A, B, and C, with several of the fourth-order terms cumbersome to evaluate because of the many components (Table 4).

Table 2.
Evaluation of JTOT(ε)-JD = 1 and 2 terms in multinomial DNA damage model for SSB, DSB, and BD. The constant factors, pA, pB, and pC, are suppressed in the formulas and are found easily by considering the definition of the term defined in the second column. The addition of probabilities is shown, while marginal distributions are selected for lesions of specific types.

Table 3.
Evaluation of JTOT(ε)-JD = 3 terms in multinomial DNA damage model for SSB, DSB, and BD. The constant factors, pA, pB, and pC, are suppressed in the formulas and are found easily by considering the definition of the term defined in the left-hand column. The addition of probabilities is shown, while marginal distributions are selected for lesions of specific types.

Table 4.
Evaluation of JTOT-JD = 4 terms in multinomial DNA damage model for SSB and DSB. The constant factors, pA, pB, and pC, are suppressed in the formulas and are found easily by considering the definition of the term defined in the left-hand column. The addition of probabilities is shown, while marginal distributions are selected for lesions of specific types.
The terms fifth order and higher order in the A probability become increasingly difficult to evaluate. However, at large values of energy imparted, the dominance of complex clustered DNA damage is expected. This observation leads to an approximation method to evaluate these probabilities. First, I note that terms to order JA must follow an inherent binomial probability rule for the factor . Therefore, the expansion in terms of increasing powers of q0(2q1) should be the basis for evaluating higher terms. This expansion is described using the binomial coefficients:
This form occurs in Equation (9) for A3 and the fourth-order term in the A-probability, which is found as:
with
As noted above, the value of q0 decreases as JA increases. Therefore, the fifth-order and higher-order terms are dominated by SSBs and DSBs of increasing complexity and are limited to complex DSB++ or larger lesions for JA >> 1. It follows that for JA > 4, an accurate approximation is to evaluate contributions in powers up to the third order in q1 (i.e., up to q13) and tally all the higher-order terms in the binomial expansion into the nDSB(++) and nSSB(++) categories using the binomial expansion coefficients (Equation (16)) with terms similar to Equation (17). This summation is quite transparent when one notes that the summation of the binomial coefficients is given by 2J, while q1 is limited to ½ at large JA. Therefore, for JA >> 1 where q0~0, the summation of the series limits to an effective population of highly complex DSBs or SSBs. To facilitate the calculation of higher-order terms in JA, the following is useful:
With the approximation that the cubic terms in q1 (q13) and higher powers are counted in the nDSB(++) population.
2.2. Summations of Probabilities for Simple and Complex Damage Probabilities
Total yields for SSBs, DSBs, and BD or mixtures are found using marginal distributions formed by summing various probabilities where at least a lesion type of interest occurs or other criteria. For example, the probability for one or more DSBs is:
where indicates only to include combinations of the A and B probabilities where a DSB occurs.
3. Results
To estimate the pj probabilities, the molecular weight of each component is considered. The average molecular weight of each of the eight histone proteins is 14 kDa, and of DNA, 0.65 kDa per bp. The number of water molecules varies under specific conditions, with estimates of ~3000 per nucleosome [32]. Based on these estimates, calculations were made with approximate values of pA = 0.2, pB = 0.2, pC = 0.2, and pD = 0.4, representing estimates of the fraction of energy imparted to the 5 × 5 nm target volume by each component. Figure 1A,B show the probabilities for SSBs and DSBs of various complexity as a function of JTOT. The results show the dominance of DSB++ for JTOT > ~6. In Figure 1C, the results for the fraction of complex SSBs and DSBs versus JTOT are shown. Complex DSBs dominate with increasing JTOT due to the impacts of clustering, which reduces the probability of complex SSBs at large JTOT. Large damage clusters are more likely to form complex DSBs, as predicted by the higher-order terms described above. Isolated SSBs are found with some frequency for JTOT up to ~10, as they can occur in the 73 bp segment at some distance from a main cluster.
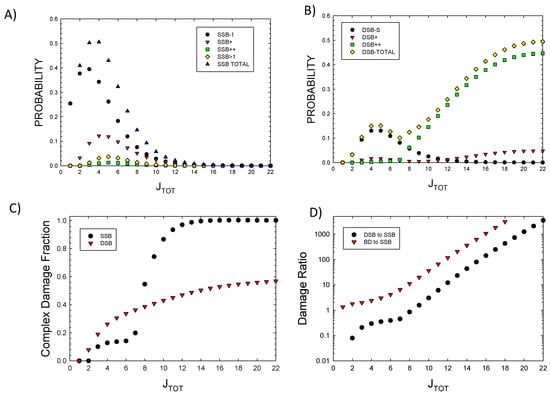
Figure 1.
Probabilities of various types of DNA lesions versus JTOT. (A) Single-strand breaks, (B) double-strand breaks, (C) the fraction of complex SSBs and DSBs. (D) The ratios of DSBs to SSBs and BD to SSBs.
In Figure 1D, the prediction of the ratio of DSBs to SSBs and BD to SSBs is shown. SSBs and BD occur with similar probability at a low JTOT (<5), while BD and DSB probabilities greatly exceed SSBs at a large JTOT. DSBs exceed SSBs due to increased clustering, leading to the dominance of a complex DSB relative to SSB at a large JTOT. Detailed considerations of BD clustering will be described in a future report. Here, preliminary observations can be made based on the results of Figure 2A, where probabilities for 1, 2, 3, or >3 BDs are plotted versus JTOT. A more detailed analysis of BD clustering and their occurrence near SSBs or DSBs is not possible at small values of JTOT; however, for a JTOT > 10, which is important for high LET radiation, these results suggest BD will be co-located within 10 bp to SSBs or DSBs in almost all events. In Figure 2B, the probability of a DSB occurrence with and without BD formation is estimated by setting r2 = 0 in applying the multinomial probabilities for cluster formalism. As expected, very few DSBs are predicted to be formed at a large JTOT with the BD not co-located.
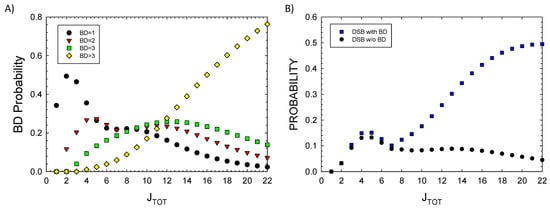
Figure 2.
Model results for (A) probability of single or multiple base damage (BD) showing contributions from the number clustered BD frequencies for increasing damage numbers, JTOT, and (B) DSB probability with or without BD. Calculations assume a 73 bp segment.
Predictions for Radiation-Induced DSBs
Predictions for 100 keV electrons representative of X-rays and 4He and 12C ions with energies from 0.1 to 10,000 MeV/u were made and compared to the experimental data. The electron results for the frequency distributions from the Monte-Carlo results of Nikjoo et al. [29] were fitted, assuming the integral spectrum is an exponential function. For ions, we used the formalism developed by Cucinotta et al. [30], which combines the direct effects, where the ion passes through the target volume, and the δ-ray effects, where the ion passes outside of the target volume. For these δ-ray events, electron spectra as a function of radial distance from the ions’ path are folded with Monte-Carlo results for the electron energy-imparted spectra from [29]. In Figure 3, representative frequency distributions are shown for 100 keV electrons 4He of kinetic energy 1 MeV (LET = 104 keV/μm), 12C ions of kinetic energy 10 MeV/u (LET = 166 keV/μm), and 12C ions of kinetic energy 1000 MeV/u (LET = 8 keV/μm). The results of Figure 3 show that the analytic formalism is in good agreement with the MC simulations for low-energy 4He ions [28]. Table 5 shows the spectra of DNA yields for the radiation types considered in Figure 3. The integral DSB yield for 100 keV electrons of 9.9 DSB per Gy per Gbp can be compared to the values from the experiments on human skin fibroblasts or V79 cells of 6.0 for 250 kVp X-rays, 7.6 for 60Co gamma-rays, 11.9 for 137Cs gamma-rays, and for 15 MeV electrons, 6.01 [33,34,35,36], which were reported using several experimental methods. Optimization of the values of pi by fits to the experimental data was not made. However, we note that introducing relative variations of ±20% leads to similar relative changes in the predicted break yields. Yields of BD compared to the DSBs are about 10-fold higher, dependent on the radiation quality. If complex BD is considered as two or more BDs in a small DNA segment, a much higher probability of complex BD compared to complex DSBs is suggested; however, a large fraction of both these types will occur in the same lesion.
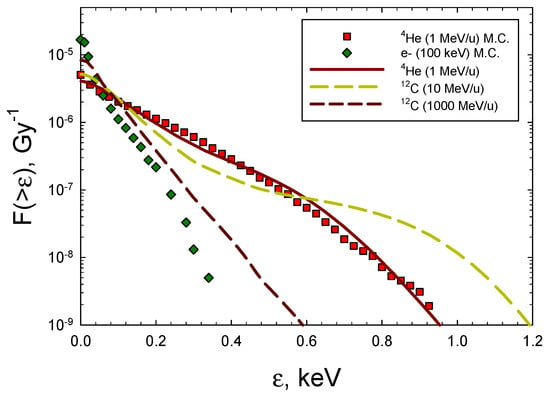
Figure 3.
Frequency distributions of energy imparted to a 5 × 5 nm cylindrical volume for 100 keV electrons, 4He, and 12C ions. Symbols are Monte-Carlo results from Charlton et al. [28] for 4He and Nikjoo et al. [29] for electrons. Lines show results from calculations of the model of Cucinotta et al. [30].

Table 5.
Predictions of yields of several types of DNA lesions per Gbp per Gy for several types of ionizing radiation.
For ions, we considered the damage frequencies expressed as an action cross-section in units of the number of breaks per Gbp per particle, which is found as:
where dF/dε is normalized to unity, nBP = 73, and is the frequency mean specific energy to the volume. Figure 4 shows the LET dependence of the DSB formation for 4He and 12C ions compared to the experimental data [33,34,35,36,37,38,39]. Agreement of the model to the measurements is good, especially when the variation in data reported from different labs employing PFGE or sedimentation is considered [33]. At the highest LET values for both ions, experimental methods are expected to undercount the number of DSBs that occur. Here, experimental methods such as PFGE and sedimentation are expected to underestimate the DSB counts because more than one DSB in an extended region of DNA will be identified as a single DSB. A preliminary estimate correction for multiple DSBs within the 73 bp segment suggests a correction of ~50% at high LET if the DSB++ is counted as a single DSB. Future studies with the present model will estimate the correction considering larger regions of DNA, which will be especially important for high energy and charge (HZE) ions. Action cross-sections σ decrease at a high LET as the ion’s velocity decreases and indicates an overkill effect, which leads to a decrease in relative biological effectiveness (RBE) ~σ/LET.
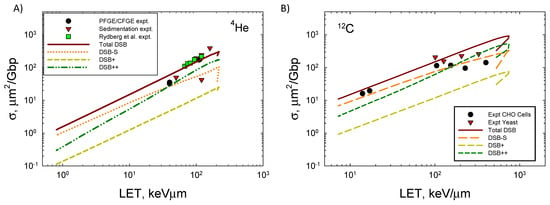
Figure 4.
Comparison of model to experimental data [32,33,34,35,36,37] for (A) 4He ions and (B) 12C ions of action cross-section versus LET for DSBs. Calculations correspond to 40 ion energies from 0.1 MeV/u to 10,000 MeV/u.
In Figure 5, we consider the prediction of action cross-sections for the DSBs induced by 12C with and without the occurrence of base damage in the same 73 bp DNA structure using the approach described in Figure 2B. Reductions of about 2-fold occur at high LET and reductions of ~30% for relativistic 12C ions. The largest reduction is for DSB++ lesions, which is more than 4-fold at LET > 100 keV/μm. These results reveal the expected severe clustering that occurs for high LET ions that go beyond the contributions of clustered breaks alone.
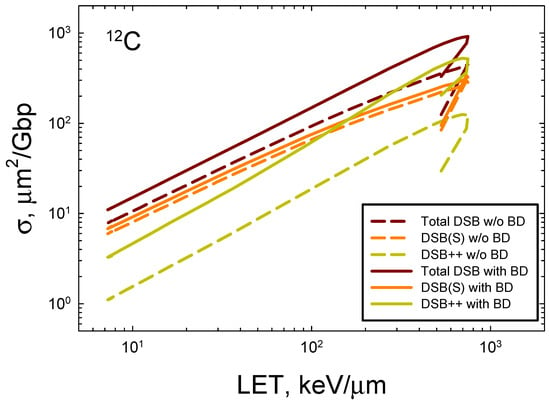
Figure 5.
Prediction of action cross-sections for DSBs with and without (w/o) the occurrence of base damage in the 73 bp DNA structure for 12C ions.
4. Discussion
In this paper, a novel approach to describing clustered DNA damage using multinomial probabilities was developed. The use of energy-imparted spectra for a 5 × 5 nm cylindrical volume offers a fast-computational approach for any radiation type in comparison to the more computationally expensive application of stochastic MC-based radiation tracks to model DNA damage [9,10,11,12,13,14]. The order of averaging made using frequency distributions is a basic difference compared to full MC track-structure simulations, which average the results over many MC histories using either volume models of DNA or scoring ionizations in atomistic DNA model structures. These descriptions are often combined with kinetics models of early chemical reactions leading to indirect effects. The MC approach averages over the orientation of the track relative to the DNA structures, while simulations take many hours of CPU time on typical computer workstations and often ignore the role of BD.
The developed model uses frequency spectra that average the energy imparted over a similar volume used in MC track-structure simulations, which are then combined with the multinomial probability functions to predict DNA lesions. This results in predictions of the full DNA damage spectra obtained in a computationally efficient manner (CPU time ~1 s) for any radiation type. This aspect is highly favorable for space radiation studies where 28 elemental groups over wide energy ranges (<0.1 MeV/u to ~50 GeV/u) are typically considered [40]. Also, in hadron therapy with 12C or other ions, the extensive distribution of secondary particles and energies arising from Coulomb slowing down, nuclear fragmentation [41], and spallation necessitate computationally efficient models.
Measurements with the PFGE are the main source of experimental data for DSB yields; however, they are expected to underestimate the yields when multiple DSBs are produced within several 10s of kbp [33,42,43]. Therefore, a comparison to heavy ions, such as 56Fe, is not included in the present work. In future work, radial distributions of the energy imparted for high-charge and energy (HZE) ions [30] and models of higher-order DNA structures will be used to make comparisons to heavy ion DNA damage experiments [38,39,44].
The present approach is similar to full MC track-structure simulations in the use of a simple energy threshold for SSBs, BD, and radical formation. However, in the present calculations, a normal distribution of energy thresholds is used because it is unlikely that a single energy threshold occurs in the ionizations leading to SSBs or BD formation when one considers the complexity of the molecules involved. The use of an identical threshold in Equations (4) and (5) could be relaxed by allowing the Ji indexes to increase with a more complex dependency on the energy imparted; however, this is unlikely to lead to important changes at the higher values of energy imparted where many terms contribute to damage production.
The use of cluster probabilities (q0 or q1) based on simple random probability criteria ignores the possible details of radiation tracks, such as low-energy electrons and their distinct angular trajectories versus straight-line trajectories of higher-energy electrons produced by ions. It is likely that the estimates of q0 for increasing JA/JB based on a random distribution overestimate the clustering that occurs, which is suggested by the predictions of a higher probability of DSB++ compared to the MC track-structure simulation predictions [10,11,12,13,14]. An alternative can be considered using a weighted combination of random distribution and a probability of straight-line motion of radiation tracks. We used the values of r1 and r2 related to the indirect effects of radical production on water molecules based on the MC estimates [10,11] and the estimate from Scholes et al. [31]. In future work, the values of various parameters, as fitted to experimental data, can be considered to investigate if a deviation from a random pattern or the MC model estimates are suggested.
The use of enzymatic probes, such as endonuclease III (Nth) to detect oxidized pyrimidines, formamidopyrimidine-DNA glycosylase (Fpg) to detect oxidized purines, and Nfo protein (endonuclease IV) to detect abasic sites, have revealed higher frequencies of clustered BD compared to DSBs [5,6,8,17,18,35,45]. The present model only predicts a generic category of BD. For 137Cs gamma-rays, Tsao et al. [35] report 9.5, 11.87, and 10.68 per Gbp per Gy for endo IV, Fpg, and endo III clusters, respectively. As seen in Table 5, 100 keV electrons show yields of 17.2, 8.7, and 4.4 per Gbp per Gy for the BD clusters of 2, 3, and >3, respectively. These values would be increased in an approximately linear fashion with increases in the value of the r2 parameter. Radiation yields for all possible base modifications have not been reported, and additional BD lesions are likely [46,47]. It would be interesting to introduce an empirical approach to model-specific base lesions for X-rays or gamma-rays to explore their ability to predict equivalent lesions for high LET radiation using the present approach. In addition, additional damages are produced in the processing of SSBs or BD in base excision repair (BER) or other pathways [5,46], and it is useful to predict the initial rates of production for comparison purposes.
A main focus of the current approach is to develop a model that can be compared to experimental data while considering the distribution of DNA end-structures that are substrates for various repair pathways for use in mathematical models of DNA repair [48,49,50]. The repair of DSBs is cell cycle-dependent, with NHEJ being dominant in the G0/G1 phases and HR in the late S phase and G2. The NHEJ pathway is error-prone, while HR is the only faithful repair pathway. The alternative end-joining pathway (alt-EJ) and single-strand annealing (SSA) are more error-prone and expected to play an increased role in complex DSB processing when NHEJ or HR are inhibited. The presence of BD near SSBs [8,51] or BD and SSBs near DSBs are possible impairments to faithful repair [4,7,8,19,51,52]. The position of the BD relative to the ligated ends, the multitude (1, 2, 3, etc.) of BD clusters, including bi-stranded clusters, along with the clustering of SSBs and DSBs, likely play impairment roles in the impairment of NHEJ or HR pathways, leading to error-prone repair, such as alt-EJ or SSA. The high frequency of complex DSBs leading to small DNA fragments is shown to reduce the efficiency of Ku70/80 from binding to DNA [53,54]. Differences in clustered DSBs, such as DSB++, between 100 keV electrons and high LET alpha particles and 12C ions, are only about 2-fold in the present results; however, larger differences will occur when larger DNA structures are considered, or for lesions such as DSB+++. These aspects will be considered in future work using the present approach.
The wide range of distinct DNA lesions that will occur across a cell thus points to the differences between low and high doses and low and high LET radiation. The higher frequency of BD or SSBs is likely dominant at low doses of low LET irradiation where few DSBs per cell are formed, while, as the dose is increased, the number of clustered DSBs increases, such that DSB repair likely becomes more dominant in cellular responses. For high LET radiation, clustered DSBs will occur at all doses, and the importance of the additional BD and clustered SSBs is suggested to play a smaller role. However, an exception is the large transverse distribution of the delta-rays (high energy electrons) produced about the path of HZE ions, leading to frequent low-dose cellular energy deposition in many cells not traversed by the ion [55]. This aspect should play an important role in risk assessments for the low dose and dos-rate space radiation exposures.
The range of complexity shown here that increases with ionization density (or LET) is consistent with the so-called “overkill effect” used to describe the high LET dependence on radiation effects. The increase in ionization density (or LET) presents a transition from the dominance of simple DNA damage to highly complex DSBs, as shown by the developed formalism. Saturation due to highly complex DSBs is predicted as the energy imparted increases to high levels (>~200 eV), and highly complex DSBs are predicted to dominate the initial damage [1,56]. In addition, saturation of biological action cross sections often reflects an underlying geometric damage area such as observed for cell inactivation and mutation [56,57] and a similar effect is observed for DSB yields from heavy ions [38]. The more complex damage likely favors cell death, while intermediate damage levels favor misrepair and mutation in the repair of complex SSBs and BD and single DSBs with additional BD.
5. Conclusions
In this paper a biophysics model for predicting yields of simple and complex clustered DNA damage induced by arbitrary radiation types was described. In this novel approach, multinomial probabilities are combined with a frequency distribution for a small DNA segment represented by a 5 × 5 nm cylindrical volume. The model calculations showed good agreement with the experimental data for DSB induction. The approach leads to an accurate, fast-computational approach with several orders of magnitude less computational expense compared to the stochastic Monte-Carlo track-structure simulations. The current paper focused on complex DSBs. Future work will extend the approach to provide more detailed descriptions of BD clustering and specific BD lesions. Parameters for radical attack leading to SSBs and BD were based on the Monte-Carlo model fits reported by others [10,11]. Future efforts will focus on considering the parameter values based on experimental data as a function of oxygen tensions. Values for parameters describing SSB clustering, q0 and q1, used here, were based on the random clustering of SSBs in the volume. An alternative model will be developed in future work to consider the balance between the random induction of SSBs in the volume and those produced along straight-line radiation track motion in the volume. Ultimately, the developed models will be used to consider clustered DNA damage processing and resulting mutations.
Funding
This research was funded by the U.S. Department of Energy Award DE-SC0025298 and the University of Nevada Las Vegas.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Request can be made to the author.
Acknowledgments
Useful discussions with Dudley T. Goodhead and Peter O’Neill are acknowledged over the course of this work.
Conflicts of Interest
The author declares no conflict of interest.
References
- Goodhead, D.T. Initial events in the cellular effects of ionizing radiations: Clustered damage in DNA. Int. J. Radiat. Biol. 1994, 65, 7–17. [Google Scholar] [CrossRef] [PubMed]
- Goodhead, D.T.; Nikjoo, H. Track structure analysis of ultrasoft X-rays compared to high- and low-LET radiations. Int. J. Radiat. Biol. 1989, 55, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Ward, J.F. DNA damage produced by ionizing radiation in mammalian cells: Identities, mechanisms of formation, and reparability. Prog. Nucleic Acid Res. Mol. Biol. 1988, 35, 95–125. [Google Scholar] [PubMed]
- Nickoloff, J.A.; Sharma, N.; Taylor, L. Clustered DNA double-strand breaks: Biological effects and relevance to cancer radiotherapy. Genes 2020, 11, 99. [Google Scholar] [CrossRef] [PubMed]
- Gulston, M.; de Lara, C.; Jenner, T.; Davis, E.; O’Neill, P. Processing of clustered DNA damage generates additional double-strand breaks in mammalian cells post-irradiation. Nucleic Acids Res. 2004, 32, 1602–1609. [Google Scholar] [CrossRef]
- Cunnife, S.; Walker, A.; Stabler, R.; O’Neill, P.; Lomax, M.E. Increased mutability and decreased repairability of a three-lesion clustered DNA-damage site comprised of an AP site and bi-stranded 8-oxoG lesions. Int. J. Radiat. Biol. 2014, 90, 468–479. [Google Scholar] [CrossRef][Green Version]
- Mladenova, V.; Mladenov, E.; Chaudhary, S.; Stuschke, M.; Iliakis, G. The high toxicity of DSB-clusters modelling high-LET-DNA damage derives from inhibition of c-NHEJ and promotion of alt-EJ and SSA despite increases in HR. Front. Cell Dev. Biol. 2022, 10, 1016951. [Google Scholar] [CrossRef]
- Dobbs, T.A.; Palmer, P.; Maniou, Z.; Lomax, M.E.; O’Neill, P. Interplay of two major repair pathways in the processing of complex double-strand DNA breaks. DNA Repair 2008, 7, 1372–1383. [Google Scholar] [CrossRef]
- Charlton, D.E.; Nikjoo, H.; Humm, J.J. Calculation of initial yields of single- and double strand breaks in nuclei from electrons, protons, and alpha particles. Int. J. Radiat. Biol. 1989, 56, 1–19. [Google Scholar] [CrossRef]
- Nikjoo, H.; O’Neill, P.; Terrisol, M.; Goodhead, D.T. Modeling of radiation-induced DNA damage: The early physical and chemical event. Int. J. Radiat. Biol. 1994, 66, 453–457. [Google Scholar] [CrossRef]
- Nikjoo, H.; O’Neill, P.; Goodhead, D.T.; Terissol, M. Computational modeling of low energy electron induced DNA damage by early physical and chemical events. Int. J. Radiat. Biol. 1997, 71, 467–483. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, R.; Rahmanian, S.; Nikjoo, H. Spectrum of radiation-induced clustering non-DNA damage- A Monte Carlo track structure modeling and calculations. Radiat. Res. 2015, 183, 525–540. [Google Scholar] [CrossRef] [PubMed]
- Friedland, W.; Dingfelder, M.; Kundrat, P.; Jacob, P. Track structures, DNA targets and radiation effects in the biophysical Monte Carlo simulation code PARTRAC. Mutat. Res. 2011, 711, 28–40. [Google Scholar] [CrossRef] [PubMed]
- Chatzipapas, K.P.; Papadimitroulas, P.; Obeidat, M.; McConnell, K.A.; Kirby, N.; Loudos, G.; Papanikolaou, N.; Kagadis, G.C. Quantification of DNA double-strand breaks using Geant4-DNA. Med. Phys. 2019, 46, 405–413. [Google Scholar] [CrossRef] [PubMed]
- Schuemann, J.; McNamara, A.L.; Warmenhoven, J.W.; Henthorn, N.T.; Kirkby, K.J.; Merchant, M.J.; Ingram, S.; Paganetti, H.; Held, K.D.; Ramos-Mendez, J.; et al. A New Standard DNA Damage (SDD) Format. Radiat. Res. 2019, 191, 76–92. [Google Scholar] [CrossRef] [PubMed]
- Lobrich, M.; Cooper, P.K.; Rydberg, B. Joining of correct and incorrect DNA ends at double-strand breaks produced by high-linear energy transfer radiation in human fibroblasts. Radiat. Res. 1998, 150, 619–626. [Google Scholar] [CrossRef]
- Sutherland, B.M.; Bennett, P.V.; Sidorkina, O.; Laval, J. Clustered DNA damages induced in isolated DNA and in human cells by low doses of ionizing radiation. Proc. Natl. Acad. Sci. USA 2000, 97, 103–108. [Google Scholar] [CrossRef]
- Datta, K.; Purkayastha, S.; Neumann, R.D.; Pastwa, E.; Winters, T.A. Base damage immediately upstream from double-strand break ends is a more severe impediment to nonhomologous end joining than blocked 30-termini. Radiat. Res. 2011, 175, 97–112. [Google Scholar] [CrossRef]
- Mladenova, V.; Mladenova, E.; Stucshke, M.; Illiakis, G. DNA damage clustering after ionizing radiation and consequences in the processing of chromatin breaks. Molecules 2022, 27, 1540. [Google Scholar] [CrossRef]
- Schipler, A.; Mladenova, V.; Soni, A.; Nikolov, V.; Saha, J.; Mladenov, E.; Iliakis, G. Chromosome thripsis by DNA double strand break clusters causes enhanced cell lethality, chromosomal translocations and 53BP1-recruitment. Nucleic Acids Res. 2016, 44, 7673–7690. [Google Scholar] [CrossRef]
- Nakano, T.; Akamatsu, K.; Tsuda, M.; Tujimoto, A.; Hirayama, R.; Hiromoto, T.; Tamada, T.; Ide, H.; Shikazono, N. Formation of clustered DNA damage in vivo upon irradiation with ionizing radiation: Visualization and analysis with atomic force microscopy. Proc. Natl. Acad. Sci. USA 2022, 119, e2119132119. [Google Scholar] [CrossRef] [PubMed]
- Rogakou, E.P.; Pilch, D.R.; Orr, A.H.; Ivanova, V.S.; Bonner, W.M. DNA double-stranded breaks induce histone H2AX phosphorylation on serine 139. J. Biol. Chem. 1998, 273, 5858–5868. [Google Scholar] [CrossRef]
- Desai, N.; Davis, E.; O’Neill, P.; Durante, M.; Cucinotta, F.A.; Wu, H. Immunofluorescent detection of DNA double strand breaks induced by high-LET radiation. Radiat. Res. 2005, 164, 518–521. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Zhou, P. DNA damage response signaling pathways and targets for radiotherapy sensitization in cancer. Signal Transd. Targeted Ther. 2020, 5, 60. [Google Scholar] [CrossRef] [PubMed]
- Asaithamby, A.; Hu, B.; Chen, D.J. Unrepaired clustered DNA lesions induce chromosome breakage in human cells. Proc. Natl. Acad. Sci. USA 2011, 108, 8293–9298. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Saha, J.; Hada, M.; Pluth, J.M.; Anderson, J.; O’Neill, P.; Cucinotta, F.A. Novel Smad proteins localize to IR-induced double-strand breaks: Interplay between TGFß and ATM pathways. Nucleic Acids Res. 2013, 41, 933–942. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.A.; Krishnakumar, E. Communication: Electron ionization of DNA bases. J. Chem. Phys. 2016, 144, 161102. [Google Scholar] [CrossRef]
- Charlton, D.E.; Goodhead, D.T.; Wilson, W.E.; Paretzke, H.G. Energy Deposition in Cylindrical Volumes: a) Protons Energy 0.3 MeV to 4.0 MeV, b) Alpha Particles Energy 1.0 MeV to 20.0 MeV; 85/1; MRC Radiobiology Unit Monograph: Chilton, UK, 1985. [Google Scholar]
- Nikjoo, H.; Goodhead, D.T.; Charlton, D.E.; Paretzke, H.G. Energy Deposition by Monoenergetic Electrons in Cylindrical Volumes; 94/1; MRC Radiobiology Unit Monograph: Chilton, UK, 1994. [Google Scholar]
- Cucinotta, F.A.; Nikjoo, H.; Goodhead, D.T. Model of the radial distribution of energy imparted in nanometer volumes from HZE particles. Radiat. Res. 2000, 153, 459–468. [Google Scholar] [CrossRef]
- Scholes, G.; Ward, J.F.; Weiss, J. Mechanism of the radiation-induced degradation of nucleic acids. J. Mol. Biol. 1960, 2, 379–391. [Google Scholar] [CrossRef]
- Davey, C.A.; Sargent, D.F.; Luger, K.; Maeder, A.W.; Richmond, T.J. Solvent mediated interactions in the structure of the nucleosome core particle at 1.9 Angstrom resolution. J. Mol. Biol. 2002, 319, 1097–1113. [Google Scholar] [CrossRef]
- Prise, K.M.; Ahnström, G.; Belli, M.; Carlsson, J.; Frankenberg, D.; Kiefer, J.; Loöbrich, M.; Michael, B.D.; Nygren, J.; Simone, G.; et al. A review of dsb induction data for varying quality radiations. Int. J. Radiat. Biol. 1998, 74, 173–184. [Google Scholar] [CrossRef] [PubMed]
- Jenner, T.J.; deLara, C.M.; O’Neill, P.; Stevens, D.L. Induction and rejoining of DNA double-strand breaks in V79-4 mammalian cells following γ– and α-irradiation. Int. J. Radiat. Biol. 1993, 64, 265–273. [Google Scholar] [CrossRef] [PubMed]
- Tsao, D.; Kalogerinis, P.; Tabrizi, I.; Dingfelder, M.; Stewart, R.D.; Georgakilas, A.G. Induction and processing of oxidative clustered DNA lesions in 56Fe-ion-irradiated human monocytes. Radiat. Res. 2007, 168, 87–97. [Google Scholar] [CrossRef]
- Frankenberg, D.; Brede, H.J.; Schrewe, U.J.; Steinmetz, C.; Frankenberg-Schwager, M.; Kasten, G.; Pralle, E. Induction of DNA double-strand breaks by 1H and 4He ions in primary human skin fibroblasts in the LET range of 8 to 124 keV/μm. Radiat. Res. 1999, 151, 540–549. [Google Scholar] [CrossRef]
- Rydberg, B.; Heilbronn, L.; Holley, W.R.; Lobrich, M.; Zeitlin, C.; Chatterjee, A.; Cooper, P.K. Spatial distribution and yield of DNA double-strand breaks induced by 3–7 MeV helium ions in human fibroblasts. Radiat. Res. 2002, 158, 32–42. [Google Scholar] [CrossRef]
- Ikpeme, S.; Lobrich, M.; Akpa, T.; Schneider, E.; Kiefer, J. Heavy ion-induce DNA double-strand breaks with yeast as a model system. Radiat. Envion. Biophys. 1995, 34, 95–99. [Google Scholar] [CrossRef] [PubMed]
- Heilmann, J.; Taucher-Scholz, G.; Kraft, G. Induction of DNA double-strand breaks in CHO-K1 cells by carbon ions. Int. J. Radiat. Biol. 1995, 68, 153–162. [Google Scholar] [CrossRef]
- Cucinotta, F.A.; Wilson, J.W.; Saganti, P.; Hu, X.; Kim, M.Y.; Cleghorn, T.; Zeitlin, C.; Tripathi, R.K. Isotopic dependence of GCR fluence behind shielding. Radiat. Meas. 2006, 41, 1235–1249. [Google Scholar] [CrossRef][Green Version]
- Cucinotta, F.A.; Plante, I.; Ponomarev, A.; Kim, M.Y. Nuclear interactions in heavy ion transport and event-based risk models. Radiat. Protect. Dosim. 2011, 143, 384–390. [Google Scholar] [CrossRef]
- Rydberg, B. Clusters of DNA damage induced by ionizing radiation: Formation of short DNA fragments, I.I. Experimental detection. Radiat. Res. 1996, 145, 200–209. [Google Scholar] [CrossRef]
- Stenerlow, B.; Hoglund, E.; Carlsson, J. Induction and rejoining of larger DNA fragments after ion irradiation. Radiat. Res. 1999, 151, 642–648. [Google Scholar] [CrossRef] [PubMed]
- Belli, M.; Campa, A.; Dini, V.; Esposito, G.; Furusawa, Y.; Simone, G.; Sorrentino, E.; Tabocchini, M.A. DNA fragmentation induced in human fibroblasts by accelerated 56Fe ions of differing energy. Radiat. Res. 2006, 165, 713–720. [Google Scholar] [CrossRef] [PubMed]
- Georgakilas, A.G.; Bennett, P.V.; Sutherland, B.M. High efficiency detection of bistranded abasic clusters in irradiated DNA by putrescine. Nucleic Acids Res. 2002, 30, 2800–2808. [Google Scholar] [CrossRef]
- Wallace, S.S. DNA damages processed by base excision repair: Biological consequences. Int. J. Radiat. Biol. 1994, 66, 579–589. [Google Scholar] [CrossRef]
- Douki, T.; Ravanat, J.; Pouget, J.; Testard, I.; Cadet, J. Minor contribution of direct ionization to DNA base damage induced by heavy ions. Int. J. Radiat. Biol. 2006, 82, 119–127. [Google Scholar] [CrossRef]
- Cucinotta, F.A.; Pluth, J.M.; Anderson, J.; Harper, J.V.; O’Neill, P. Biochemical kinetics model of DSB repair and γH2AX foci by non-homologous end joining. Radiat. Res. 2008, 169, 214–222. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Reynolds, P.; O’Neill, P.; Cucinotta, F.A. Modeling damage complexity-dependent nonhomologous end-joining repair pathway. PLoS ONE 2014, 9, e85816. [Google Scholar]
- Li, Y.; Cucinotta, F.A. Mathematical modeling ATM activation and chromatin relaxation by ionizing radiation. Int. J. Molec. Sci. 2020, 21, 1214. [Google Scholar] [CrossRef]
- Lomax, M.E.; Folkes, L.K.; O’Neill, P. Biological consequences of radiation-induced DNA damage: Relevance to radiotherapy. Clin. Onc. 2023, 25, 578–585. [Google Scholar] [CrossRef]
- Schipler, A.; Illiakis, G. DNA double-strand–break complexity levels and their possible contributions to the probability for error-prone processing and repair pathway choice. Nucl. Acids Res. 2013, 41, 7589–7605. [Google Scholar] [CrossRef]
- Wang, H.; Wang, X.; Zhang, P.; Wang, Y. The Ku-dependent nonhomologous end-joining but not other repair pathway is inhibited by high linear energy transfer ionizing radiation. DNA Repair 2008, 7, 725–733. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Qian, H.; Wang, Y.; Cucinotta, F.A. A stochastic model of DNA fragment rejoining. PLoS ONE 2012, 7, e44293. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Cucinotta, F.A.; Nikjoo, H.; Goodhead, D.T. Comment on the effects of delta-rays on the number of particle-track transversals per cell in laboratory and space exposures. Radiat. Res. 1998, 150, 115–119. [Google Scholar] [CrossRef] [PubMed]
- Goodhead, D.T. Relationship of radiation track structure to biological effect: A re-interpretation of the parameters of the Katz model. Nuclear Tracks Radiat. Meas. 1989, 116, 177–184. [Google Scholar] [CrossRef]
- Cucinotta, F.A.; Wilson, J.W.; Shavers, M.R.; Katz, R. The effects of track structure and cell inactivation on the calculation of heavy ion mutation rates in mammalian cells. Int. J. Radiat. Biol. 1996, 69, 593–600. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).